The Influence of the Ionic Core on Structural and Thermodynamic Properties of Dense Plasmas
Abstract
:1. Introduction
2. Materials and Methods
3. Results
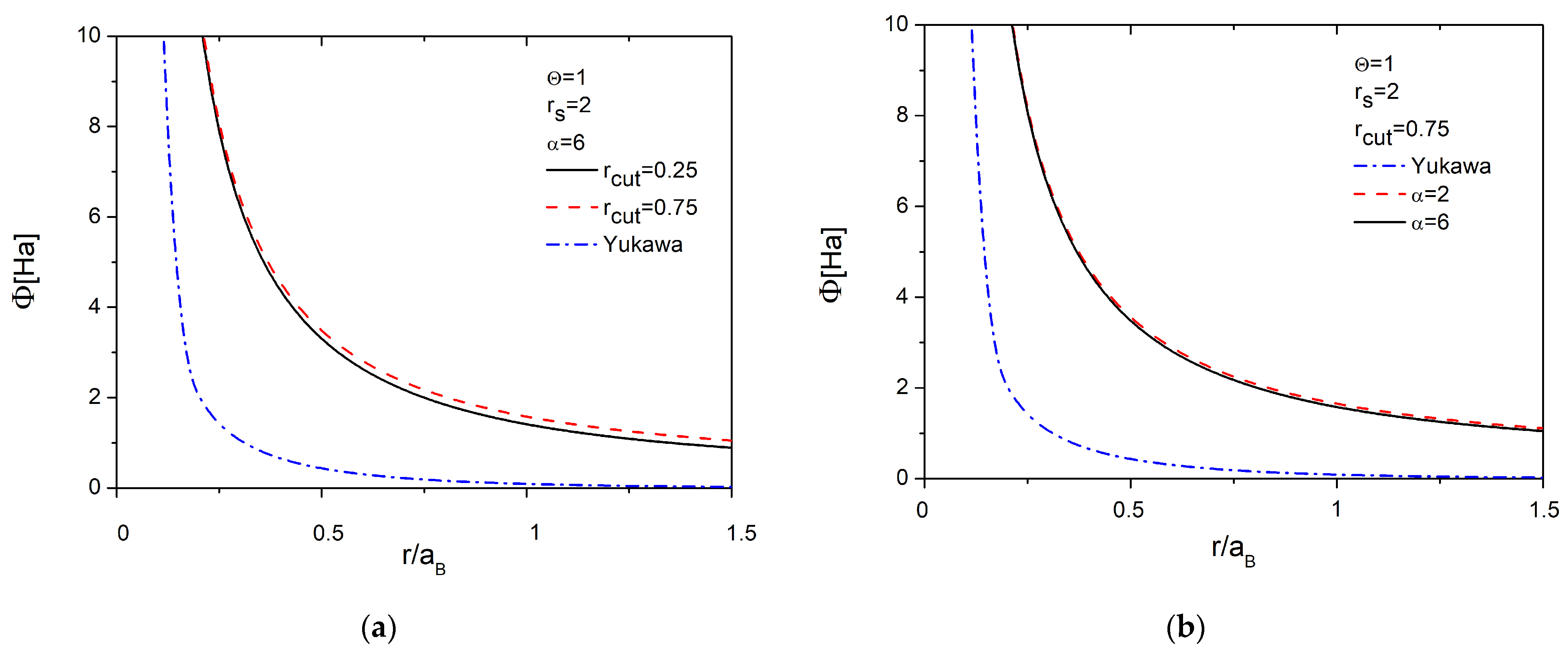
3.1. Ion–Ion Interaction Potential
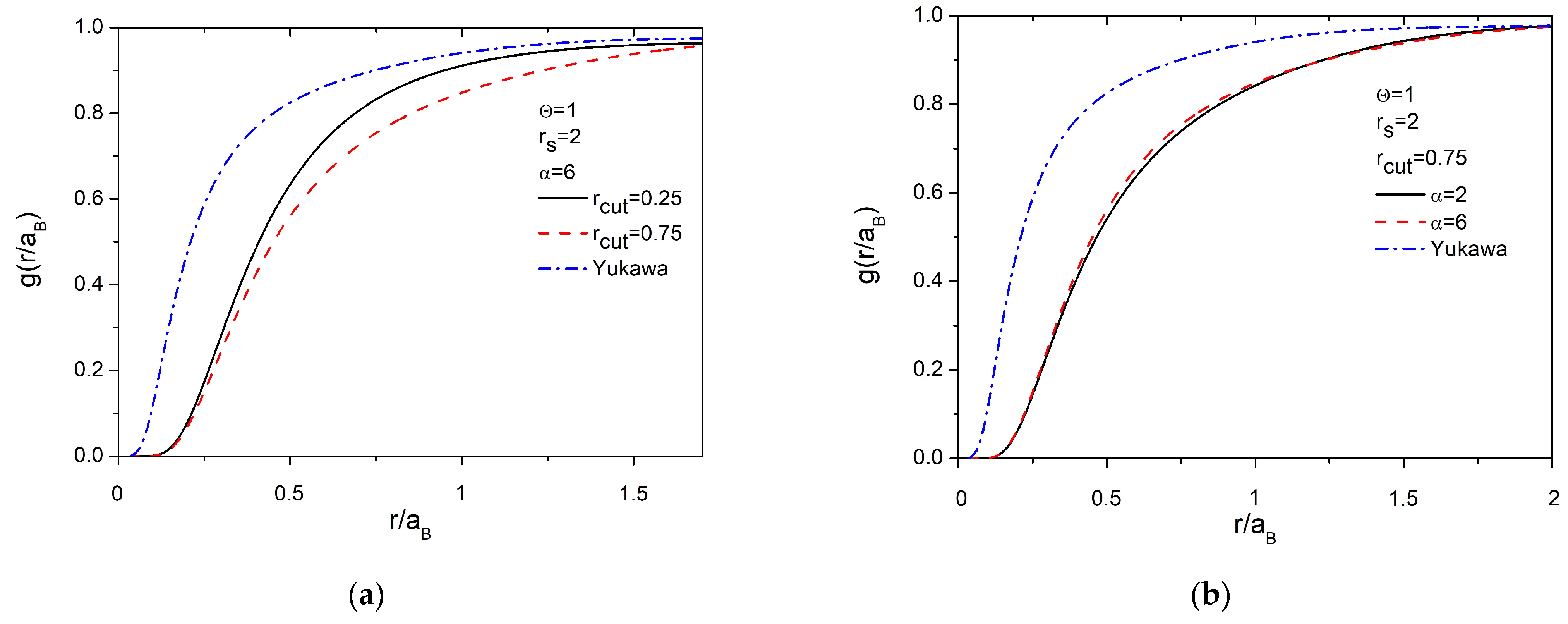
3.2. The Radial Distribution Functions of Ions
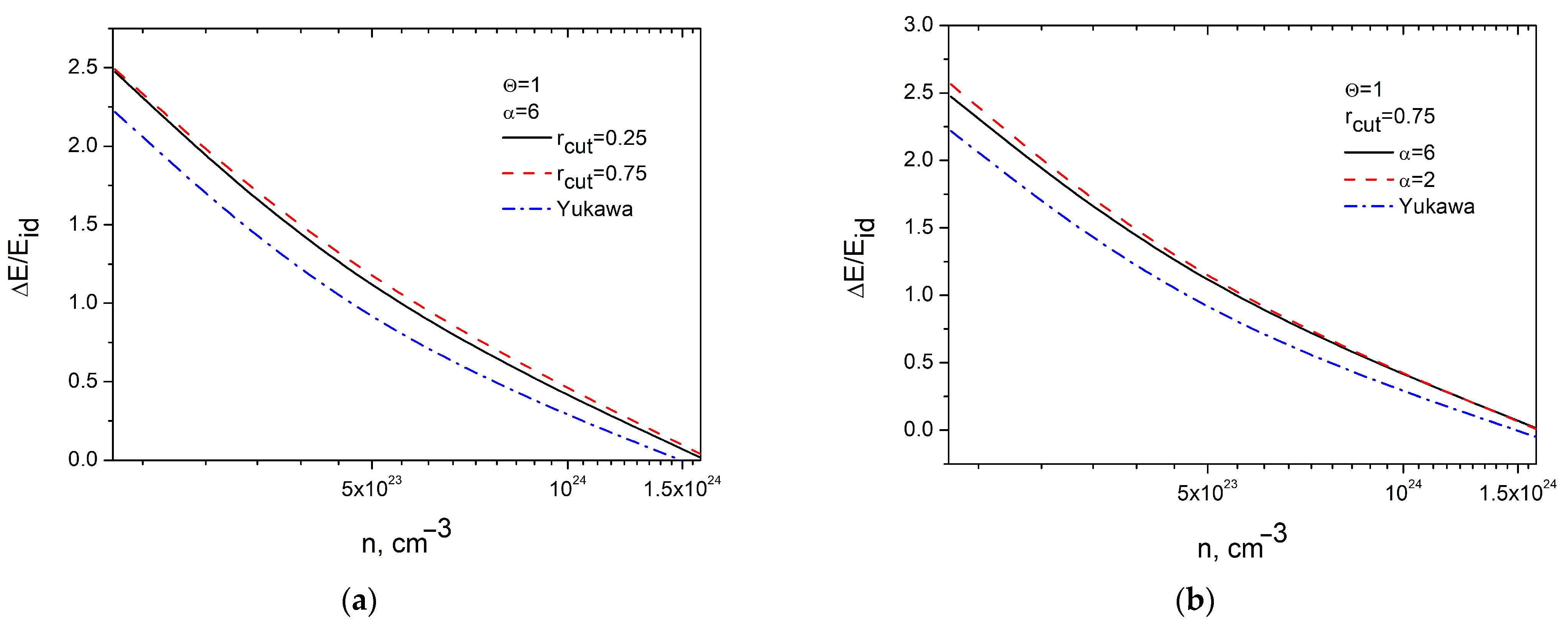
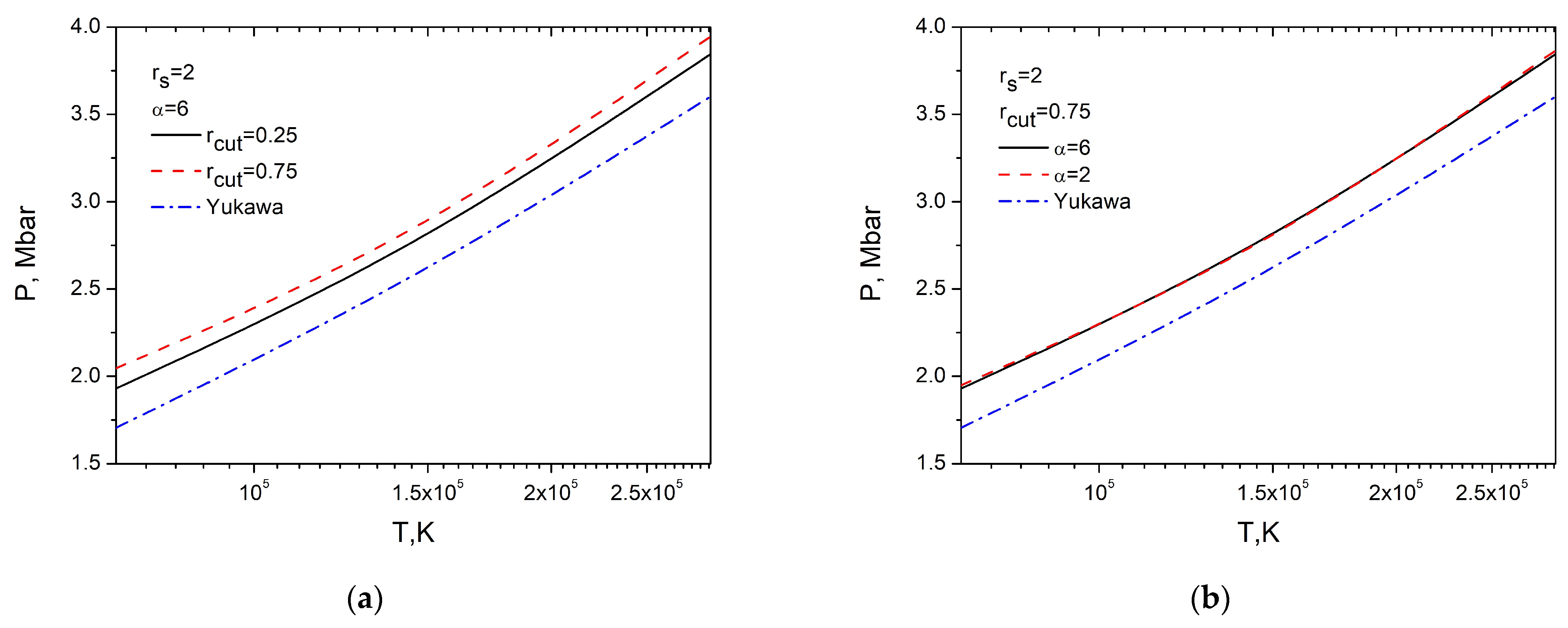
3.3. Thermodynamic Properties
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tahir, N.A.; Stöhlker, T.; Shutov, A.; Lomonosov, I.V.; Fortov, V.E.; French, M.; Nettelmann, N.; Redmer, R.; Piriz, A.R.; Deutsch, C. Laboratory planetary physics using intense heavy ion beams at the Facility for Antiprotons and Ion Research at Darmstadt: The HEDgeHOB collaboration. Astrophys. Space Sci. 2011, 336, 61–65. [Google Scholar] [CrossRef]
- Hurricane, O.A.; Callahan, D.A.; Casey, D.T.; Celliers, P.M.; Cerjan, C.; Dewald, E.L.; Dittrich, T.R.; Döppner, T.; Hinkel, D.E.; Hopkins, L.F.B.; et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 2014, 506, 343–348. [Google Scholar] [CrossRef] [PubMed]
- Cuneo, M.E.; Herrmann, M.C.; Sinars, D.B.; Slutz, S.A.; Stygar, W.A.; Vesey, R.A.; Sefkow, A.B.; Rochau, G.A.; Chandler, G.A.; Bailey, J.E.; et al. Magnetically Driven Implosions for Inertial Confinement Fusion at Sandia National Laboratories. IEEE Trans. Plasma Sci. 2012, 40, 3222–3245. [Google Scholar] [CrossRef]
- Lyon, M.; Bergeson, S.D.; Murillo, M.S. Limit of strong ion coupling due to electron shielding. Phys. Rev. E 2013, 87, 033101. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Dzhumagulova, K.N.; Gabdullin, M.T. Effective potentials for ion-ion and charge-atom interactions of dense semiclassical plasma. Phys. Plasmas 2010, 17, 042703. [Google Scholar] [CrossRef]
- Ismagambetova, T.N.; Moldabekov, Z.A.; Amirov, S.M.; Ramazanov, T.S.; Gabdullin, M.T.; Temirbek, A.; Tikhonov, A. Dense plasmas with partially degenerate semiclassical ions: Screening and structural properties. Jpn. J. Appl. Phys. 2020, 59, SHHA10. [Google Scholar] [CrossRef]
- Wünsch, K.; Hilse, P.; Schlanges, M.; Gericke, D.O. Structure of strongly coupled multicomponent plasmas. Phys. Rev. E 2008, 77, 056404. [Google Scholar] [CrossRef]
- Ramazanov, T.; Dzhumagulova, K.; Moldabekov, Z. Generalized pair potential between charged particles in dense semiclassical plasma. Phys. Sci. Technol. 2018, 1, 48–54. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Dzhumagulova, K.N.; Gabdullin, M.T.; Moldabekov, Z.A.; Ismagambetova, T.N. Development of effective potentials for complex plasmas. Phys. Sci. Technol. 2019, 6, 44–53. [Google Scholar] [CrossRef]
- Sharkov, B.Y.; Hoffmann, D.H.; Golubev, A.A.; Zhao, Y. High energy density physics with intense ion beams. Matter Radiat. Extrem. 2016, 1, 28–47. [Google Scholar] [CrossRef]
- Kawata, S.; Karino, T.; Ogoyski, A.I. Review of heavy-ion inertial fusion physics. Matter Radiat. Extrem. 2016, 1, 89–113. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Kodanova, S.K.; Nurusheva, M.M.; Issanova, M.K. Ion core effect on scattering processes in dense plasmas. Phys. Plasmas 2021, 28, 092702. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Issanova, M.K.; Aldakul, Y.K.; Kodanova, S.K. Ion core effect on transport characteristics in warm dense matter. Phys. Plasmas 2022, 29, 112706. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Kodanova, S.K.; Issanova, M.K.; Kenzhegulov, B.Z. Influence of the ion core on relaxation processes in dense plasmas. Contrib. Plasma Phys. 2024, 64, e202300127. [Google Scholar] [CrossRef]
- Gericke, D.O.; Vorberger, J.; Wünsch, K.; Gregori, G. Screening of ionic cores in partially ionized plasmas within linear response. Phys. Rev. E 2010, 81, 065401. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Holt, Rinehart, and Winston: New York, NY, USA, 1976. [Google Scholar]
- Ashcroft, N.W.; Stroud, D. Theory of the Thermodynamics of Simple Liquid Metals. Solid State Phys. 1977, 33, 1–81. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I.R. Theory of Simple Liquids; Academic Press: London, UK, 2000. [Google Scholar]
- Ramazanov, T.S.; Dzhumagulova, K.N. Effective screened potentials of strongly coupled semiclassical plasma. Phys. Plasmas 2002, 9, 3758–3761. [Google Scholar] [CrossRef]
- Moldabekov, Z.A.; Groth, S.; Dornheim, T.; Kählert, H.; Bonitz, M.; Ramazanov, T.S. Structural characteristics of strongly coupled ions in a dense quantum plasma. Phys. Rev. E 2018, 98, 023207. [Google Scholar] [CrossRef]
- Moldabekov, Z.A.; Dornheim, T.; Bonitz, M. Screening of a test charge in a free-electron gas at warm dense matter and dense non-ideal plasma conditions. Contrib. Plasma Phys. 2022, 62, e202000176. [Google Scholar] [CrossRef]
- Groth, S.; Dornheim, T.; Sjostrom, T.; Malone, F.D.; Foulkes, W.M.C.; Bonitz, M. Ab initio Exchange-Correlation Free Energy of the Uniform Electron Gas at Warm Dense Matter Conditions. Phys. Rev. Lett. 2017, 119, 135001. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley and Sons: New York, NY, USA, 2005. [Google Scholar]
- Springer, J.F.; Pokrant, M.A.; Stevens, F.A. Integral equation solutions for the classical electron gas. J. Chem. Phys. 1973, 58, 4863–4867. [Google Scholar] [CrossRef]
- Ng, K.-C. Hypernetted chain solutions for the classical one-component plasma up to Γ = 7000. J. Chem. Phys. 1974, 61, 2680–2689. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Ismagambetova, T.N.; Gabdullin, M.T. The Influence of the Effects of the Bound Electrons on the Ion Structural and Thermodynamic Properties. IEEE Trans. Plasma Sci. 2023, 51, 1208–1211. [Google Scholar] [CrossRef]
- Isihara, A. Statistical Physics; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Boehly, T.; Brown, D.; Craxton, R.; Keck, R.; Knauer, J.; Kelly, J.; Kessler, T.; Kumpan, S.; Loucks, S.; Letzring, S.; et al. Initial performance results of the OMEGA laser system. Opt. Commun. 1997, 133, 495. [Google Scholar] [CrossRef]
- Hu, S.X.; Militzer, B. Strong Coupling and Degeneracy Effects in Inertial Confinement Fusion Implosions. Phys. Rev. Lett. 2010, 104, 235003. [Google Scholar] [CrossRef]
- Paisner, J.A. National ignition facility would boost United-states industrial competitiveness. Laser Focus World 1994, 30, 75. [Google Scholar]
- Landen, O.; Glenzer, S.; Edwards, M.; Lee, R.; Collins, G.; Cauble, R.; Hsing, W.; Hammel, B. Dense matter characterization by x-ray Thomson scattering. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 465. [Google Scholar] [CrossRef]
- Ma, T.; Döppner, T.; Falcone, R.W.; Fletcher, L.; Fortmann, C.; Gericke, D.O.; Landen, O.L.; Lee, H.J.; Pak, A.; Vorberger, J.; et al. X-Ray Scattering Measurements of Strong Ion-Ion Correlations in Shock-Compressed Aluminum. Phys. Rev. Lett. 2013, 110, 065001. [Google Scholar] [CrossRef]
- Glenzer, S.H.; Landen, O.L.; Neumayer, P.; Lee, R.W.; Widmann, K.; Pollaine, S.W.; Wallace, R.J.; Gregori, G.; Höll, A.; Bornath, T.; et al. Observations of Plasmons in Warm Dense Matter. Phys. Rev. Lett. 2007, 98, 065002. [Google Scholar] [CrossRef]
- Fletcher, L.B.; Lee, H.J.; Döppner, T.; Galtier, E.; Nagler, B.; Heimann, P.; Fortmann, C.; LePape, S.; Ma, T.; Millot, M.; et al. X-Ray Thomson-Scattering Measurements of Density and Temperature in Shock-Compressed Beryllium. Phys. Rev. Lett. 2009, 102, 115001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismagambetova, T.; Muratov, M.; Gabdullin, M. The Influence of the Ionic Core on Structural and Thermodynamic Properties of Dense Plasmas. Plasma 2024, 7, 858-866. https://doi.org/10.3390/plasma7040046
Ismagambetova T, Muratov M, Gabdullin M. The Influence of the Ionic Core on Structural and Thermodynamic Properties of Dense Plasmas. Plasma. 2024; 7(4):858-866. https://doi.org/10.3390/plasma7040046
Chicago/Turabian StyleIsmagambetova, Tomiris, Mukhit Muratov, and Maratbek Gabdullin. 2024. "The Influence of the Ionic Core on Structural and Thermodynamic Properties of Dense Plasmas" Plasma 7, no. 4: 858-866. https://doi.org/10.3390/plasma7040046
APA StyleIsmagambetova, T., Muratov, M., & Gabdullin, M. (2024). The Influence of the Ionic Core on Structural and Thermodynamic Properties of Dense Plasmas. Plasma, 7(4), 858-866. https://doi.org/10.3390/plasma7040046





