Mechanics of Fluid-Conveying Microtubes: Coupled Buckling and Post-Buckling
Abstract
:1. Introduction
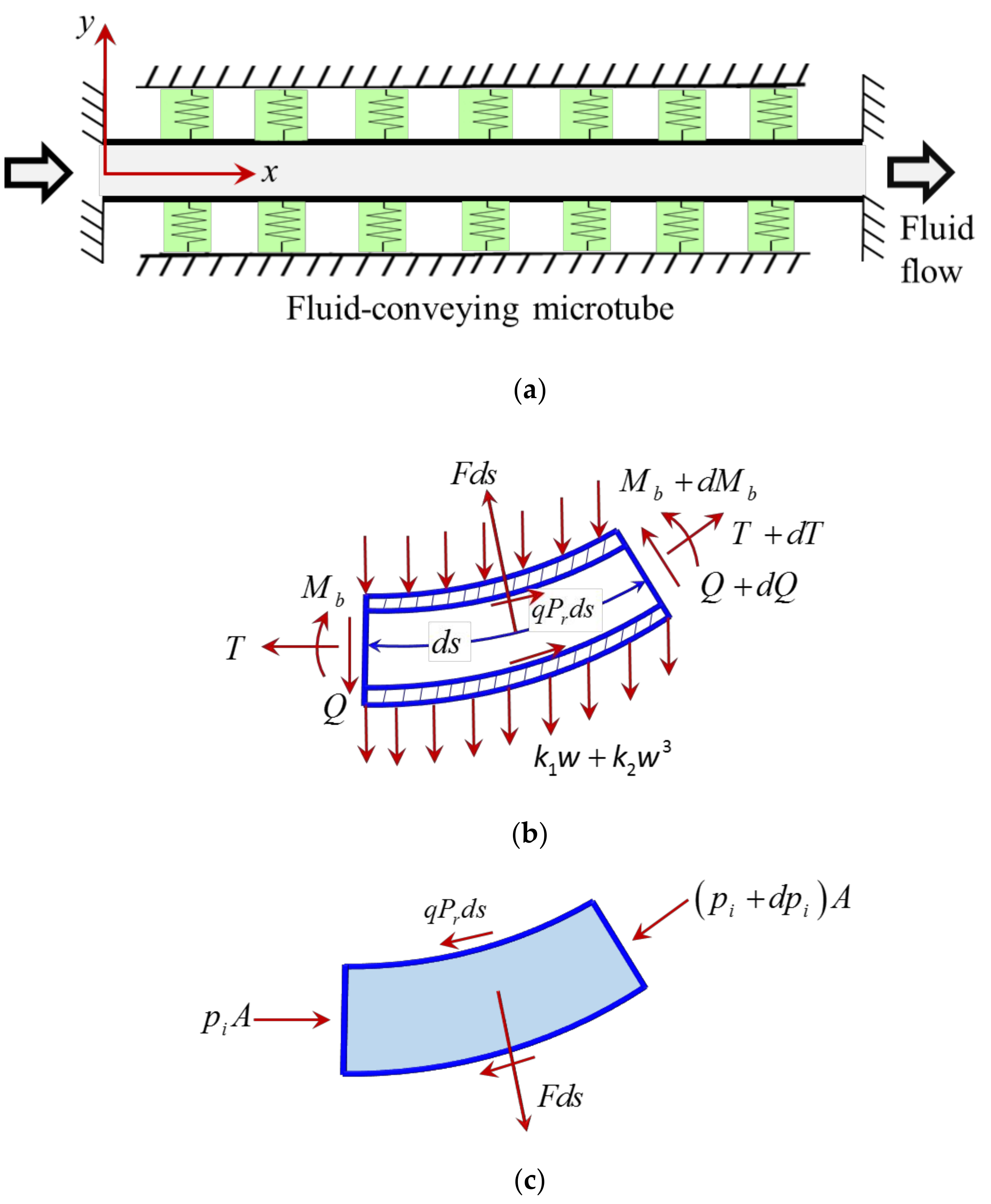
2. Fluid-Structure Interaction Model of the Microtube
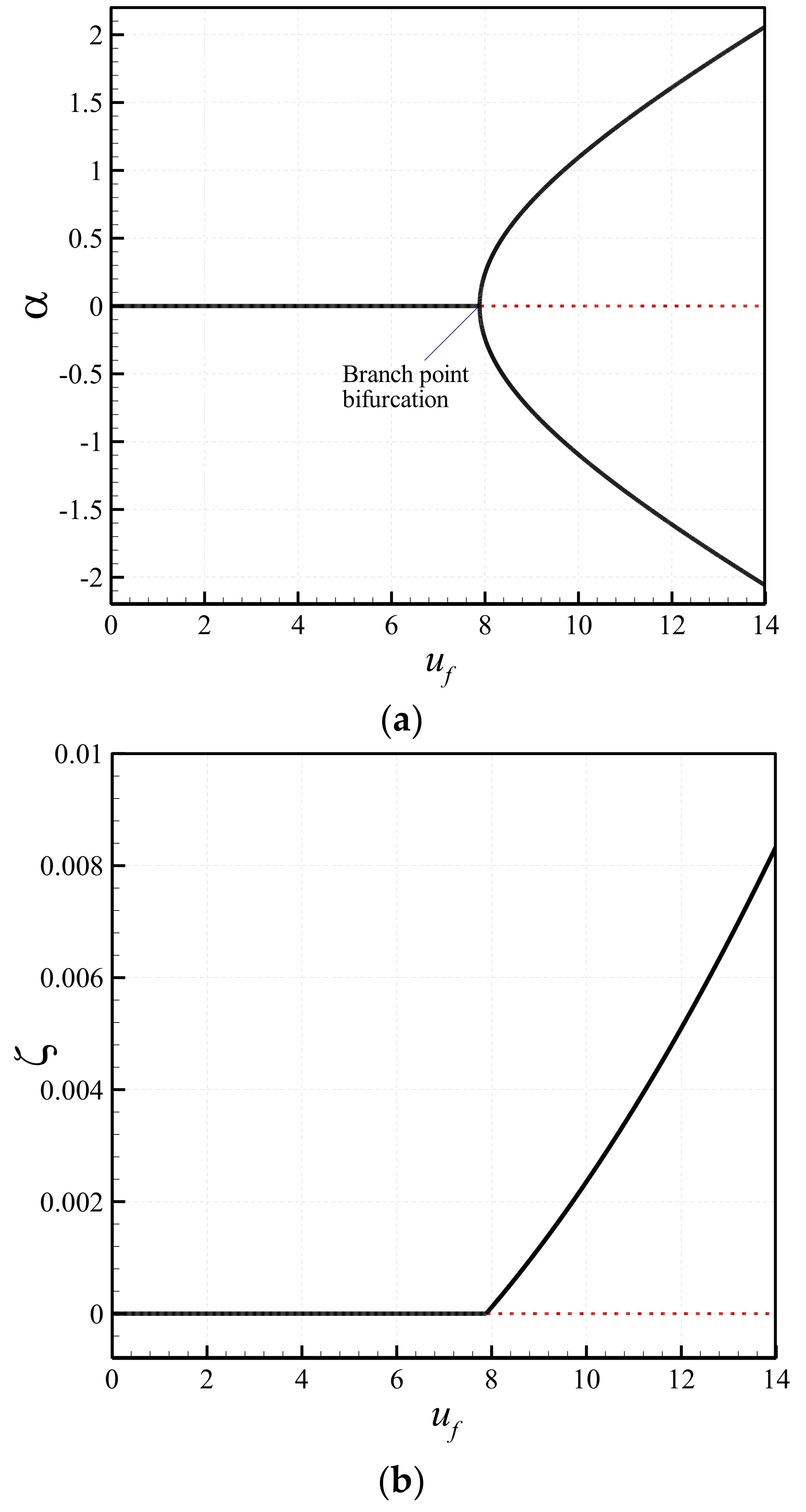
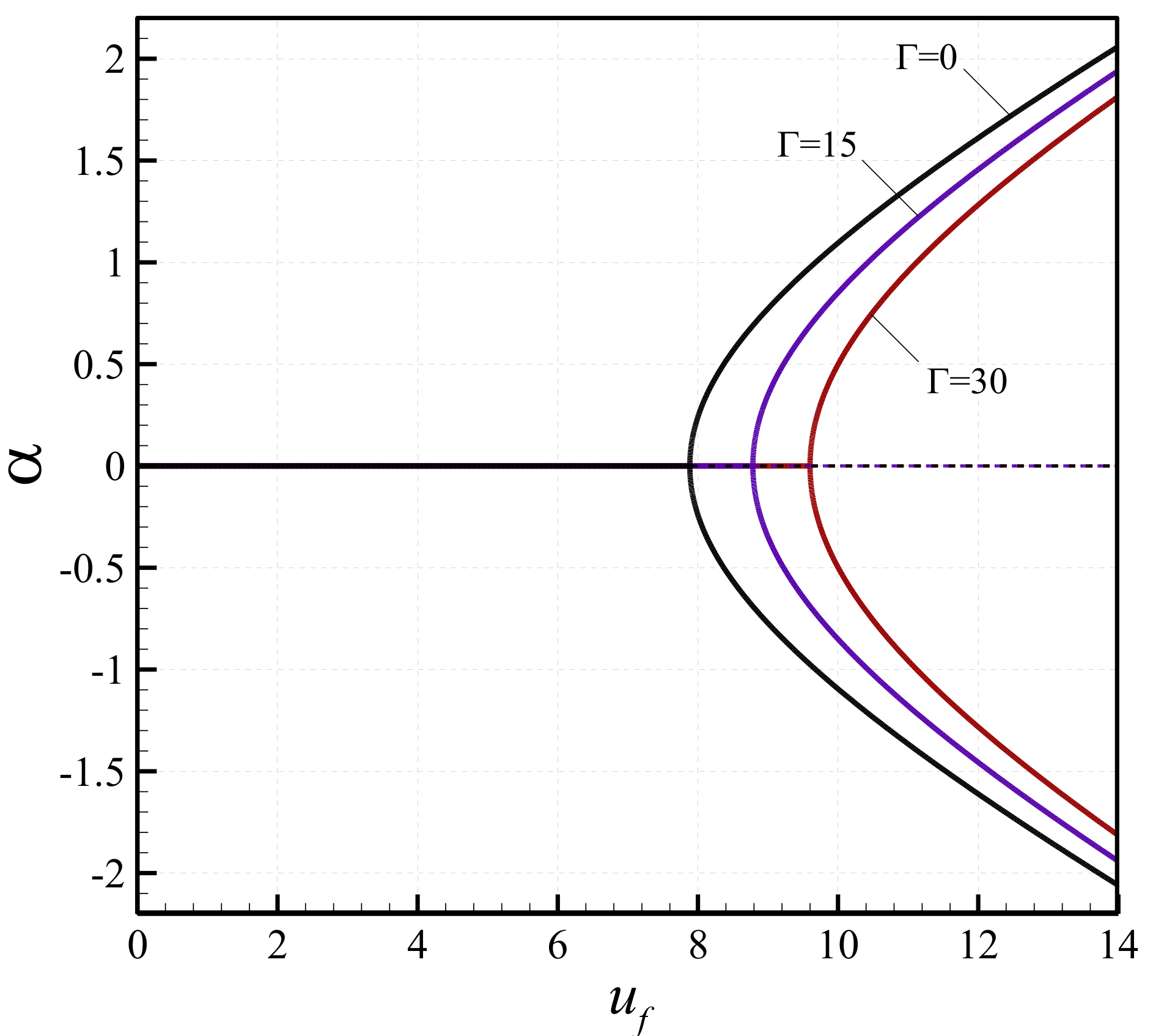
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
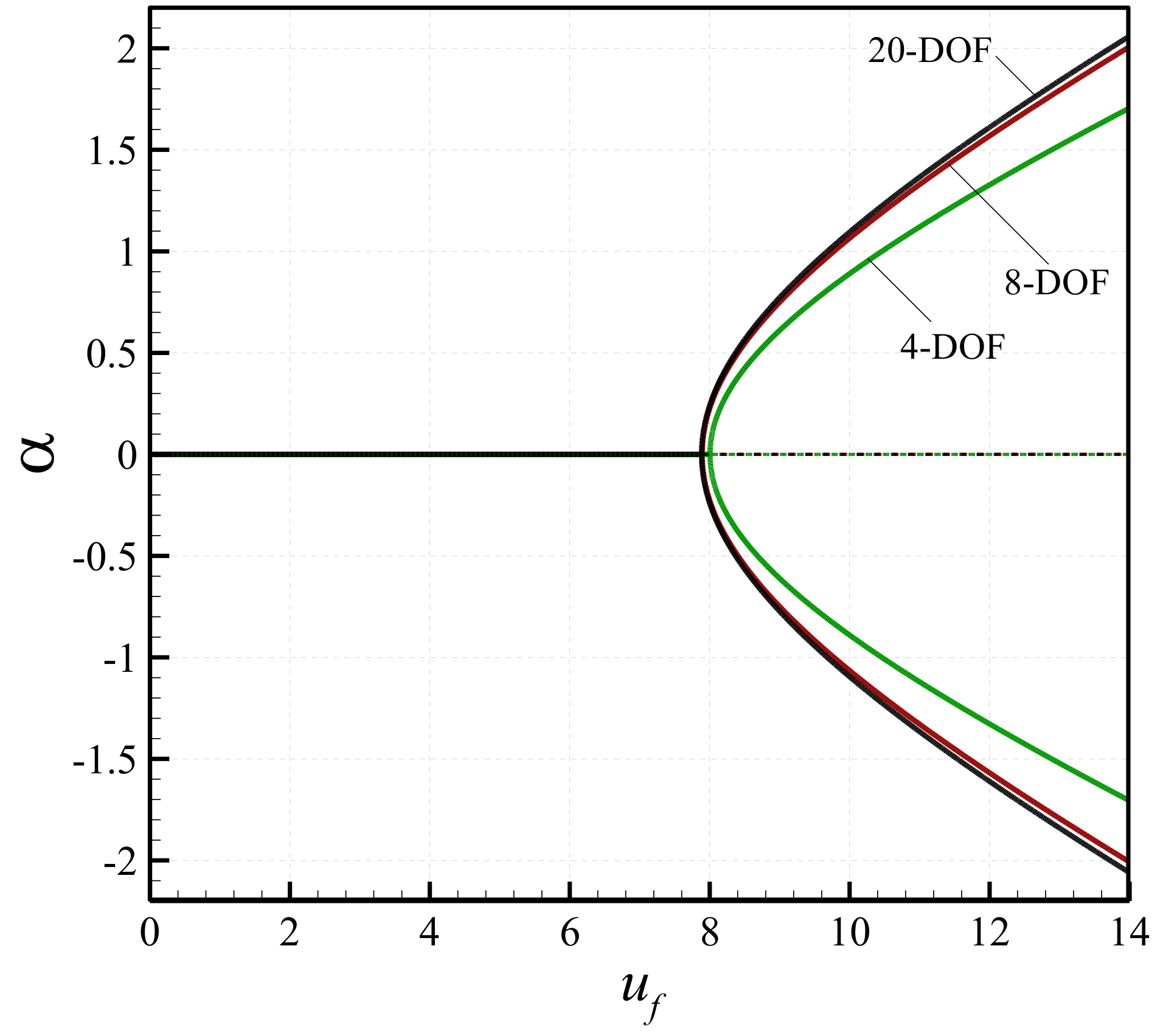
Appendix A. Convergence Analysis
Appendix B. Experiment Setup for Obtaining the Small-Scale Parameter

References
- Shi, Q.; Wang, T.; Lee, C. MEMS based broadband piezoelectric ultrasonic energy harvester (pueh) for enabling self-powered implantable biomedical devices. Sci. Rep. 2016, 6, 24946. [Google Scholar] [CrossRef] [PubMed]
- Bognash, M.; Asokanthan, S. Stochastic stability of a class of mems-based vibratory gyroscopes under input rate fluctuations. Vibration 2018, 1, 69–80. [Google Scholar] [CrossRef]
- Ho, C.-M.; Tai, Y.-C. Micro-electro-mechanical-systems (MEMS) and fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 579–612. [Google Scholar] [CrossRef]
- Martínez-Ayuso, G.; Haddad Khodaparast, H.; Zhang, Y.; Bowen, C.R.; Friswell, M.I.; Shaw, A.D.; Madinei, H. Model validation of a porous piezoelectric energy harvester using vibration test data. Vibration 2018, 1, 123–137. [Google Scholar] [CrossRef]
- Naranjo-Pérez, J.; Jiménez-Manfredi, J.; Jiménez-Alonso, J.F.; Sáez, A. Motion-based design of passive damping devices to mitigate wind-induced vibrations in stay cables. Vibration 2018, 1, 269–289. [Google Scholar] [CrossRef]
- Tophøj, L.; Grathwol, N.; Hansen, S.O. Effective mass of tuned mass dampers. Vibration 2018, 1, 192–206. [Google Scholar] [CrossRef]
- Zaghari, B.; Rustighi, E.; Ghandchi Tehrani, M. Improved modelling of a nonlinear parametrically excited system with electromagnetic excitation. Vibration 2018, 1, 157–171. [Google Scholar] [CrossRef]
- Farajpour, A.; Farokhi, H.; Ghayesh, M.H. Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. Eur. J. Mech. A/Solids 2019, 74, 281–296. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanical behaviour of microshells. Int. J. Eng. Sci. 2018, 127, 127–144. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear coupled mechanics of nanotubes incorporating both nonlocal and strain gradient effects. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Hussain, S. On the nonlinear mechanics of layered microcantilevers. Int. J. Eng. Sci. 2017, 120, 1–14. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A coupled nonlinear continuum model for bifurcation behaviour of fluid-conveying nanotubes incorporating internal energy loss. Microfluid. Nanofluid. 2019, 23, 34. [Google Scholar] [CrossRef]
- Ahangar, S.; Rezazadeh, G.; Shabani, R.; Ahmadi, G.; Toloei, A. On the stability of a microbeam conveying fluid considering modified couple stress theory. Int. J. Mech. Mater. Des. 2011, 7, 327. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Three-dimensional nonlinear size-dependent behaviour of timoshenko microbeams. Int. J. Eng. Sci. 2013, 71, 1–14. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Compos. Part B Eng. 2013, 50, 318–324. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. In-plane and out-of-plane motion characteristics of microbeams with modal interactions. Compos. Part B Eng. 2014, 60, 423–439. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear dynamics of multilayered microplates. J. Comput. Nonlinear Dyn. 2017, 13, 021006. [Google Scholar] [CrossRef]
- Gholipour, A.; Farokhi, H.; Ghayesh, M.H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dyn. 2015, 79, 1771–1785. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
- Kural, S.; Özkaya, E. Size-dependent vibrations of a micro beam conveying fluid and resting on an elastic foundation. J. Vib. Control 2017, 23, 1106–1114. [Google Scholar] [CrossRef]
- Xia, W.; Wang, L. Microfluid-induced vibration and stability of structures modeled as microscale pipes conveying fluid based on non-classical Timoshenko beam theory. Microfluid. Nanofluid. 2010, 9, 955–962. [Google Scholar] [CrossRef]
- Hosseini, M.; Bahaadini, R. Size dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory. Int. J. Eng. Sci. 2016, 101, 1–13. [Google Scholar] [CrossRef]
- Abbasnejad, B.; Shabani, R.; Rezazadeh, G. Stability analysis of a piezoelectrically actuated micro-pipe conveying fluid. Microfluid. Nanofluid. 2015, 19, 577–584. [Google Scholar] [CrossRef]
- Wang, L. Size-dependent vibration characteristics of fluid-conveying microtubes. J. Fluid. Struct. 2010, 26, 675–684. [Google Scholar] [CrossRef]
- Dai, H.; Wang, L.; Ni, Q. Dynamics and pull-in instability of electrostatically actuated microbeams conveying fluid. Microfluid. Nanofluid. 2015, 18, 49–55. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Li, X.; Ling, L. Size-dependent effects on critical flow velocity of fluid-conveying microtubes via nonlocal strain gradient theory. Microfluid. Nanofluid. 2016, 20, 76. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid. Microfluid. Nanofluid. 2018, 22, 72. [Google Scholar] [CrossRef]
- Deng, J.; Liu, Y.; Liu, W. Size-dependent vibration analysis of multi-span functionally graded material micropipes conveying fluid using a hybrid method. Microfluid. Nanofluid. 2017, 21, 133. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Nikkhah-Bahrami, M.; Yazdi, M.R.H. On nonlinear stability of fluid-conveying imperfect micropipes. Int. J. Eng. Sci. 2017, 120, 254–271. [Google Scholar] [CrossRef]
- Mashrouteh, S.; Sadri, M.; Younesian, D.; Esmailzadeh, E. Nonlinear vibration analysis of fluid-conveying microtubes. Nonlinear Dyn. 2016, 85, 1007–1021. [Google Scholar] [CrossRef]
- Yang, T.-Z.; Ji, S.; Yang, X.-D.; Fang, B. Microfluid-induced nonlinear free vibration of microtubes. Int. J. Eng. Sci. 2014, 76, 47–55. [Google Scholar] [CrossRef]
- Setoodeh, A.; Afrahim, S. Nonlinear dynamic analysis of fg micro-pipes conveying fluid based on strain gradient theory. Compos. Struct. 2014, 116, 128–135. [Google Scholar] [CrossRef]
- Rajabi, F.; Ramezani, S. A nonlinear microbeam model based on strain gradient elasticity theory with surface energy. Arch. Appl. Mech. 2012, 82, 363–376. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Moradian, N. Nonlinear dynamic response of axially moving, stretched viscoelastic strings. Arch. Appl. Mech. 2011, 81, 781–799. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Global dynamics of fluid conveying nanotubes. Int. J. Eng. Sci. 2019, 135, 37–57. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanics of electrically actuated microplates. Int. J. Eng. Sci. 2018, 123, 197–213. [Google Scholar] [CrossRef]
- Kazemirad, S.; Ghayesh, M.H.; Amabili, M. Thermo-mechanical nonlinear dynamics of a buckled axially moving beam. Arch. Appl. Mech. 2013, 83, 25–42. [Google Scholar] [CrossRef]
- Farajpour, A.; Rastgoo, A.; Farajpour, M. Nonlinear buckling analysis of magneto-electro-elastic CNT-MT hybrid nanoshells based on the nonlocal continuum mechanics. Compos. Struct. 2017, 180, 179–191. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Large-amplitude coupled scale-dependent behaviour of geometrically imperfect nsgt nanotubes. Int. J. Mech. Sci. 2019, 150, 510–525. [Google Scholar] [CrossRef]
- Farajpour, A.; Farokhi, H.; Ghayesh, M.H.; Hussain, S. Nonlinear mechanics of nanotubes conveying fluid. Int. J. Eng. Sci. 2018, 133, 132–143. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Subharmonic dynamics of an axially accelerating beam. Arch. Appl. Mech. 2012, 82, 1169–1181. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. On the dynamics of imperfect shear deformable microplates. Int. J. Eng. Sci. 2018, 133, 264–283. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Supercritical nonlinear parametric dynamics of Timoshenko microbeams. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 592–605. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastic dynamics of axially FG microbeams. Int. J. Eng. Sci. 2019, 135, 75–85. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. On the viscoelastic dynamics of fluid-conveying microtubes. Int. J. Eng. Sci. 2018, 127, 186–200. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Hussain, S. Complex motion characteristics of three-layered Timoshenko microarches. Microsyst. Technol. 2017, 23, 3731–3744. [Google Scholar] [CrossRef]
- Irschik, H.; Holl, H.J. The equations of Lagrange written for a non-material volume. Acta Mech. 2002, 153, 231–248. [Google Scholar] [CrossRef]
- Seydel, R. Practical Bifurcation and Stability Analysis; Springer Science & Business Media: Berlin, Germany, 2009; Volume 5. [Google Scholar]
- Lam, D.C.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Hussain, S. Motion characteristics of bilayered extensible Timoshenko microbeams. Int. J. Eng. Sci. 2017, 112, 1–17. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Vibrations of shear deformable FG viscoelastic microbeams. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
- Farajpour, M.R.; Shahidi, A.; Farajpour, A. Resonant frequency tuning of nanobeams by piezoelectric nanowires under thermo-electro-magnetic field: A theoretical study. Micro Nano Lett. 2018, 13, 1627–1632. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A. Oscillations of functionally graded microbeams. Int. J. Eng. Sci. 2017, 110, 35–53. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 129, 84–95. [Google Scholar] [CrossRef]
- Paidoussis, M.P. Fluid-Structure Interactions: Slender Structures and Axial Flow; Academic Press: Cambridge, MA, USA, 1998; Volume 1. [Google Scholar]
- Li, Z.; He, Y.; Lei, J.; Han, S.; Guo, S.; Liu, D. Experimental investigation on size-dependent higher-mode vibration of cantilever microbeams. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farajpour, A.; Farokhi, H.; Ghayesh, M.H. Mechanics of Fluid-Conveying Microtubes: Coupled Buckling and Post-Buckling. Vibration 2019, 2, 102-115. https://doi.org/10.3390/vibration2010007
Farajpour A, Farokhi H, Ghayesh MH. Mechanics of Fluid-Conveying Microtubes: Coupled Buckling and Post-Buckling. Vibration. 2019; 2(1):102-115. https://doi.org/10.3390/vibration2010007
Chicago/Turabian StyleFarajpour, Ali, Hamed Farokhi, and Mergen H. Ghayesh. 2019. "Mechanics of Fluid-Conveying Microtubes: Coupled Buckling and Post-Buckling" Vibration 2, no. 1: 102-115. https://doi.org/10.3390/vibration2010007
APA StyleFarajpour, A., Farokhi, H., & Ghayesh, M. H. (2019). Mechanics of Fluid-Conveying Microtubes: Coupled Buckling and Post-Buckling. Vibration, 2(1), 102-115. https://doi.org/10.3390/vibration2010007





