Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions
Abstract
:1. Introduction
2. Nonlocal Elasticity Theory
Hamilton’s Principle
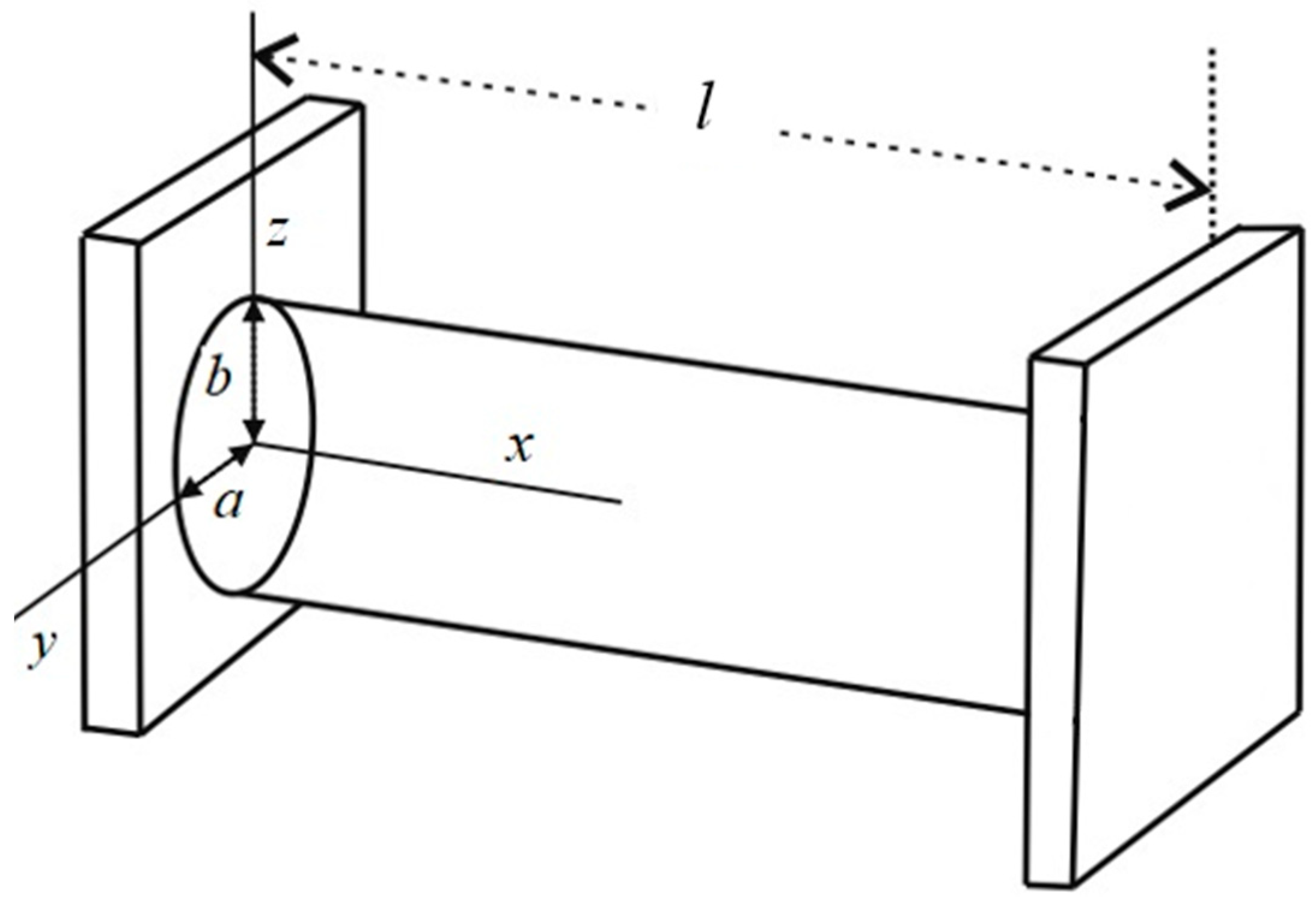
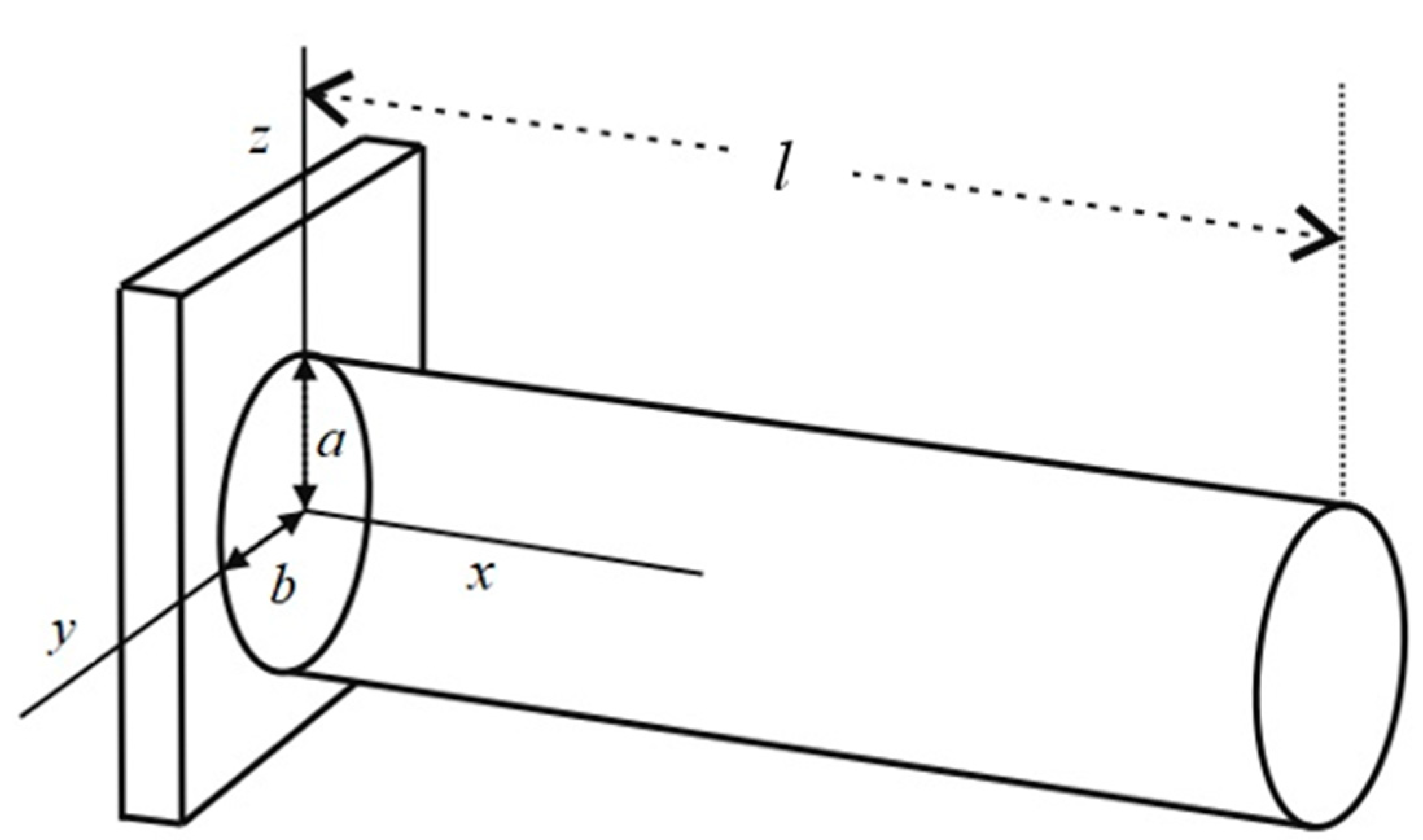
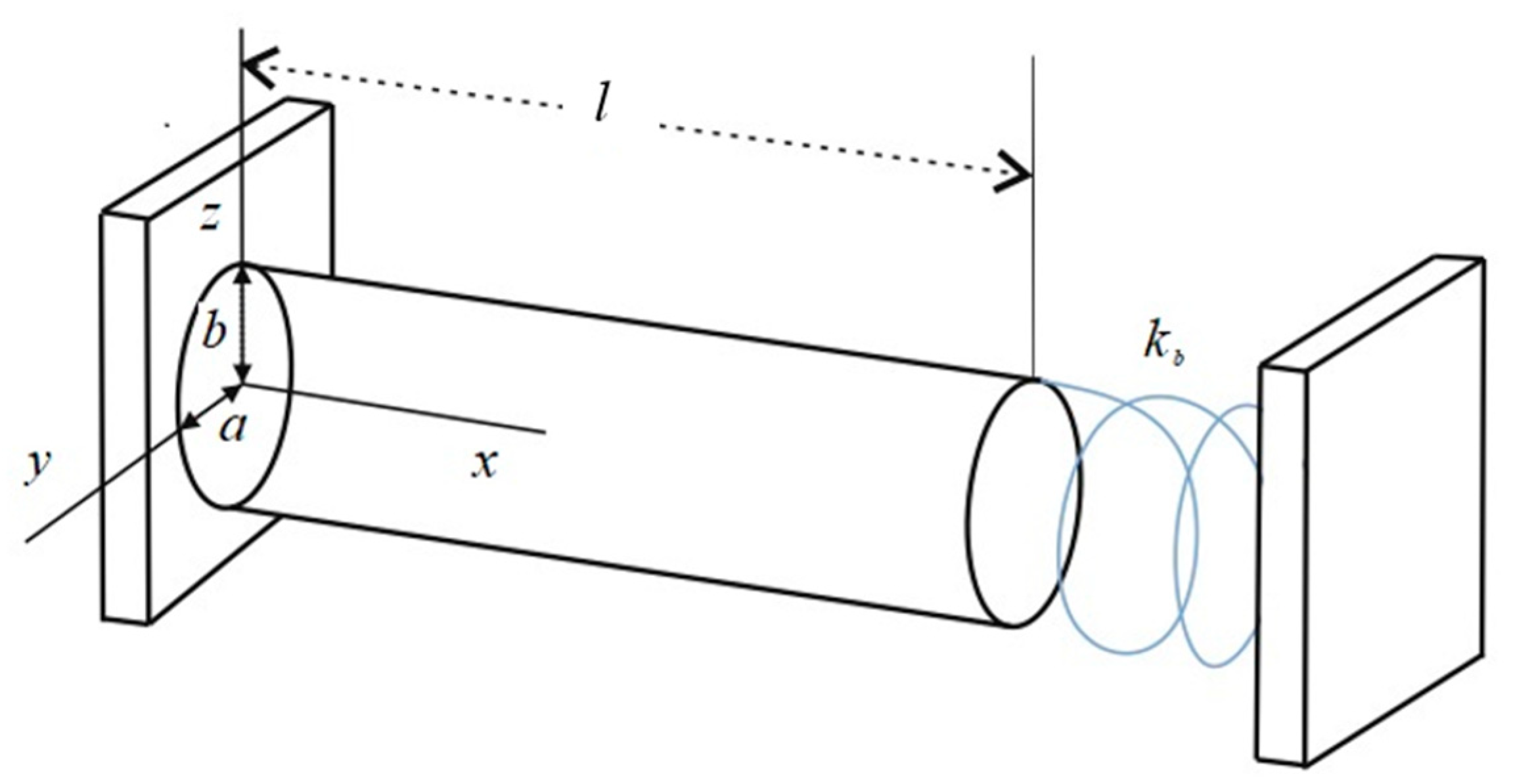
3. Analytical Solution
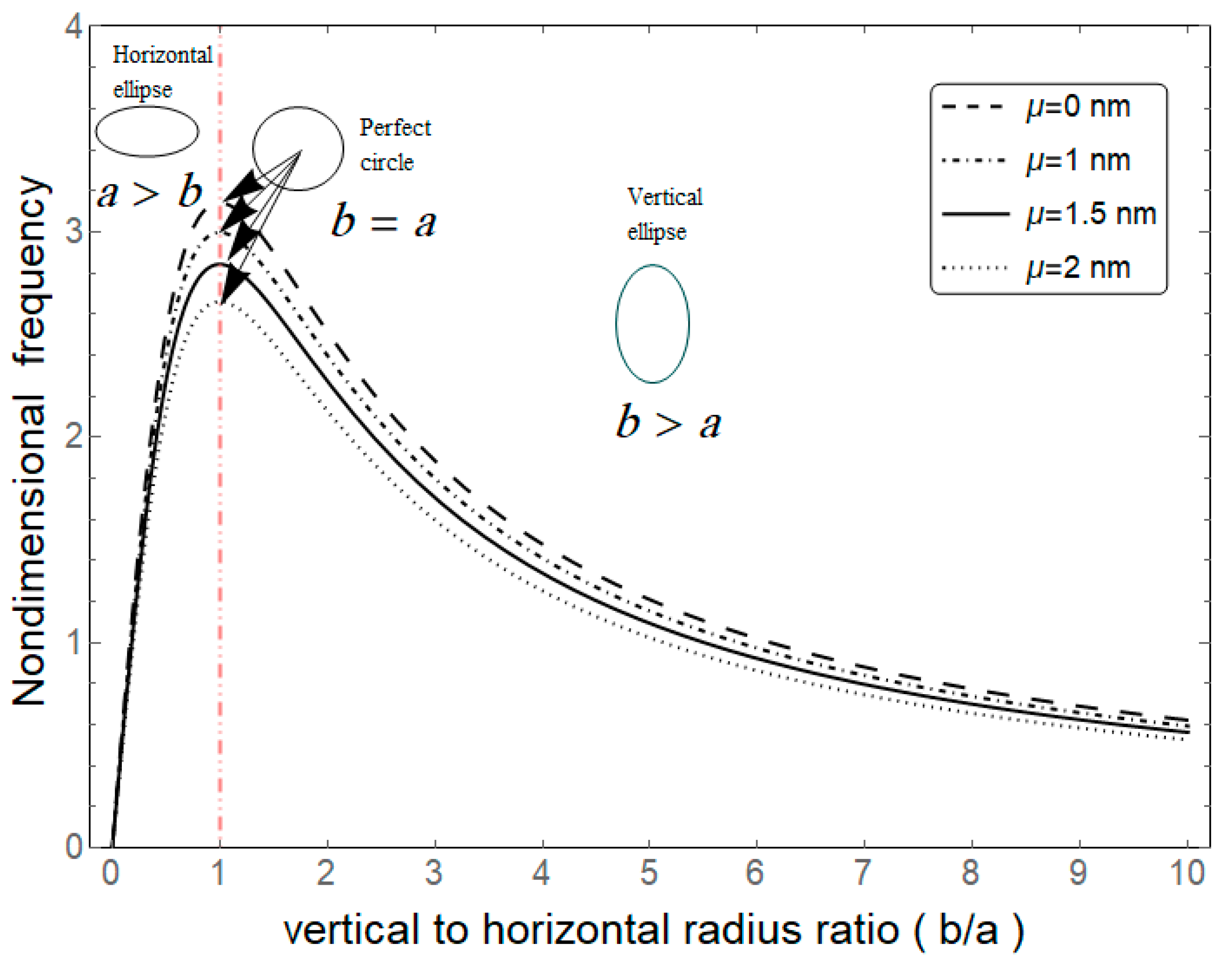
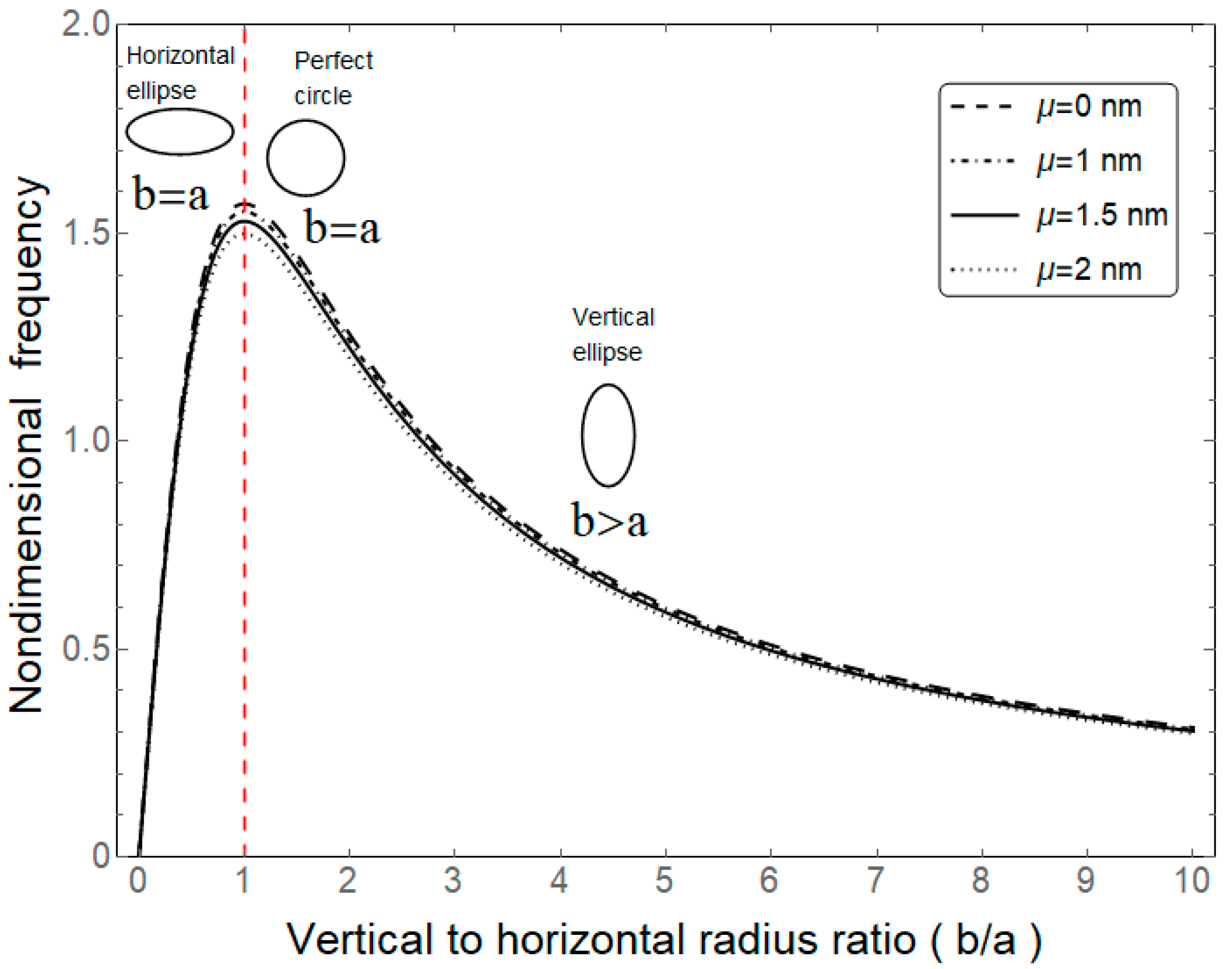
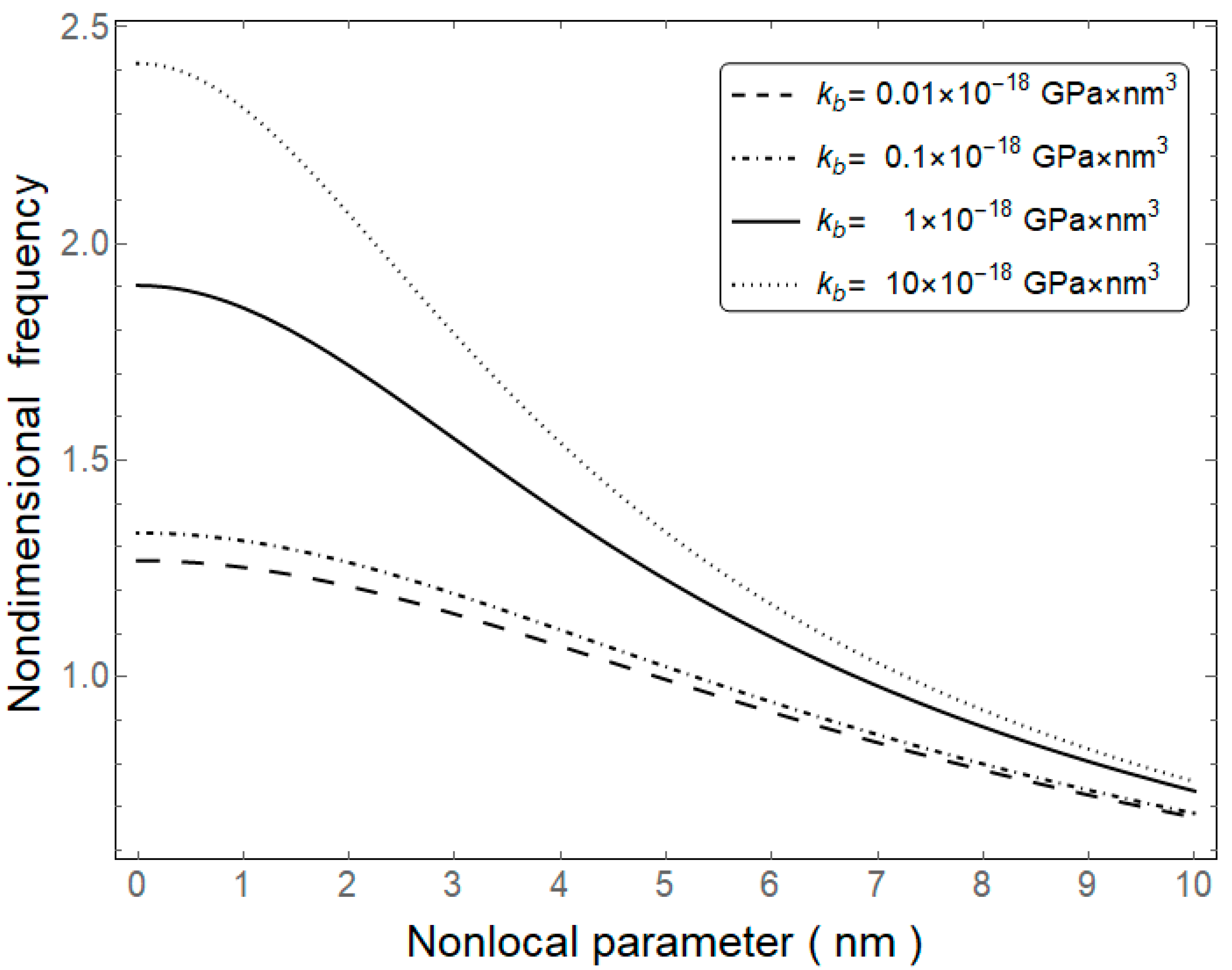
4. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Chopra, N.G.; Zettl, A. Measurement of the elastic modulus of a multi-wall boron nitride nanotube. Solid State Commun. 1998, 105, 297–300. [Google Scholar] [CrossRef]
- Zhi, C.; Bando, Y.; Tang, C.; Golberg, D. Engineering of electronic structure of boron-nitride nanotubes by covalent functionalization. Phys. Rev. B 2006, 74, 153413. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.L.; Dai, Z.R.; Gao, R.P.; Ba, Z.G. Side-by-side silicon carbide–silica biaxial nanowires: Synthesis, structure, and mechanical properties. Appl. Phys. Lett. 2000, 77, 3349. [Google Scholar] [CrossRef]
- Latu-Romain, L.; Ollivier, M. Silicon carbide based one-dimensional nanostructure growth: Towards electronics and biology perspectives. J. Phys. D. Appl. Phys. 2014, 47, 203001. [Google Scholar] [CrossRef]
- Krasavin, S.E.; Osipov, V.A. Vacancy-induced enhancement of thermal conductivity in grapheme. EPL (Europhys. Lett.) 2016, 113, 66002. [Google Scholar] [CrossRef] [Green Version]
- Korobeynikov, S.N.; Alyokhin, V.V.; Babichev, A.V. On the molecular mechanics of single layer graphene sheets. Int. J. Eng. Sci. 2018, 133, 109–131. [Google Scholar] [CrossRef]
- Salvetat, J.P.; Bonard, J.M.; Thomson, N.H.; Kulik, A.J.; Forrò, L.; Benoit, W.; Zuppiroli, L. Mechanical properties of carbon nanotubes. Appl. Phys. A 1999, 69, 255–260. [Google Scholar] [CrossRef]
- Song, Y.W. Single-walled carbon nanotubes for high-energy optical pulse formation. Appl. Phys. Lett. 2008, 92, 021115. [Google Scholar] [CrossRef]
- Kinoshita, Y.; Murashima, M.; Kawachi, M.; Ohno, N. First-principles study of mechanical properties of one-dimensional carbon nanotube intramolecular junctions. Comput. Mater. Sci. 2013, 70, 1–7. [Google Scholar] [CrossRef]
- Férec, J.; Bertevas, E.; Khoo, B.C.; Ausias, G.; Phan-Thien, N. Thermal or electrical bulk properties of rod-filled composites. Int. J. Eng. Sci. 2018, 133, 219–230. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Baughman, R.H.; Cui, C.; Zakhidov, A.A.; Iqbal, Z.; Barisci, J.N.; Spinks, G.M.; Wallace, G.G.; Mazzoldi, A.; de Rossi, D.; Rinzler, A.G.; et al. Carbon nanotube actuators. Science 1999, 284, 1340–1344. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Hta, K.; Tkakura, A.; Yotani, J.; Uemura, S. Field emission of carbon nanotubes and its application as electron sources of ultra-high luminance light-source devices. Physica B 2002, 323, 30–37. [Google Scholar] [CrossRef]
- Wang, J. Carbon-nanotube based electrochemical biosensors: A review. Electroanal. An Int J. Dev. Fundam. Pract. Asp. Electroanal. 2005, 17, 7–14. [Google Scholar] [CrossRef]
- Arnold, M.S.; Green, A.A.; Hulvat, J.F.; Stupp, I.S.; Hersam, M.C. Sorting carbon nanotubes by electronic structure using density differentiation. Nat. Nanotech 2006, 1, 60–65. [Google Scholar] [CrossRef]
- Yan, J.; Zhou, H.; Yu, P. Rational functionalization of carbon nanotubes leading to electrochemical devices with striking applications. Adv. Mater. 2008, 20, 2899–2906. [Google Scholar] [CrossRef]
- Eatemadi, A.; Daraee, H.; Karimkhanloo, H.; Kouhi, M.; Zarghami, N.; Akbarzadeh, A.; Abasi, M.; Hanifehpour, Y.; Joo, S.W. Carbon nanotubes: Properties, synthesis, purification, and medical applications. Nanoscale Res. Lett. 2014, 9, 393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bianco, A.; Kostarelos, K.; Partidos, C.D.; Prato, M. Biomedical applications of functionalised carbon nanotubes. Chem. Commun. 2005, 5, 571–577. [Google Scholar] [CrossRef] [PubMed]
- Miyako, E.; Hosokawa, C.; Kojima, M.; Yudasaka, M.; Funahashi, R.; Oishi, I.; Hagihara, Y.; Shichiri, M.; Takashima, M.; Nishio, K.; et al. A Photo-Thermal-Electrical Converter Based On Carbon Nanotubes for Bioelectronic Applications. Angew. Chem. Int. Ed. 2011, 50, 12266–12270. [Google Scholar] [CrossRef] [PubMed]
- Gooding, J.J. Nanostructuring electrodes with carbon nanotubes: A review on electrochemistry and applications for sensing. Electrochim. Acta 2005, 50, 3049–3060. [Google Scholar] [CrossRef]
- Paradise, M.; Goswami, T. Carbon nanotubes–production and industrial applications. Mat. Des. 2007, 28, 1477–1489. [Google Scholar] [CrossRef]
- He, H.; Pham-Huy, L.A.; Dramou, P.; Xiao, D.; Zuo, P.; Pham-Huy, C. Carbon nanotubes: Applications in pharmacy and medicine. BioMed Res. Int. 2013, 578290. [Google Scholar] [CrossRef] [Green Version]
- Braun, M.; Aranda-Ruiz, J.; Rodriguez-Millan, M.; Loya, J.A. On the bulk modulus and natural frequency of fullerene and nanotube carbon structures obtained with a beam based method. Compos. Struct. 2018, 187, 10–17. [Google Scholar] [CrossRef]
- Avouris, P.; Hertel, T.; Martel, R.; Schmidt, T.; Shea, H.R.; Walkup, R.E. Carbon nanotubes: Nanomechanics, manipulation, and electronic devices. Appl. Surf. Sci. 1999, 141, 201–209. [Google Scholar] [CrossRef] [Green Version]
- Dai, H.; Hafner, J.H.; Rinzler, A.G.; Colbert, D.T.; Smalley, R.E. Nanotubes as nanoprobes in scanning probe microscopy. Nature 1996, 384, 147–150. [Google Scholar] [CrossRef]
- Lau, A.K.T.; Hui, D. The revolutionary creation of new advanced materials-carbon nanotube composites. Compos. Part B Eng. 2002, 33, 263–277. [Google Scholar] [CrossRef]
- Sun, C.H.; Li, F.; Cheng, H.M. Axial Young’s modulus prediction of single-walled carbon nanotube arrays with diameters from nanometer to meter scales. Appl. Phys. Lett. 2005, 87, 193101. [Google Scholar] [CrossRef] [Green Version]
- De Volder, M.F.; Tawfick, S.H.; Baughman, R.H.; Hart, A.J. Carbon nanotubes: Present and future commercial applications. Science 2013, 339, 535–539. [Google Scholar] [CrossRef] [Green Version]
- Hibbeler, R.C. Statics and Mechanics of Materials, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Flügge, W. Tatik und Dynamik der Schalen; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Danesh, M.; Farajpour, A.; Mohammadi, M. Axial vibration analysis of a tapered nanorod based on nonlocal elasticity theory and differential quadrature method. Mech. Res. Commun. 2012, 39, 23–27. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Farajpour, A. Axisymmetric free and forced vibrations of initially stressed circular nanoplates embedded in an elastic medium. Acta Mech. 2012, 223, 2311–2330. [Google Scholar] [CrossRef]
- Mohammadi, M.; Moradi, A.; Ghayour, M.; Farajpour, A. Exact solution for thermo-mechanical vibration of orthotropic mono-layer graphene sheet embedded in an elastic medium. Lat. Am. J. Solids Struct. 2014, 11, 437–458. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, M.; Farajpour, A.; Goodarzi, M.; Dinari, F. Thermo-mechanical vibration analysis of annular and circular graphene sheet embedded in an elastic medium. Lat. Am. J. Solids Struct. 2014, 11, 659–682. [Google Scholar] [CrossRef] [Green Version]
- Farajpour, A.; Rastgoo, A. Influence of carbon nanotubes on the buckling of microtubule bundles in viscoelastic cytoplasm using nonlocal strain gradient theory. Results Phys. 2017, 7, 1367–1375. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Large-amplitude coupled scale-dependent behaviour of geometrically imperfect NSGT nanotubes. Int. J. Mech. Sci. 2019, 150, 510–525. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Plane waves in nonlocal micropolar elasticity. Int. J. Eng. Sci. 1984, 22, 1113–1121. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Sudak, L.J. Column buckling of multiwalled carbon nanotubes using nonlocal continuum mechanics. J. Appl. Phys. 2003, 94, 7281–7287. [Google Scholar] [CrossRef]
- Li, C.Y.; Chou, T.W. Vibrational behaviors of multi-walled carbon nanotube-based nanomechancial resonators. Appl. Phys. Lett. 2004, 84, 121–123. [Google Scholar] [CrossRef]
- He, X.Q.; Kitipornchai, S.; Liew, K.M. Buckling analysis of multi-walled carbon nanotubes: A continuum model accounting for van der Waals interaction. J. Mech. Phys. Solid 2005, 53, 303–326. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liu, G.R.; Xie, X.Y. Free transverse vibrations of double-walled carbon nanotubes using a theory of nonlocal elasticity. Phys. Rev. B 2005, 71, 195404. [Google Scholar] [CrossRef]
- Wang, Q.; Varadan, V.K. Vibration of carbon nanotubes studied using nonlocal continuum mechanics. Smart Mat. Struct. 2006, 15, 659–666. [Google Scholar] [CrossRef]
- Aranda-Ruiz, J.; Loya, J.A.; Fernández-Sáez, J. Bending vibrations of rotating nonuniform nanocantilevers using the Eringen nonlocal elasticity theory. Compos. Struct. 2012, 94, 2990–3001. [Google Scholar] [CrossRef] [Green Version]
- Numanoğlu, H.M.; Akgöz, B.; Civalek, Ö. On dynamic analysis of nanorods. Int. J. Eng. Sci. 2018, 130, 33–50. [Google Scholar] [CrossRef]
- Malikan, M.; Dimitri, R.; Tornabene, F. Transient response of oscillated carbon nanotubes with an internal and external damping. Compos. Part B-Eng. 2019, 158, 198–205. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Civalek, Ö. On dynamic instability of magnetically embedded viscoelastic porous FG nanobeam. Int. J. Eng. Sci. 2019, 143, 14–32. [Google Scholar] [CrossRef]
- Numanoğlu, H.M.; Civalek, Ö. On the dynamics of small-sized structures. Int. J. Eng. Sci. 2019, 145, 103164. [Google Scholar] [CrossRef]
- Lim, C.W. Equilibrium and static deflection for bending of a nonlocal nanobeam. Adv. Vib. Eng. 2009, 8, 277–300. [Google Scholar]
- Kiani, K.; Mehri, B. Assessment of nanotube structures under a moving nanoparticle using nonlocal beam theories. J. Sound Vib. 2010, 329, 2241–2264. [Google Scholar] [CrossRef]
- Lim, C.W.; Niu, J.C.; Yu, Y.M. Nonlocal stress theory for buckling instability of nanotubes: New predictions on stiffness strengthening effects of nanoscales. J. Comput. Theor. Nanosci. 2010, 7, 2104–2111. [Google Scholar] [CrossRef]
- Li, C.; Lim, C.W.; Yu, J.L. Dynamics and stability of transverse vibrations of nonlocal nanobeams with a variable axial load. Smart Mat. Struct. 2011, 20, 015023. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Demir, Ç.; Civalek, Ö. On the analysis of microbeams. Int. J. Eng. Sci. 2017, 121, 14–33. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Nonlocal bending analysis of curved nanobeams reinforced by graphene nanoplatelets. Compos. Part B Eng. 2019, 166, 1–12. [Google Scholar] [CrossRef]
- Pinnola, F.P.; Faghidian, S.A.; Barretta, R.; de Sciarra, F.M. Variationally consistent dynamics of nonlocal gradient elastic beams. Int. J. Eng. Sci. 2020, 149, 103220. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M. Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on nonlocal plate theory. Nanotechnology 2007, 18, 385704. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Vibration analysis of nanoplates under uniaxial prestressed conditions via nonlocal elasticity. J. Appl. Phys. 2009, 106, 104301. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Express 2018, 5, 095006. [Google Scholar] [CrossRef]
- Srividhya, S.; Raghu, P.; Rajagopal, A.; Reddy, J.N. Nonlocal nonlinear analysis of functionally graded plates using third-order shear deformation theory. Int. J. Eng. Sci. 2018, 125, 1–22. [Google Scholar] [CrossRef]
- Dindarloo, M.H.; Li, L.; Dimitri, R.; Tornabene, F. Nonlocal elasticity response of doubly-curved nanoshells. Symmetry 2020, 12, 466. [Google Scholar] [CrossRef] [Green Version]
- Malikan, M.; Krasheninnikov, M.; Eremeyev, V.A. Torsional stability capacity of a nano-composite shell based on a nonlocal strain gradient shell model under a three-dimensional magnetic field. Int. J. Eng. Sci. 2020, 148, 103210. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. Free Vibration of Flexomagnetic Nanostructured Tubes Based on Stress-Driven Nonlocal Elasticity, In Analysis of Shells, Plates, and Beams; Springer: Berlin/Heidelberg, Germany, 2020; pp. 215–226, Chapter 12. [Google Scholar]
- Ansari, R.; Gholami, R.; Ajori, S. Torsional vibration analysis of carbon nanotubes based on the strain gradient theory and molecular dynamic simulations. J. Vib. Acoustic. 2013, 135, 051016. [Google Scholar] [CrossRef]
- Fatahi-Vajari, A.; Imam, A. Torsional vibration of single-walled carbon nanotubes using doublet mechanics. Z. Angew. Math. Phys. 2016, 67, 81. [Google Scholar] [CrossRef]
- Arda, M.; Aydogdu, M. Torsional vibration of double CNT system embedded in an elastic medium. Noise Theory Pract. 2018, 4, 4. [Google Scholar]
- Li, C. Torsional vibration of carbon nanotubes: Comparison of two nonlocal models and a semi-continuum model. Int. J. Eng. Sci. 2014, 82, 25–31. [Google Scholar] [CrossRef]
- Aydogdu, M.; Arda, M. Torsional vibration analysis of double walled carbon nanotubes using nonlocal elasticity. Int. J. Mech. Mater. Design 2016, 12, 71–84. [Google Scholar] [CrossRef]
- Demir, C.; Civalek, Ö. Torsional and longitudinal frequency and wave response of microtubules based on the nonlocal continuum and nonlocal discrete models. Appl. Math. Model. 2013, 37, 9355–9367. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S.; Wang, C. Torsional vibration of carbon nanotube–buckyball systems based on nonlocal elasticity theory. Phys. E Low Dimens. Syst. Nanostruct. 2011, 43, 1276–1280. [Google Scholar] [CrossRef]
- Suzuki, N.; Yokoi, H.; Shamoto, E. Micro/nano sculpturing of hardened steel by controlling vibration amplitude in elliptical vibration cutting. Precis. Eng. 2011, 35, 44–50. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, T.; Ge, C.; Sui, Y.; Yang, H. Review of micro/nano machining by utilizing elliptical vibration cutting. Int. J. Mach. Tool Manufact. 2016, 196, 109–126. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, Y.; Guo, P. Structural coloration of metallic surfaces with micro/nano-structures induced by elliptical vibration texturing. Appl. Surf. Sci. 2017, 402, 400–409. [Google Scholar] [CrossRef]
- Mikeš, K.; Jirásek, M. Free warping analysis and numerical implementation. Appl. Mech. Mat. 2016, 825, 141–148. [Google Scholar] [CrossRef]
- Barr, A. Torsional waves in uniform rods of non-circular section. J. Mech. Eng. Sci. 1962, 4, 127–135. [Google Scholar] [CrossRef]
- Stephen, N. Comparison of dynamic torsion theories for beams of elliptical cross-section. J. Sound Vib. 1985, 100, 1–6. [Google Scholar] [CrossRef]
- Francu, J.; Novácková, P.; Janicek, P. Torsion of a non-circular bar. Eng. Mech. 2012, 19, 45–60. [Google Scholar]
- Christides, S.; Barr, A. Torsional vibration of cracked beams of non-circular cross-section. Int. J. Mech. Sci. 1986, 28, 473–490. [Google Scholar] [CrossRef]
- Loya, J.A.; Aranda-Ruiz, J.; Fernández-Sáez, J.F. Torsion of cracked nanorods using a nonlocal elasticity model. J. Phys. D Appl. Phys. 2014, 47, 115304. [Google Scholar] [CrossRef]
- Loya, J.; López-Puente, J.; Zaera, R.; Fernández-Sáez, J. Free transverse vibrations of cracked nanobeams using a nonlocal elasticity model. J. Appl. Phys. 2009, 105, 044309. [Google Scholar] [CrossRef] [Green Version]
- Loya, J.A.; Rubio, L.; Fernández-Sáez, J. Natural frequencies for bending vibrations of Timoshenko cracked beams. J. Sound Vib. 2006, 290, 640–653. [Google Scholar] [CrossRef] [Green Version]
- Ogata, Y.; Mizutani, G. Control of cross-sections and optical nonlinearity of Pt Nanowires and the Roughness Effect. Phys. Res. Int. 2012, 2012, 969835. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; Wiley Online Library: Hoboken, NJ, USA, 2007. [Google Scholar]
- Mir, M.; Hosseini, A.; Majzoobi, G. A numerical study of vibrational properties of single-walled carbon nanotubes. Comp. Mater. Sci. 2008, 43, 540–548. [Google Scholar] [CrossRef]
- Ruoff, R.S.; Qian, D.; Liu, W.K. Mechanical properties of carbon nanotubes: Theoretical predictions and experimental measurements. Comptes. Rendus. Phys. 2003, 4, 993–1008. [Google Scholar] [CrossRef]
- El Khoury, E.; Messager, T.; Cartraud, P. Derivation of the Young’s and shear moduli of single-walled carbon nanotubes through a computational homogenization approach. Int. J. Multisc. Comput. Eng. 2011, 9, 97–118. [Google Scholar] [CrossRef]
- Khosravi, F.; Hosseini, S.A.; Tounsi, A. Torsional dynamic response of viscoelastic SWCNT subjected to linear and harmonic torques with general boundary conditions via Eringen’s nonlocal differential model. Eur. Phys. J. Plus 2020, 135, 183. [Google Scholar] [CrossRef]

| n = 1 | n = 2 | n = 3 | n = 4 | |
|---|---|---|---|---|
| Present | 2.9971 | 5.3201 | 6.8586 | 7.8247 |
| Ref. [95] | 2.9971 | 5.3201 | 6.8586 | 7.8247 |
| 0 | 0.6220 | 1.2082 | 3.1415 | 1.2062 | 0.6208 |
| 1 | 0.6145 | 1.1935 | 3.1035 | 1.1916 | 0.6133 |
| 1.5 | 0.6055 | 1.1760 | 3.0578 | 1.1741 | 0.6043 |
| 2 | 0.5934 | 1.1526 | 2.9971 | 1.1508 | 0.5923 |
| 0 | 0.3110 | 1.2565 | 1.5708 | 1.2564 | 0.3108 |
| 1 | 0.3100 | 1.2527 | 1.5659 | 1.2525 | 0.3099 |
| 1.5 | 0.3089 | 1.2479 | 1.5600 | 1.2478 | 0.3087 |
| 2 | 0.3072 | 1.2413 | 1.5517 | 1.2412 | 0.3071 |
| 0 | 1 | 1.5 | 2 | |
|---|---|---|---|---|
| 0.01 | 1.2815 | 1.2774 | 1.2723 | 1.2653 |
| 0.1 | 1.4690 | 1.4628 | 1.4552 | 1.4448 |
| 1 | 2.1225 | 2.1040 | 2.0817 | 2.0515 |
| 10 | 2.4638 | 2.4351 | 2.4006 | 2.3547 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosravi, F.; Hosseini, S.A.; Hamidi, B.A.; Dimitri, R.; Tornabene, F. Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions. Vibration 2020, 3, 189-203. https://doi.org/10.3390/vibration3030015
Khosravi F, Hosseini SA, Hamidi BA, Dimitri R, Tornabene F. Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions. Vibration. 2020; 3(3):189-203. https://doi.org/10.3390/vibration3030015
Chicago/Turabian StyleKhosravi, Farshad, Seyyed Amirhosein Hosseini, Babak Alizadeh Hamidi, Rossana Dimitri, and Francesco Tornabene. 2020. "Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions" Vibration 3, no. 3: 189-203. https://doi.org/10.3390/vibration3030015
APA StyleKhosravi, F., Hosseini, S. A., Hamidi, B. A., Dimitri, R., & Tornabene, F. (2020). Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions. Vibration, 3(3), 189-203. https://doi.org/10.3390/vibration3030015







