Simulation of Torsional Vibration of Driven Railway Wheelsets Respecting the Drive Control Response on the Vibration Excitation in the Wheel-Rail Contact Point
Abstract
:1. Introduction
1.1. Vogel’s Law
1.2. Simulation Model of Schneider
1.3. Simulation Model of Weinhardt
1.4. Simulation Model of Yu and Breuer
1.5. Motivation of the Model at Hand
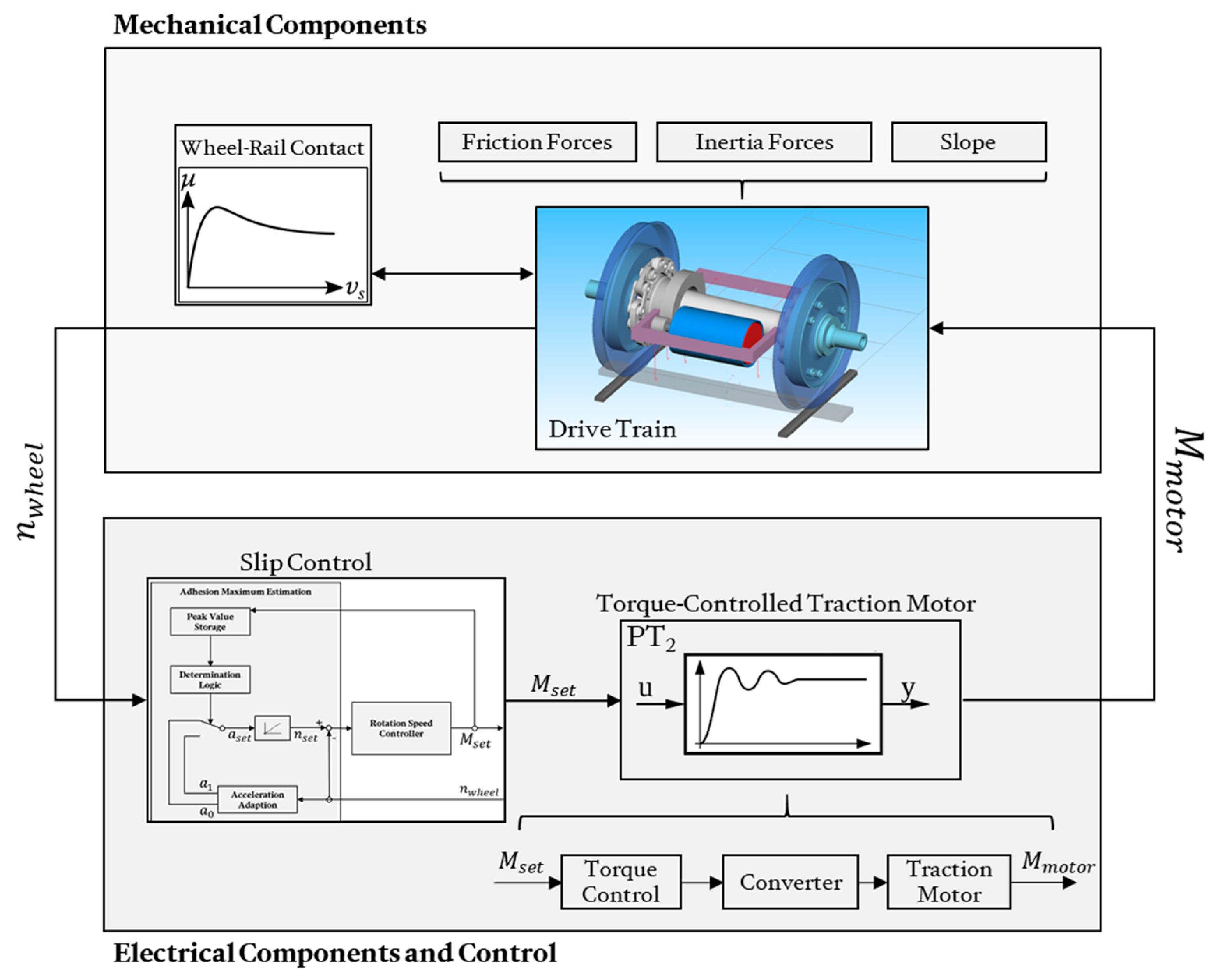
2. Simulation Model Setup
- The mechanical drive train;
- The wheel-rail contact;
- Friction and inertia forces of the train set.
- The traction motor,
- The torque control of the traction motor,
- A wheel slip control.
2.1. Mechanical Model
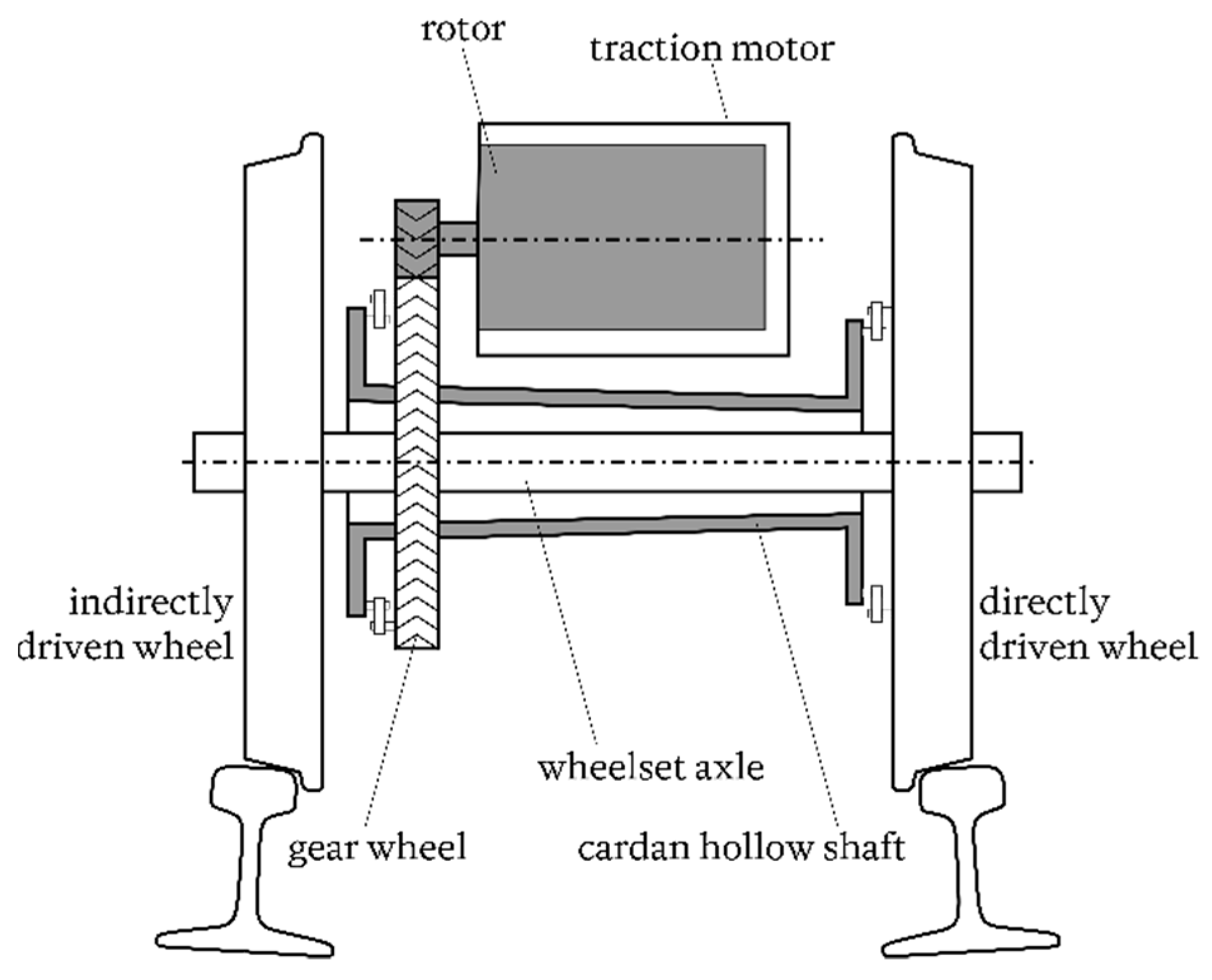
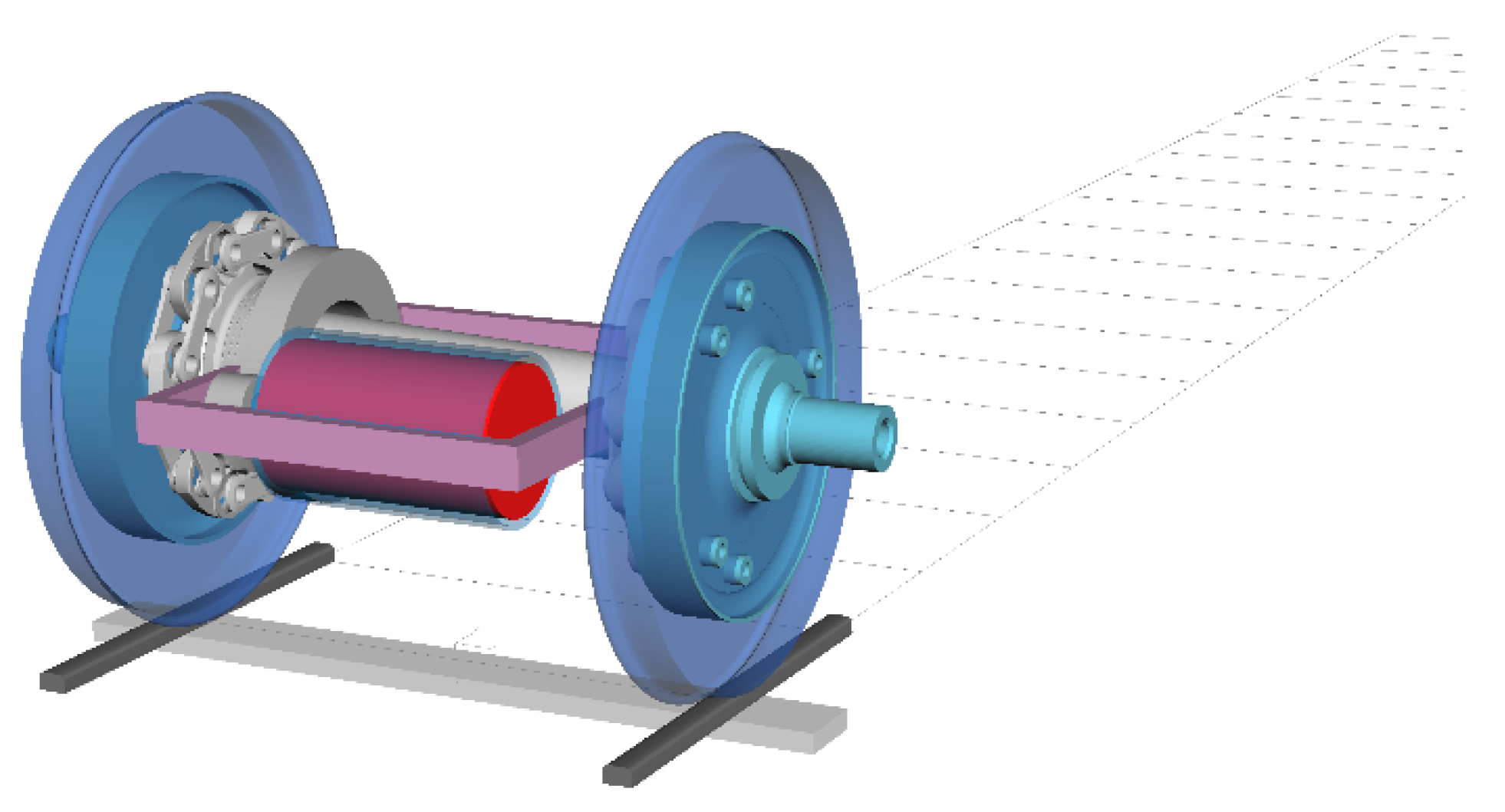
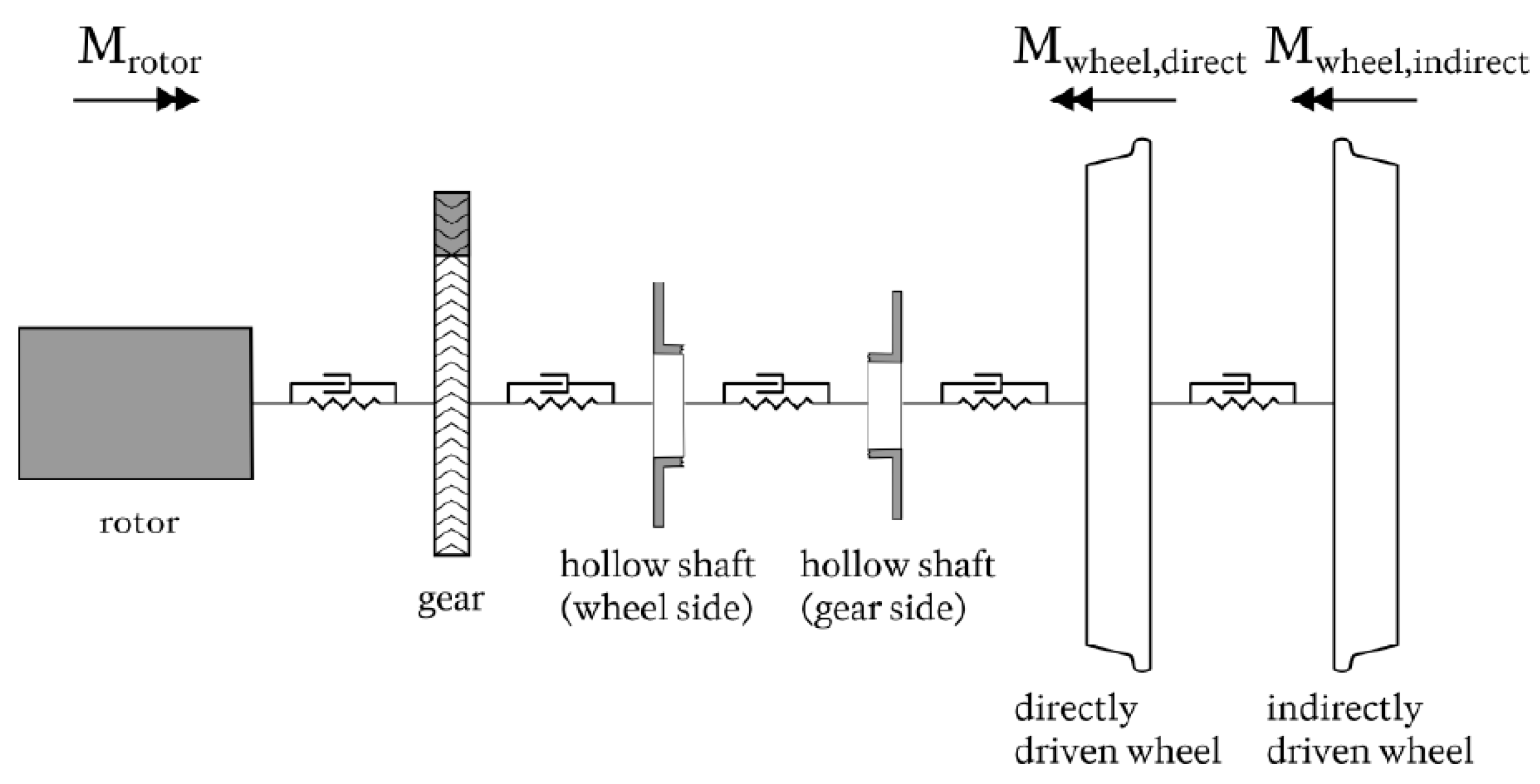
2.1.1. Mechanical Drive Train
- Rotor;
- Gear wheels;
- Coupling;
- Hollow shaft;
- Wheelset axle;
- Both wheels.
- Gear;
- Coupling;
- Hollow shaft;
- Wheelset axle.
2.1.2. Wheel-Rail Contact
- The rail conditions (dry, wet, dirty, etc.);
- The overall vehicle speed;
- Material properties;
- The relative position between wheel and rail;
- Further operational quantities (e.g., rail temperature).
2.1.3. Friction and Inertia Forces of the Train Set
- for cargo trains,
- for passenger trains.
2.2. Model of the Electrical Components
2.2.1. Torque-Controlled Traction Motor
2.2.2. Slip Control
2.3. Overall Model Implementation
3. Simulation Model Verification
3.1. Verification of the Mechanical Drive Train (Modal Analysis)
3.2. Comparison of the Wheel-Rail Contact Implementation
3.3. Verification of the Overall Model
4. Results on Torsional Vibration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eisenbahn-Bundesamt Bericht des Eisenbahn-Bundesamts—Berichtsjahr 2010: Gemäß Artikel 18 der Richtlinie Über Eisenbahnsicherheit in der Gemeinschaft (Richtlinie 2004/49/EG, Sicherheitsrichtlinie über die Tätigkeit als Sicherheitsbehörde). Available online: https://www.eba.bund.de/SharedDocs/Downloads/DE/Allgemeines/Sicherheitsberichte/sicherheitsbericht_2010.pdf?__blob=publicationFile&v=3 (accessed on 25 December 2020).
- Trimpe, F.; Salander, C. Wheel-rail adhesion during torsional vibration of driven railway wheelsets. Veh. Syst. Dyn. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- DIN Deutsches Institut für Normung e.V. DIN Taschenbuch 491/1—Schienenfahrzeuge 1—Radsätze; Beuth Verlag GmbH: Berlin, Germany, 2013. [Google Scholar]
- Friedrich, S.; Traupe, M. Dynamic Torsional Loads on Wheelsets—Recent Findings for the Assessment; DB Systemtechnik GmbH: Milan, Italy, 2014; Available online: http://esistc24.mecc.polimi.it/Milan_2014/Torsional_Loads.pdf (accessed on 25 December 2020).
- Saur, F.; Weber, J.; Schlecht, B. Selbsterregte Radsatz-Torsionsschwingungen von Schienenfahrzeugen mit Hoher Kraftschlussausnutzung, HTWG Sommerkolloquium. 2017. Available online: https://promotionskolleg.htwg-konstanz.de/wp-content/uploads/2017/07/Sommerkolloquium2017_FelixSaur.pdf (accessed on 25 December 2020).
- Trimpe, F.; Friedrich, S.; Traupe, M. Untersuchung der Gleitgeschwindigkeit während dynamischer Torsionsbelastungen von Radsatzwellen. In Proceedings of the 17 Internationale Schienenfahrzeugtagung, Dresden, Germany, 11 February 2020; pp. 61–63. [Google Scholar]
- Schneider, R. Rollierschwingungen von Radsätzen; Ein neuer integrierter und systematischer Ansatz. In Proceedings of the 13 Internationale Schienenfahrzeugtagung, Dresden, Germany, 26 February 2014; pp. 50–52. [Google Scholar]
- Weinhardt, M. Torsionsschwingung in Radsätzen—Fakten und Thesen zur Anregung durch den Rad/Schiene-Kraftschluss. In Proceedings of the 15 Internationale Schienenfahrzeugtagung, Dresden, Germany, 1–3 March 2017; pp. 49–51. [Google Scholar]
- Yu, M.; Breuer, W. Energy based approach to evaluate self oscillations of wheelsets caused by adhesion characteristics. ZEVrail 2018, 142, 164–172. [Google Scholar]
- Liu, J.; Zhao, H.; Zhai, W. Mechanism of self-excited torsional vibration of locomotive driving system. Front. Mech. Eng. China 2010, 5, 465–469. [Google Scholar] [CrossRef]
- Konowrocki, R.; Szolc, T. An Analysis of the Self-Excited Torsional Vibrations of the Electromechanical Drive System. Vib. Phys. Syst. 2016, 27, 187–194. [Google Scholar]
- Xu, K.; Zeng, J.; Wei, L. An analysis of the self-excited torsional vibration of high-speed train drive system. J. Mech. Sci. Technol. 2019, 33, 1149–1158. [Google Scholar] [CrossRef]
- Meierhofer, A.; Bernsteiner, C.; Müller, G.; Semrad, F.; Weber, F.-J.; Rosenberger, M.; Six, K. Prediction of Maximum Torsional Wheel-Set Axle Vibrations Considering Non-linear Adhesion Characteristics. In Proceedings of the IAVSD 2019: Advances in Dynamics of Vehicles on Roads and Tracks, Gothenburg, Sweden, 12–16 August 2019; pp. 970–976. [Google Scholar]
- Körner, E. Reibschwingungen Eines Elektrischen Triebfahrzeuges an der Haftwertgrenze. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 1988. [Google Scholar]
- Polach, O. Creep forces in simulations of traction vehicles running on adhesion limit. Wear 2005, 258, 992–1000. [Google Scholar] [CrossRef]
- Polach, O. A Fast Wheel-Rail Forces Calculation Computer Code. Veh. Syst. Dyn. 1999, 33, 728–739. [Google Scholar] [CrossRef]
- Kalker, J.J. A Fast Algorithm for the Theory of Rolling Contact. Veh. Syst. Dyn. 1982, 11, 1–13. [Google Scholar] [CrossRef]
- Schwartz, H.J. Regelung der Radsatzdrehzahl zur Maximalen Kraftschlußausnutzung bei Elektrischen Triebfahrzeugen; VDI-Verlag GmbH: Düsseldorf, Germany, 1992. [Google Scholar]
- Dassault Systèmes Simulia Corp. Simpack 2021: Simulia User Assistance; Dassault Systèmes: Vélizy-Villacoublay Cedex, France, 2020. [Google Scholar]
- Sachs, K. Elektrische Triebfahrzeuge; Kommissionsverlag Huber & Co: Frauenfeld, Switzerland, 1953. [Google Scholar]
- Filipovic, Z. Elektrische Bahnen, Grundlagen, Triebfahrzeuge, Stromversorgung; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Buscher, M. Radschlupfregelung zur Maximalen Kraftschlussausnutzung bei Elektrischen Traktionsantrieben; Verlag Shaker: Aachen, Germany, 1995. [Google Scholar]


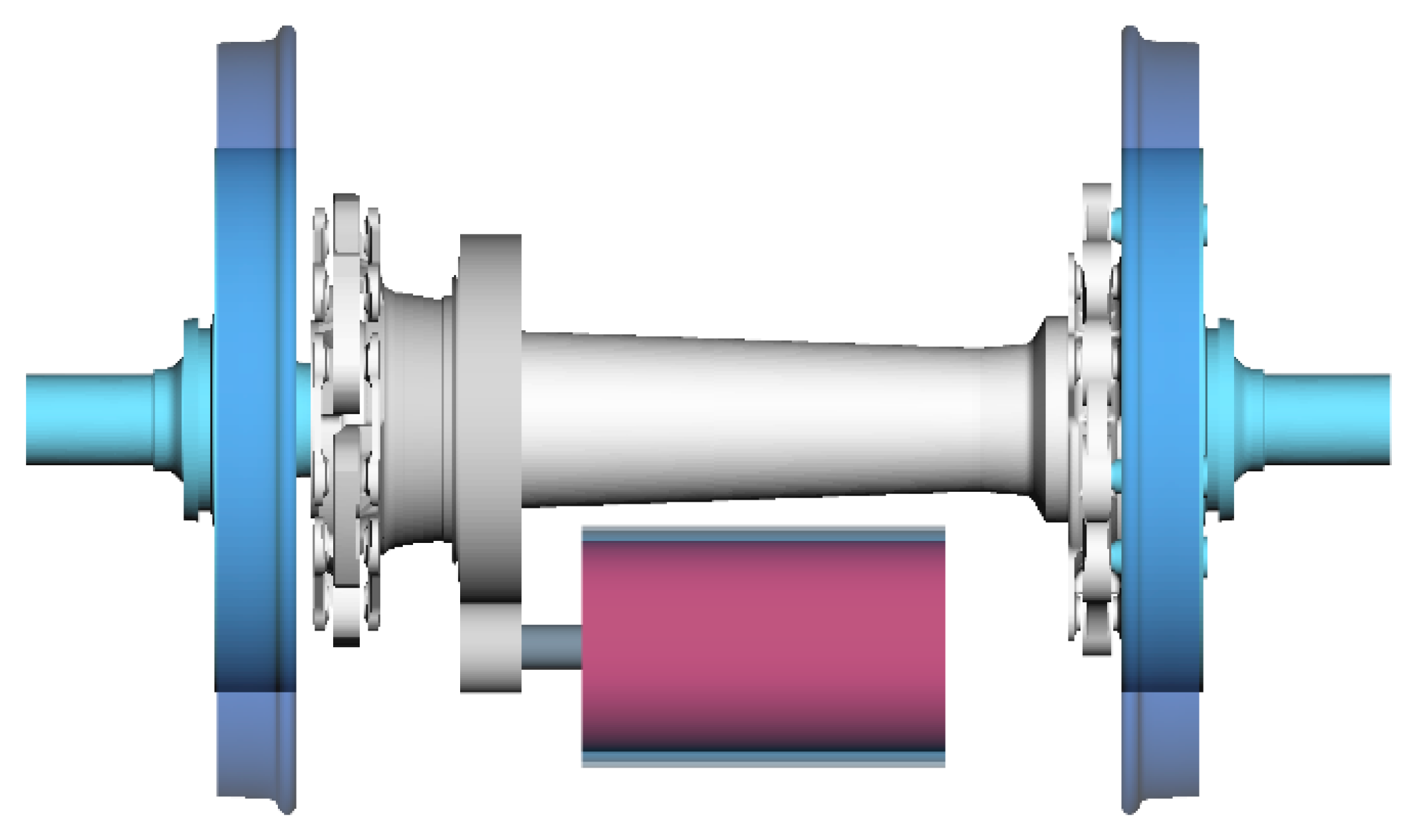



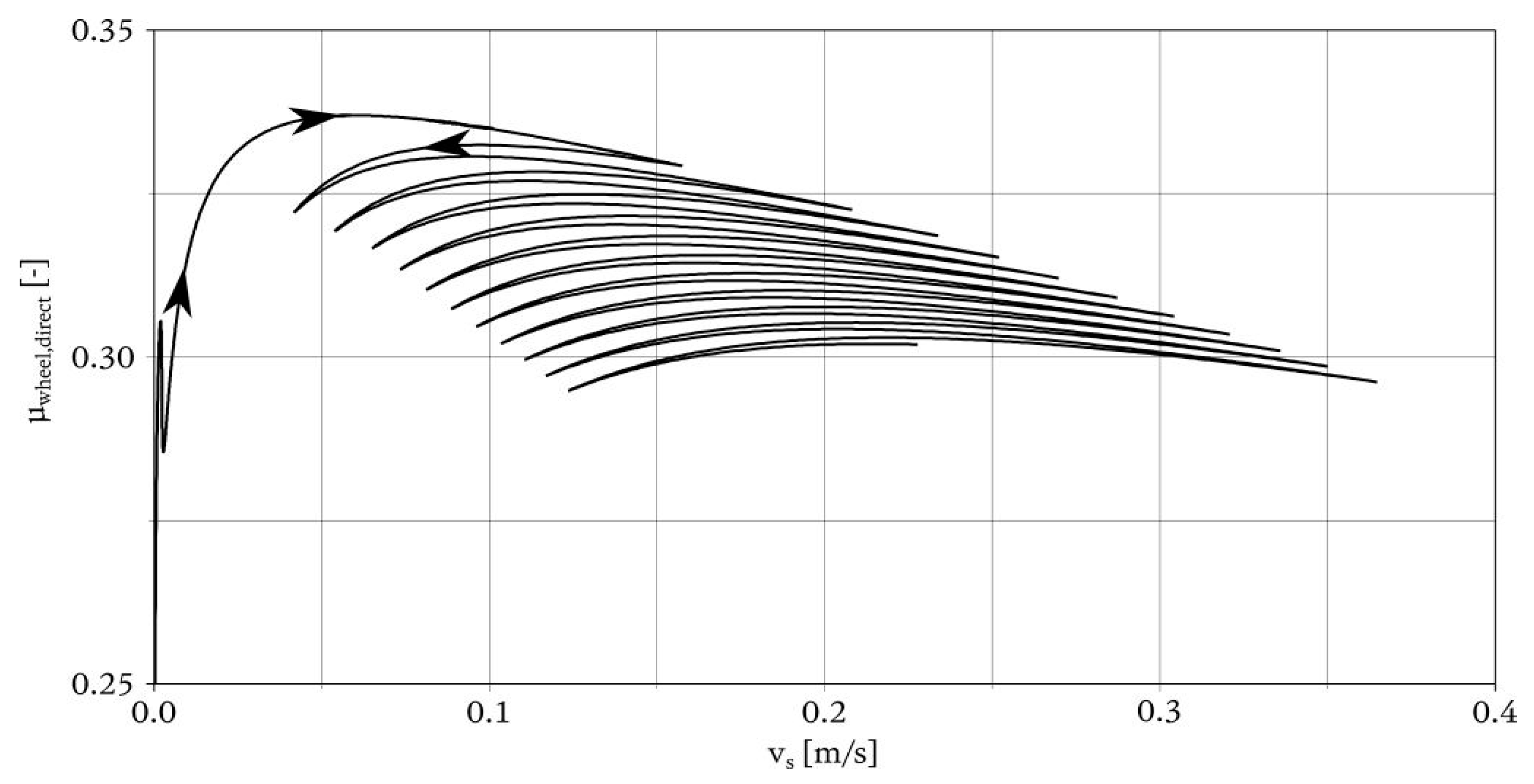
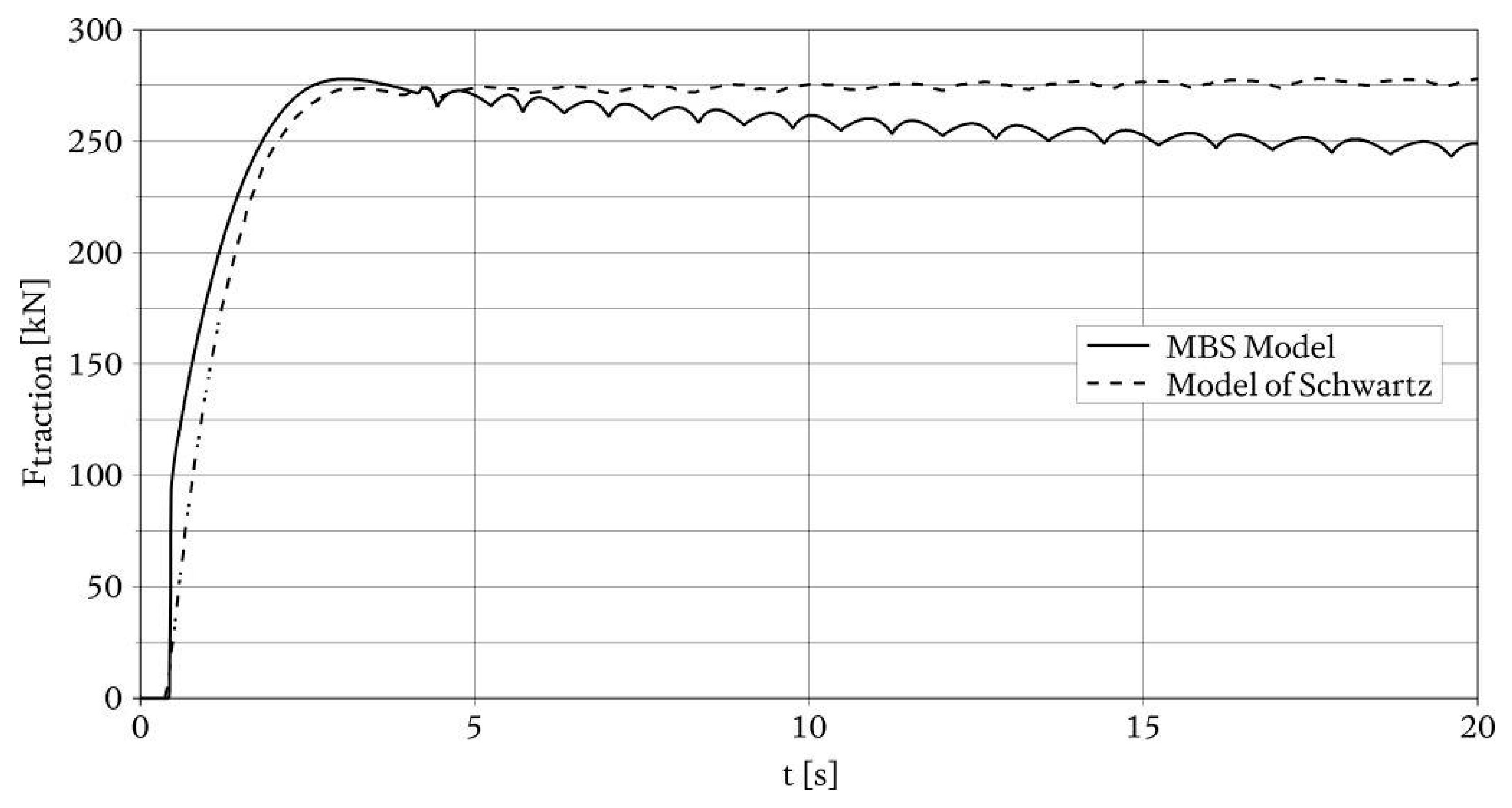
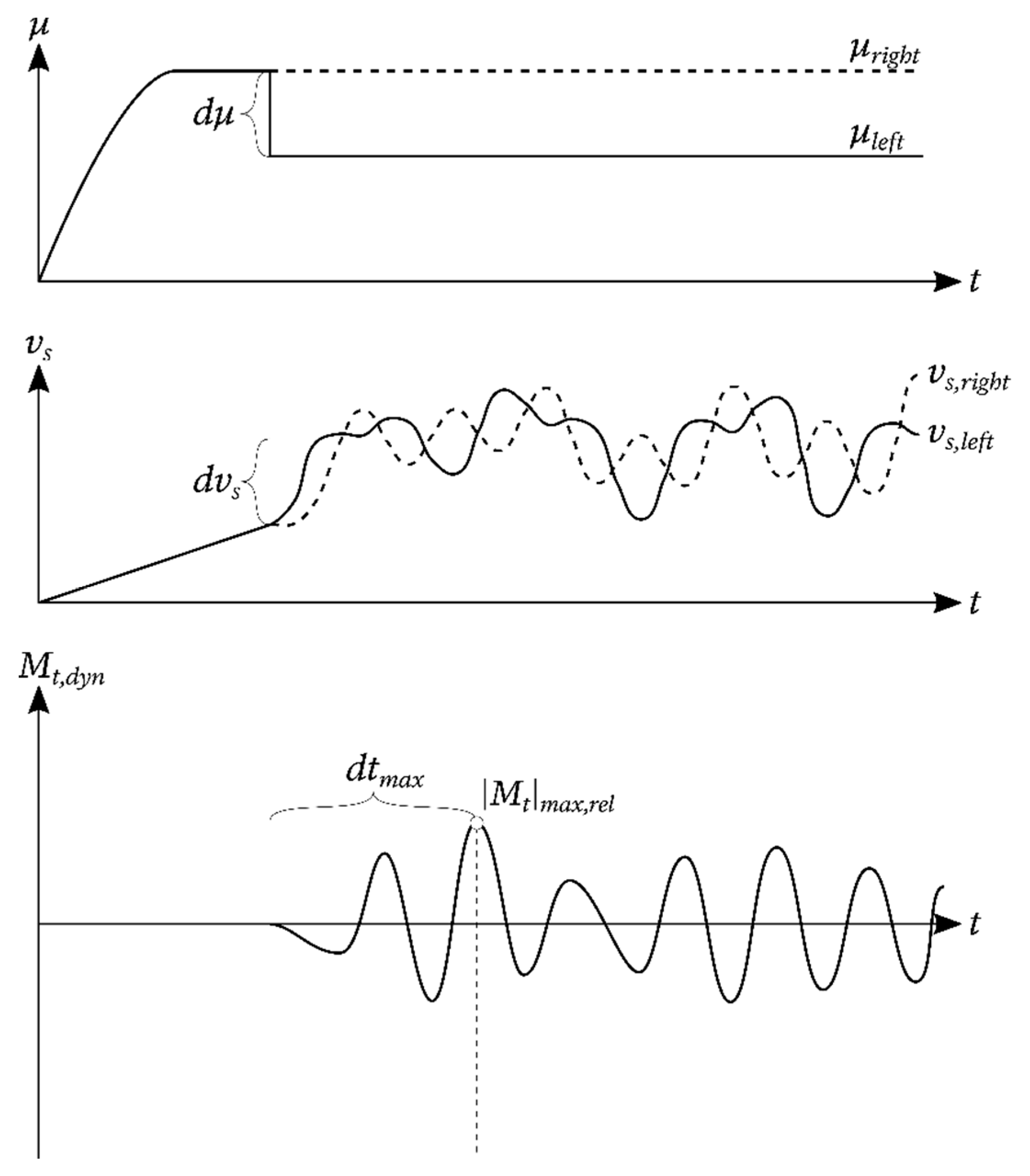


| Mechanical Drive Train Part | Torsional Stiffness | Torsional Damping Rate |
|---|---|---|
| Motor Shaft | 88.12 × 106 Nm | 920.30 Nm s |
| Coupling (Gear Side) | 15.10 × 106 Nm | 4730.80 Nm s |
| Hollow Shaft | 10.10 × 106 Nm | 105.50 Nm s |
| Coupling (Wheel Side) | 15.70 × 106 Nm | 11,731.40 Nm s |
| Wheelset Axle | 7.06 × 106 Nm | 73.70 Nm s |
| Parameter | Numerical Value |
|---|---|
| 100 Nm | |
| 13.3 kNm s |
| i | fi [Hz] | |
|---|---|---|
| Schwartz | MBS | |
| 1 | 0 | 0 |
| 2 | 21.3 | 21.28 |
| 3 | 50.8 | 50.76 |
| 4 | 181.8 | 181.77 |
| 5 | 238.3 | 238.28 |
| 6 | 307.2 | 307.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trimpe, F.; Lück, S.; Naumann, R.; Salander, C. Simulation of Torsional Vibration of Driven Railway Wheelsets Respecting the Drive Control Response on the Vibration Excitation in the Wheel-Rail Contact Point. Vibration 2021, 4, 30-48. https://doi.org/10.3390/vibration4010003
Trimpe F, Lück S, Naumann R, Salander C. Simulation of Torsional Vibration of Driven Railway Wheelsets Respecting the Drive Control Response on the Vibration Excitation in the Wheel-Rail Contact Point. Vibration. 2021; 4(1):30-48. https://doi.org/10.3390/vibration4010003
Chicago/Turabian StyleTrimpe, Fritz, Sönke Lück, Rolf Naumann, and Corinna Salander. 2021. "Simulation of Torsional Vibration of Driven Railway Wheelsets Respecting the Drive Control Response on the Vibration Excitation in the Wheel-Rail Contact Point" Vibration 4, no. 1: 30-48. https://doi.org/10.3390/vibration4010003
APA StyleTrimpe, F., Lück, S., Naumann, R., & Salander, C. (2021). Simulation of Torsional Vibration of Driven Railway Wheelsets Respecting the Drive Control Response on the Vibration Excitation in the Wheel-Rail Contact Point. Vibration, 4(1), 30-48. https://doi.org/10.3390/vibration4010003






