Frequency-Adaptable Tuned Mass Damper Using Metal Cushions
Abstract
:1. Introduction
2. Materials and Methods
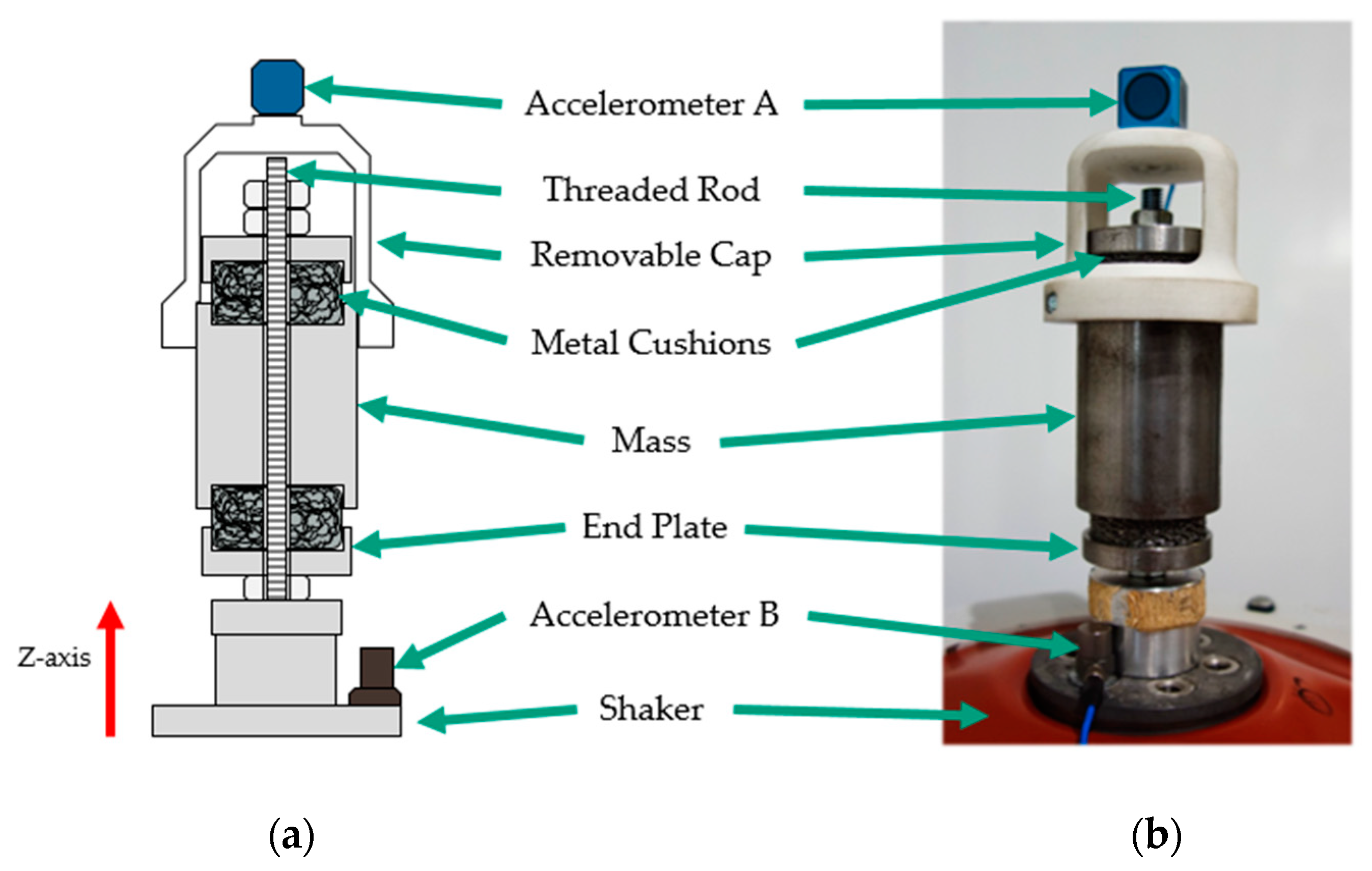
2.1. Experimental Set-Up
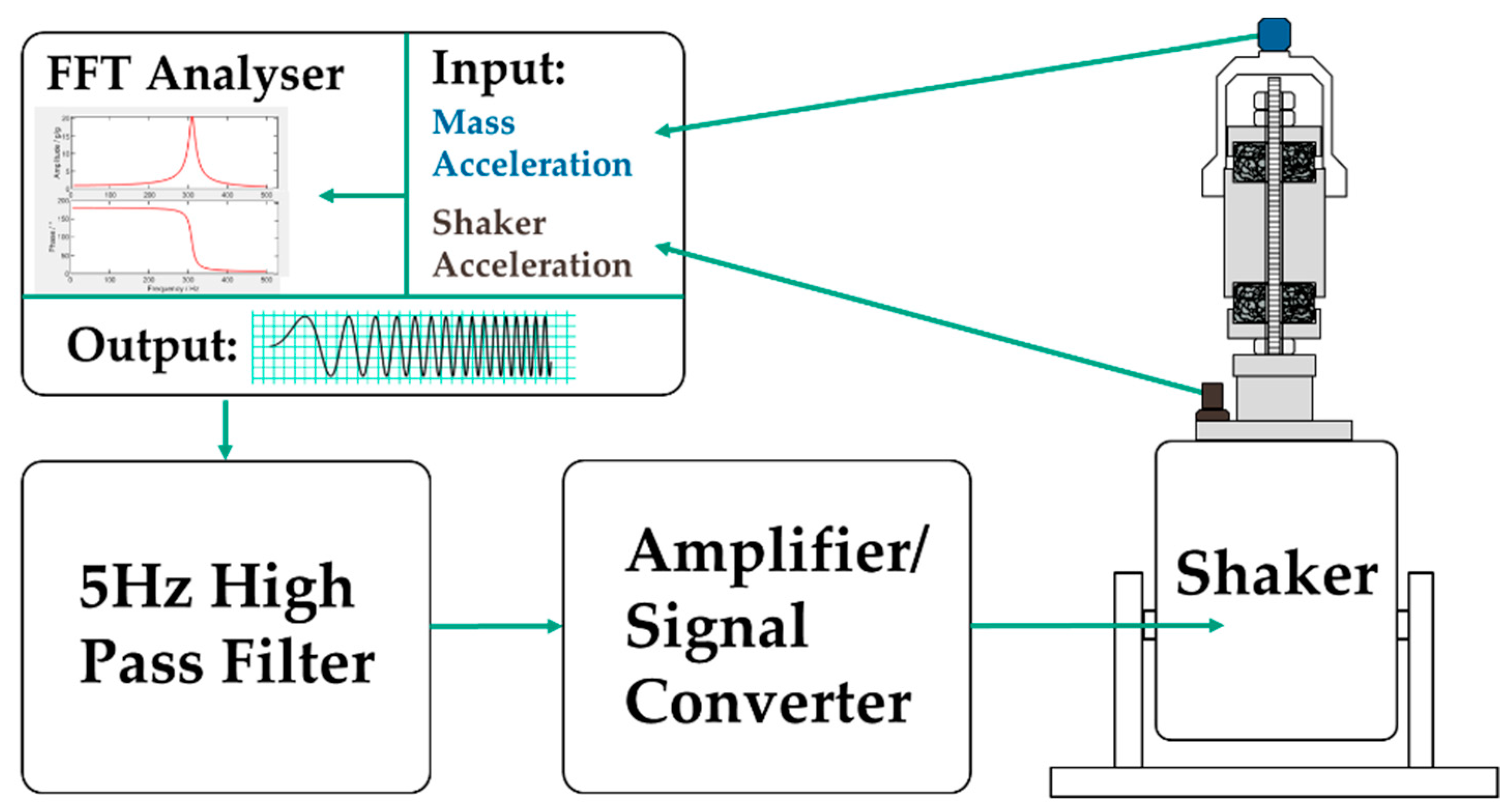
2.2. Experimental Method
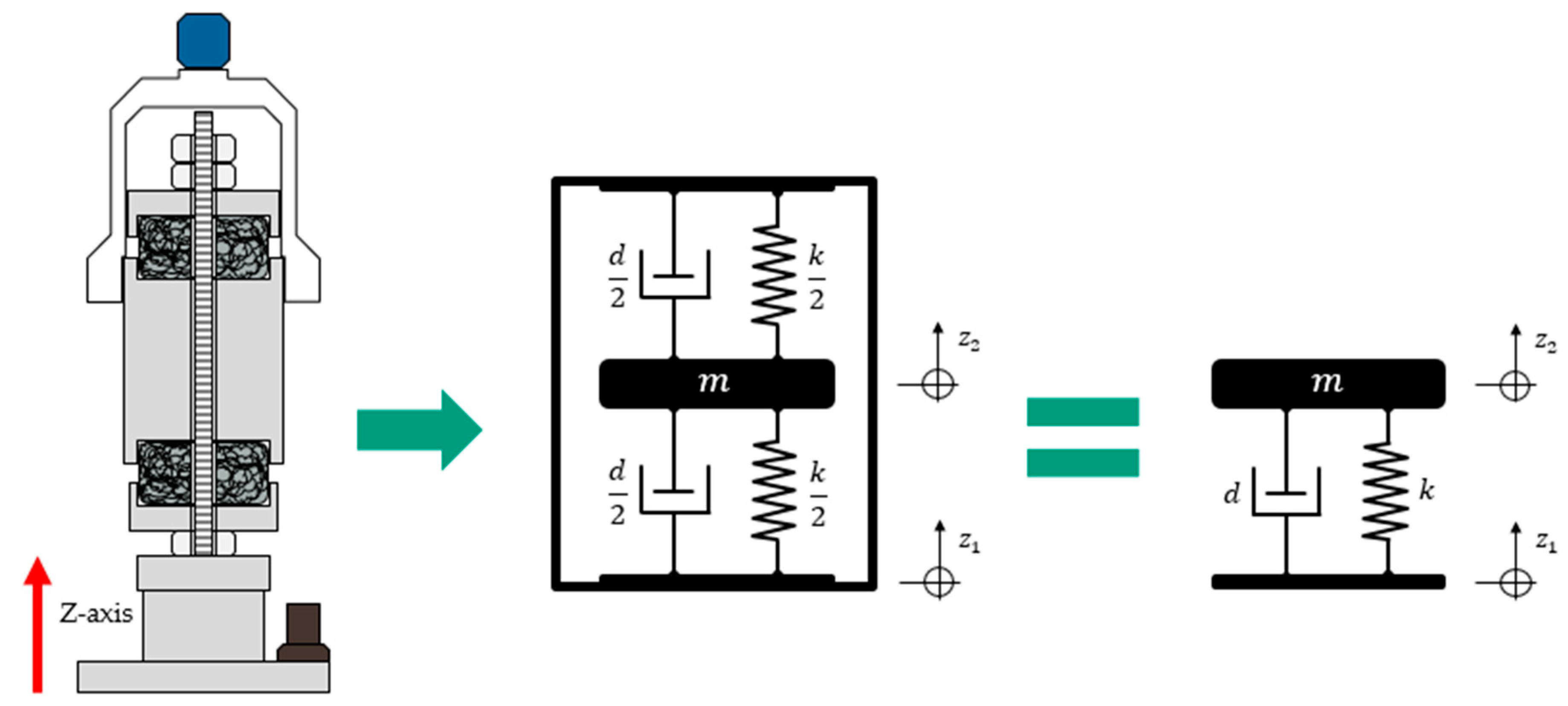
2.3. Analytical Modelling
2.4. Methods of Analysis
- (1)
- First, the damping ratio of the system is determined by regarding the magnitude of the measured frequency response and identifying the peak. Its value is evaluated according to the equation
- (2)
- Second, the stiffness is evaluated using the equation
- (3)
- Third, the damping factor is evaluated by rearranging Equation (2). All components necessary to produce the model curves using the transfer function (Equation (1)) are now at hand.
2.5. Methods of Error Calculation
3. Results and Discussion
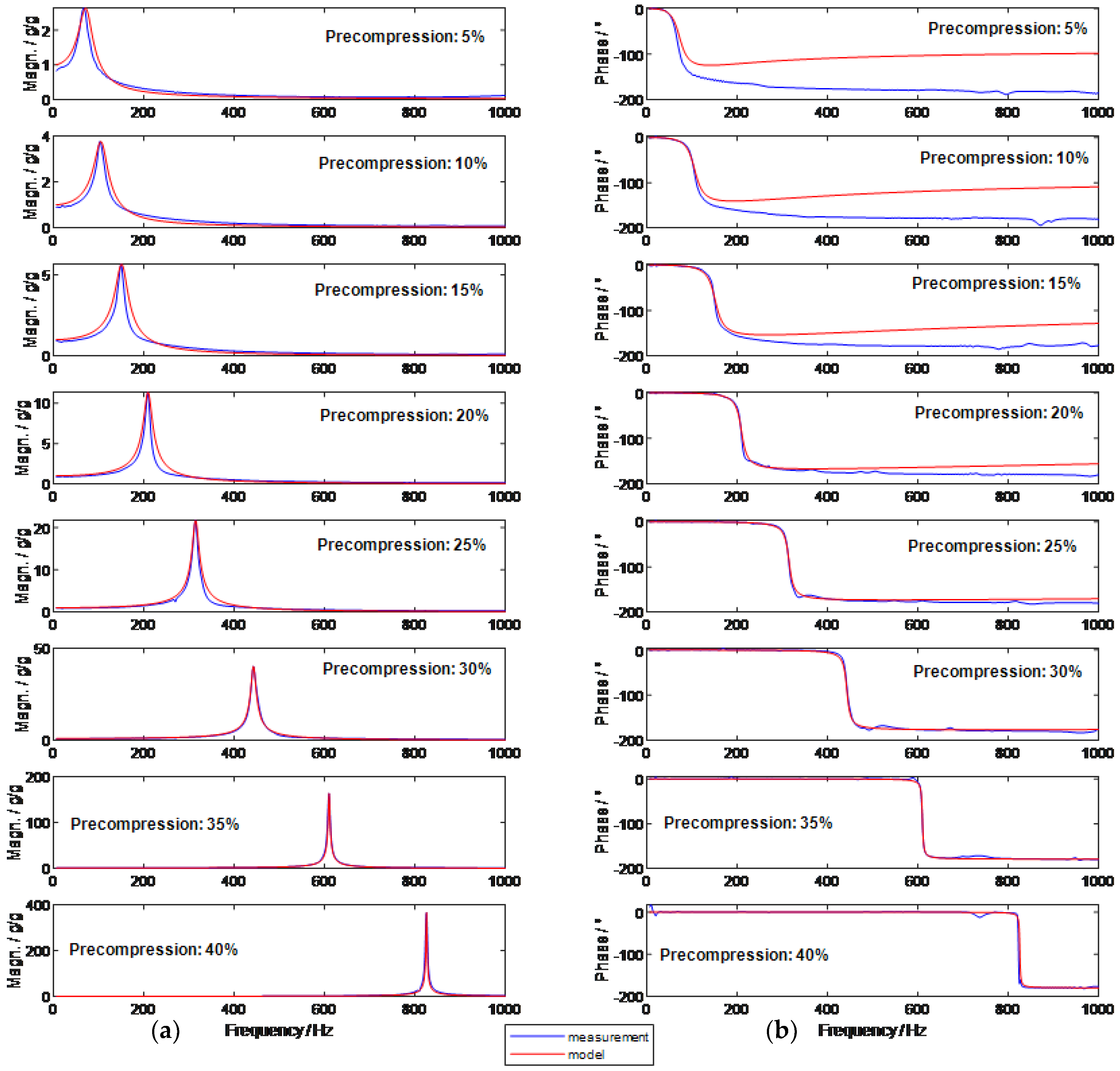
3.1. Effect of Precompression on Resonant Frequency, Stiffness and Damping Ratio
3.2. Effect of Input Amplitude on Resonant Frequency
3.3. Effect of Precompression and Amplitude on Error between Data and Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ormondroyd, J.; Den Hartog, J. The theory of the vibration absorber. Trans. Am. Soc. Mech. Eng. 1928, 49, A9–A22. [Google Scholar]
- Leung, A.Y.T.; Zhang, H.; Cheng, C.C.; Lee, Y.Y. Particle swarm optimization of TMD by non—stationary base excitation during earthquake. Earthq. Eng. Struct. Dyn. 2008, 37, 1223–1246. [Google Scholar] [CrossRef]
- Yurchenko, D. Tuned Mass and Parametric Pendulum Dampers under Seismic Vibrations. In Encyclopedia of Earthquake Engineering; Michael, B., Kougioumtzoglou, I.A., Patelli, E., Ivan Siu-Kui, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–22. [Google Scholar]
- Lopez, R.H.; Miguel, L.F.F.; Beck, A.T. Tuned Mass Dampers for Passive Control of Structures under Earthquake Excitations. In Encyclopedia of Earthquake Engineering; Kougioumtzoglou, I.A., Patelli, E., Beer, M., Siu-Kui, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3814–3823. [Google Scholar]
- Shi, W.; Wang, L.; Lu, Z. Study on self-adjustable tuned mass damper with variable mass. Struct. Control Health Monit. 2018, 25, e2114. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, H.; Wang, H.; Chen, Z. Development of stiffness-adjustable tuned mass dampers for frequency retuning. Adv. Struct. Eng. 2019, 22, 473–485. [Google Scholar] [CrossRef]
- Brennan, M.J. Some Recent Developments in Adaptive Tuned Vibration Absorbers/Neutralisers. Shock Vib. 2006, 13, 531–543. [Google Scholar] [CrossRef]
- Hansmann, J.; Kaal, W.; Seipel, B.; Melz, T. Tuneable Spring Element for an Adaptable Vibration Absorber. Atz Worldw. 2012, 114, 36–39. [Google Scholar] [CrossRef]
- Williams, K.; Chiu, G.; Bernhard, R. Adaptive-Passive Absorbers Using Shape-Memory alloys. J. Sound Vib. 2002, 249, 835–848. [Google Scholar] [CrossRef]
- Deng, H.X.; Gong, X.L.; Wang, L.H. Development of an adaptive tuned vibration absorber with magnetorheological elastomer. Smart Mater. Struct. 2006, 15, N111–N116. [Google Scholar] [CrossRef]
- Sun, S.; Deng, H.; Yang, J.; Li, W.; Du, H.; Alici, G.; Nakano, M. An adaptive tuned vibration absorber based on multilayered MR elastomers. Smart Mater. Struct. 2015, 24, 45045. [Google Scholar] [CrossRef]
- Shin, B.-C.; Yoon, J.-H.; Kim, Y.-K.; Kim, K.-S. Vibration suppression using tunable vibration absorber based on stiffness variable magneto-rheological gel. Rev. Sci. Instrum. 2015, 86, 106106. [Google Scholar] [CrossRef]
- Karsten, R.; Schlaak, H.F. Adaptive absorber based on dielectric elastomer stack actuator with variable stiffness. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 12–15 March 2012; p. 834020. [Google Scholar]
- Heuss, O.; Salloum, R.; Mayer, D.; Melz, T. Tuning of a vibration absorber with shunted piezoelectric transducers. Arch. Appl. Mech. 2016, 86, 1715–1732. [Google Scholar] [CrossRef] [Green Version]
- Tang, N.; Rongong, J.A.; Sims, N.D. Design of adjustable Tuned Mass Dampers using elastomeric O-rings. J. Sound Vib. 2018, 433, 334–348. [Google Scholar] [CrossRef] [Green Version]
- Carrascal, I.A.; Pérez, A.; Casado, J.A.; Diego, S.; Polanco, J.A.; Ferreño, D.; Martín, J.J. Experimental study of metal cushion pads for high speed railways. Constr. Build. Mater. 2018, 182, 273–283. [Google Scholar] [CrossRef]
- Pérez, A.; Ferreño, D.; Carrascal, I.A.; Polanco, J.A.; Casado, J.A.; Diego, S. Metal cushion dampers for railway applications: A review. Constr. Build. Mater. 2020, 238, 117711. [Google Scholar] [CrossRef]
- Wang, H.; Rongong, J.A.; Tomlinson, G.R.; Hong, J. Nonlinear Static and Dynamic Properties of Metal Rubber Dampers. Proc. ISMA 2010, 10, 1301–1315. [Google Scholar]
- Chandrasekhar, K.; Rongong, J.A.; Cross, E.J. Frequency and amplitude dependent behaviour of tangled metal wire dampers. In Proceedings of the International Conference on Noise and Vibration Engineering and International Conference on Uncertainty in Structural Dynamics, Heverlee, Belgium, 15–17 September 2014; pp. 559–572. [Google Scholar]
- Chandrasekhar, K.; Rongong, J.; Cross, E. Mechanical behaviour of tangled metal wire devices. Mech. Syst. Signal Process. 2019, 118, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.Z.; Hu, S.Y.; Zou, G.P. Research on Vibration Characteristic of Metal Rubber by Wire Mesh. AMM 2014, 633–634, 242–245. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, L.; Bai, H.; Lu, C.; Li, S. Mechanical Behavior of Entangled Metallic Wire Materials under Quasi-Static and Impact Loading. Materials 2019, 12, 3392. [Google Scholar] [CrossRef] [Green Version]
- Xue, X.; Ruan, S.; Bai, H.; Chen, X.; Shao, Y.; Lu, C. An enhanced constitutive model for the nonlinear mechanical behavior of the elastic-porous metal rubber. Mech. Mater. 2020, 148, 103447. [Google Scholar] [CrossRef]
- Hong, J.; Chen, L.; Ma, Y.; Tomlinson, G.R.; Rongong, J.A. Hysteretic properties of metal rubber particles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 693–702. [Google Scholar] [CrossRef]
- Tang, N.; Rongong, J.A. Feasibility study on the use of tangled metal wire particles as the adjustable elements in tuned mass dampers. J. Sound Vib. 2019, 457, 1–14. [Google Scholar] [CrossRef]
- Hou, J.F.; Bai, H.B.; Li, D.W. Damping capacity measurement of elastic porous wire-mesh material in wide temperature range. J. Mater. Process. Technol. 2008, 206, 412–418. [Google Scholar] [CrossRef]
- Ding, Z.; Bai, H.; Wu, Y.; Ren, Z.; Shao, Y. A Constitutive Model of Plate-Like Entangled Metallic Wire Material in Wide Temperature Range. Materials 2019, 12, 2538. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuyan, L.; Xieqing, H.; Wenxiong, M. A Theoretical Model and Experimental Investigation of a Nonlinear Constitutive Equation for Elastic Porous Metal Rubbers. Mech. Compos. Mater. 2005, 41, 303–312. [Google Scholar] [CrossRef]
- Markert, R. Strukturdynamik; Shaker-Verlag: Aachen, Germany, 2013. [Google Scholar]


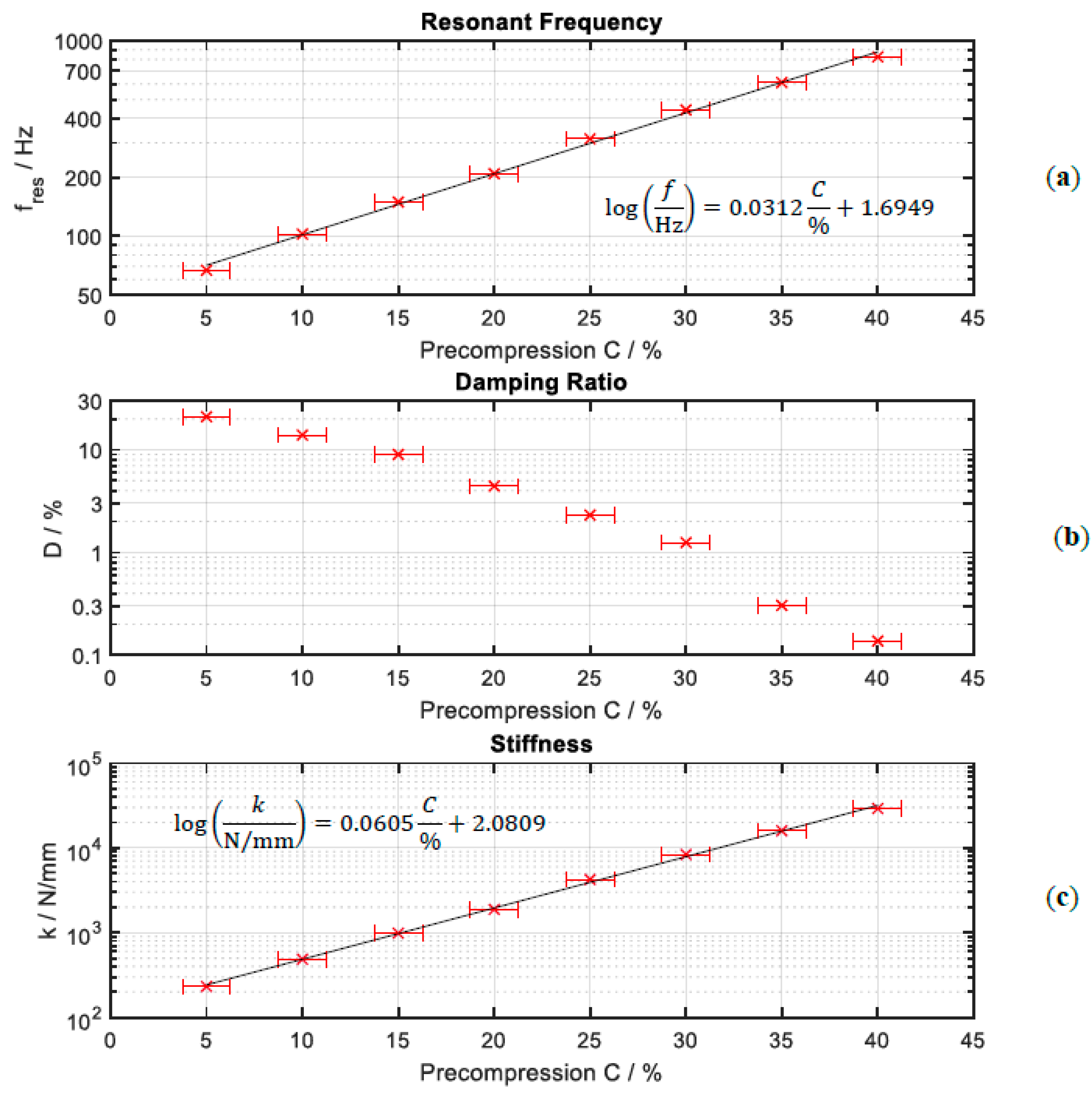
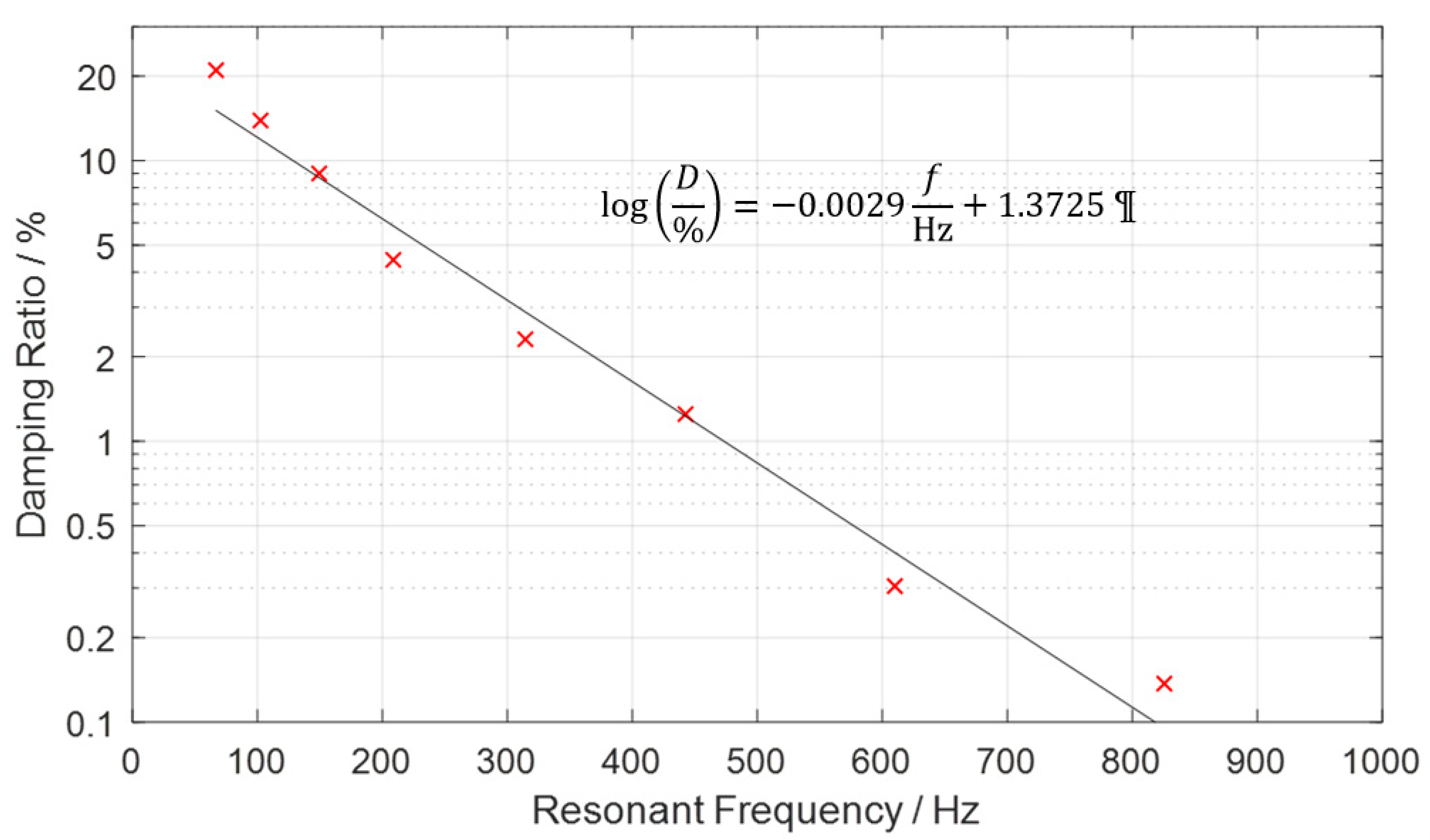
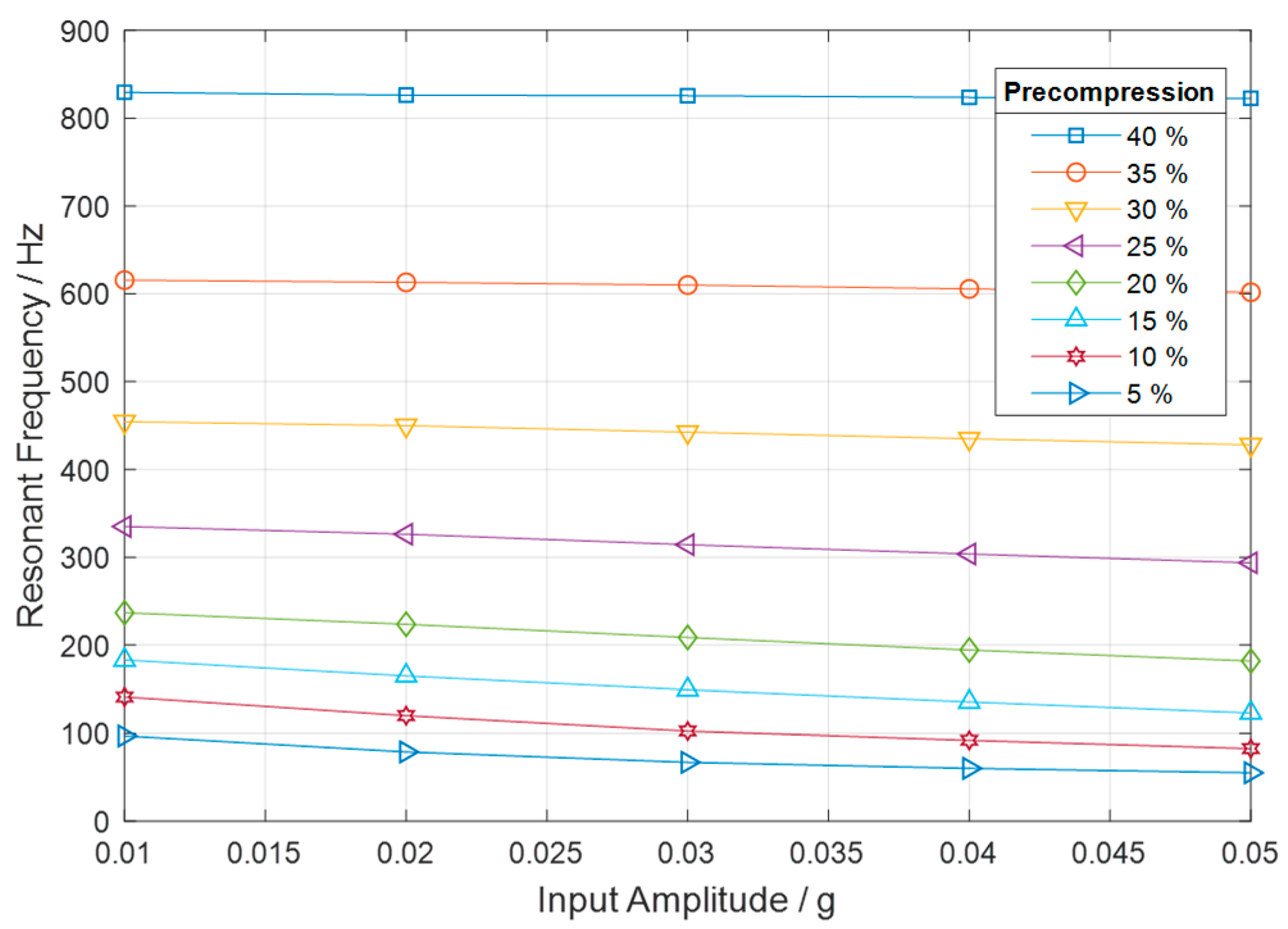
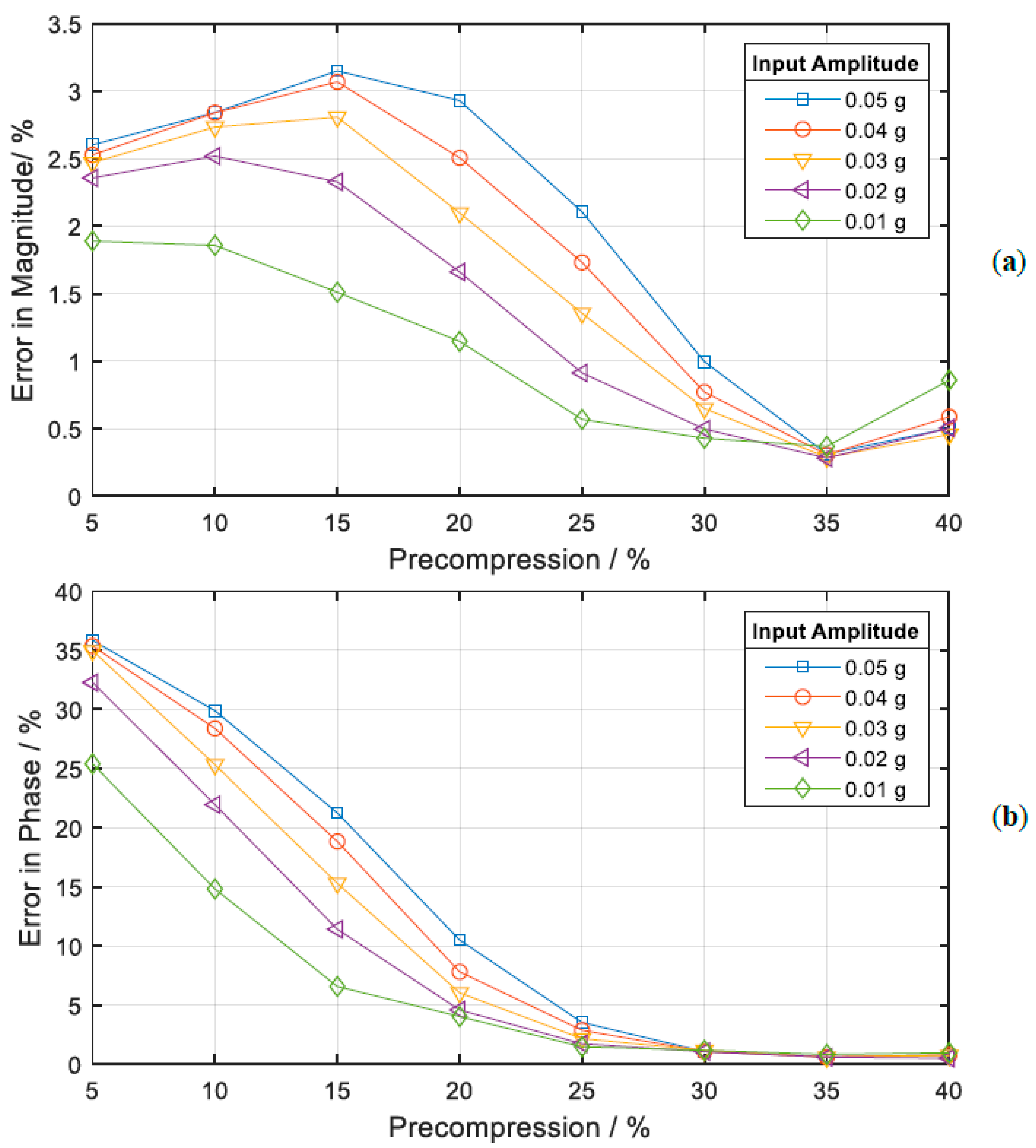
| Parameter | Value | Unit |
|---|---|---|
| Outer diameter | 40 | mm |
| Inner diameter | 15 | mm |
| Height | 20 | mm |
| Mass | 32 | g |
| Relative density | 19 | % |
| % | Hz | − | kg | N/mm | Ns/m | % | % | % |
|---|---|---|---|---|---|---|---|---|
| 5 | 66.9 | 2.62 | 1.082 | 232 | 210 | 21.0 | 2.47 | 33.6 |
| 10 | 102.5 | 3.76 | 1.082 | 486 | 202 | 13.9 | 2.73 | 23.8 |
| 15 | 149.4 | 5.66 | 1.082 | 985 | 186 | 9.0 | 2.81 | 15.0 |
| 20 | 208.8 | 11.3 | 1.082 | 1880 | 126 | 4.4 | 2.10 | 5.97 |
| 25 | 314.4 | 21.7 | 1.082 | 4230 | 98.8 | 2.3 | 1.35 | 2.17 |
| 30 | 442.5 | 40.2 | 1.082 | 8370 | 74.9 | 1.25 | 0.65 | 1.17 |
| 35 | 610.0 | 163.7 | 1.082 | 15900 | 25.3 | 0.31 | 0.29 | 0.60 |
| 40 | 825.6 | 365.8 | 1.082 | 29100 | 15.3 | 0.14 | 0.46 | 0.80 |
| Bandwidth | 758.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rieß, S.; Kaal, W.; Herath, K. Frequency-Adaptable Tuned Mass Damper Using Metal Cushions. Vibration 2021, 4, 77-90. https://doi.org/10.3390/vibration4010007
Rieß S, Kaal W, Herath K. Frequency-Adaptable Tuned Mass Damper Using Metal Cushions. Vibration. 2021; 4(1):77-90. https://doi.org/10.3390/vibration4010007
Chicago/Turabian StyleRieß, Sebastian, William Kaal, and Kristian Herath. 2021. "Frequency-Adaptable Tuned Mass Damper Using Metal Cushions" Vibration 4, no. 1: 77-90. https://doi.org/10.3390/vibration4010007
APA StyleRieß, S., Kaal, W., & Herath, K. (2021). Frequency-Adaptable Tuned Mass Damper Using Metal Cushions. Vibration, 4(1), 77-90. https://doi.org/10.3390/vibration4010007





