An Experimental Approach for the Determination of the Mechanical Properties of Base-Excited Polymeric Specimens at Higher Frequency Modes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
2.2. Experimental Apparatus and Procedure
2.3. Beam Vibrations
2.3.1. Euler–Bernoulli Beam Theory
2.3.2. Timoshenko Beam Theory
3. Results and Discussion
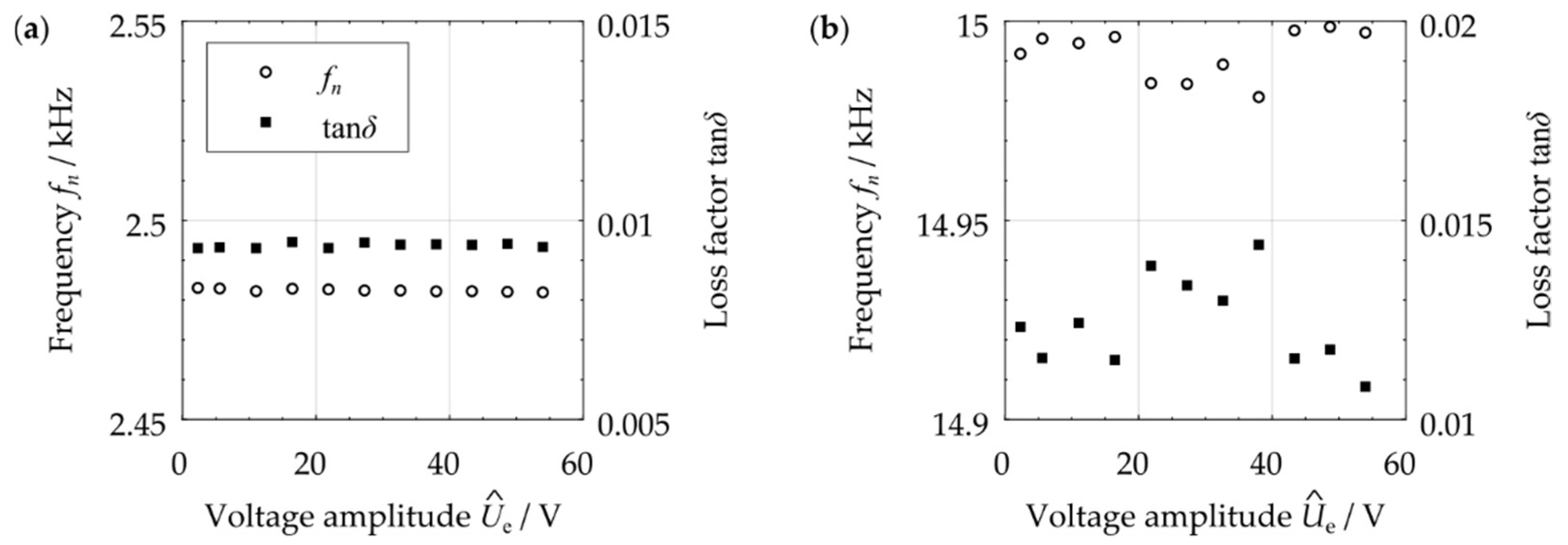
3.1. Influence of Applied Base Excitation of Beam’s Vibration Behavior
3.2. Influence of Specimen’s Tension Torque
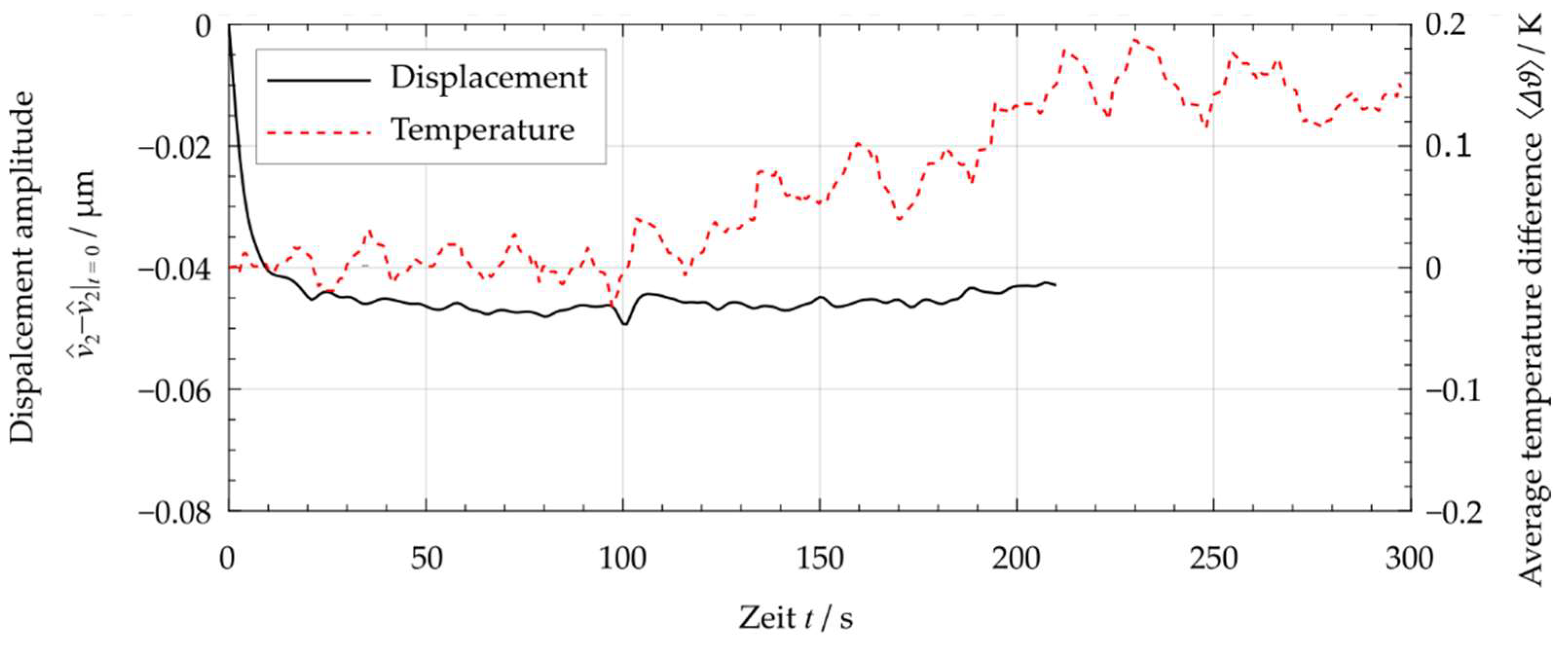
3.3. Thermal Behavior during Excitation
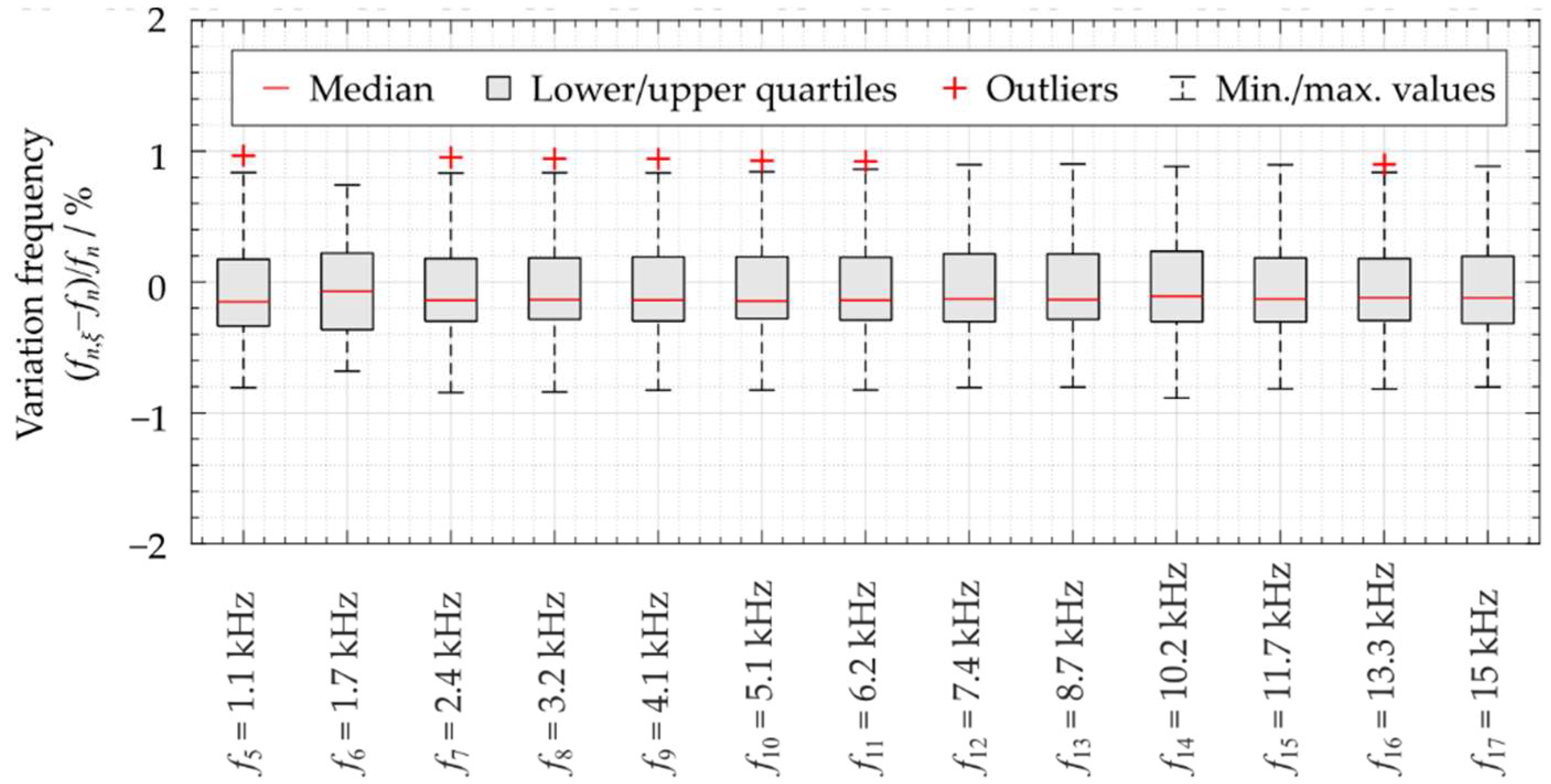
3.4. Resulting Velocity Amplitudes and Resonance Frequencies
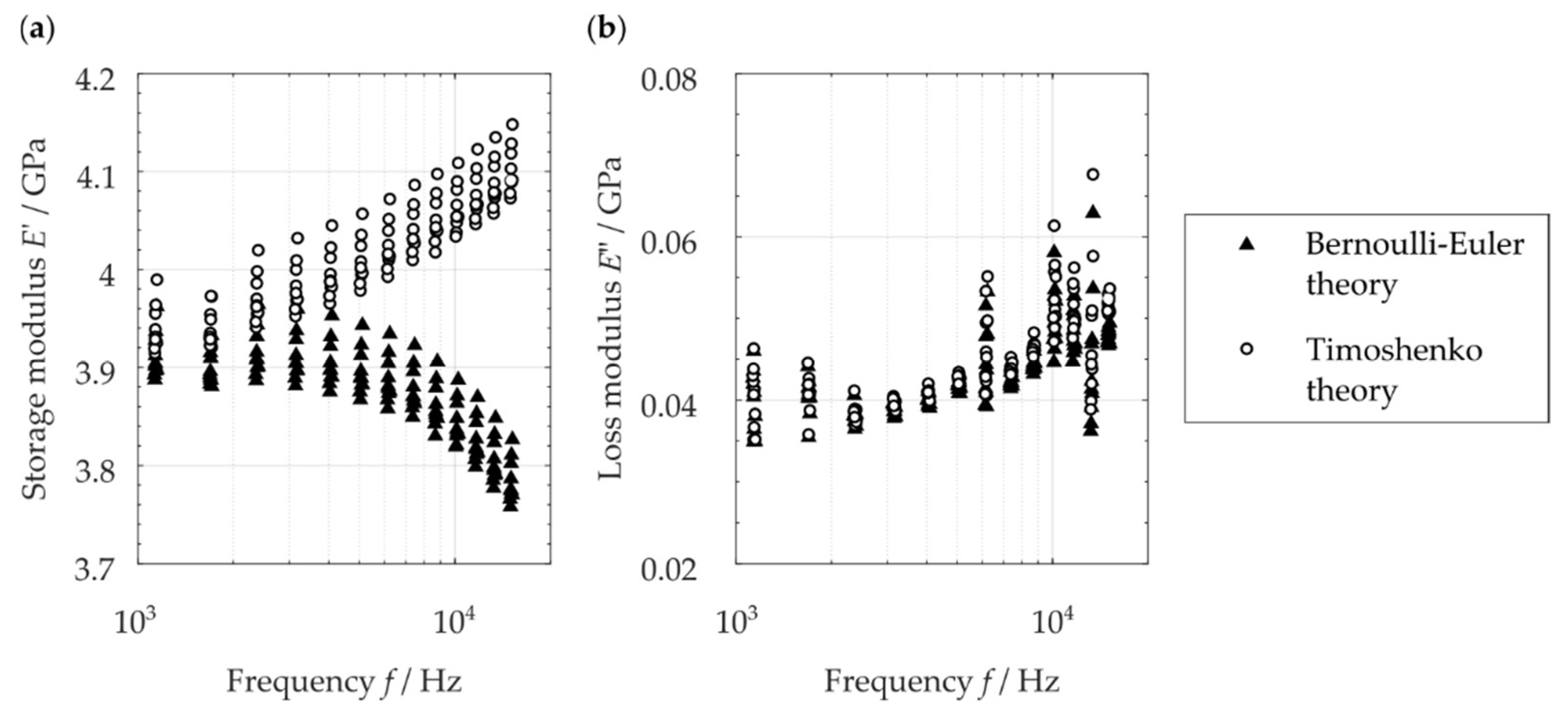
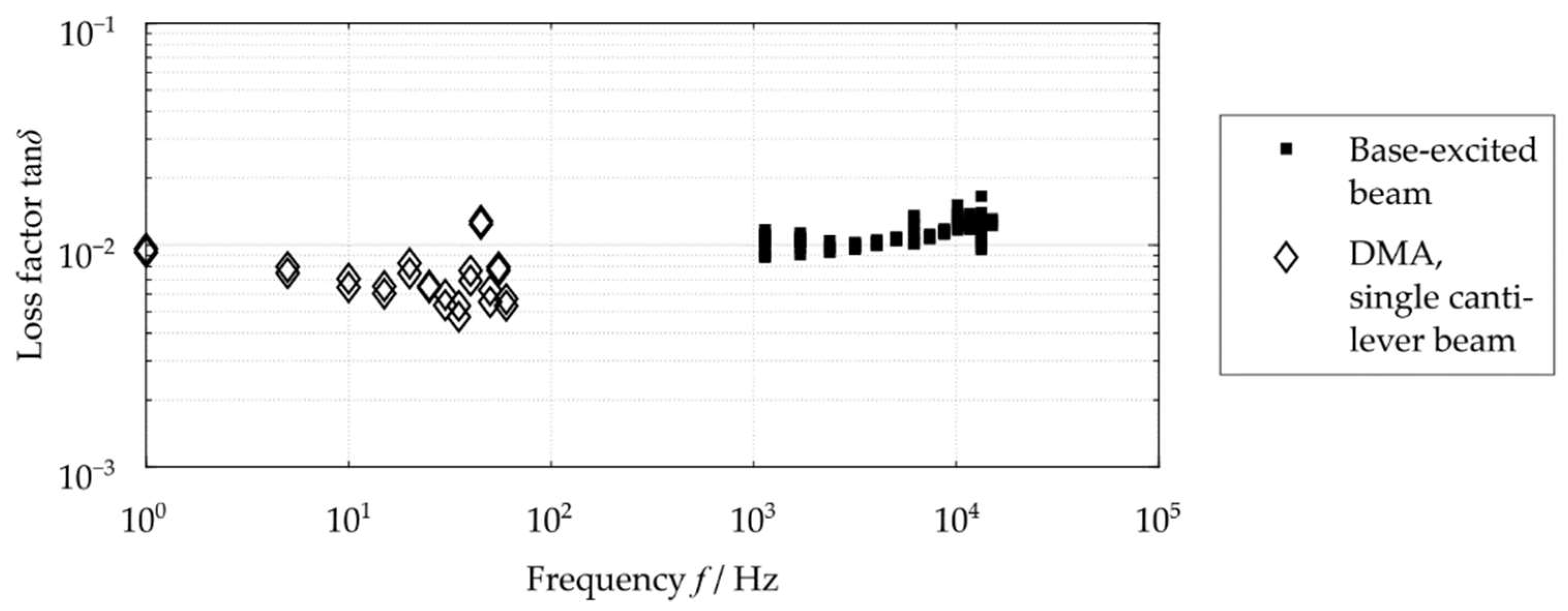
3.5. Dynamic Mechanical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Menard, K.P.; Menard, N.R. Dynamic Mechanical Analysis; CRC Press: Boca Raton, FL, USA, 2020; ISBN 9780429190308. [Google Scholar]
- Kostka, P.; Holeczek, K.; Höhne, R.; Filippatos, A.; Modler, N. Extension and application of dynamic mechanical analysis for the estimation of spatial distribution of material properties. Polym. Test. 2016, 52, 184–191. [Google Scholar] [CrossRef]
- Sessner, V.; Liebig, W.V.; Jackstadt, A.; Schmid, D.; Ehrig, T.; Holeczek, K.; Gräbner, N.; Kostka, P.; von Wagner, U.; Weidenmann, K.A.; et al. Wide Scale Characterization and Modeling of the Vibration and Damping Behavior of CFRP-Elastomer-Metal Laminates—Comparison and Discussion of Different Test Setups. Appl. Compos. Mater. 2021, 28, 1715–1746. [Google Scholar] [CrossRef]
- Read, B.E.; Dean, G.D. The Determination of Dynamic Properties of Polymers and Composites; Wiley: Hoboken, NJ, USA, 1978; ISBN 0-470-26543-4. [Google Scholar]
- Hufenbach, W.; Böhm, R.; Langkamp, A.; Kroll, L.; Ritschel, T. Ultrasonic evaluation of anisotropic damage in multiaxially textile-reinforced thermoplastic composites made from hybrid yarns. Mech. Compos. Mater. 2006, 42, 151–162. [Google Scholar] [CrossRef]
- Almaraz, G.M.D.; Martínez, A.G.; Sánchez, R.H.; Gómez, E.C.; Tapia, M.G.; Juárez, J.C.V. Ultrasonic Fatigue Testing on the Polymeric Material PMMA, Used in Odontology Applications. Proced. Struct. Integ. 2017, 3, 562–570. [Google Scholar] [CrossRef]
- Backe, D.; Balle, F.; Eifler, D. Fatigue testing of CFRP in the Very High Cycle Fatigue (VHCF) regime at ultrasonic frequencies. Compos. Sci. Technol. 2015, 106, 93–99. [Google Scholar] [CrossRef]
- Almaraz, G.M.D.; Gómez, E.C.; Juárez, J.C.V.; Ambriz, J.L. Crack initiation and propagation on the polymeric material ABS (Acrylonitrile Butadiene Styrene), under ultrasonic fatigue testing. Frat. Ed Integrità Strutt. 2015, 34, 498–506. [Google Scholar] [CrossRef]
- Mignogna, R.B.; Green, R.E.; Duke, J.C.; Henneke, E.G.; Reifsnider, K.L. Thermographic investigation of high-power ultrasonic heating in materials. Ultrasonics 1981, 19, 159–163. [Google Scholar] [CrossRef]
- B, V.; Jade, N.; Bhirodkar, S. Measurement of damping properties of beeswax and cosmetic wax using Oberst beam method. Vibroeng. Procedia 2019, 29, 54–59. [Google Scholar] [CrossRef]
- Ozer, M.S.; Koruk, H.; Sanliturk, K.Y. Testing non-magnetic materials using Oberst Beam Method utilising electromagnetic excitation. J. Sound. Vib. 2019, 456, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Dannemann, M.; Holeczek, K.; Leimert, J.; Friebe, S.; Modler, N. Adapted measuring sequence for the determination of directional-dependent dynamic material properties using a bending resonance method. Polym. Test. 2019, 79, 1–10. [Google Scholar] [CrossRef]
- Katunin, A. Evaluation of Criticality of Self-Heating of Polymer Composites by Estimating the Heat Dissipation Rate. Mech. Compos. Mater. 2018, 54, 53–60. [Google Scholar] [CrossRef]
- Katunin, A.; Pawlak, S.; Wronkowicz, A. Evaluation of Structural Degradation of Polymeric Composites Subjected to Self-Heating by the Thermal Diffusivity Analysis. Arab J. Sci. Eng. 2018, 43, 4541–4547. [Google Scholar] [CrossRef] [Green Version]
- Boccardi, S.; Carlomagno, G.M.; Meola, C.; Russo, P.; Simeoli, G. Evaluation of polypropylene based composites from thermal effects developing under cyclic bending tests. Compos. Struct. 2017, 182, 628–635. [Google Scholar] [CrossRef]
- Ledi, K.S.; Hamdaoui, M.; Robin, G.; Daya, E.M. An identification method for frequency dependent material properties of viscoelastic sandwich structures. J. Sound. Vib. 2018, 428, 13–25. [Google Scholar] [CrossRef]
- Liao, Y.; Wells, V. Estimation of complex Young’s modulus of non-stiff materials using a modified Oberst beam technique. J. Sound Vib. 2008, 316, 87–100. [Google Scholar] [CrossRef]
- Wojtowicki, J.-L.; Jaouen, L.; Panneton, R. New approach for the measurement of damping properties of materials using the Oberst beam. Rev. Sci. Instrum. 2004, 75, 2569–2574. [Google Scholar] [CrossRef] [Green Version]
- Kucher, M. Hochfrequent beanspruchte Polymerstrukturen für den Einsatz als endodontische Instrumente. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2022. [Google Scholar]
- Curtis, D.C.; Moore, D.R.; Slater, B.; Zahlan, N. Fatigue testing of multi-angle laminates of CF/PEEK. Composites 1988, 19, 446–452. [Google Scholar] [CrossRef]
- Kenny, J.M.; Marchetti, M. Elasto-plastic behavior of thermoplastic composite laminates under cyclic loading. Compos. Struct. 1995, 32, 375–382. [Google Scholar] [CrossRef]
- Leveuf, L.; Marco, Y.; Le Saux, V.; Navrátil, L.; Leclercq, S.; Olhagaray, J. Fast screening of the fatigue properties of thermoplastics reinforced with short carbon fibers based on thermal measurements. Polym. Test. 2018, 68, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N. Load history and sequence effects on cyclic deformation and fatigue behavior of a thermoplastic polymer. Polym. Test. 2016, 56, 99–109. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N. Mean strain effects on cyclic deformation and fatigue behavior of polyether ether ketone (PEEK). Polym. Test. 2016, 55, 69–77. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N.; Moser, R.D. Cyclic deformation and fatigue behavior of polyether ether ketone (PEEK). Int. J. Fatigue 2016, 82, 411–427. [Google Scholar] [CrossRef]
- Simsiriwong, J.; Shrestha, R.; Shamsaei, N.; Lugo, M.; Moser, R.D. Effects of microstructural inclusions on fatigue life of polyether ether ketone (PEEK). J. Mech. Behav. Biomed. Mater. 2015, 51, 388–397. [Google Scholar] [CrossRef] [PubMed]
- Abbasnezhad, N.; Khavandi, A.; Fitoussi, J.; Arabi, H.; Shirinbayan, M.; Tcharkhtchi, A. Influence of loading conditions on the overall mechanical behavior of polyether-ether-ketone (PEEK). Int. J. Fatigue 2018, 109, 83–92. [Google Scholar] [CrossRef]
- Röchling Sustaplast. Technical Data Sheet—SustaPEEK. Available online: https://www.roechling.com/de/industrial/werkstoffe/thermoplastische-kunststoffe/showpdf?selectedUid=1756&slang=0&cHash=2150716fb11be797f9bddb6b83e018a4 (accessed on 10 June 2021).
- Lakes, R. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780511626722. [Google Scholar]
- Dresig, H.; Holzweißig, F.; Rockhausen, L. Maschinendynamik. Symposium Universität-GH- Essen, 26–28 June 1984; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-16010-3. [Google Scholar]
- Möser, M.; Kropp, W.; Cremer, L.; Heckl, M. Körperschall. Physikalische Grundlagen und Technische Anwendungen (German Edition); Springer: Dordrecht, The Netherlands, 2009; ISBN 978-3-540-49048-7. [Google Scholar]
- Magnus, K.; Popp, K.; Sextro, W. Kontinuumsschwingungen. In Schwingungen; Magnus, K., Popp, K., Sextro, W., Eds.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2016; pp. 269–309. [Google Scholar]
- Wauer, J. Kontinuumsschwingungen. Vom Einfachen Strukturmodell Zum Komplexen Mehrfeldsystem, Mit 74 Aufgaben und 41 Beispielen; Vieweg+Teubner: Wiesbaden, Germany, 2008. [Google Scholar]
- Kaneko, T. On Timoshenko’s correction for shear in vibrating beams. J. Phys. D Appl. Phys. 1975, 8, 1927–1936. [Google Scholar] [CrossRef]
- Baur, E.; Brinkmann, S.; Osswald, T.A.; Schmachtenberg, E.; Saechtling, H. Saechtling Kunststoff Taschenbuch; Hanser: München, Germany, 2007; ISBN 978-3-446-40352-9. [Google Scholar]




| Parameter 1 | Used Value/Description |
|---|---|
| General settings | |
| From 2.3 V to 54 V | |
| Investigated frequency range | From 1 kHz to 16 kHz |
| Scanning laser vibrometer (SLV) | |
| One-point laser vibrometer (OLV) | |
| From 0.5 Nm to 1.7 Nm | |
| Linear sweep | |
| Measuring time | 12.8 s |
| 1 kHz to 16 kHz | |
| Sampling frequency | 128 kHz |
| Signal filter | No filter |
| Window function | Rectangular window |
| Data collection mode | Fast Fourier transform (FFT) |
| Determination of natural bending vibration modes | |
| Harmonic mono-frequency excitation, Equation (1) | |
| Measuring time | 0.512 s |
| Resonant excitation | |
| Sampling frequency | 128 kHz |
| Signal filter | No filter |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kucher, M.; Dannemann, M.; Böhm, R.; Modler, N. An Experimental Approach for the Determination of the Mechanical Properties of Base-Excited Polymeric Specimens at Higher Frequency Modes. Vibration 2022, 5, 429-441. https://doi.org/10.3390/vibration5030024
Kucher M, Dannemann M, Böhm R, Modler N. An Experimental Approach for the Determination of the Mechanical Properties of Base-Excited Polymeric Specimens at Higher Frequency Modes. Vibration. 2022; 5(3):429-441. https://doi.org/10.3390/vibration5030024
Chicago/Turabian StyleKucher, Michael, Martin Dannemann, Robert Böhm, and Niels Modler. 2022. "An Experimental Approach for the Determination of the Mechanical Properties of Base-Excited Polymeric Specimens at Higher Frequency Modes" Vibration 5, no. 3: 429-441. https://doi.org/10.3390/vibration5030024
APA StyleKucher, M., Dannemann, M., Böhm, R., & Modler, N. (2022). An Experimental Approach for the Determination of the Mechanical Properties of Base-Excited Polymeric Specimens at Higher Frequency Modes. Vibration, 5(3), 429-441. https://doi.org/10.3390/vibration5030024








