Vibrational Effects on the Acoustic Performance of Multi-Layered Micro-Perforated Metamaterials
Abstract
:1. Introduction
2. Methods
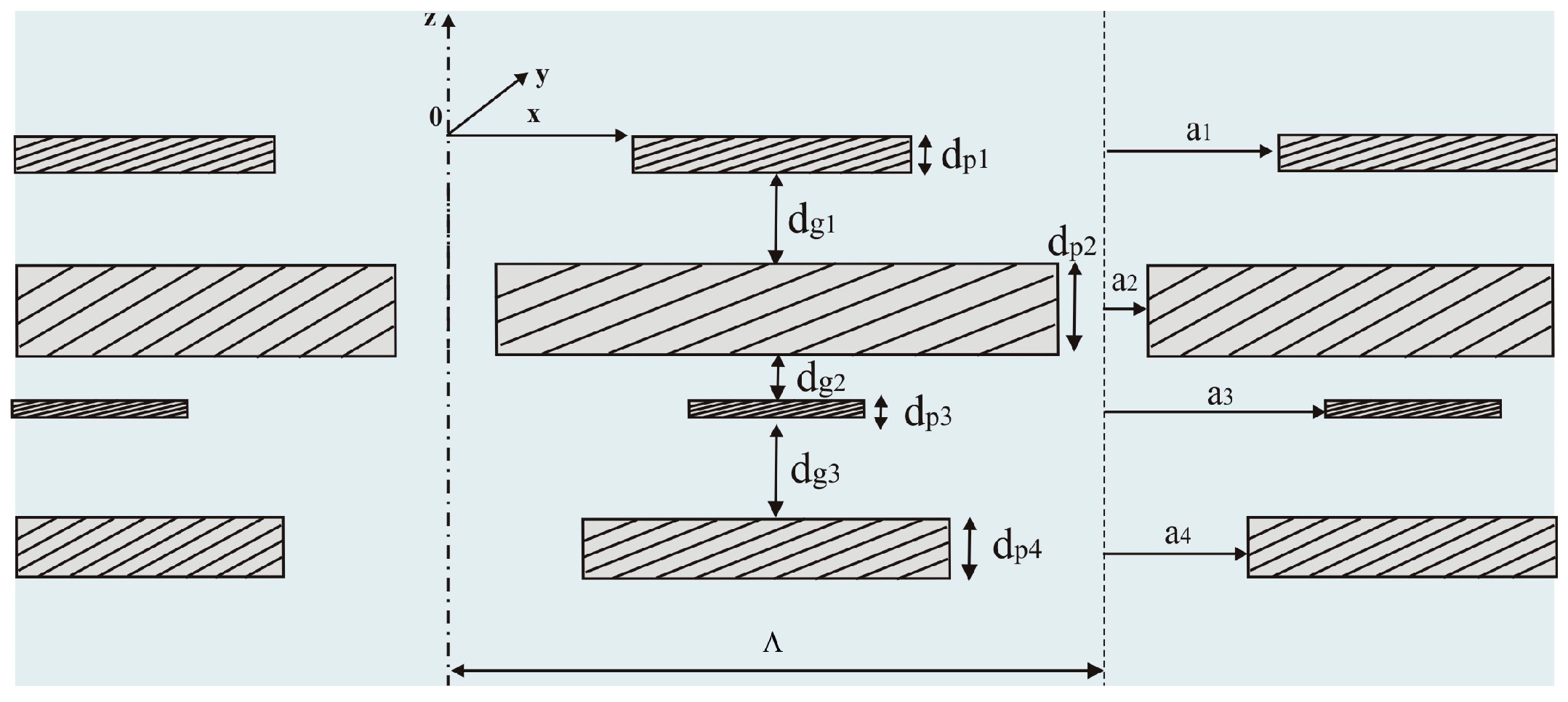
2.1. Impedance Translation Method
2.2. Scattering Matrix Formulation
3. Acoustic Performance of Multi-Layered Identical MPPs
3.1. The Acoustic Fishnet Performance
3.2. Influence of the MPP Vibrations on the Acoustic Fishnet Performance
4. Acoustic Performance of Multi-Layered Functionally Graded (M)PPs
4.1. Broadband Optimization of FGPs
4.2. Vibrational Effects on the Broadband Optimization of FGPs
4.3. Critical Coupling Analysis
4.3.1. Optimization of Rigid FGPs
4.3.2. Optimization of FGPs with Elastic Limp Membranes
4.3.3. Optimization of FGPs with Thin Resonant Vibrating Panels
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gardonio, P. Review of Active Techniques for Aerospace Vibro-Acoustic Control. J. Aircr. 2002, 39, 206–214. [Google Scholar] [CrossRef]
- Sadeghian, M.; Bandpy, M.G. Technologies for Aircraft Noise Reduction: Review Paper. J. Aeronaut. Aerospace Eng. 2020, 9, 218. [Google Scholar]
- Giesecke, D.; Lehmler, M.; Friedrichs, J.; Blinstrub, J.; Bertsch, L.; Heinze, W. Evaluation of ultra-high bypass ratio engines for an over-wing aircraft configuration. J. Glob. Power Propuls. Soc. 2018, 2, 493–515. [Google Scholar] [CrossRef]
- Oettle, N.; Sims-Williams, D. Automotive aeroacoustics: An overview. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2017, 231, 1177–1189. [Google Scholar] [CrossRef]
- Christensen, J.; Martinez-Moreno, L.; Garcia-Vidal, F.J. All-angle blockage of sound by an acoustic double-fishnet metamaterial. Appl. Phys. Lett. 2010, 97, 134106. [Google Scholar] [CrossRef]
- Bell, J.S.; Summers, I.R.; Murray, A.R.J.; Hendry, E.; Sambles, J.R.; Hibbins, A.P. Low acoustic transmittance through a holey structure. Phys. Rev. B 2012, 85, 214305. [Google Scholar] [CrossRef]
- Akozbek, N.; Mattiucci, N.; Bloemer, M.J.; Sanghadasa, M.; D’Aguanno, G. Manipulating the extraordinary acoustic transmission through metamaterial-based acoustic band gap structures. Appl. Phys. Lett. 2014, 104, 161906. [Google Scholar] [CrossRef]
- Fan, L.; Chen, Z.; Zhang, S.Y.; Ding, J.; Li, X.J.; Zhang, H. An acoustic metamaterial composed of multi-layer membrane-coated perforated plates for low-frequency sound insulation. Appl. Phys. Lett. 2015, 106, 151908. [Google Scholar] [CrossRef]
- Romero-García, V.; Theocharis, G.; Richoux, O.; Pagneux, V. Use of complex frequency plane to design broadband and sub-wavelength absorbers. J. Acoust. Soc. Am. 2016, 139, 3395–3403. [Google Scholar] [CrossRef]
- Romero-García, V.; Jiménez, N.; Theocharis, G.; Achilleos, V.; Merkel, A.; Richoux, O.; Tournat, V.; Groby, J.-P.; Pagneux, V. Design of acoustic metamaterials made of Helmholtz resonators for perfect absorption by using the complex frequency plane. Comptes Rendus Phys. 2020, 21, 713–749. [Google Scholar] [CrossRef]
- Jiménez, N.; Romero-García, V.; Cebrecos, A.; Picó, R.; Sánchez Morcillos, V.J.; García-Raffi, L.M. Broadband quasi perfect absorption using chirped multi-layer porous materials. AIP Adv. 2016, 6, 121605. [Google Scholar] [CrossRef]
- Yang, M.; Chen, S.; Fu, C.; Sheng, P. Optimal sound-absorbing structures. Mater. Horiz. 2017, 4, 673–680. [Google Scholar] [CrossRef]
- Bravo, T.; Maury, C. Causally-guided acoustic optimization of rigidly-backed micro-perforated partitions: Case studies and experiments. J. Sound Vib. 2022, 523, 116735. [Google Scholar] [CrossRef]
- Takahashi, D.; Tanaka, M. Flexural vibrations of perforated plates and porous elastic materials under acoustic loading. J. Acoust. Soc. Am. 2002, 112, 1456–1464. [Google Scholar] [CrossRef] [PubMed]
- Toyoda, M.; Tanaka, M.; Takahashi, D. Reduction of acoustic radiation by perforated board and honeycomb layer systems. Appl. Acoust. 2007, 68, 71–85. [Google Scholar] [CrossRef]
- Toyoda, M.; Mu, R.L.; Takahashi, D. Relationship between Helmholtz-resonance absorption and panel-type absorption in finite flexible microperforated-panel absorbers. Appl. Acoust. 2010, 71, 315–320. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, E.W.M.; Ng, C.F. Sound absorption of a finite flexible micro-perforated panel backed by an air cavity. J. Sound Vib. 2005, 287, 227–243. [Google Scholar] [CrossRef]
- Bravo, T.; Maury, C.; Pinhede, C. Enhancing sound absorption and transmission through flexible multi-layer micro-perforated structures. J. Acoust. Soc. Am. 2013, 134, 3363–3373. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.Y.; Lee, E.W.M. Widening the sound absorption bandwidths of flexible micro-perforated curved absorbers using structural and acoustic resonances. Int. J. Mech. Sci. 2007, 49, 925–934. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.F.; Sheng, Z.H.; Zhu, Z.Y.; Li, G.F.; Ni, J.F. Analysis of the sound absorption characteristics of the curved microperforated panel with elastically restrained edges. Thin. Walled Struct. 2023, 182, 110147. [Google Scholar] [CrossRef]
- Bolton, J.S. The effect of flexibility on the acoustical performance of microperforated materials (A). J. Acoust. Soc. Am. 2012, 132, 1887. [Google Scholar] [CrossRef]
- Tournadre, J.; Temiz, M.A.; Martınez-Lera, P.; De Roeck, W.; Desmet, W. Vibro-acoustic response of flexible Micro-Perforated Plates: Impact of the boundary condition at the perforation walls. In Proceedings of the ISMA 2019, Leuven, Belgium, 19–20 September 2019. [Google Scholar]
- Ren, S.W.; Van Belle, L.; Claeys, C.; Xin, F.X.; Lu, T.J.; Deckers, E.; Desmet, W. Improvement of the sound absorption of flexible micro-perforated panels by local resonances. Mech. Syst. Signal Process. 2019, 117, 138–156. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J.L. Acoustic properties of multilayer sound absorbers with a 3D printed micro-perforated panel. Appl. Acoust. 2017, 121, 25–32. [Google Scholar] [CrossRef]
- Bucciarelli, F.; Malfense Fierro, G.P.; Meo, M. A multilayer microperforated panel prototype for broadband sound absorption at low frequencies. Appl. Acoust. 2019, 146, 134–144. [Google Scholar] [CrossRef]
- Yang, W.; Bai, X.; Zhu, W.; Kiran, R.; An, J.; Chua, C.K.; Zhou, K. 3D Printing of Polymeric Multi-Layer Micro-Perforated Panels for Tunable Wideband Sound Absorption. Polymers 2020, 12, 360. [Google Scholar] [CrossRef]
- Quian, Y.J.; Kong, D.Y.; Liu, Y.; Liu, S.M.; Li, Z.B.; Shao, D.S.; Sun, S.M. Improvement of sound absorption characteristics under low frequency for micro-perforated panel absorbers using super-aligned carbon nanotube arrays. Appl. Acoust. 2014, 82, 23–27. [Google Scholar] [CrossRef]
- Singh, S.K.; Prakash, O.; Bhattacharya, S. Hybrid fractal acoustic metamaterials for low-frequency sound absorber based on cross mixed micro-perforated panel mounted over the fractals structure cavity. Sci. Rep. 2022, 12, 20444. [Google Scholar] [CrossRef]
- Duan, H.; Shen, X.; Wang, E.; Yang, F.; Zhang, X.; Yin, Q. Acoustic multi-layer Helmholtz resonance metamaterials with multiple adjustable absorption peaks. Appl. Phys. Lett. 2021, 118, 241904. [Google Scholar] [CrossRef]
- Kim, H.; Ma, P.S.; Kim, B.K.; Kim, S.R.; Lee, S.H. Low-frequency sound absorption of elastic micro-perforated plates in a parallel arrangement. J. Sound Vib. 2019, 460, 114884. [Google Scholar] [CrossRef]
- Gallerand, L.; Legrand, M.; Dupont, T.; Leclaire, P. Vibration and damping analysis of a thin finite-size microperforated plate. J. Sound Vib. 2022, 541, 117295. [Google Scholar] [CrossRef]
- Lee, F.-C.; Chen, W.-H. Acoustic transmission analysis of multi-layer absorbers. J. Sound Vib. 2001, 248, 621–634. [Google Scholar] [CrossRef]
- Asdrubali, F.; Pispola, G. Properties of transparent sound-absorbing panels for use in noise barriers. J. Acoust. Soc. Am. 2007, 121, 214–221. [Google Scholar] [CrossRef]
- Mechel, P.; Ver, I.L. Sound-absorbing materials and sound absorbers. In Noise and Vibration Control Engineering: Principles and Applications; Beranek, L.L., Vér, I.L., Eds.; Wiley and Sons: New York, NY, USA, 1992; Chapter 8. [Google Scholar]
- Maa, D.Y. Potential of microperforated panel absorber. J. Acoust. Soc. Am. 1998, 104, 2861–2866. [Google Scholar] [CrossRef]
- Melling, T.H. The acoustic impedance of perforates at medium and high sound pressure levels. J. Sound Vib. 1973, 29, 1–65. [Google Scholar] [CrossRef]
- Åbom, M. Measurement of the scattering-matrix of acoustical two-ports. Mech. Syst. Signal Process. 1991, 5, 89–104. [Google Scholar] [CrossRef]
- Maury, C.; Bravo, T. Enhanced modal matching method for macro- and micro-perforated plates. J. Sound Vib. 2021, 500, 116042. [Google Scholar] [CrossRef]
- Li, C.; Cazzolato, B.; Zander, A. Acoustic impedance of micro perforated membranes: Velocity continuity condition at the perforation boundary. J. Acoust. Soc. Am. 2016, 139, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Dupont, T.; Pavic, G.; Laulagnet, B. Acoustic properties of lightweight micro-perforated plate systems. Acta Acust. United Acust. 2003, 89, 201–212. [Google Scholar]
- Leissa, A.W. Vibrations of Plates; NASA Technical Report SP-160; Scientific and Technical Information Division, National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Mi, Y.; Zhai, W.; Cheng, L.; Xi, C.; Yu, X. Wave trapping by acoustic black hole: Simultaneous reduction of sound reflection and transmission. Appl. Phys. Lett. 2021, 118, 114101. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maury, C.; Bravo, T. Vibrational Effects on the Acoustic Performance of Multi-Layered Micro-Perforated Metamaterials. Vibration 2023, 6, 695-712. https://doi.org/10.3390/vibration6030043
Maury C, Bravo T. Vibrational Effects on the Acoustic Performance of Multi-Layered Micro-Perforated Metamaterials. Vibration. 2023; 6(3):695-712. https://doi.org/10.3390/vibration6030043
Chicago/Turabian StyleMaury, Cédric, and Teresa Bravo. 2023. "Vibrational Effects on the Acoustic Performance of Multi-Layered Micro-Perforated Metamaterials" Vibration 6, no. 3: 695-712. https://doi.org/10.3390/vibration6030043




