Analytical Study of Nonlinear Flexural Vibration of a Beam with Geometric, Material and Combined Nonlinearities
Abstract
:1. Introduction
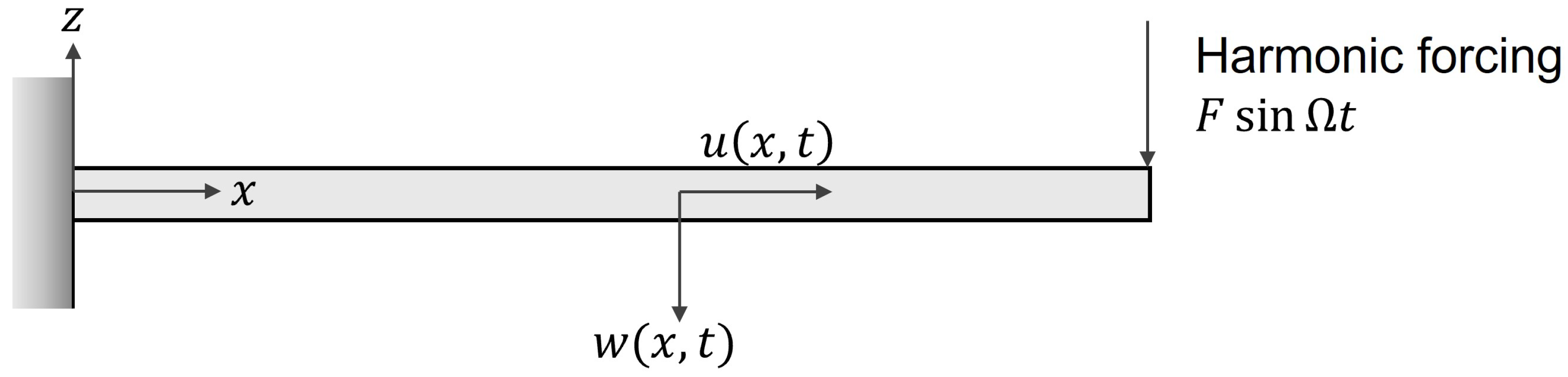
2. Models
2.1. Geometric Nonlinearity
2.2. Material Nonlinearity
2.2.1. Third-Order Elasticity
2.2.2. Fourth-Order Elasticity
2.3. Combined Geometric and Material Nonlinearity
3. Results and Discussions
3.1. Model Evaluation
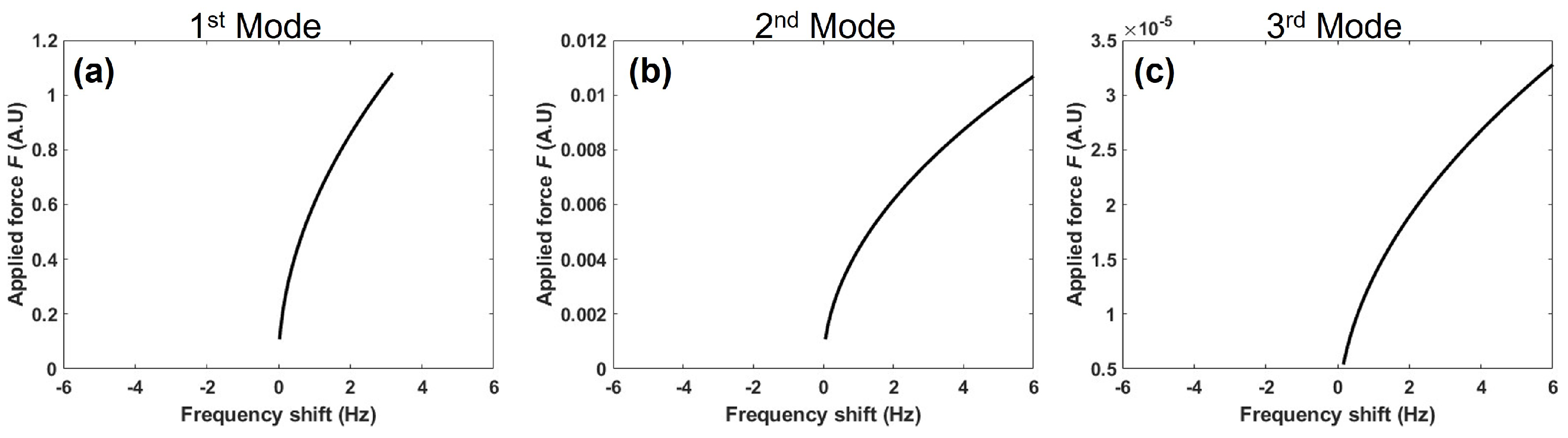
3.2. Geometric Nonlinearity
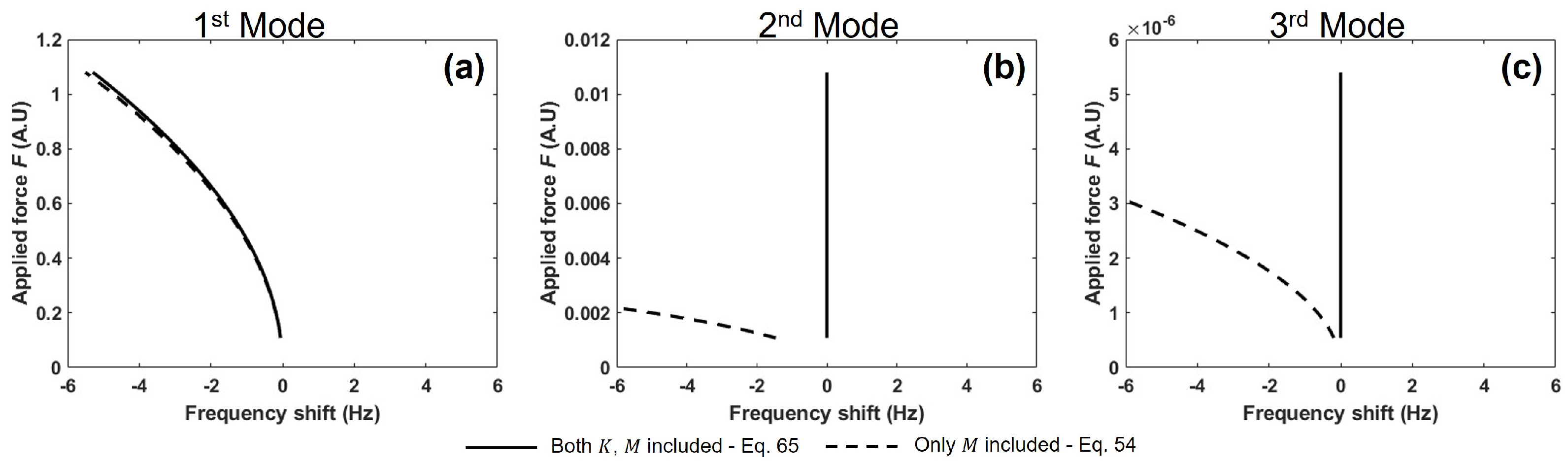
3.3. Material Nonlinearity
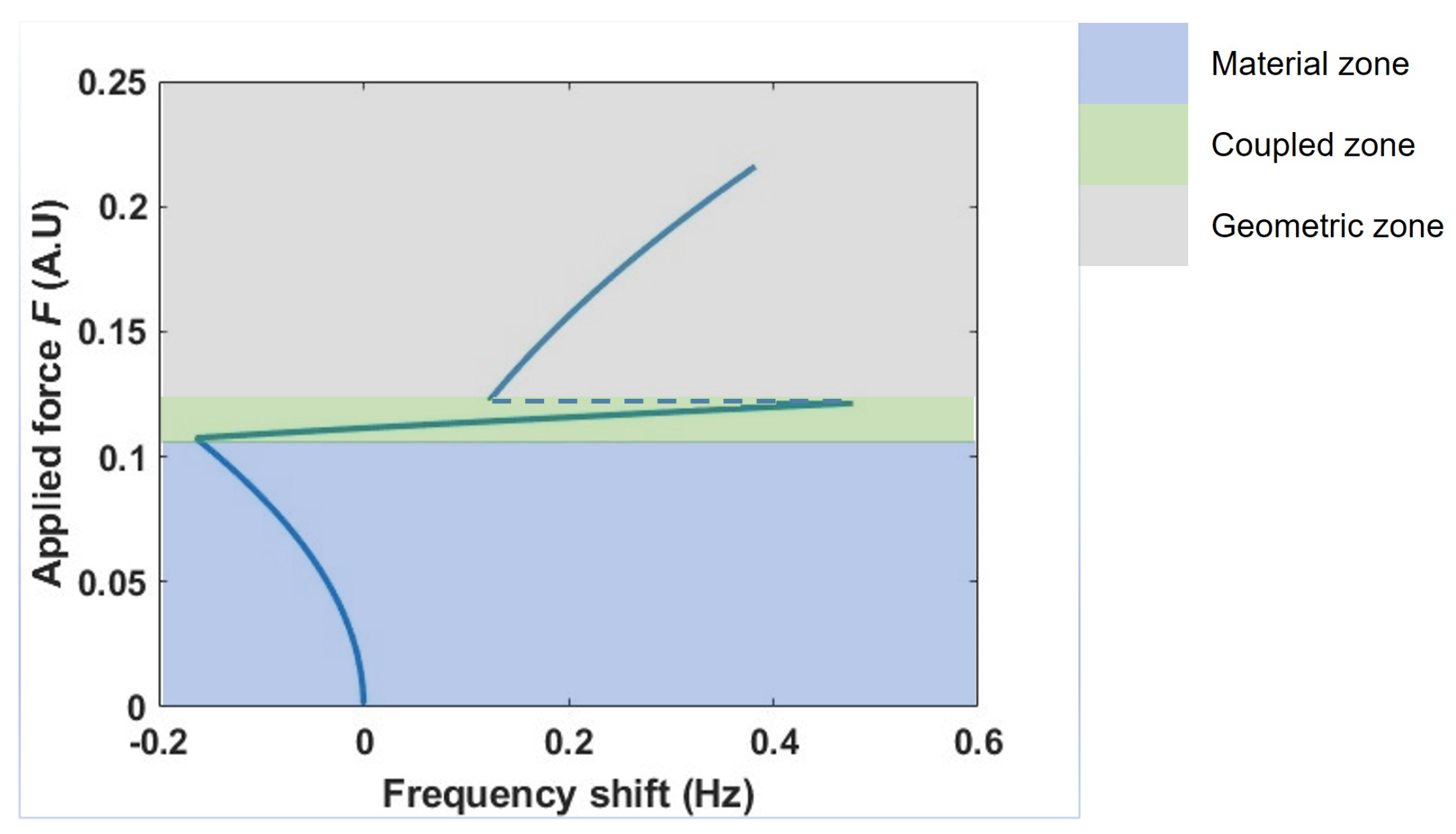
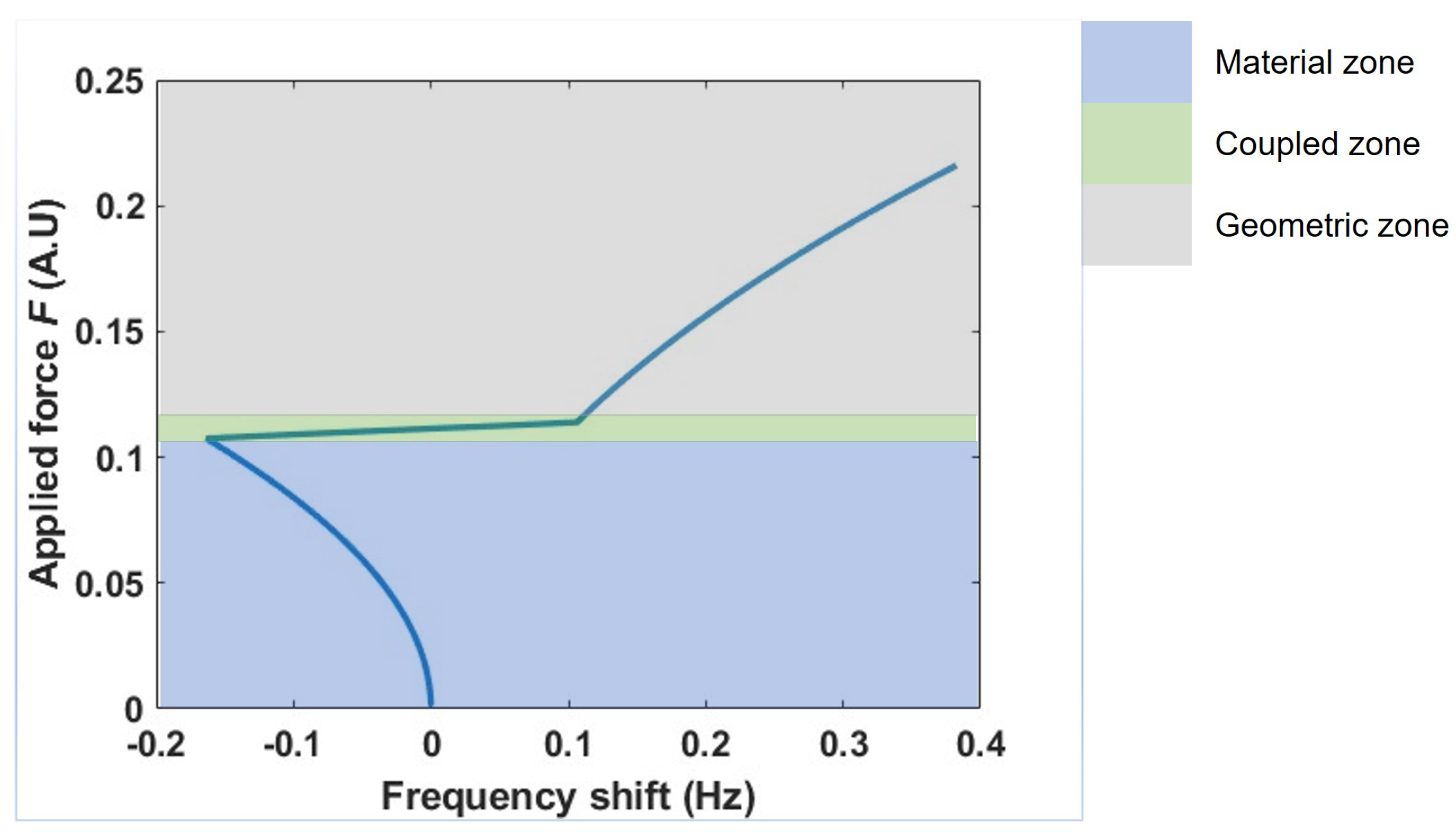
3.4. Combined Nonlinearity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Strutt, J.W. The Theory of Sound; Cambridge University Press: Cambridge, UK, 2011; Volume 1. [Google Scholar] [CrossRef]
- Strutt, J.W. The Theory of Sound; Cambridge University Press: Cambridge, UK, 2011; Volume 2. [Google Scholar] [CrossRef]
- Chakrapani, S.K.; Barnard, D.J. Determination of acoustic nonlinearity parameter ( β ) using nonlinear resonance ultrasound spectroscopy: Theory and experiment. J. Acoust. Soc. Am. 2017, 141, 919–928. [Google Scholar] [CrossRef] [PubMed]
- Schmerr, L.W. Fundamentals of Ultrasonic Nondestructive Evaluation; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Nayfeh, S.A. Nonlinear Normal Modes of a Cantilever Beam. J. Vib. Acoust. 1995, 117, 477–481. [Google Scholar] [CrossRef]
- Hui, D. Effects of Geometric Imperfections on Large-Amplitude Vibrations of Rectangular Plates with Hysteresis Damping. J. Appl. Mech. 1984, 51, 216–220. [Google Scholar] [CrossRef]
- Hui, D. Effects of Geometric Imperfections on Frequency-Load Interaction of Biaxially Compressed Antisymmetric Angle Ply Rectangular Plates. J. Appl. Mech. 1985, 52, 155–162. [Google Scholar] [CrossRef]
- Hui, D.; Du, I.H.Y. Effects of Axial Imperfections on Vibrations of Anti-Symmetric Cross-Ply, Oval Cylindrical Shells. J. Appl. Mech. 1986, 53, 675–680. [Google Scholar] [CrossRef]
- Reddy, J.N. Geometrically nonlinear transient analysis of laminated composite plates. AIAA J. 1983, 21, 621–629. [Google Scholar] [CrossRef]
- Hui, D. Influence of Geometric Imperfections and In-Plane Constraints on Nonlinear Vibrations of Simply Supported Cylindrical Panels. J. Appl. Mech. 1984, 51, 383–390. [Google Scholar] [CrossRef]
- Andreaus, U.; Casini, P.; Vestroni, F. Non-linear dynamics of a cracked cantilever beam under harmonic excitation. Int. J.-Non-Linear Mech. 2007, 42, 566–575. [Google Scholar] [CrossRef]
- Zaǐtsev, V.Y.; Matveev, L.A.; Matveev, A.L.; Arnold, W. Cascade cross modulation due to the nonlinear interaction of elastic waves in samples with cracks. Acoust. Phys. 2008, 54, 398–406. [Google Scholar] [CrossRef]
- Rudenko, O.V.; Korobov, A.I.; Izosimova, M.Y. Nonlinearity of solids with micro- and nanodefects and characteristic features of its macroscopic manifestations. Acoust. Phys. 2010, 56, 151–157. [Google Scholar] [CrossRef]
- Abeele, K.E.A.V.D.; Carmeliet, J.; Cate, J.A.T.; Johnson, P.A. Nonlinear Elastic Wave Spectroscopy (NEWS) Techniques to Discern Material Damage, Part II: Single-Mode Nonlinear Resonance Acoustic Spectroscopy. Res. Nondestruct. Eval. 2000, 12, 31–42. [Google Scholar] [CrossRef]
- Long, H.; Liu, Y.; Liu, K. Nonlinear vibration analysis of a beam with a breathing crack. Appl. Sci. 2019, 9, 3874. [Google Scholar] [CrossRef]
- Chia, C.Y. Geometrically Nonlinear Behavior of Composite Plates: A Review. Appl. Mech. Rev. 1988, 41, 439–451. [Google Scholar] [CrossRef]
- Varghaei, P.; Kharazmi, E.; Suzuki, J.L.; Zayernouri, M. Vibration Analysis of Geometrically Nonlinear and Fractional Viscoelastic Cantilever Beams. arXiv 2019, arXiv:1909.02142. [Google Scholar]
- Gonzalez-Cruz, C.A.; Jauregui-Correa, J.C.; Herrera-Ruíz, G. Nonlinear response of cantilever beams due to large geometric deformations: Experimental validation. Stroj. Vestnik/J. Mech. Eng. 2016, 62, 187–196. [Google Scholar] [CrossRef]
- Stojanović, V. Geometrically nonlinear vibrations of beams supported by a nonlinear elastic foundation with variable discontinuity. Commun. Nonlinear Sci. Numer. Simul. 2015, 28, 66–80. [Google Scholar] [CrossRef]
- Mahmoodi, S.; Khadem, S.; Jalili, N. Theoretical development and closed-form solution of nonlinear vibrations of a directly excited nanotube-reinforced composite cantilevered beam. Arch. Appl. Mech. 2006, 75, 153–163. [Google Scholar] [CrossRef]
- Azrar, L.; Benamar, R.; White, R. A semi-analytical approach to the nonlinear dynamic response problem of S-S and C-C beams at large vibration amplitudes part1: General theory and application to the single mode approach to free and forced vibration analysis. J. Sound Vib. 1999, 224, 183–207. [Google Scholar] [CrossRef]
- Azrar, L.; Benamar, R.; White, R. A semi-analytical approach to the non-linear dynamic response problem of beams at large vibration amplitudes, part II: Multimode approach to the steady state forced periodic response. J. Sound Vib. 2002, 255, 1–41. [Google Scholar] [CrossRef]
- Shooshtari, A.; Rafiee, M. Nonlinear forced vibration analysis of clamped functionally graded beams. Acta Mech. 2011, 221, 23–38. [Google Scholar] [CrossRef]
- Youzera, H.; Meftah, S.A.; Challamel, N.; Tounsi, A. Nonlinear damping and forced vibration analysis of laminated composite beams. Compos. Part B Eng. 2012, 43, 1147–1154. [Google Scholar] [CrossRef]
- Arafat, H.N.; Nayfeh, A.H.; Chin, C.M. Nonlinear Nonplanar Dynamics of Parametrically Excited Cantilever Beams. Nonlinear Dyn. 1998, 15, 31–61. [Google Scholar] [CrossRef]
- Nematollahi, M.S.; Mohammadi, H.; Dimitri, R.; Tornabene, F. Nonlinear vibration of functionally graded graphene nanoplatelets polymer nanocomposite sandwich beams. Appl. Sci. 2020, 10, 5669. [Google Scholar] [CrossRef]
- Shen, Y.; Vizzaccaro, A.; Kesmia, N.; Yu, T.; Salles, L.; Thomas, O.; Touzé, C. Comparison of Reduction Methods for Finite Element Geometrically Nonlinear Beam Structures. Vibration 2021, 4, 175–204. [Google Scholar] [CrossRef]
- Dolbachian, L.; Harizi, W.; Aboura, Z. Experimental Linear and Nonlinear Vibration Methods for the Structural Health Monitoring (SHM) of Polymer-Matrix Composites (PMCs): A Literature Review. Vibration 2024, 7, 281–325. [Google Scholar] [CrossRef]
- Rincón-Casado, A.; González-Carbajal, J.; García-Vallejo, D.; Domínguez, J. Analytical and numerical study of the influence of different support types in the nonlinear vibrations of beams. Eur. J. Mech.-A/Solids 2021, 85, 104113. [Google Scholar] [CrossRef]
- Kloda, L.; Lenci, S.; Warminski, J. Hardening vs. softening dichotomy of a hinged-simply supported beam with one end axial linear spring: Experimental and numerical studies. Int. J. Mech. Sci. 2020, 178, 105588. [Google Scholar] [CrossRef]
- Ogden, R.W. Nonlinear Elasticity, Anisotropy, Material Stability and Residual Stresses in Soft Tissue; Springer: Vienna, Austria, 2003; pp. 65–108. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Hiki, Y. Higher Order Elastic Constants of Solids. Annu. Rev. Mater. Sci. 1981, 11, 51–73. [Google Scholar] [CrossRef]
- Chakrapani, S.K.; Barnard, D.J.; Dayal, V. Nonlinear forced vibration of carbon fiber/epoxy prepreg composite beams: Theory and experiment. Compos. Part B Eng. 2016, 91, 513–521. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite Deformation of an Elastic Solid; John Wiley and Sons: Hoboken, NJ, USA, 1951. [Google Scholar]
- Thurston, R.N.; Mason, W.P. Physical Acoustics: Principles and Methods, 1st ed.; Academic Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Brugger, K. Thermodynamic Definition of Higher Order Elastic Coefficients. Phys. Rev. 1964, 133, A1611–A1612. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermoelastic Theory of Stressed Crystals and Higher-Order Elastic Constants; Academic Press: Cambridge, MA, USA, 1970; pp. 301–404. [Google Scholar] [CrossRef]
- Mahmoodi, S.N.; Jalili, N.; Daqaq, M.F. Modeling, nonlinear dynamics, and identification of a piezoelectrically actuated microcantilever sensor. IEEE/ASME Trans. Mechatron. 2008, 13, 58–65. [Google Scholar] [CrossRef]
- Ali, H. Nayfeh, B.B. Applied Nonlinear Dynamics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1995; Chapter 3; pp. 147–230. [Google Scholar] [CrossRef]
- Delsanto, P.P.; Scalerandi, M. Modeling nonclassical nonlinearity, conditioning, and slow dynamics effects in mesoscopic elastic materials. Phys. Rev. B 2003, 68, 064107. [Google Scholar] [CrossRef]
- Khandelwal, A.; Chakrapani, S.K. Nonclassical nonlinear elasticity of crystalline structures. Phys. Rev. E 2021, 104, 045002. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.T.; Stern, R.; Stephens, R.W.B. Third-Order Elastic Moduli of Polycrystalline Metals from Ultrasonic Velocity Measurements. J. Acoust. Soc. Am. 2005, 40, 1002–1008. [Google Scholar] [CrossRef]
- Garber, J.A.; Granato, A.V. Fourth-order elastic constants and the temperature dependence of second-order elastic constants in cubic materials. Phys. Rev. B 1975, 11, 3998–4007. [Google Scholar] [CrossRef]
- Landau, L.D.; Pitaevskii, L.; Kosevich, A.M.; Lifshitz, E.M. Theory of Elasticity; Elsevier: Amsterdam, The Netherlands, 2012; Volume 7. [Google Scholar]

| Symbol | Description | Value |
|---|---|---|
| Material Density | ||
| (E) | Second Order Elastic Constant | |
| M | Third Order Elastic Constant | |
| K | Fourth Order Elastic Constant | |
| G | Shear Modulus | |
| Damping Coefficient | ||
| L | Length of beam | |
| W | Width of beam | |
| H | Thickness of beam |
| Parameters | Nonlinearity | 1st Mode | 2nd Mode | 3rd Mode |
|---|---|---|---|---|
| Geometric | ||||
| Third order material | ||||
| Fourth order material | ||||
| Combined (material) | _ | _ | ||
| Combined (geometric) | _ | _ | ||
| Combined (coupled) | _ | _ | ||
| Combined | _ | _ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madhuranthakam, Y.; Chakrapani, S.K. Analytical Study of Nonlinear Flexural Vibration of a Beam with Geometric, Material and Combined Nonlinearities. Vibration 2024, 7, 464-478. https://doi.org/10.3390/vibration7020025
Madhuranthakam Y, Chakrapani SK. Analytical Study of Nonlinear Flexural Vibration of a Beam with Geometric, Material and Combined Nonlinearities. Vibration. 2024; 7(2):464-478. https://doi.org/10.3390/vibration7020025
Chicago/Turabian StyleMadhuranthakam, Yoganandh, and Sunil Kishore Chakrapani. 2024. "Analytical Study of Nonlinear Flexural Vibration of a Beam with Geometric, Material and Combined Nonlinearities" Vibration 7, no. 2: 464-478. https://doi.org/10.3390/vibration7020025
APA StyleMadhuranthakam, Y., & Chakrapani, S. K. (2024). Analytical Study of Nonlinear Flexural Vibration of a Beam with Geometric, Material and Combined Nonlinearities. Vibration, 7(2), 464-478. https://doi.org/10.3390/vibration7020025






