Simulation on Buffet Response and Mitigation of Variant-Tailed Aircraft in Maneuver State
Abstract
1. Introduction
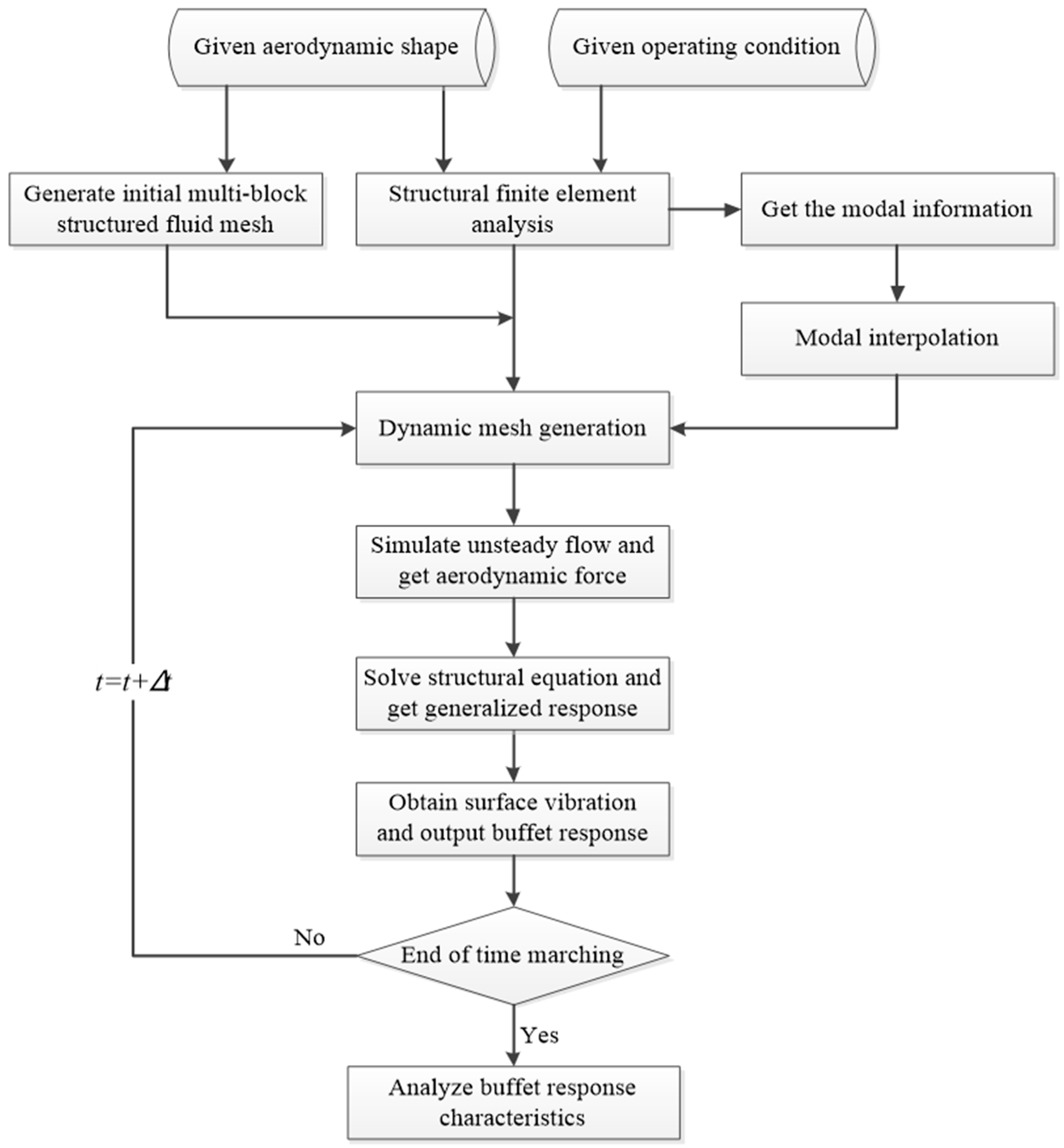
2. Numerical Method
2.1. Unsteady Flow Simulation Method
2.2. Dynamic Grid Generation Technology
- (1)
- Properly select feature points on the edge interface of the grid block (far-field, object surface, and symmetry plane) as the control points required for RBF interpolation;
- (2)
- Use the RBF interpolation method to solve the deformation of grid block edges based on the deformation of control points;
- (3)
- Use the two-dimensional TFI method to solve the deformation of the grid block surface based on the deformation of the grid block edges;
- (4)
- Use the three-dimensional TFI method to calculate the deformation of all internal points of the grid block based on its surface deformation.
2.3. Flow Field Structural Field Coupling
3. Calculation Results and Analysis
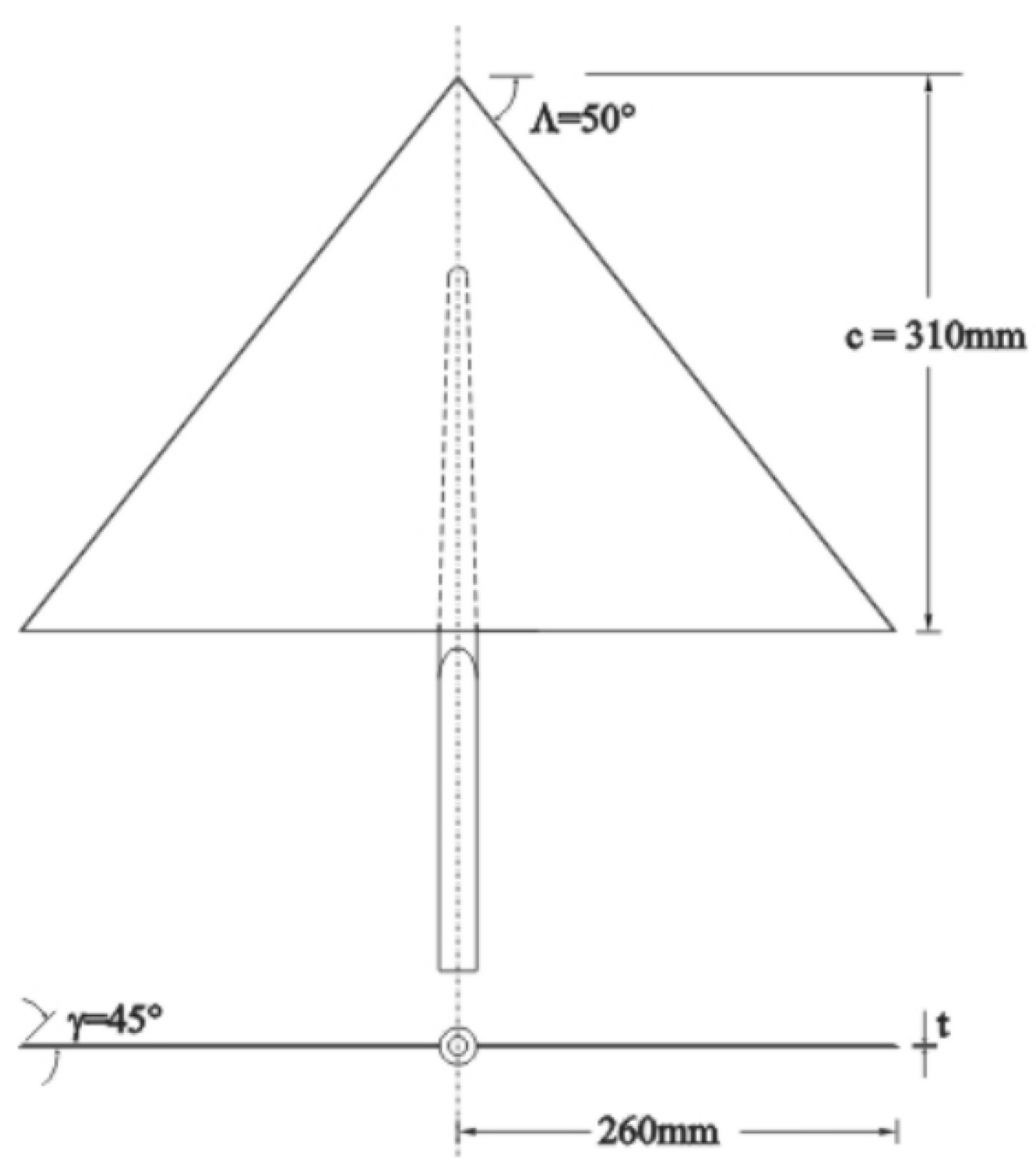
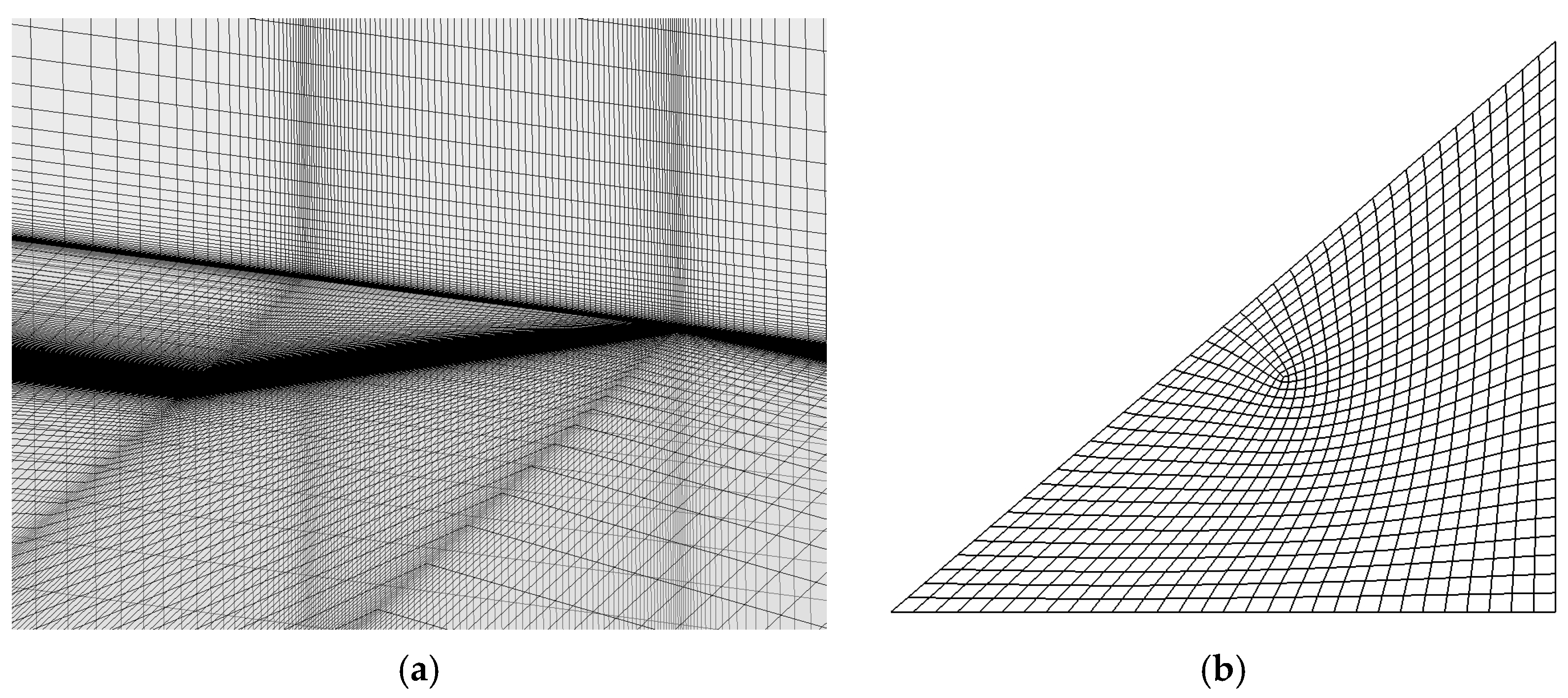
3.1. Verification Example of High-Angle-of-Attack Buffet Response of Delta Wing
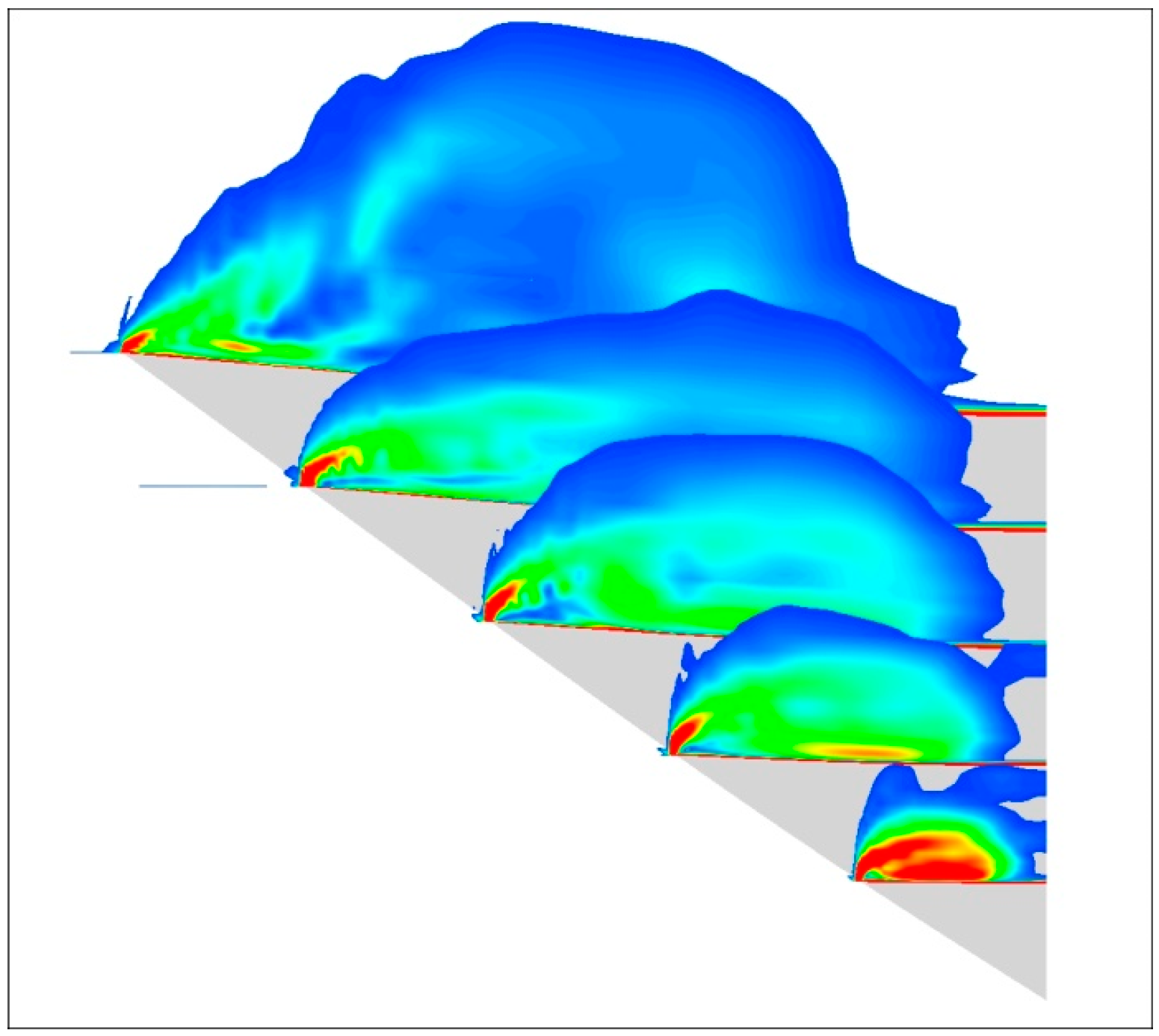
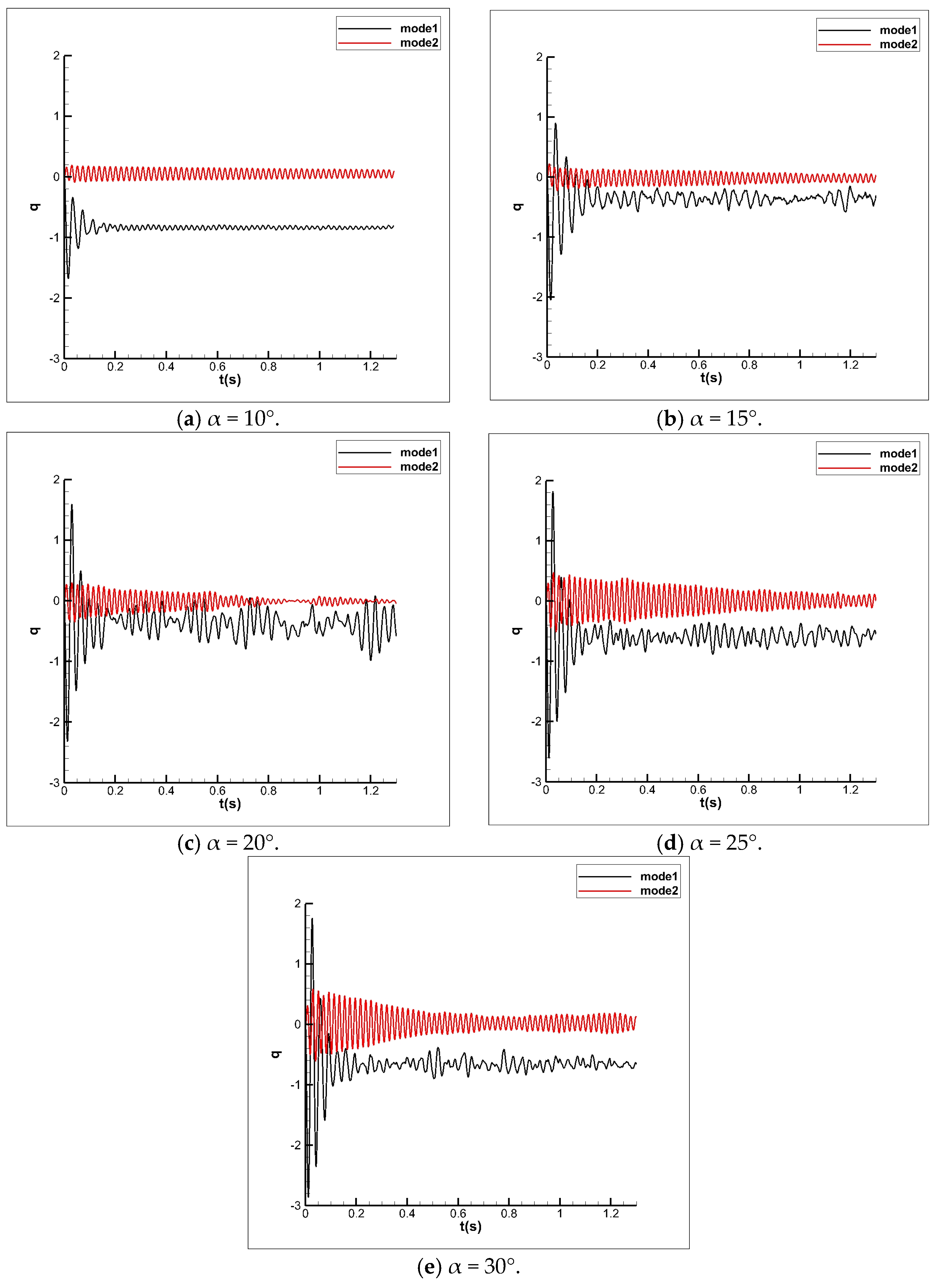
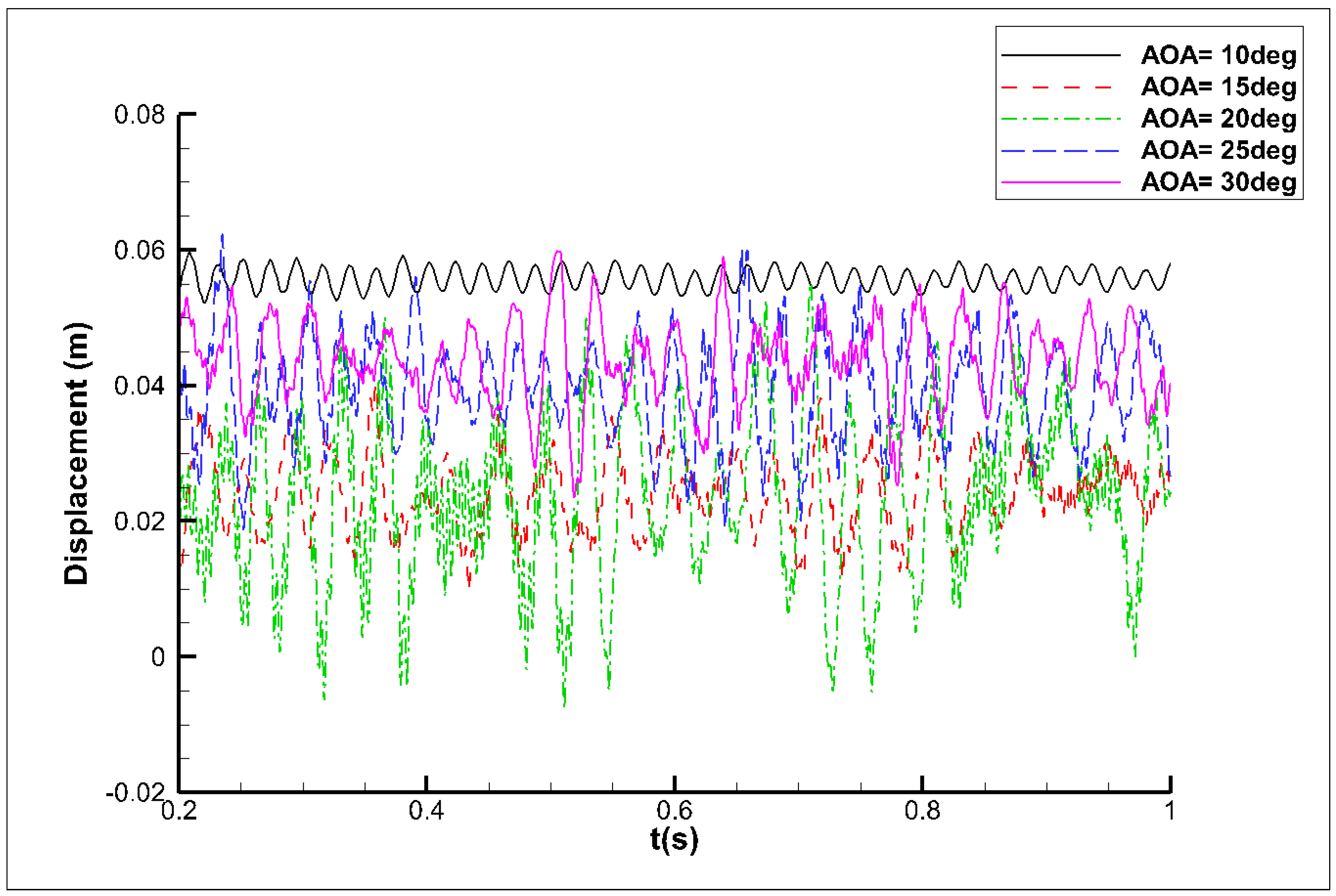
3.2. Simulation of Buffet Response of Variant-Tailed Aircraft
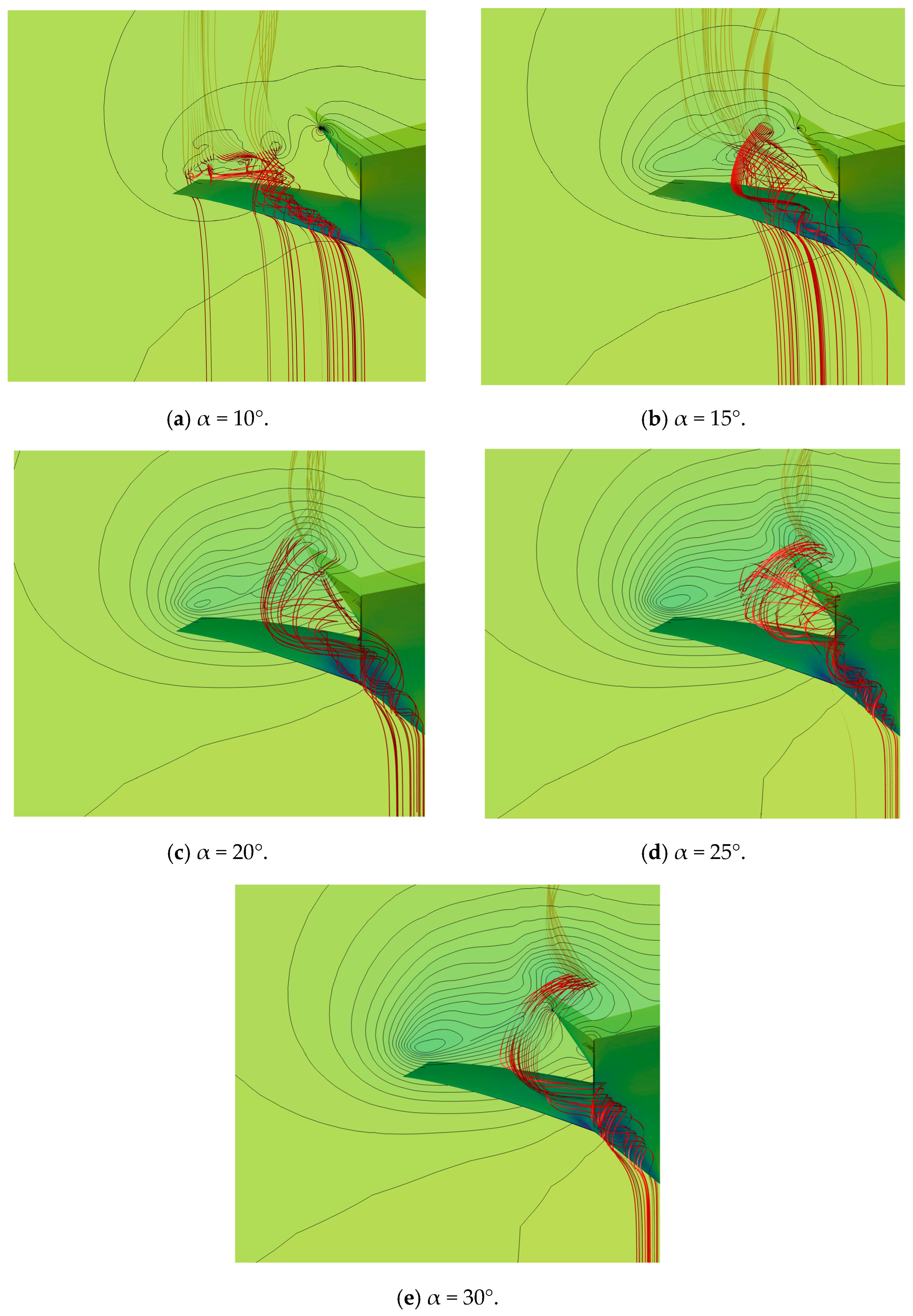
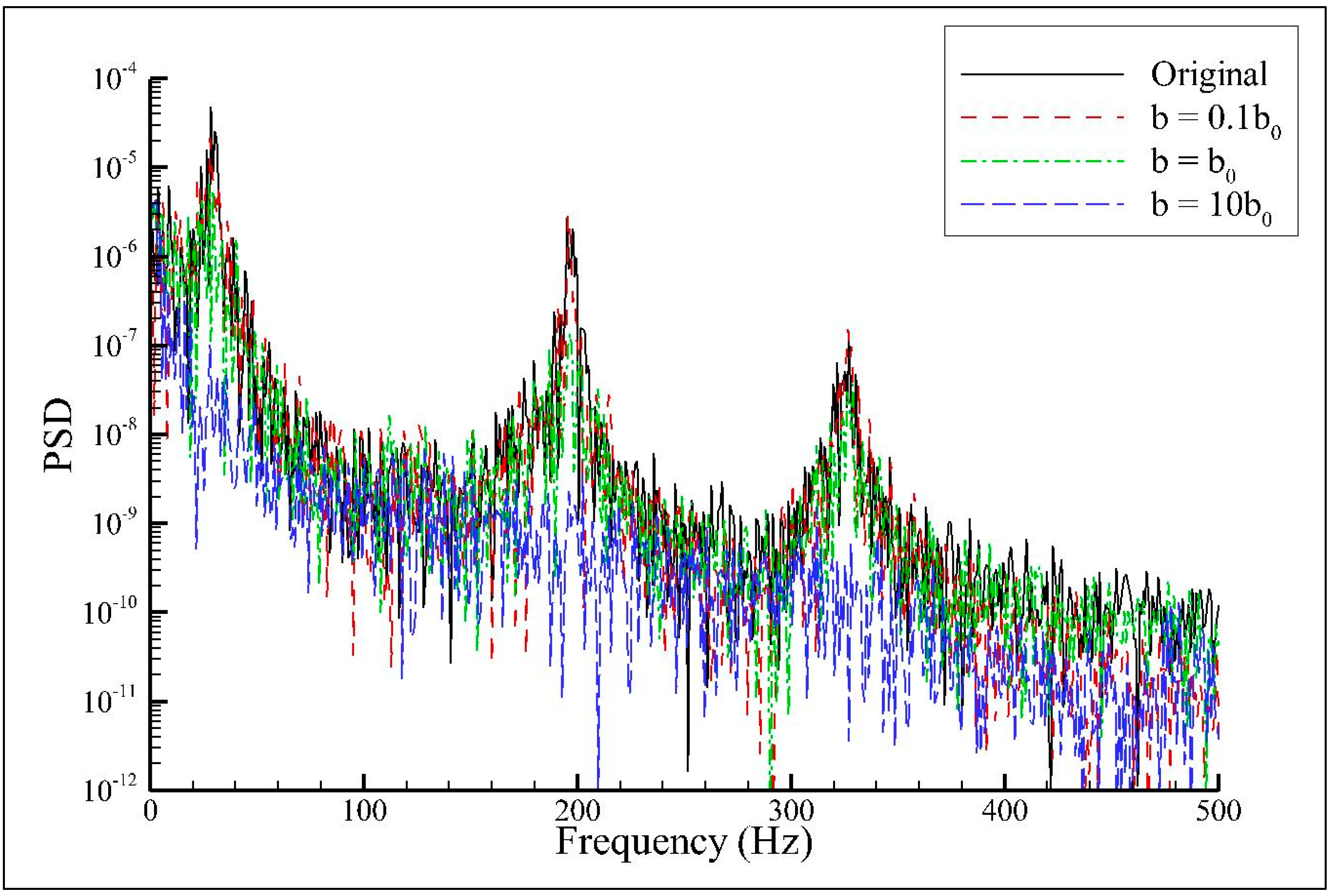
3.3. Simulation of Buffet Response Reduction for Variant-Tailed Aircraft
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sivanandi, P.; Gupta, C.; Durai, H. A review on evolution of aeroelastic assisted wing. Int. J. Aeronaut. Space Sci. 2023, 24, 652–688. [Google Scholar] [CrossRef]
- Scarlett, J.; Canfield, R.; Sanders, B. Multibody dynamic aeroelastic simulation of a folding wing aircraft. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 14th AIAA/ASME/AHS Adaptive Structures Conference 7th, Newport, RI, USA, 1–4 May 2006; p. 2135. [Google Scholar]
- Reich, G.; Bowman, J.; Sanders, B.; Frank, G. Development of an integrated aeroelastic multi-body morphing simulation tool. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 14th AIAA/ASME/AHS Adaptive Structures Conference 7th, Honolulu, HI, USA, 23–26 April 2007; p. 1892. [Google Scholar]
- Wilson, T.; Castrichini, A.; Paterson, J.; Arribas Ardura, R. Non-linear aeroelastic behaviour of hinged wing tips. In Proceedings of the 6th Aircraft Structural Design Conference, We The Curious, Bristol, UK, 9–11 October 2018. [Google Scholar]
- Castrichini, A.; Cooper, J.E.; Wilson, T.; Carrella, A.; Lemmens, Y. Nonlinear negative stiffness wingtip spring device for gust loads alleviation. J. Aircr. 2017, 54, 627–641. [Google Scholar] [CrossRef]
- Lee, D.H.; Chen, P. Nonlinear aeroelastic studies on a folding wing configuration with free-play hinge nonlinearity. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 14th AIAA/ASME/AHS Adaptive Structures Conference 7th, Newport, RI, USA, 1–4 May 2006; p. 1734. [Google Scholar]
- Tang, D.; Dowell, E.H. Theoretical and experimental aeroelastic study for folding wing structures. J. Aircr. 2008, 45, 1136–1147. [Google Scholar] [CrossRef]
- Wang, I.; Gibbs, S.C.; Dowell, E.H. Aeroelastic model of multisegmented folding wings: Theory and experiment. J. Aircr. 2012, 49, 911–921. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H. Prediction of transient responses of a folding wing during the morphing process. Aerosp. Sci. Technol. 2013, 24, 89–94. [Google Scholar] [CrossRef]
- Huang, R.; Yang, Z.; Yao, X.; Zhao, Y.; Hu, H. Parameterized modeling methodology for efficient aeroservoelastic analysis of a morphing wing. AIAA J. 2019, 57, 5543–5552. [Google Scholar]
- Lee, B. Statistical analysis of wing/fin buffeting response. Prog. Aerosp. Sci. 2002, 38, 305–345. [Google Scholar] [CrossRef]
- Pototzky, A.; Moses, R. An analysis method to predict tail buffet loads of fighter aircraft. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; p. 2291. [Google Scholar]
- Guo, T.; Lu, Z.; Tang, D.; Wang, T.; Dong, L. A CFD/CSD model for aeroelastic calculations of large-scale wind turbines. Sci. China Technol. Sci. 2013, 56, 205–211. [Google Scholar] [CrossRef]
- Lv, B.; Lu, Z.; Guo, T.; Tang, D.; Yu, L.; Guo, H. Investigation of winglet on the transonic flutter characteristics for a wind tunnel test model CHNT-1. Aerosp. Sci. Technol. 2019, 86, 430–437. [Google Scholar] [CrossRef]
- Liu, F.; Cai, J.; Zhu, Y.; Tsai, H.; Wong, A. Calculation of wing flutter by a coupled fluid-structure method. J. Aircr. 2001, 38, 334–342. [Google Scholar] [CrossRef]
- Yang, G.; Zheng, G.; Li, G. Computational methods and engineering applications of static/dynamic aeroelasticity based on CFD/CSD coupling solution. Sci. China Technol. Sci. 2012, 55, 2453–2461. [Google Scholar] [CrossRef]
- Gordnier, R.; Visbal, M. Computation of the aeroelastic response of a flexible delta wing at high angles of attack. J. Fluids Struct. 2004, 19, 785–800. [Google Scholar] [CrossRef]
- Kandil, O.; Massey, S.; Kandil, H. Computations of vortex-breakdown induced tail buffet undergoing bending and torsional vibrations. In Proceedings of the 35th Structures, Structural Dynamics, and Materials Conference, Hilton Head, SC, USA, 18–20 April 1994; p. 1428. [Google Scholar]
- Sheta, E.F.; Kandil, O.A. Effect of dynamic rolling oscillations on twin-tail buffet response. J. Sound Vib. 2002, 252, 261–280. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: London, UK, 2015. [Google Scholar]
- Taylor, G.; Kroker, A.; Gursul, I. Passive flow control over flexible nonslender delta wings. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 865. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Ding, L.; Lu, Z.; Guo, T. An efficient dynamic mesh generation method for complex multi-block structured grid. Adv. Appl. Math. Mech. 2014, 6, 120–134. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, Y.; Ye, Z. Two better loosely coupled solution algorithms of CFD based aeroelastic simulation. Eng. Appl. Comput. Fluid Mech. 2007, 1, 253–262. [Google Scholar] [CrossRef][Green Version]
- Smith, M.J.; Hodges, D.H.; Cesnik, C.E. Evaluation of computational algorithms suitable for fluid-structure interactions. J. Aircr. 2000, 37, 282–294. [Google Scholar] [CrossRef]
- Gordnier, R.; Visbal, M. Numerical simulation of nonslender delta wing buffet at high angle of attack. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; p. 2047. [Google Scholar]
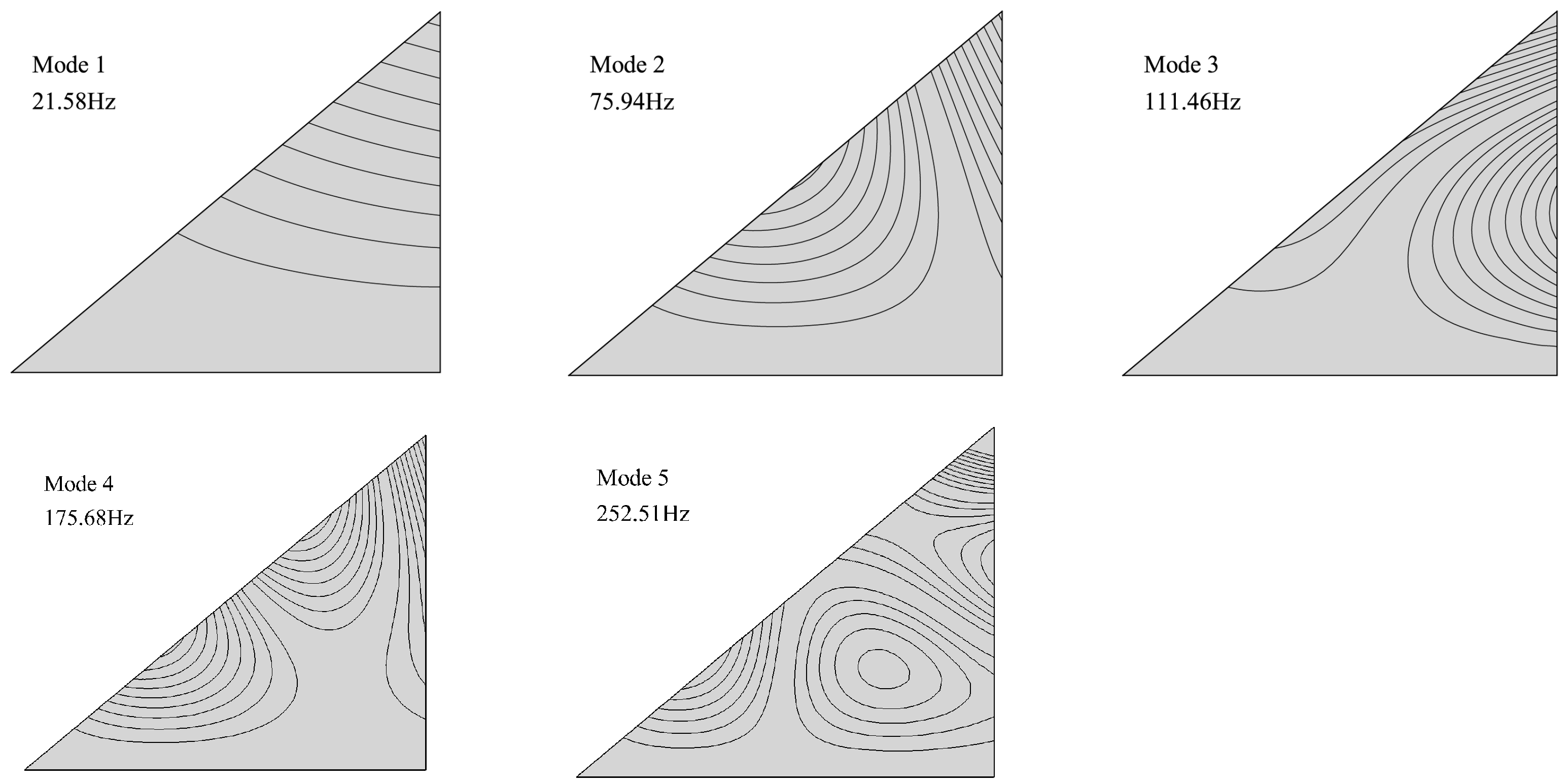
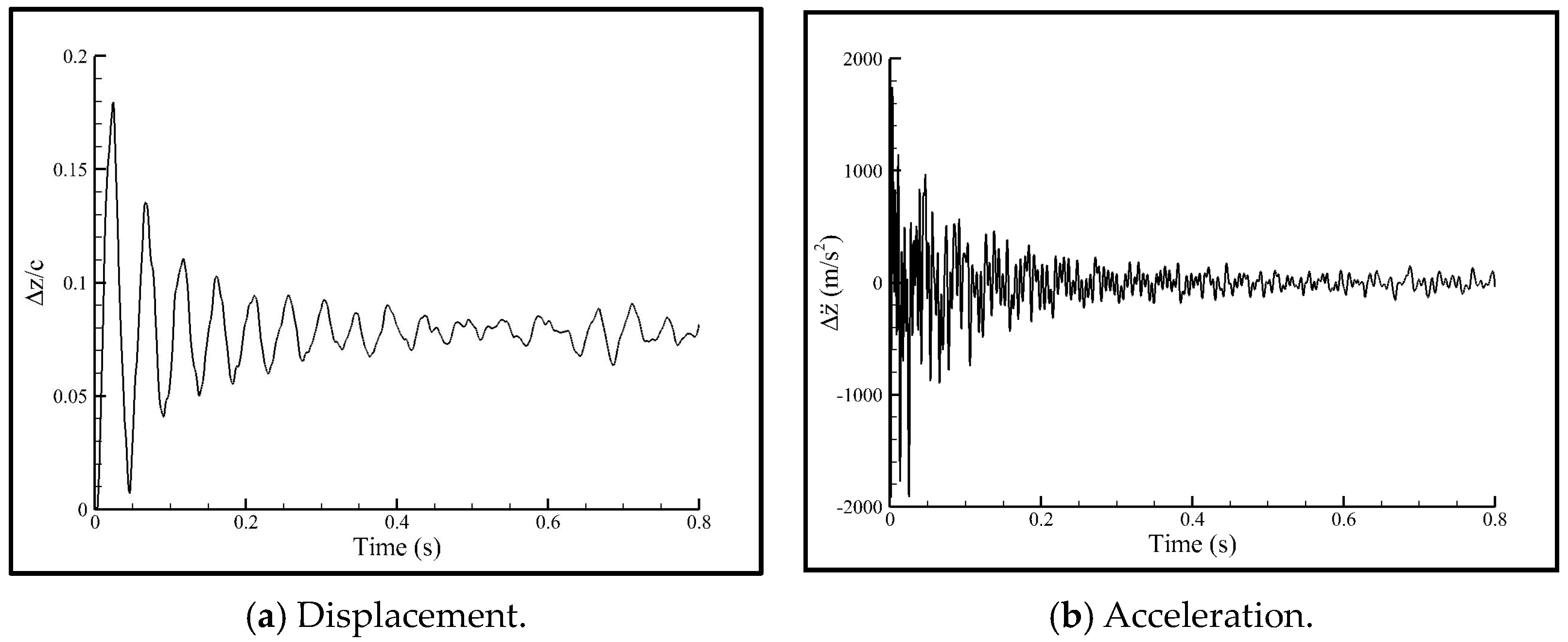
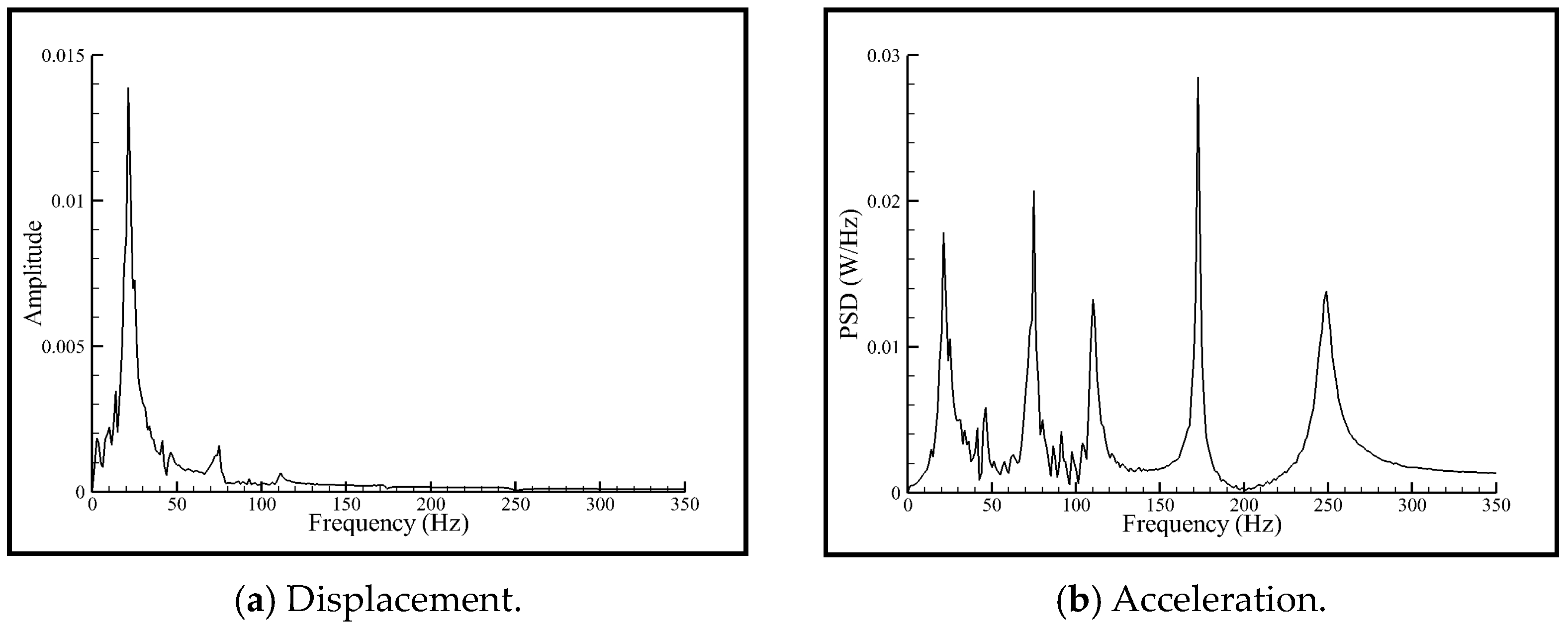


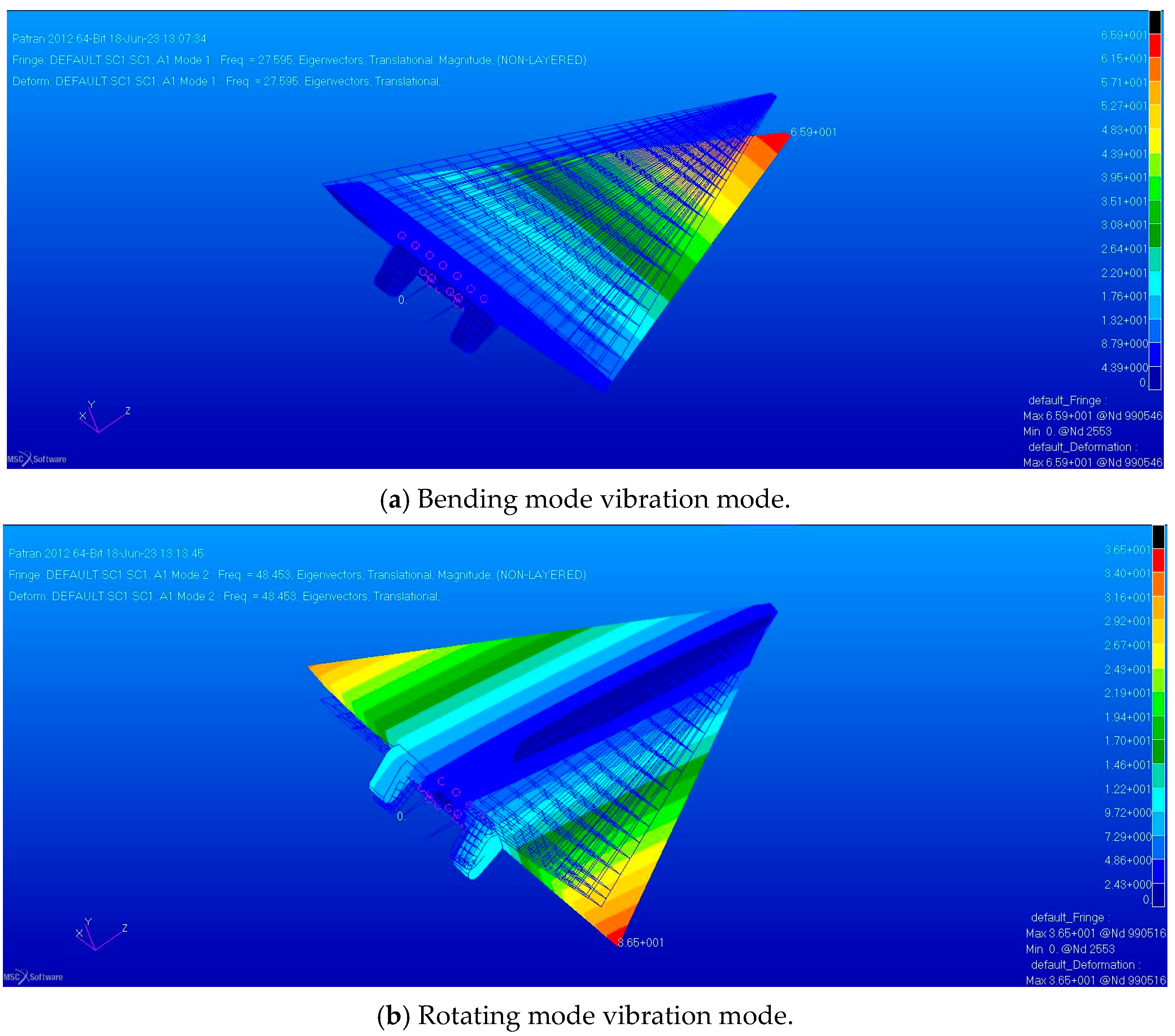


| Mode-Order | Frequency (Hz) | |
|---|---|---|
| Calculated Value | Literature Value [26] | |
| 1 | 21.58 | 21.28 |
| 2 | 75.94 | 75.79 |
| 3 | 111.46 | 111.82 |
| 4 | 175.68 | 176.15 |
| 5 | 252.51 | 255.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhang, P.; Lv, B.; Guo, H.; Yu, L.; Chen, Y.; Lu, B. Simulation on Buffet Response and Mitigation of Variant-Tailed Aircraft in Maneuver State. Vibration 2024, 7, 503-520. https://doi.org/10.3390/vibration7020027
Liu D, Zhang P, Lv B, Guo H, Yu L, Chen Y, Lu B. Simulation on Buffet Response and Mitigation of Variant-Tailed Aircraft in Maneuver State. Vibration. 2024; 7(2):503-520. https://doi.org/10.3390/vibration7020027
Chicago/Turabian StyleLiu, Dawei, Peng Zhang, Binbin Lv, Hongtao Guo, Li Yu, Yanru Chen, and Bo Lu. 2024. "Simulation on Buffet Response and Mitigation of Variant-Tailed Aircraft in Maneuver State" Vibration 7, no. 2: 503-520. https://doi.org/10.3390/vibration7020027
APA StyleLiu, D., Zhang, P., Lv, B., Guo, H., Yu, L., Chen, Y., & Lu, B. (2024). Simulation on Buffet Response and Mitigation of Variant-Tailed Aircraft in Maneuver State. Vibration, 7(2), 503-520. https://doi.org/10.3390/vibration7020027





