Numerical Simulation of Folding Tail Aeroelasticity Based on the CFD/CSD Coupling Method
Abstract
:1. Introduction
2. CFD/CSD Coupling Method
2.1. Aerodynamic Model
2.1.1. Governing Equations
2.1.2. Numerical Technique
2.1.3. Dynamic Mesh Method
- (1)
- Select some characteristic points at the surface boundaries (e.g., farfield, wall, and symmetry) as the control points needed by the RBF interpolation, whose deformations are known.
- (2)
- Use the RBF method to calculate the deformations at all edges of grid blocks according to the deformations at control points.
- (3)
- Use the two-dimensional TFI method to calculate the deformations at all domains of grid blocks according to the deformations at all edges.
- (4)
- Use the three-dimensional TFI method to calculate the deformations at all interior points of grid blocks according to the deformations at all domains.
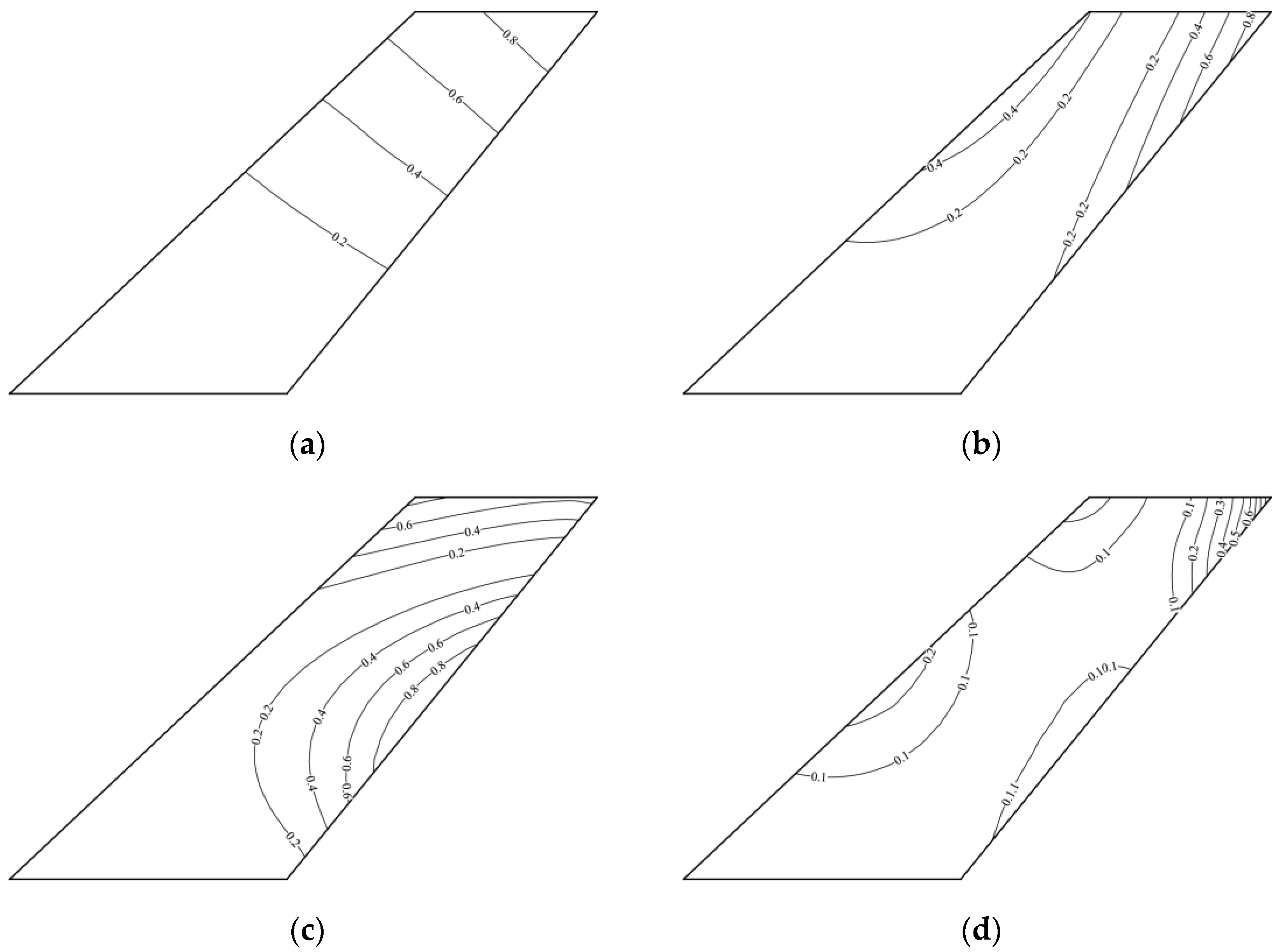
2.2. Structural Model
2.3. CFD/CSD Coupling for Folding Tail Morphing Aircraft
- (1)
- Given the range and rate of tail fold motion, generate the initial computational mesh for the unfolded configuration.
- (2)
- Calculate the rigid deformation according to the instantaneous folding angle at time t and transform the mode shape matrix.
- (3)
- Calculate the elastic deformation according to the instantaneous aerodynamic force at time t for the current folded configuration.
- (4)
- Combine the folding and elastic deformations and update the aerodynamic mesh using the RBF-TFI method.
- (5)
- Calculate the unsteady flow field and obtain the instantaneous aerodynamic force at time t + ∆t.
- (6)
- Repeat the procedures (2)–(5) until the entire tail folding process is finished.
2.4. Code Validation
3. Results and Discussions
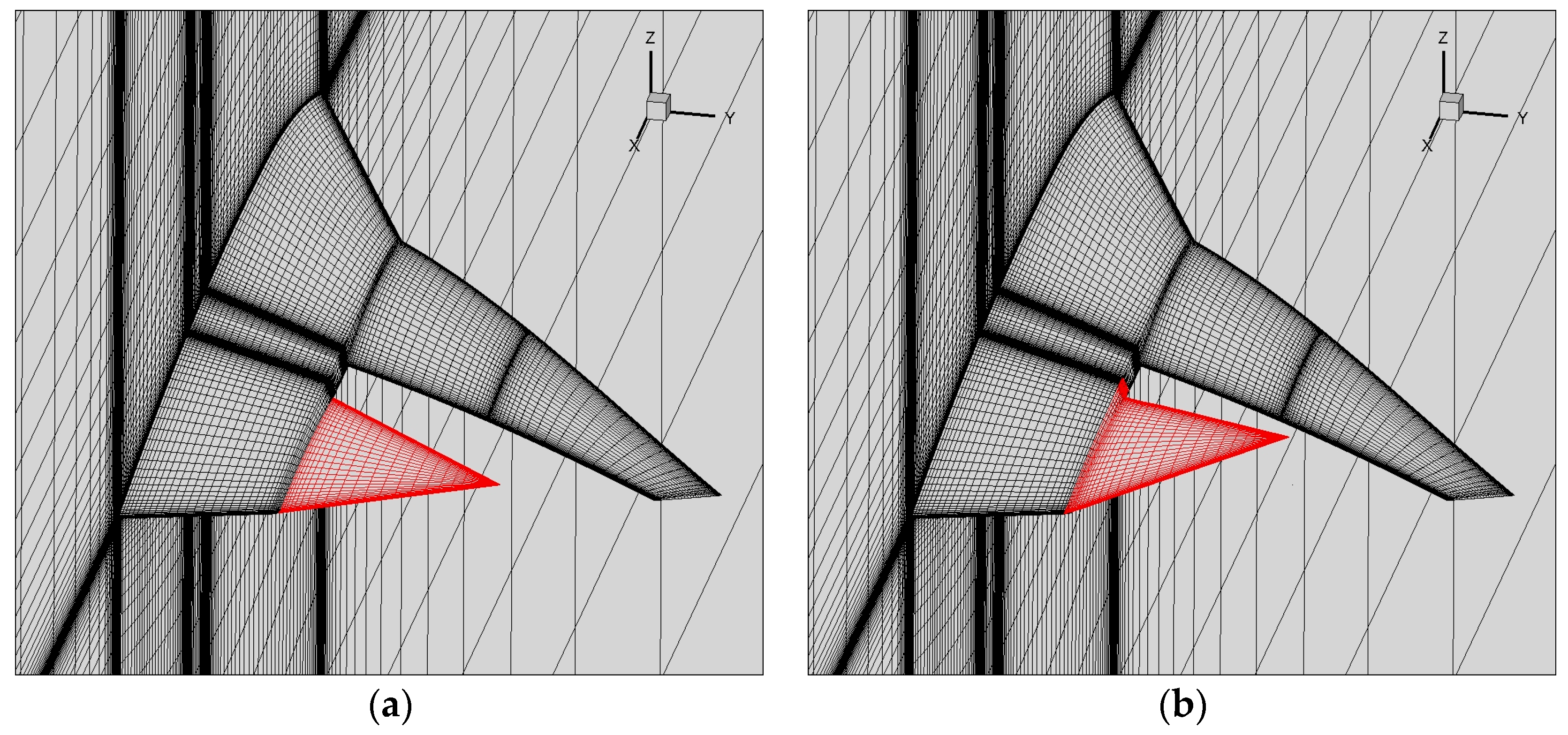
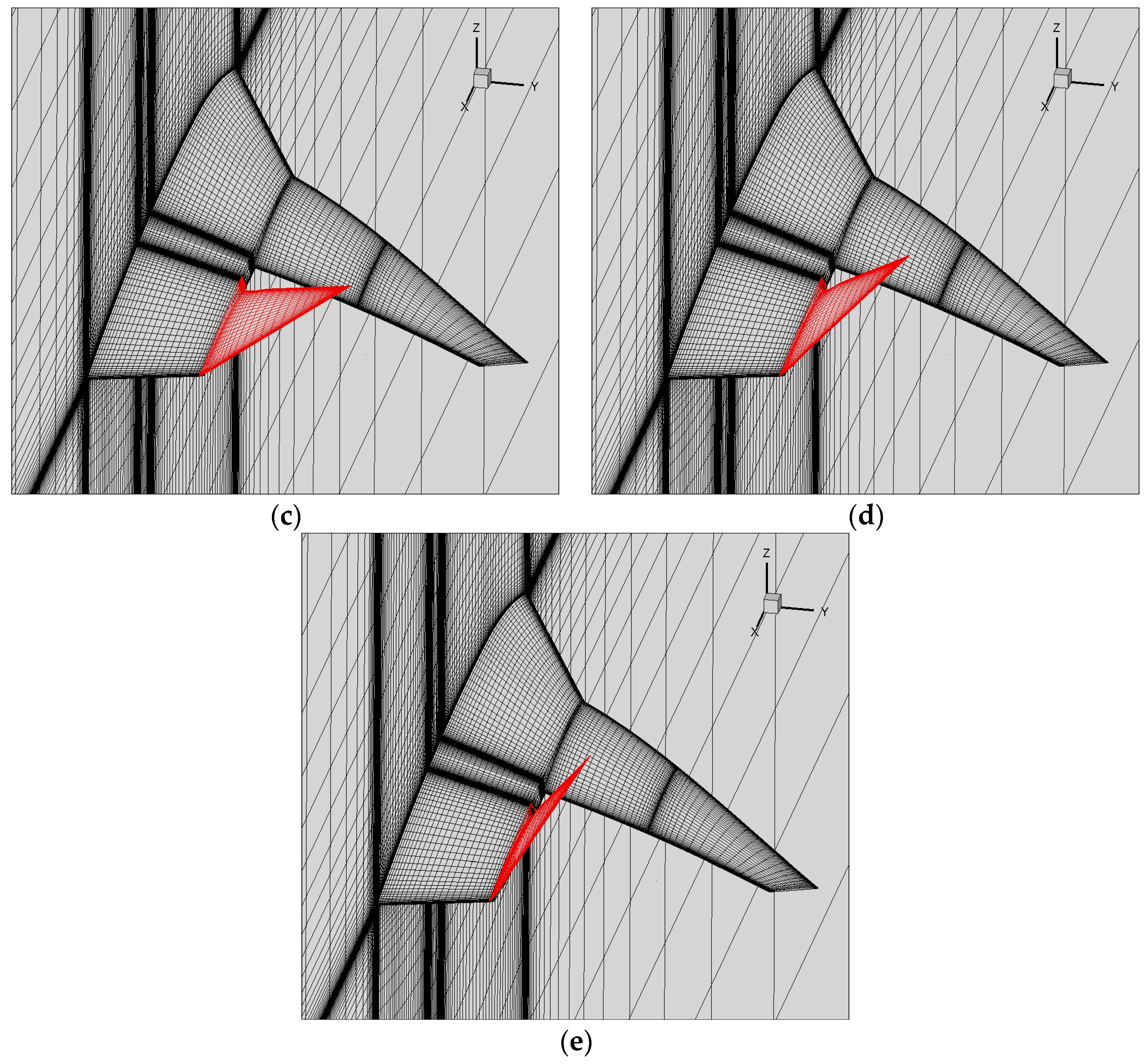
3.1. Model Description
3.2. Aeroelastic Simulation and Mechanism Analysis
3.2.1. Flutter Characteristics at Fixed Folding Angles
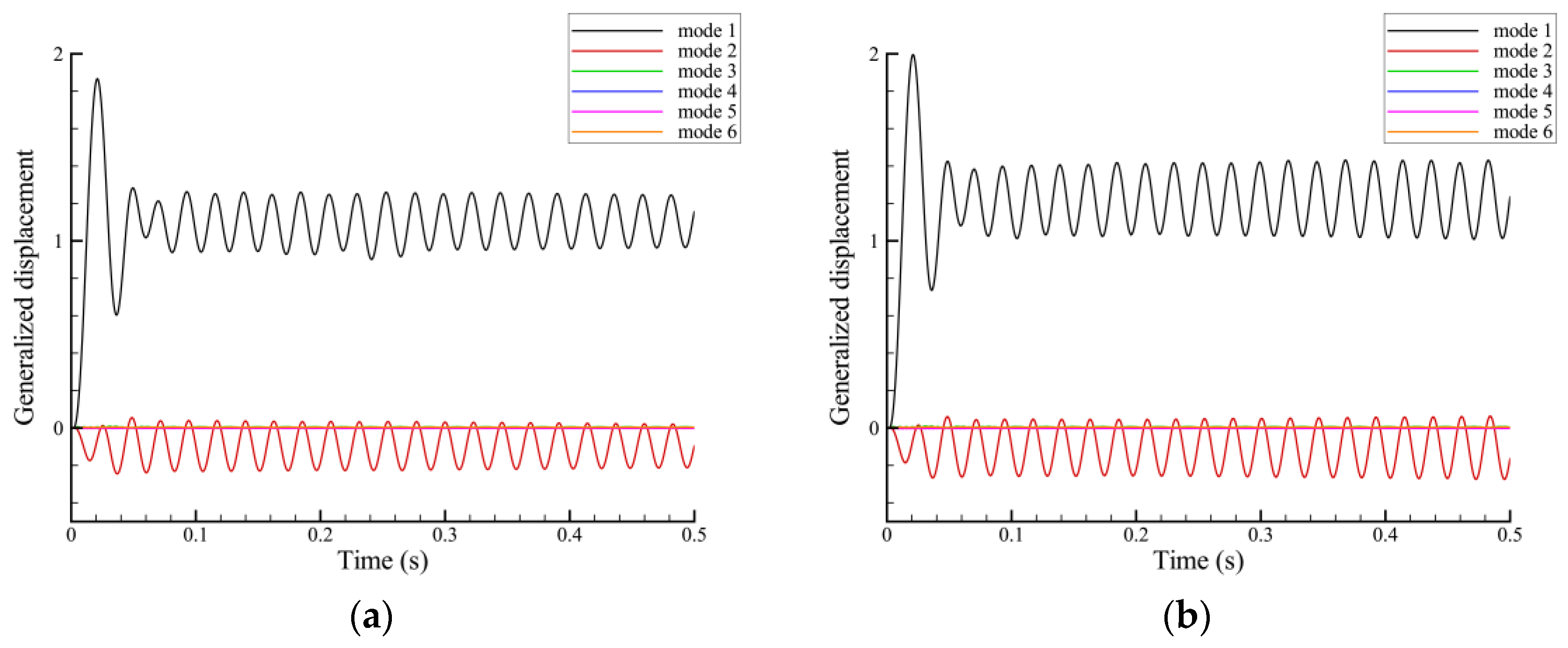
3.2.2. Response Characteristics during the Folding Process
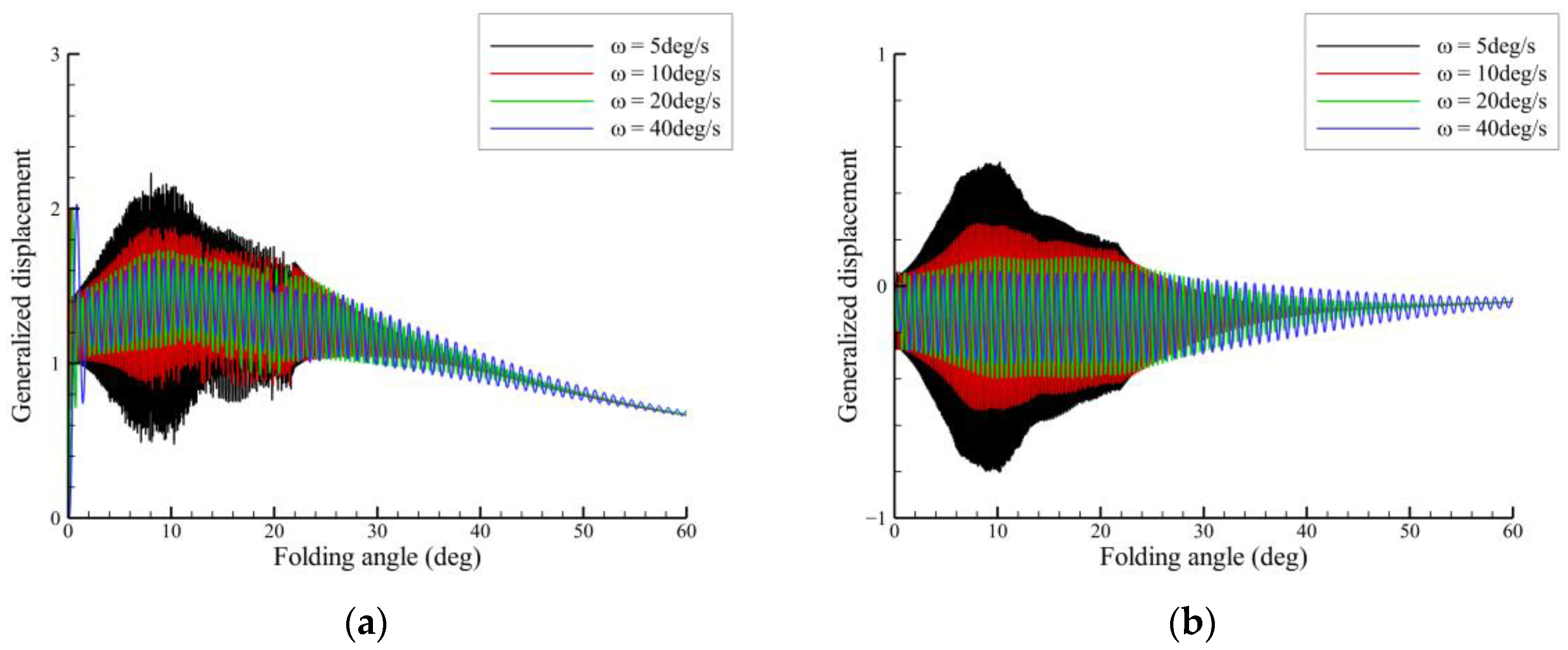
3.2.3. Influence of Folding Rate and Influence Mechanism
4. Conclusions
- (1)
- For a very slow folding (quasi-static) process, the increase in tail folding angle reduced the aerodynamic load and improves the aeroelastic stability. The wing interference had negative effects on the aeroelastic stability, at least for this case.
- (2)
- The dynamic process of tail folding had a significant influence on the aeroelastic characteristics, and the responses exhibited nonlinear behaviors.
- (3)
- The influence of the tail folding process became greater as the folding rate increased, and generally it had a positive effect on the aeroelastic stability, at least for this case.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodriguez, A. Morphing Aircraft Technology Survey. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Liu, D.; Chen, P.-C.; Zhang, Z.; Wang, Z.; Yang, S.; Lee, D.-H.; Mignolet, M.; Liu, F.; Lindsley, N.; Beran, P. Continuous Dynamic Simulation for Morphing Wing Aeroelasticity. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar]
- Love, M.; Zink, S.; Stroud, R.; Bye, D.; Chase, C. Impact of Actuation Concepts on Morphing Aircraft Structures. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004. [Google Scholar]
- Snyder, M.P.; Sanders, B.; Eastep, F.E.; Frank, G.J. Vibration and Flutter Characteristics of a Folding Wing. J. Aircr. 2009, 46, 791–799. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Theoretical and Experimental Aeroelastic Study for Folding Wing Structures. J. Aircr. 2008, 45, 1136–1147. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H. Prediction of transient responses of a folding wing during the morphing process. Aerosp. Sci. Technol. 2013, 24, 89–94. [Google Scholar] [CrossRef]
- Hu, W.; Yang, Z.; Gu, Y. Aeroelastic study for folding wing during the morphing process. J. Sound Vib. 2016, 365, 216–229. [Google Scholar] [CrossRef]
- Reich, G.; Bowman, J.; Sanders, B.; Frank, G. Development of an Integrated Aeroelastic Multi-Body Morphing Simulation Tool. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006. [Google Scholar]
- Bowman, J.; Reich, G.; Sanders, B.; Frank, G. Simulation Tool for Analyzing Complex Shape-Changing Mechanisms in Aircraft. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Xu, H.; Han, J.; Yun, H.; Chen, X. Calculation of the Hinge Moments of a Folding Wing Aircraft during the Flight-Folding Process. Int. J. Aerosp. Eng. 2019, 9362629. [Google Scholar] [CrossRef]
- Baldelli, D.H.; Lee, D.-H.; Pena, R.S.S.; Cannon, B. Modeling and Control of an Aeroelastic Morphing Vehicle. J. Guid. Control Dyn. 2008, 31, 1687–1699. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M.; Skelton, R.E. Markov data-based reference tracking control to tensegrity morphing airfoils. Eng. Struct. 2023, 291, 116430. [Google Scholar] [CrossRef]
- Chen, M.; Shen, Y.; Skelton, R.E. Model-Based and Markov Data-Based Linearized Tensegrity Dynamics and Analysis of Morphing Airfoils. In Proceedings of the AIAA SCITECH 2024 Forum 2024, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Liu, F.; Cai, J.; Zhu, Y.; Tsai, H.M.; Wong, A.S.F. Calculation of Wing Flutter by a Coupled Fluid-Structure Method. J. Aircr. 2001, 38, 334–342. [Google Scholar] [CrossRef]
- Yang, G.; Zheng, G.; Li, G. Computational methods and engineering applications of static/dynamic aeroelasticity based on CFD/CSD coupling solution. Sci. China Technol. Sci. 2012, 55, 2453–2461. [Google Scholar] [CrossRef]
- Guruswamy, G.P. Perspective on CFD/CSD-Based Computational Aeroelasticity during 1977–2020. J. Aerosp. Eng. 2021, 34, 06021005. [Google Scholar] [CrossRef]
- Guo, T.; Lu, Z.; Tang, D.; Wang, T.; Dong, L. A CFD/CSD model for aeroelastic calculations of large-scale wind turbines. Sci. China Technol. Sci. 2013, 56, 205–211. [Google Scholar] [CrossRef]
- Lv, B.; Lu, Z.; Guo, T.; Tang, D.; Yu, L.; Guo, H. Investigation of winglet on the transonic flutter characteristics for a wind tunnel test model CHNT-1. Aerosp. Sci. Technol. 2019, 86, 430–437. [Google Scholar] [CrossRef]
- Zhou, D.; Lu, Z.; Guo, T.; Chen, G. Aeroelastic prediction and analysis for a transonic fan rotor with the “hot” blade shape. Chin. J. Aeronaut. 2021, 34, 50–61. [Google Scholar] [CrossRef]
- Ma, X.; Su, J.; Zhong, S.; Huang, Y.; Zhang, Y. Study of aerodynamic and stealthy performance for a multifunctional morphing tail. Acta Aerodyn. Sin. 2020, 38, 896–900. [Google Scholar]
- Jiang, Q.-F.; Chen, S.-S.; Yang, H.; Zhang, Z.-G.; Gao, Z.-H. Unsteady aerodynamic characteristics of a morphing tail configuration. Phys. Fluids 2024, 36, 036133. [Google Scholar] [CrossRef]
- Ding, L.; Guo, T.; Lu, Z. An Efficient Dynamic Mesh Generation Method for Complex Multi-Block Structured Grid. Adv. Appl. Math. Mech. 2015, 6, 120–134. [Google Scholar] [CrossRef]
- Harder, R.L.; Desmarais, R.N. Interpolation using surface splines. J. Aircr. 1972, 9, 189–191. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, Y.; Ye, Z. Two better loosely coupled solution algorithms of CFD based aeroelastic simulation. Eng. Appl. Comput. Fluid Mech. 2007, 1, 253–262. [Google Scholar] [CrossRef]
- Yates, E.C., Jr. AGARD Standard Aeroelastic Configurations for Dynamic Response I-Wing 445.6, Proceedings of the 61st Meeting of the Structures and Materials Panel, Oberammergau, Germany, 8–13 September 1985; Advisory Group for Aerospace Research and Development: Neuilly sur Seine, France, 1988. [Google Scholar]
- Silva, W.A.; Chwalowski, P.; Perry, B., III. Evaluation of linear, inviscid, viscous, and reduced-order modelling aeroelastic solutions of the AGARD 445.6 wing using root locus analysis. Int. J. Comput. Fluid Dyn. 2014, 28, 122–139. [Google Scholar] [CrossRef]
- Silva, W.A.; Bartels, R.E. Development of reduced-order models for aeroelastic analysis and flutter prediction using the CFL3Dv6.0 code. J. Fluids Struct. 2004, 19, 729–745. [Google Scholar] [CrossRef]
- Lee-Rausch, E.M.; Batina, J.T. Wing flutter boundary prediction using unsteady Euler aerodynamic method. J. Aircr. 1995, 32, 416–422. [Google Scholar] [CrossRef]







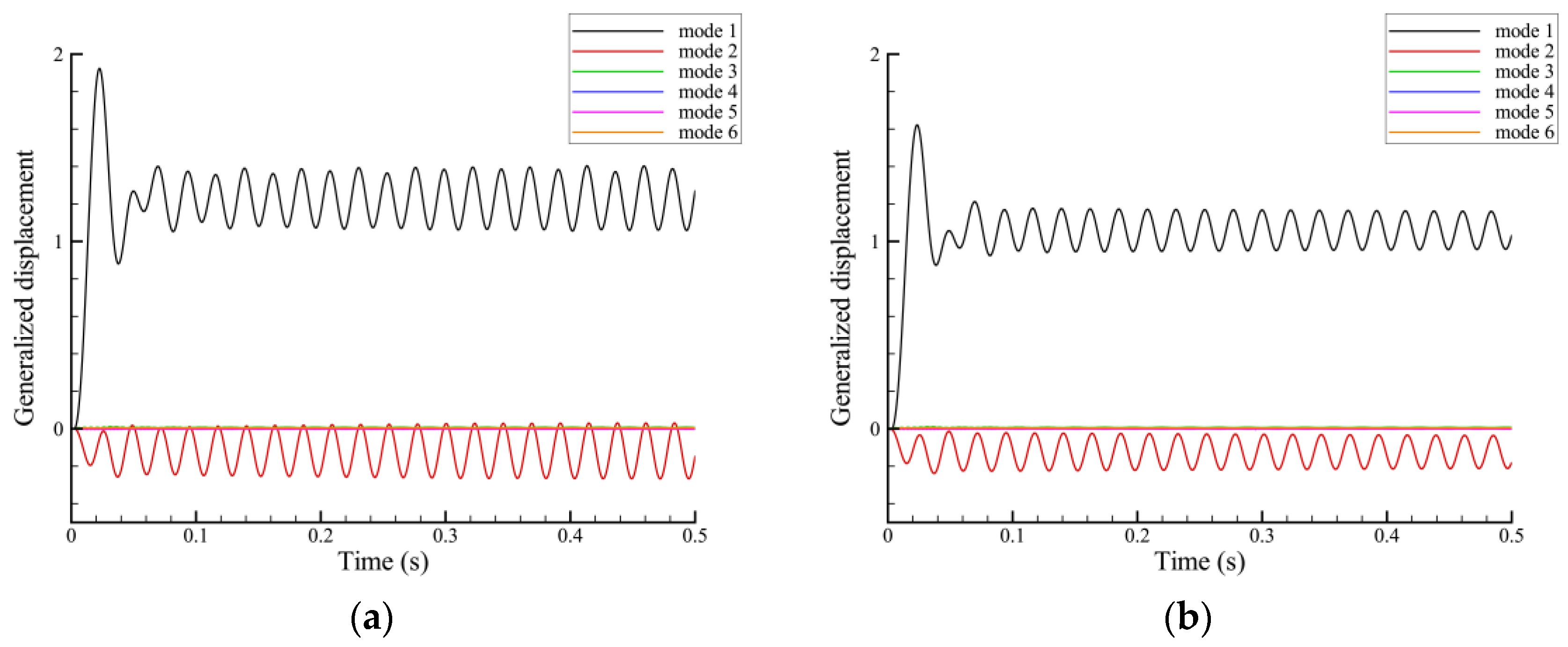
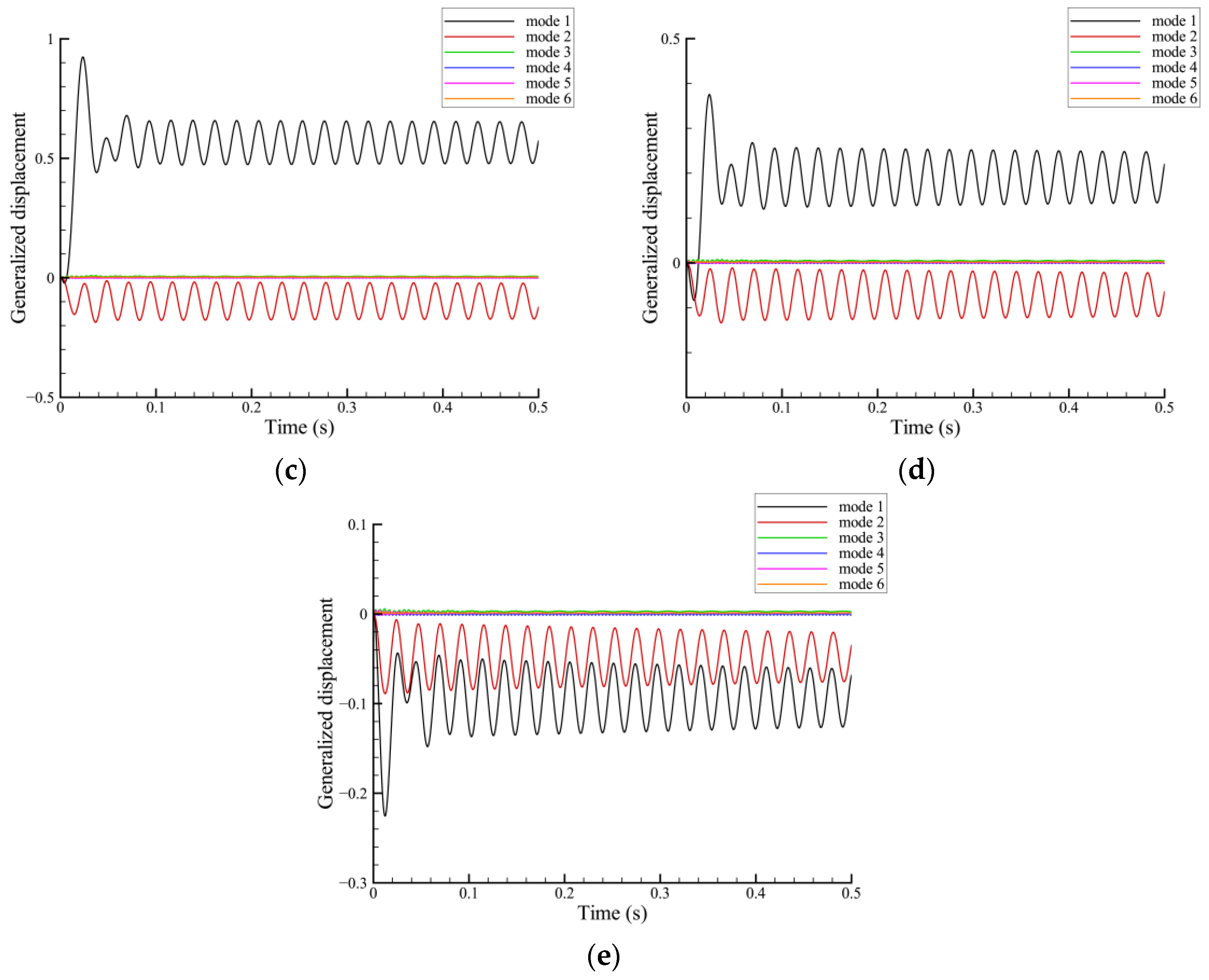

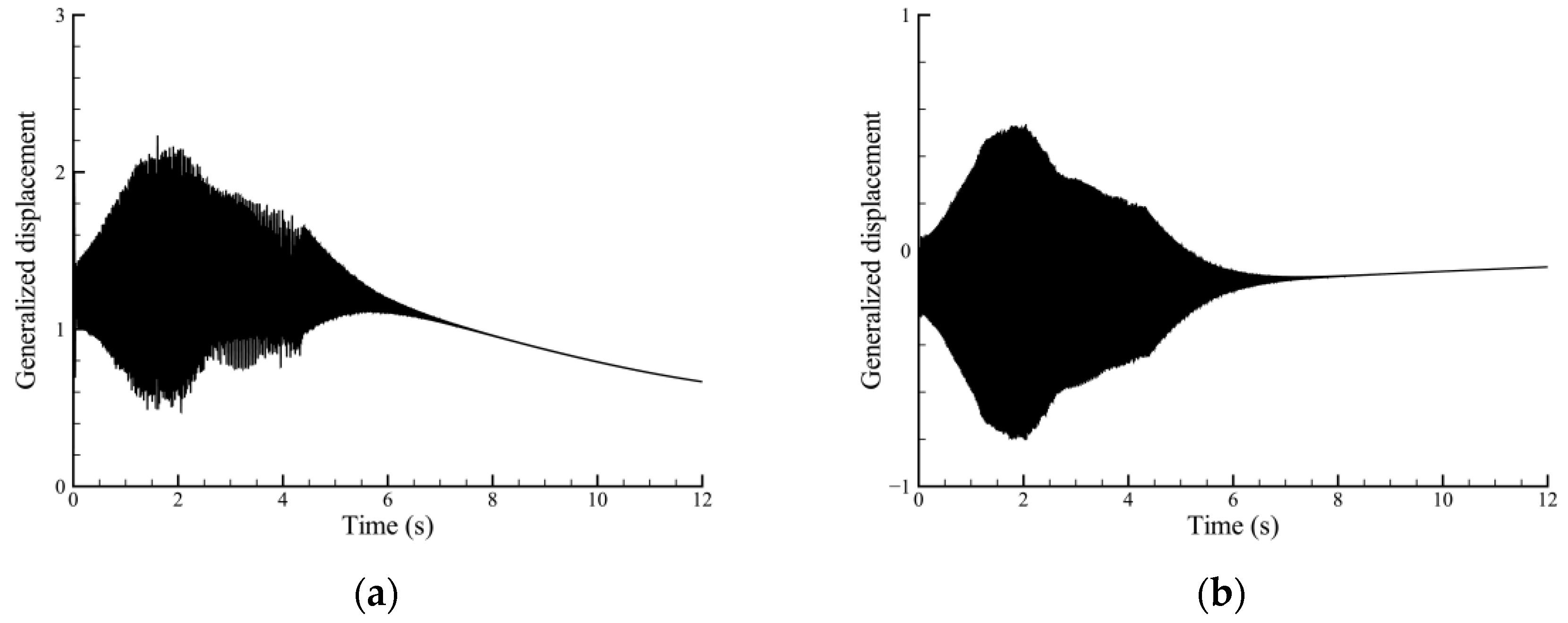
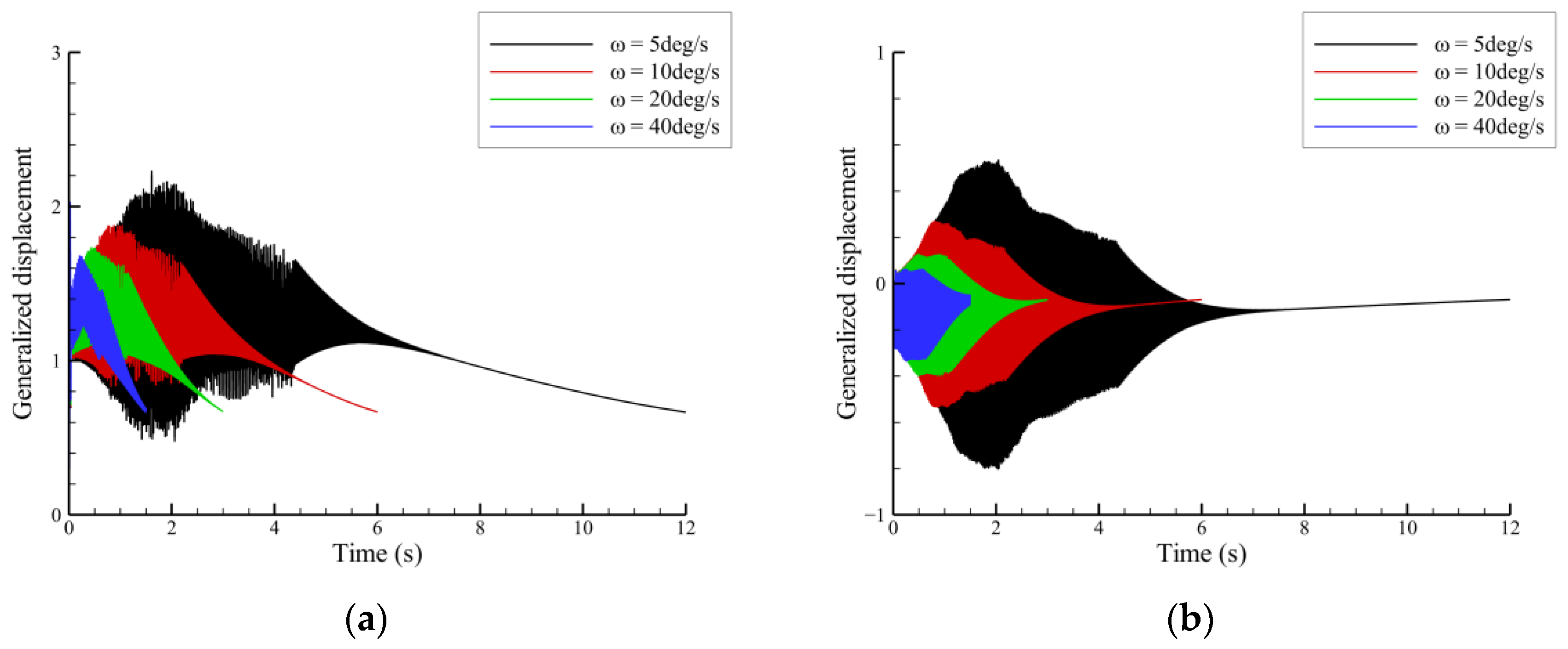
| Mode Order | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Natural frequency (Hz) | 27.595 | 48.453 | 196.89 | 273.51 | 327.72 | 483.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Lu, W.; Wu, J.; Guo, T.; Lv, B.; Guo, H.; Xia, H. Numerical Simulation of Folding Tail Aeroelasticity Based on the CFD/CSD Coupling Method. Vibration 2024, 7, 705-721. https://doi.org/10.3390/vibration7030037
Zhou D, Lu W, Wu J, Guo T, Lv B, Guo H, Xia H. Numerical Simulation of Folding Tail Aeroelasticity Based on the CFD/CSD Coupling Method. Vibration. 2024; 7(3):705-721. https://doi.org/10.3390/vibration7030037
Chicago/Turabian StyleZhou, Di, Weitao Lu, Jiangpeng Wu, Tongqing Guo, Binbin Lv, Hongtao Guo, and Hongya Xia. 2024. "Numerical Simulation of Folding Tail Aeroelasticity Based on the CFD/CSD Coupling Method" Vibration 7, no. 3: 705-721. https://doi.org/10.3390/vibration7030037
APA StyleZhou, D., Lu, W., Wu, J., Guo, T., Lv, B., Guo, H., & Xia, H. (2024). Numerical Simulation of Folding Tail Aeroelasticity Based on the CFD/CSD Coupling Method. Vibration, 7(3), 705-721. https://doi.org/10.3390/vibration7030037






