Rat-Tail Models for Studying Hand-Arm Vibration Syndrome: A Comparison between Living and Cadaver Rat Tails
Abstract
:1. Introduction
2. Materials and Methods
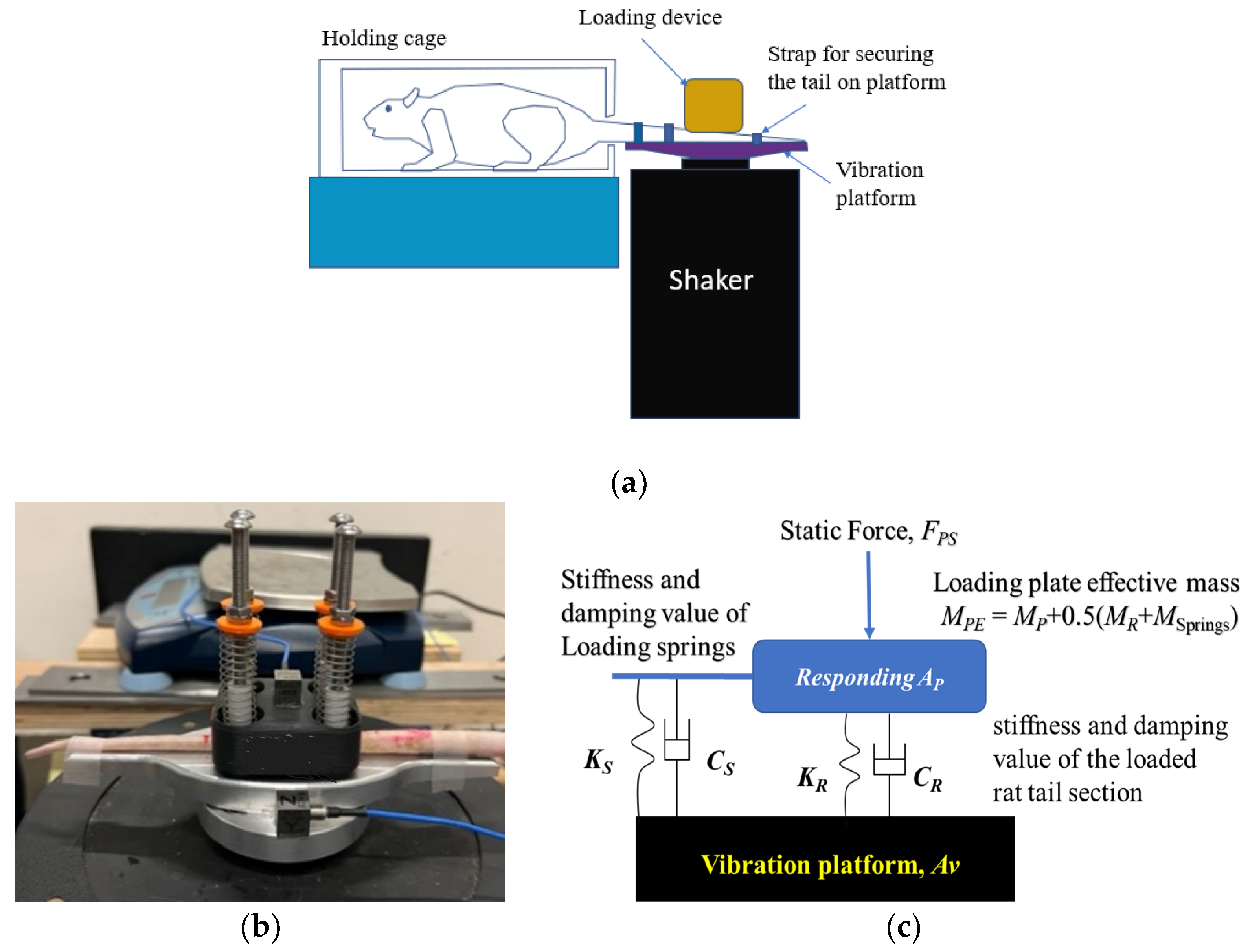
2.1. Rat-Tail Vibration Exposure System and Modeling Method
2.2. Tests with the Tails of Cadaver Rats
2.3. Tests with the Tails of Living Rats
2.4. Statistical Analyses
3. Results
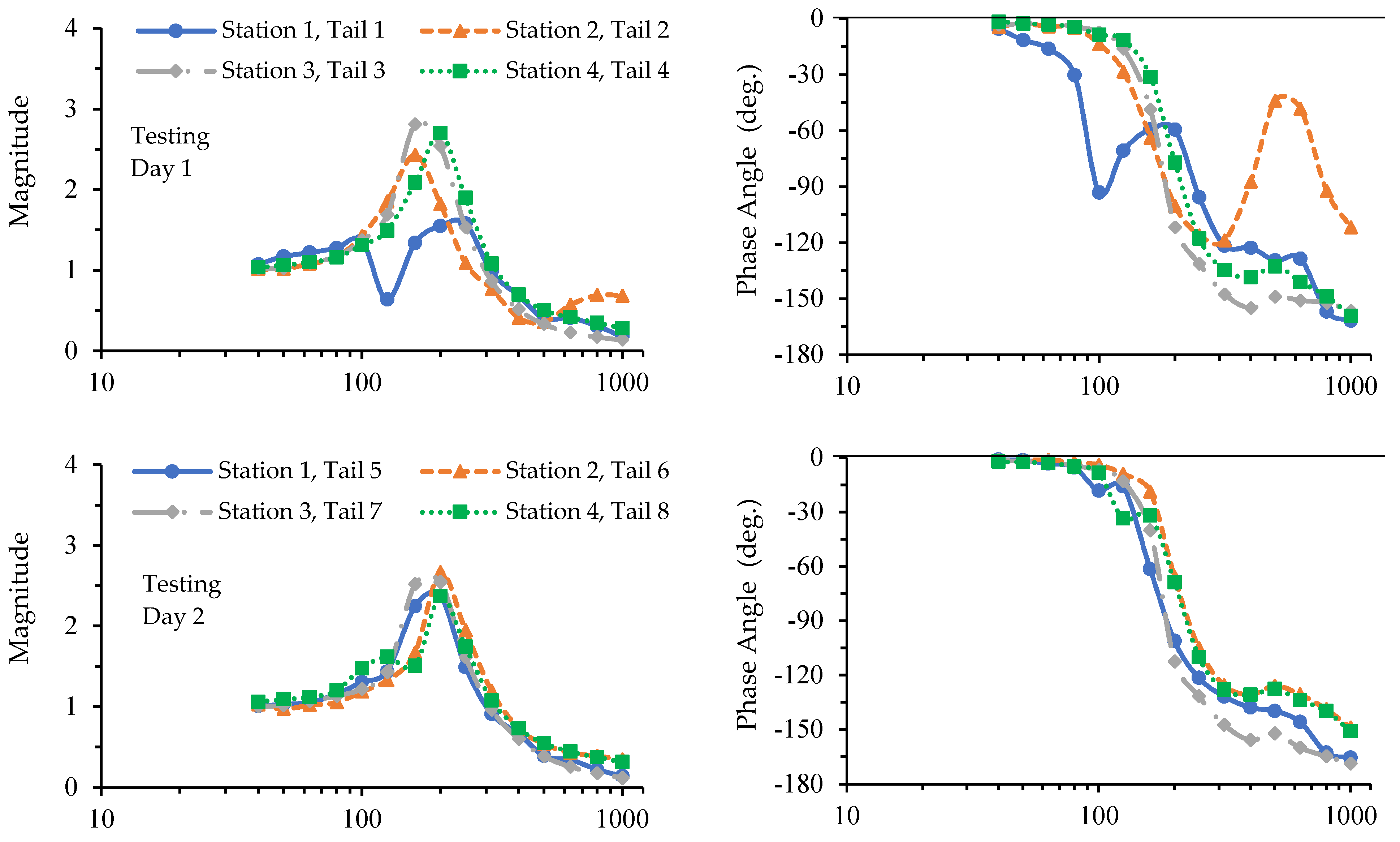
3.1. Results of the Tests with Cadaver Tails
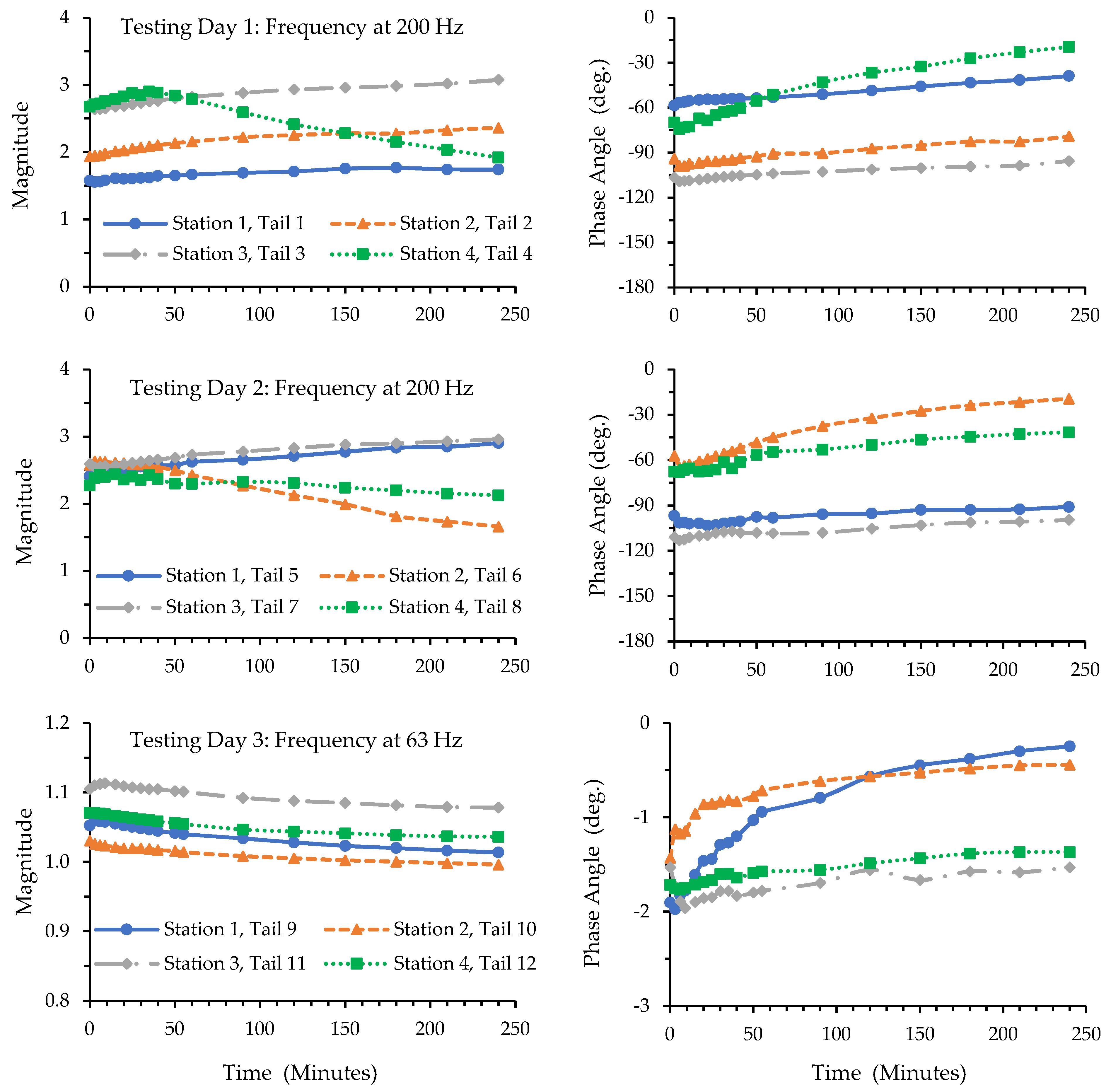
3.2. Results of the Tests with Living Rat Tails
4. Discussion
4.1. The Similarities and Differences between the Biodynamic Responses of Cadaver and Living Rat Tails
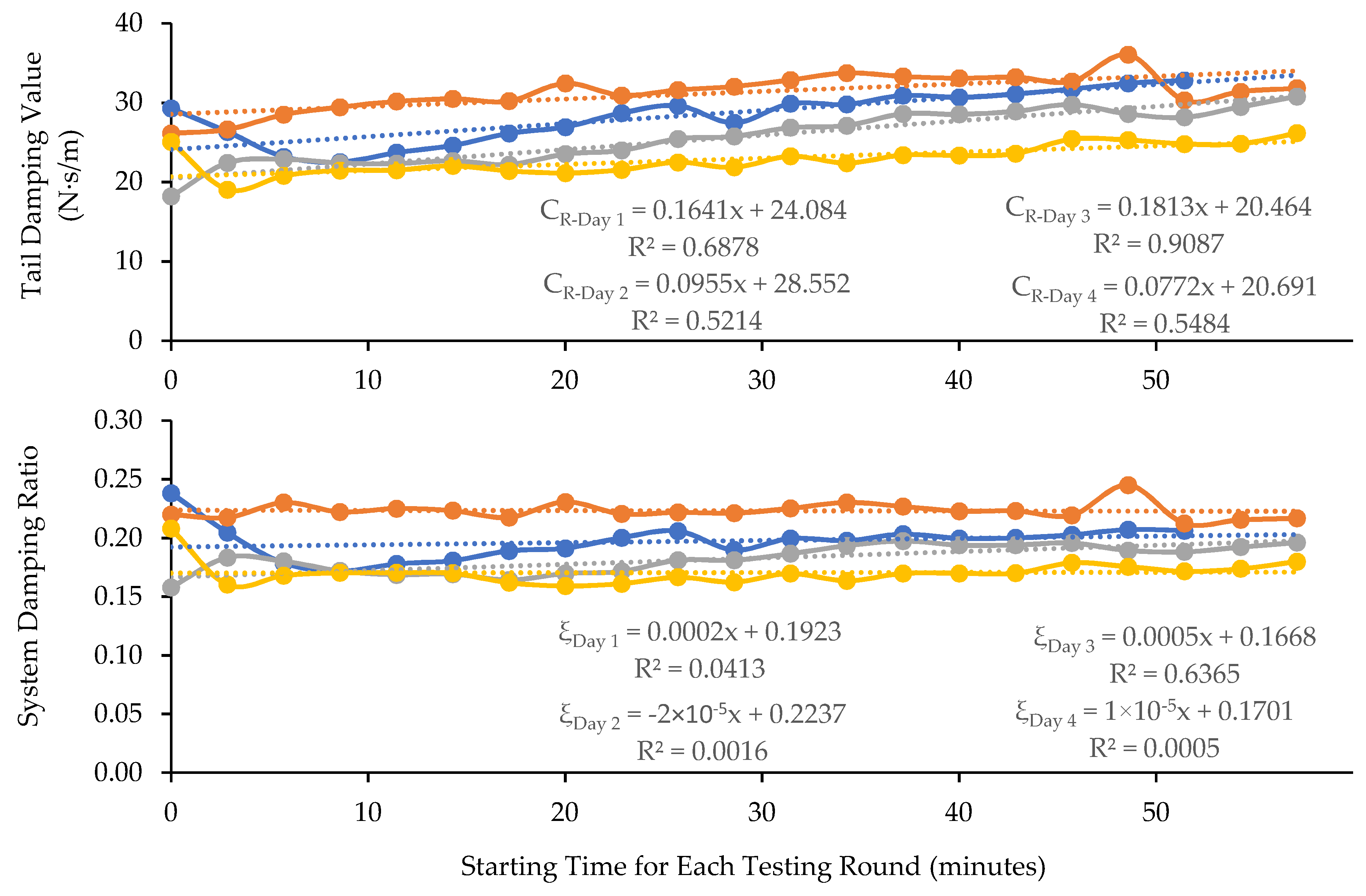
4.2. The Time Dependencies of Rat-Tail Biodynamic Responses
4.3. Improvement to the Rat-Tail Vibration Exposure System
- (I)
- Confirm that the loading devices work normally during each test by continuously monitoring the transfer function or loading plate response. A warning signal should be designed in exposure software. The rat for each testing station should not be changed so that the measured responses are directly comparable. If an abnormal or unreasonably large variation is detected, the testing station should be checked. If the loading plate is locked by friction, it can be released by adding lubricant to the frictional interfaces and/or adjusting the position/angle of the loading plate. The living tail may change its position, which could result in changes in the loading portion and the plate response. This can be corrected by adjusting the tail position and loading portion.
- (II)
- Redesign the loading device by eliminating the friction interfaces. The vibration displacements in the frequency range of interest are usually small. For small displacements, a flexible support structure can be applied to replace the friction interfaces for holding the loading plate while allowing the required displacements.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Griffin, M.J. Handbook of Human Vibration; Academic Press: London, UK, 1990; 988p, ISBN-13: 978-0123030412. [Google Scholar]
- Pelmear, P.L.; Wasserman, D.E. Hand-Arm Vibration: A Comprehensive Guide for Occupational Health Professionals, 2nd ed.; OEM Press: Beverly Farms, MA, USA, 1998; ISBN-13: 978-1883595227. [Google Scholar]
- Bovenzi, M.; Zadini, A.; Franzinelli, A.; Borgogni, F. Occupational musculoskeletal disorders in the neck and upper limbs of forestry workers exposed to hand arm vibration. Ergonomics 1991, 34, 547–562. [Google Scholar] [CrossRef] [PubMed]
- Stoyneva, Z.; Lyapina, M.; Tzvetkov, D.; Tzvetkov, D.; Vodenicharov, E. Current pathophysiological views on vibration-induced Raynaud’s phenomenon. Cardiovasc. Res. 2003, 57, 615–624. [Google Scholar] [CrossRef] [PubMed]
- 5349-1 ISO 5349-1; Mechanical Vibration–Measurement and Evaluation of Human Exposure to Hand-Transmitted Vibration–Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 2001.
- Bovenzi, M. Exposure-response relationship in the hand-arm vibration syndrome: An overview of current epidemiology research. Int. Arch. Occup. Environ. Health 1998, 71, 509–519. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.G.; Warren, C.; Xu, X.S.; Wu, J.Z.; Welcome, D.E.; Waugh, S.; Krajnak, K. A novel rat-tail model for studying human finger vibration health effects. J. Eng. Med. Proc. Inst. Mech. Eng. 2023, 237, 890–904. [Google Scholar] [CrossRef] [PubMed]
- Krajnak, K.; Warren, C.; Xu, X.S.; Chapman, P.; Waugh, S.; Boots, T.; Welcome, D.E.; Dong, R.G. Applied force alters sensorineural and peripheral vascular function in a rat model of hand-arm vibration syndrome. J. Occup. Environ. Med. 2024, 66, 93–104. [Google Scholar] [CrossRef] [PubMed]
- Moore, K.D.; Wu, J.Z.; Krajnak, K.; Warren, C.; Dong, R.G. Quantification of mechanical behavior of rat tail under compression. Biomed. Mater. Eng. 2024in press. [CrossRef] [PubMed]
- Pacurari, M.; Waugh, S.; Krajnak, K. Acute Vibration Induces Peripheral Nerve Sensitization in a Rat Tail Model: Possible Role of Oxidative Stress and Inflammation. Neuroscience 2019, 398, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.G.; Dong, J.H.; Wu, J.Z.; Rakheja, S. Modeling of biodynamic responses distributed at the fingers and the palm of the human hand-arm system. J. Biomech. 2007, 40, 2335–2340. [Google Scholar] [CrossRef] [PubMed]
- Welcome, D.E.; Krajnak, K.; Kashon, M.L.; Dong, R.G. An investigation on the biodynamic foundation of a rat tail vibration model. J. Eng. Med. Proc. Inst. Mech. Eng. H 2008, 222, 1127–1141. [Google Scholar] [CrossRef] [PubMed]




| Tail ID | Proximal Diameter (mm) | Distal Diameter (mm) | Exposed Tail Segment Length (mm) | Mean Diameter (dt) (mm) | Tail Mass of Exposed Segment Portion (Lt = 53 mm), MR (g) |
|---|---|---|---|---|---|
| 1 | 6.1 | 4.28 | 40.78 | 5.19 | 2.37 |
| 2 | 7.38 | 4.66 | 41.55 | 6.02 | 2.44 |
| 3 | 6.58 | 4.89 | 40.35 | 5.74 | 2.75 |
| 4 | 7.78 | 3.99 | 39.37 | 5.89 | 2.52 |
| 5 | 7.52 | 4.25 | 41.24 | 5.89 | 2.47 |
| 6 | 6.98 | 4.44 | 40.15 | 5.71 | 2.50 |
| 7 | 7.15 | 4.59 | 42.11 | 5.87 | 2.51 |
| 8 * | |||||
| 9 | 6.98 | 4.12 | 43.15 | 5.55 | 2.44 |
| 10 | 7.51 | 4.5 | 42.22 | 6.01 | 2.38 |
| 11 | 7.57 | 3.99 | 43.17 | 5.78 | 2.65 |
| 12 | 7.24 | 4.36 | 42.11 | 5.8 | 2.50 |
| Mean | 7.16 | 4.37 | 41.47 | 5.77 | 2.50 |
| Tail ID | Tail Stiffness, KR (N/m) | Tail Damping Value, CR (N·s/m) | Natural Frequency, fn (Hz) | Damping Ratio, ζ |
|---|---|---|---|---|
| Tail 1 * | ||||
| Tail 2 | 65,103 | 30 | 175 | 0.27 |
| Tail 3 | 72,465 | 18 | 185 | 0.16 |
| Tail 4 | 98,133 | 25 | 215 | 0.19 |
| Tail 5 | 86,127 | 28 | 202 | 0.23 |
| Tail 6 | 103,644 | 26 | 221 | 0.19 |
| Tail 7 | 83,074 | 24 | 198 | 0.19 |
| Tail 8 | 101,416 | 32 | 219 | 0.23 |
| Tail 9 | 82,167 | 33 | 197 | 0.27 |
| Tail 10 | 53,040 | 38 | 158 | 0.38 |
| Tail 11 | 64,205 | 23 | 174 | 0.21 |
| Tail 12 | 78,008 | 18 | 192 | 0.16 |
| Mean | 80,671 | 27 | 194 | 0.23 |
| STD | 16,286 | 6 | 20 | 0.06 |
| CV | 0.20 | 0.23 | 0.10 | 0.28 |
| Tail ID | Tail Stiffness, KR (N/m) | Tail Damping Value, CR (N·s/m) | Natural Frequency, fn (Hz) | Damping Ratio, ζ |
|---|---|---|---|---|
| Tail 1 | 83,454 | 33 | 198 | 0.27 |
| Tail 2 | 85,586 | 31 | 201 | 0.25 |
| Tail 3 | 95,494 | 21 | 212 | 0.17 |
| Tail 4 | 85,912 | 22 | 201 | 0.18 |
| Tail 5 | 68,911 | 35 | 180 | 0.31 |
| Tail 6 | 86,176 | 33 | 202 | 0.26 |
| Mean | 84,256 | 29 | 199 | 0.24 |
| STD | 8609 | 6 | 10 | 0.05 |
| CV | 0.10 | 0.20 | 0.05 | 0.23 |
| Difference = (Living mean − Cadaver mean)/Living mean | 4.3% (Insignificant: p = 0.63) | 8.1% (Insignificant: p = 0.46) | 2.4% (Insignificant: p = 0.59) | 6.1% (Insignificant: p = 0.64) |
| Tail Stiffness, KR (N/m) | |||||||
|---|---|---|---|---|---|---|---|
| IDs | Tail 1 | Tail 2 | Tail 3 | Tail 4 | Tail 5 | Tail 6 | Mean |
| Station 1 | 83,454 | 68,971 | 72,340 | 74,470 | 68,911 | 69,305 | 72,908 |
| Station 2 | 68,353 | 85,586 | 78,846 | 71,372 | 83,918 | 86,176 | 79,042 |
| Station 3 | 107,189 | 82,954 | 95,494 | 93,590 | 83,805 | 80,784 | 90,636 |
| Station 4 | 52,827 * | 71,261 | 73,798 | 85,912 | 89,719 | 38,831 * | 68,725 |
| Tail Damping Value, CR (N·s/m) | |||||||
| Station 1 | 33 | 15 | 18 | 29 | 35 | 21 | 25 |
| Station 2 | 50 | 31 | 22 | 19 | 30 | 33 | 31 |
| Station 3 | 16 | 18 | 21 | 25 | 36 | 25 | 24 |
| Station 4 | 65 * | 20 | 29 | 22 | 42 | 90 * | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Warren, C.M.; Xu, X.S.; Jackson, M.; McKinney, W.G.; Wu, J.Z.; Welcome, D.E.; Waugh, S.; Chapman, P.; Sinsel, E.W.; Service, S.; et al. Rat-Tail Models for Studying Hand-Arm Vibration Syndrome: A Comparison between Living and Cadaver Rat Tails. Vibration 2024, 7, 722-737. https://doi.org/10.3390/vibration7030038
Warren CM, Xu XS, Jackson M, McKinney WG, Wu JZ, Welcome DE, Waugh S, Chapman P, Sinsel EW, Service S, et al. Rat-Tail Models for Studying Hand-Arm Vibration Syndrome: A Comparison between Living and Cadaver Rat Tails. Vibration. 2024; 7(3):722-737. https://doi.org/10.3390/vibration7030038
Chicago/Turabian StyleWarren, Christopher M., Xueyan S. Xu, Mark Jackson, Walter G. McKinney, John Z. Wu, Daniel E. Welcome, Stacey Waugh, Phillip Chapman, Erik W. Sinsel, Samantha Service, and et al. 2024. "Rat-Tail Models for Studying Hand-Arm Vibration Syndrome: A Comparison between Living and Cadaver Rat Tails" Vibration 7, no. 3: 722-737. https://doi.org/10.3390/vibration7030038
APA StyleWarren, C. M., Xu, X. S., Jackson, M., McKinney, W. G., Wu, J. Z., Welcome, D. E., Waugh, S., Chapman, P., Sinsel, E. W., Service, S., Krajnak, K., & Dong, R. G. (2024). Rat-Tail Models for Studying Hand-Arm Vibration Syndrome: A Comparison between Living and Cadaver Rat Tails. Vibration, 7(3), 722-737. https://doi.org/10.3390/vibration7030038







