Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring
Abstract
:1. Introduction
2. Equation of Motion for Base Exited System
3. Response Analysis of Nonlinear Isolation System for Base Excited
4. Results and Discussion
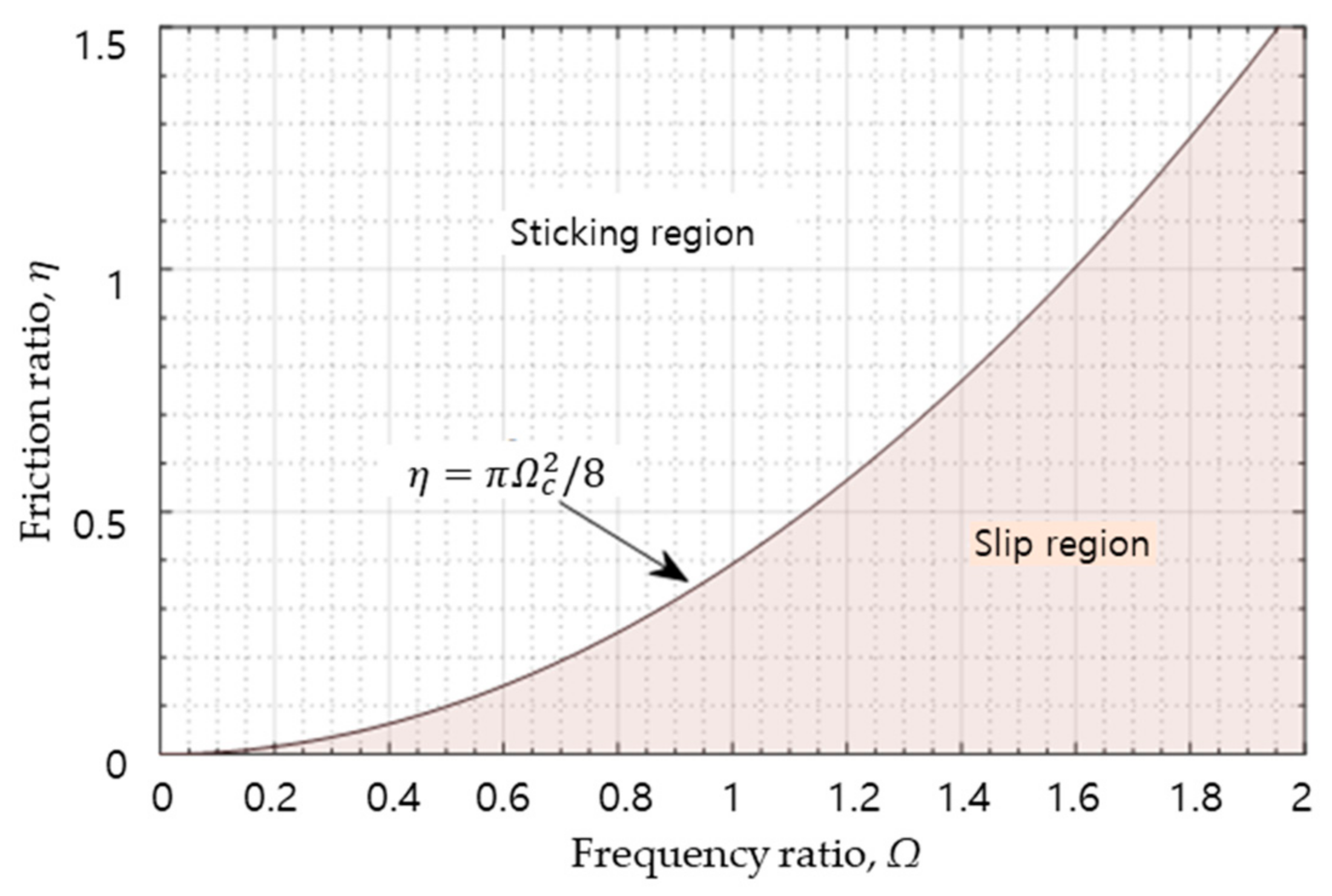
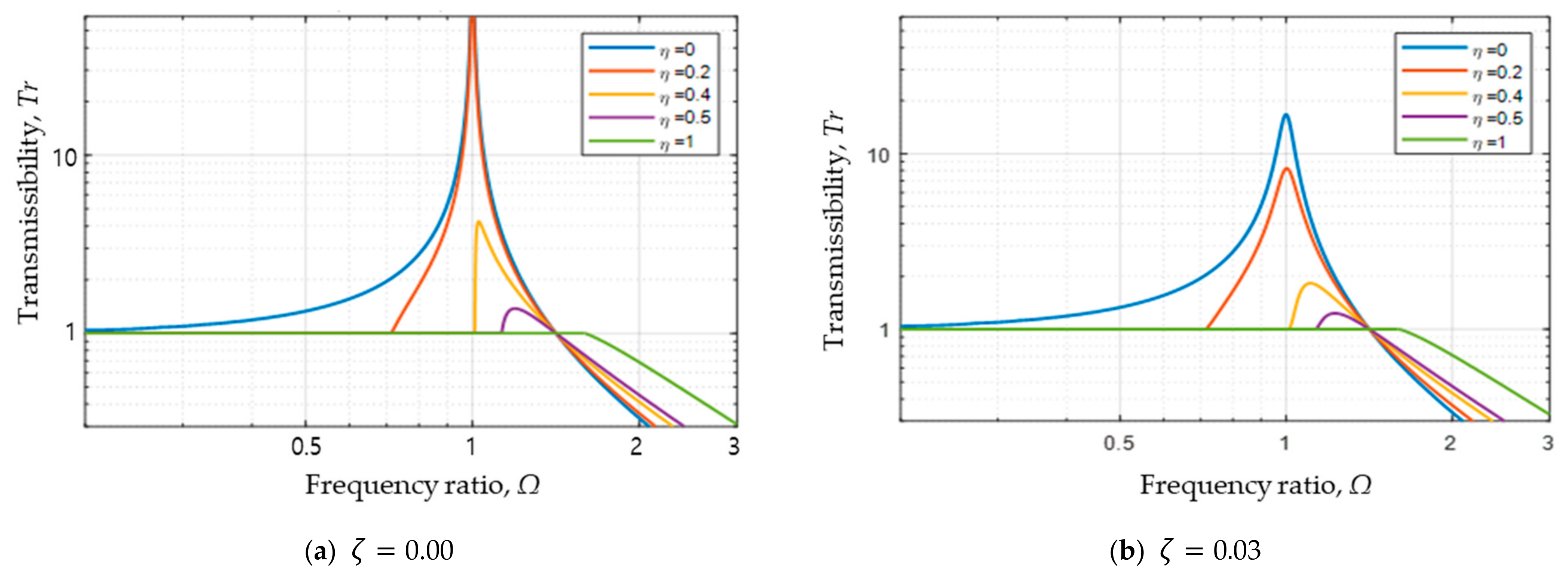
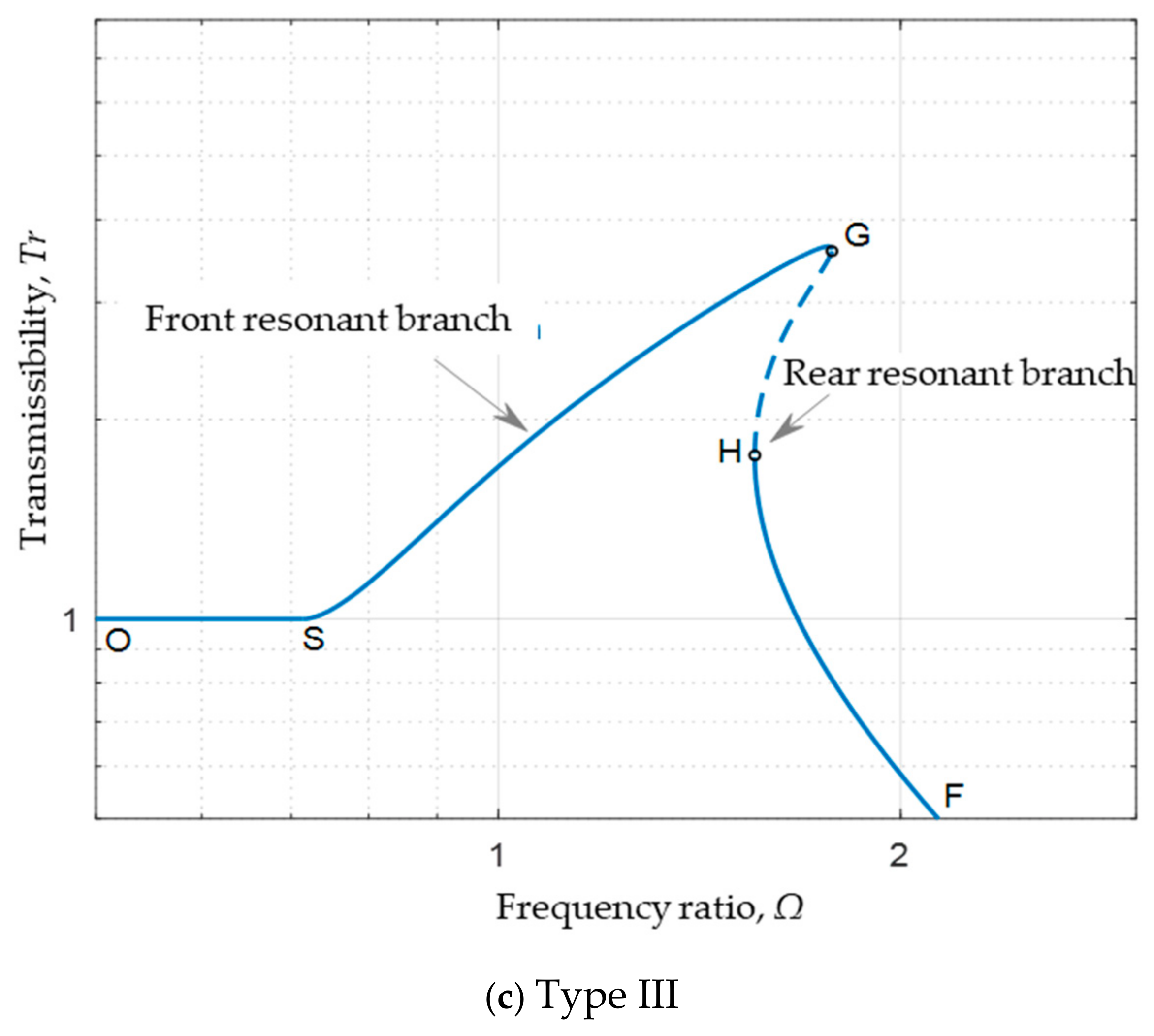
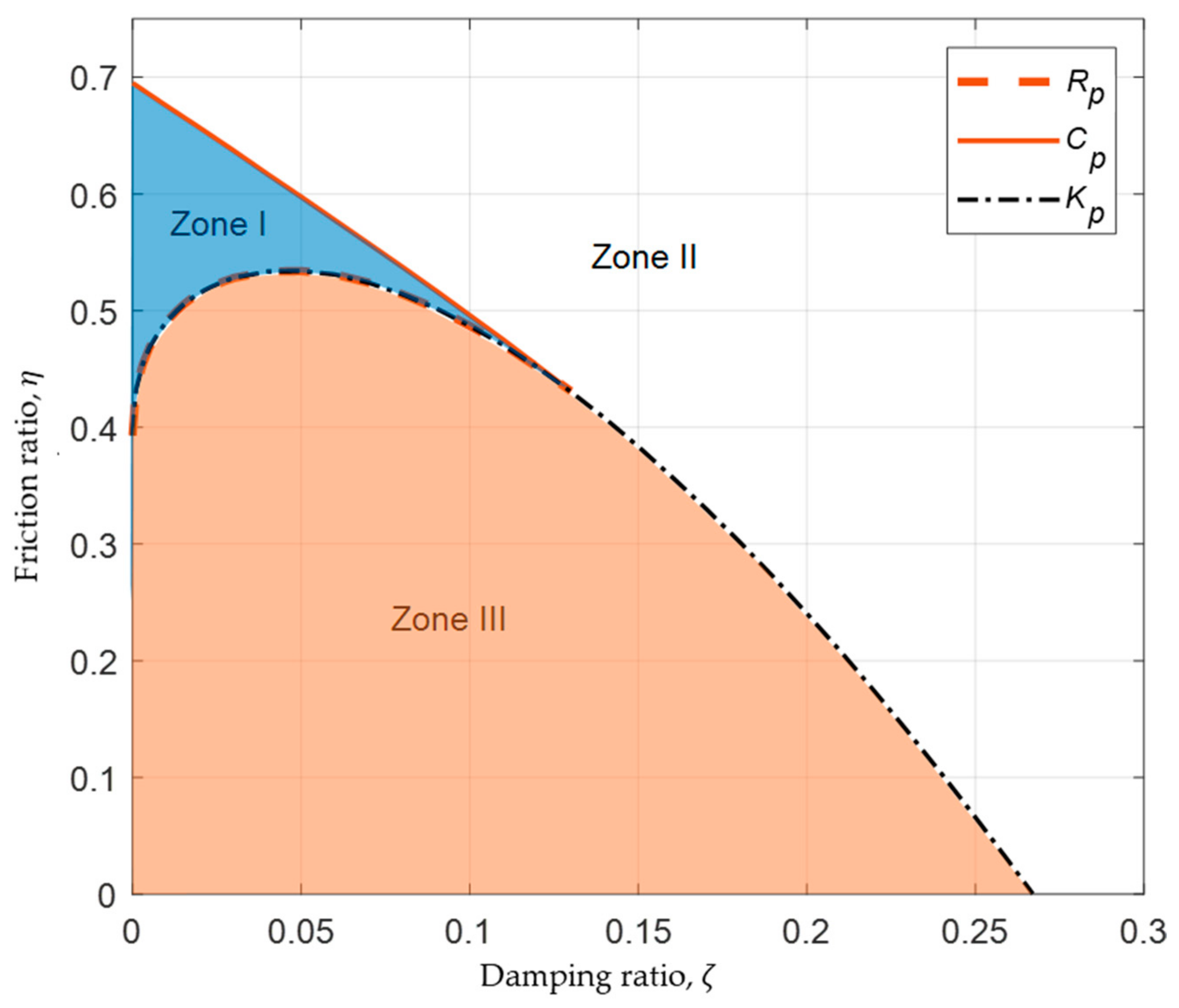
4.1. System with Zero Nonlinear Spring Coefficient (
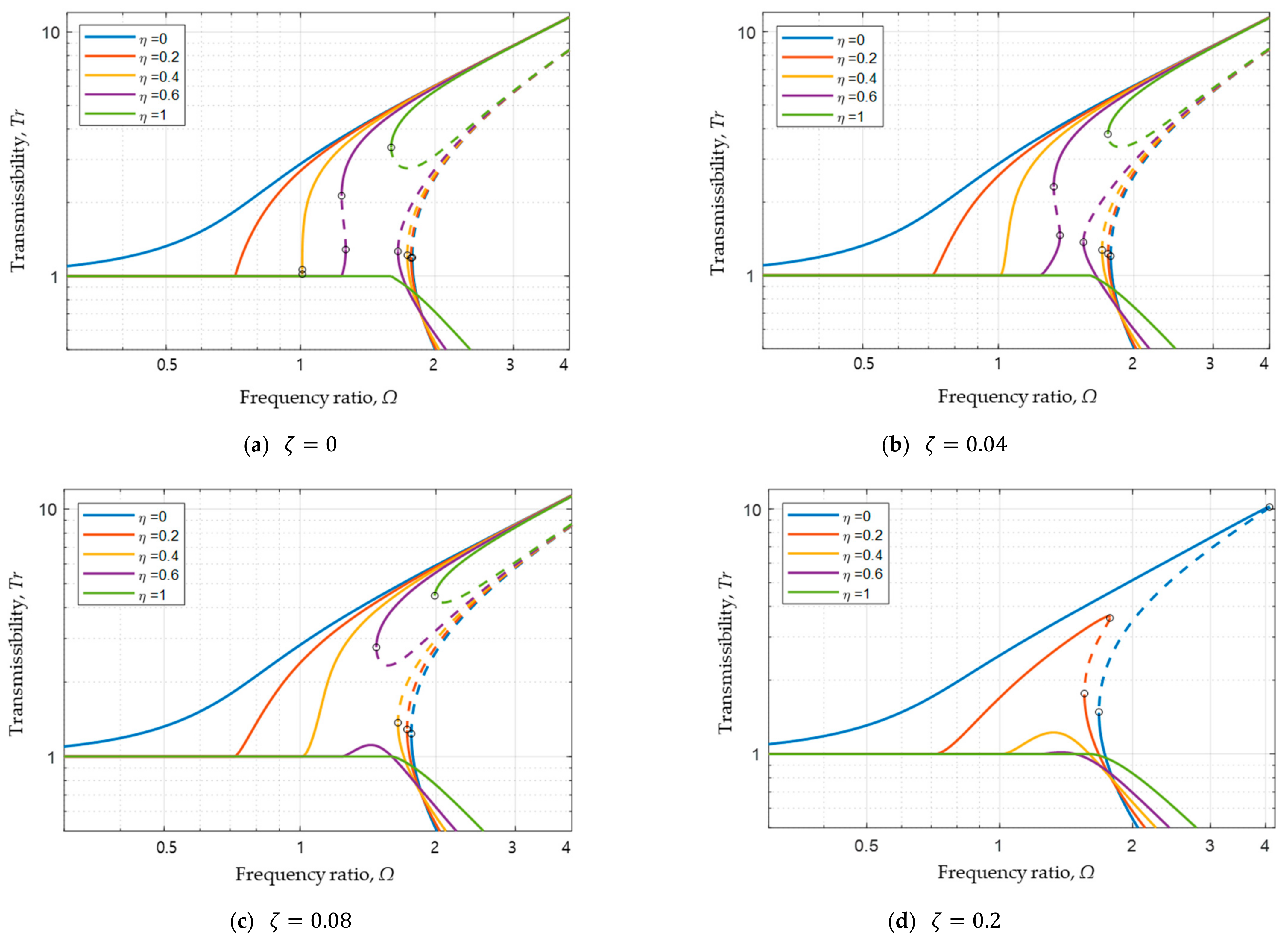
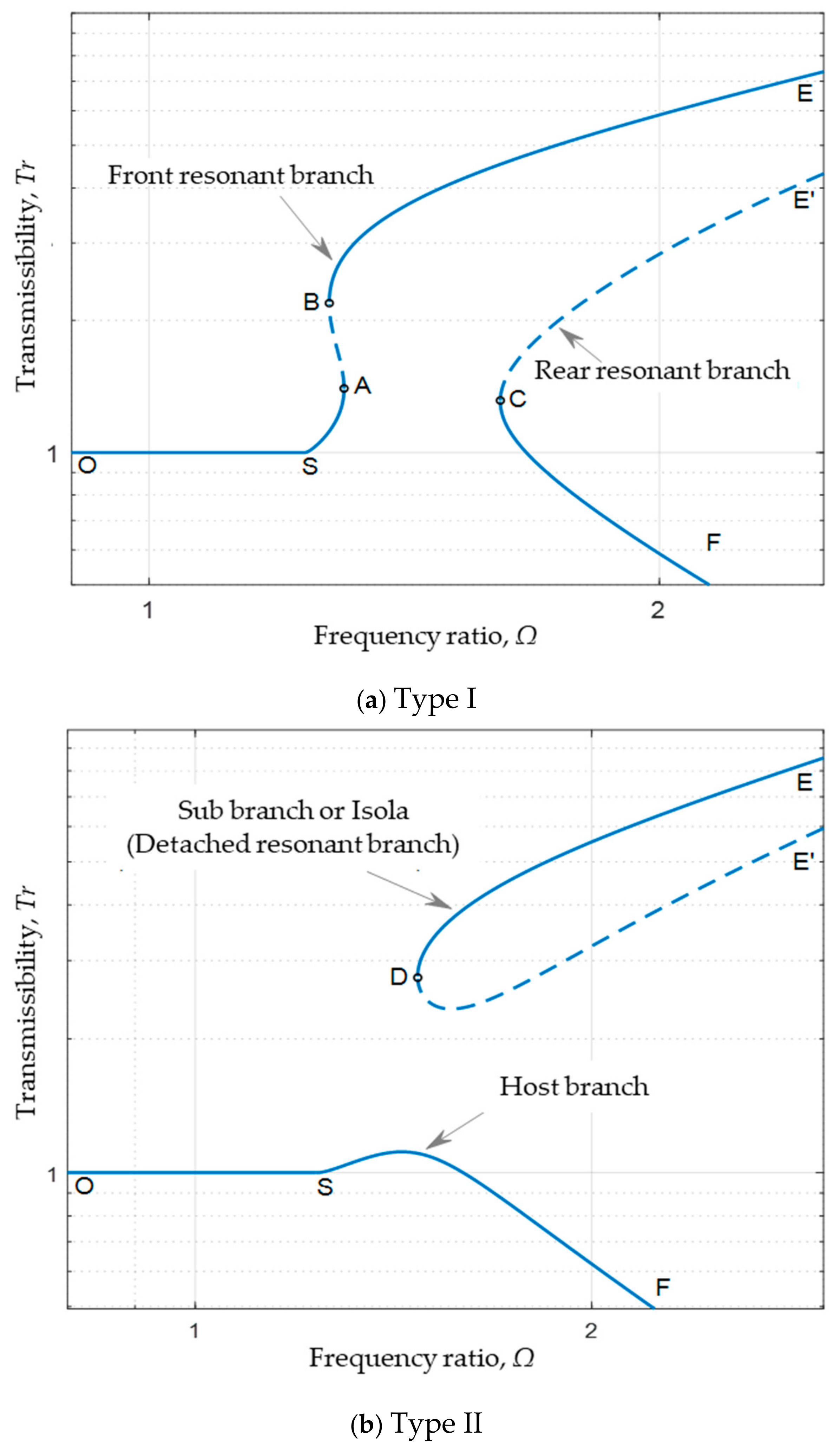
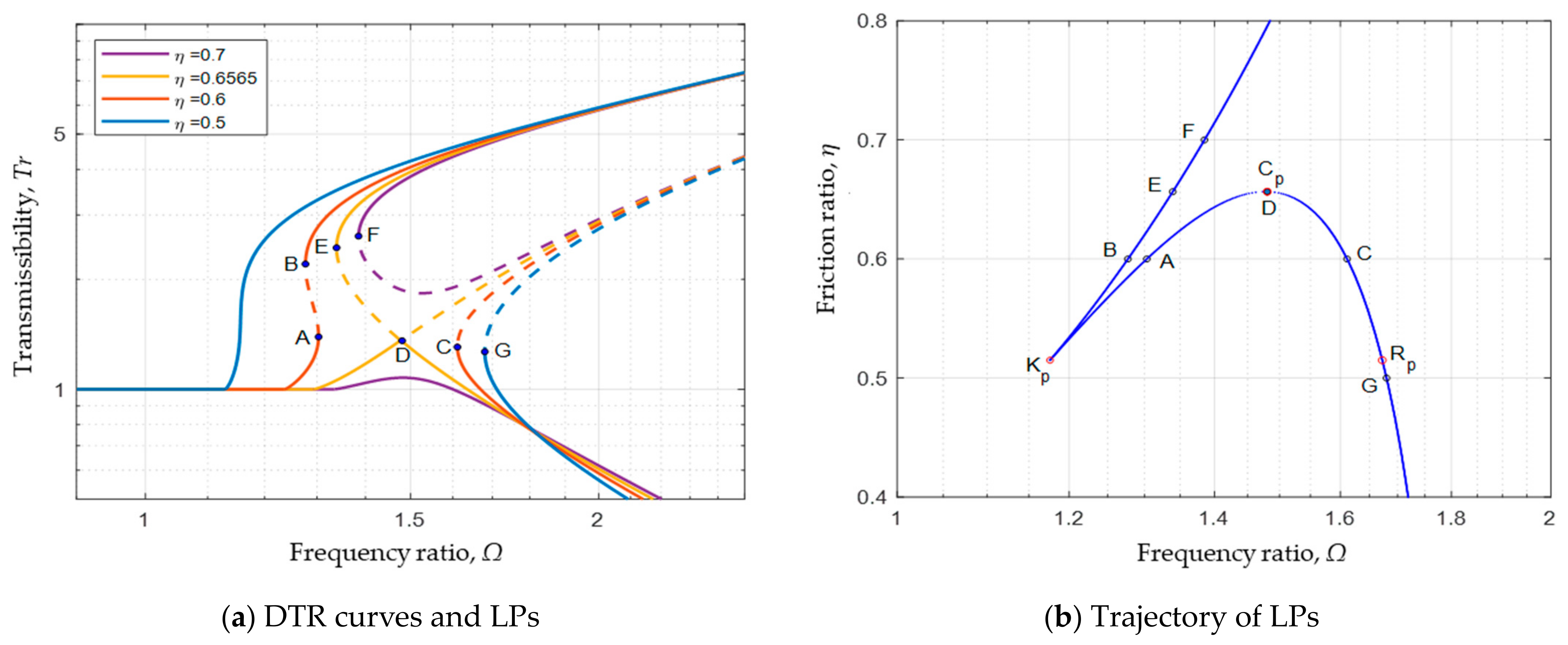
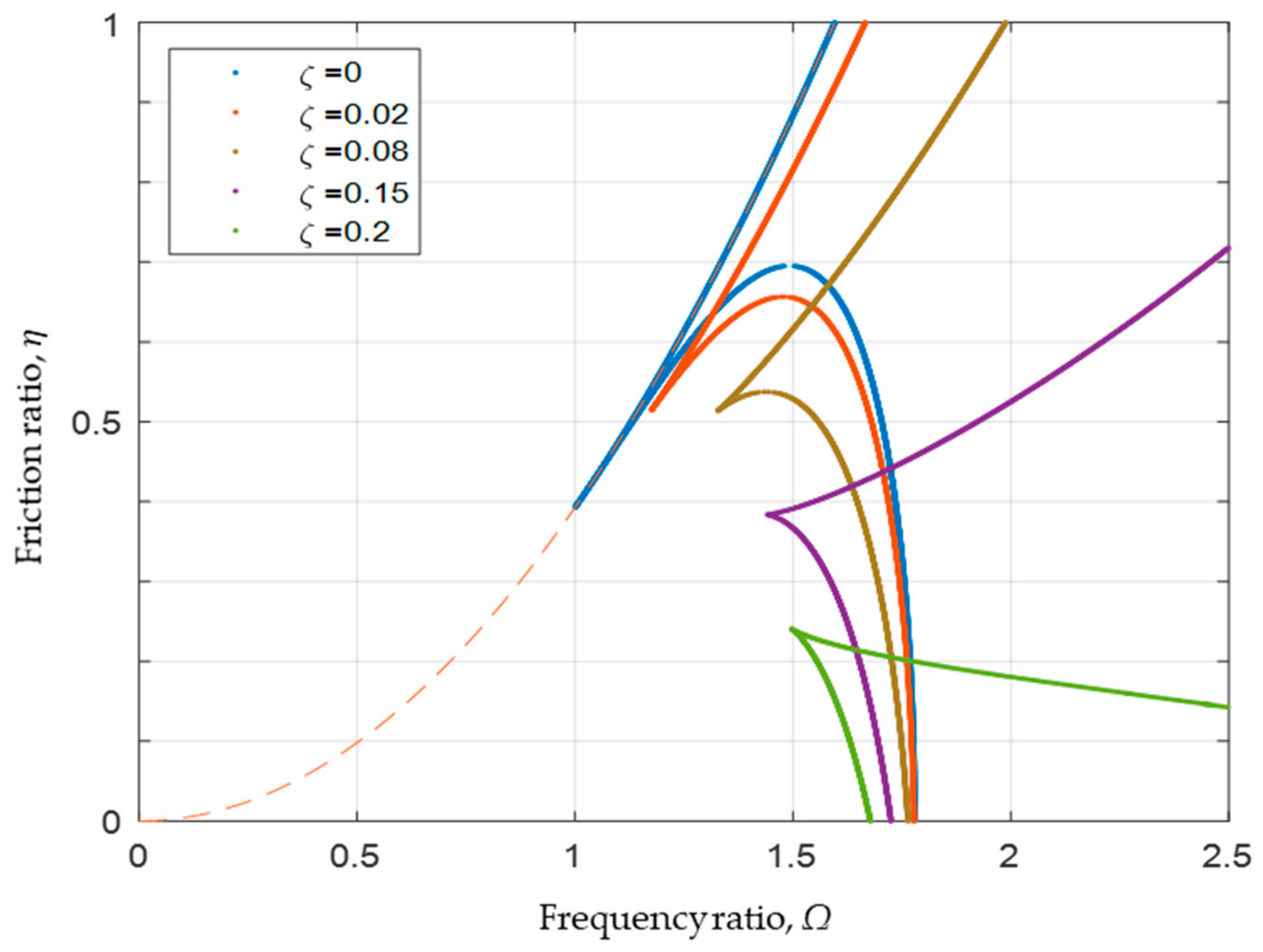
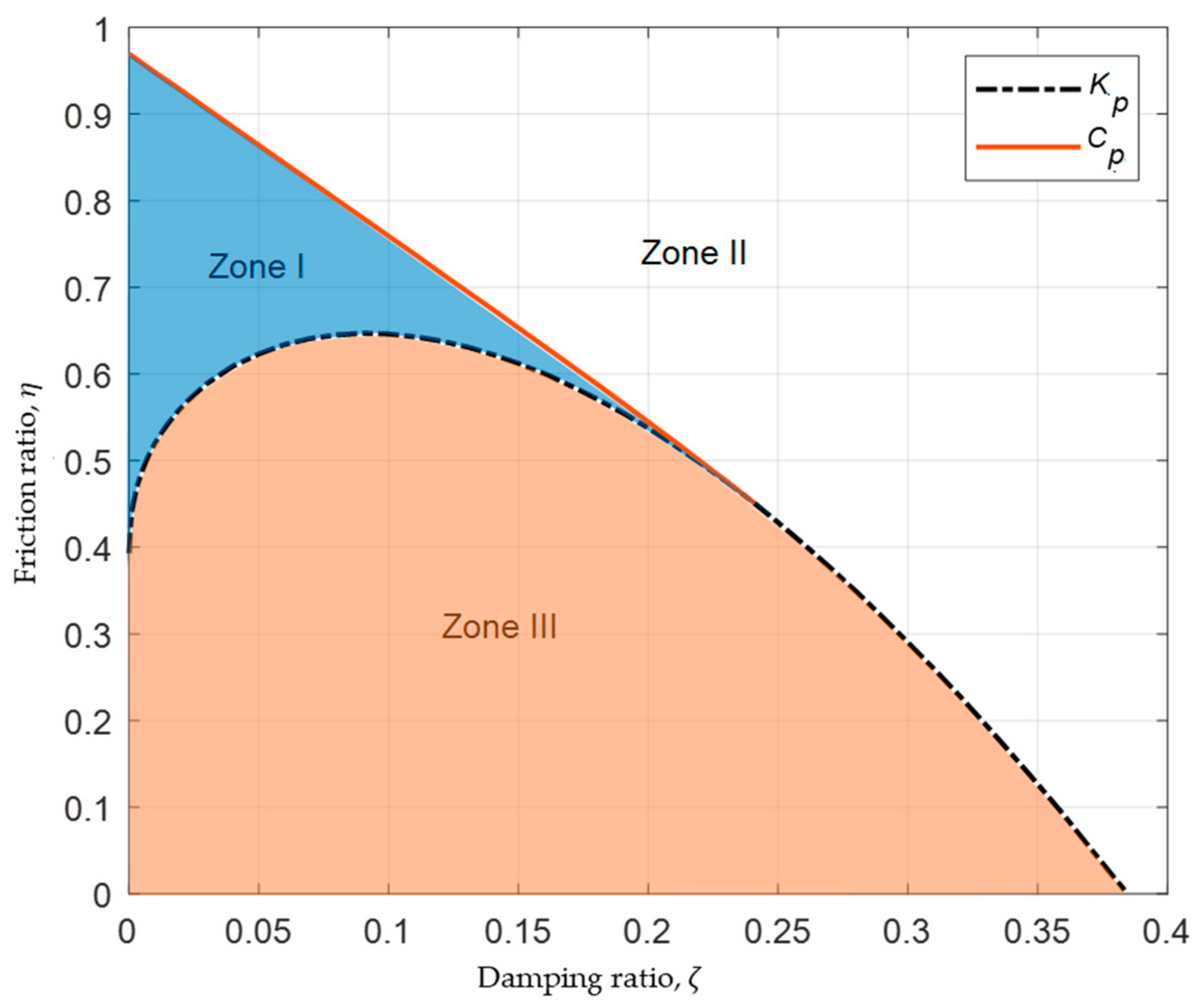
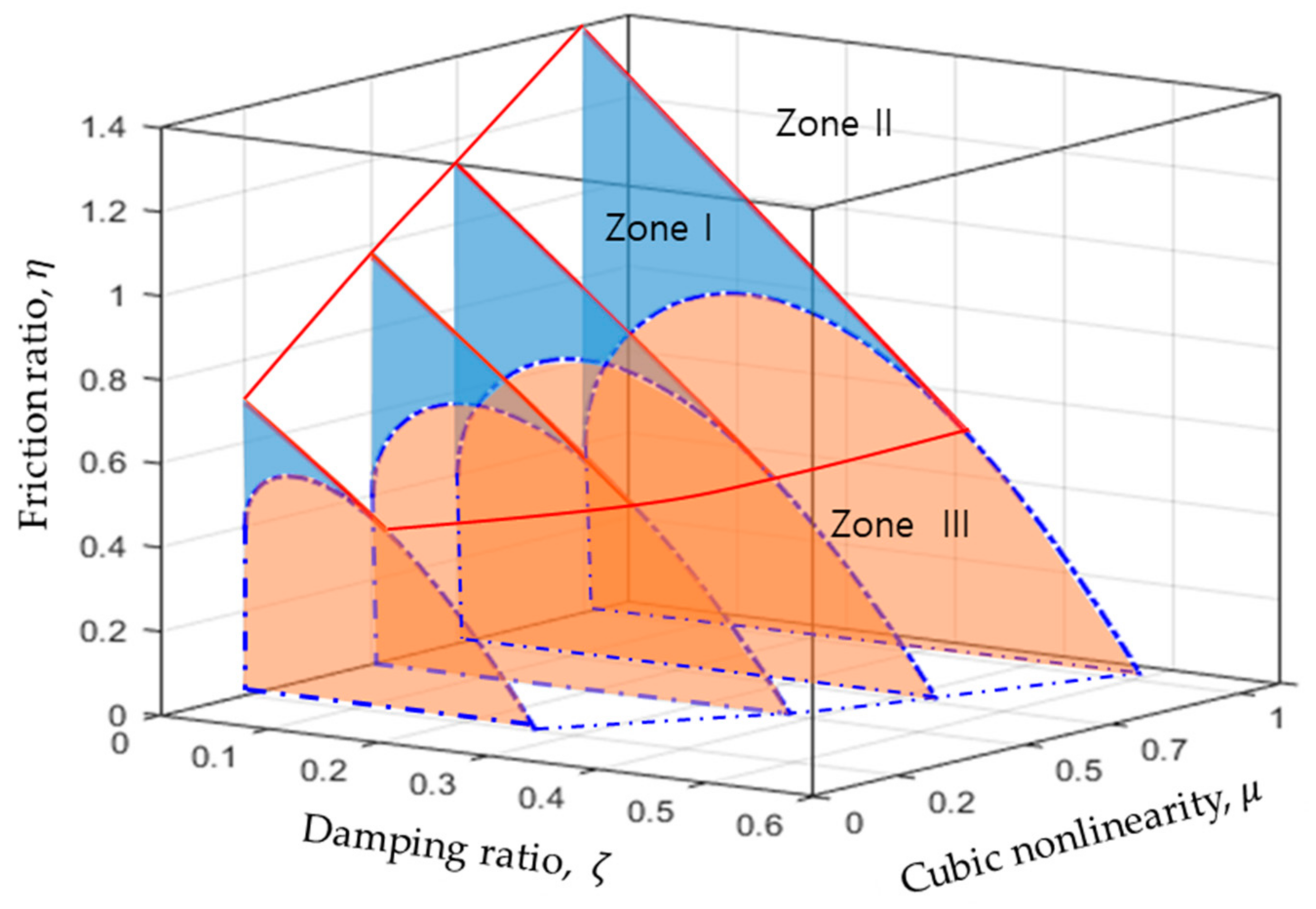
4.2. System with Positive Nonlinear Spring Coefficient (
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| m | mass of system |
| c | viscous damping coefficient |
| stiffness coefficient | |
| coefficient of cubic nonlinear stiffness | |
| friction force | |
| displacement of mass | |
| displacement of base | |
| relative displacement of the mass with respect to the base | |
| excitation frequency | |
| amplitude of base displacement | |
| dimensionless relative displacement | |
| natural frequency | |
| dimensionless time | |
| frequency ratio | |
| damping ratio | |
| friction ratio | |
| coefficient of cubic nonlinearity | |
| amplitude of relative displacement response | |
| phase of relative displacement response | |
| steady-state amplitude of relative displacement response | |
| steady-state phase of relative displacement response | |
| break-loose frequency, starting frequency of motion, or critical frequency | |
| absolute displacement transmissibility (ADTR) | |
| SVAP | slowly varying amplitude and phase |
| DTR | displacement transmissibility |
| LP | Limit Point |
| kink point | |
| critical point | |
| intersection point |
References
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wu, C. A state-of-the-art review on low-frequency nonlinear vibration isolation with electromagnetic mechanisms. Appl. Math. Mech.-Engl. 2022, 43, 1045–1062. [Google Scholar] [CrossRef]
- Santhosh, B.; Narayanan, S.; Padmanabhan, C. Nonlinear Dynamics of Shrouded Turbine Blade System with Impact and Friction. Appl. Mech. Mater. 2014, 76, 81–92. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vib. 2011, 330, 6311–6335. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 2013, 70, 99–112. [Google Scholar] [CrossRef]
- Lang, Z.Q.; Jing, X.J.; Billings, S.A.; Tomlinson, G.R.; Peng, Z.K. Theoretical study of the effects of nonlinear viscous damping on vibration isolation of sdof systems. J. Sound Vib. 2009, 323, 352–365. [Google Scholar] [CrossRef]
- Yuvaraju, B.A.G.; Srinivas, J.; Nanda, B.K. Nonlinear dynamics of friction-induced regenerative chatter in internal turning with process damping forces. J. Sound Vib. 2023, 544, 117386. [Google Scholar] [CrossRef]
- Ruzicka, J.E.; Derby, T.F. Influence of Damping in Vibration Isolation, SVM-7; Shock and Vibration Information Center: Washington DC, USA, 1971. [Google Scholar]
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Ledezma-Ramírez, D.F.; Tapia-González, P.E.; Ferguson, N.; Brennan, M.; Tang, B. Recent advances in shock vibration isolation: An overview and future possibilities. Appl. Mech. Rev. 2019, 71, 060802. [Google Scholar] [CrossRef]
- Rivin, E.I. Passive Vibration Isolation; ASME Press: New York, NY, USA, 2003. [Google Scholar]
- Hong, S.C.; Hur, D.J. Dynamic behavior of a simple rolling seismic isolator with a position restoring device. Appl. Sci. 2018, 8, 1910. [Google Scholar] [CrossRef]
- Hur, D.J.; Hong, S.C. Analysis of an isolation system with vertical spring-viscous dampers in horizontal and vertical ground motion. Appl. Sci. 2020, 10, 1141. [Google Scholar] [CrossRef]
- Shin, Y.H.; Lee, J.H.; Jung, B.C.; Moon, S.J. Design of passive vibration isolation element by wire mesh material for developing a hybrid mount. Trans. Korean Soc. Noise Vib. Eng. 2020, 30, 75–81. [Google Scholar] [CrossRef]
- Alrajhi, J.; Alhaifi, K.; Alardhi, M.; Alhaifi, N.; Alazmi, J.; Khalfan, A.; Alkhulaifi, K. The numerical analysis of single degree of freedom vibration system with non-linearity. J. Mech. Eng. Autom. 2023, 12, 6–19. [Google Scholar]
- Min, K.W.; Kim, H.S. Performance based design of friction dampers for seismically excited structures. J. Earthq. Eng. Soc. Korea 2003, 7, 17–24. [Google Scholar]
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Mickens, R.E. Truly Nonlinear Oscillations, Harmonic Balance, Parameter Expansions, Iteration, and Averaging Methods; World Scientific Publishing Company: Danvers, MA, USA, 2010. [Google Scholar]
- Hagedorn, P. Non-Linear Oscillations; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Sanders, J.A.; Verhulst, F.; Murdock, J. Averaging Methods in Nonlinear Dynamical Systems, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Shahraeeni, M.; Sorokin, V.; Mace, B.; Ilanko, S. Effect of damping nonlinearity on the dynamics and performance of a quasi-zero-stiffness vibration isolator. J. Sound Vib. 2022, 526, 116822. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, R.; Yang, Q. Recent advances in quasi-zero stiffness vibration isolation systems: An overview and future possibilities. Machines 2022, 10, 813. [Google Scholar] [CrossRef]
- Brennan, M.J.; Kovacic, I.; Carrella, A.; Waters, T.P. On the jump-up and jump-down frequencies of the Duffing oscillator. J. Sound Vib. 2008, 318, 1250–1261. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Barquist, C.S.; Jiang, W.G.; Gunther, K.; Lee, Y. Determining the source of phase noise: Response of a driven Duffing oscillator to low-frequency damping and resonance frequency fluctuations. Phys. D Nonlinear Phenom. 2021, 427, 13299. [Google Scholar] [CrossRef]
- Liu, S.; Peng, G.; Li, Z.; Li, W. Analytical jump-avoidance criteria of Duffing-type vibration isolation systems under base and force excitations based on concave-convex property. J. Vib. Control 2023, 29, 4082–4092. [Google Scholar] [CrossRef]
- Murata, A.; Kume, Y.; Hashimoto, F. Application of catastrophe theory to forced vibration of a diaphragm air spring. J. Sound Vib. 1987, 112, 31–44. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Lineton, B. On the resonance response of an asymmetric Duffing oscillator. Int. J. Non-Linear Mech. 2008, 43, 858–867. [Google Scholar] [CrossRef]
- Shi, B.; Yang, J.; Li, T. Enhancing Vibration Isolation Performance by Exploiting Novel Spring-Bar Mechanism. Appl. Sci. 2021, 11, 8852. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A.; Hills, D.A. Displacement transmissibility of a Coulomb friction oscillator subject to jointed base-wall motion. Nonlinear Dyn. 2019, 98, 2595–2612. [Google Scholar] [CrossRef]
- Wang, D.; Song, L.; Zhu, R.; Cao, P. Nonlinear dynamics and stability analysis of dry friction damper for supercritical transmission shaft. Nonlinear Dyn. 2022, 110, 3135–3149. [Google Scholar] [CrossRef]
- Uzdin, A.M.; Kuznetsova, I.O.; Frese, M.; Nazarova, S.S.; Nazarov, A.A. Analysis of the behaviour of seismic isolated structure on bearings connected to the structure with a dry friction damper. AIP Conf. Proc. 2023, 2612, 040012. [Google Scholar]
- Benacchio, S.; Giraud-Audine, C.; Thomas, O. Effect of dry friction on a parametric nonlinear oscillator. Nonlinear Dyn. 2022, 108, 1005–1026. [Google Scholar] [CrossRef]
- Zucca, S.; Firrone, C.M. Nonlinear dynamics of mechanical systems with friction contacts: Coupled static and dynamic multi-harmonic balance method and multiple solutions. J. Sound Vib. 2014, 333, 916–926. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Zucca, S. Determination of periodic response limits among multiple solutions for mechanical systems with wedge dampers. J. Sound Vib. 2021, 494, 115900. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Groß, J.; Krack, M. Frequency response variability in friction-damped structures due to non-unique residual tractions: Obtaining conservative bounds using a nonlinear-mode-based approach. Mech. Syst. Signal Process. 2013, 201, 110651. [Google Scholar] [CrossRef]
- Starossek, U. Exact analytical solutions for forced cubic restoring force oscillator. Nonlinear Dyn. 2016, 83, 2349–2359. [Google Scholar] [CrossRef]
- Ravindra, B.; Mallik, A.K. Hard Duffing-type Vibration Isolator with Combined Coulomb and Viscous Damping. Int. J. Non-Linear Mech. 1993, 28, 427–440. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, L. Free resonance analysis of bilinear hysteresis dry friction damper. J. Vib. Shock 2016, 3, 92–95. [Google Scholar]
- Huang, X.; Sun, J.; Hua, H.; Zhang, Z. The isolation performance of vibration systems with general velocity-displacement-dependent nonlinear damping under base excitation: Numerical and experimental study. Nonlinear Dyn. 2016, 85, 777–796. [Google Scholar] [CrossRef]
- Yu, H.; Xu, Y.; Sun, X. Analysis of the non-resonance of nonlinear vibration isolation system with dry friction. J. Mech. Sci. Technol. 2018, 32, 1489–1497. [Google Scholar] [CrossRef]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A. MATCONT: A Matlab Package for Numerical Bifurcation Analysis of ODEs. ACM Trans. Math. Softw. 2003, 29, 141–164. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hur, D.J.; Hong, S.C. Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring. Vibration 2024, 7, 1210-1225. https://doi.org/10.3390/vibration7040062
Hur DJ, Hong SC. Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring. Vibration. 2024; 7(4):1210-1225. https://doi.org/10.3390/vibration7040062
Chicago/Turabian StyleHur, Deog Jae, and Sung Chul Hong. 2024. "Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring" Vibration 7, no. 4: 1210-1225. https://doi.org/10.3390/vibration7040062
APA StyleHur, D. J., & Hong, S. C. (2024). Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring. Vibration, 7(4), 1210-1225. https://doi.org/10.3390/vibration7040062







