Integrating Density Functional Theory Modeling with Experimental Data to Understand and Predict Sorption Reactions: Exchange of Salicylate for Phosphate on Goethite
Abstract
1. Introduction
1.1. Macroscopic Data—Adsorption Isotherms, pH Edges, Calorimetry, Adsorption/Desorption Kinetics
1.2. Molecular Data—IR/Raman, EXAFS/XANES
1.3. Classical Molecular Mechanics Simulations
1.4. DFT
2. Methods
2.1. Adsorption and Exchange Experiments
2.2. DFT
2.3. Basis Sets
2.4. Exchange-Correlation Functionals
2.5. Model Construction
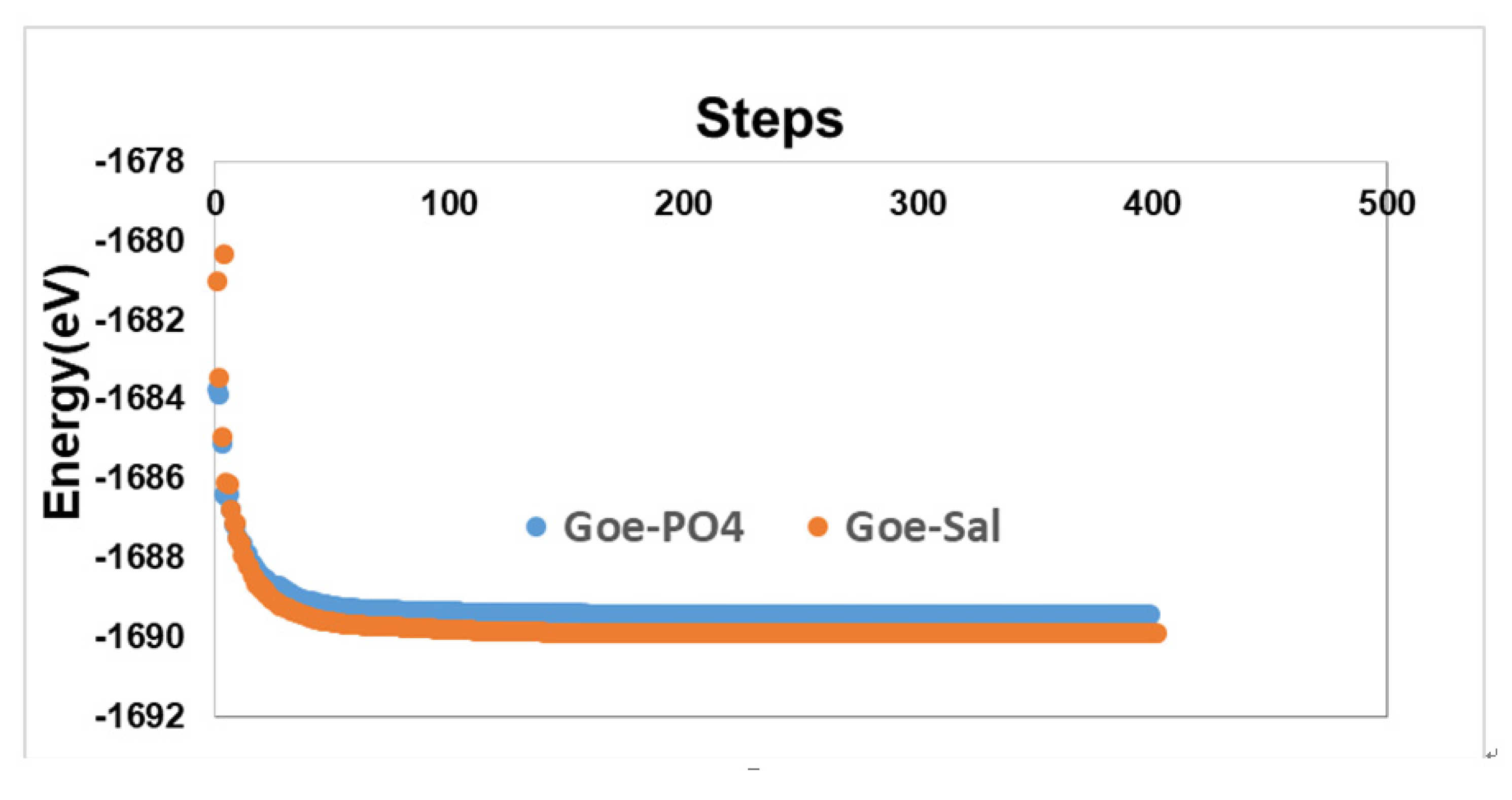
2.6. Energy Minimization and Molecular Dynamics
2.7. Frequency Analysis
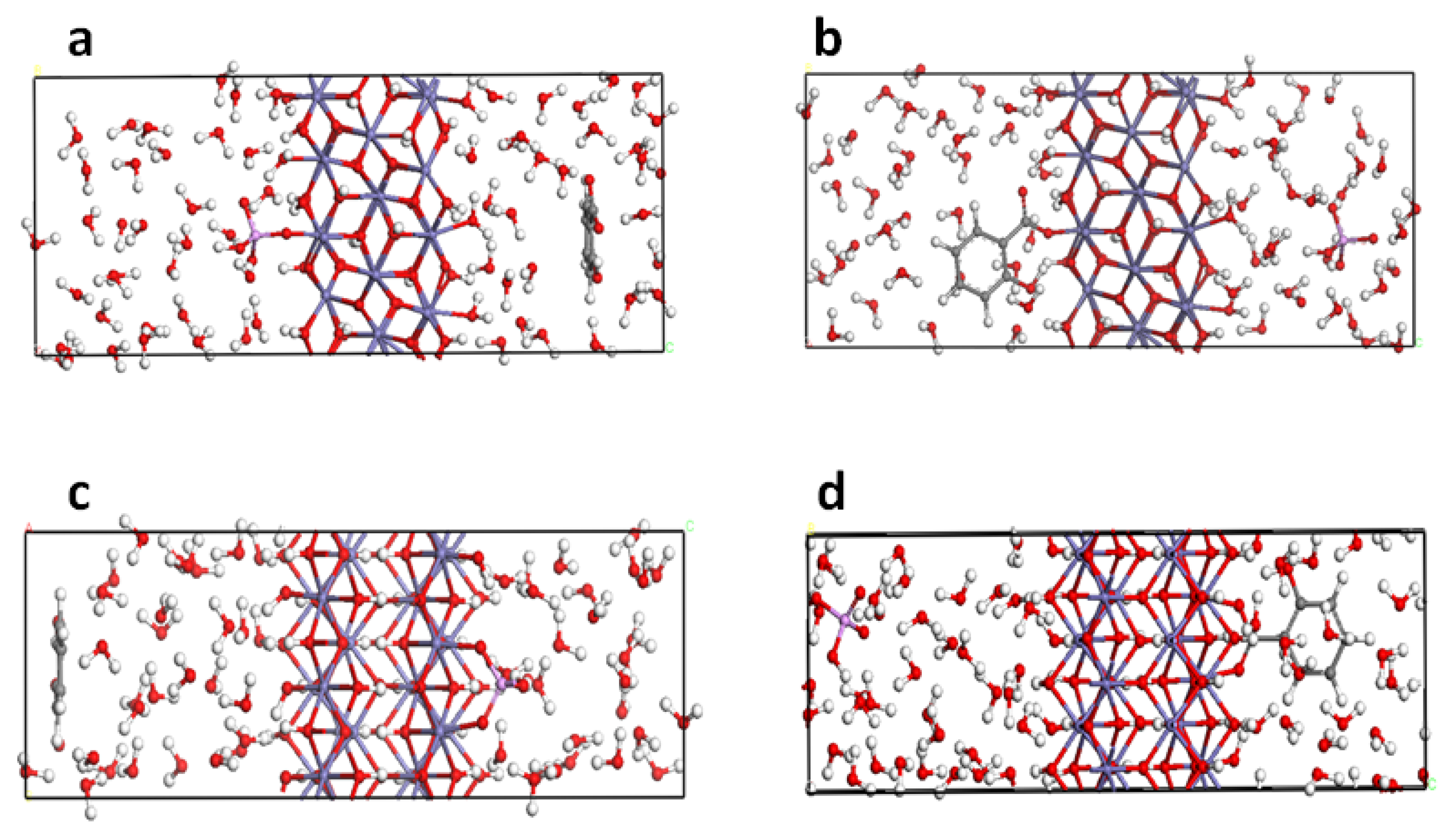
2.8. Model and Computational Details
3. Results
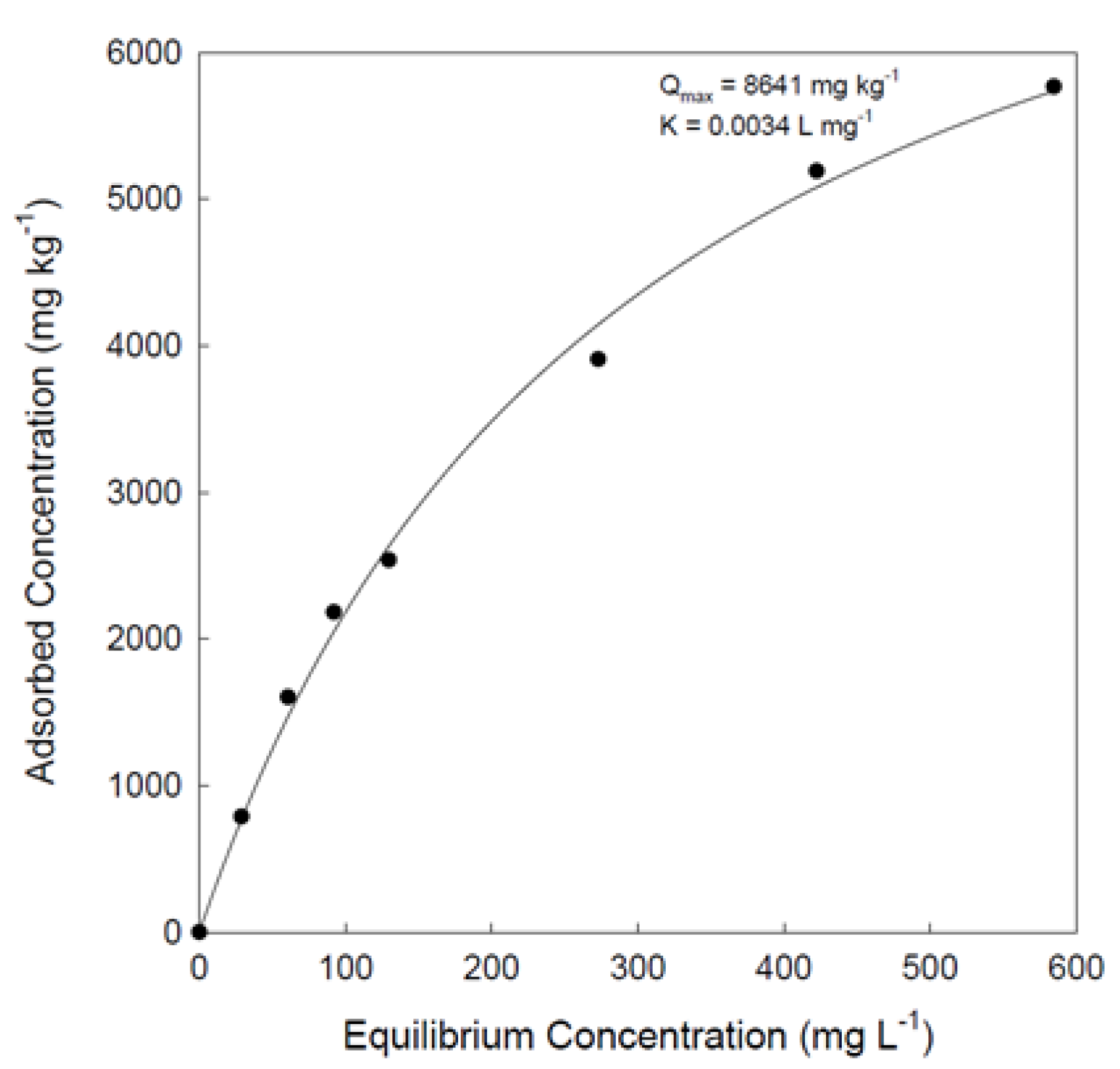
Adsorption Data
4. DFT Results
4.1. Energetics
4.2. Vibrational Frequencies
5. Implications and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rabotyagov, S.; Kling, C.; Gassman, P.; Turner, G. The economics of dead zones: Causes, impacts, policy challenges, and a model of the Gulf of Mexico Hypoxic Zone. Rev. Environ. Econ. Policy 2014, 8, 58–79. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, D.; van Griensven, A.; Van, L.; et al. SWAT: Model use, calibration, and validation. Biol. Syst. Eng. Pap. Publ. 2012, 406, 1491–1508. [Google Scholar]
- Hanna, K.; Martin, S.; Quilès, F.; Boily, J.-F. Sorption of phthalic acid at goethite surfaces under flow-through conditions. Langmuir 2014, 30, 6800–6807. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.G.; Sanderman, J.; Chadwick, O.A.; Chorover, J.; Vitousek, P.M. Long-term carbon storage through retention of dissolved aromatic acids by reactive particles in soil. Global Change Biol. 2012, 18, 2594–2605. [Google Scholar] [CrossRef]
- Barber, S. Soil Nutrient Bioavailability: A Mechanistic Approach; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Tinker, P.B.; Nye, P.H. Solute Movement in the Rhizosphere; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Goldberg, S.; Sposito, G. On the mechanism of specific phosphate adsorption by hydroxylate mineral surfaces: A review. Commun. Soil Sci. Plant Anal. 1985, 16, 801–821. [Google Scholar] [CrossRef]
- Baldock, J.A.; Skjemstad, J.O. Role of the soil matrix and minerals protecting natural organic materials against biological attack. Org. Geochem. 2000, 31, 697–710. [Google Scholar] [CrossRef]
- Zsolnay, A.; Gorlitz, H. Water extractable organic matter in arable soils: Effects of drought and long-term fertilization. Soil Biol. Biochem. 1994, 26, 1257–1261. [Google Scholar] [CrossRef]
- Fox, T.R.; Comerford, N.B.; McFee, W.W. Phosphorus and aluminum release from a spodic horizon mediated by organic acids. Soil Sci. Soc. Am. J. 1990, 54, 1763–1767. [Google Scholar] [CrossRef]
- Hue, N.V. Effects of organic acids/anions on P sorption and phytoavailability in soils with different mineralogies. Soil Sci. 1991, 152, 463–471. [Google Scholar] [CrossRef]
- Bolan, N.S.; Naidu, S.M.; Baskaran, S. Influence of low-molecular weight organic acids on the solubilization of phosphates. Biol. Fertil. Soils 1994, 18, 311–319. [Google Scholar] [CrossRef]
- Hue, N.V.; Craddock, G.R.; Adams, F. Effect of organic acids on aluminum toxicity in subsoils. Soil Sci. Soc. Am. J. 1986, 50, 28–34. [Google Scholar] [CrossRef]
- Sunda, W.G.; Tester, P.A.; Huntsman, S.A. Toxicity of trace metals to Acartia tonsa in the Elizabeth River and southern Chesapeake Bay. Estuar. Coast. Shelf Sci. 1990, 30, 207–221. [Google Scholar] [CrossRef]
- Parker, D.R.; Bertsch, P.M. Identification and quantification of the Al13 tridecameric aluminum polycation using Ferron. Environ. Sci. Technol. 1992, 26, 908–914. [Google Scholar] [CrossRef]
- Parikh, S.J.; Goyne, K.W.; Margenot, A.J.; Mukome, F.N.D.; Calderon, F.J. Soil chemical insights provided through vibration spectroscopy. Adv. Agron. 2014, 126, 1–148. [Google Scholar]
- Bleam, W.F. Soil science applications of nuclear magnetic resonance spectroscopy. Adv. Agron. 1991, 46, 91–155. [Google Scholar]
- Lombi, E.; Susini, J. Synchrotron-based techniques for plant and soil science: Opportunities, challenges and future perspectives. Plant Soil 2009, 320, 1–35. [Google Scholar] [CrossRef]
- Nielsen, U.G.; Paik, Y.; Julmis, K.; Schoonen, M.A.A.; Reeder, R.J.; Grey, C.P. Investigating Sorption on Iron-Oxyhydroxide Soil Minerals by Solid-State NMR Spectroscopy: A 6Li MAS NMR Study of Adsorption and Absorption on Goethite. J. Phys. Chem. B 2005, 109, 18310–18315. [Google Scholar] [CrossRef]
- Kim, J.; Gro Nielsen, U.; Grey, C.P. Local Environments and Lithium Adsorption on the Iron Oxyhydroxides Lepidocrocite (γ-FeOOH) and Goethite (α-FeOOH): A 2H and 7Li Solid State MAS NMR Study. J. Am. Chem. Soc. 2008, 130, 1285–1295. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Mueller, K.T. Computational Spectroscopy in Environmental Chemistry. In Computational Spectroscopy; Grunenberg, J., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Molinari, M.; Brukhno, A.V.; Parker, S.C.; Spagnoli, D. Force field application and development. In Molecular Modeling of Geochemical Reactions; Kubicki, J.D., Ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 33–75. [Google Scholar]
- Cygan, R.T.; Liang, J.-J.; Kalinichev, A.G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M.; et al. The ReaxFF reactive force-field: Development, applications and future directions. Comput. Mater. 2016, 2, 15011. [Google Scholar] [CrossRef]
- Achtyl, J.L.; Unocic, R.R.; Xu, L.; Cai, Y.; Raju, M.; Zhang, W.; Sacci, R.L.; Vlassiouk, I.V.; Fulvio, P.F.; Ganesh, P.; et al. Aqueous proton transfer across single-layer graphene. Nat. Commun. 2015, 6, 6539. [Google Scholar] [CrossRef] [PubMed]
- Van Gunsteren, W.F.; Daura, X.; Mark, A.E. Computation of Free Energy. Helv. Chim. Acta 2002, 85, 3113–3129. [Google Scholar] [CrossRef]
- Shock, E.L.; Koretsky, C.M. Metal-organic complexes in geochemical processes – Calculation of standard partial molal thermodynamic properties of aqueous acetate complexes at high temperatures and pressures. Geochim. Cosmochim. Acta 1993, 57, 66–74. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; Wiley: West Sussex, England, 2002. [Google Scholar]
- Sherman, D. Introduction to the Theory and Methods of Computational Chemistry. In Molecular Modelling of Geochemical Reactions: An Introduction; Kubicki, J.D., Ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 1–32. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B. Condens. Matter 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 09 Revision, E01; Wallingford, CT, USA, 2009. Available online: http://gaussian.com/ (accessed on 22 April 2020).
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wires Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Demichelis, R.; Civalleri, B.; Ferrabone, M.; Dovesi, R. On the performance of eleven DFT functionals in the descrption of the vibrational properties of aluminosilicates. Int. J. Quantum Chem. 2010, 110, 406–415. [Google Scholar] [CrossRef]
- Lo, C.S.; Tanwar, K.S.; Chaka, A.M.; Trainor, T.P. Density functional theory study of the clean and hydrated hematite surfaces. Phys. Rev. B 2007, 75, 075425. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Paul, K.W.; Sparks, D.L. Periodic density functional theory calculations of bulk and the (010) surface of goethite. Geochem. Trans. 2008, 9, 4. [Google Scholar] [CrossRef]
- Marcus, Y. Ionic radii in aqueous solutions. Chem Rev. 1988, 8, 1475–1498. [Google Scholar] [CrossRef]
- Zhang, Z.; Fenter, P.; Kelly, S.D.; Catalano, J.G.; Bandura, A.V.; Kubicki, J.D.; Sofo, J.O.; Wesolowski, D.J.; Machesky, M.L.; Sturchio, N.C.; et al. Structure of hydrated Zn2+ at the rutile TiO2 (110)-aqueous solution interface: Comparison of X-ray standing wave, X-ray absorption spectroscopy, and density functional theory results. Geochim. Cosmochim. Acta 2006, 70, 4039–4056. [Google Scholar] [CrossRef]
- Scalmani, G.; Frisch, M.J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C.W. Refinement and Parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Klamt, A. The COSMO and COSMO-RS solvation models. Wires Comput. Mol. Sci. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Paul, K.W.; Kabalan, L.; Zhu, Q.; Mrozik, M.K.; Aryanpour, M.; Pierre-Louis, A.M.; Strongin, D.R. ATR-FTIR and density functional theory study of the structures, energetics, and vibrational spectra of phosphate adsorbed onto goethite. Langmuir 2012, 28, 14573–14587. [Google Scholar] [CrossRef] [PubMed]
- Kubicki, J.D.; Lasaga, A.C. Molecular dynamics and diffusion in silicate melts. In Diffusion, Defects, and Mass Transport. Adv. Phys. Geochem. 1990, 8, 1–50. [Google Scholar]
- Rustad, J.R.; Yuen, D.A.; Spera, F.J. The sensitivity of physical and spectroscopic properties of silica glass to variations of interatomic potentials under high pressure. Phys. Earth Planet. Inter. 1991, 65, 210–230. [Google Scholar] [CrossRef]
- Wilson, E.B., Jr.; Decius, J.D.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; Dover: New York, NY, USA, 1955. [Google Scholar]
- Kubicki, J.D.; Watts, H.D. Quantum mechanical modeling of the vibrational spectra of minerals with a focus on clays. Minerals 2019, 9, 141. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Trout, C.C.; Kubicki, J.D. Correlation of observed and model vibrational frequencies for aqueous organic acids: UV resonance Raman spectra and molecular orbital calculations of benzoic, salicylic, and phthalic acids. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2005, 61, 2622–2633. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical gga-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 2006, 27, 1787. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Becke’s three parameter hybrid method using the LYP correlation functional. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Sparks, D.L. Environmental Soil Chemistry, 2nd ed.; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Sposito, G. The Surface Chemistry of Soils; Oxford University Press: New York, NY, USA, 1984. [Google Scholar]
- Kubicki, J.D.; Itoh, M.J.; Schroeter, L.M.; Apitz, S.E. Bonding mechanisms of salicylic acid adsorbed onto illite clay: An ATR-FTIR and molecular orbital study. Environ. Sci. Technol. 1997, 31, 1151–1156. [Google Scholar] [CrossRef]
- Villalobos, M.; Perez-Gallegos, A. Goethite surface reactivity: A macroscopic investigation unifying proton, chromate, carbonate, and lead(II) adsorption. J. Colloid Interface Sci. 2008, 326, 307–323. [Google Scholar] [CrossRef] [PubMed]
- Villalobos, M.; Cheney, M.A.; Alcaraz-Cienfuego, J. Goethite surface reactivity: II. A microscopic site-density model that describes its surface area-normalized variability. J. Colloid Interface Sci. 2009, 336, 412–422. [Google Scholar] [CrossRef]
- Kwon, K.D.; Kubicki, J.D. Molecular orbital theory study on complexation structures of phosphates to iron hydroxides: Calculation of vibrational frequencies and adsorption energies. Langmuir 2004, 20, 9249–9254. [Google Scholar] [CrossRef] [PubMed]
- Paul, K.; Kubicki, J.D.; Sparks, D.L. Sulphate adsorption at the Fe (hydr)oxide-H2O interface: Comparison of cluster and periodic slab DFT predictions. Eur. J. Soil Sci. 2007, 58, 978–988. [Google Scholar] [CrossRef]
- Abdala, D.B.; Northrup, P.A.; Arai, Y.; Sparks, D.L. Surface loading effects on orthophosphate surface complexation at the goethite/water interface as examined by extended X-ray absorption fine structure (EXAFS) spectroscopy. J. Coll. Interface Sci. 2015, 437, 297–303. [Google Scholar] [CrossRef] [PubMed]
- Loring, J.S.; Sandstrom, M.H.; Noren, K.; Persson, P. Rethinking arsenate coordination at the surface of goethite. Chem. –A Eur. J. 2009, 15, 5063–5072. [Google Scholar] [CrossRef]
- Whipps, J.M. Carbon economy. In The Rhizosphere; Lynch, J.M., Ed.; John Wiley & Sons Ltd: Essex, UK, 1990; pp. 59–97. [Google Scholar]
- Marschner, H. Mineral Nutrition of Higher Plants; Academic Press: London, UK, 1995. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubicki, J.D.; Ohno, T. Integrating Density Functional Theory Modeling with Experimental Data to Understand and Predict Sorption Reactions: Exchange of Salicylate for Phosphate on Goethite. Soil Syst. 2020, 4, 27. https://doi.org/10.3390/soilsystems4020027
Kubicki JD, Ohno T. Integrating Density Functional Theory Modeling with Experimental Data to Understand and Predict Sorption Reactions: Exchange of Salicylate for Phosphate on Goethite. Soil Systems. 2020; 4(2):27. https://doi.org/10.3390/soilsystems4020027
Chicago/Turabian StyleKubicki, James D., and Tsutomu Ohno. 2020. "Integrating Density Functional Theory Modeling with Experimental Data to Understand and Predict Sorption Reactions: Exchange of Salicylate for Phosphate on Goethite" Soil Systems 4, no. 2: 27. https://doi.org/10.3390/soilsystems4020027
APA StyleKubicki, J. D., & Ohno, T. (2020). Integrating Density Functional Theory Modeling with Experimental Data to Understand and Predict Sorption Reactions: Exchange of Salicylate for Phosphate on Goethite. Soil Systems, 4(2), 27. https://doi.org/10.3390/soilsystems4020027



