Soil as an Archetype of Complexity: A Systems Approach to Improve Insights, Learning, and Management of Coupled Biogeochemical Processes and Environmental Externalities
Abstract
:1. Introduction
“The impression may be that our scientific knowledge on soil processes and how they produce emergent soil functions is pretty much settled, and it is only insufficient how to translate this knowledge into sustainable management practices. We are convinced that this is a misimpression…we stress the fact that our knowledge on soil processes is fragmented throughout various disciplines and the system perspective required to truly capture the reaction of soils to external forcing through land use and climate change is still in its infancy. This systemic approach is furthermore necessary considering the need to distinguish the enormous variety of different soil types in various geographic and climatic regions, all of whose functioning reacts specifically in response to external forcing….Such a systemic approach, providing a clear perspective on how soil functions emerge from small-scale process interactions, is a prerequisite to actually understanding the basic controls and to developing science-based strategies towards sustainable soil management. This will also have an enormous potential for facilitating communication towards stakeholders and policy makers by replacing the cacophony generated by a disciplinarily fragmented research community with harmonized information on the soil system’s behavior.”
1.1. Characteristics of Complex Systems
1.1.1. Constantly Changing
1.1.2. Tightly Coupled
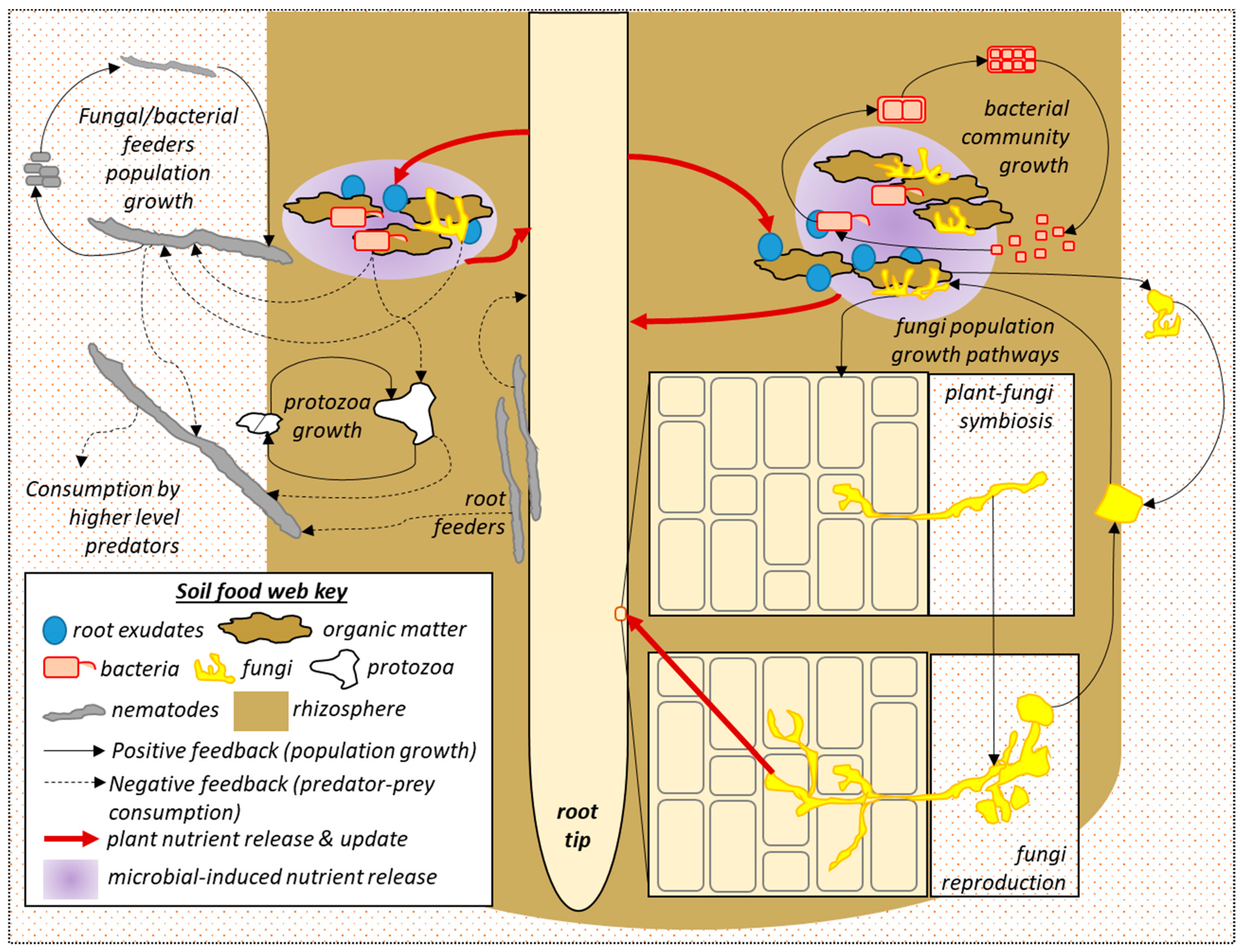
1.1.3. Governed by Feedback
1.1.4. Nonlinear
1.1.5. History Dependent
1.1.6. Self-Organizing
1.1.7. Adaptive
1.1.8. Exhibit Trade-Offs
1.1.9. Counterintuitive
1.1.10. Policy or Management Resistant
- Fertilization overcomes soil nutrient deficiencies by providing nutrients in plant-available form, but artificially high resource conditions shift microbial community structure and activity away from guilds specializing in decomposition of organic compounds or potential synergistic plant root–microorganism symbioses; under reduced nutrient cycling, plant production increasingly relies on fertilization to meet nutrient needs at the field scale [36,80,81,82] and can contribute nutrient-driven externalities at larger scales.
- Irrigation overcomes soil moisture deficiencies that limit plant transpiration but often introduces salts and other chemicals into the rooting zone that accumulate over time with subsequent irrigation events (especially in situations with poor drainage and water quality, an effect known as secondary salinization). Eventually, the accumulated salts limit plant transpiration, trading one problem (soil moisture availability) for a more challenging one (salt accumulation) [43,83,84,85,86,87,88].
- Tillage provides beneficial results by opening soil pore spaces, breaking up compacted layers, and accelerating nutrient release. However, continued tillage eventually destroys soil aggregates by decoupling soil aggregation processes, reducing pore space and increasing bulk density, which in turn minimizes microbial community habitat and nutrient capture and release. This biophysical trade-off alters nutrient management in the short term [89]; and in the long run, such degradation processes have contributed to the growth and collapse of societies [90].
- Biochar has increasingly been suggested as an amendment to accelerate soil carbon storage. However, short-term carbon emissions often increase after biochar application and other management factors may override benefits of biochar to improving soil functions (e.g., more difficult weed control, introduction of contaminants, microbial community shifts, and rapid pH change) [91].
2. Materials and Methods
2.1. Model Overview
2.2. Model Nutrient and Chemical Components
2.3. Model Biological Components
2.4. Model Soil Physical and Hydraulic Component
2.5. Model Economic and Decision-Making Component
2.6. Model Performance Evaluation
2.7. Case Study Applications in Soil System Investigations
2.7.1. Case Study Experiment 1: Why Do More Agricultural Producers Not Adopt Micro- or Drip Irrigation Systems?
2.7.2. Case Study Experiment 2: Why Do More Agricultural Producers Not Adopt No-Tillage Practices in Their Crop Production Systems?
3. Results
3.1. Why Do More Agricultural Producers Not Adopt Micro- or Drip Irrigation Systems?
3.2. Why Do More Agricultural Producers Not Adopt No-Tillage Practices in Their Crop Production Systems?
3.3. Summary of the Nutrient Cycling Dynamics and Implications for Environmental Externalities
4. Discussion
4.1. Viewing the Complexity of Soil Systems through an Integrative Lens
4.2. Case Study Modeling Applications: Insights, Strengths and Weaknesses
4.3. Frontiers in Soil Science Complexity Research and Education
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| List of Symbols | Description | Value | Units | Source Model or Reference Material |
|---|---|---|---|---|
| a | scaling parameter | - | dmnl | |
| B | crop biomass | - | kg/m2 | Pelak et al., 2017 |
| be | the power law exponent | - | dmnl | Pelak and Porporato 2019 |
| bc | the parameter value at OM equal to 0 | 0.9 | dmnl | Pelak and Porporato 2019 |
| C | crop canopy cover, the percentage of soil surface covered | - | dmnl | Pelak et al., 2017 |
| Cs | surface tension of water | 0.072 | Newton/m | |
| D | natural deposition rate (assumed constant) | 15 × 10−6 | kg/m2/day | Pelak et al., 2017 |
| d | an empirically derived parameter value for the exponential term for saturated conductivity | 13 | dmnl | Brooks and Corey, 1964, Rodriguez et al., 2004 |
| dr | change in radii | - | μm | Pelak and Porporato 2019 |
| E | evaporation rate | - | cm/day | Porporato et al. 2001, Porporato, A et al. 2015, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b |
| ET | coupled water losses form evaporation and transpiration | - | cm/day | Porporato et al. 2001, Porporato, A et al. 2015, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b |
| ET0 | potential evapotranspiration | - | cm/day | Hargreaves, 1975, Hargreaves and Allen, 2003 |
| ETs | water stress coefficient due to limited soil water availability | - | cm/day | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| Etw | reduced evapotranspiration rate under wilting conditions | - | cm/day | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| f | pore size distribution | - | μm | Pelak and Porporato 2019 |
| Fm | fraction of plant residue that is metabolic | - | dmnl | Parton et al., 1987; Parton et al., 1994; Kelly et al., 1997 |
| Fr | fertilization rate at time t of fertilizer application | - | kg/m2/day | Pelak et al., 2017 |
| Fs | fraction of plant residue that is structural | - | dmnl | Parton et al., 1987; Parton et al., 1994; Kelly et al., 1997 |
| f(η) | limitation of nitrogen uptake beyond the critical threshold | 0.054 | kg/m2/day | Pelak et al., 2017 |
| G | canopy growth rate | - | 1/day | Pelak et al., 2017 |
| Ge | empirically derived value following the Hagen-Poiseuille equation for porous flow | 1/8 | dmnl | Brutsaert 2005; Pelak and Porporato 2019 |
| H | harvest | - | kg/m2/day | Pelak et al., 2017 |
| hi | harvest index | 0.5 | dmnl | Pelak et al., 2017 |
| Hd | day of harvest | 270 | day | Pelak et al., 2017 |
| Hv | percentage of biomass removed | 1 | dmnl | |
| I | irrigation applications | - | cm/day | Porporato et al., 2015; Vico and Porporato 2011a; Vico and Porporato 2011b |
| K | hydraulic conductivity | - | m/day | Brooks and Corey, 1964, Rodriguez et al., 2004 |
| kb | the rate of soil particle settling | 0.001 | dmnl | Pelak and Porporato 2019 |
| Kcb | basal crop coefficient | 1.03 | dmnl | Allen et al., 1998 |
| Kg | Gapon selectivity coefficient | 0.0147−1/2 | mmol/L | Mau and Porporato, 2015 |
| Ki | the maximum SOM decomposition rate for the ith SOM state variable (1 surface/soil litter; 2 active C; 3 slow C; 4 passive C) | - | 1/day | Parton et al., 1987; Parton et al., 1994; Kelly et al., 1997 |
| Kr(S) | evaporation reduction coefficient | - | dmnl | Pelak et al. 2017 |
| Ksat | saturated hydraulic conductivity | - | m/day | Brooks and Corey, 1964, Rodriguez et al., 2004 |
| L | leakage term used in N balance equation | - | kg/m/day | Pelak et al., 2017 |
| Lfi | fraction of structural material that is lignin (a-above-ground biomass; r- root biomass) | - | dmnl | Parton et al., 1987; Parton et al., 1994 |
| LR/N | litter lignin to nitrogen ration | - | dmnl | Melillo et al., 1984; Parton et al., 1987; Parton et al., 1994 |
| INfraction | fraction of the gap between observed and desired soil conditions to be recovered | - | - | - |
| INr | changes in input rates or soil management practices given dynamic decision making | - | - | - |
| INtime | mean application time of inputs given dynamic decision making | - | - | - |
| m | source-sink term (gain or loss of pores at given radius, r) | - | μm/day | Pelak and Porporato 2019 |
| Ms | metabolic and senescence rate | - | 1/day | Pelak et al. 2017 |
| Md | the effect of the ratio of monthly precipitation to potential evapotranspiration rate on SOM decomposition | - | dmnl | Parton et al., 1987; Parton et al., 1994; Kelly et al., 1997 |
| n | soil porosity (initial) | 0.43 | dmnl | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| Nc | total mineral nitrogen level per unit area soil | - | kg/m2 | Pelak et al. 2017 |
| P | price per unit of crop | 0.15 | $/kg | |
| PPT | annual precipitation | - | cm | Parton et al., 1987; Parton et al., 1994 |
| Q(S(t)) | represents the coupled losses from runoff and percolation below the rooting zone Zr, | - | cm/day | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| qs | salt dissolved in water in the soil column | - | mmol/L | Mau and Porporato, 2015 |
| r | soil pore radius | - | μm | Pelak and Porporato 2019 |
| R(t) | inflow of rainfall over time | - | cm/day | Porporato et al. 2001, Porporato, A et al. 2015, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b |
| rb | the ratio of the parameter value in an untilled state to the base value | 0.9 | dmnl | Pelak and Porporato 2019 |
| rg | represents a scaler of canopy cover growth per unit of nitrogen utilization | 560 | m2/kg | Pelak et al., 2017 |
| rm | the metabolic constant used in plant senescence | 0.2 | 1/day | Pelak et al., 2017 |
| Rm(t) | maximum effective pore radius | - | μm | Pelak and Porporato 2019 |
| RAT | root available water | - | dmnl | Parton et al., 1987; Parton et al., 1994 |
| S | soil moisture expressed as percentage of field capacity | - | dmnl | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| S* | soil moisture value below which plants become stressed and begin stomatal closure | 0.46 | dmnl | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| SCdesired | desired soil condition from which input rate decisions are based | - | - | - |
| SCobserved | observed soil condition from input rate decision are based | - | - | - |
| sfc | full soil moisture saturation | - | cm | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| sh | the soil moisture value crossing the plant hygroscopic point beyond which moisture losses cease | 0.14 | dmnl | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| Sw | soil moisture value inducing plant wilting point | 0.18 | dmnl | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b, Pelak et al. 2017 |
| SOM | soil organic matter | - | kg C/m3 | Parton et al., 1987; Parton et al., 1994; Kelly et al., 1997; Pelak and Porporato 2019 |
| SOMslow | effect of soil texture on the efficiency of stabilizing SOM from the active to slow states | - | dmnl | Parton et al., 1987; Parton et al., 1994; |
| T | transpiration | - | cm/day | Pelak et al., 2017 |
| Td | the effect of monthly average soil temperature on SOM decomposition | - | 1/day | Parton et al., 1987; Parton et al., 1994; Kelly et al., 1997 |
| ts | temperature in degrees °C | - | °C | Parton et al., 1987; Parton et al., 1994 |
| tsen | estimated time of senescence (day of year) | 275 | day | Pelak et al., 2017 |
| temp1 | parameter input to Td | - | dmnl | Parton et al., 1987; Parton et al., 1994 |
| temp2 | parameter input to Td | - | dmnl | Parton et al., 1987; Parton et al., 1994 |
| ttd | time since tillage in days | - | day | Pelak and Porporato 2019 |
| U | nitrogen uptake by plant | - | kg/m2/day | Pelak et al., 2017 |
| v | soil drift term for shrinking pore radii | - | μm | Pelak and Porporato 2019 |
| V | the dissolved salt concentration | - | mmol/L | Mau and Porporato, 2015 |
| Vi | salt concentration in irrigation water | 1 | mmol/L | Mau and Porporato, 2015 |
| w* | volumetric water content. | - | L/m2 | Mau and Porporato, 2015 |
| Y | yield | - | kg/m2 | Pelak et al., 2017 |
| Zr | soil depth | 90 | cm | Porporato et al. 2001, Porporato et al. 2005, Rodriguez-Iturbe et al. 2001, Laio et al. 2001a, Laio et al. 2001b |
| γ | slope of the senescence curve post-tsen | 0.005 | 1/day | Pelak et al., 2017 |
| γb | management factor used in the b term | - | dmnl | Pelak and Porporato 2019 |
| γw | specific weight of water | 0.001 | kg/cm3 | Pelak and Porporato 2019 |
| η | nitrogen content of soil moisture | 1 | kg/m2 | Pelak et al., 2017 |
| ηc | critical threshold of nitrogen beyond which plant uptake does not occur | 1 | kg/m3/day | Pelak et al., 2017 |
| Θ | step function that causes crop canopy senescence to begin | - | 1/day | Pelak et al., 2017 |
| μ | dynamic viscosity of water | 8.9 × 10−4 | Pa | Pelak and Porporato 2019 |
| σb | slope of the b–OM relationship | −0.001 | dmnl | Pelak and Porporato 2019 |
| ψs | matric potential | - | MPa | Pelak and Porporato 2019 |


References
- Matson, P.A. Agricultural Intensification and Ecosystem Properties. Science. 1997, 277, 504–509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartemink, A.E.; McBratney, A. A soil science renaissance. Geoderma 2008, 148, 123–129. [Google Scholar] [CrossRef]
- Schröder, J.J.; Schulte, R.P.; Creamer, R.E.; Delgado, A.; Leeuwen, J.; Lehtinen, T. The elusive role of soil quality in nutrient cycling: A review. Soil Use Manag. 2016, 32, 476–486. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E. Linking soils to ecosystem services—A global review. Geoderma 2016, 262, 101–111. [Google Scholar] [CrossRef]
- Power, A.G. Ecosystem services and agriculture: Tradeoffs and synergies. Philos. Trans. R. Soc. B 2010, 365, 2959–2971. [Google Scholar] [CrossRef]
- Swift, M.J.; Izac, A.-M.N.; van Noordwijk, M. Biodiversity and ecosystem services in agricultural landscapes—are we asking the right questions? Agric. Ecosyst. Environ. 2004, 104, 113–134. [Google Scholar] [CrossRef]
- Alexander, P.; Rounsevell, M.D.; Dislich, C.; Dodson, J.R.; Engström, K.; Moran, D. Drivers for global agricultural land use change: The nexus of diet; population; yield and bioenergy. Glob. Environ. Chang. 2015, 35, 138–147. [Google Scholar] [CrossRef] [Green Version]
- Turner, B.L.; Fuhrer, J.; Wuellner, M.; Menendez, H.M.; Dunn, B.H.; Gates, R. Scientific case studies in land-use driven soil erosion in the central United States: Why soil potential and risk concepts should be included in the principles of soil health. Int. Soil Water Conserv. Res. 2018, 6, 63–78. [Google Scholar] [CrossRef]
- Turner, B.L.; Wuellner, M.; Malo, D.D.; Herrick, J.E.; Dunn, B.H.; Gates, R. Ecosystem functions in mixed cropland–grassland systems influenced by soil legacies of past crop cultivation decisions. Ecosphere. 2018, 9, e02521. [Google Scholar] [CrossRef]
- Vogel, H.-J.; Bartke, S.; Daedlow, K.; Helming, K.; Kögel-Knabner, I.; Lang, B. A systemic approach for modeling soil functions. SOIL 2018, 4, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Adewopo, J.B.; VanZomeren, C.; Bhomia, R.K.; Almaraz, M.; Bacon, A.R.; Eggleston, E. Top-Ranked Priority Research Questions for Soil Science in the 21st Century. Soil Sci. Soc. Am. J. 2014, 78, 337–347. [Google Scholar] [CrossRef] [Green Version]
- Baveye, P.C. Grand challenges in the research on soil processes. Front. Environ. Sci. 2015, 3. [Google Scholar] [CrossRef] [Green Version]
- Bridges, E.M.; Catizzone, M. Soil science in a holistic framework: Discussion of an improved integrated approach. Geoderma 1996, 71, 275–287. [Google Scholar] [CrossRef]
- Sterman, J.D. System Dynamics Modeling: Tools for Learning in a Complex World. Calif. Manag. Rev. 2001, 43, 8–25. [Google Scholar] [CrossRef]
- Sterman, J.D. Sustaining Sustainability: Creating a Systems Science in a Fragmented Academy and Polarized World. In Sustainability Science; Springer: New York, NY, USA, 2012; pp. 21–58. [Google Scholar] [CrossRef]
- Foster, J. From simplistic to complex systems in economics. Camb. J. Econ. 2005, 29, 873–892. [Google Scholar] [CrossRef] [Green Version]
- Turner, B.L.; Goodman, M.; Machen, R.; Mathis, C.; Rhoades, R.; Dunn, B. Results of Beer Game Trials Played by Natural Resource Managers Versus Students: Does Age Influence Ordering Decisions? Systems 2020, 8, 37. [Google Scholar] [CrossRef]
- Kahneman, D. Thinking Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Cronin, M.A.; Gonzalez, C.; Sterman, J.D. Why don’t well-educated adults understand accumulation? A challenge to researchers, educators, and citizens. Organ. Behav. Hum. Decis. Process. 2009, 108, 116–130. [Google Scholar] [CrossRef]
- Manzoni, S.; Porporato, A.; D’Odorico, P.; Laio, F.; Rodriguez-Iturbe, I. Soil nutrient cycles as a nonlinear dynamical system. Nonlinear Process. Geophys. 2004, 11, 589–598. [Google Scholar] [CrossRef] [Green Version]
- Churchman, G.J. The philosophical status of soil science. Geoderma 2010, 157, 214–221. [Google Scholar] [CrossRef]
- Senge, P.M. The leader’s new work: Building learning organizations. Sloan Manag. Rev. 1990, 31, 7–23. [Google Scholar]
- Barlas, Y. System dynamics: Systemic feedback modeling for policy analysis. System 2007, 1, 1–29. [Google Scholar]
- Sterman, J.D. Learning in and about complex systems. Syst. Dyn. Rev. 1994, 10, 291–330. [Google Scholar] [CrossRef] [Green Version]
- Bar-Yam, Y. General features of complex systems. In Encyclopeida of Life Support Systems (EOLSS); UNESCO, EOLSS Pubblishers: Oxford, UK, 2002. [Google Scholar]
- Stockmann, U.; Minasny, B.; McBratney, A.B. How fast does soil grow? Geoderma 2014, 216, 48–61. [Google Scholar] [CrossRef]
- Montgomery, D.R. Soil erosion and agricultural sustainability. Proc. Natl. Acad. Sci. USA 2007, 104, 13268–13272. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, D.R. Dirt: The Erosion of Civilizations; University of California Press: Oakland, CA, USA, 2007. [Google Scholar]
- Zhang, R.; Wienhold, B.J. The effect of soil moisture on mineral nitrogen, soil electrical conductivity, and pH. Nutr. Cycl. Agroecosyst. 2002, 63, 251–254. [Google Scholar] [CrossRef]
- Zhang, K.; Maltais-Landry, G.; Liao, H.-L. How soil biota regulate C cycling and soil C pools in diversified crop rotations. Soil Biol. Biochem. 2021, 156, 108219. [Google Scholar] [CrossRef]
- Balestrini, R.; Lumini, E.; Borriello, R.; Bianciotto, V. Plant-Soil Biota Interactions. In Soil Microbiology; Ecology and Biochemistry; Elsevier: Amsterdam, The Netherlands, 2015; pp. 311–338. [Google Scholar] [CrossRef]
- Wagg, C.; Bender, S.F.; Widmer, F.; van der Heijden, M.G. Soil biodiversity and soil community composition determine ecosystem multifunctionality. Proc. Natl. Acad. Sci. USA 2014, 111, 5266–5270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bücking, H.; Kafle, A. Role of Arbuscular Mycorrhizal Fungi in the Nitrogen Uptake of Plants: Current Knowledge and Research Gaps. Agronomy 2015, 5, 587–612. [Google Scholar] [CrossRef] [Green Version]
- Massalha, H.; Korenblum, E.; Tholl, D.; Aharoni, A. Small molecules below-ground: The role of specialized metabolites in the rhizosphere. Plant J. 2017, 90, 788–807. [Google Scholar] [CrossRef] [Green Version]
- Giovannini, L.; Palla, M.; Agnolucci, M.; Avio, L.; Sbrana, C.; Turrini, A. Arbuscular Mycorrhizal Fungi and Associated Microbiota as Plant Biostimulants: Research Strategies for the Selection of the Best Performing Inocula. Agronomy 2020, 10, 106. [Google Scholar] [CrossRef] [Green Version]
- Chandra, P. Soil-Microbes-Plants: Interactions and ecological diversity. In Plant Microbes Interface; Springer: Cham, Switzerland; pp. 145–176.
- Turner, B.L.; Kodali, S. Soil system dynamics for learning about complex; feedback-driven agricultural resource problems: Model development, evaluation, and sensitivity analysis of biophysical feedbacks. Ecol. Model. 2020, 428, 109050. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress II. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Porporato, A.; Laio, F.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress III. Vegetation water stress. Adv. Water Resour. 2001, 24, 725–744. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Fernandez-Illescas, C.P.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress IV. Discussion of real cases. Adv. Water Resour. 2001, 24, 745–762. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Manzoni, S.; Porporato, A. Soil carbon and nitrogen mineralization: Theory and models across scales. Soil Biol. Biochem. 2009, 41, 1355–1379. [Google Scholar] [CrossRef]
- Mau, Y.; Porporato, A. A dynamical system approach to soil salinity and sodicity. Adv. Water Resour. 2015, 83, 68–76. [Google Scholar] [CrossRef] [Green Version]
- Pelak, N.; Revelli, R.; Porporato, A. A dynamical systems framework for crop models: Toward optimal fertilization and irrigation strategies under climatic variability. Ecol. Model. 2017, 365, 80–92. [Google Scholar] [CrossRef] [Green Version]
- Pelak, N.; Porporato, A. Dynamic evolution of the soil pore size distribution and its connection to soil management and biogeochemical processes. Adv. Water Resour. 2019, 131, 103384. [Google Scholar] [CrossRef]
- Porporato, A.; Feng, X.; Manzoni, S.; Mau, Y.; Parolari, A.J.; Vico, G. Ecohydrological modeling in agroecosystems: Examples and challenges. Water Resour. Res. 2015, 51, 5081–5099. [Google Scholar] [CrossRef] [Green Version]
- Forrester, J.W. Policies, decisions and information sources for modeling. Eur. J. Oper. Res. 1992, 59, 42–63. [Google Scholar] [CrossRef]
- Fernald, A.; Tidwell, V.; Rivera, J.; Rodríguez, S.; Guldan, S.; Steele, C.; Ochoa, C.; Hurd, B.; Ortiz, M.; Boykin, K.; et al. Modeling Sustainability of Water, Environment, Livelihood, and Culture in Traditional Irrigation Communities and Their Linked Watersheds. Sustainability 2012, 4, 2998–3022. [Google Scholar] [CrossRef] [Green Version]
- Gunda, T.; Turner, B.L.; Tidwell, V.C. The Influential Role of Sociocultural Feedbacks on Community-Managed Irrigation System Behaviors During Times of Water Stress. Water Resour. Res. 2018, 54, 2697–2714. [Google Scholar] [CrossRef]
- Ferguson, I.M.; Maxwell, R.M. Role of groundwater in watershed response and land surface feedbacks under climate change. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Hooper, B.P.; Lant, C. Integrated, Adaptive Watershed Management. In Fostering Integration: Concepts and Practice in Resource and Environmental Management; Hanna, K., Scott Slocombe, D., Eds.; Oxford University Press: Oxford, UK; Toronto, ON, Canada, 2007. [Google Scholar]
- Calkin, D.E.; Thompson, M.P.; Finney, M.A. Negative consequences of positive feedbacks in US wildfire management. For Ecosyst. 2015, 2, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Fernald, A.G.; Cevik, S.Y.; Ochoa, C.G.; Tidwell, V.C.; King, J.P.; Guldan, S.J. River Hydrograph Retransmission Functions of Irrigated Valley Surface Water–Groundwater Interactions. J. Irrig. Drain. Eng. 2010, 136, 823–835. [Google Scholar] [CrossRef]
- Fernald, A.; Guldan, S.; Boykin, K.; Cibils, A.; Gonzales, M.; Hurd, B.; Lopez, S.; Ochoa, C.; Ortiz, M.; Rivera, J.; et al. Linked hydrologic and social systems that support resilience of traditional irrigation communities. Hydrol. Earth Syst. Sci. 2015, 19, 293–307. [Google Scholar] [CrossRef] [Green Version]
- Ochoa, C.G.; Guldan, S.J.; Cibils, A.F.; Lopez, S.C.; Boykin, K.G.; Tidwell, V.C.; Fernald, A.G. Hydrologic Connectivity of Head Waters and Floodplains in a Semi-Arid Watershed. J. Contemp. Water Res. Educ. 2013, 152, 69–78. [Google Scholar] [CrossRef]
- Menendez, H.M.; Wuellner, M.R.; Turner, B.L.; Gates, R.N.; Dunn, B.H.; Tedeschi, L.O. A spatial landscape scale approach for estimated erosion, water quantity, and quality in response to South Dakota grassland conversion. Nat. Resour. Model. 2019, 33, e12243. [Google Scholar] [CrossRef]
- Popp, A.; Blaum, N.; Jeltsch, F. Ecohydrological feedback mechanisms in arid rangelands: Simulating the impacts of topography and land use. Basic Appl. Ecol. 2009, 10, 319–329. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, J.; Liu, G.; Zhou, L. The behavioural causes of bullwhip effect in supply chains: A systematic literature review. Int. J. Prod. Econ. 2021, 236, 108120. [Google Scholar] [CrossRef]
- Jenny, H. Factors of Soil Formation: A System of Quantitative Pedology; Dover Publications, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Kaisermann, A.; Vries, F.T.; Griffiths, R.I.; Bardgett, R.D. Legacy effects of drought on plant–soil feedbacks and plant–plant interactions. New Phytol. 2017, 215, 1413–1424. [Google Scholar] [CrossRef] [Green Version]
- Kleinschroth, F.; Gourlet-Fleury, S.; Sist, P.; Mortier, F.; Healey, J.R. Legacy of logging roads in the Congo Basin: How persistent are the scars in forest cover? Ecosphere 2015, 6, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Monger, C.; Sala, O.E.; Duniway, M.C.; Goldfus, H.; Meir, I.A.; Poch, R.M.; Throop, H.L.; Vivoni, E.R. Legacy effects in linked ecological–soil–geomorphic systems of drylands. Front. Ecol. Environ. 2015, 13, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Steel, Z.L.; Safford, H.D.; Viers, J.H. The fire frequency-severity relationship and the legacy of fire suppression in California forests. Ecosphere 2015, 6, 1–23. [Google Scholar] [CrossRef]
- Angeler, D.G.; Fried-Petersen, H.B.; Allen, C.R.; Garmestani, A.; Twidwell, D.; Chuang, W.-C.; Donovan, V.M.; Eason, T.; Roberts, C.P.; Sundstrom, S.M.; et al. Adaptive capacity in ecosystems. In Resilience in Complex Socio-Ecological Systems; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–24. [Google Scholar] [CrossRef]
- Holling, C.S. Simplifying the complex: The paradigms of ecological function and structure. Eur. J. Oper. Res. 1987, 30, 139–146. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, Y.; Li, F.; Yang, G.; Wang, J.; Yu, J.; Zhou, G.; Yang, Y. Changes in above-/below-ground biodiversity and plant functional composition mediate soil respiration response to nitrogen input. Funct. Ecol. 2021, 35, 1171–1182. [Google Scholar] [CrossRef]
- Wade, T.; Classen, R.; Wallander, S. Conservation-Practice Adoption Rates Vary Widely by Crop and Region; EIB-147; U.S. Department of Agriculture, Economic Research Service: Washington, DC, USA, 2015.
- Ward, P.S.; Bell, A.R.; Droppelmann, K.; Benton, T.G. Early adoption of conservation agriculture practices: Understanding partial compliance in programs with multiple adoption decisions. Land Use Policy 2018, 70, 27–37. [Google Scholar] [CrossRef]
- Lahmar, R. Adoption of conservation agriculture in Europe. Land Use Policy 2010, 27, 4–10. [Google Scholar] [CrossRef]
- Knowler, D.; Bradshaw, B. Farmers’ adoption of conservation agriculture: A review and synthesis of recent research. Food Policy 2007, 32, 25–48. [Google Scholar] [CrossRef]
- Giller, K.E.; Andersson, J.A.; Corbeels, M.; Kirkegaard, J.; Mortensen, D.; Erenstein, O.; Vanlauwe, B. Beyond conservation agriculture. Front. Plant Sci. 2015, 6, 870. [Google Scholar] [CrossRef] [Green Version]
- Pittelkow, C.M.; Linquist, B.A.; Lundy, M.E.; Liang, X.; van Groenigen, K.J.; Lee, J.; van Gestal, N.; Six, J.; Venterea, R.T.; van Kessel, C. When does no-till yield more? A global meta-analysis. Field Crop. Res. 2015, 183, 156–168. [Google Scholar] [CrossRef] [Green Version]
- Ismail, I.; Blevins, R.L.; Frye, W.W. Long-Term No-tillage Effects on Soil Properties and Continuous Corn Yields. Soil Sci. Soc. Am. J. 1994, 58, 193–198. [Google Scholar] [CrossRef]
- West, T.O.; Post, W.M. Soil Organic Carbon Sequestration Rates by Tillage and Crop Rotation. Soil Sci. Soc. Am. J. 2002, 66, 1930–1946. [Google Scholar] [CrossRef] [Green Version]
- Turner, B.L.; Wuellner, M.; Nichols, T.; Gates, R. Dueling Land Ethics: Uncovering Agricultural Stakeholder Mental Models to Better Understand Recent Land Use Conversion. J. Agric. Environ. Ethics 2014, 27, 831–856. [Google Scholar] [CrossRef]
- Wright, C.K.; Wimberly, M.C. Recent land use change in the Western Corn Belt threatens grasslands and wetlands. Proc. Natl. Acad. Sci. USA 2013, 110, 4134–4139. [Google Scholar] [CrossRef] [Green Version]
- Gilovich, T.; Griffin, D.; Kahneman, D. (Eds.) Heuristics and Biases: The Psychology of Intuitive Judgment; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Tversky, A.; Kahneman, D. Judgment under Uncertainty: Heuristics and Biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef]
- Malik, Z.; Ahmad, M.; Abassi, G.H.; Dawood, M.; Hussain, A.; Jamil, M. Agrochemicals and Soil Microbes: Interaction for Soil Health. In Soil Biology; Springer International Publishing: New York, NY, USA, 2017; pp. 139–152. [Google Scholar] [CrossRef]
- Wood, S.A.; Bradford, M.A.; Gilbert, J.A.; McGuire, K.L.; Palm, C.A.; Tully, K.L.; Zhou, J.; Naeem, S. Agricultural intensification and the functional capacity of soil microbes on smallholder African farms. J. Appl. Ecol. 2015, 52, 744–752. [Google Scholar] [CrossRef]
- Hartmann, M.; Frey, B.; Mayer, J.; Mäder, P.; Widmer, F. Distinct soil microbial diversity under long-term organic and conventional farming. ISME J. 2014, 9, 1177–1194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maas, E.V. Salt tolerance of plants. In Handbook of Plant Science in Agriculture; Christie, B.R., Ed.; CRC Press: Boca Raton, FL, USA, 1987; Volume 2, pp. 57–75. [Google Scholar]
- Abrol, I.P.; Yadav, J.S.; Massoud, F.I. Salt-Affected Soils and Their Management; FAO Soils Bulletin 39; Food & Agriculture Organization: Rome, Italy, 1988. [Google Scholar]
- Bernstein, L. Effects of Salinity and Sodicity on Plant Growth. Annu. Rev. Phytopathol. 1975, 13, 295–312. [Google Scholar] [CrossRef]
- Levy, G.J. Sodicity. In Handbook of Soil Sciences: Resource Management and Environmental Impacts; Huang, P.M., Li, Y., Sumner, M.E., Eds.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- Ghassemi, F.; Jakeman, A.J.; Nix, H.A. Salinisation of Land and Water Resources: Human Causes, Extent, Management and Case Studies; Cab International: Wallingford, UK, 1995. [Google Scholar]
- Bekle, H.; Mulcock, J.; Phillips, H. The Salinity Crisis: Landscapes, Communities and Politics; UWA Publishing: Crawley, Australia, 2004. [Google Scholar]
- Abbas, F.; Hammad, H.M.; Ishaq, W.; Farooque, A.A.; Bakhat, H.F.; Zia, Z.; Fahad, S.; Farhad, W.; Cerdà, A. A review of soil carbon dynamics resulting from agricultural practices. J. Environ. Manag. 2020, 268, 110319. [Google Scholar] [CrossRef] [PubMed]
- Lowdermilk, W.C. Conquest of the Land through 7000 Years: (No. 99); Soil Conservation Service, US Department of Agriculture: Washington, DC, USA, 1953.
- Kookana, R.S.; Sarmah, A.K.; Van Zwieten, L.; Krull, E.; Singh, B. Biochar Application to Soil. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2011; pp. 103–143. [Google Scholar] [CrossRef]
- Turner, B.; Menendez, H.; Gates, R.; Tedeschi, L.; Atzori, A. System Dynamics Modeling for Agricultural and Natural Resource Management Issues: Review of Some Past Cases and Forecasting Future Roles. Resources 2016, 5, 40. [Google Scholar] [CrossRef] [Green Version]
- Turner, B.L. Model laboratories: A quick-start guide for design of simulation experiments for dynamic systems models. Ecol. Model. 2020, 434, 109246. [Google Scholar] [CrossRef]
- Parton, W.J.; Schimel, D.S.; Cole, C.V.; Ojima, D.S. Analysis of factors controlling soil organic matter levels in Great Plains grasslands. Soil Sci. Soc. Am. J. 1987, 51, 1173–1179. [Google Scholar] [CrossRef]
- Parton, W.J.; Ojima, D.S.; Cole, C.V.; Schimel, D.S. A General Model for Soil Organic Matter Dynamics: Sensitivity to Litter Chemistry, Texture and Management. In Quantitative Modeling of Soil Forming Processes; Soil Science Society of America: Madison, WI, USA, 1994; pp. 147–167. [Google Scholar] [CrossRef] [Green Version]
- Parton, W.J. The CENTURY model. In Evaluation of Soil Organic Matter Models; Springer: Berlin/Heidelberg, Germany, 1996; pp. 283–291. [Google Scholar] [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y.; Dagan, G. Hydraulic Conductivity of Soils: Unified Approach to the Statistical Models. Soil Sci. Soc. Am. J. 1978, 42, 392–395. [Google Scholar] [CrossRef]
- Mohaghegh, M.; Größler, A. The Dynamics of Operational Problem-Solving: A Dual-Process Approach. Syst. Pract. Action Res. 2019, 33, 27–54. [Google Scholar] [CrossRef]
- Choo, A.S. Defining Problems Fast and Slow: The U-shaped Effect of Problem Definition Time on Project Duration. Prod. Oper. Manag. 2014, 23, 1462–1479. [Google Scholar] [CrossRef]
- Repenning, N.P.; Sterman, J.D. Capability Traps and Self-Confirming Attribution Errors in the Dynamics of Process Improvement. Adm. Sci. Q. 2002, 47, 265. [Google Scholar] [CrossRef]
- Althoff, T.D.; Menezes, R.S.; de Pinto, A.S.; Pareyn, F.G.; de Carvalho, A.L.; Martins, J.C.; Carvalho, E.; Samuel, A.; da Silva, A.; Dutra, E.; et al. Adaptation of the century model to simulate C and N dynamics of Caatinga dry forest before and after deforestation. Agric. Ecosyst. Environ. 2018, 254, 26–34. [Google Scholar] [CrossRef]
- Dimassi, B.; Guenet, B.; Saby, N.P.; Munoz, F.; Bardy, M.; Millet, F.; Martin, M.P. The impacts of CENTURY model initialization scenarios on soil organic carbon dynamics simulation in French long-term experiments. Geoderma 2018, 311, 25–36. [Google Scholar] [CrossRef]
- Nicoloso, R.S.; Amado, T.J.; Rice, C.W. Assessing strategies to enhance soil carbon sequestration with the DSSAT-CENTURY model. Eur. J. Soil Sci. 2020, 71, 1034–1049. [Google Scholar] [CrossRef]
- Franzluebbers, A.J.; Follett, R.F.; Johnson, J.M.; Liebig, M.A.; Gregorich, E.G.; Parkin, T.B.; Smith, J.L.; Del Grosso, S.J.; Jawson, M.D.; Martens, D.A. Agricultural exhaust: A reason to invest in soil. J. Soil Water Conserv. 2006, 61, 98A–101A. [Google Scholar]
- Six, J.; Conant, R.T.; Paul, E.A.; Paustian, K. Stabilization mechanisms of soil organic matter: Implications for C-saturation of soils. Plant Soil 2002, 241, 155–176. [Google Scholar] [CrossRef]
- Delgado, J.A. Crop residue is a key for sustaining maximum food production and for conservation of our biosphere. J. Soil Water Conserv. 2010, 65, 111A–116A. [Google Scholar] [CrossRef] [Green Version]
- Smith, P.; House, J.I.; Bustamante, M.; Sobocká, J.; Harper, R.; Pan, G.; West, P.C.; Clark, J.M.; Adhya, T.; Rumpel, C.; et al. Global change pressures on soils from land use and management. Glob. Chang. Biol. 2015, 22, 1008–1028. [Google Scholar] [CrossRef]
- Franzluebbers, A.J.; Wendroth, O.; Creamer, N.G.; Feng, G.G. Focusing the future of farming on agroecology. Agric. Environ. Lett. 2020, 5, e20034. [Google Scholar] [CrossRef]
- McGill, W.B.; Hunt, W.W.; Woodmansee, R.G.; Reuss, J.O. PHOENIX, a model of the dynamics of carbon and nitrogen in grassland soils. Ecol. Bull. 1981, 33, 49–115. [Google Scholar]
- Martin, J.P.; Haider, K. Influence of mineral colloids on turnover rates of soil organic carbon. In Interactions of Soil Minerals with Natural Organics and Microbes; Huang, P.M., Schnitzer, M., Eds.; Soil Science Society of America Special Publication 17; SSSA: Madison, WI, USA, 1986; pp. 283–304. [Google Scholar]
- Lane, D. Can we have confidence in generic structure? J. Oper. Res. Soc. 1998, 49, 936–947. [Google Scholar] [CrossRef]
- Senge, P. The Fifth Discipline, The Art and Practice of the Learning Organization; Currency/Doubleday: New York, NY, USA, 1990. [Google Scholar]
- Richardson, G.P. System Dynamics. In Encyclopedia of Operations Research and Management Science; Springer Science and Business Media: Berlin, Germany, 2013; pp. 1519–1522. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Farm and Ranch Irrigation Survey 2013. Special Studies, Part 1, AC-12-SS-1; November 2014; Volume 3. Available online: https://www.nass.usda.gov/Publications/AgCensus/2012/Online_Resources/Farm_and_Ranch_Irrigation_Survey/ (accessed on 20 October 2019).
- Brilli, L.; Bechini, L.; Bindi, M.; Carozzi, M.; Cavalli, D.; Conant, R.; Dorich, C.D.; Doro, L.; Ehrhardt, F.; Farina, R.; et al. Review and analysis of strengths and weaknesses of agro-ecosystem models for simulating C and N fluxes. Sci. Total Environ. 2017, 598, 445–470. [Google Scholar] [CrossRef] [Green Version]











| Equation | Equation No. | Soil Nutrient/Chemical Component |
|---|---|---|
| nZr (dS/dt) = R(t) + I(S(t)) − ET(S(t), C(t)) − Q(S(t)) | (1) | Water balance * |
| ET(S(t), C(t)) = ETs * C(t) * Kcb * ET0 | (2) | Total ET |
| (3) | Soil moisture-regulated transpiration | |
| E(S, C, t) = Kr(S) * (1 − C) * Eb * ET0(t) | (4) | Evaporation driven by soil cover |
| (5) | Evaporation reduction coefficient | |
| K(S) = Ksat * Sd | (6) | Hydraulic conductivity |
| dC/dt = G(C, S, N, t) − −Ms(C, t) − H(C, t) | (7) | Plant canopy cover |
| G(C, S, N, t) = rg * U(C, S, N, t) | (8) | Plant growth rate |
| Ms(C, t) = (rm + γ (t − tsen) * Θ (t − tsen)) * C2 | (9) | Plant senescence |
| Hi = C * Hv * Hd | (10) | Plant harvest |
| dNc/dt = D(C, t) + F(N, t) − L(S, N) − U(S, N, C, t) | (11) | Nitrogen balance * |
| L(S, N) = η * Q(S) | (12) | Nitrogen leaching |
| η = aN/SnZ | (13) | Soil water nitrogen content |
| U(S, N, C, t) = f(η) * T(S, C, t) | (14) | Plant nitrogen uptake |
| (15) | Nitrogen uptake limitation function | |
| dqs/dt = IVi – Q * V | (16) | Soil salinity |
| dB/dt = W * U(S, N, C, t)/ηcET0(t) = W/ηc Ks(S)Kcbf(η)C | (17) | Crop biomass |
| Y = B * Hi | (18) | Crop yield * |
| (19) | Irrigation efficiency | |
| (20) | Nitrogen use efficiency |
| Equation | Equation No. | Soil Biology Component |
|---|---|---|
| dSOMi/dt = Ki * Md * Td * SOMi | (21) | Organic matter dynamics |
| (22) | Soil moisture effect on decomposition rate | |
| Td = (t1 * 0.2) * t2 | (23) | Soil temperature effect on decomposition rate |
| Ki1 = K1 * exp (−3.0 * Lf) | (24) | Litter layer decomposition rate |
| Ki5 = K5 * (1 − 0.75 * (silt + clay fraction)) | (25) | Soil texture effect on active carbon decomposition * |
| Lfa = 2 + 0.12 * PPT; where PPT is the annual precipitation | (26) | Precipitation effect on above-ground lignin biomass |
| Lfr = 26 − 0.15 * PPT; where PPT is the annual precipitation | (27) | Precipitation effect on root lignin biomass |
| Fm = 0.85 − 0.018 * LR/N | (28) | Residue microbial metabolic supply * |
| Fs = 1 − Fm | (29) | Residue structural component |
| SOMslow = (0.85 − 0.68 * (silt + clay fraction)) | (30) | Soil texture effect on stabilizing slow SOM * |
| RAT = (S(t) + R(t))/ET0 | (31) | Md inputs * |
| temp1 = (45 − ts)/(45 − 35); temp2 = e^(0.076 * (1 − temp1 * 2.63)); where ts is temperature degrees °C | (32) | Td inputs |
| Equation | Equation No. | Soil Physical and Hydraulic Component |
|---|---|---|
| dr/dt = d(vf)/dr − mf | (33) | Pore radius distribution |
| n(t) = a(t)r−b(t)dr | (34) | Soil porosity dynamics * |
| v(r, t) = r/(a(t)b(t)) * (a(t)b’(t)ln(r) − a’(t)) | (35) | Soil particle space drift and shrink term |
| m(r,t) = b’(t)/b(t) * (1 − ln(r)) − a’(t)/(a(t)b(t)) | (36) | Soil particle space source-sink term |
| ψs (S, t) = −(Cs/Rm(t)) * s−1/(1 − b(t)) | (37) | Matric potential |
| Ksat (s, t) = [(γw * Ge * n(t)2 * Rm(t)2 * (1 − b(t))2]/μ (3 − b(t))(2 − b(t))) * s(4 − 2b(t))/(1 − b(t)) | (38) | Saturated conductivity * |
| γb = rb + (1 − rb) * exp(−kb(ttd)) | (39) | Management (tillage) influence on porosity |
| bc(SOM(t)) = b0 + σbOM(t) | (40) | Soil organic matter influence on porosity |
| b(ttd, SOM(t)) = γb * bc | (41) | Combined b-term for management and SOM effect on porosity * |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Threshold S (% of Field Capacity) | Target S (% of Field Capacity) | Application Freq (days) | Day of Tillage | Harvest Volume (%) | ||
| Exp. 1 | Control (flood) | 0.35 | 0.45 | 21 | 115 | 0.67 |
| Drip irrigation | 0.35 * | 0.45 * | 3 | 115 | 0.67 | |
| Exp. 2 | Control (conv. tillage) | 0.35 | 0.45 | 21 | 115 | 0.67 |
| No-tillage | 0.35 | 0.45 | 21 | n/a | 0.34 * | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turner, B.L. Soil as an Archetype of Complexity: A Systems Approach to Improve Insights, Learning, and Management of Coupled Biogeochemical Processes and Environmental Externalities. Soil Syst. 2021, 5, 39. https://doi.org/10.3390/soilsystems5030039
Turner BL. Soil as an Archetype of Complexity: A Systems Approach to Improve Insights, Learning, and Management of Coupled Biogeochemical Processes and Environmental Externalities. Soil Systems. 2021; 5(3):39. https://doi.org/10.3390/soilsystems5030039
Chicago/Turabian StyleTurner, Benjamin L. 2021. "Soil as an Archetype of Complexity: A Systems Approach to Improve Insights, Learning, and Management of Coupled Biogeochemical Processes and Environmental Externalities" Soil Systems 5, no. 3: 39. https://doi.org/10.3390/soilsystems5030039
APA StyleTurner, B. L. (2021). Soil as an Archetype of Complexity: A Systems Approach to Improve Insights, Learning, and Management of Coupled Biogeochemical Processes and Environmental Externalities. Soil Systems, 5(3), 39. https://doi.org/10.3390/soilsystems5030039






