Abstract
Algae-based products have applications in the food and pharmaceutical industries, bioremediation of waste streams and biofuel production. Drying has been recognised to constitute the largest energy cost in algae processing, yet there is limited data or modelling characterising the drying kinetics of macroalgae. This research modelled the equilibrium moisture content of two macroalgae species, Ulva ohnoi, a saltwater alga and Oedogonium intermedium, a freshwater alga. The Guggenheim–Anderson–de Boer model was found to best represent experimental equilibrium moisture contents. Drying rate curves obtained under both convective and radiative conditions were fitted to an analytical solution of Fick’s second law, including the modelled equilibrium moisture values. Effective diffusivity values for the two species are presented.
1. Introduction
Algae have been identified as a renewable resource that can be utilised for a range of products such as fertilisers and animal feeds, human food supplements, nutraceuticals, specialty chemicals, and bioenergy [1,2,3]. Historically the majority of research has focused on the development of microalgae, which are small single-celled algae. However, the commercial development of microalgae has been limited to high-value niche applications due to the technical difficulties and cost of large-scale cultivation and dewatering [4]. More recently, research effort in bioprocessing has broadened to include macroalgae, which are large multicellular alga found in both marine and freshwater environments. Due to their larger size and ease of harvesting, macroalgae are well suited to large-scale outdoor cultivation.
Macroalgae have the capacity to complement existing industries and drive sustainability and circular economy objectives by utilising their waste nutrients and water, effectively creating a sustainable source of high-protein biomass from waste inputs [5,6]. Neveux et al. [7] found that a freshwater species of macroalgae, Oedogonium intermedium (Chlorophyta), had the highest biocrude yield of a range of species, using hydrothermal liquefaction. Zeraatkar et al. [8] performed a review of algae in bioremediation of heavy metals from wastewater, which concluded both macro- and micro-algae were suitable candidates. Castine et al. [9] considered the use of macroalgae to treat wastewater from aquaculture, including added value from algae products. An assessment of the potential for algae in bioremediation was performed by Lawton et al. [10], where the saltwater macroalga Ulva ohnoi (Chlorophyta) was found to have the highest growth rates of a range of local species. Several macroalgae species including O. intermedium and Asparagopsis taxiformis (Rhodophyta) have potential for use as a supplement to livestock feed, leading to improved growth rates and lower livestock methane emissions [11,12].
A significant barrier to the development of industry based around macroalgal production is the design of energy efficient and well-controlled drying systems that can transition freshly harvested biomass into a product suitable for storage and transport. The drying step of a process was recognised as the single biggest energy usage for the processing of algal biomass, due to the large amounts of moisture requiring removal [13]. The drying step can constitute up to 70–75% of processing costs in some cases. As such, optimisation of this step would lead to the largest gain in efficiency for the overall process.
Drying models are an effective way to understand and define the drying process and design drying equipment for industry. Industrial drying equipment can be broadly divided into drying via radiative and convective heating methods, with convective drying typically faster. Diffusion-based modelling has been extensively used in literature to describe both convective and radiative drying of food and biomaterials. This has been through the fitting of theoretical models based on Fick’s law of diffusion, or fitting moisture data to empirical models with mathematical formulations that are identical to the first term in the analytical solution to Fick’s law of diffusion, such as the Henderson and Pabis model [14].
Many studies in the literature have used diffusion modelling approaches to successfully represent macroalgae drying [15,16,17,18,19]. Other drying studies utilising diffusion-based modelling of algae include several covering the drying kinetics of the microalga Arthrospira platensis (Cyanobacteria) [20,21]. The use of diffusion modelling of other materials such as fibre, fruit, and vegetables is widespread in the literature.
The theoretical method of modelling diffusion-based drying kinetics is based on Fick’s second law of diffusion [22]. A commonly used analytical series solution to Fick’s second law, adapted to apply to the drying of an infinite slab of constant thickness, was derived by Sherwood [23] and is shown in Equation (1).
In the equation MR is the dimensionless moisture ratio, M, Me, and M0 are moisture contents (% dry basis) at current, equilibrium, and initial times respectively. L is the material thickness (m), De is effective diffusivity (m2/s), and t is drying time (s).
Me is another important parameter in modelling drying kinetics as it defines the limits to which a material can be dried, given the conditions of the surroundings. Its value is important for product preservation, packaging, and storage. The equilibrium moisture content depends on the material as well as the relative humidity and temperature of the surroundings. It is typically modelled using adaptions of gas surface adsorption models. Lemus et al. [24] studied the equilibrium moisture content of the red alga Agarophyton chilense (Rhodophyta) between 5 and 40 °C and between 10% and 95% relative humidity. Other equilibrium moisture studies of macroalgae include the brown alga Fucus vesiculosus and Macrocystis pyrifera (Ochrophyta, Phaeophyceae) [15,16]. The best-fit equations in equilibrium moisture studies are typically the Guggenheim–Anderson–de Boer (GAB) or Bruenauer–Emmett–Teller models [25]. In the GAB model (Equation (2)) A, B, and C are model constants, ERH is the relative humidity as decimal and Me is the equilibrium moisture content in % dry basis. As an equilibrium moisture model, the GAB model has been shown to well represent Me values over relative humidities between 5% and 90% for a range of different biomaterials [26].
The aim of this work is to model experimentally determined equilibrium moisture contents over a range of temperature and relative humidity conditions for two previously undescribed but commercially important macroalgae species, U. ohnoi and O. intermedium. In this work, diffusion modelling and critical model parameters (effective diffusivities and activation energy) are experimentally determined and used to compare radiative and convective drying. These values are essential to determine safe storage moisture content limits and for obtaining accurate drying rate models. These model parameters are compared to results for other macroalgae.
2. Experiments
The algal biomass used in this study was obtained from stock cultures sourced from the Marine and Aquaculture Research Facilities Unit (MARFU) at James Cook University in Townsville, Australia. The two species used in the study were U. ohnoi and O. intermedium. U. ohnoi is a saltwater alga that forms thin, roughly rectangular blades up to 10 cm wide, with the thickness of each blade being two cells wide. It was selected from a range of saltwater species based on its high growth rates and high biocrude yield as well as high resistance to bacterial ingress [27,28]. O. intermedium is a freshwater alga that forms single filaments one cell wide, which can significantly clump together when harvested. Both species have potential for use as livestock feed supplement [11,29].
In both kinetic and equilibrium tests, surface moisture was removed from the algae samples via use of lab-scale centrifuge (Koh-I-Noor Engineering Works, Punjab, Pakistan) at 2800 RPM. Algae samples were dewatered in the centrifuge until outlet moisture flow completely stopped, which provided a consistent starting point for the drying and equilibrium moisture trials. Nine dewatered subsamples of the algae were used to determine the initial moisture content (M0) and to evaluate consistency in the determination of moisture content following the dewatering step. Dry weights were obtained using a moisture analyser (MA-45, Sartorius AG, 37075 Goettingen, Germany) drying at 110 °C to ensure complete moisture removal. Average initial moisture content (following dewatering) and 95% confidence interval for U. onhoi was 81.73% weight ± 1.4% (relative), and 83.54% weight ± 1.1% (relative) for O. intermedium. The low variance in these starting-point (dewatered) moisture contents demonstrated both consistency in the dewatering process and in the use of the MA-45 to obtain moisture content and dry basis algae mass values.
2.1. Equilibrium Moisture Content
The setup used for the equilibrium moisture experiments consists of twelve sealed containers fully immersed in a hot water bath to control internal temperature. Each container was 500 ml in volume and had a mesh platform suspended above a saturated salt solution filling a third of the container volume. At a given temperature, a saturated salt solution will achieve equilibrium with the air inside the container, giving a fixed humidity [30]. Temperature (T) and humidity (ERH) inside the sample containers were measured using a humidity probe (Center 313, Center Technology Corporation, Taipei, Taiwan). Fresh centrifuged algae samples weighing approximately 4 g each were placed on the mesh platforms inside each container. Excess salts were used as a visual indicator to ensure saturated solutions during each experiment. The solutions used (and their respective relative humidities) at equilibrium were lithium chloride (11%); sodium acetate (20%); magnesium chloride (31%); sodium carbonate (43%); and sodium bromide (52%). Three containers of each solution were used to obtain triplicate results for each temperature and humidity.
The mass of the algae samples was measured daily after being left for a week to reach equilibrium. Three consecutive and constant measurements were obtained to ensure equilibrium. The measured equilibrium masses were converted to moisture content in % dry basis via Equation (3);
where Me,g is the equilibrium mass of the algae in grams, and D is the dry weight of the algae in grams. Algae dry weight was determined using the Sartorius MA-45.
2.2. Drying Kinetics
Freshly centrifuged algae was used to experimentally investigate drying kinetics. Given proteins in algae are prone to denaturation at high temperature, and characteristics such as colour also deteriorate (changing from green to brown) at high temperature, temperatures used for the experimental runs were 40, 50, and 60 °C. Three repeats were performed for each temperature. The initial material thickness (L = 0.01 m) and the initial fresh mass were kept constant between runs.
A Sartorius MA-45 moisture analyser was used for the radiation drying experiments. Relevant technical details for the moisture analyser are as follows: frequency 48–60 Hz, temperature range 40–230 °C in 1 °C increments, mass measurement accuracy of 0.2%, balance resolution 1 mg. Initial fresh masses were set at 1.5 g. Triplicates of moisture ratio versus time showed excellent consistency in experimental moisture profiles obtained under radiative drying conditions (Figure 1).
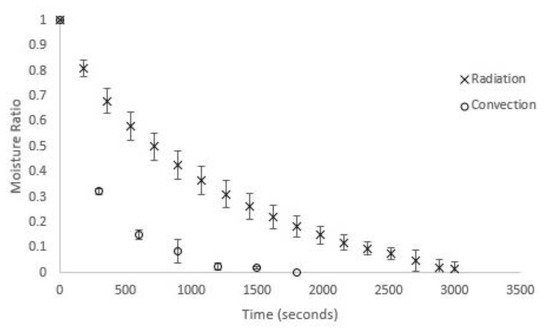
Figure 1.
Triplicate moisture profiles for U. ohnoi at 40 °C for radiative and convective drying.
A convective food desiccator (Ezi-Dri FD-1000, Hydraflow Industries Limited, Upper Hutt, New Zealand) was used for the convection drying experiments. The equipment passes heated air through vertically stacked trays on which the algal material is placed. Gas temperature (40, 50, 60 °C) and flow rate (0.7 m/s) were confirmed from measurement of outlet conditions via hot-wire anemometer (AM-4214SD, Lutron Electronics Enterprise, Taipei, Taiwan). Initial biomass weight was measured before placement in the stacked trays. Trays were removed in a randomised order at discrete time intervals and material weight was obtained at each interval. Randomisation was chosen to reduce any potential effects of tray positions on the drying kinetics. Humidity of the exhaust air was measured directly using a handheld humidity meter and probe (Center 313, Center Technology Corp., Taipei, Taiwan). Initial fresh masses on each tray were set at 7 g.
2.3. Analysis Methods
2.3.1. Equilibrium Moisture
For each algae type, two equilibrium moisture content models (BET and GAB) were fitted to the experimentally determined equilibrium moisture content at each temperature and relative humidity. Model fitting was performed by adjusting model parameter values to minimise the total sum of square errors between the model and the triplicate experimental data sets. Initial guess values for the model fit process were chosen to represent the expected parameter range for the equations, and a wide range of different initial parameter values was tested to ensure the global minimum was found. These calculations were performed using Microsoft Excel using the solver function with GRG nonlinear solver method. The objective function is summarised in Equation (4), where m corresponds to a given data set, and the objective function (Obj) is minimised by varying the model constants.
2.3.2. Drying Kinetics
The raw experimental data of mass against time in the convective and radiative drying experiments were converted to moisture ratio versus time. An analytical solution to the Fick’s second law model (Equation (1)) was fitted to moisture ratio versus time data sets. Model fitting was performed by minimisation of the total sum of square errors between the model and experimental data, with the model representing the best fit to all three sets of data at a given condition. Ten terms of the infinite series were used in modelling to ensure convergence in the infinite series solution [31]. These calculations were performed using Microsoft Excel with the solver function and GRG nonlinear solver method, assuming constant relative variance in the experimental data. The objective function is summarised in Equation (5), where m corresponds to the number of data sets. The objective function (Obj) was minimised by varying the magnitude of the effective diffusivity parameter (De).
3. Results
3.1. Equilibrium Moisture Modelling
Of the models used, the best fit (i.e., demonstrating the highest R2 value) for both species over the conditions tested was the GAB model. We recommend this model to be adopted for both species. The model constants and the goodness of fit (R2) for the GAB equation are summarised in Table 1. Graphs of the experimental equilibrium moisture compared with the GAB model predictions are shown in Figure 2 for both species.

Table 1.
Guggenheim–Anderson–de Boer (GAB) model coefficients and fit.
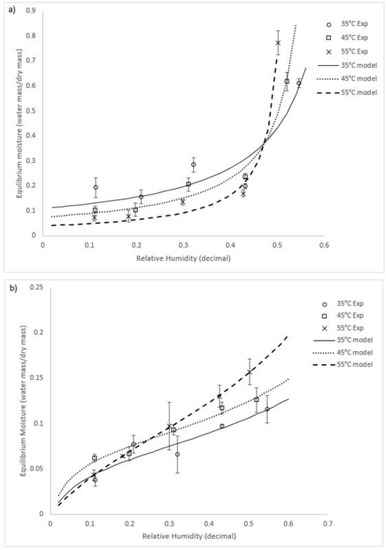
Figure 2.
GAB model and experimental data for (a) U. ohnoi and (b) O. intermedium (Exp = experimental; model = modelling outcome).
A statistical analysis was performed using SPSS software to determine the significance of temperature and relative humidity for determining the equilibrium moisture. A general linear univariate model analysis was used, which provided regression and variance analysis of the equilibrium moisture as the dependent variable against temperature and relative humidity. The analysis showed that both temperature and relative humidity were statistically significant in their ability to predict changes in the equilibrium value for both species (significance < 0.05 for all variables for both species). F–tests (a measure of the relative predictive ability) showed that, of the two variables, relative humidity was the best single predictor of the equilibrium moisture content. Comparing between the two types of algae, U. ohnoi exhibited a significantly higher equilibrium moisture content than O. intermedium. It is assumed that this was because U. ohnoi has reduced surface area (algal sheets are two cells thick rather than the single cell strings of O. intermedium) and is a saltwater alga.
At around 50% humidity for Ulva and 30% humidity for O. intermedium, there was a crossover point where higher temperatures resulted in higher equilibrium moisture than those observed at lower temperatures. Lemus et al. [24] had a similar crossover effect at higher humidities in a study of the red macroalga Agarophyton chilense, as did Moreira [15] for Fucus vesiculosus. They reasoned that this was due to solubility effects of polysaccharides and proteins that make up the majority of the alga solids mass. The crossover point would then be where these solubility effects on the equilibrium point become larger than effects of the surrounding atmospheric conditions. Similar results have been shown for other algae biomass, including Gelidium corneum (Rhodophyta), as well as other biomaterial with soluble components [32,33]. Both U. ohnoi and O. intermedium have polysaccharide and protein content totalling about 60% of dry mass [7]. It should be noted that the GAB equation is not designed to represent these interactions. As such, it follows that the parameters of the GAB equation are semi-empirical or empirical in this application, reinforcing the importance of experimental characterisation of algal species.
In general, equilibrium moisture isotherms and equilibrium moisture magnitudes for both species were similar to those for other macroalgae and biomaterials. Table 2 provides equilibrium moisture content values for this work and also for a variety of biomass types.

Table 2.
Examples of equilibrium moisture contents for various biomaterials and algae.
3.2. Drying Kinetics Modelling
The model-predicted effective diffusivities for both Ulva and O. intermedium at each temperature were determined by including the GAB-modelled equilibrium moisture contents (Me). The parameter-estimated effective diffusivities are shown in Table 3 for both species. The effective diffusivity was lower for O. intermedium than U. ohnoi and this is likely due to the tendency for O. intermedium to clump together when harvested, which reduces overall contact area for drying compared with individual blades of U. ohnoi.

Table 3.
Effective diffusivity from radiative and convective drying.
Diffusivity values for the two species were similar to those of other macroalgae, summarised in Table 4. However, diffusivities for both algae species were high compared to those determined for microalgae drying. For example, effective diffusivities for spirulina drying under convective conditions were in the range 3 × 10−10 to 7 × 10−10 m2/s [21]. Both species of macroalgae had relatively high effective diffusivities compared to other biomaterials, such as wood and fruit slices, which indicates a lower internal resistance to diffusion for macroalgae. This was likely due to the comparative simplicity of the algae material combined with the large discrete particles giving a high void fraction. The algae cells also use diffusion across cell walls to transfer water and nutrients from their surroundings. This predisposition could be enhancing the drying rate in comparison to material like wood and fruits. Generally, biomaterials with comparatively lower effective diffusivities have outer solid surfaces (e.g., bark) that do not facilitate moisture transfer (to the same extent that algae does), as well as being materials with more complex structures (e.g., lignin, fibres) that include multiple different internal layers.

Table 4.
Examples of effective diffusivity values for various biomaterials during convective drying.
Graphs of the experimental data for radiative and convective drying of both algae species are compared to each fitted model in Figure 3 and Figure 4, respectively. The general fit of the Fick’s second law model to the experimental data is excellent (R2 values in all runs except for 40 °C radiative heating for O. intermedium were between 0.945 and 0.99). However, the model had a tendency to under-predict the experimental data for moisture ratios between one and 0.3, then over-predict as the moisture ratio approached zero. Worst fit was O. intermedium at 40 °C under radiation drying, where the tendency of the algal biomass to clump unevenly caused an increase in the variance of the experimental data. Convection drying rates were higher than for radiation, with increased heat transfer and slab penetration likely to be the cause.
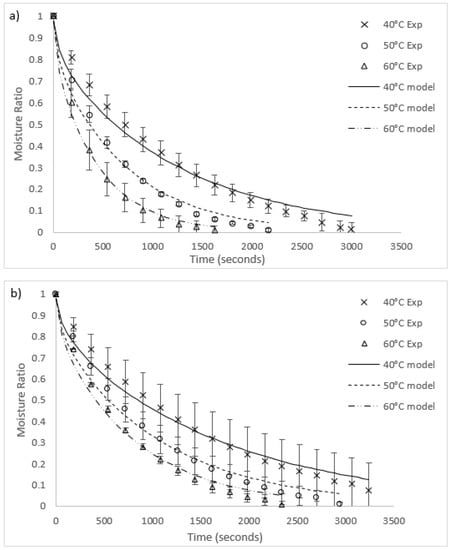
Figure 3.
Comparison of radiation drying results and models for (a) U. ohnoi and (b) O. intermedium (Exp = experimental; model = modelling outcome).
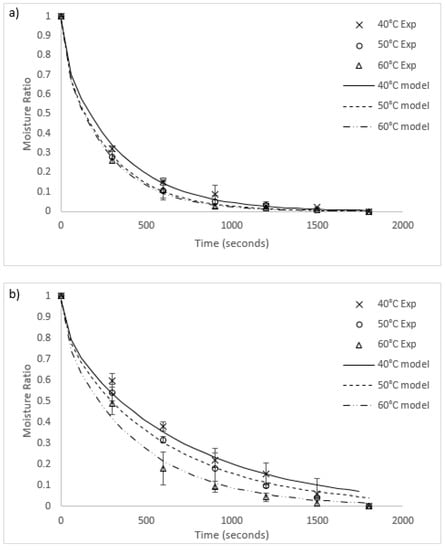
Figure 4.
Comparison of convection drying results and models for (a) U. ohnoi and (b) O. intermedium (Exp = experimental; model = modelling outcome).
The assumptions made in the derivation of this analytical solution are: initial moisture distribution is even; internal moisture transport is by diffusion only; drying gas volumes are large enough that surrounding environmental conditions are not changed by moisture transfer; slab thickness is constant throughout the drying process; temperature of the slab is isothermal and equal to the temperature of the surroundings; and bulk transfer of moisture (by convection) to the surroundings is sufficiently fast that drying is only limited by the internal rate of diffusion. These conditions are rarely if ever fully satisfied, and De is used in drying kinetics to pragmatically represent a global effective diffusivity, which accounts for these deviations. In this way, the diffusion coefficient consolidates the effects of deviations from these assumptions into a single (lumped) parameter model. This covers internal effects such as resistance to diffusion from material layers and a biomaterial’s binding strength holding moisture internally, as well as external effects of temperature gradients, drying gas velocity and humidity. The effective diffusivity approach requires new experimental results for new materials, due to the influence of material properties. In the case of biomaterial drying there is typically some volume loss or material shrinkage that occurs, and there is also an initial heating period required to bring the biomaterial up to the gas temperature. Despite these physical and mechanistic deviations from ideal behaviour, model accuracy remains typically high and any errors introduced by using this modelling approach are widely considered to be acceptable. Both materials undergo significant shrinkage during drying, which is not accounted for in the analytical model. This shrinking would reduce the effective slab thickness as the material dries, which would lead to increased effective diffusivity values as drying progresses. A solution of the original Fick’s second law partial differential equations by including time-variant boundary conditions would be required to account for this effect. However, the complexity of this approach would limit its utility for industry practitioners seeking to use model equations to design drying operations.
Radiative drying was measured as slower than convection drying. There are two potential explanations as to why this could be the case. The first is that drying was not a diffusion-limited process and was instead controlled by moisture removal at the surface. This would lead to accumulation of moisture on the surface, and result in constant-rate drying. This was investigated by numerically calculating the drying rate using second order Taylor approximation. Figure 5 includes graphs of the rate of change of drying for both algae species, shown as absolute values. In these graphs, a constant-rate drying period would show as a horizontal trend in the initial drying stage. The graphs in Figure 5 show that drying was in a single falling-rate period for both species and all temperatures. The shape is the same as the expected rate of change from the Fick’s law model. This shows the assumption of diffusion-limited drying is correct.
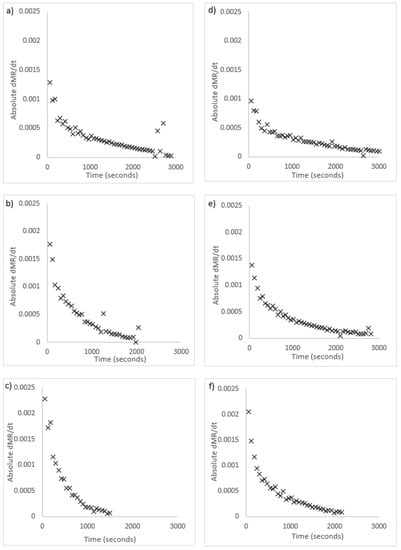
Figure 5.
Dimensionless moisture ratio (MR) rate of change vs time for radiative drying; U. ohnoi (a) 40 °C (b) 50 °C (c) 60 °C; O. intermedium (d) 40 °C (e) 50 °C (f) 60 °C.
Given that diffusion-limited drying was occurring, the addition of air flow must then have been affecting the material in a way that led to an apparent increase in effective diffusivity. Several other studies have shown increases in air velocity cause an increase in effective diffusivity, including for eggplant, potato slices, and other macroalgae [17,39,40]. Other materials have been studied with results showing little to no effect with flow rate changes, including a selection of vegetables and a differently structured macroalga [32,41]. There is little discussion on possible mechanisms for this in literature. The most likely explanation is that airflow causes an increase in penetration through the material slab, which results in a reduction of the average distance moisture is required to diffuse through (i.e., the parameter L, the slab width reduces with increasing gas velocity). In this case, we are choosing a pragmatic approach, leaving L as the initial slab width and representing the effect as an increase in the effective diffusivity. Comparing this work with other observations of the effect of convection indicates that materials composed of particulates or with porous structure show increased diffusivity with air flow, while those closer to solid slabs of material do not.
The Fick’s law analytical model enables a mechanistic or theoretical description of the influence of temperature, through the determination of activation energy of drying. Studies of drying kinetics typically show temperature has an Arrenhius-type relationship to the effective diffusivity, shown in Equation (6);
where D0 is the diffusion pre-exponential factor (m2/s), Ea is the activation energy (J/mol), R is the ideal gas constant (8.314 J/mol.K), and T is temperature in Kelvin.
Assuming this type of relationship holds true for diffusivity and temperature and no other compounding effects exist (for example, material degradation from high temperature), D0 represents the effective diffusivity at an infinitely high temperature and Ea is the energy to overcome the “barrier” to diffusion. This barrier is the energy to overcome the initial moisture binding in the case of internally bound moisture in macroalgae and other biomaterials. These values were estimated by plotting the natural log of the parameter-estimated effective diffusivity versus 1/T from radiative drying trials (shown in Figure 6). The slope of the fitted line is then equivalent to –Ea/R, and the y-intercept is equivalent to ln(D0). For a complete radiative drying model description, the recommended values of Ea and D0 for both species are shown in Table 5. A comparison of the Ea values with literature results for other macroalgae and biomaterials is shown in Table 6. For convective drying at 0.7 m/s, it is recommended to use the diffusivity values (De) at the appropriate drying temperature, shown in Table 3.
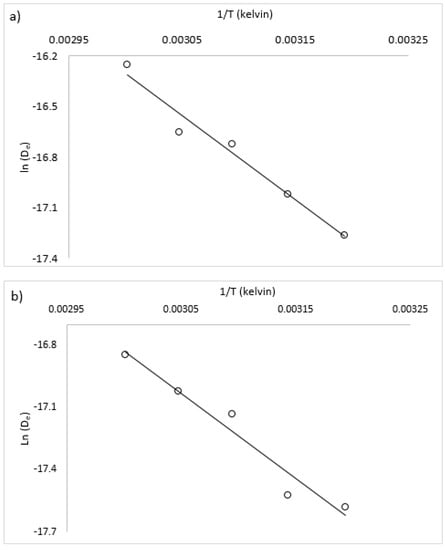
Figure 6.
Graphical solution method for calculation of activation energy and diffusion pre-exponent, (a) U. ohnoi and (b) O. intermedium.

Table 5.
Activation energy and diffusion pre-exponent for radiative drying.

Table 6.
Comparison of D0 and Ea for other biomaterials.
4. Conclusions
Important drying and moisture equilibrium properties of two commercially important macroalgae species were characterised in lab-based trials. The GAB moisture sorption model showed the best fit to experimentally determined equilibrium moisture contents for both U. ohnoi and O. intermedium macroalgae over industry-relevant temperature and relative humidity ranges (35–55 °C and 10–60% RH). Relative humidity was found to be the most significant variable in predicting equilibrium moisture content for both types of algae, and environmental limits for safe algae storage were clearly identified. An analytical solution to Fick’s second law of diffusion was used to model both convective and radiative drying kinetics for both algae species with a high degree of correlation. Moisture ratio versus time data showed that drying for both species occurs in a falling-rate period at all times and temperatures (40–60 °C), indicating diffusion-limited drying and reinforcing the validity of the analytical model for these biomaterials. Convective drying at 0.7 m/s demonstrated an increased drying rate compared to radiative drying at the same temperature, reinforcing the value in gas-assisted drying technologies. Diffusion coefficients under both radiative and convective conditions, as well as activation energies, were determined for both species. These model parameters were compared to literature values for other biomaterials and showed consistency. Increased rates of diffusion under convective conditions were attributed to the drying gas flow penetrating into the material “slab” and reducing diffusion distance (i.e., slab thickness). Given the significant influence of gas velocity on the drying rates observed in this study, the effects of both gas velocity and material thickness should be more extensively investigated for both macro- and microalgae.
Author Contributions
Conceptualization, M.S.; methodology, C.W. and M.S.; formal analysis, C.W.; writing—original draft preparation, M.S. and C.W.; writing—review and editing, M.S., E.A., A.C.; supervision, M.S. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The algal biomass used in this research was supplied by Pacific Bio Pty Ltd. as part of their research and development program on algal bioremediation and bio-products.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Angell, A.; Angell, S.; de Nys, R.; Paul, N. Seaweed as a protein source for mono-gastric livestock. Trends Food Sci. Technol. 2016, 54, 74–84. [Google Scholar] [CrossRef]
- Mabeau, S.; Fleurence, J. Seaweed in food products: Biochemical and nutritional aspects. Trends Food Sci. Technol. 1993, 4, 103–107. [Google Scholar] [CrossRef]
- Garcia-Vaquero, M.; Hayes, M. Red and green macroalgae for fish and animal feed and human functional food development. Food Rev. Int. 2016, 32, 15–45. [Google Scholar] [CrossRef]
- Rawat, I.; Ranjith Kumar, R.; Mutanda, T.; Bux, F. Biodiesel from microalgae: A critical evaluation from laboratory to large scale production. Appl. Energy 2013, 103, 444–467. [Google Scholar] [CrossRef]
- Cole, A.J.; Neveux, N.; Whelan, A.; Morton, J.; Vis, M.; de Nys, R.; Paul, N.A. Adding value to the treatment of municipal wastewater through the intensive production of freshwater macroalgae. Algal Res. 2016, 20, 100–109. [Google Scholar] [CrossRef]
- Lawton, R.J.; Cole, A.J.; Roberts, D.A.; Paul, N.A.; de Nys, R. The industrial ecology of freshwater macroalgae for biomass applications. Algal Res. 2017, 24, 486–491. [Google Scholar] [CrossRef]
- Neveux, N.; Magnusson, M.; Maschmeyer, T.; de Nys, R.; Paul, N.A. Comparing the potential production and value of high-energy liquid fuels and protein from marine and freshwater macroalgae. GCB Bioenergy 2014, 7, 673–689. [Google Scholar] [CrossRef]
- Zeraatkar, A.K.; Ahmadzadeh, H.; Talebi, A.F.; Moheimani, N.R.; McHenry, M.P. Potential use of algae for heavy metal bioremediation, a critical review. J. Env. Manag. 2016, 181, 817–831. [Google Scholar] [CrossRef]
- Castine, S.A.; Paul, N.A.; Magnusson, M.; Bird, I.; de Nys, R. Algal bioproducts derived from suspended solids in intensive land-based aquaculture. Bioresour. Technol. 2013, 131, 113–120. [Google Scholar] [CrossRef]
- Lawton, R.J.; Mata, L.; de Nys, R.; Paul, N.A. Algal bioremediation of waste waters from land-based aquaculture using Ulva; selecting target species and strains. PLoS ONE 2013, 8, e77344. [Google Scholar] [CrossRef]
- Machado, L.; Kinley, R.; Magnusson, M.; de Nys, R.; Tomkins, N. The potential of macroalgae for beef production systems in Northern Australia. J. Appl. Phycol. 2015, 27, 2001–2005. [Google Scholar] [CrossRef]
- Machado, L.; Magnusson, M.; Paul, N.; Kinley, R.; de Nys, R.; Tomkins, N. Dose-response effects of asparagopsis taxiformis and oedogonium sp. on in vitro fermentation and methane production. J. Appl. Phycol. 2016, 28, 1443–1452. [Google Scholar] [CrossRef]
- Show, K.; Lee, D.; Chang, J. Algal biomass dehydration. Bioresour. Technol. 2013, 135, 720–729. [Google Scholar] [CrossRef] [PubMed]
- Henderson, S.M.; Pabis, S. Grain drying theory I: Temperature effects on drying coefficients. J. Agric. Eng. Res. 1961, 6, 169–174. [Google Scholar]
- Moreira, R.; Chenlo, F.; Sineiro, J.; Arufe, S.; Sexto, S. Water sorption isotherms and air drying kinetics of fucus vesiculosus brown seaweed. J. Food Process. Preserv. 2017, 41, e12997. [Google Scholar] [CrossRef]
- Vega-Gálvez, A.; Ayala-Aponte, A.; Notte, E.; Fuente, L.; Lemus-Mondaca, R. Mathematical Modeling of Mass Transfer during Convective Dehydration of Brown Algae Macrocystis Pyrifera. Dry. Technol. 2008, 26, 1610–1616. [Google Scholar] [CrossRef]
- Djaeni, M.; Sari, D.A. Low temperature seaweed drying using dehumidified air. Procedia Env. Sci. 2015, 23, 2–10. [Google Scholar] [CrossRef]
- Uribe, E.; Vega-Gálvez, A.; Vásquez, V.; Lemus-Mondaca, R.; Callejas, L.; Pastén, A. Hot-air drying characteristics and energetic requirement of the edible brown seaweed Durvillaea antarctica. J. Food Process. Preserv. 2017, 41, e13313. [Google Scholar] [CrossRef]
- Gupta, S.; Cox, S.; Abu-Ghannam, N. Effect of different drying temperatures on the moisture and phytochemical constituents of edible Irish brown seaweed. Food Sci. Technol. 2011, 44, 1266–1272. [Google Scholar] [CrossRef]
- Oliveira, E.; Rosa, G.; Moraes, M.; Pinto, L. Characterization of thin layer drying of spirulina platensis utilizing perpendicular air flow. Bioresour. Technol. 2009, 100, 1297–1303. [Google Scholar] [CrossRef]
- Dissa, O.; Compaore, A.; Tiendrebeogo, E.; Koulidiati, J. An effective moisture diffusivity model deduced from experiment and numerical solution of mass transfer equations for a shrinkable drying slab of microalgae spirulina. Dry. Technol. 2014, 32, 1231–1244. [Google Scholar] [CrossRef]
- Fick, A.V. On liquid diffusion. Philos. Mag. 1855, 10, 30–39. [Google Scholar] [CrossRef]
- Sherwood, T.K. The drying of solids–I. Ind. Eng. Chem. 1932, 24, 307–310. [Google Scholar] [CrossRef]
- Lemus, R.A.; Pérez, M.; Andrés, A.; Roco, T.; Tello, C.M.; Vega, A. Kinetic study of dehydration and desorption isotherms of red alga Gracilaria. Food Sci. Technol. 2008, 41, 1592–1599. [Google Scholar] [CrossRef]
- Anderson, R.B. Modifications of the Brunauer, Emmett and Teller equation. J. Am. Chem. Soc. 1946, 68, 686–691. [Google Scholar] [CrossRef]
- Guillard, V.; Bourlieu, C.; Gontard, N. Food Structure and Moisture Transfer: A Modelling Approach; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Neveux, N.; Yuen, A.K.L.; Jazrawi, C.; Magnusson, M.; Haynes, B.S.; Masters, A.F.; Montoya, A.; Paul, N.A.; Maschmeyer, T.; de Nys, R. Biocrude yield and productivity from the hydrothermal liquefaction of marine and freshwater green macroalgae. Bioresour. Technol. 2014, 155, 334–341. [Google Scholar] [CrossRef]
- Lawton, R.J.; de Nys, R.; Paul, N.A. Selecting reliable and robust freshwater macroalgae for biomass applications. PLoS ONE 2013, 8, e64168. [Google Scholar] [CrossRef]
- Vucko, M.; Cole, A.; Moorhead, J.; Pit, J.; de Nys, R. The freshwater macroalga Oedogonium intermedium can meet the nutritional requirements of the herbivorous fish Ancistrus cirrhosus. Algal Res. 2017, 27, 21–31. [Google Scholar] [CrossRef]
- Greenspan, L. Humidity set points of binary aqueous solutions. J. Res. Natl. Inst. Stand. Technol. 1976, 81, 89–96. [Google Scholar] [CrossRef]
- Walker, C.; Cole, A.; Sheehan, M. Modelling of thin layer drying of macroalgae. Presetend at the Asia Pacific Confederation of Chemical Engineering Congress 2015, Melbourne, Australia, 27 September–1 October 2015. [Google Scholar]
- Mohamed, L.A.; Kouhila, M.; Lahsasni, S.; Jamali, A.; Idlimam, A.; Rhazi, M.; Aghfir, M.; Mahrouz, M. Equilibrium moisture content and heat of sorption of Gelidium sesquipedale. J. Stored Prod. Res. 2005, 41, 199–209. [Google Scholar] [CrossRef]
- Al–Muhtaseb, A.H.; McMinn, W.A.M.; Magee, T.R.A. Moisture sorption isotherm characteristics of food products: A review. Food Bioprod. Process. 2002, 80, 118–128. [Google Scholar] [CrossRef]
- Kiranoudis, C.; Tsami, E.; Maroulis, Z.; Marinos-Kouris, D. Drying kinetics of some fruits. Dry. Technol. 1997, 15, 1399–1418. [Google Scholar] [CrossRef]
- Moussaoui, H.; Bahammou, Y.; Idlimam, A.; Lamharrar, A.; Abdenouri, N. Investigation of hygroscopic equilibrium and modeling sorption isotherms of the argan products: A comparative study of leaves, pulps, and fruits. Food Bioprod. Process. 2019, 114, 12–22. [Google Scholar] [CrossRef]
- Zomorodian, A.; Kavoosi, Z.; Momenzadeh, L. Determination of EMC isotherms and appropriate mathematical models for canola. Food Bioprod. Process. 2011, 89, 407–413. [Google Scholar] [CrossRef]
- Xanthopoulos, G.; Yanniotis, S.; Lambrinos, G.R. Water diffusivity and drying kinetics of air drying of figs. Dry. Technol. 2009, 27, 502–512. [Google Scholar] [CrossRef]
- Cárcel, J.; García-Pérez, J.; Riera, E.; Mulet, A. Influence of high intensity ultrasound on drying kinetics of persimmon. Dry. Technol. 2007, 25, 185–193. [Google Scholar] [CrossRef]
- Santacatalina, J.; Soriano, J.; Cárcel, J.; Garcia-Perez, J. Influence of air velocity and temperature on ultrasonically assisted low temperature drying of eggplant. Food Bioprod. Process. 2016, 100, 282–291. [Google Scholar] [CrossRef]
- Hassini, L.; Azzouz, S.; Peczalski, R.; Belghith, A. Estimation of potato moisture diffusivity from convective drying kinetics with correction for shrinkage. J. Food Eng. 2007, 79, 47–56. [Google Scholar] [CrossRef]
- Krokida, M.; Karathanos, V.; Maroulis, Z.; Marinos-Kouris, D. Drying kinetics of some vegetables. J. Food Eng. 2003, 59, 391–403. [Google Scholar] [CrossRef]
- Scala, K.; Crapiste, G. Drying kinetics and quality changes during drying of red pepper. Food Sci. Technol. 2008, 41, 789–795. [Google Scholar] [CrossRef]
- Rosa, D.; Cantú-Lozano, D.; Luna-Solano, G.; Polachini, T.; Telis-Romero, J. Mathematical modeling of orange seed drying kinetics. Ciênc. Agrotecnol. 2015, 39, 291–300. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).