Developing a Hybrid Optimization Algorithm for Optimal Allocation of Renewable DGs in Distribution Network
Abstract
:1. Introduction
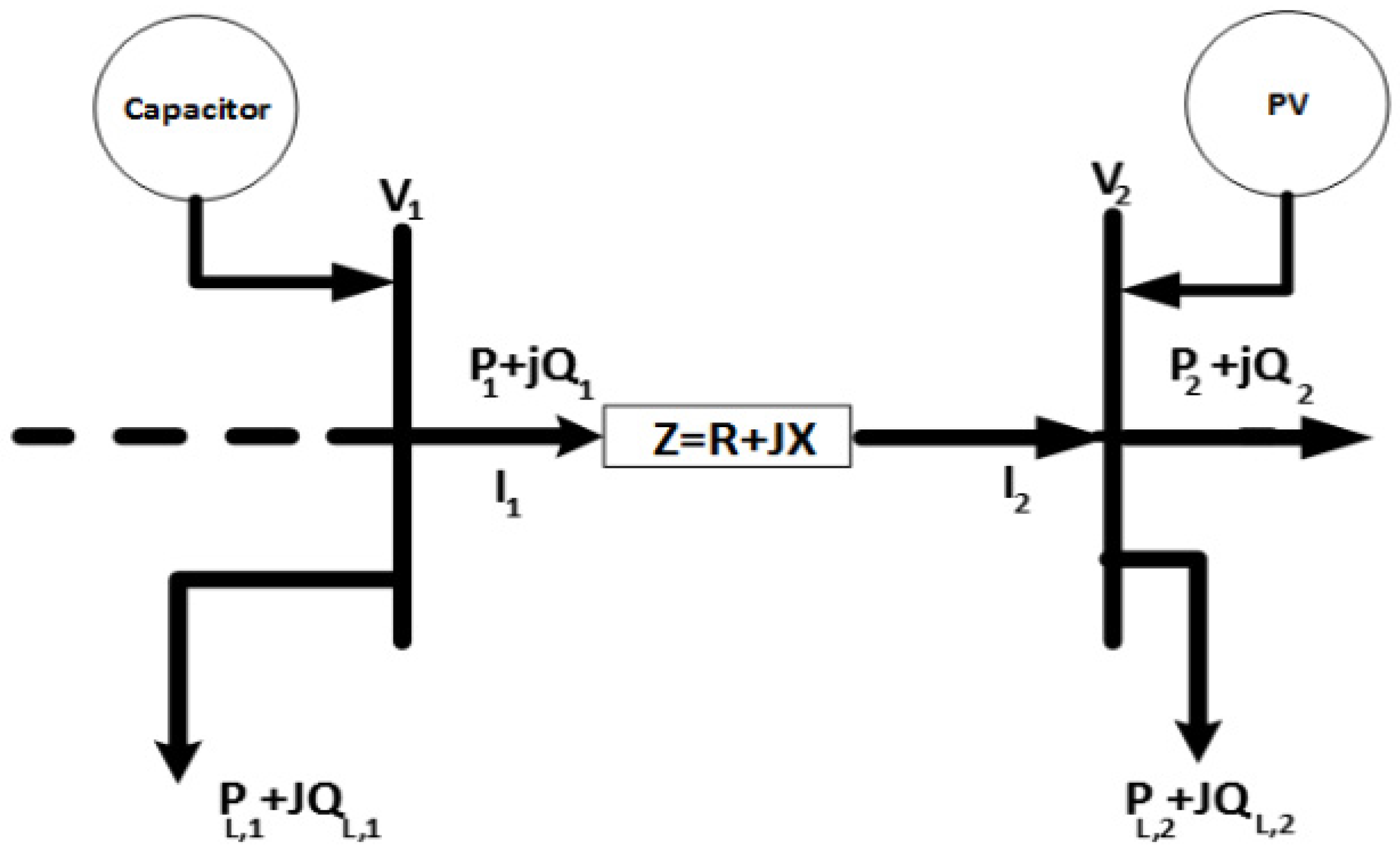
2. Problem Formulation
2.1. Equality Constraints
2.2. Inequality Constraints
2.2.1. System Voltage Constraints
2.2.2. Line Capacity Limits
3. TSA-SCA Algorithm
3.1. Tunicate Swarm Algorithm (TSA)
3.2. Sine-Cosine Algorithm (SCA)
3.3. Improved TSA-SCA Algorithm
- Read the system data, maximum iteration (I), and number of search agents (S).
- Produce the initial population of slime mold between the lower-(w) and upper (p)-controlled variables by Equation (36).where, represents a random value between the values of 0 and 1. and are the number of tunicates and the problem dimension.
- The produced population represents the tunicate position that can be formulated as follows:where, is the position of the tunicate.
- Evaluate the fitness for all locations of tunicates, and obtain the superior position of tunicates and the superior objective function.
- Evaluate the new position of each tunicate by Equation (35).
- Return to step 4 until the final iteration is reached.
- Obtain the best location of tunicates (sizes and positions of DG).
4. Testing and Evaluation
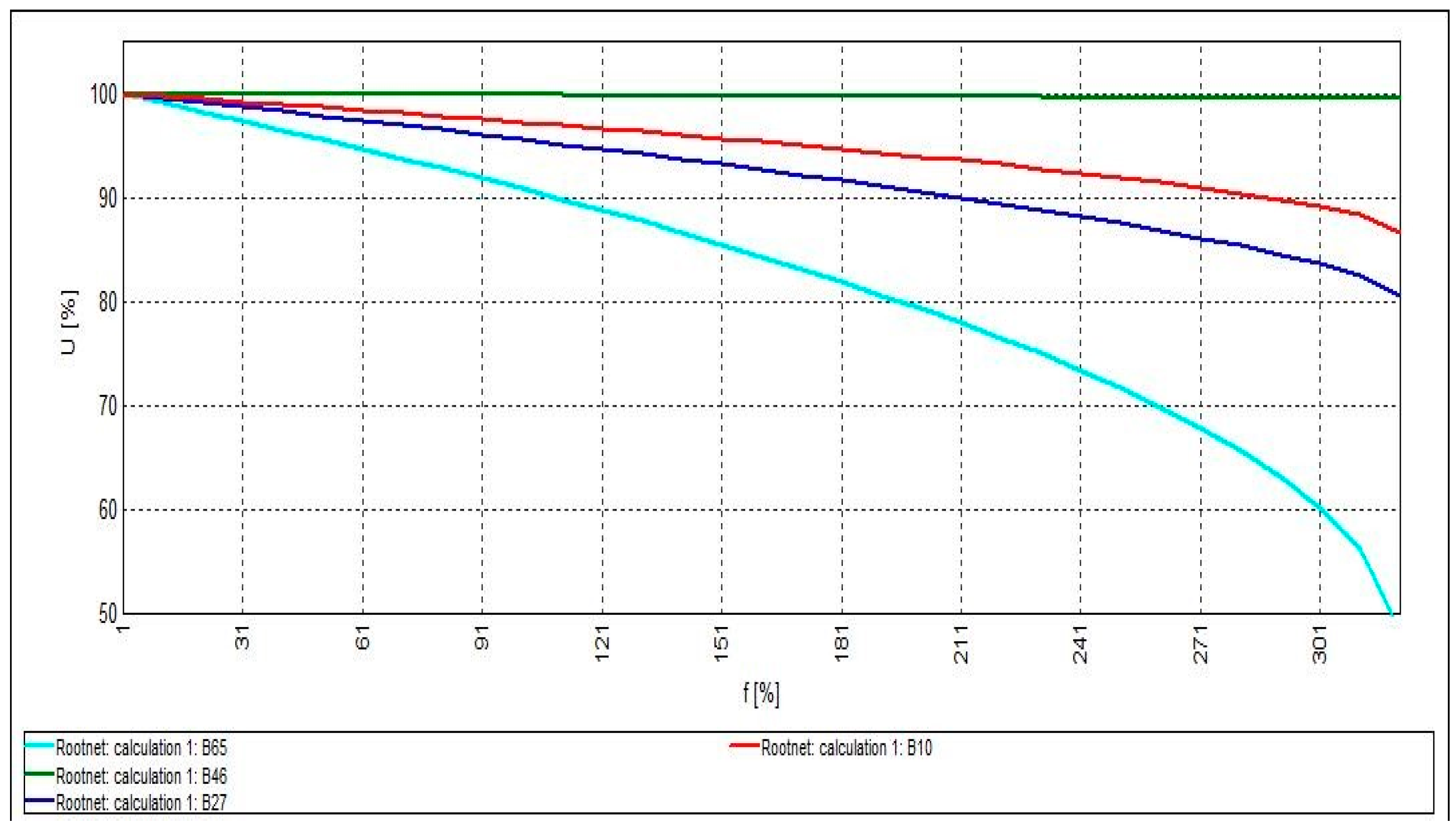
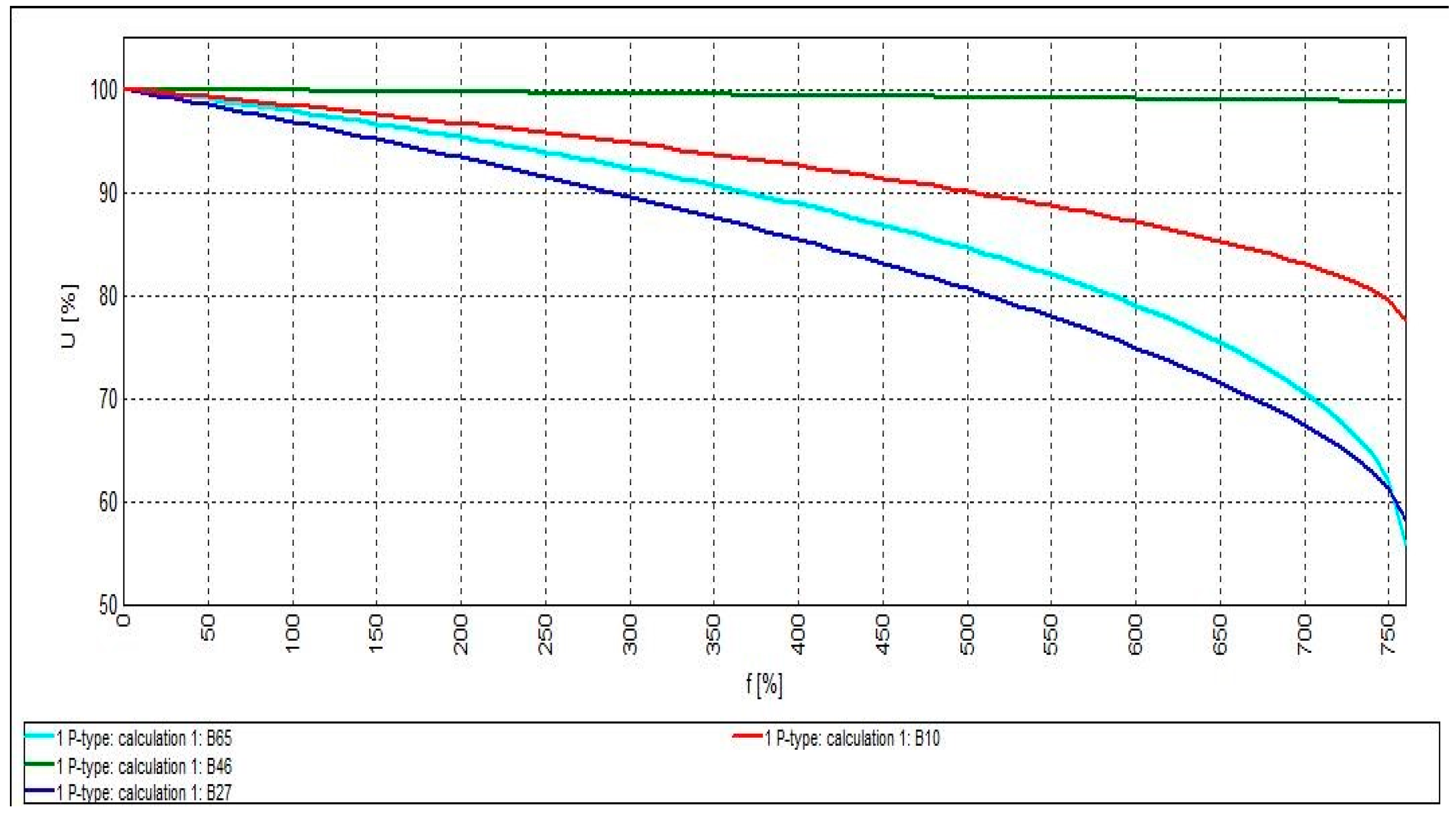
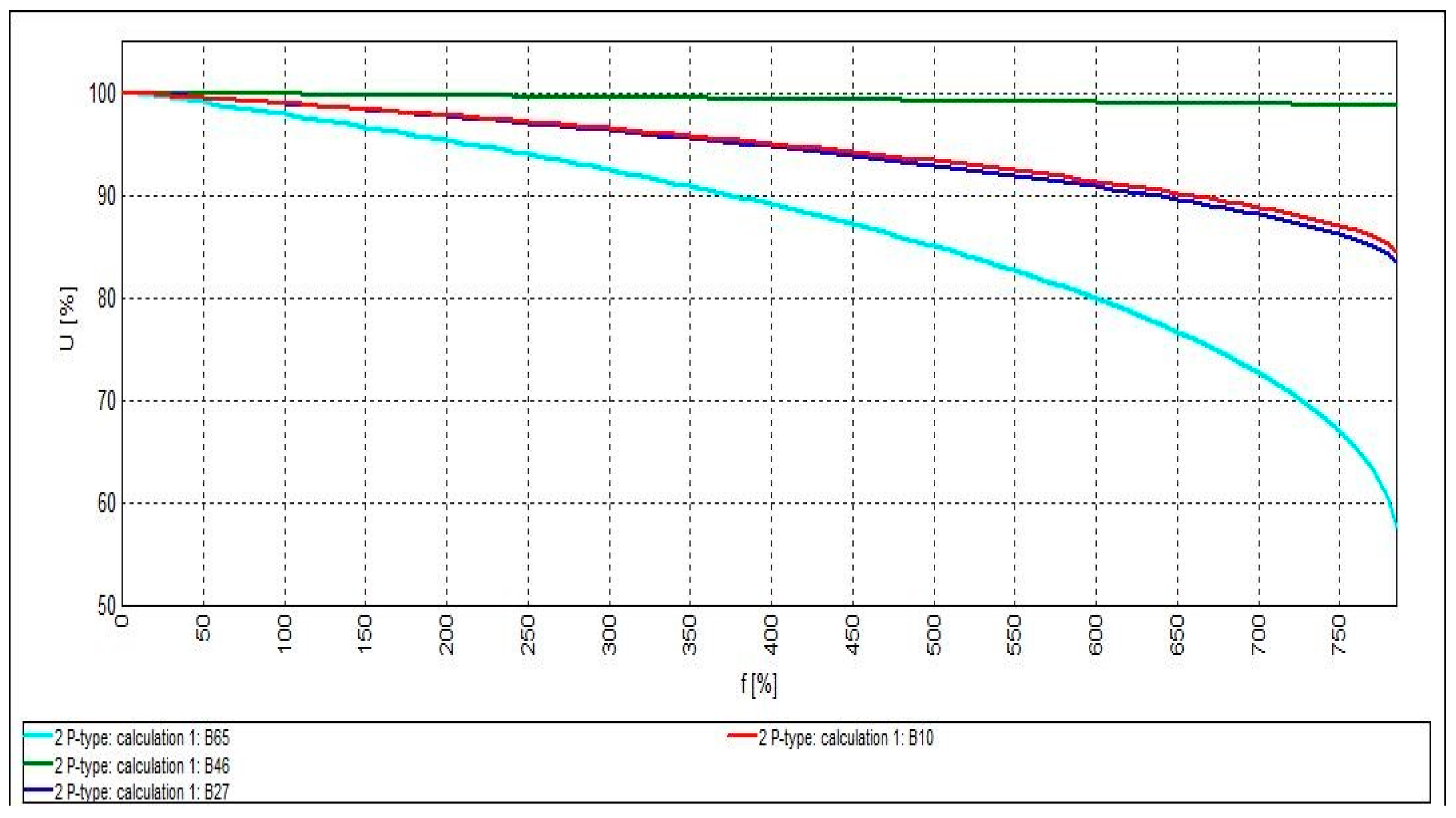
4.1. System Optimization with Active Power-Generating DG (P-Type Mode)
4.2. System Optimization with Reactive Power-Generating DGs (Q-Type Mode)
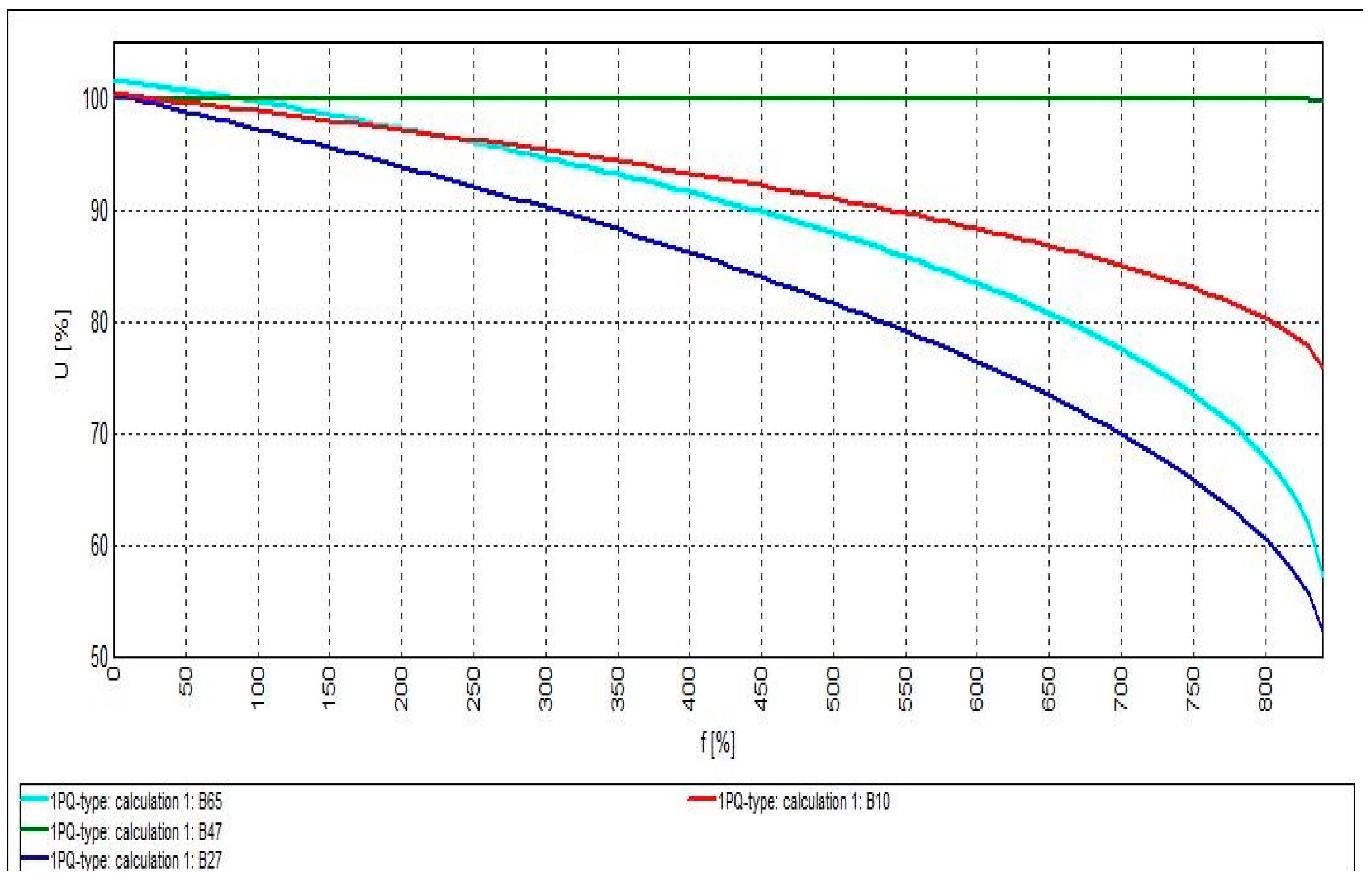
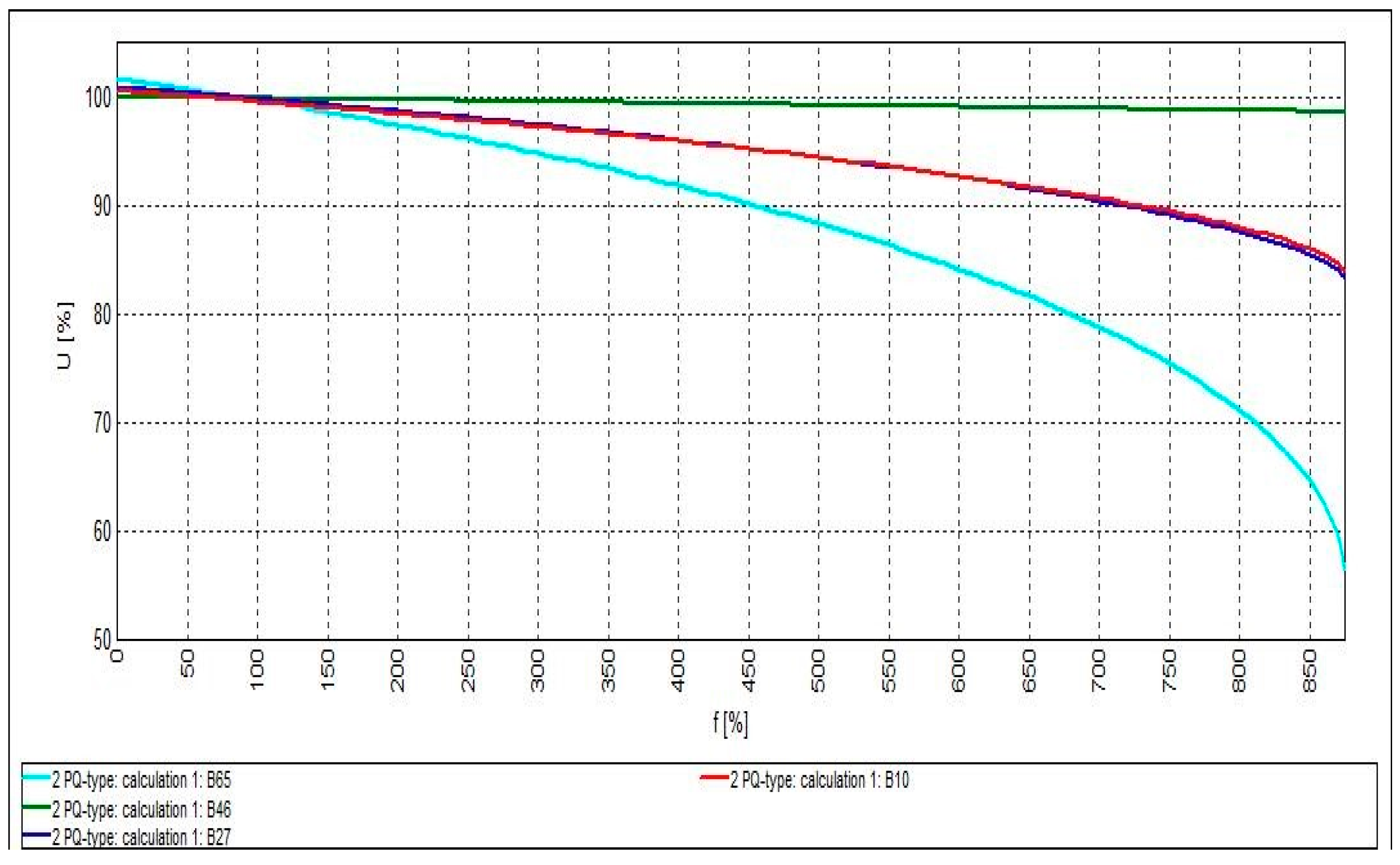
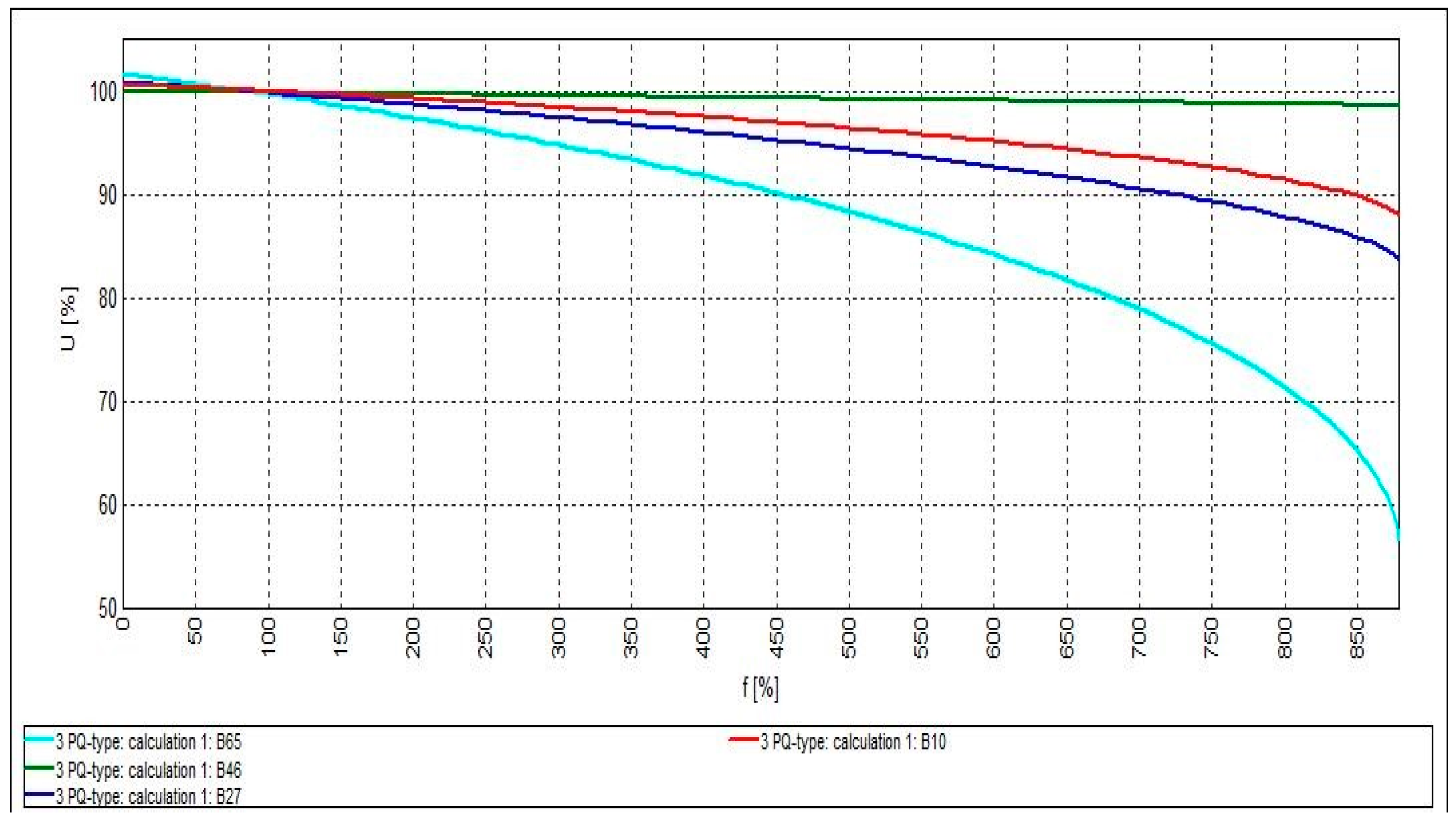
4.3. System Optimization with Active and Reactive Power-Generating DG (PQ-Type Mode)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Mekhilef, S.; Saidur, R.; Kamalisarvestani, M. Effect of dust, humidity and air velocity on efficiency of photovoltaic cells. Renew. Sustain. Energy Rev. 2012, 16, 2920–2925. [Google Scholar] [CrossRef]
- Rizzi, F.; van Eck, N.J.; Frey, M. The production of scientific knowledge on renewable energies: Worldwide trends, dynamics and challenges and implications for management. Renew. Energy 2014, 62, 657–671. [Google Scholar] [CrossRef]
- Paska, J.; Biczel, P.; Kłos, M. Hybrid power systems–An effective way of utilising primary energy sources. Renew. Energy 2009, 34, 2414–2421. [Google Scholar] [CrossRef]
- Raheem, A.; Abbasi, S.A.; Memon, A.; Samo, S.R.; Taufiq-Yap, Y.H.; Danquah, M.K.; Harun, R. Renewable energy deployment to combat energy crisis in Pakistan. Energy Sustain. Soc. 2016, 6, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Ashfaq, A.; Ianakiev, A. Features of fully integrated renewable energy atlas for Pakistan; wind, solar and cooling. Renew. Sustain. Energy Rev. 2018, 97, 14–27. [Google Scholar] [CrossRef] [Green Version]
- Zaharim, A.; Sopian, K. Prospects of life cycle assessment of renewable energy from solar photovoltaic technologies: A review. Renew. Sustain. Energy Rev. 2018, 96, 11–28. [Google Scholar]
- Abdel-mawgoud, H.; Kamel, S.; Ebeed, M.; Aly, M.M. An efficient hybrid approach for optimal allocation of DG in radial distribution networks. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; pp. 311–316. [Google Scholar]
- Engelen, P.J.; Kool, C.; Li, Y. A barrier options approach to modeling project failure: The case of hydrogen fuel infrastructure. Resour. Energy Econ. 2016, 43, 33–56. [Google Scholar] [CrossRef] [Green Version]
- Ranieri, L.; Mossa, G.; Pellegrino, R.; Digiesi, S. Energy recovery from the organic fraction of municipal solid waste: A real options-based facility assessment. Sustainability 2018, 10, 368. [Google Scholar] [CrossRef] [Green Version]
- Di Corato, L.; Moretto, M. Investing in biogas: Timing, technological choice and the value of flexibility from input mix. Energy Econ. 2011, 33, 1186–1193. [Google Scholar] [CrossRef]
- Huisman, K.J.; Kort, P.M. Strategic technology adoption taking into account future technological improvements: A real options approach. Eur. J. Oper. Res. 2004, 159, 705–728. [Google Scholar] [CrossRef] [Green Version]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Reddy, P.D.P.; Reddy, V.V.; Manohar, T.G. Whale optimization algorithm for optimal sizing of renewable resources for loss reduction in distribution systems. Renew. Wind Water Sol. 2017, 4, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Thangaraj, Y.; Kuppan, R. Multi-objective simultaneous placement of DG and DSTATCOM using novel lightning search algorithm. J. Appl. Res. Technol. 2017, 15, 477–491. [Google Scholar] [CrossRef]
- Syed, M.S.; Injeti, S.K. Simultaneous optimal placement of DGs and fixed capacitor banks in radial distribution systems using BSA optimization. Int. J. Comput. Appl. 2014, 108. [Google Scholar]
- Lalitha, M.P.; Babu, P.S.; Adivesh, B. Optimal distributed generation and capacitor placement for loss minimization and voltage profile improvement using Symbiotic Organisms Search Algorithm. Int. J. Electr. Eng. 2016, 9, 249–261. [Google Scholar]
- Barati, H.; Shahsavari, M. Simultaneous Optimal placement and sizing of distributed generation resources and shunt capacitors in radial distribution systems using Crow Search Algorithm. Int. J. Ind. Electron. Control Optim. 2018, 1, 27–40. [Google Scholar]
- Krueasuk, W.; Ongsakul, W. Optimal placement of distributed generation using particle swarm optimization. In Proceedings of the Australian Universities Power Engineering Conference, Melbourne, Australia, 10–13 December 2006; pp. 10–13. [Google Scholar]
- El-Fergany, A. Optimal allocation of multi-type distributed generators using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 1197–1205. [Google Scholar] [CrossRef]
- Kumar Injeti, S.; Shareef, S.M.; Kumar, T.V. Optimal allocation of DGs and capacitor banks in radial distribution systems. Distrib. Gener. Altern. Energy J. 2018, 33, 6–34. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Ali, E.S.; Abd Elazim, S.M. Flower pollination algorithm and loss sensitivity factors for optimal sizing and placement of capacitors in radial distribution systems. Int. J. Electr. Power Energy Syst. 2016, 78, 207–214. [Google Scholar] [CrossRef]
- Eminoglu, U.; Hocaoglu, M.H. Distribution systems forward/backward sweep-based power flow algorithms: A review and comparison study. Electr. Power Compon. Syst. 2008, 37, 91–110. [Google Scholar] [CrossRef]
- Abdel-mawgoud, H.; Kamel, S.; Ebeed, M.; Youssef, A.R. Optimal allocation of renewable dg sources in distribution networks considering load growth. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1236–1241. [Google Scholar]
- Ali, E.S.; Abd Elazim, S.M.; Abdelaziz, A.Y. Ant lion optimization algorithm for renewable distributed generations. Energy 2016, 116, 445–458. [Google Scholar] [CrossRef]
- Kansal, S.; Kumar, V.; Tyagi, B. Hybrid approach for optimal placement of multiple DGs of multiple types in distribution networks. Int. J. Electr. Power Energy Syst. 2016, 75, 226–235. [Google Scholar] [CrossRef]
- Reddy, V.V.C. Optimal renewable resources placement in distribution networks by combined power loss index and whale optimization algorithms. J. Electr. Syst. Inf. Technol. 2018, 5, 175–191. [Google Scholar]
- Biswal, S.R.; Shankar, G. Optimal Sizing and Allocation of Capacitors in Radial Distribution System using Sine Cosine Algorithm. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–4. [Google Scholar]
- Aman, M.M.; Jasmon, G.B.; Solangi, K.H.; Bakar, A.H.A.; Mokhlis, H. Optimum simultaneous DG and capacitor placement on the basis of minimization of power losses. Int. J. Comput. Electr. Eng. 2013, 5, 516. [Google Scholar] [CrossRef]
- Nawaz, S.A.R.F.A.R.A.Z.; Bansal, A.K.; Sharma, M.P. Optimal Allocation of Multiple DGs and Capacitor Banks in Distribution Network. Eur. J. Sci. Res. 2016, 142, 153–162. [Google Scholar]

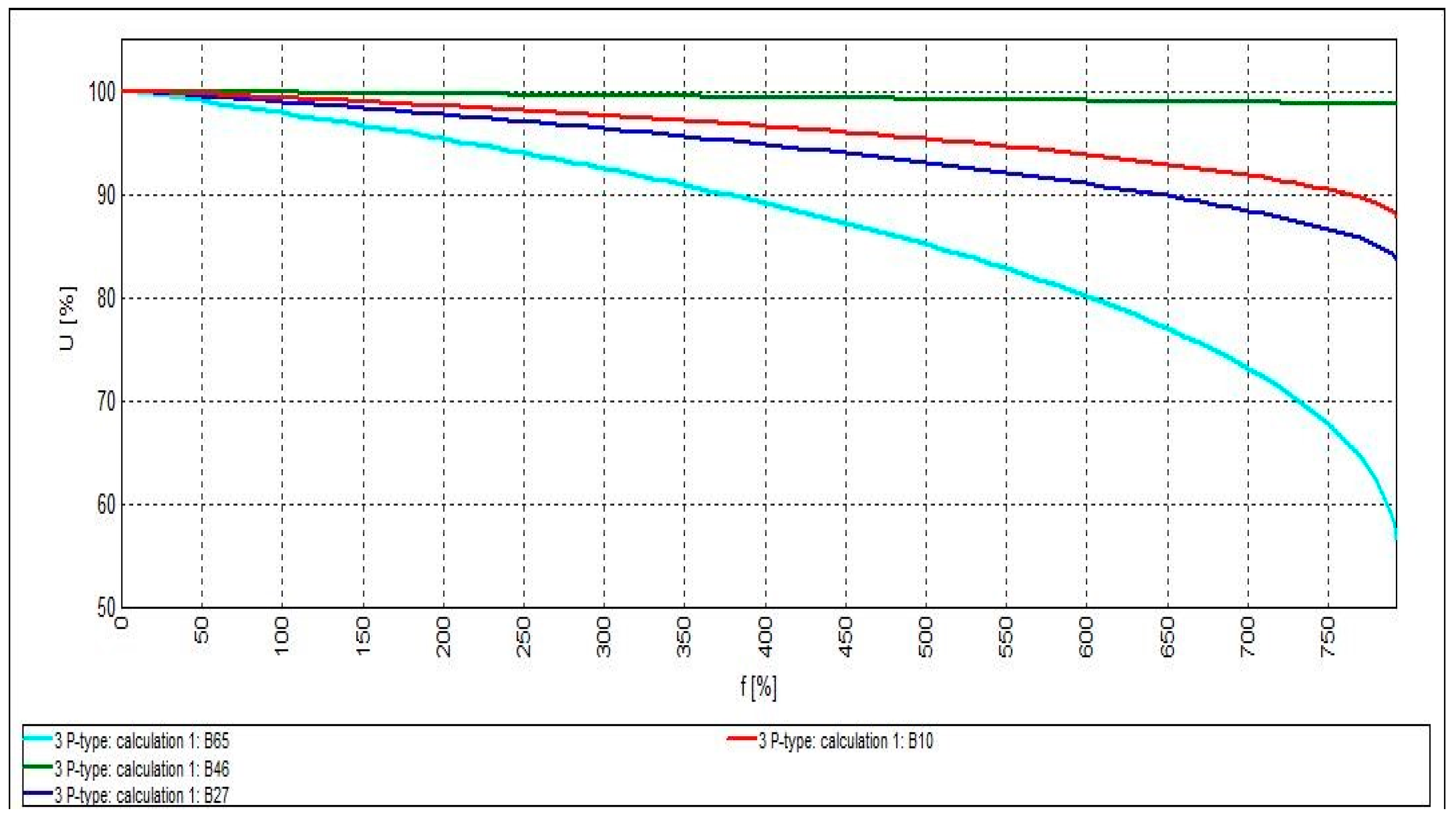
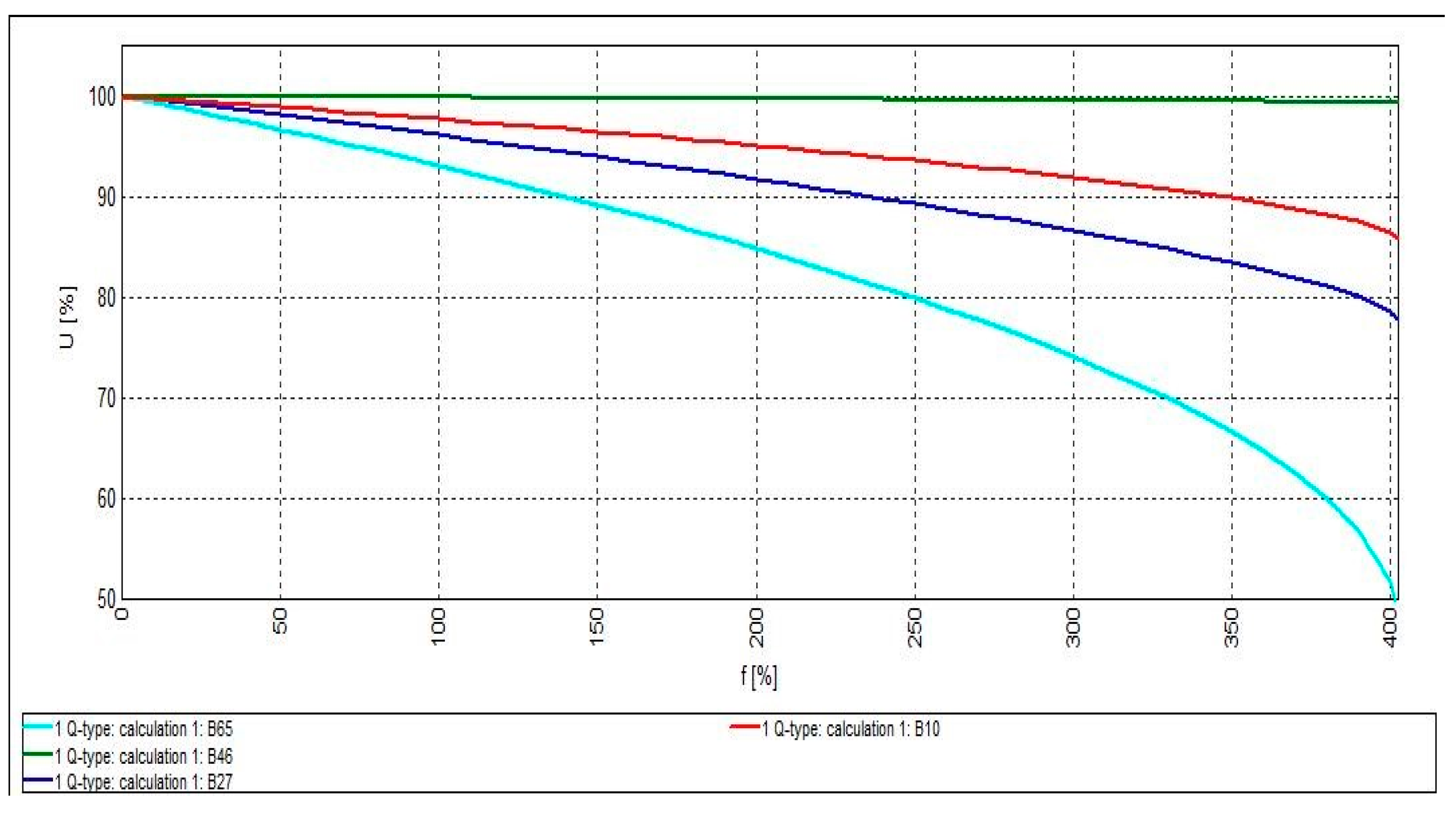
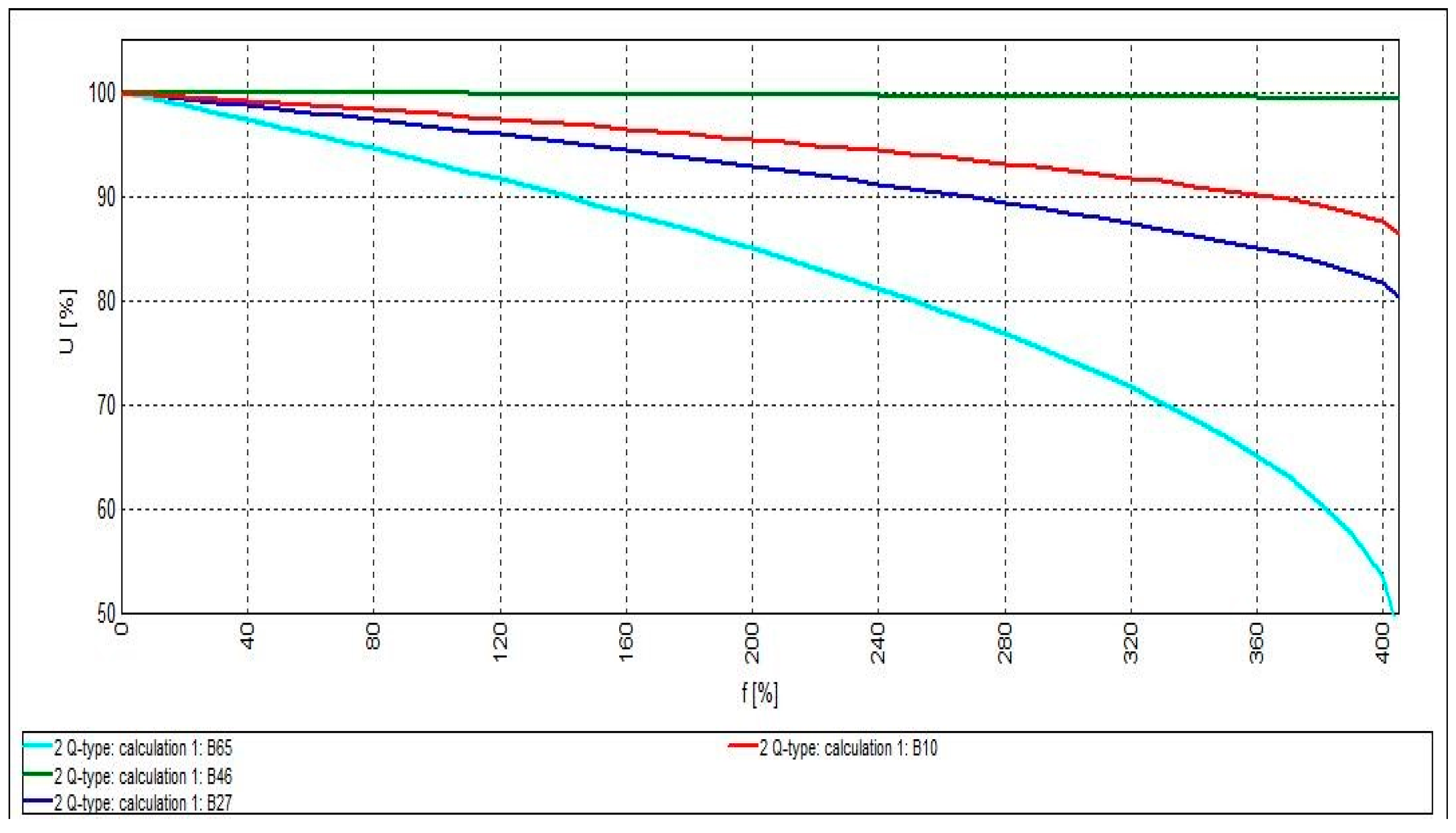
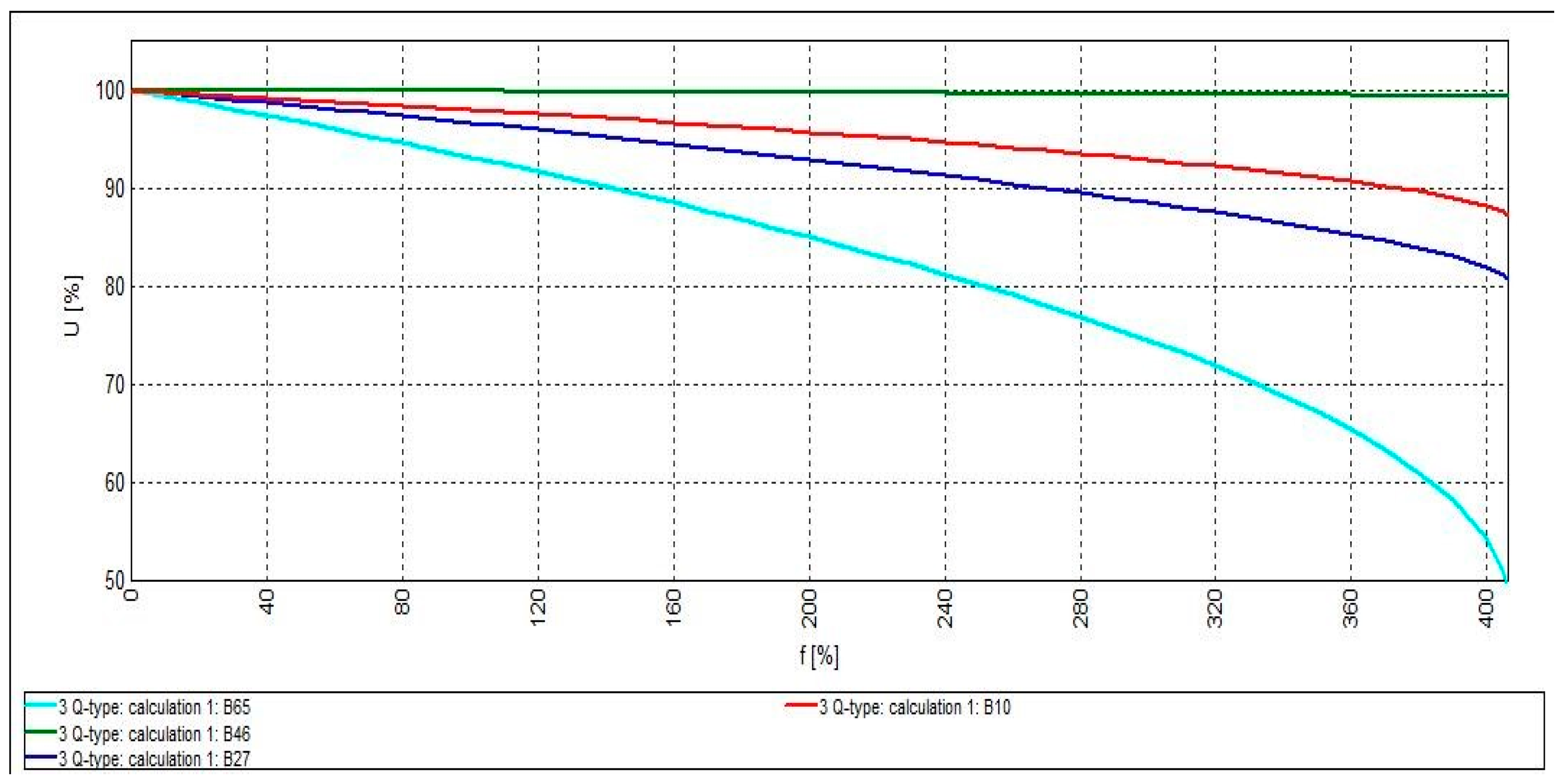
| Number of DGs | 1 | 2 | 3 |
|---|---|---|---|
| Location/Size (kW) | 61/1873.32 | 61/1781.2 17/530.5 | 61/1718.8 17/380.5 11/525 |
| Power Losses (kW) | 83.2224 | 71.6745 | 69. 4266 |
| Power Losses Reduction (%) | 63.012 | 68.145 | 69.144 |
| Number of DGs | 1 | 2 | 3 |
|---|---|---|---|
| Location/Size (kVAr) | 61/1330 | 61/1276 17/361 | 61/1233 17/253 11/391 |
| Power Losses (kW) | 152.041 | 146.441 | 145.129 |
| Power Losses Reduction (%) | 32.426 | 34.915 | 35.498 |
| Number of DGs | 1 | 2 | 3 |
|---|---|---|---|
| Location/Size (kVAr)/P.F | 61/1828.44/0.8149 | 61/1735/0.8138 17/523.24/0.829 | 61/1673.2/0.8136 17/377.86/0.8312 11/497.33/0.8155 |
| Power Losses (kW) | 23.169 | 7.2013 | 4.2665 |
| Power Losses Reduction (%) | 89.702 | 96.799 | 98.104 |
| Item | TSA-SCA | MFO [8] | Hybrid [27] | WOA [28] | SCA [29] | PSO [30] | PVSC [31] |
|---|---|---|---|---|---|---|---|
| 1P-type | 83.2224 | 83.224 | 83.372 | - | - | - | - |
| 2P-type | 71.6745 | 71.679 | 71.82 | - | - | - | - |
| 3P-type | 69.4266 | - | 69.52 | - | - | - | - |
| 1Q-type | 152.041 | - | - | 152.064 | - | - | - |
| 2Q-type | 146.441 | - | - | - | 147.762 | - | - |
| 3Q-type | 145.129 | - | - | - | - | - | - |
| 1PQ-type | 23.169 | - | - | - | - | 25.9 | - |
| 2PQ-type | 7.201 | - | - | - | - | - | - |
| 3PQ-type | 4.253 | - | - | - | - | - | 9.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awad, A.; Abdel-Mawgoud, H.; Kamel, S.; Ibrahim, A.A.; Jurado, F. Developing a Hybrid Optimization Algorithm for Optimal Allocation of Renewable DGs in Distribution Network. Clean Technol. 2021, 3, 409-423. https://doi.org/10.3390/cleantechnol3020023
Awad A, Abdel-Mawgoud H, Kamel S, Ibrahim AA, Jurado F. Developing a Hybrid Optimization Algorithm for Optimal Allocation of Renewable DGs in Distribution Network. Clean Technologies. 2021; 3(2):409-423. https://doi.org/10.3390/cleantechnol3020023
Chicago/Turabian StyleAwad, Ayman, Hussein Abdel-Mawgoud, Salah Kamel, Abdalla A. Ibrahim, and Francisco Jurado. 2021. "Developing a Hybrid Optimization Algorithm for Optimal Allocation of Renewable DGs in Distribution Network" Clean Technologies 3, no. 2: 409-423. https://doi.org/10.3390/cleantechnol3020023
APA StyleAwad, A., Abdel-Mawgoud, H., Kamel, S., Ibrahim, A. A., & Jurado, F. (2021). Developing a Hybrid Optimization Algorithm for Optimal Allocation of Renewable DGs in Distribution Network. Clean Technologies, 3(2), 409-423. https://doi.org/10.3390/cleantechnol3020023








