Impact of Battery Energy System Integration in Frequency Control of an Electrical Grid with Wind Power
Abstract
:1. Introduction
2. Materials and Methods
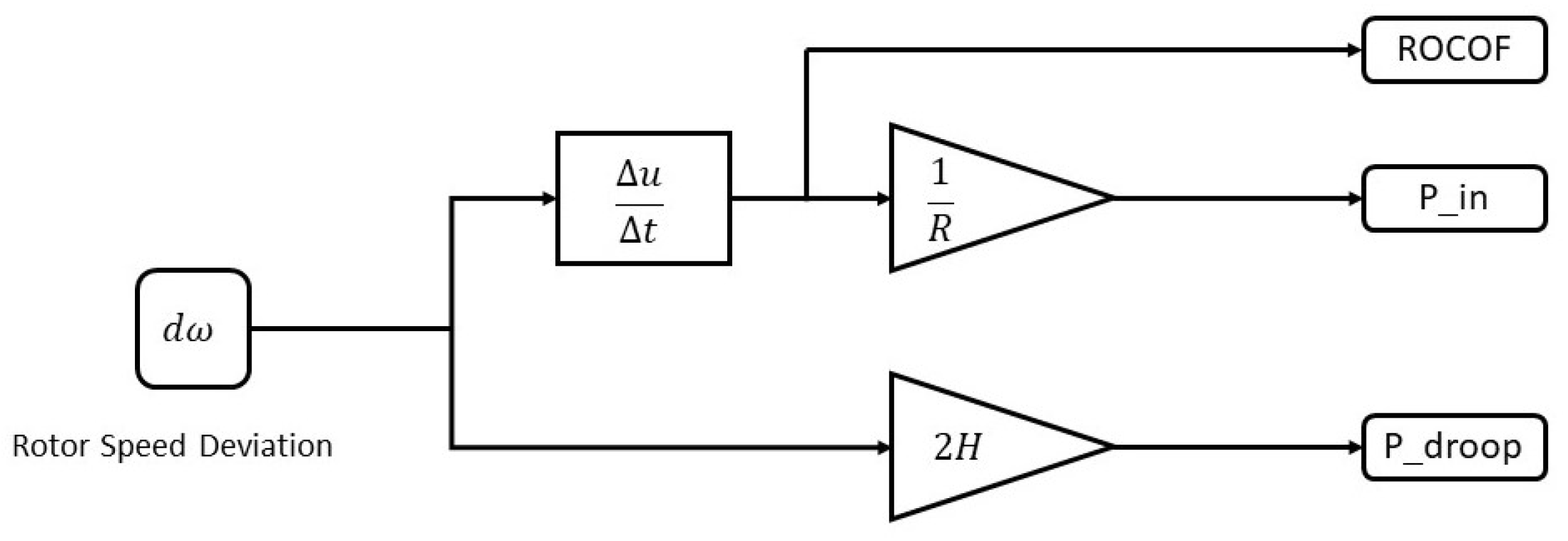
Frequency Support from Wind Turbine Control and BESS
3. Case Study and Sensitivity Analysis
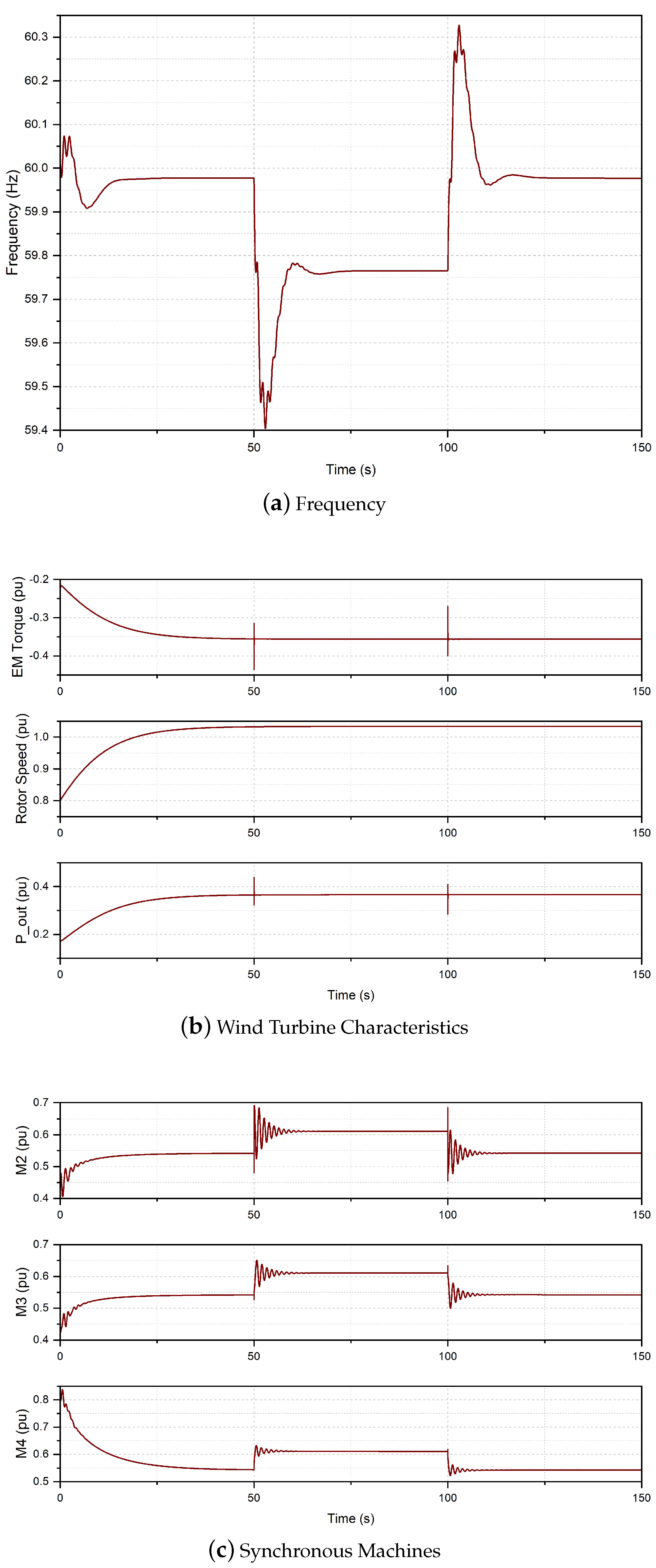
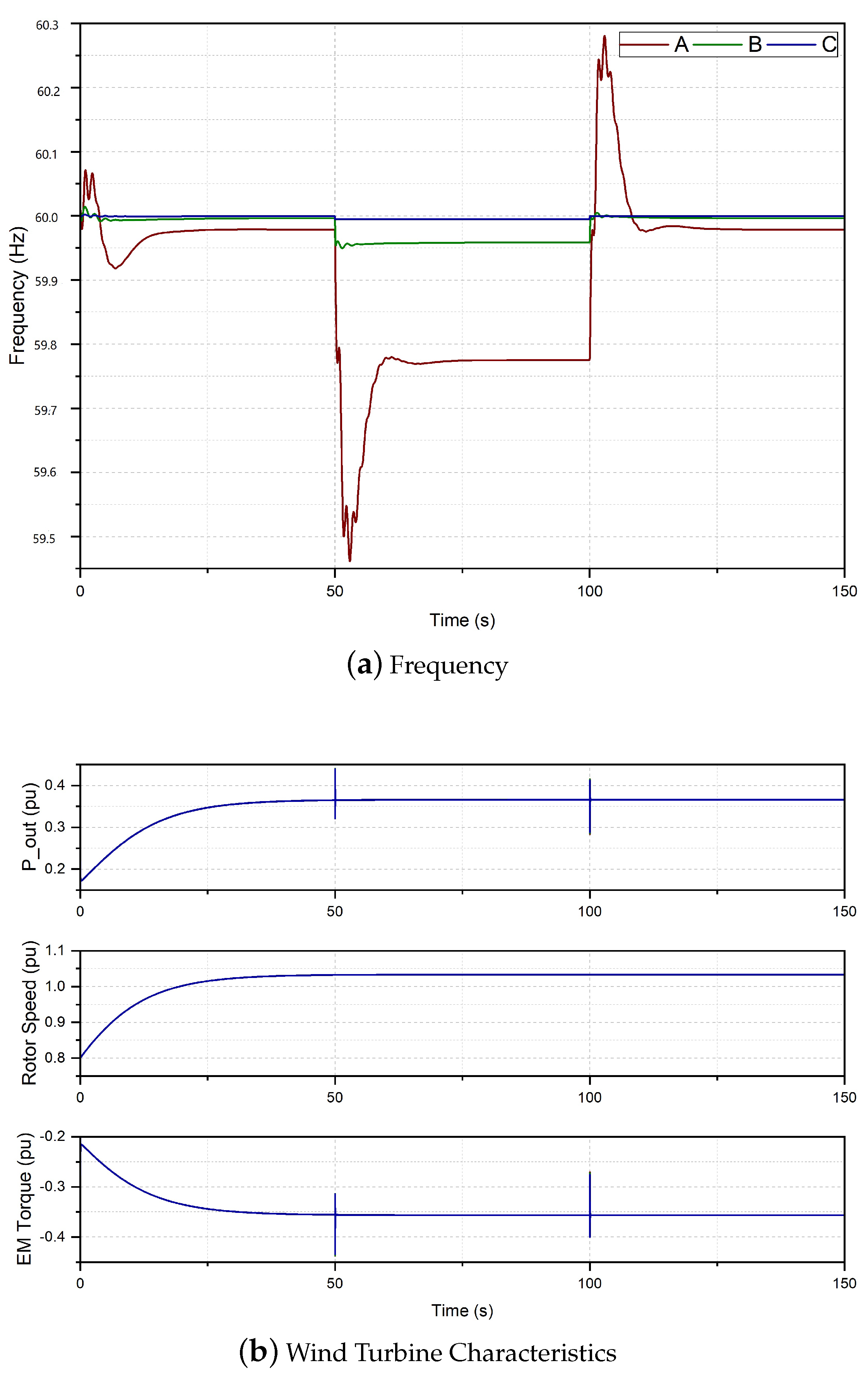
3.1. Case I: No Frequency Control
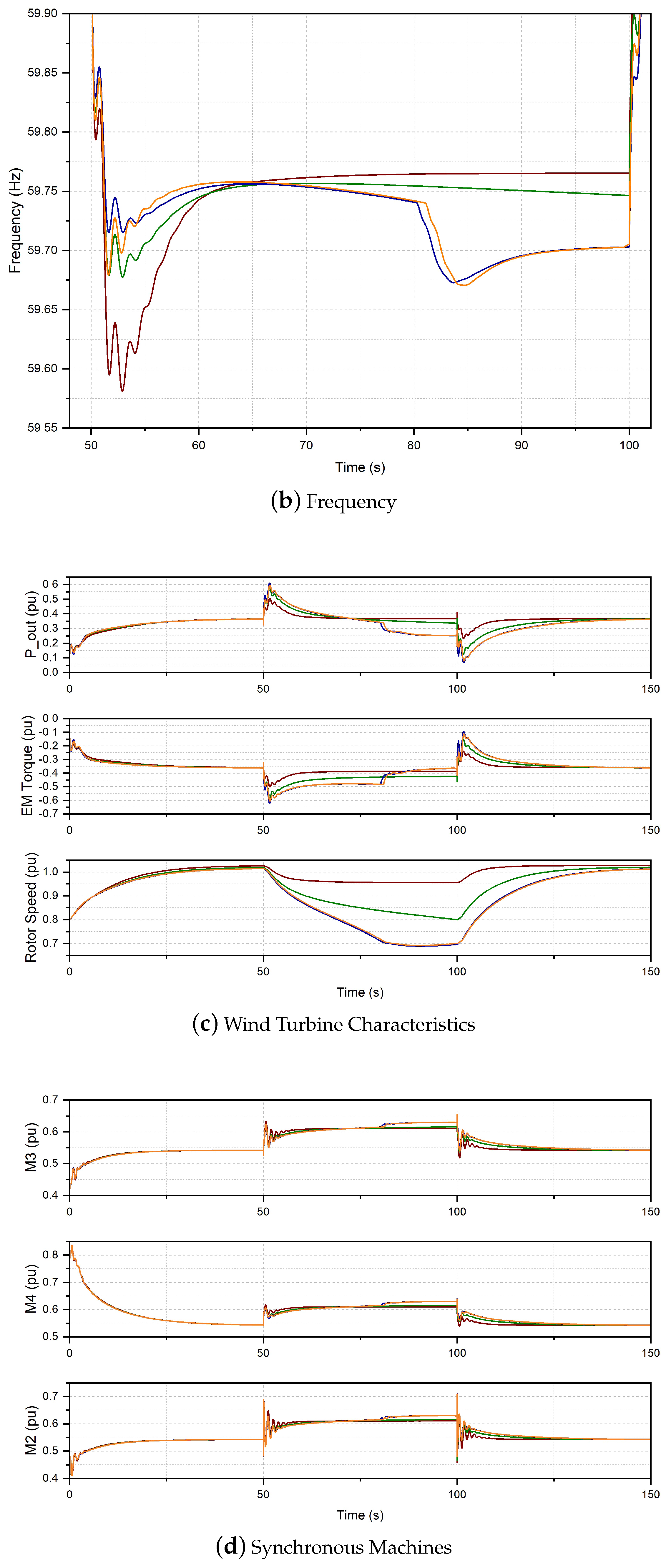
3.2. Case II: Inertia and Droop Control
3.3. Case III: Battery Control
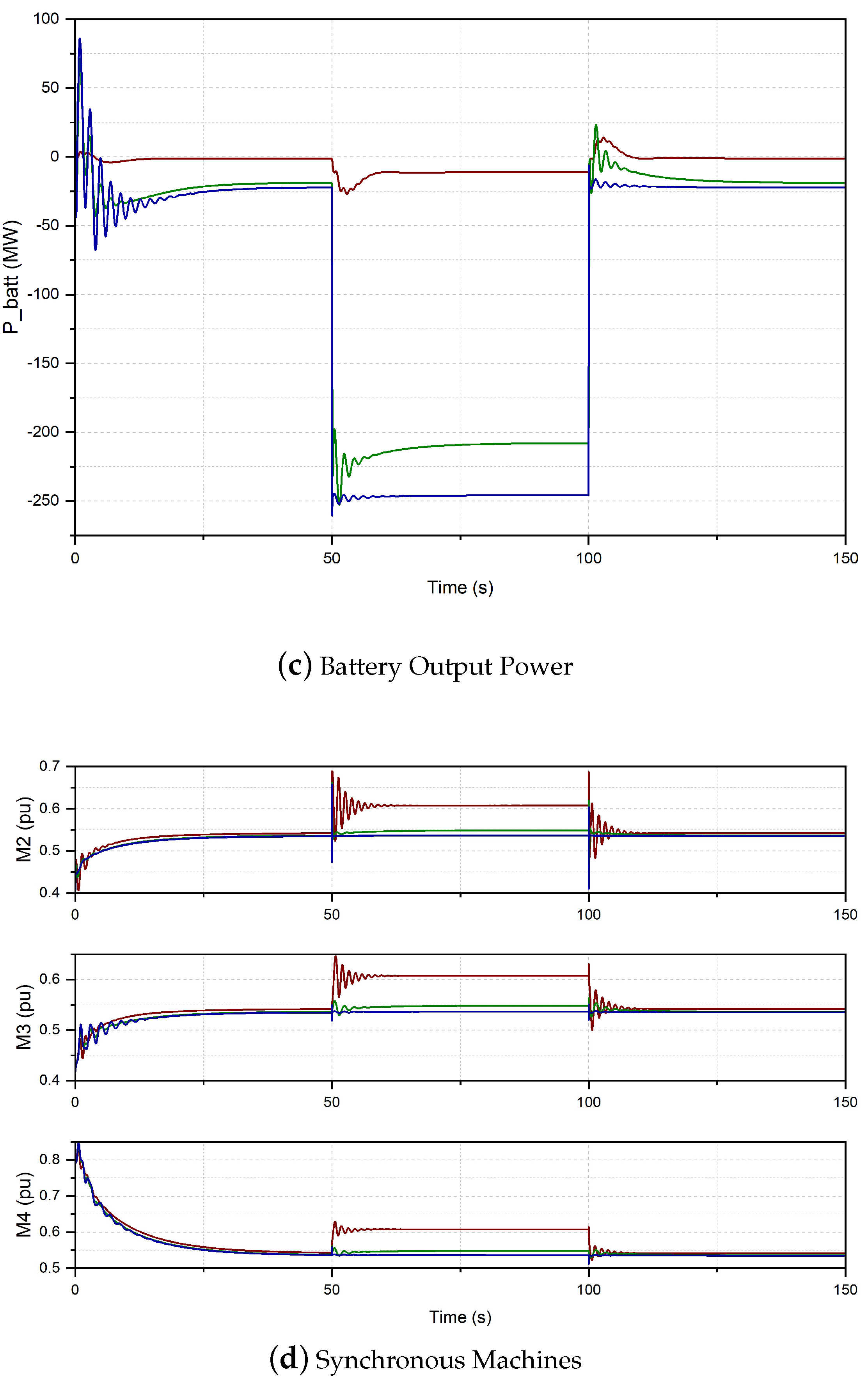
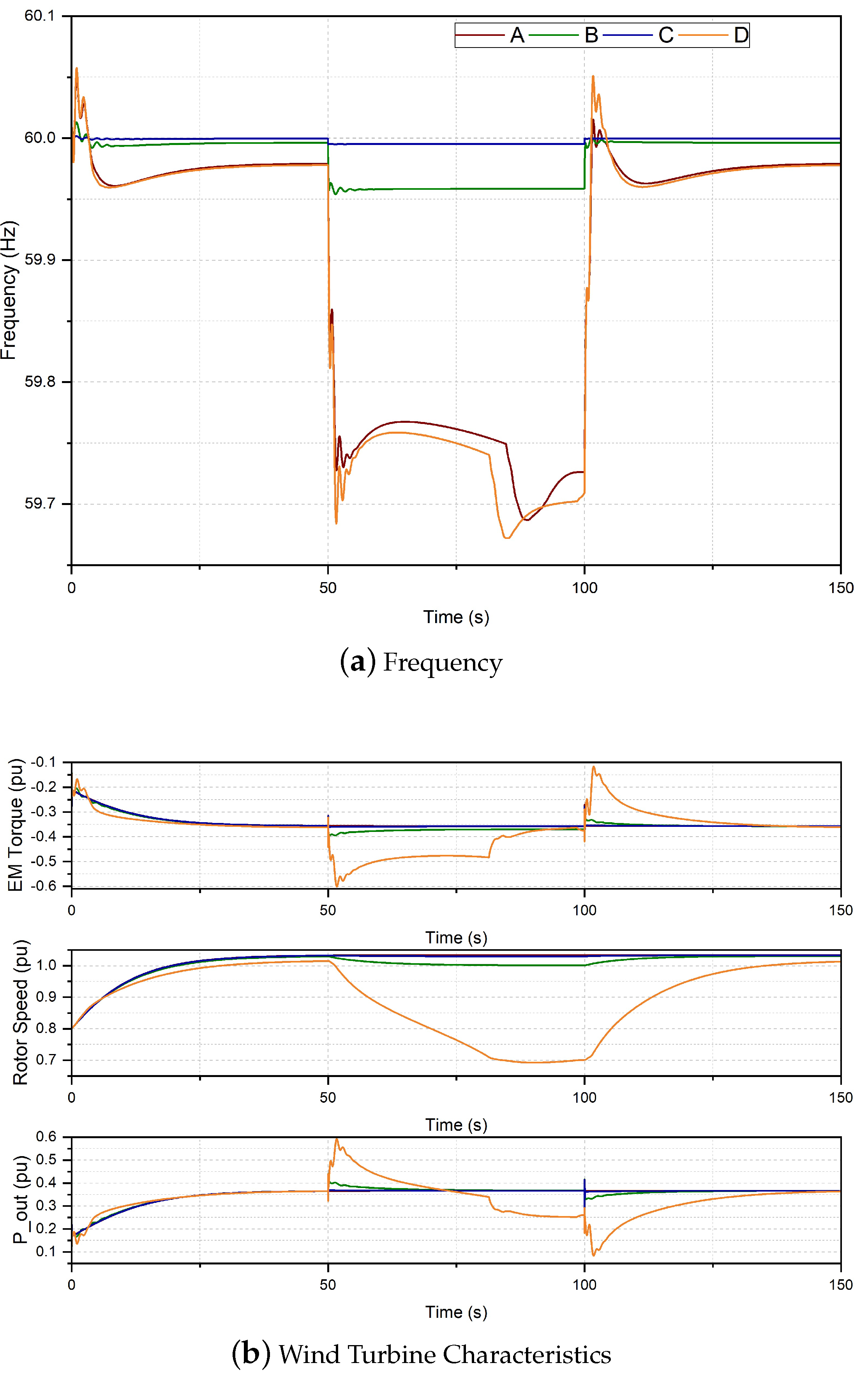
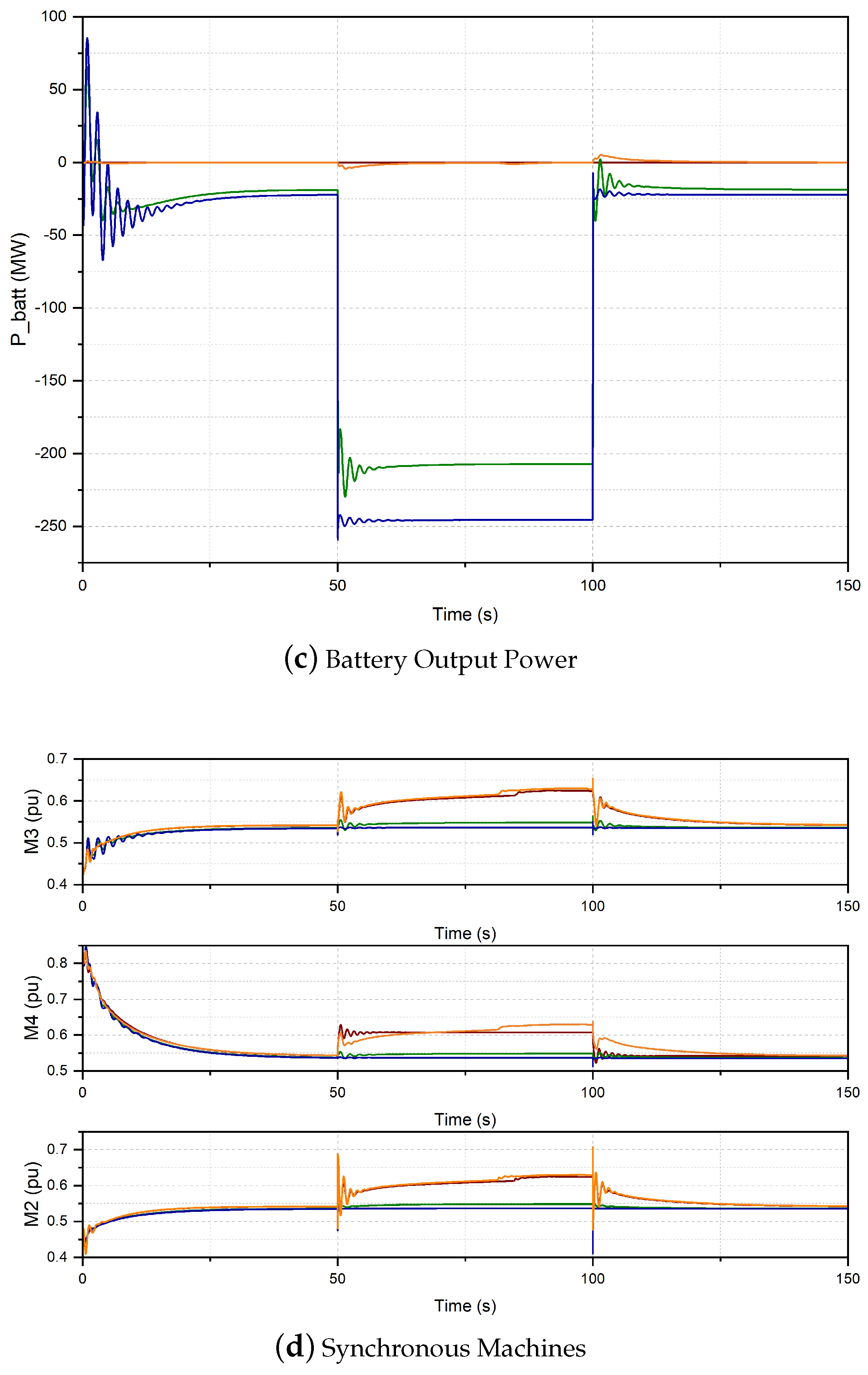
3.4. Case IV: Inertia, Droop and Battery Control
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future low-inertia power systems: Requirements, issues, and solutions—A review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Europe Faces Gas Supply Disruption after Russia Imposes Sanctions. Al Jazeera 2022. Available online: https://www.aljazeera.com/news/2022/5/12/europes-gas-supply-crisis-grows-after-russia-imposes-sanctions (accessed on 12 May 2022).
- Denholm, P.; Mai, T.; Kenyon, R.W.; Kroposki, B.; O’Malley, M. Inertia and the Power Grid: A Guide Without the Spin; Technical Report NREL/TP-6A20-73856; National Renewable Energy Laboratory: Golden, CO, USA, 2020.
- Wu, Z.; Gao, W.; Wang, J.; Gu, S. A coordinated primary frequency regulation from Permanent Magnet Synchronous Wind Turbine Generation. In Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 16–18 July 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Attya, A.; Dominguez-Garcia, J.; Anaya-Lara, O. A review on frequency support provision by wind power plants: Current and future challenges. Renew. Sustain. Energy Rev. 2018, 81, 2071–2087. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Ángel Molina-García. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Gao, W.; Gao, T.; Yan, W.; Zhang, H.; Yan, S.; Wang, X. State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean Energy 2018. [Google Scholar] [CrossRef] [Green Version]
- Conroy, J.F.; Watson, R. Frequency Response Capability of Full Converter Wind Turbine Generators in Comparison to Conventional Generation. IEEE Trans. Power Syst. 2008, 23, 649–656. [Google Scholar] [CrossRef]
- Akram, U.; Nadarajah, M.; Shah, R.; Milano, F. A review on rapid responsive energy storage technologies for frequency regulation in modern power systems. Renew. Sustain. Energy Rev. 2020, 120, 109626. [Google Scholar] [CrossRef]
- Díaz-González, F.; Hau, M.; Sumper, A.; Gomis-Bellmunt, O. Participation of wind power plants in system frequency control: Review of grid code requirements and control methods. Renew. Sustain. Energy Rev. 2014, 34, 551–564. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M. Effects of the synthetic inertia from wind power on the total system inertia: Simulation study. In Proceedings of the 2012 2nd International Symposium On Environment Friendly Energies And Applications, Newcastle Upon Tyne, UK, 25–27 June 2012; pp. 389–395. [Google Scholar] [CrossRef]
- Yao, W.; Lee, K.Y. A control configuration of wind farm for load-following and frequency support by considering the inertia issue. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, Y.; Xu, L.; Zhang, X.; Li, H. Virtual inertia control of DFIG-based wind turbines for dynamic grid frequency support. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Hu, W.; Hu, R.; Huang, Q.; Yao, J.; Chen, Z. Strategy for wind power plant contribution to frequency control under variable wind speed. Renew. Energy 2019, 130, 1226–1236. [Google Scholar] [CrossRef]
- de Almeida, R.G.; Pecas Lopes, J.A. Participation of Doubly Fed Induction Wind Generators in System Frequency Regulation. IEEE Trans. Power Syst. 2007, 22, 944–950. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.K.; Yang, W.H.; Hu, Y.L.; Dzung, P.Q. Frequency Regulation at a Wind Farm Using Time-Varying Inertia and Droop Controls. IEEE Trans. Ind. Appl. 2019, 55, 213–224. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gomez-Exposito, A.; Martinez Ramos, J.L. Frequency Regulation Contribution Through Variable-Speed Wind Energy Conversion Systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Shao, C.; Li, Z.; Hao, R.; Qie, Z.; Xu, G.; Hu, J. A Wind Farm Frequency Control Method Based on the Frequency Regulation Ability of Wind Turbine Generators. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 592–596. [Google Scholar] [CrossRef]
- Hu, Y.L.; Wu, Y.K. Inertial Response Identification Algorithm for the Development of Dynamic Equivalent Model of DFIG-Based Wind Power Plant. IEEE Trans. Ind. Appl. 2021, 57, 2104–2113. [Google Scholar] [CrossRef]
- Poullikkas, A. A comparative overview of large-scale battery systems for electricity storage. Renew. Sustain. Energy Rev. 2013, 27, 778–788. [Google Scholar] [CrossRef]
- Hesse, H.C.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion Battery Storage for the Grid—A Review of Stationary Battery Storage System Design Tailored for Applications in Modern Power Grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef] [Green Version]
- Palizban, O.; Kauhaniemi, K. Energy storage systems in modern grids—Matrix of technologies and applications. J. Energy Storage 2016, 6, 248–259. [Google Scholar] [CrossRef]
- Behnam Zakeri, S.S. Electrical energy storage systems: A comparative life cycle cost analysis. Renew. Sustain. Energy Rev. 2015, 42, 569–596. [Google Scholar] [CrossRef]
- Dang, J.; Seuss, J.; Suneja, L.; Harley, R.G. SOC feedback control for wind and ESS hybrid power system frequency regulation. In Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 16–18 July 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Li, W.; Joos, G. Comparison of Energy Storage System Technologies and Configurations in a Wind Farm. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1280–1285. [Google Scholar] [CrossRef]
- Sun, J.; Sheng, L.; Sun, Y.; Zhou, Z.; Fu, R. Stability Simulation Analysis of a Hybrid Wind-Battery System. In Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems; Zhang, L., Song, X., Wu, Y., Eds.; Springer: Singapore, 2016; pp. 154–163. [Google Scholar]
- Liang, L.; Zhong, J.; Jiao, Z. Frequency Regulation for a Power System with Wind Power and Battery Energy Storage. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012. [Google Scholar]
- Toge, M.; Kurita, Y.; Iwamoto, S. Supplementary load frequency control with storage battery operation considering SOC under large-scale wind power penetration. In Proceedings of the 2013 IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Ono, T.; Arai, J. Frequency Control with Dead Band Characteristic of Battery Energy Storage System for Power System Including Large Amount of Wind Power Generation. Electr. Eng. Jpn. 2013, 185, 1–10. [Google Scholar] [CrossRef]
- Li, W.; Joos, G. A power electronic interface for a battery supercapacitor hybrid energy storage system for wind applications. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1762–1768. [Google Scholar] [CrossRef]
- He, G.; Chen, Q.; Kang, C.; Xia, Q.; Poolla, K. Cooperation of Wind Power and Battery Storage to Provide Frequency Regulation in Power Markets. IEEE Trans. Power Syst. 2017, 32, 3559–3568. [Google Scholar] [CrossRef]
- Singarao, V.Y.; Nimmagadda, S.; Rao, V. Economic Comparison of Deloaded-Wind and Wind-Battery Systems. In Proceedings of the 2014 Sixth Annual IEEE Green Technologies Conference, Corpus Christi, TX, USA, 3–4 April 2014; pp. 126–131. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, Y. Coordinated Control Strategy of a Battery Energy Storage System to Support a Wind Power Plant Providing Multi-Timescale Frequency Ancillary Services. IEEE Trans. Sustain. Energy 2017, 8, 1140–1153. [Google Scholar] [CrossRef]
- Li, W.; Joos, G.; Belanger, J. Real-Time Simulation of a Wind Turbine Generator Coupled With a Battery Supercapacitor Energy Storage System. IEEE Trans. Ind. Electron. 2010, 57, 1137–1145. [Google Scholar] [CrossRef]
- Mendis, N.; Muttaqi, K.M.; Perera, S. Management of Battery-Supercapacitor Hybrid Energy Storage and Synchronous Condenser for Isolated Operation of PMSG Based Variable-Speed Wind Turbine Generating Systems. IEEE Trans. Smart Grid 2014, 5, 944–953. [Google Scholar] [CrossRef]
- Hajiaghasi, S.; Salemnia, A.; Hamzeh, M. Hybrid energy storage system for microgrids applications: A review. J. Energy Storage 2019, 21, 543–570. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy Management in the Decentralized Generation Systems Based on Renewable Energy—Ultracapacitors and Battery to Compensate the Wind/Load Power Fluctuations. IEEE Trans. Ind. Appl. 2015, 51, 1817–1827. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A Battery/Ultracapacitor Hybrid Energy Storage System for Implementing the Power Management of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Zhang, S.; Mishra, Y.; Shahidehpour, M. Fuzzy-Logic Based Frequency Controller for Wind Farms Augmented With Energy Storage Systems. IEEE Trans. Power Syst. 2016, 31, 1595–1603. [Google Scholar] [CrossRef]
- Mohammad Dreidy, H. Mokhlis, S.M. Inertia response and frequency control techniques for renewable energy sources: A review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Zhan, S.; Hou, P.; Enevoldsen, P.; Yang, G.; Zhu, J.; Eichman, J.; Jacobson, M.Z. Co-optimized trading of hybrid wind power plant with retired EV batteries in energy and reserve markets under uncertainties. Int. J. Electr. Power Energy Syst. 2020, 117, 105631. [Google Scholar] [CrossRef]
- Atieh, A.; Charfi, S.; Chaabene, M. Chapter 8—Hybrid PV/Batteries Bank/Diesel Generator Solar-Renewable Energy System Design, Energy Management, and Economics. In Advances in Renewable Energies and Power Technologies; Yahyaoui, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 257–294. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Zhang, S.S. The effect of the charging protocol on the cycle life of a Li-ion battery. J. Power Sources 2006, 161, 1385–1391. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, N.C.; Liu, J.H. Optimal Sizing of PV/Wind/Battery Hybrid Microgrids Considering Lifetime of Battery Banks. Energies 2021, 14, 6655. [Google Scholar] [CrossRef]
- Stroe, D.I.; Świerczyński, M.; Stan, A.I.; Teodorescu, R.; Andreasen, S.J. Accelerated Lifetime Testing Methodology for Lifetime Estimation of Lithium-Ion Batteries Used in Augmented Wind Power Plants. IEEE Trans. Ind. Appl. 2014, 50, 4006–4017. [Google Scholar] [CrossRef]
- Bouchhima, N.; Gossen, M.; Schulte, S.; Birke, K.P. Lifetime of self-reconfigurable batteries compared with conventional batteries. J. Energy Storage 2018, 15, 400–407. [Google Scholar] [CrossRef]
- Alramlawi, M.; Gabash, A.; Mohagheghi, E.; Li, P. Optimal operation of hybrid PV-battery system considering grid scheduled blackouts and battery lifetime. Sol. Energy 2018, 161, 125–137. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, L.; Chen, J.; Xiong, Y.; Zhang, X.; Qian, Y. An aqueous rechargeable lithium ion battery with long cycle life and overcharge self-protection. Mater. Chem. Front. 2021, 5, 2749–2757. [Google Scholar] [CrossRef]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Xiong, R.; Chen, H.; Wang, C.; Sun, F. Towards a smarter hybrid energy storage system based on battery and ultracapacitor—A critical review on topology and energy management. J. Clean. Prod. 2018, 202, 1228–1240. [Google Scholar] [CrossRef]
- Wind Energy and On-Site Energy Storage. Exploring Market Opportunities; Technical Report; Wind Europe: Brussels, Belgium, 2017.


| Parameter | Value |
|---|---|
| Rated Power | 300 MW |
| Rated Capacity | 50 MWh |
| Efficiency | 95% |
| 80% | |
| 20% |
| Parameter | Value |
|---|---|
| Wind Turbine Nominal Power | 1.5 MW |
| Number of wind turbines | 321 |
| Wind speed | 10 m/s |
| Grid Frequency | 60 Hz |
| Initial Load | 1600 MW |
| Rated Power of Synchronous Turbines | 900 MVA |
| Inertia Constant (H) | Droop Constant (R) | |
|---|---|---|
| A | 5.04 | 0.05 |
| B | 10.08 | 0.025 |
| C | 13.104 | 0.019 |
| D | 0 | 0.019 |
| Frequency Deviation Multiplier | ROCOF Multiplier | |
|---|---|---|
| A | ||
| B | ||
| C |
| H | R | Frequency Deviation Multiplier | ROCOF Multiplier | |
|---|---|---|---|---|
| A | 13.104 | 0.019 | ||
| B | 13.104 | 0.019 | ||
| C | 13.104 | 0.019 | ||
| D | 0 | 0.019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pokhriyal, A.; Domínguez-García, J.L.; Gómez-Romero, P. Impact of Battery Energy System Integration in Frequency Control of an Electrical Grid with Wind Power. Clean Technol. 2022, 4, 972-986. https://doi.org/10.3390/cleantechnol4040060
Pokhriyal A, Domínguez-García JL, Gómez-Romero P. Impact of Battery Energy System Integration in Frequency Control of an Electrical Grid with Wind Power. Clean Technologies. 2022; 4(4):972-986. https://doi.org/10.3390/cleantechnol4040060
Chicago/Turabian StylePokhriyal, Anukriti, José Luis Domínguez-García, and Pedro Gómez-Romero. 2022. "Impact of Battery Energy System Integration in Frequency Control of an Electrical Grid with Wind Power" Clean Technologies 4, no. 4: 972-986. https://doi.org/10.3390/cleantechnol4040060
APA StylePokhriyal, A., Domínguez-García, J. L., & Gómez-Romero, P. (2022). Impact of Battery Energy System Integration in Frequency Control of an Electrical Grid with Wind Power. Clean Technologies, 4(4), 972-986. https://doi.org/10.3390/cleantechnol4040060








