Influence of Dimple Diameter and Depth on Heat Transfer of Impingement-Cooled Turbine Leading Edge with Cross-Flow and Dimple
Abstract
:1. Introduction
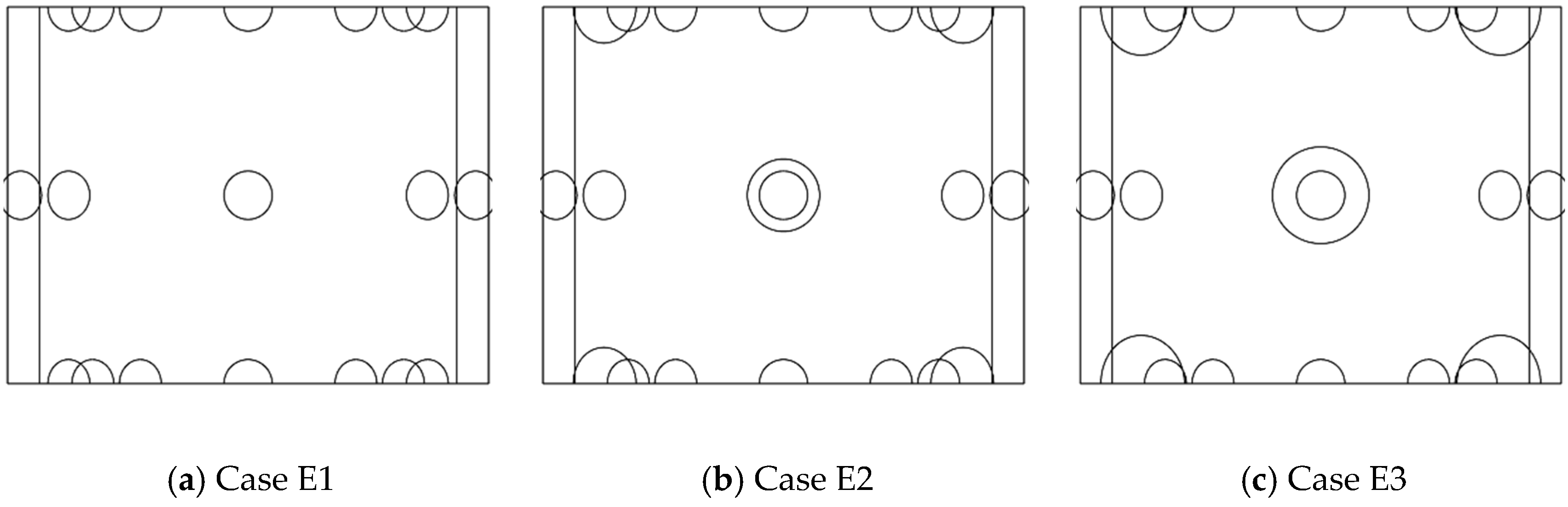
2. Research Method and Scheme Design
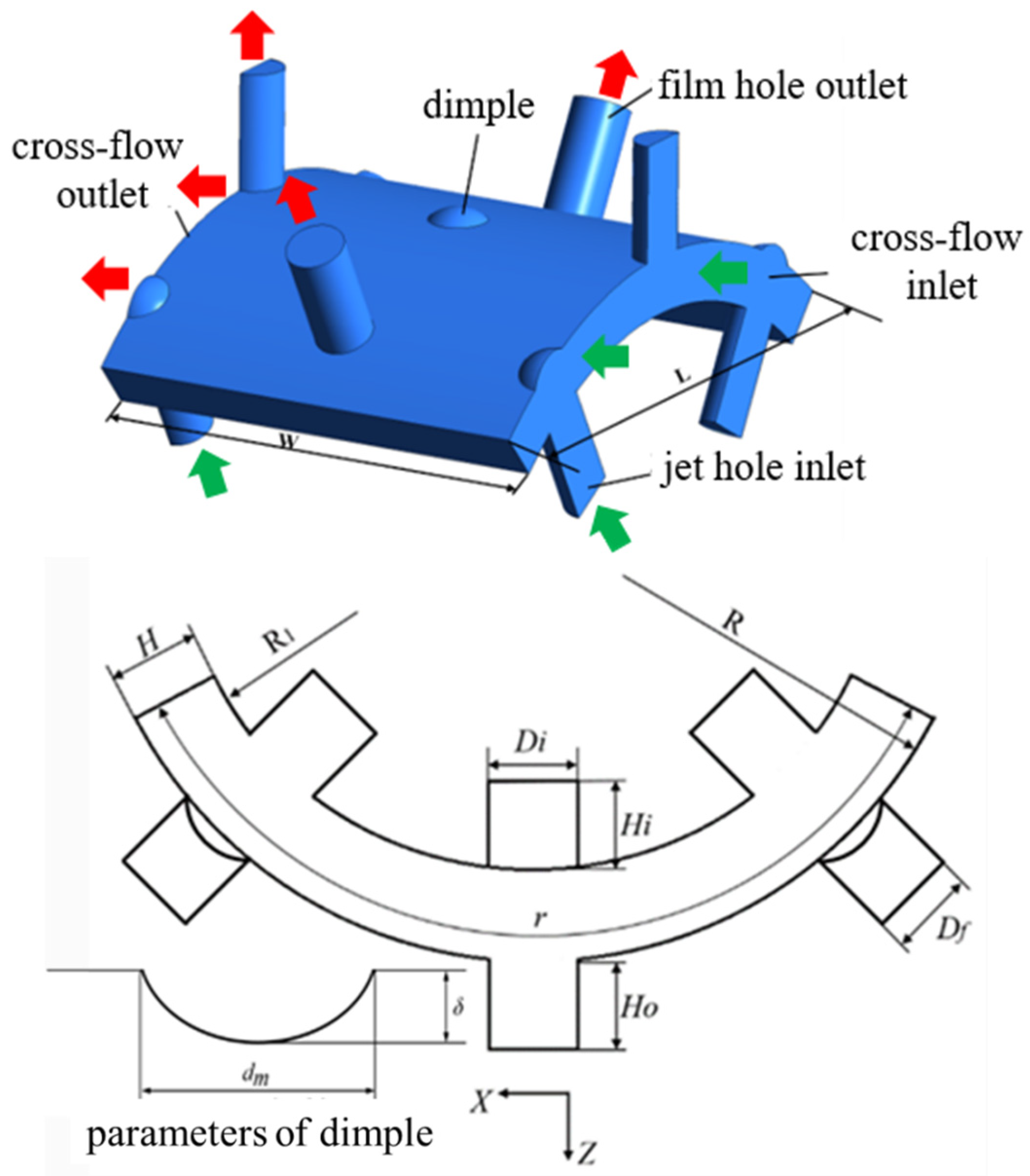
2.1. Geometry Model
2.2. Parameters Definition
2.3. Boundary Conditions
2.4. Mesh Generation
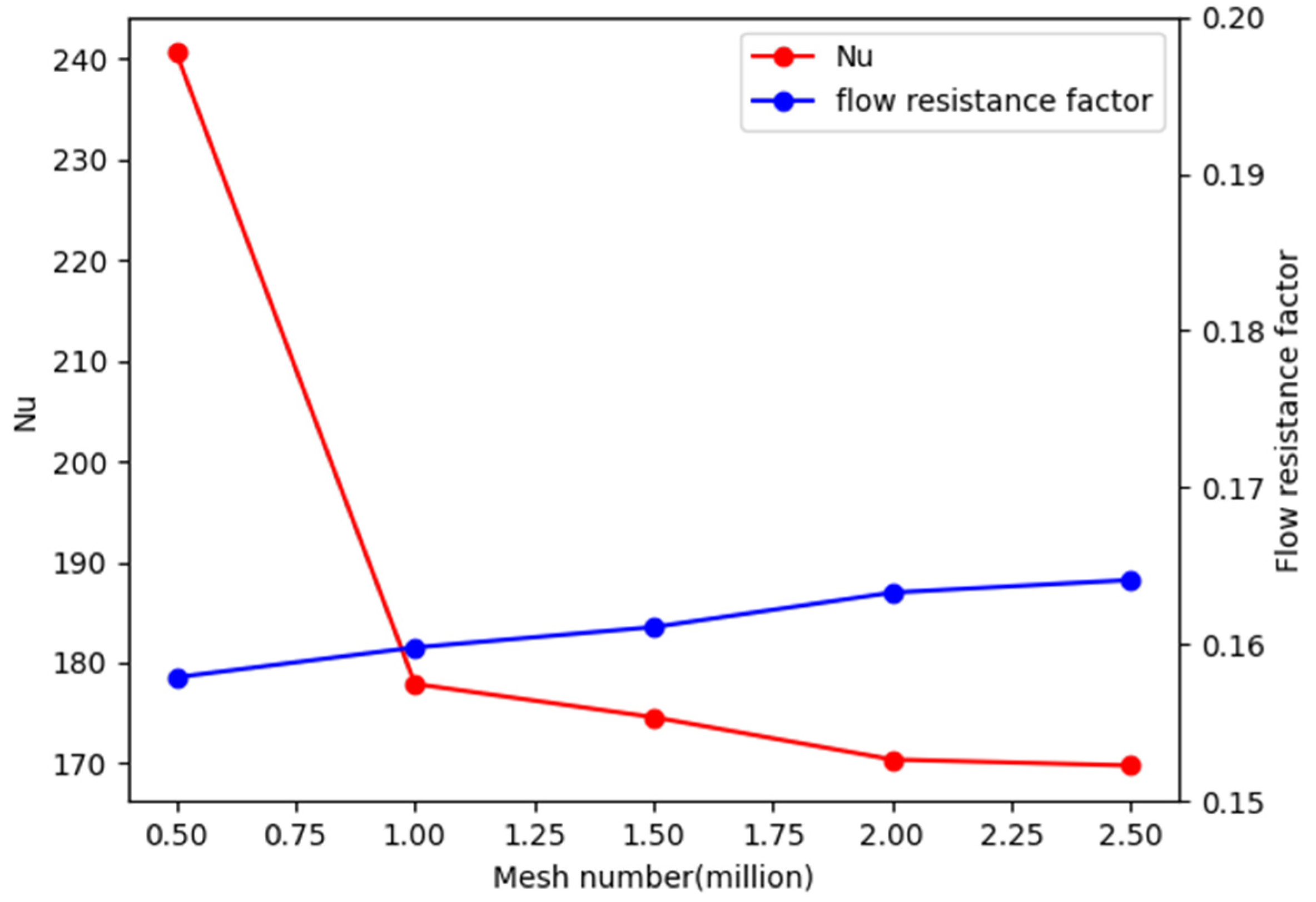
2.5. Grid Independency Test
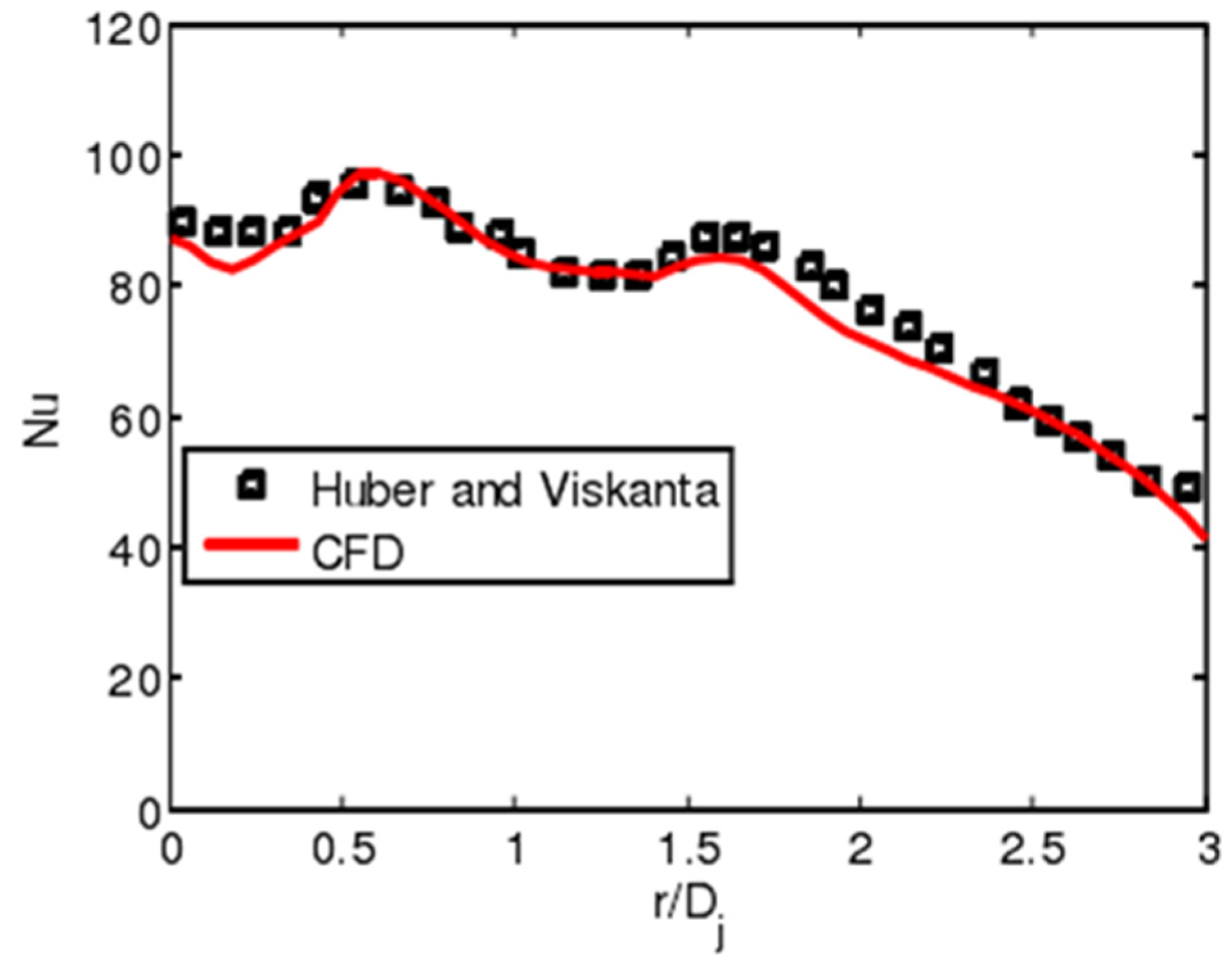
2.6. Numerical Validation
3. Analysis of Calculated Results
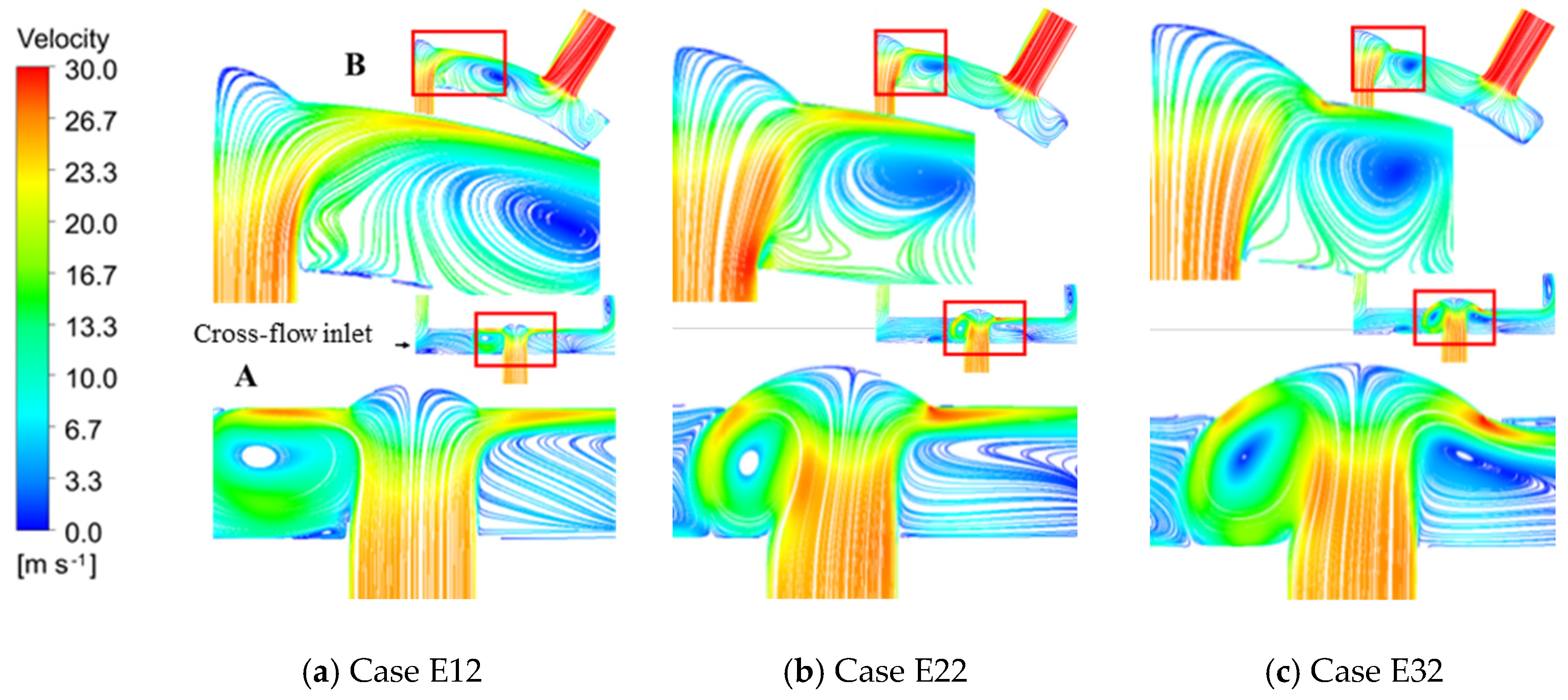
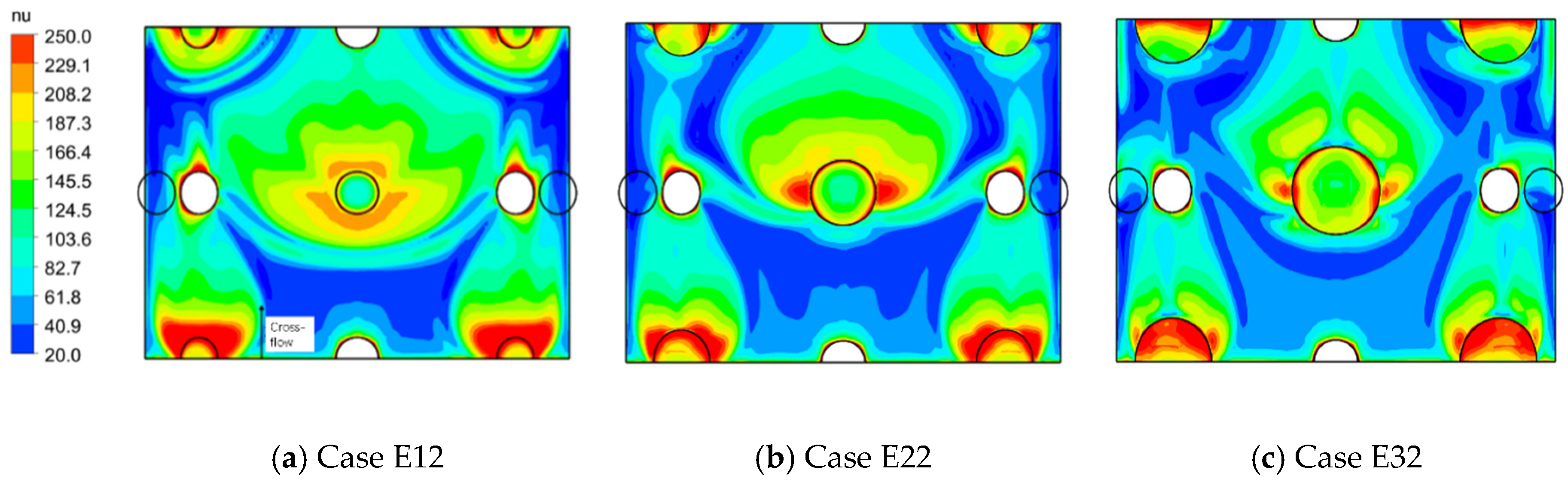
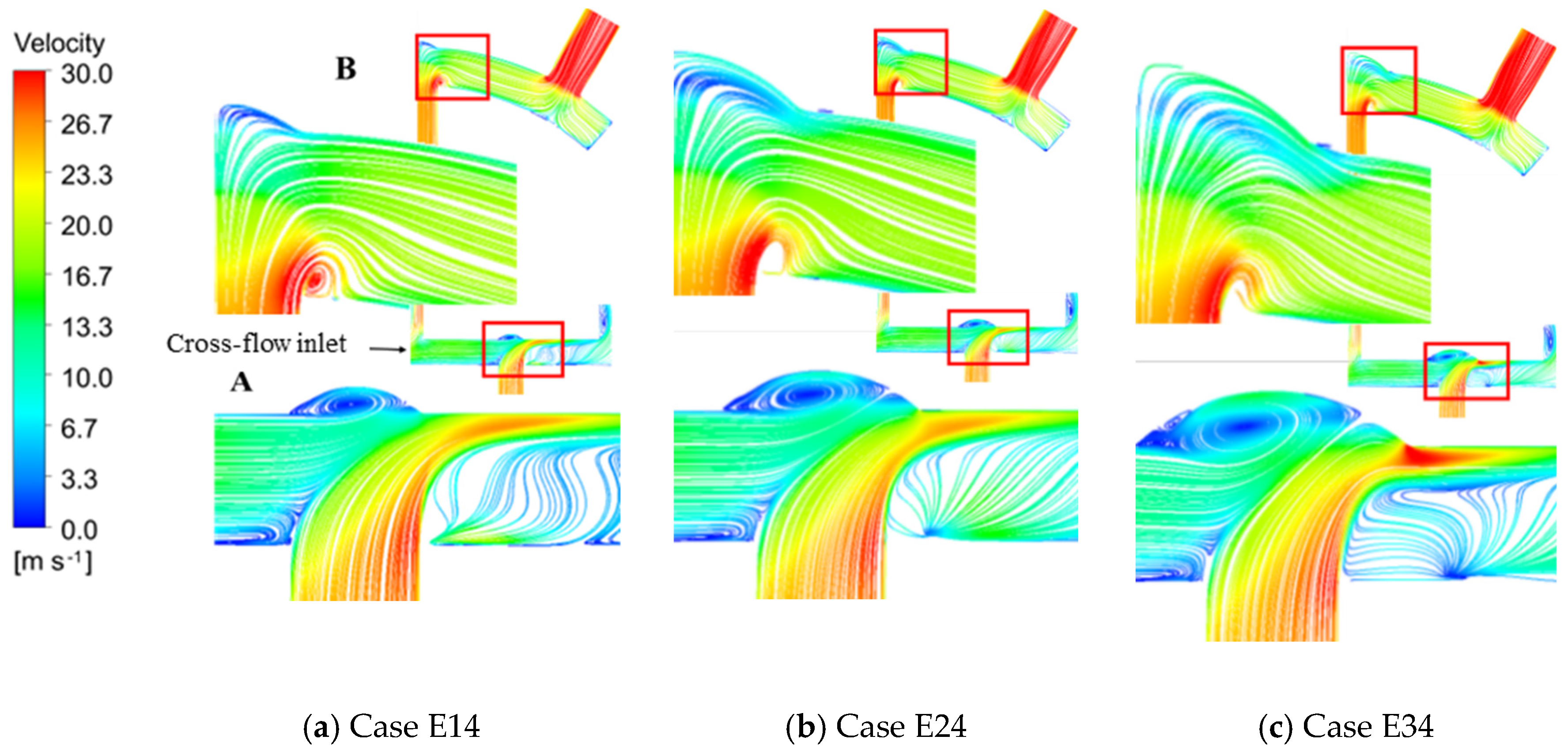
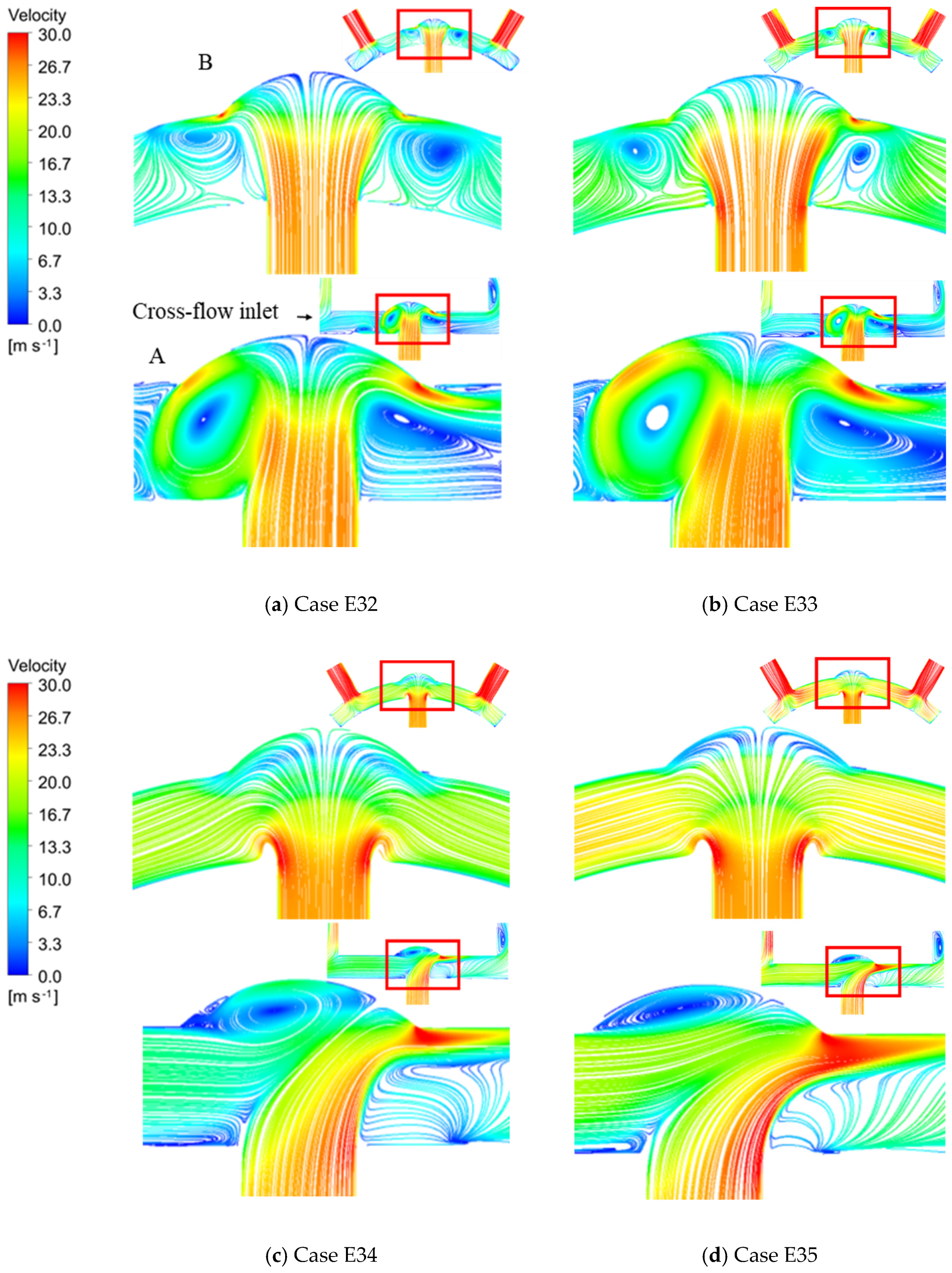
3.1. The Influence of Dimple Diameter on Heat Transfer at Target Surface under Cross-Flow
3.1.1. Flow Field and Heat Transfer
3.1.2. The Influence of
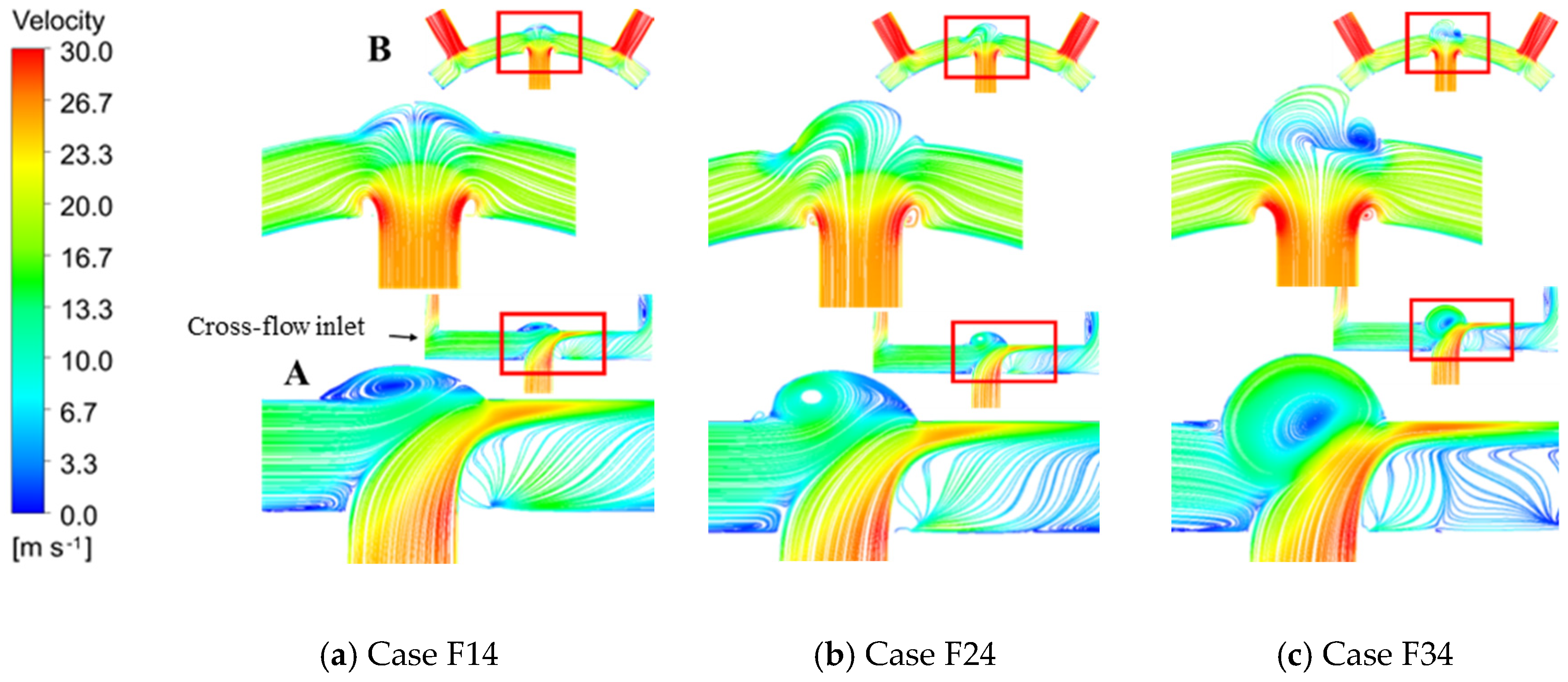
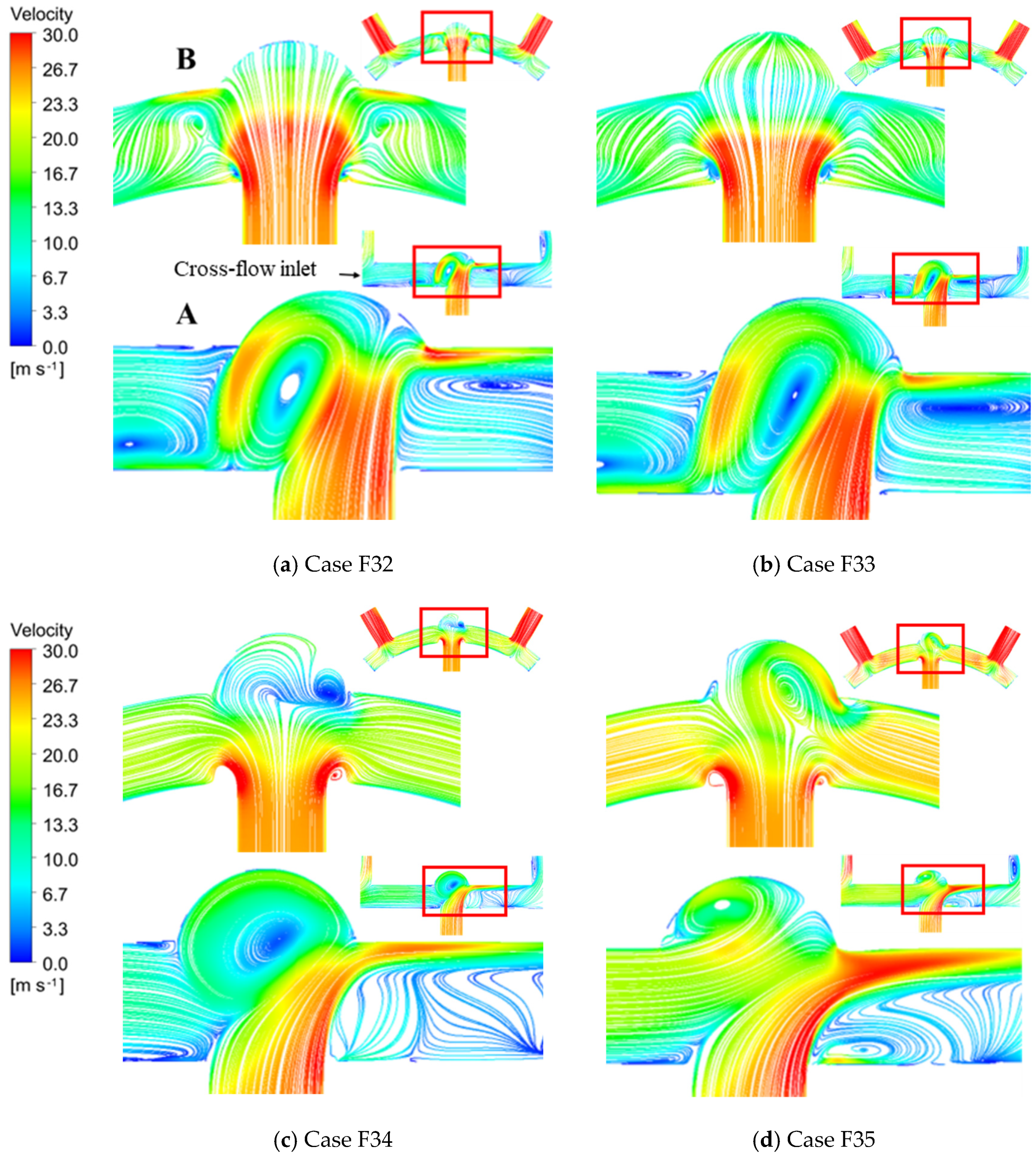
3.2. The Influence of Dimple Depth on Heat Transfer at Target Surface under Cross-Flow
3.2.1. Flow Field and Heat Transfer
3.2.2. The Influence of
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of symbols and abbreviations | |
| Dimple depth | |
| Dimple diameter | |
| Jet hole diameter | |
| Jet Reynolds number | |
| Impact jet velocity | |
| Jet motion viscosity | |
| Cross-flow Reynolds number | |
| Cross-flow velocity | |
| Cross-flow motion viscosity | |
| Jet-to-space spacing | |
| Target surface Nusselt number | |
| Fluid convention heat transfer coefficient | |
| Width of target surface | |
| Fluid thermal conductivity | |
References
- Basir, H.; Alaviyoun, S.; Rosen, M.A. Thermal Investigation of a Turbocharger Using IR Thermography. Clean Technol. 2022, 4, 329–344. [Google Scholar] [CrossRef]
- Kim, M.; Dong, H.S.; Jin, S.K.; Lee, B.J.; Lee, J. Experimental investigation of effusion and transpiration air cooling for single turbine blade. J. Appl. Therm. Eng. 2021, 182, 116156. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, J.; Tan, X. Numerical assessment of round-to-slot film cooling performances on a turbine blade under engine representative conditions. J. Int. Commun. Heat Mass Transf. 2019, 100, 98–110. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, O. Enhancement of combined cycle performance using transpiration cooling of gas turbine blades with steam. J. Mech. Sci. Technol. 2014, 28, 2429–2437. [Google Scholar] [CrossRef]
- He, J.; Luo, X.; Peng, Y. Investigation on the relation of transpiration cooling of sintered woven wire mesh and particle deposition. J. Gas Turbine Exp. Res. 2018, 31, 40–45. [Google Scholar]
- Goldstein, R.J.; Sobolik, K.A.; Seol, W.S. Effect of entrainment on the heat transfer to a heated circular air jet impinging on a flat surface. J. Heat Transf. 1990, 112, 608–611. [Google Scholar] [CrossRef]
- Martini, P.; Schulz, A.; Bauer, H.J. Film cooling effectiveness and heat transfer on the trailing edge cut-back of gas turbine airfoils with various internal cooling designs. J. Turbomach. 2014, 128, 87–96. [Google Scholar]
- Shen, Z.; Xie, Y.; Zhang, D. Numerical predictions on fluid flow and heat transfer in U-shaped channel with the combination of ribs, dimples and protrusions under rotational effects. J. Int. J. Heat Mass Transf. 2015, 80, 494–512. [Google Scholar] [CrossRef]
- Alaskari, M.; Kadhim, A.M.; Farhan, A.A.; Al-Damook, M.; Al Qubeissi, M. Performance Evaluation of Roughened Solar Air Heaters for Stretched Parameters. Clean Technol. 2022, 4, 555–569. [Google Scholar] [CrossRef]
- Luo, L.; Wang, C.; Wang, L.; Bengt, S.; Wang, S. Effects of pin fin configurations on heat transfer and friction factor in an improved lamilloy cooling structure. J. Heat Transf. Res. 2017, 48, 657–679. [Google Scholar] [CrossRef]
- Wu, W.; Xu, H.; Wang, J. Numerical investigation of pin-fin influences on cooling air flow characteristics in turbine blade trailing edge region. J. Propuls. Technol. 2021, 42, 163–172. [Google Scholar]
- Han, J.C. Heat transfer and friction in channels with two opposite rib-roughened walls. J. Heat Transf. 1984, 106, 774–781. [Google Scholar] [CrossRef]
- Lee, D.H.; Rhee, D.H.; Cho, H.H.; Moon, H.K. Heat transfer measurements in a rotating equilateral triangular channel with various rib arrangements. In Proceedings of the American Society of Mechanical Engineers Digital Collection, ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Afanasyev, V.N.; Chudnovsky, Y.P.; Leontiev, A.I.; Roganov, P.S. Turbulent flow friction and heat transfer characteristics for spherical cavities on a flat plate. J. Exp. Therm. Fluid Sci. 1993, 7, 1–8. [Google Scholar] [CrossRef]
- Rao, Y.; Xu, Y.; Wan, C. A numerical study of the flow and heat transfer in the pin fin-dimple channels with various dimple depths. J. Heat Transf. 2012, 134, 071902. [Google Scholar] [CrossRef]
- Lan, J.; Xie, Y.; Zhang, D. Heat transfer enhancement in a rectangular channel with the combination of ribs, dimples and protrusions. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Murata, A.; Nishida, S.; Saito, H.; Iwamoto, K.; Okita, Y.; Nakamata, C. Heat transfer enhancement due to combination of dimples, protrusions, and ribs in narrow internal passage of gas turbine blade. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Xie, G.; Sundén, B.; Wang, Q. Predictions of enhanced heat transfer of an internal blade tip-wall with hemispherical dimples or protrusions. J. Turbomach. 2011, 133, 041005. [Google Scholar] [CrossRef]
- Kanokjaruvijit, K.; Martinez-Botas, R.F. Heat transfer and pressure investigation of dimple impingement. J. Turbomach. 2008, 130, 011003. [Google Scholar] [CrossRef]
- Fazli, M.; Raisee, M. Computation of flow and heat transfer through channels with periodic dimple/protrusion walls using low-Reynolds number turbulence models. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 1178–1207. [Google Scholar] [CrossRef]
- Luo, L.; Du, W.; Wang, S.; Wang, L.; Sundén, B.; Zhang, X. Multi-objective optimization of a solar receiver considering both the dimple/protrusion depth and delta-winglet vortex generators. J. Energy 2017, 137, 1–19. [Google Scholar] [CrossRef]
- Kim, S.M.; Kim, K.Y. Evaluation of cooling performance of impinging jet array over various dimpled surfaces. J. Heat Mass Transf. 2016, 52, 845–854. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, J.; Li, H.; Mao, H. Investigation on heat transfer mechanism of impinging jet with cross-flow. J. Aerosp. Power 2011, 21, 528–532. [Google Scholar]
- Florschuetz, L.W.; Su, C.C. Effects of crossflow temperature on heat transfer within an array of impinging jets. J. Heat Transf. 1987, 109, 74–82. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, J.; Tan, X. Numerical investigation of jet impingement cooling with non-uniform crossflow. J. Aerosp. Power 2006, 21, 528–532. [Google Scholar]
- Wang, C.; Luo, L.; Wang, L.; Sundén, B. Effects of vortex generators on the jet impingement heat transfer at different cross-flow Reynolds numbers. Int. J. Heat Mass Transf. 2016, 96, 278–286. [Google Scholar] [CrossRef]
- Lee, J.; Zhong, R.; Ligrani, P.; Lee, D.H.; Fox, M.D.; Moon, H.K. Cross-flow effects on impingement array heat transfer with varying jet-to-target plate distance and hole spacing. Int. J. Heat Mass Transf. 2014, 75, 534–544. [Google Scholar] [CrossRef]
- Luo, L. On the Design Method and Heat Transfer Mechanism of High Efficiency Cooling Structure in a Gas Turbine. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Funazaki, K.; Tarukawa, Y.; Kudo, T.; Matsuno, S.; Imai, R.; Yamawaki, S. Heat transfer characteristics of an integrated cooling configuration for ultra-high temperature turbine blades: Experimental and numerical investigations. In Proceedings of the American Society of Mechanical Engineers Digital Collection, ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, LA, USA, 4–7 June 2001. [Google Scholar]
- Huber, A.M.; Viskanta, R. Convective heat transfer to a confined impinging array of air jets with spent air exits. ASME J. Heat Transf. 1994, 116, 570–576. [Google Scholar] [CrossRef]





| Case | Dimensionless Diameter | Jet Reynolds Number | Cross-Flow Reynolds Number |
|---|---|---|---|
| E12 | 1.0 | 30,000 | 15,000 |
| E13 | 1.0 | 30,000 | 30,000 |
| E14 | 1.0 | 30,000 | 45,000 |
| E15 | 1.0 | 30,000 | 60,000 |
| E22 | 1.5 | 30,000 | 15,000 |
| E23 | 1.5 | 30,000 | 30,000 |
| E24 | 1.5 | 30,000 | 45,000 |
| E25 | 1.5 | 30,000 | 60,000 |
| E32 | 2.0 | 30,000 | 15,000 |
| E33 | 2.0 | 30,000 | 30,000 |
| E34 | 2.0 | 30,000 | 45,000 |
| E35 | 2.0 | 30,000 | 60,000 |
| Case | Dimensionless Depth | Jet Reynolds Number | Cross-Flow Reynolds Number |
|---|---|---|---|
| F12 | 0.2 | 30,000 | 15,000 |
| F13 | 0.2 | 30,000 | 30,000 |
| F14 | 0.2 | 30,000 | 45,000 |
| F15 | 0.2 | 30,000 | 60,000 |
| F22 | 0.3 | 30,000 | 15,000 |
| F23 | 0.3 | 30,000 | 30,000 |
| F24 | 0.3 | 30,000 | 45,000 |
| F25 | 0.3 | 30,000 | 60,000 |
| F32 | 0.4 | 30,000 | 15,000 |
| F33 | 0.4 | 30,000 | 30,000 |
| F34 | 0.4 | 30,000 | 45,000 |
| F35 | 0.4 | 30,000 | 60,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, B.; Chen, Z.; He, D.; Zeng, F.; Song, Y.; Ouyang, Y.; Luo, L. Influence of Dimple Diameter and Depth on Heat Transfer of Impingement-Cooled Turbine Leading Edge with Cross-Flow and Dimple. Clean Technol. 2023, 5, 1012-1027. https://doi.org/10.3390/cleantechnol5030051
Qu B, Chen Z, He D, Zeng F, Song Y, Ouyang Y, Luo L. Influence of Dimple Diameter and Depth on Heat Transfer of Impingement-Cooled Turbine Leading Edge with Cross-Flow and Dimple. Clean Technologies. 2023; 5(3):1012-1027. https://doi.org/10.3390/cleantechnol5030051
Chicago/Turabian StyleQu, Bin, Zilong Chen, Dengke He, Fei Zeng, Youfu Song, Yuqing Ouyang, and Lei Luo. 2023. "Influence of Dimple Diameter and Depth on Heat Transfer of Impingement-Cooled Turbine Leading Edge with Cross-Flow and Dimple" Clean Technologies 5, no. 3: 1012-1027. https://doi.org/10.3390/cleantechnol5030051
APA StyleQu, B., Chen, Z., He, D., Zeng, F., Song, Y., Ouyang, Y., & Luo, L. (2023). Influence of Dimple Diameter and Depth on Heat Transfer of Impingement-Cooled Turbine Leading Edge with Cross-Flow and Dimple. Clean Technologies, 5(3), 1012-1027. https://doi.org/10.3390/cleantechnol5030051





