Chernobyl’s Lesser Known Design Flaw: The Chernobyl Liquidator Medal—An Educational Essay
Abstract
1. Introduction
1.1. The Chernobyl Power Station Accident and the Liquidators
1.2. Nuclear Decay Background
2. Analysis
2.1. The Lorentz Force—Charged Particle Dynamics in External Fields
2.2. Relativistic Equations of Motion in a Static, Uniform Magnetic Field
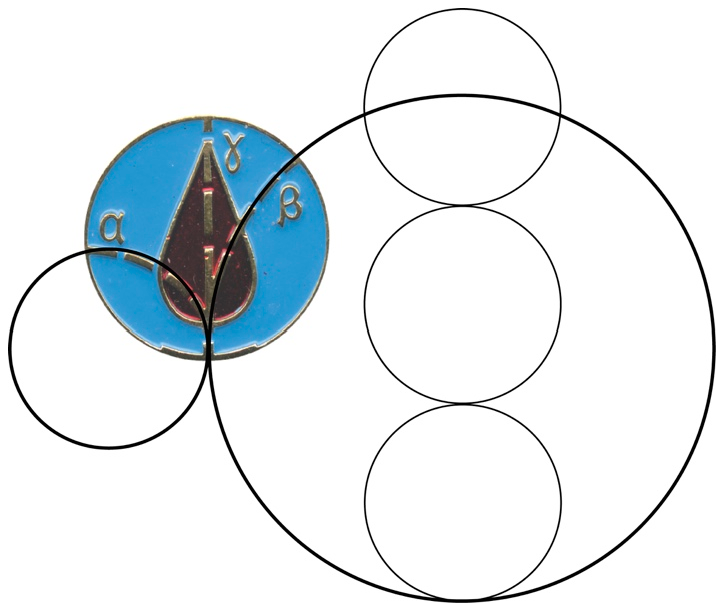
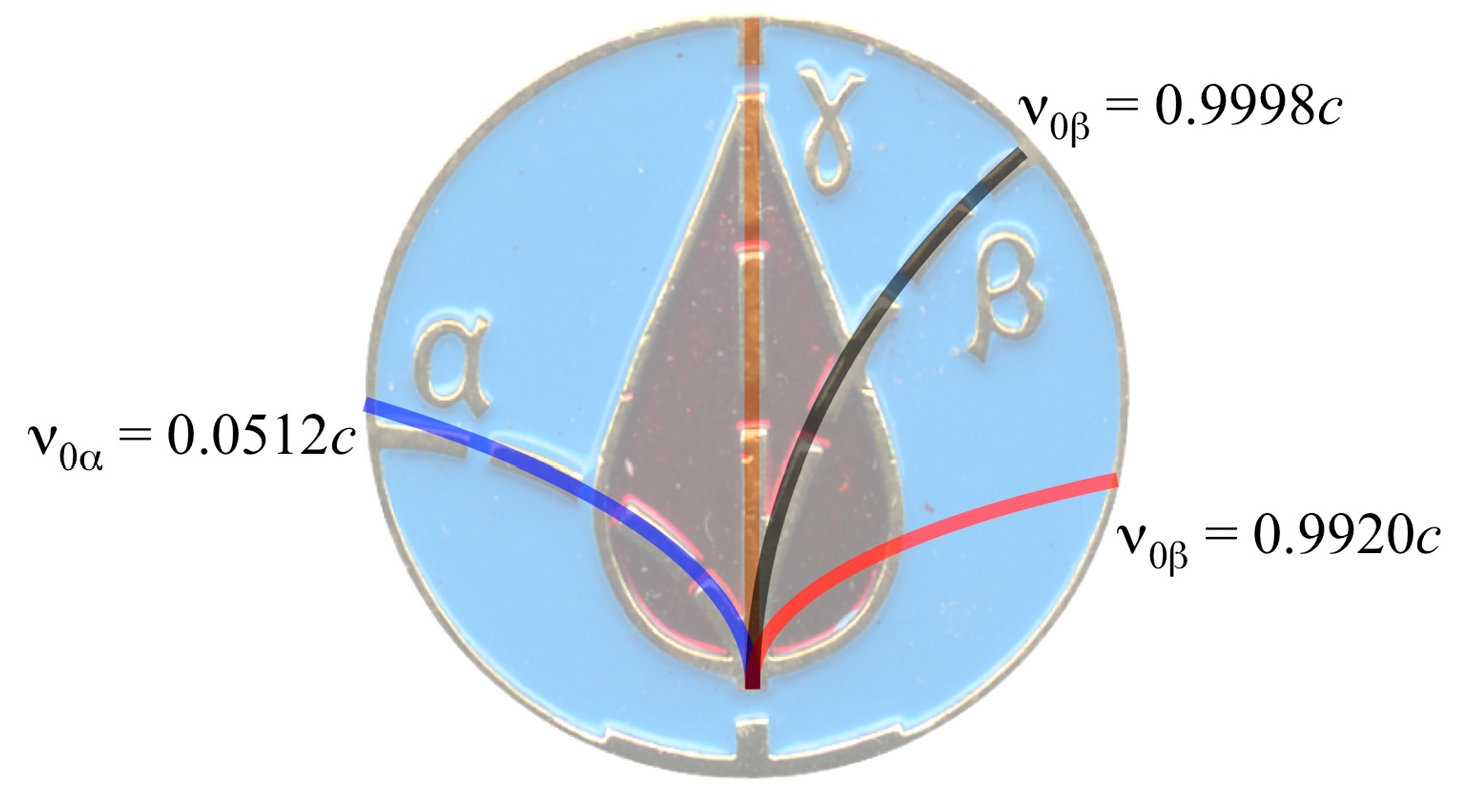
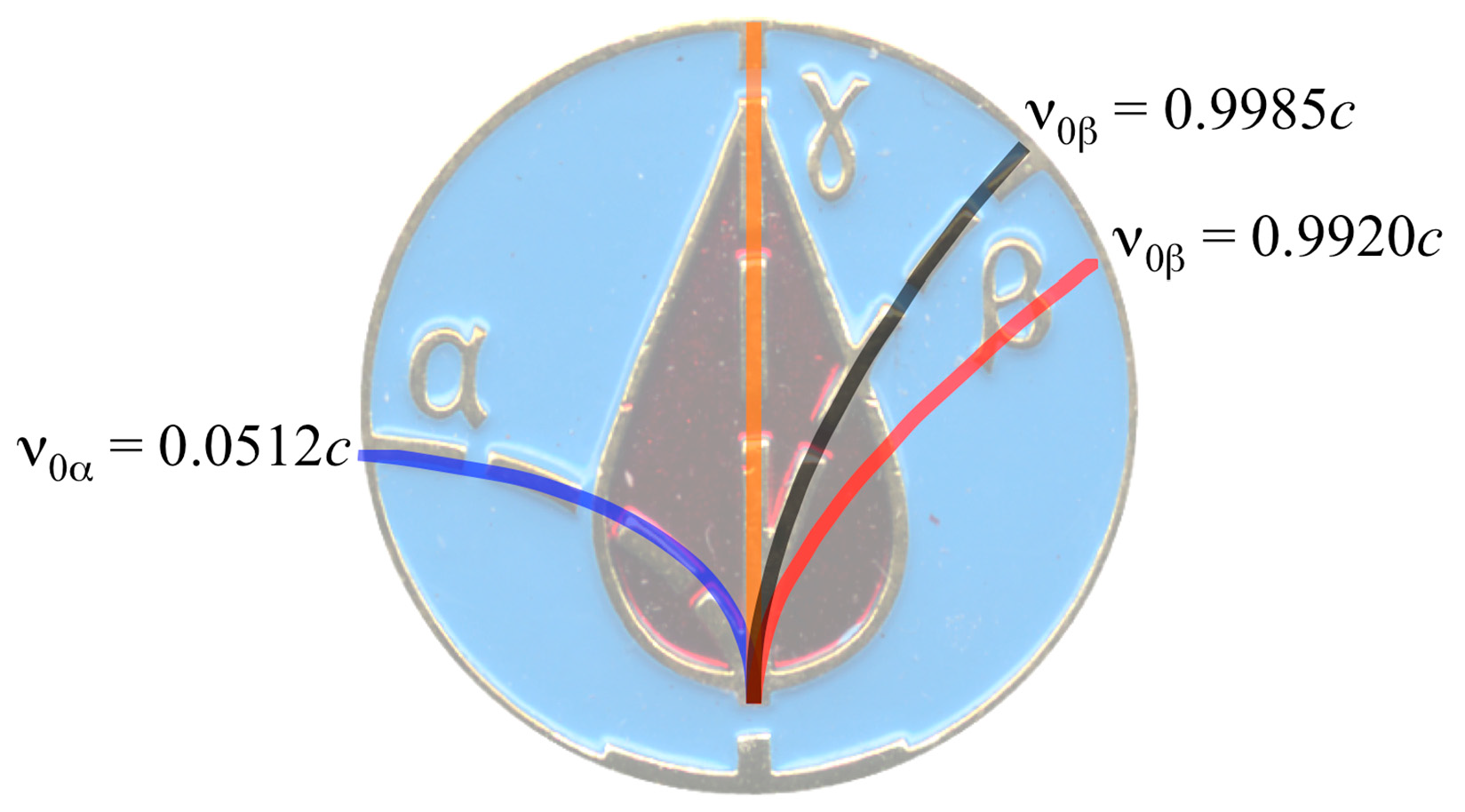
2.3. CLM Trajectory Analysis
2.4. Relativistic Motion of a Charged Particle in a Static Uniform Electric Field
3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ElBaradei, M. The Enduring Lessons of Chernobyl. In Proceedings of the Chernobyl: Looking Back to Go Forward, Proceedings of an International Conference, Vienna, Austria, 6–7 September 2005; International Atomic Energy Agency: Vienna, Austria, 2008. ISBN 978-92-0-110807-4. Available online: http://www-pub.iaea.org/MTCD/publications/PDF/Pub1312_web.pdf (accessed on 11 June 2019).
- The Chernobyl Forum: 2003–2005 (Second Revised Version). In Proceedings of the Chernobyl’s Legacy: Health, Environmental and Socio-Economic Impacts and Recommendations to the Governments of Belarus, the Russian Federation and Ukraine; International Atomic Energy Agency: Vienna, Austria, 2005; p. 57. Available online: https://www.iaea.org/sites/default/files/chernobyl.pdf (accessed on 11 June 2019).
- Rutherford, E. Radioactive Substances and Their Radiations; Cambridge University Press: Cambridge, UK, 1913; p. 116. ISBN 978-1-40674-805-5. [Google Scholar]
- Walker, J. Physics, 4th ed.; Addison-Wesley: San Francisco, CA, USA, 2010; p. 1122. ISBN 032161111X. [Google Scholar]
- Knight, R.D.; Jones, B.; Field, S. College Physics—A Strategic Approach, 2nd ed.; Pearson: Boston, MA, USA, 2017; p. 1011. ISBN 978-0-134-14332-3. [Google Scholar]
- Cutnell, J.D.; Johnson, K.W. Physics, 9th ed.; John Wiley & Sons: New York, NY, USA, 2012; p. 959. ISBN 0470879521. [Google Scholar]
- Silberberg, M.; Amateis, P. Chemistry: The Molecular Nature of Matter and Change, 7th ed.; McGraw-Hill: New York, NY, USA, 2016; p. 1099. ISBN 978-1-259-70264-8. [Google Scholar]
- Nave, R.V. HyperPhysics. 2005. Available online: http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html (accessed on 28 March 2016).
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1975; p. 531. ISBN 047143132X. [Google Scholar]
- Neary, G.J. The β-Ray Spectrum of Radium E. Proc. R. Soc. Lond. A 1940, 175, 71–87. [Google Scholar] [CrossRef]
- Chernobyl Forum Expert Group. ‘Environment’, Environmental Consequences of the Chernobyl Accident and Their Remediation: Twenty years of Experience, Report of the UN Chernobyl Forum Expert Group ‘Environment’, 2005. 2006. Available online: http://www-pub.iaea.org/MTCD/publications/PDF/Pub1239_web.pdf (accessed on 11 June 2019).
- Magill, J.; Galy, J. Radioactivity Radionuclides Radiation; Springer: New York, NY, USA, 2005; p. 264. ISBN 978-3-540-26881-9. [Google Scholar]
- Bé, M.M.; Chisté, V.; Dulieu, C.; Browne, E.; Chechev, V.; Kuzmenko, N.; Helmer, R.; Nichols, A.; Schonfeld, E.; Dersch, R. Table of Radionuclides (Vol. 1-A = 1 to 150); Bureau International des Poids et Mesures (BIPM): Sevres, France, 2004; p. 285. Available online: http://www.bipm.org/en/publications/scientific-output/monographie-ri-5.html (accessed on 11 June 2019).
- Bé, M.M.; Chisté, V.; Dulieu, C.; Browne, E.; Chechev, V.; Kuzmenko, N.; Helmer, R.; Nichols, A.; Schonfeld, E.; Dersch, R. Table of Radionuclides (Vol. 2-A = 151 to 242); Bureau International des Poids et Mesures (BIPM): Sevres, France, 2004; p. 282. Available online: http://www.bipm.org/en/publications/scientific-output/monographie-ri-5.html (accessed on 11 June 2019).
- Laboratoire National Henri Becquerel: Recommended Data (Atomic & Nuclear Data). Available online: http://www.nucleide.org/DDEP_WG/DDEPdata.htm (accessed on 11 June 2019).
- Nica, N. Nuclear Data Sheets for A = 140. Nucl. Data Sheets 2007, 108, 1287–1470. [Google Scholar] [CrossRef]
- Nica, N. Nuclear Data Sheets for A = 141. Nucl. Data Sheets 2014, 122, 151–204. [Google Scholar] [CrossRef]
- Bé, M.M.; Chisté, V.; Dulieu, C.; Mougeot, X.; Chechev, V.P.; Kondev, F.G.; Nichols, A.L.; Huang, X.; Wang, B. Table of Radionuclides (Vol. 7-A = 14 to 245); Bureau International des Poids et Mesures (BIPM): Sevres, France, 2013; p. 216. Available online: http://www.bipm.org/en/publications/scientific-output/monographie-ri-5.html (accessed on 11 June 2019).
- Tuli, J.K. Nuclear Data Sheets for A = 144. Nucl. Data Sheets 1979, 21, 97–153. [Google Scholar] [CrossRef]
- Sonzogni, A.A. Nuclear Data Sheets for A = 134. Nucl. Data Sheets 2004, 103, 1–182. [Google Scholar] [CrossRef]
- Sonzogni, A.A. Nuclear Data Sheets for A = 136. Nucl. Data Sheets 2002, 95, 837–994. [Google Scholar] [CrossRef]
- National Nuclear Data Center at Brookhaven National Labs. Interactive Chart of the Nuclides. Available online: http://www.nndc.bnl.gov/nudat2/ (accessed on 11 June 2019).
- Bé, M.M.; Chisté, V.; Dulieu, C.; Browne, E.; Baglin, C.; Chechev, V.; Kuzmenko, N.; Helmer, R.; Kondev, F.; MacMahon, D.; et al. Table of Radionuclides (Vol. 3-A = 3 to 244); Bureau International des Poids et Mesures (BIPM): Sevres, France, 2006; p. 210. Available online: http://www.bipm.org/en/publications/scientific-output/monographie-ri-5.html (accessed on 11 June 2019).
- Browne, E.; Tuli, J.K. Nuclear Data Sheets for A = 137. Nucl. Data Sheets 2007, 108, 2173–2318. [Google Scholar] [CrossRef]
- Khazov, Y.; Mitropolsky, I.; Rodionov, A. Nuclear Data Sheets for A = 131. Nucl. Data Sheets 2006, 107, 2715–2930. [Google Scholar] [CrossRef]
- Khazov, Y.; Rodionov, A.; Kondev, F.G. Nuclear Data Sheets for A = 133. Nucl. Data Sheets 2011, 112, 855–1113. [Google Scholar] [CrossRef]
- Bé, M.M.; Chisté, V.; Dulieu, C.; Browne, E.; Chechev, V.; Kuzmenko, N.; Kondev, F.; Luca, A.; Galán, M.; Pearce, A.; et al. Table of Radionuclides (Vol. 4-A = 133 to 252); Bureau International des Poids et Mesures (BIPM): Sevres, France, 2008; p. 282. Available online: http://www.bipm.org/en/publications/scientific-output/monographie-ri-5.html (accessed on 11 June 2019).
- Singh, B.; Chen, J. Nuclear Data Sheets for A = 85. Nucl. Data Sheets 2014, 116, 1–162. [Google Scholar] [CrossRef]
- Browne, E.; Tuli, J.K. Nuclear Data Sheets for A = 99. Nucl. Data Sheets 2011, 112, 275–446. [Google Scholar] [CrossRef]
- Browne, E.; Tuli, J.K. Nuclear Data Sheets for A = 239. Nucl. Data Sheets 2006, 107, 2649–2714. [Google Scholar] [CrossRef]
- De Frenne, D. Nuclear Data Sheets for A = 103. Nucl. Data Sheets 2009, 110, 2081–2256. [Google Scholar] [CrossRef]
- De Frenne, D.; Negret, A. Nuclear Data Sheets for A = 106. Nucl. Data Sheets 2008, 109, 943–1102. [Google Scholar] [CrossRef]
- Singh, B. Nuclear Data Sheets for A = 89. Nucl. Data Sheets 1998, 85, 1–170. [Google Scholar] [CrossRef]
- Browne, E. Nuclear Data Sheets for A = 90. Nucl. Data Sheets 1997, 82, 379–546. [Google Scholar] [CrossRef]
- Bé, M.M.; Chisté, V.; Dulieu, C.; Mougeot, X.; Chechev, V.P.; Kuzmenko, N.K.; Kondev, F.G.; Luca, A.; Galán, M.; Nichols, A.L.; et al. Table of Radionuclides (Vol. 6-A = 22 to 244); Bureau International des Poids et Mesures (BIPM): Sevres, France, 2011; p. 278. Available online: http://www.bipm.org/en/publications/scientific-output/monographie-ri-5.html (accessed on 11 June 2019).
- Khazov, Y.; Rodionov, A.A.; Sakharov, S.; Singh, B. Nuclear Data Sheets for A = 132. Nucl. Data Sheets 2005, 104, 497–790. [Google Scholar] [CrossRef]
- Basu, S.K.; Mukherjee, G.; Sonzogni, A.A. Nuclear Data Sheets for A = 95. Nucl. Data Sheets 2010, 111, 2555–2737. [Google Scholar] [CrossRef]
- Bé, M.M.; Chisté, V.; Dulieu, C.; Mougeot, X.; Browne, E.; Chechev, V.; Kuzmenko, N.; Kondev, F.; Luca, A.; Galán, M.; et al. Table of Radionuclides (Vol. 5-A = 22 to 244); Bureau International des Poids et Mesures (BIPM): Sevres, France, 2010; p. 228. Available online: http://www.bipm.org/en/publications/scientific-output/monographie-ri-5.html (accessed on 11 June 2019).
- Tsang, T. Classical Electrodynamics; World Scientific Publishing Co. Pte. Ltd.: River Edge, NJ, USA, 1997; ISBN 981-02-3041-9. [Google Scholar]
- Klein, R.; Kuske, P.; Thornagel, R.; Brandt, G.; Gorgen, R.; Ulm, G. Measurement of the BESSY II electron beam energy by Compton-backscattering of laser photons. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 486, 545–551. [Google Scholar] [CrossRef]
- Marshall, T.C.; Stolzenburg, M.; Maggio, C.R.; Coleman, L.M.; Krehbiel, P.R.; Hamlin, T.; Thomas, R.J.; Rison, W. Observed electric fields associated with lightning initiation. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Treagust, D.F. Development and Use of Diagnostic Tests to Evaluate Students’ Misconceptions in Science. Int. J. Sci. Educ. 1988, 10, 159–169. [Google Scholar] [CrossRef]




| Isotope | References | Emitted Particle Energy (MeV) | Particle speed (c 1) |
|---|---|---|---|
| Ba-140 | [15,16] | 0.281 (average), 0.828 (maximum) | 0.764c, 0.924c |
| Ce-141 | [15,17,18] | 0.145 (average), 0.479 (maximum) | 0.627c, 0.856c |
| Ce-144 | [15,19] | 0.082 (average), 0.290 (maximum) | 0.508c, 0.770c |
| Cs-134 | [15,18,20] | 0.157 (average), 0.498 (maximum) | 0.644c, 0.862c |
| Cs-136 | [15,21,22] | 0.118 (average), 0.396 (maximum) | 0.583c, 0.826c |
| Cs-137 | [15,23,24] | 0.188 (average), 0.551 (maximum) | 0.682c, 0.877c |
| I-131 | [15,25] | 0.182 (average), 0.578 (maximum) | 0.675c, 0.883c |
| I-133 | [15,26,27] | 0.405 (average), 1.140 (maximum) | 0.830c, 0.951c |
| Kr-85 | [13,15,28] | 0.251 (average), 0.685 (maximum) | 0.741c, 0.904c |
| Mo-99 | [13,15,29] | 0.389 (average), 1.080 (maximum) | 0.823c, 0.947c |
| Np-239 | [15,27,30] | 0.118 (average), 0.407 (maximum) | 0.583c, 0.831c |
| Ru-103 | [15,31] | 0.064 (average), 0.224 (maximum) | 0.458c, 0.719c |
| Ru-106 * | [15,32] | 0.010 (average), 0.039 (maximum) | 0.195c, 0.372c |
| Sr-89 | [13,15,33] | 0.585 (average), 1.495 (maximum) | 0.885c, 0.967c |
| Sr-90 | [15,23,34] | 0.196 (average), 0.546 (maximum) | 0.691c, 0.875c |
| Te-132 | [15,35,36] | 0.067 (average), 0.240 (maximum) | 0.467c, 0.733c |
| Xe-133 | [15,26,27] | 0.100 (average), 0.346 (maximum) | 0.549c, 0.803c |
| Zr-95 | [15,37] | 0.117 (average), 0.388 (maximum) | 0.581c, 0.823c |
| Isotope | Emitted Particle Energy (MeV) | Particle Speed (c 1) |
|---|---|---|
| Am-241 | 5.479 | 0.0542c |
| Cm-242 | 6.101 | 0.0572c |
| Pu-238 | 5.487 | 0.0542c |
| Pu-239 | 5.236 | 0.0530c |
| Pu-240 | 5.155 | 0.0526c |
| Pu-242 | 4.892 | 0.0512c |
| U-235 | 4.394 | 0.0485c |
| U-238 | 4.187 | 0.0474c |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McIntire, M.; Luczaj, J. Chernobyl’s Lesser Known Design Flaw: The Chernobyl Liquidator Medal—An Educational Essay. J 2019, 2, 340-351. https://doi.org/10.3390/j2030023
McIntire M, Luczaj J. Chernobyl’s Lesser Known Design Flaw: The Chernobyl Liquidator Medal—An Educational Essay. J. 2019; 2(3):340-351. https://doi.org/10.3390/j2030023
Chicago/Turabian StyleMcIntire, Michael, and John Luczaj. 2019. "Chernobyl’s Lesser Known Design Flaw: The Chernobyl Liquidator Medal—An Educational Essay" J 2, no. 3: 340-351. https://doi.org/10.3390/j2030023
APA StyleMcIntire, M., & Luczaj, J. (2019). Chernobyl’s Lesser Known Design Flaw: The Chernobyl Liquidator Medal—An Educational Essay. J, 2(3), 340-351. https://doi.org/10.3390/j2030023





