Risk Prediction Model for Dengue Transmission Based on Climate Data: Logistic Regression Approach
Abstract
:1. Introduction
2. Source of Data and Methodology
2.1. Data and Method
2.2. Overview of the Logistic Regression Model
2.2.1. Logistic Regression
- the outcome is a binary variable;
- there is a linear relationship between the logit of the outcome and each predictor variable;
- there are no influential values (extreme values or outliers) in the continuous predictors; and
- there is no high intercorrelation (multicollinearity) among predictors.
2.2.2. Estimation of Parameters and Goodness-Of-Fit of the Model
- Pearson chi-square goodness-of-fit test,
- Deviance goodness-of-fit test,
- Hosmer–Lemeshow goodness-of-fit test,
- Pseudo R2, and
- Receiver operating characteristic (ROC) curve.
3. Data Analysis and Discussion of Results
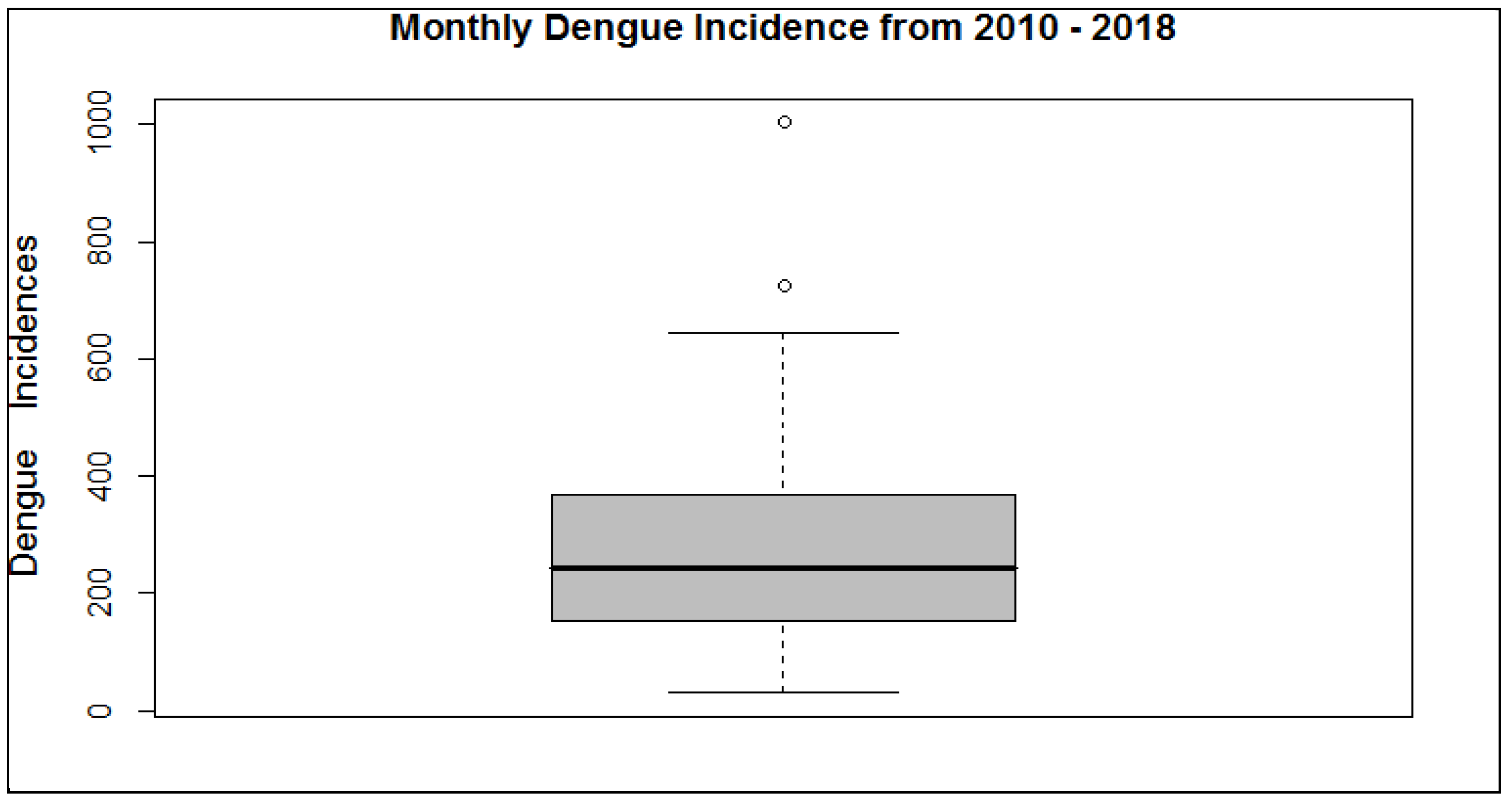
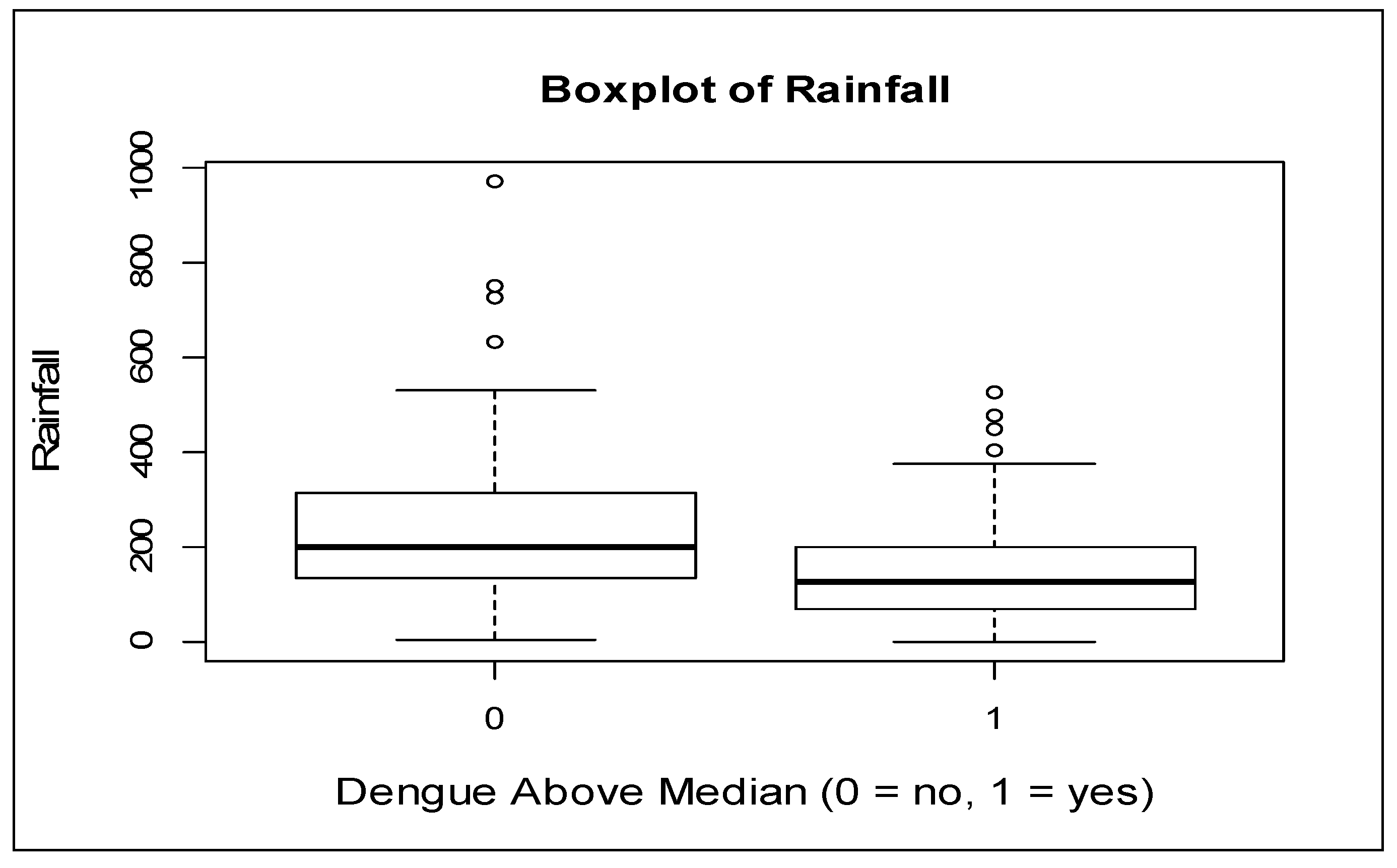
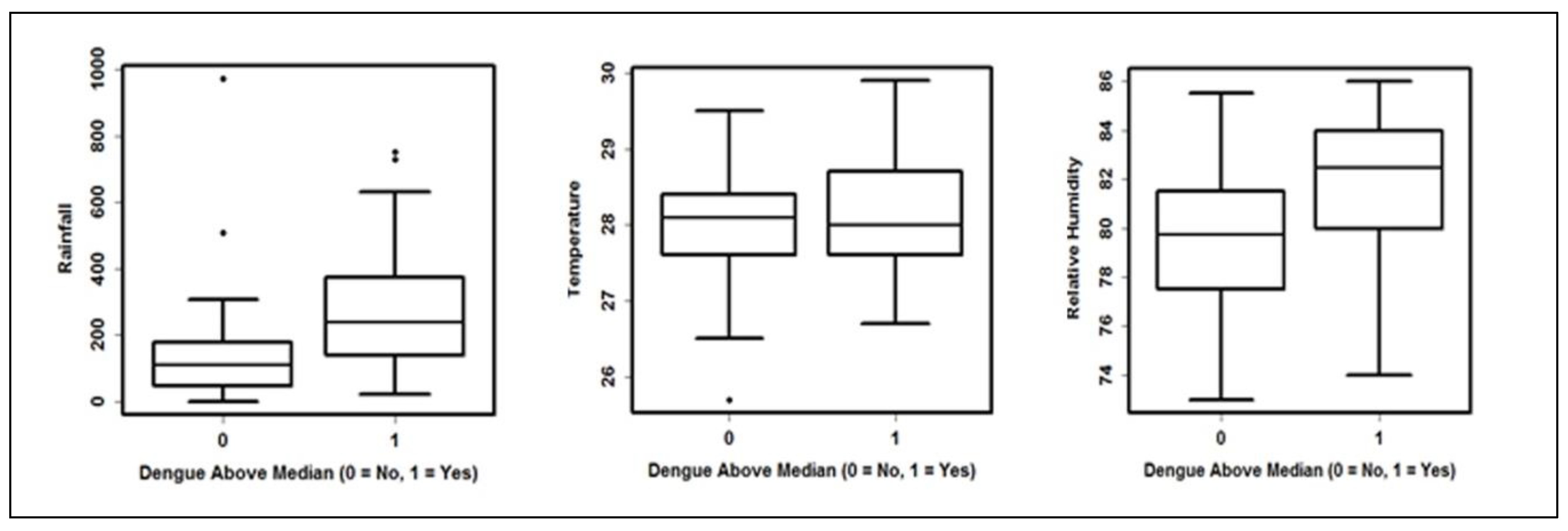
3.1. Data Analysis
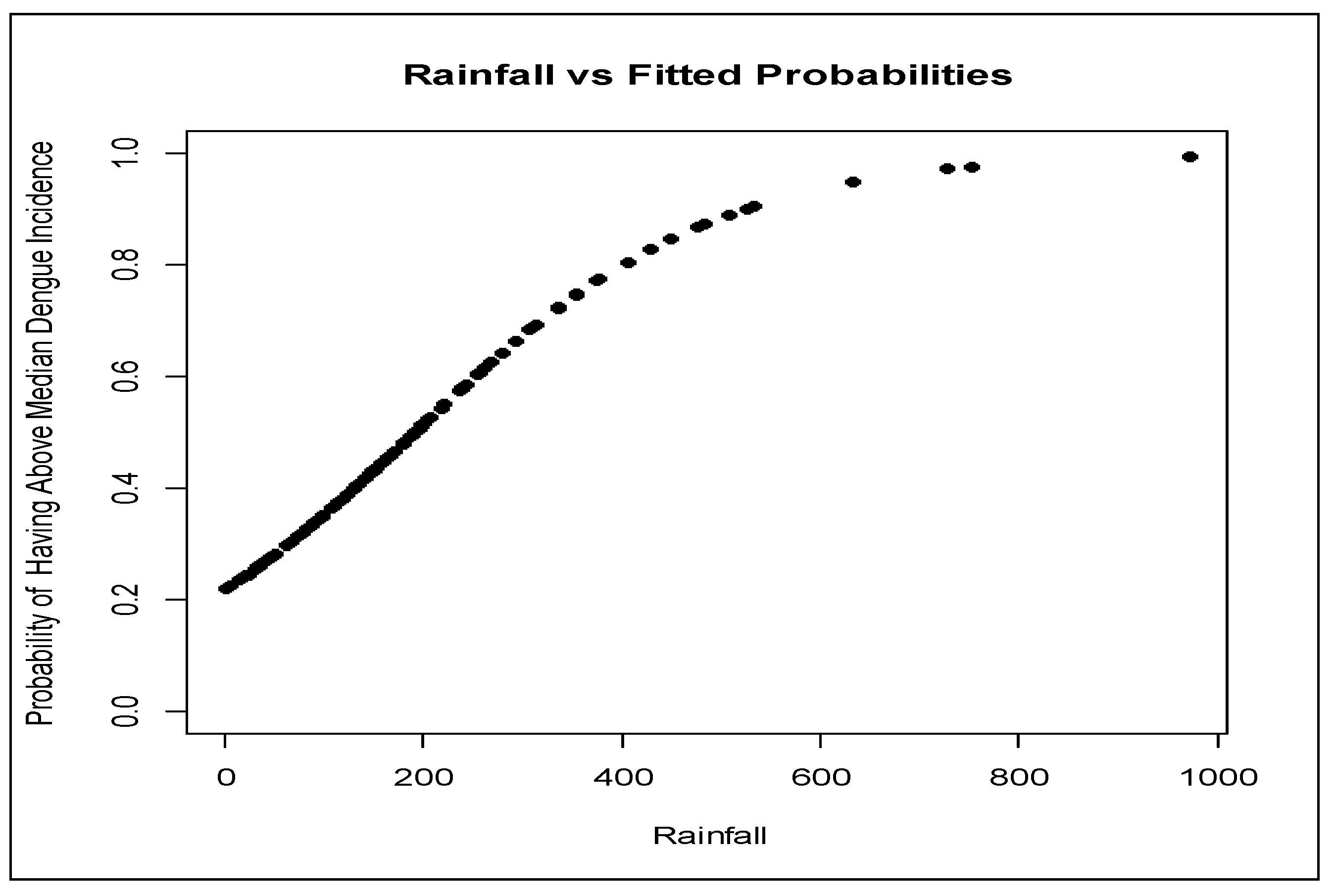
3.2. Interpreting Coefficients
3.3. Discussion
4. Conclusions
Funding
Conflicts of Interest
References
- CDC. Centers for Disease Control and Prevention. Available online: https://www.cdc.gov/dengue/index.html (accessed on 15 March 2019).
- Endy, T.P.; Anderson, K.B.; Nisalak, A.; Yoon, I.K.; Green, S.; Rothman, A.L.; Thomas, S.J.; Jarman, R.G.; Libraty, D.H.; Gibbons, R.V. Determinants of inapparent and symptomatic dengue infection in a prospective study of primary school children in Kamphaeng Phet, Thailand. PLoS Negl. Trop. Dis. 2011, 5. [Google Scholar] [CrossRef] [PubMed]
- World Mosquito Program. Available online: http://www.eliminatedengue.com/our-research/dengue-fever (accessed on 10 March 2019).
- Gubler, D.J. Dengue and dengue hemorrhagic fever. Clin. Microbial. Rev. 1998, 11, 480–496. [Google Scholar] [CrossRef]
- Sirisena, P.P.N.N.; Noordeen, F. Evolution of Dengue in Sri Lanka—Changes in the Virus, Vector, and Climate. Int. J. Infect. Dis. 2014, 19, 6–12. [Google Scholar] [CrossRef] [PubMed]
- International Federation of Red Cross And Red Crescent Societies: Sri Lanka/Dengue DREF Final Report (MDRLK007). Available online: https://reliefweb.int/report/sri-lanka/sri-lanka-dengue-dref-final-report-mdrlk007 (accessed on 20 March 2019).
- Epidemiology Unit of Ministry of Health of Sri Lanka. Available online: http://www.epid.gov.lk/web/ (accessed on 10 March 2019).
- Wu, P.C.; Guo, H.R.; Lung, S.C.; Lin, C.Y.; Su, H.J. Weather as an effective predictor for occurrence of dengue fever in Taiwan. Acta Tropica. 2007, 103, 50–57. [Google Scholar] [CrossRef] [PubMed]
- Chandrakantha, L. Statistical analysis of climate factors influencing dengue incidences in Colombo, Sri Lanka: Poisson and negative binomial regression approach. Int. J. Sci. Res. Publ. 2019, 9, 133–144. [Google Scholar] [CrossRef]
- Goto, K.; Kumarrendran, B.; Mettananda, S.; Gunasekara, D.; Fujii, Y.; Kaneko, S. Analysis of Effects of Meteorological Factors on Dengue Incidence in Sri Lanka Using Time Series Data. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Withanage, G.P.; Wishwakula, S.D.; Gunawardena, Y.I.; Hapugoda, M.D. A Forecasting Model for Dengue Incidence in the District of Gampaha, Sri Lanka. Parasit. Vector. 2018, 11. [Google Scholar] [CrossRef] [PubMed]
- Kavinga, H.W.B.; Jayasundara, D.D.M.; Jayakody, D.K.N. A New Dengue Outbreak Statistical Model using the Time Series Analysis. Eur. Int. J. Sci. Technol. 2013, 2, 35–52. [Google Scholar]
- Sun, W.; Xue, L.; Xie, X. Spatial-temporal Distribution of Dengue and Climate Characteristics for Two Clusters in Sri Lanka from 2012 to 2016. Sci. Rep. 2017, 7, 12884. [Google Scholar] [CrossRef] [PubMed]
- Iguchi, A.; Seposo, X.T.; Honda, Y. Meteorological Factors Affecting Dengue Incidence in Davao, Philippines. BMC Pub. Health 2018, 18, 629. [Google Scholar] [CrossRef] [PubMed]
- Campbell, K.M.; Lin, C.; Iamsirithawom, S.; Scott, T.W. The complex relationship between weather and dengue virus transmission in Thailand. Am. J. Trop. Med. Hyg. 2013, 89, 1066–1080. [Google Scholar] [CrossRef] [PubMed]
- Vu, H.H.; Okumura, J.; Hashizume, M.; Tran, D.N.; Yamamoto, T. Regional differences in the growing incidences of dengue fever in Vietnam explained by weather variability. Trop. Med. Health 2014, 42, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Department of Census and Statistics of Sri Lanka. Available online: http://www.statistics.gov (accessed on 10 March 2019).
- Hosmer, D.W., Jr.; Lemeshow, S. Applied Logistic Regression, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2013. [Google Scholar]
- Cordeiro, G.M.; Simas, A.B. The distribution of Pearson residuals in generalized linear models. Comput. Stat. Data Anal. 2009, 53, 3397–3411. [Google Scholar] [CrossRef]
- Menard, S. Applied Logistic Regression Analysis, 2nd ed.; SAGE Publications: New York, NY, USA, 2001. [Google Scholar]
- Nakhapakorn, K.; Tripathi, N.K. An Information Value Based Analysis of Physical and Climatic Factors Affecting Dengue Fever and Dengue Haemorrhagic Fever Incidence. Int. J. Health Geogr. 2005, 4. [Google Scholar] [CrossRef] [PubMed]
- Focks, D.; Barrera, R. Report on Scientific Working Group Meeting on Dengue. Geneva: WHO: 2007 Dengue Transmission Dynamics: Assessment and Implications for Control. 2007, pp. 92–108. Available online: https://www.who.int/tdr/publications/documents/swg_dengue_2.pdf (accessed on 7 March 2019).
- Choi, Y.; Tang, C.S.; McIve, L.; Hashizume, M.; Chan, V.; Abeyasinghe, R.R.; Iddings, S.; Huy, R. Effects of Weather Factors on Dengue Fever Incidence and Implications for Interventions in Cambodia. BMC Public Health 2016, 16. [Google Scholar] [CrossRef] [PubMed]




| Estimate | p-Value | |
|---|---|---|
| Intercept | 12.89567 | 0.1848 |
| Average Temperature | −0.53593 | 0.0622 |
| Rainfall | −0.00518 | 0.0114 |
| Average Relative Humidity | 0.03913 | 0.6518 |
| Estimate | p-Value | |
|---|---|---|
| Intercept | −1.26622 | 0.00085 |
| Rainfall | 0.00666 | 0.00024 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chandrakantha, L. Risk Prediction Model for Dengue Transmission Based on Climate Data: Logistic Regression Approach. Stats 2019, 2, 272-283. https://doi.org/10.3390/stats2020021
Chandrakantha L. Risk Prediction Model for Dengue Transmission Based on Climate Data: Logistic Regression Approach. Stats. 2019; 2(2):272-283. https://doi.org/10.3390/stats2020021
Chicago/Turabian StyleChandrakantha, Leslie. 2019. "Risk Prediction Model for Dengue Transmission Based on Climate Data: Logistic Regression Approach" Stats 2, no. 2: 272-283. https://doi.org/10.3390/stats2020021
APA StyleChandrakantha, L. (2019). Risk Prediction Model for Dengue Transmission Based on Climate Data: Logistic Regression Approach. Stats, 2(2), 272-283. https://doi.org/10.3390/stats2020021





