Negative Spatial Autocorrelation: One of the Most Neglected Concepts in Spatial Statistics
Abstract
1. Introduction
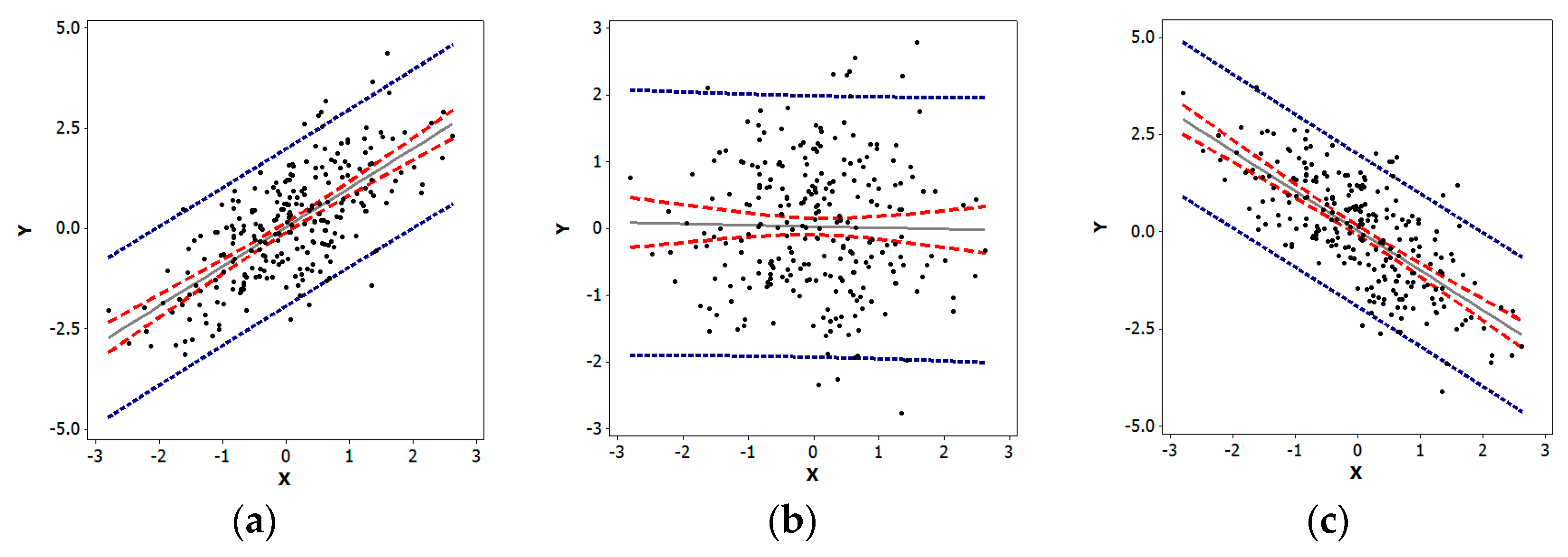
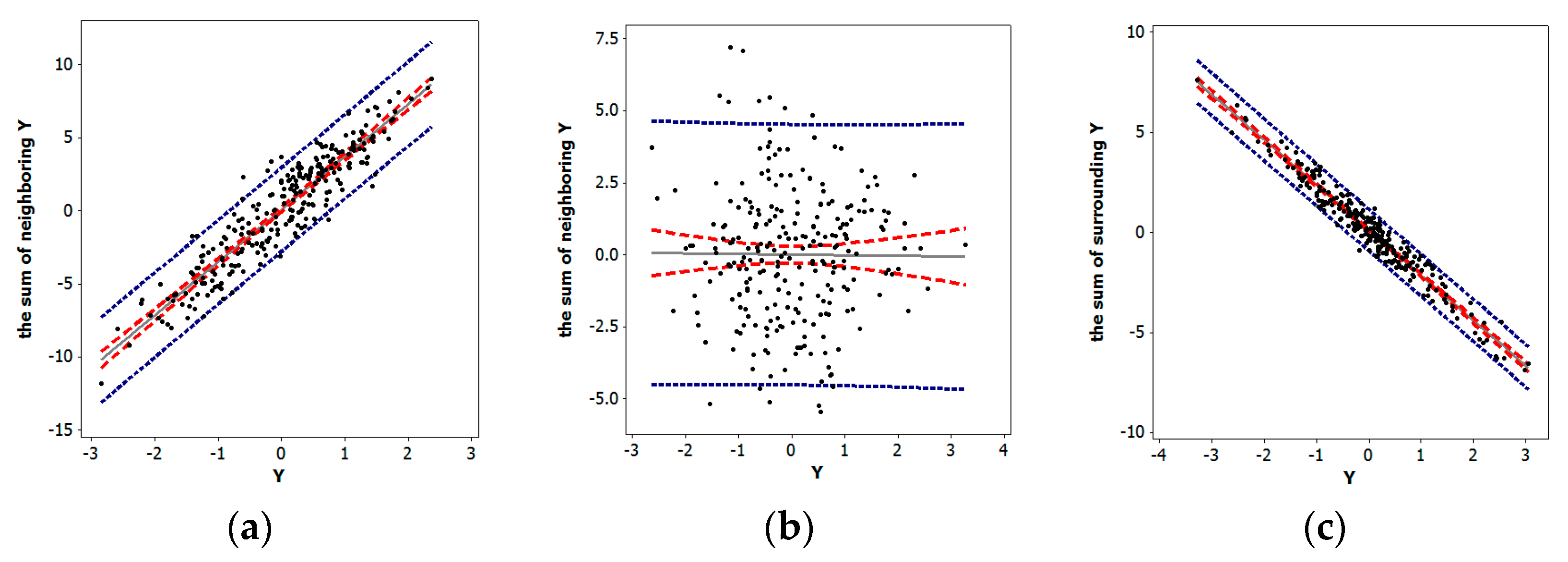
1.1. Visualizing Correlation
1.2. What Is Special About Negative Correlation?
- Linear regression residuals are negatively correlated;
- Multinomial indicator variables yield a correlation matrix with all negative off-diagonal entries;
- Positively skewed independent variables have a strong tendency to display negative bivariate correlation;
- Negatively correlated replicates can reduce variance in simulation experiments; and,
- Negative bivariate correlation can be relative.
| 1.00 | −0.10 | −0.19 | −0.14 | −0.14 | −0.14 | −0.17 | −0.17 | −0.10 | −0.19 | −0.17 | −0.10 | −0.14 | −0.24 | −0.35 | −0.35 | −0.41 |
| −0.10 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | 0.00 | −0.01 | −0.01 | 0.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 |
| −0.19 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.01 | −0.01 | −0.01 | −0.02 | −0.03 | −0.03 | −0.03 |
| −0.14 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.02 | −0.02 |
| −0.14 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.02 | −0.02 |
| −0.14 | −0.01 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.02 | −0.02 |
| −0.17 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.03 | −0.03 | −0.03 |
| −0.17 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.03 | −0.03 | −0.03 |
| −0.10 | 0.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 |
| −0.19 | −0.01 | −0.02 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.02 | −0.03 | −0.03 | −0.03 |
| −0.17 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.02 | −0.03 | −0.03 | −0.03 |
| −0.10 | 0.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.00 | −0.01 | −0.01 | 1.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 |
| −0.14 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | 1.00 | −0.01 | −0.02 | −0.02 | −0.02 |
| −0.24 | −0.01 | −0.02 | −0.01 | −0.01 | −0.01 | −0.02 | −0.02 | −0.01 | −0.02 | −0.02 | −0.01 | −0.01 | 1.00 | −0.04 | −0.04 | −0.04 |
| −0.35 | −0.01 | −0.03 | −0.02 | −0.02 | −0.02 | −0.03 | −0.03 | −0.01 | −0.03 | −0.03 | −0.01 | −0.02 | −0.04 | 1.00 | −0.05 | −0.06 |
| −0.35 | −0.01 | −0.03 | −0.02 | −0.02 | −0.02 | −0.03 | −0.03 | −0.01 | −0.03 | −0.03 | −0.01 | −0.02 | −0.04 | −0.05 | 1.00 | −0.06 |
| −0.41 | −0.02 | −0.03 | −0.02 | −0.02 | −0.02 | −0.03 | −0.03 | −0.02 | −0.03 | −0.03 | −0.02 | −0.02 | −0.04 | −0.06 | −0.06 | 1.00 |
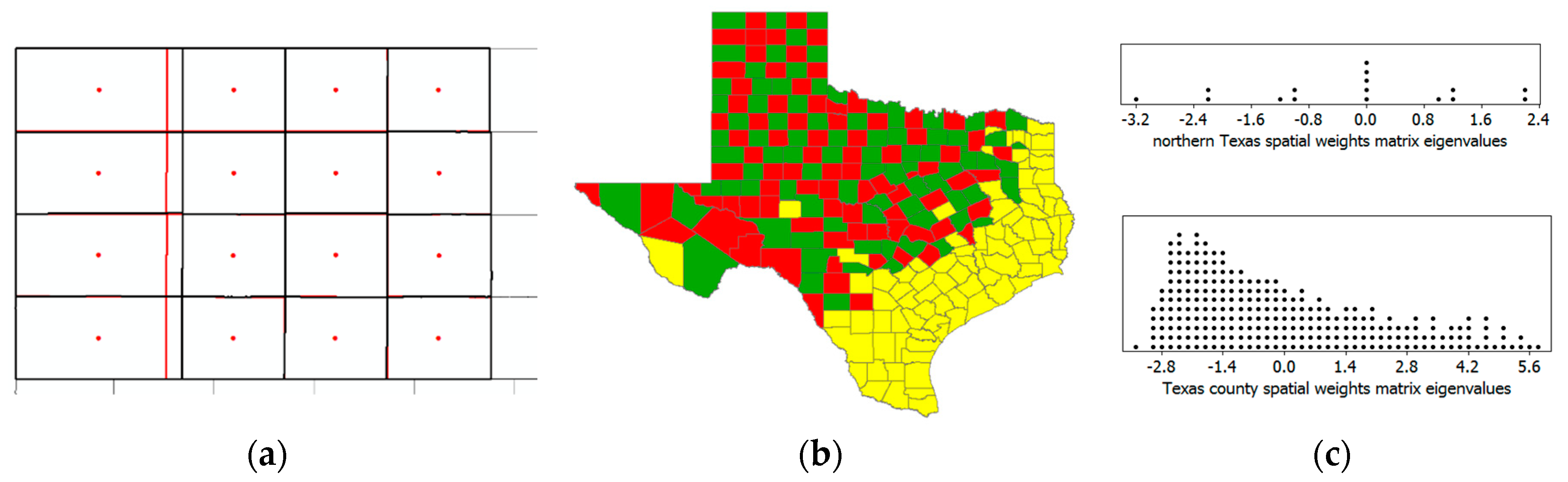
1.3. What Is Special About NSA?
- NSA manifestations differ between discrete and continuous geographic space;
- NSA links to spatial competition;
- Common spatial autocorrelation indices tend to gauge NSA on a scale shorter than [−1,0];
- Extreme NSA supports the fast calculation of the extreme eigenvalues of certain matrices;
- The boundary between PSA and NSA for the MC is zero rather than some small negative value; and,
- NSA often mixes with PSA, which tends to mask its existence.
2. A Brief Overview of Moran Eigenvector Spatial Filtering (MESF)
3. Selected Case Studies Demonstrating the Presence and Importance of NSA
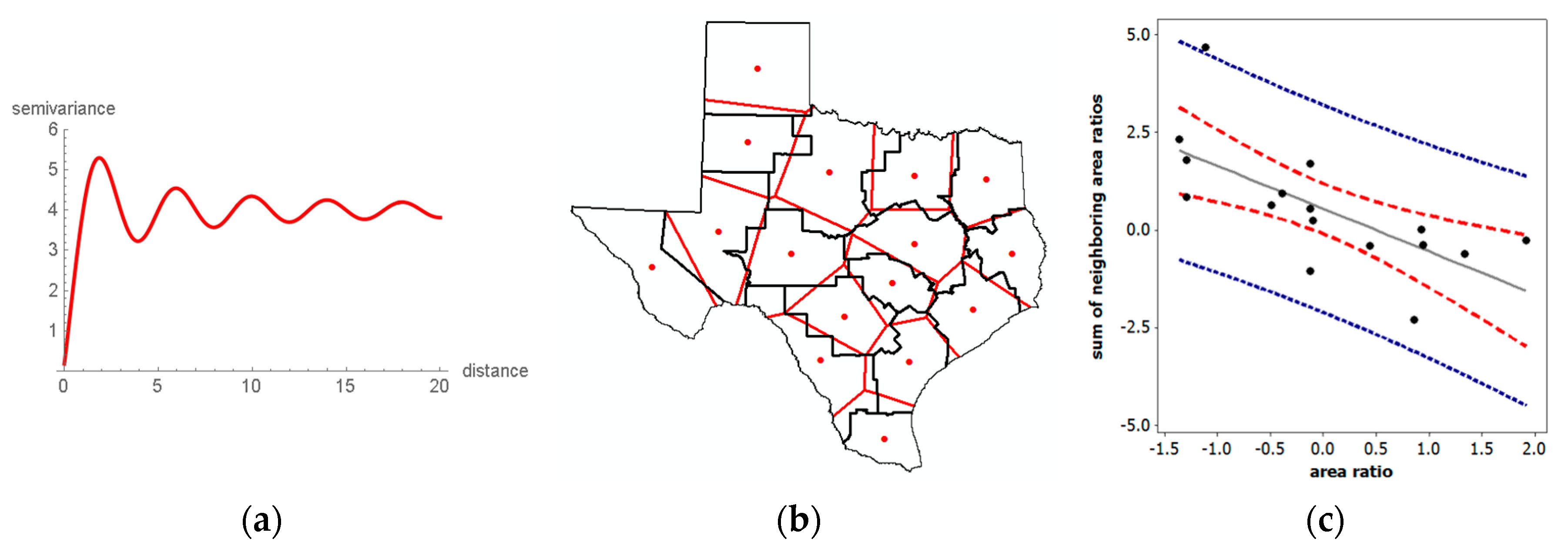
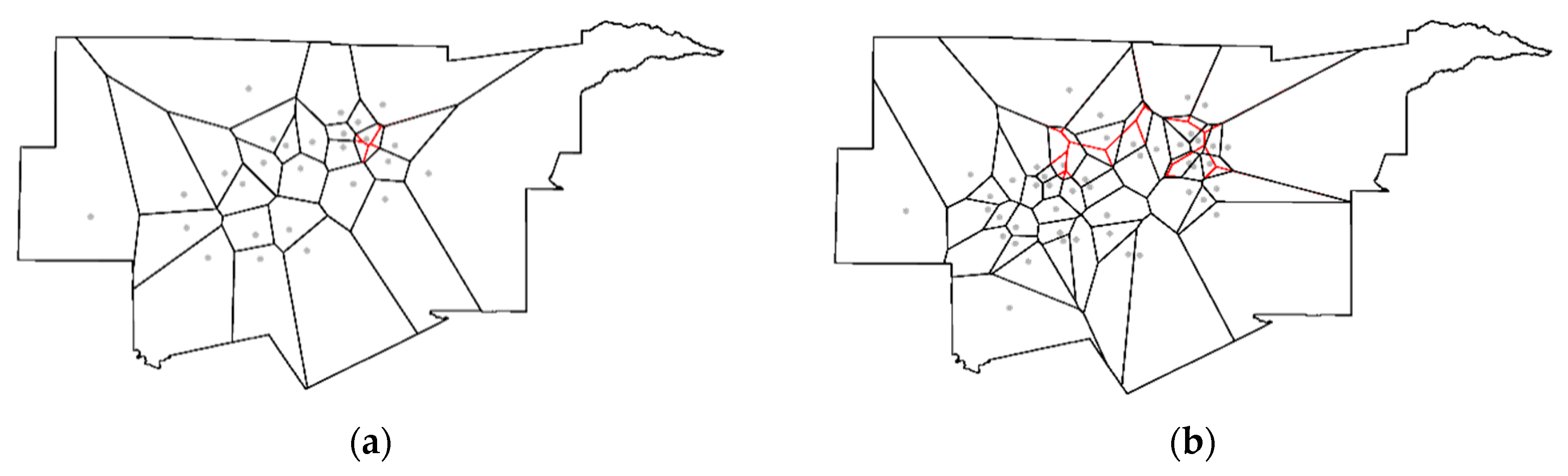
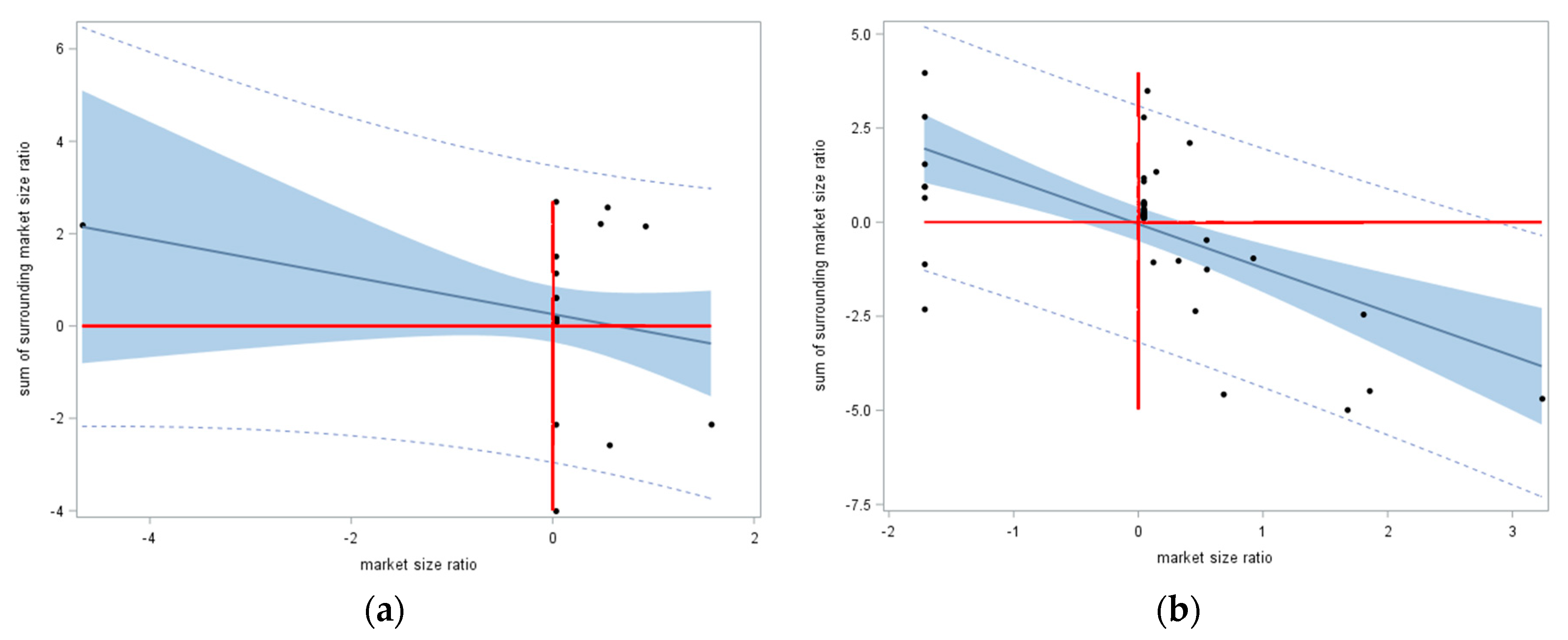
3.1. Market Area Competition: NSA and Facility Closures
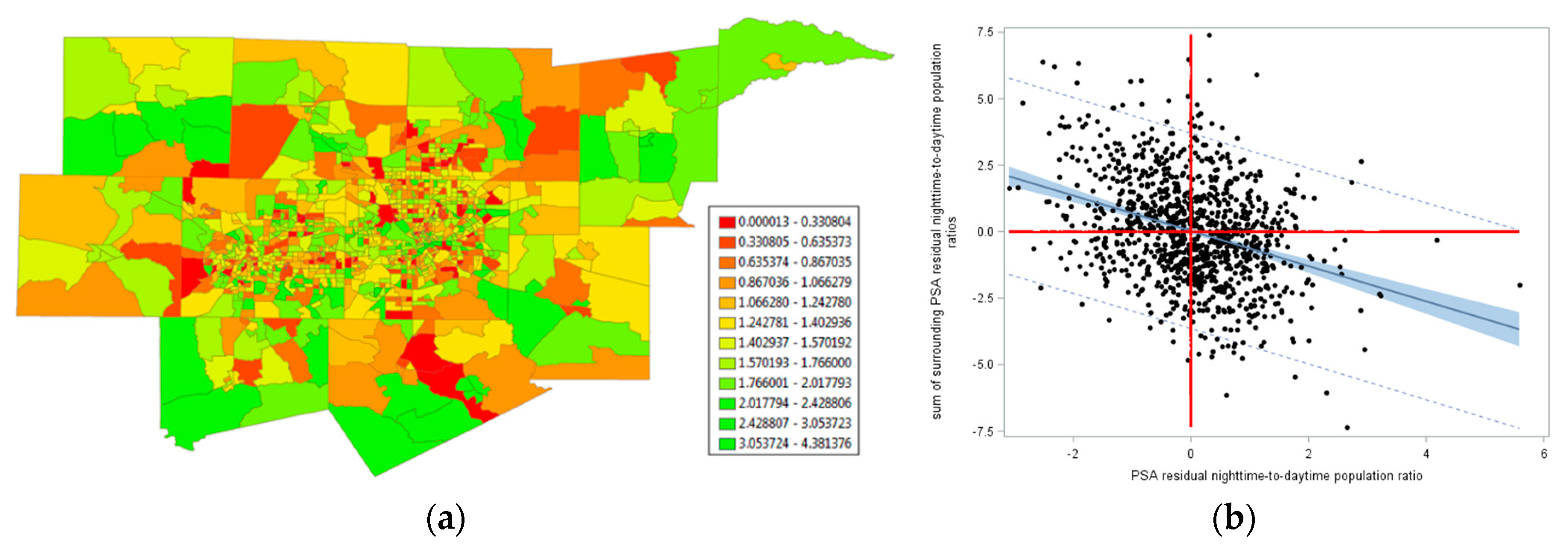
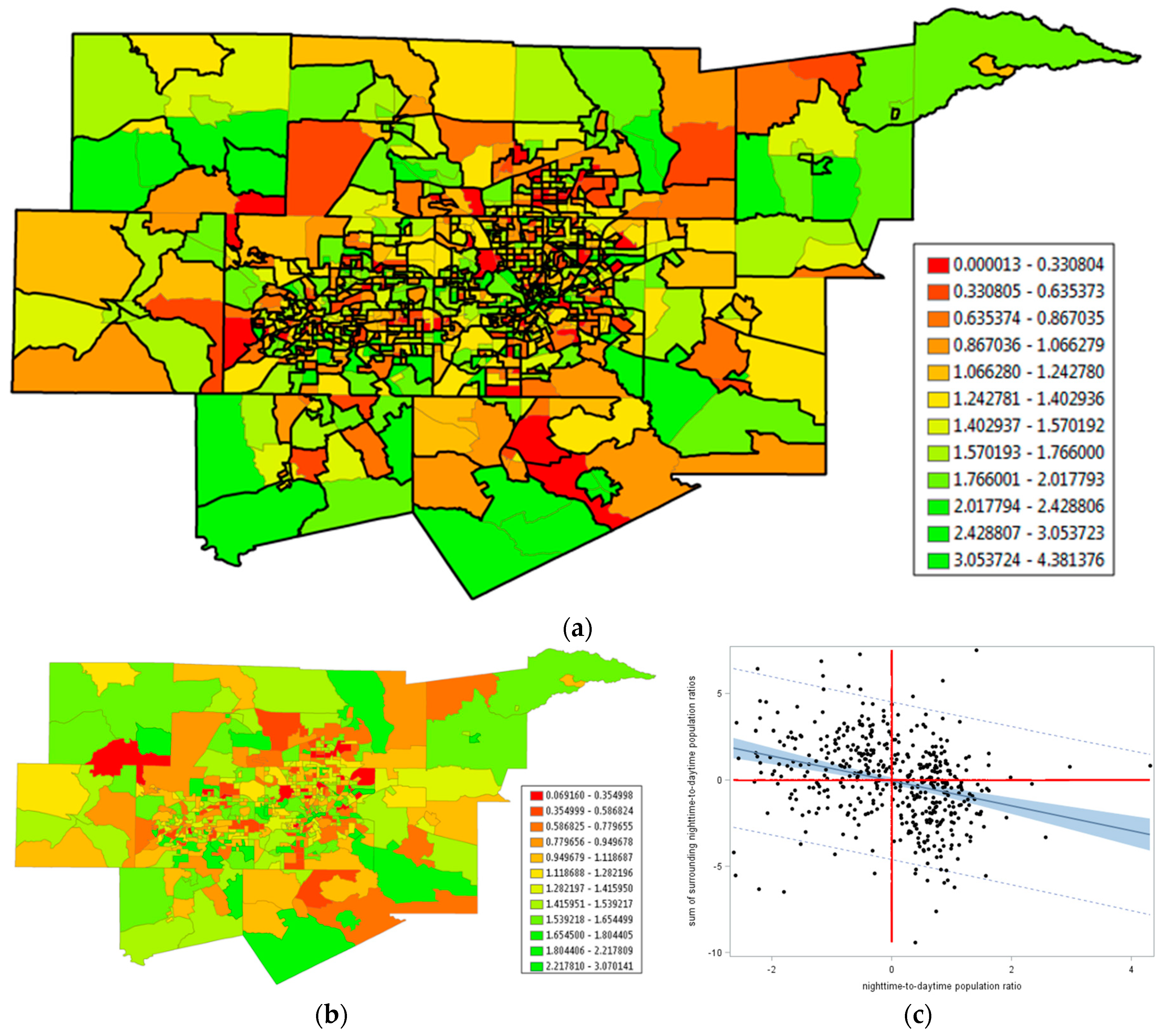
3.2. Journey-To-Work: Shifts In Daytime and Nighttime Populations
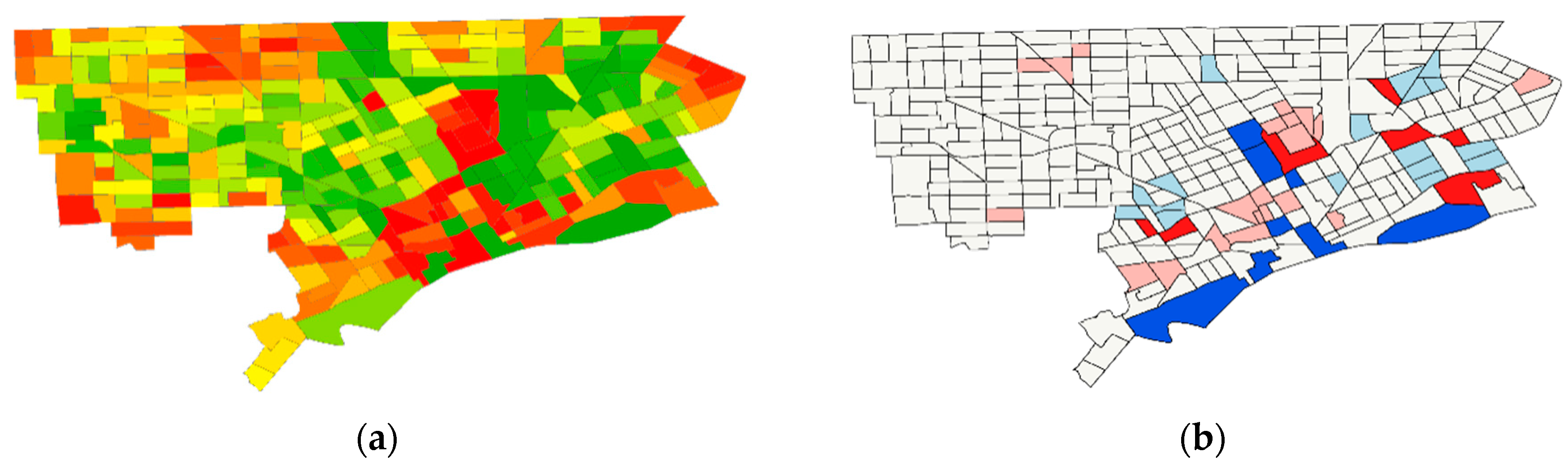
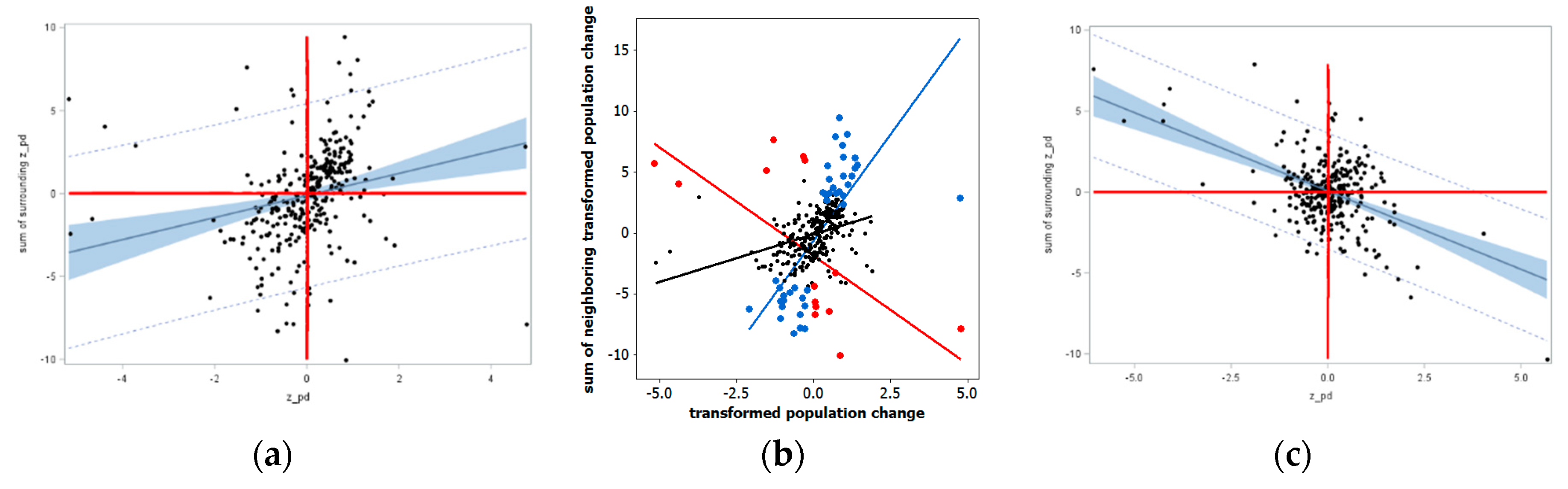
3.3. Urban Area Shrinkage
3.4. 1990. Homicide Rates in the US South Revisited
4. Conclusions; Lessons Learned, and Implications
- Developing appropriate quantification modifications that transform NSA index scales to the interval [−1, 0);
- Evaluating the impact of different definitions of spatial weights (e.g., topological adjacency, distance, and nearest neighbors), as well as distance standardization [33], on a resulting NSA value;
- Devising general map pattern descriptions for different degrees of NSA (paralleling the global, regional, and local descriptors for PSA);
- Revisiting various data analytic features that entail a change of studied variables (e.g., denominators of rates and populations at risk);
- Articulating relationships between NSA and both geographic scale and resolution, as suggested by the geostatistical wave-hole semi-variogram model and this paper’s aggregation experimental results for Detroit;
- Seeking an informed answer to the question asking whether or not areal unit polygons should be designed to mask or accentuate NSA;
- Addressing repeatability and replicability of findings by investigating case studies beyond Detroit, the DFW MSA, and the US South with exploratory spatial statistical analysis of other geographic landscapes to see if they, too, exhibit NSA;
- Expanding findings about the full range of geographic flows beyond the DFW MSA journey-to-work analysis presented here;
- Relating MC values in the cross-validation type close-one-store scenario to individual outlet attributes;
- Replacing Thiessen polygons with Huff probabilities in market area competition analyses;
- Establishing the range of PSA–NSA mixtures, and further explicating the notion of hidden NSA;
- Assessing the range of geographic variance accounted for by NSA, specifically to ascertain whether or not 10% is common, and 25% is exceptional;
- Comprehensively evaluating the strategy of separately estimating ESFPSA and ESFNSA components;
- Confirming more cases where ignoring NSA results in specification error;
- Determining the phantom/search degrees of freedom for a given nature and degree of spatial autocorrelation; and,
- Formulating a better understanding of effective geographic sample size as it relates to phantom/search degrees of freedom.
Funding
Acknowledgments
Conflicts of Interest
Appendix A. About PSA-NSA Mixtures and MESF Eigenvector Selection
| Geographic Landscape | Detroit | DFW MSA |
|---|---|---|
| Standardized response variable variance | 1 | 1 |
| SAR residual variance | 0.69799 | 0.86834 |
| ESF residual variance | 129.69892/(308 − 1 − 48) | 276.43766/(472 − 1 − 51) |
| Estimated search degrees of freedom | 73 | 102 |
| Corrected ESF residual variance | 0.69731 | 0.86930 |
| LASSO based ESF residual variance | 0.68271 | 0.90344 |
| H0 Probability | <0.0001 | 0.0001–0.0050 | 0.0050–0.0100 | 0.0100–0.0500 | 0.0500–0.1000 |
|---|---|---|---|---|---|
| PSA | |||||
| Detroit | 4 (2;1) | 6 (7;6) | 0 (1;2) | 8 (8;3) | 5 (5;6) |
| DFW MSA | 0 (0;0) | 0 (0;0) | 0 (0;0) | 10 (9;2) | 6 (7;7) |
| US South | 24 | 41 | 10 | 27 | 8 |
| NSA | |||||
| Detroit | 2 (0;0) | 2 (2;2) | 1 (2;1) | 11 (12;7) | 9 (9;6) |
| DFW MSA | 1 (1;1) | 11 (4;1) | 6 (6;3) | 14 (20;17) | 3 (4;9) |
| US South | 7 | 43 | 9 | 38 | 5 |
| Statistic | Candidate set Size | ||||||
|---|---|---|---|---|---|---|---|
| α = 0.005 | |||||||
| Detroit | −0.000 (−0.223, 0.207) | 0.999 (0.833, 1.156) | 0.548 (0.1001, 0.9998) | 1.228 (0, 10) | 80 + 135 = 215 | 0.037 (0, 0.263) | 1.015 (1.007, 1.075) |
| DFW | 0.001 (−0.171, 0.175) | 1.000 (0.872, 1.121) | 0.545 (0.1000, 0.9999) | 1.701 (0, 10) | 105 + 193 = 298 | 0.034 (0, 0.180) | 1.012 (1.004, 1.043) |
| US South | 0.000 (−0.097, 0.109) | 0.999 (0.932, 1.071) | 0.543 (0.1002, 0.9995) | 5.903 (0, 17) | 352 + 662 = 1,014 | 0.039 (0.017, 0.107) | 1.010 (1.001, 1.035) |
| α = 0.010 | |||||||
| Detroit | 0.000 (−0.219, 0.197) | 0.999 (0.844, 1.142 | 0.546 (0.1002, 0.9999) | 2.690 (0, 13) | 80 + 135 = 215 | 0.070 (0, 0.292) | 1.025 (1.007, 1.100) |
| DFW | −0.000 (−0.183, 0.176) | 0.999 (0.891, 1.113) | 0.547 (0.1001, 0.9997) | 3.618 (0, 15) | 105 + 193 = 298 | 0.062 (0, 0.242) | 1.020 (1.004, 1.074) |
| US South | −0.000 (−0.100, 0.091) | 1.000 (0.932, 1.068) | 0.542 (0.1001, 0.9999) | 12.870 (1, 30) | 352 + 662 = 1,014 | 0.073 (0.005, 0.164) | 1.020 (1.003, 1.047) |
Appendix B. The Geographic Distribution of the Spatial Means of the Census Tract Centroids

References
- Griffith, D. Better articulating normal curve theory for introductory mathematical statistics students: power transformations and their back-transformations. Am. Stat. 2013, 67, 157–169. [Google Scholar] [CrossRef]
- Hodges, J.; Reich, B. Adding spatially-correlated errors can mess up the fixed effect you love. Am. Stat. 2010, 64, 325–334. [Google Scholar] [CrossRef]
- Griffith, D. Hidden negative spatial autocorrelation. J. Geogr. Syst. 2006, 8, 335–355. [Google Scholar] [CrossRef]
- Griffith, D.; Arbia, G. Detecting negative spatial autocorrelation in georeferenced random variables. Int. J. Geogr. Inf. Sci. 2010, 24, 417–437. [Google Scholar] [CrossRef]
- Antczak, E. Building W matrices using selected geostatistical tools: Empirical examination and application. Stats 2018, 1, 112–133. [Google Scholar] [CrossRef]
- Beardsley, E. Tendency toward negative correlations for positively skewed independent random variables. J. Hydrol. N. Z. 2014, 53, 175–177. [Google Scholar]
- Ladson, T. Spurious Correlation between Skewed Independent Variables. 2015. Available online: https://tonyladson.wordpress.com/2015/03/17/spurious-correlation-between-skewed-independent-variables/ (accessed on 24 May 2019).
- Hammersley, K.; Morton, J. A new Monte Carlo technique: Antithetic variates. Proc. Camb. Philos. Soc. 1956, 52, 449–475. [Google Scholar] [CrossRef]
- Saliby, E.; Paul, R. A farewell to the use of antithetic variates in Monte Carlo simulation. J. Oper. Res. Soc. 2009, 60, 1026–1035. [Google Scholar] [CrossRef]
- Wu, T.; Mather, D.; Dutilleul, P. Application of geostatistical and neighbor analyses to data from plant breeding trials. Crop Sci. 1998, 38, 1545–1553. [Google Scholar] [CrossRef]
- Griffith, D.; Wong, D.; Whitfield, T. Exploring relationships between the global and regional measures of spatial autocorrelation. J. Reg. Sci. 2003, 43, 683–710. [Google Scholar] [CrossRef]
- Chun, Y.; Griffith, D. Impacts of negative spatial autocorrelation on frequency distributions. Chil. J. Stat. 2018, 9, 3–17. [Google Scholar]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. B 1974, 36, 192–225. [Google Scholar] [CrossRef]
- Cressie, N. Geostatistics. Am. Stat. 1989, 43, 197–202. [Google Scholar]
- Mead, R. Measurements of competition between individual plants in a population. J. Ecol. 1968, 56, 35–45. [Google Scholar] [CrossRef]
- Griffith, D. Eigenfunction properties and approximations of selected incidence matrices employed in spatial analyses. Linear Algebra Appl. 2000, 321, 95–112. [Google Scholar] [CrossRef]
- Griffith, D.; Bivand, R.; Chun, Y. Implementing approximations to extreme eigenvalues and eigenvalues of irregular surface partitionings for use in SAR and CAR Models. Procedia Environ. Sci. 2015, 26, 119–122. [Google Scholar] [CrossRef]
- Kao, Y.-H. Three Essays on Spatial Econometrics with an Emphasis on Testing. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2016. Unpublished doctoral dissertation. [Google Scholar]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Griffith, D.; Chun, Y. Spatial autocorrelation and spatial filtering. In Handbook of Regional Science; Fischer, M., Nijkamp, P., Eds.; Springer: Berlin, Germany, 2014; pp. 1477–1507. [Google Scholar]
- Hughes, J.; Haran, M. Dimension reduction and alleviation of confounding for spatial generalized linear mixed models. J. R. Stat. Soc. Ser. B 2013, 75, 139–159. [Google Scholar] [CrossRef]
- Borcard, D.; Legendre, P. All-scale spatial analysis of ecological data by means of principal coordinates of neighbour matrices. Ecol. Model. 2002, 153, 51–68. [Google Scholar] [CrossRef]
- Griffith, D. Spatial Autocorrelation and Spatial Filtering: Gaining Understanding through Theory and Scientific Visualization; Springer: Berlin, Germany, 2003. [Google Scholar]
- Griffith, D.; Peres-Neto, P. Spatial modeling in ecology: The flexibility of eigenfunction spatial analyses. Ecology 2006, 87, 2603–2613. [Google Scholar] [CrossRef]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–59. [Google Scholar] [CrossRef]
- Schelling, T. Models of segregation. Am. Econ. Rev. 1969, 59, 488–493. [Google Scholar]
- Schelling, T. Dynamic models of segregation. J. Math. Sociol. 1971, 1, 143–186. [Google Scholar] [CrossRef]
- Traun, C.; Loidl, M. Autocorrelation-based regioclassification—A self-calibrating classification approach for choropleth maps explicitly considering spatial autocorrelation. Int. J. Geogr. Inf. Sci. 2012, 26, 923–939. [Google Scholar] [CrossRef]
- Weaver, R.; Bagchi-Sen, S.; Knight, J.; Frazier, A. Shrinking Cities: Understanding Urban Decline in the United States; Routledge: London, UK, 2017. [Google Scholar]
- Manly, B. Exponential data transformations. J. R. Stat. Soc. Ser. D 1976, 25, 37–42. [Google Scholar] [CrossRef]
- Baller, R.; Anselin, L.; Messner, S.; Deane, G.; Hawkins, D. Structural covariates of U.S. County homicide rates: Incorporating spatial effects. Criminology 2001, 39, 561–588. [Google Scholar] [CrossRef]
- Diggle, P.; Milne, R. Negative binomial quadrat counts and point processes. Scand. J. Stat. 1983, 10, 257–267. [Google Scholar]
- Souris, M.; Demoraes, F. Improvement of spatial autocorrelation, kernel estimation and modeling methods by spatial standardization on distance. Int. J. Geo Inf. 2019, 8, 199. [Google Scholar] [CrossRef]
- Babyak, M. What you see may not be what you get: A brief, nontechnical introduction to overfitting in regression-type models. Psychosom. Med. 2004, 66, 411–421. [Google Scholar]
- Tibshirani, R. Degrees of freedom and model search. Stat. Sin. 2015, 25, 1265–1296. [Google Scholar] [CrossRef]
- Griffith, D. Effective geographic sample size in the presence of spatial autocorrelation. Ann. Am. Assoc. Geogr. 2005, 95, 740–760. [Google Scholar] [CrossRef]
- Chun, Y.; Griffith, D.; Lee, M.; Sinha, P. Eigenvector selection with stepwise regression techniques to construct eigenvector spatial filters. J. Geogr. Syst. 2016, 18, 67–85. [Google Scholar] [CrossRef]
- Freedman, L.; Pee, D.; Midthune, D. The problem of underestimating the residual error variance in forward stepwise regression. J. R. Stat. Soc. Ser. D (Stat.) 1992, 41, 405–412. [Google Scholar] [CrossRef]
- Blanchet, F.; Legendre, P.; Maranger, R.; Monti, D.; Pepin, P. Modelling the effect of directional spatial ecological processes at different scales. Oecologia 2011, 166, 357–368. [Google Scholar] [CrossRef] [PubMed]



| Random Variable | Parameters | Skewness | n | % of r < 0 Batches | Average % of r < 0 |
|---|---|---|---|---|---|
| exponential | λ = 1 | 2.00 | 100 | 92 | 52.2 |
| 500 | 77 | 51.2 | |||
| 1000 | 70 | 50.9 | |||
| beta | α = 0.3, β = 25 | 3.39 | 100 | 100 | 56.0 |
| gamma | α = 0.1, β = 1 | 4.47 | 100 | 100 | 59.0 |
| log-normal | μ =0, σ2 = 1 | 6.18 | 100 | 100 | 56.0 |
| Weibull | λ = 0.25, κ = 1 | 60.09 | 100 | 100 | 75.0 |
| 500 | 100 | 73.0 | |||
| 1000 | 100 | 72.0 |
| Store ID | MC | MC/|MCmin | Prob (H0) | Store ID | MC | MC/|MCmin| | Prob (H0) |
|---|---|---|---|---|---|---|---|
| 1 | −0.206 | −0.383 | 0.091 | 14 | −0.181 | −0.336 | 0.129 |
| 2 | −0.250 | −0.465 | 0.045 | 15 | −0.136 | −0.253 | 0.219 |
| 3 | −0.280 | −0.520 | 0.027 | 16 | −0.205 | −0.381 | 0.092 |
| 4 | −0.225 | −0.418 | 0.068 | 17 | −0.311 | −0.578 | 0.014 |
| 5 | −0.195 | −0.362 | 0.106 | 18 | −0.243 | −0.452 | 0.051 |
| 6 | −0.213 | −0.396 | 0.082 | 19 | −0.230 | −0.428 | 0.062 |
| 7 | −0.215 | −0.400 | 0.079 | 21 | −0.250 | −0.465 | 0.045 |
| 8 | −0.217 | −0.403 | 0.077 | 22 | −0.159 | −0.296 | 0.170 |
| 9 | −0.236 | −0.439 | 0.057 | 23 | −0.233 | −0.433 | 0.060 |
| 10 | −0.269 | −0.500 | 0.033 | 24 | −0.202 | −0.375 | 0.095 |
| 11 | −0.284 | −0.528 | 0.024 | 25 | −0.276 | −0.513 | 0.028 |
| 12 | −0.200 | −0.372 | 0.098 | 26 | −0.148 | −0.275 | 0.192 |
| 13 | −0.252 | −0.468 | 0.044 | 27 | −0.183 | −0.340 | 0.125 |
| Covariate | Model Specification | ||||
|---|---|---|---|---|---|
| Normal Approximation | Poisson | NB | NB + ESFPSA | Poisson + ESFPSA & ESFNSA | |
| Resource deprivation/affluence | 0.4239 * | 0.5250 * | 0.4649 * | 0.4733 * | 0.4937 * |
| Population size/density | 0.0806 * | 0.3003 * | 0.2108 * | 0.1825 * | 0.2095 * |
| Median age | −0.0035 * | −0.0104 * | −0.0020 * | −0.0005 * | −0.0015 * |
| Divorce rate | 0.0453 * | 0.0632 * | 0.0588 * | 0.0840 * | 0.0765 * |
| Unemployment rate | −0.0591 * | −0.0731 * | −0.0536 * | −0.0372 * | −0.0463 * |
| Deviance statistic | 3.1343 | 1.0926 | 1.1897 | 1.0874 | |
| Over-dispersion parameter | 0.1064 | 0.0256 | 0.0000 | ||
| (Pseudo)-R2 | 0.281 | 0.311 | 0.308 | 0.476 | 0.596 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Griffith, D.A. Negative Spatial Autocorrelation: One of the Most Neglected Concepts in Spatial Statistics. Stats 2019, 2, 388-415. https://doi.org/10.3390/stats2030027
Griffith DA. Negative Spatial Autocorrelation: One of the Most Neglected Concepts in Spatial Statistics. Stats. 2019; 2(3):388-415. https://doi.org/10.3390/stats2030027
Chicago/Turabian StyleGriffith, Daniel A. 2019. "Negative Spatial Autocorrelation: One of the Most Neglected Concepts in Spatial Statistics" Stats 2, no. 3: 388-415. https://doi.org/10.3390/stats2030027
APA StyleGriffith, D. A. (2019). Negative Spatial Autocorrelation: One of the Most Neglected Concepts in Spatial Statistics. Stats, 2(3), 388-415. https://doi.org/10.3390/stats2030027





