Stylometry and Numerals Usage: Benford’s Law and Beyond

Abstract

We suggest two approaches to the statistical analysis of texts, both based on the study of numerals occurrence in literary texts. The first approach is related to Benford’s Law and the analysis of the frequency distribution of various leading digits of numerals contained in the text. In coherent literary texts, the share of the leading digit 1 is even larger than prescribed by Benford’s Law and can reach 50 percent. The frequencies of occurrence of the digit 1, as well as, to a lesser extent, the digits 2 and 3, are usually a characteristic the author’s style feature, manifested in all (sufficiently long) literary texts of any author. This approach is convenient for testing whether a group of texts has common authorship: the latter is dubious if the frequency distributions are sufficiently different. The second approach is the extension of the first one and requires the study of the frequency distribution of numerals themselves (not their leading digits). The approach yields non-trivial information about the author, stylistic and genre peculiarities of the texts and is suited for the advanced stylometric analysis. The proposed approaches are illustrated by examples of computer analysis of the literary texts in English and Russian.

1. Introduction

Benford’s Law [1]—a strange manifestation of the law of large numbers (understood as the combined action of a large number of random factors leading to a result that is almost independent of the case)—is sometimes rightfully called curious, surprising and mysterious [2,3]. There is still no complete understanding of why some data sets obey this law, while others do not. The famous Hill’s theorem [4], which gives sufficient conditions for the appearance of Benford’s Law, does not give the necessary ones nor the insight into why and when Benford’s Law applies.

Incomplete understanding does not prevent the emergence of more and more proposals for the practical use of Benford’s Law in a wide area of sciences from geodesy [5] and geology [6] through genomics [7] and ecology [8,9] to scientometrics [10].

The primary goal of these attempts is to detect various falsifications (in a broad sense) and anomalies in data sets [11,12,13]. The questions addressed extends from the possibility of finding the Dyson spheres (presumably built by advanced civilizations) through anomalies in the star emission spectra to the prosaic falsifications of election results [14,15] and financial statements. In the USA, evidence based on Benford’s Law [16] has been admitted in criminal cases of financial fraud at the federal, state, and local levels. The Internal Revenue Service of the US federal government, which is responsible for collecting taxes, has been using it for decades to ferret out fraudsters.

We deliberately discard the extensive bibliography devoted to the application of Benford’s Law in various sciences, as there is an excellent, constantly updated website https://benfordonline.net/ (accessed on 10 October 2021).

In our work, we will review the works related to the analysis of numerals contained in texts in connection with Benford’s Law and present our original approach to this topic, as well as some results obtained in the framework of this approach.

The present study pertains to the scope of stylometry (statistical study of texts to find the individual peculiarities of the author’s style and, in particular, for the texts attribution). In turn, stylometry is an integral part of quantitative and, more generally, mathematical linguistics.

The work is heuristic by nature and does not aim at theoretical justification of the results (if that is even possible), which, however, does not detract from the possibility of applying the proposed methodology for stylometry tasks.

2. Benford’s Law and Texts

There have been few attempts to link Benford’s Law with text data analysis. The first belongs to Benford himself. In his classic work [1], he analyzed

• Arabic numbers (not spelled out) of consecutive front-page news items of a newspaper. “Dates were barred as not being variable, and the omission of spelled-out numbers restricted the counted digits to numbers 10 and over”;
• The first 342 street addresses given in an American Men of Science edition;
• Numeral usage (except for dates and page numbers) of an issue of the Readers’ Digest.

Benford stated that fully random data (the first and second items) had an excellent agreement with the “logarithmic law” (As we now know, it may be explained by Hill’s theorem [4]), and the third item was also in agreement with it.

An excellent introduction to Benfordology in general and to the analysis of the use of numerals in texts is contained in the paper by Hungerbühler [17]. The author studied the numerals found in the German translation of the Old and New Testaments and came to the conclusion that the distribution of their first significant digits is in good agreement with Benford’s Law. There is a noticeable difference only for two digits: 1 and 7. The author explained the excess of the share of 1 in comparison with that prescribed by Benford’s Law by two reasons:

(1)

Possible rounding of numerals starting with digits 8 and 9;

(2)

In German, the indefinite article ein coincides with the numeral ein.

The fact that the digit 7 occurs too often is explained by the biblical number symbolism in which this number occupies a dominant position.

By and large, this is all that was in the scientific literature about the analysis of the occurrence of numerals in texts in connection with Benford’s Law and in relation to stylometry problems in 2014, when our research in this area began [18]. (In papers [19,20], statistical patterns of texts have been studied, which have some, albeit remote, relation to the topic of our paper. In [19], the question is raised whether there are general patterns in different languages describing the shares of words starting with a certain letter. It is shown that when ordering these shares in descending order, their distribution resembles Benford’s, but better agreement can be achieved with the exponential distribution. For large texts written both in various human languages and in programming languages Java and C++, the total numbers of occurrence of a certain word give rise to the Benford-like distribution of their first significant digits [20]).

In contrast to Benford’s work [1],

• we take into account not only numerals expressed in digits but also those spelled (expressed verbally), both cardinal and ordinal ones—technically, a much more difficult task, especially for texts in languages in which the numerals are declined: Russian, Czech, Lithuanian, etc.;
• the object of our study is coherent literary texts (as well as compilations of such texts), not a random set of texts.

The specificity of the use of numerals in the literary text is the significant predominance of verbal numerals expression over a digital one. In the first case, we first transferred the numerals (in different word forms) into a digital record so that, for example, for the numeral seven hundred and fifty-third (753), only the first significant digit 7 was taken into account. To identify the author’s use of numerals, we previously deleted from the texts the idiomatic expressions and set expressions, accidentally containing numerals (“as clear as two and two makes four” or “to drink like seven lords”) and bullets: (1), (2), (3), etc. (Since it is not possible to decompose phraseological units into separate words without loss of general meaning, the numerals that are accidentally included in such expressions should not be taken into account. As for the list markers, they are similar to page numbers. They are not always established by the author himself (this may depend on editorial corrections) and are only a generally accepted system of designations and not a reflection of the author’s intention. In any case, deleted items (due to their comparative rarity) have little effect on the results).

Ironically, the object of our first publication [18] was also the sacred texts—the four canonical Gospels from Matthew, Mark, Luke and John in the Russian translation (during the research we did not yet know about Hungerbühler’s paper [17]). Our results:

• There are differences between the distributions (especially between the Gospels from Matthew, Mark, Luke on the one hand and that from John, on the other hand)—not very large, but statistically significant, given the amount of analyzed data.
• In general, the distribution of the first significant digit of numerals here also resembles Benford’s one, but the first significant digit 1 is noticeably predominant.
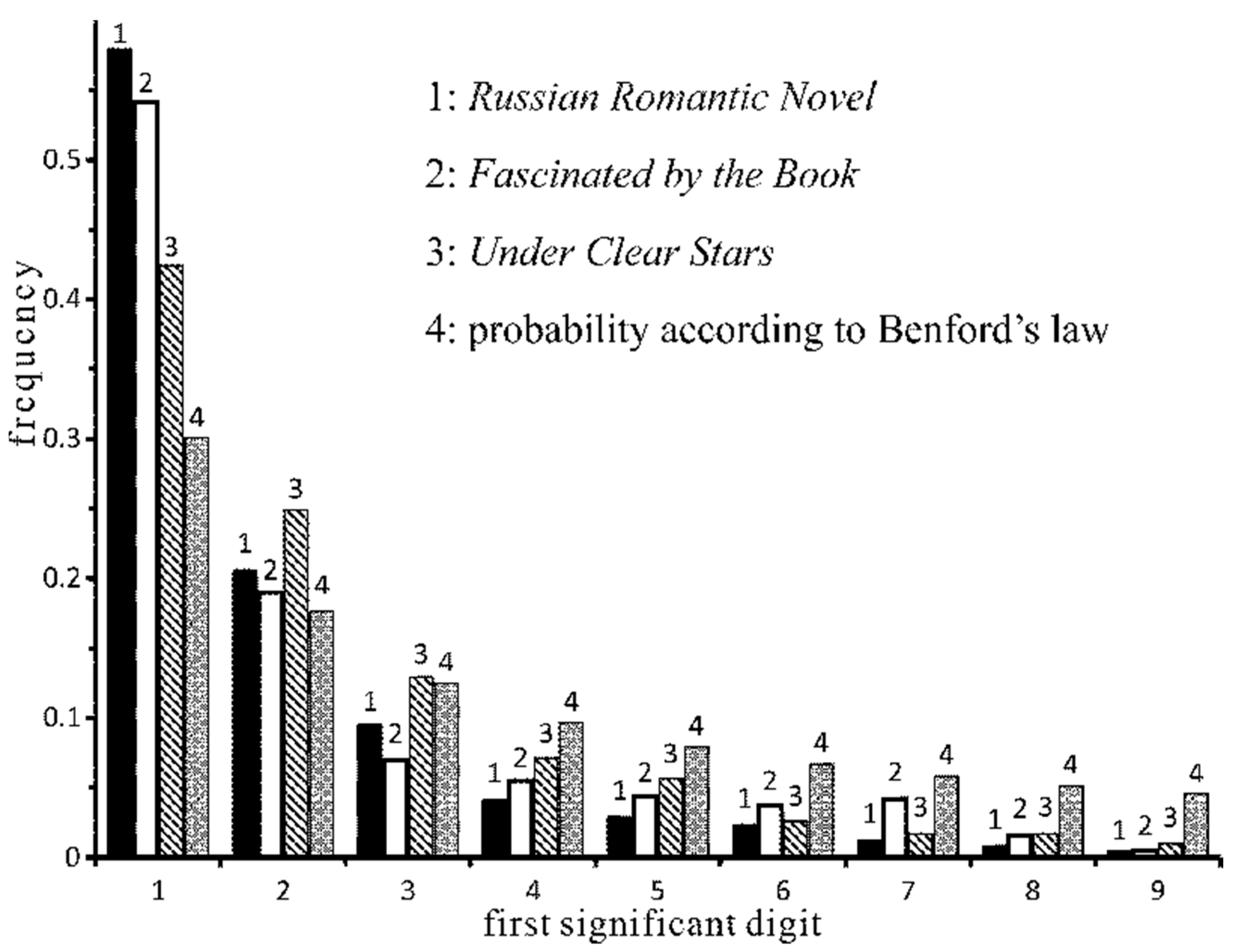
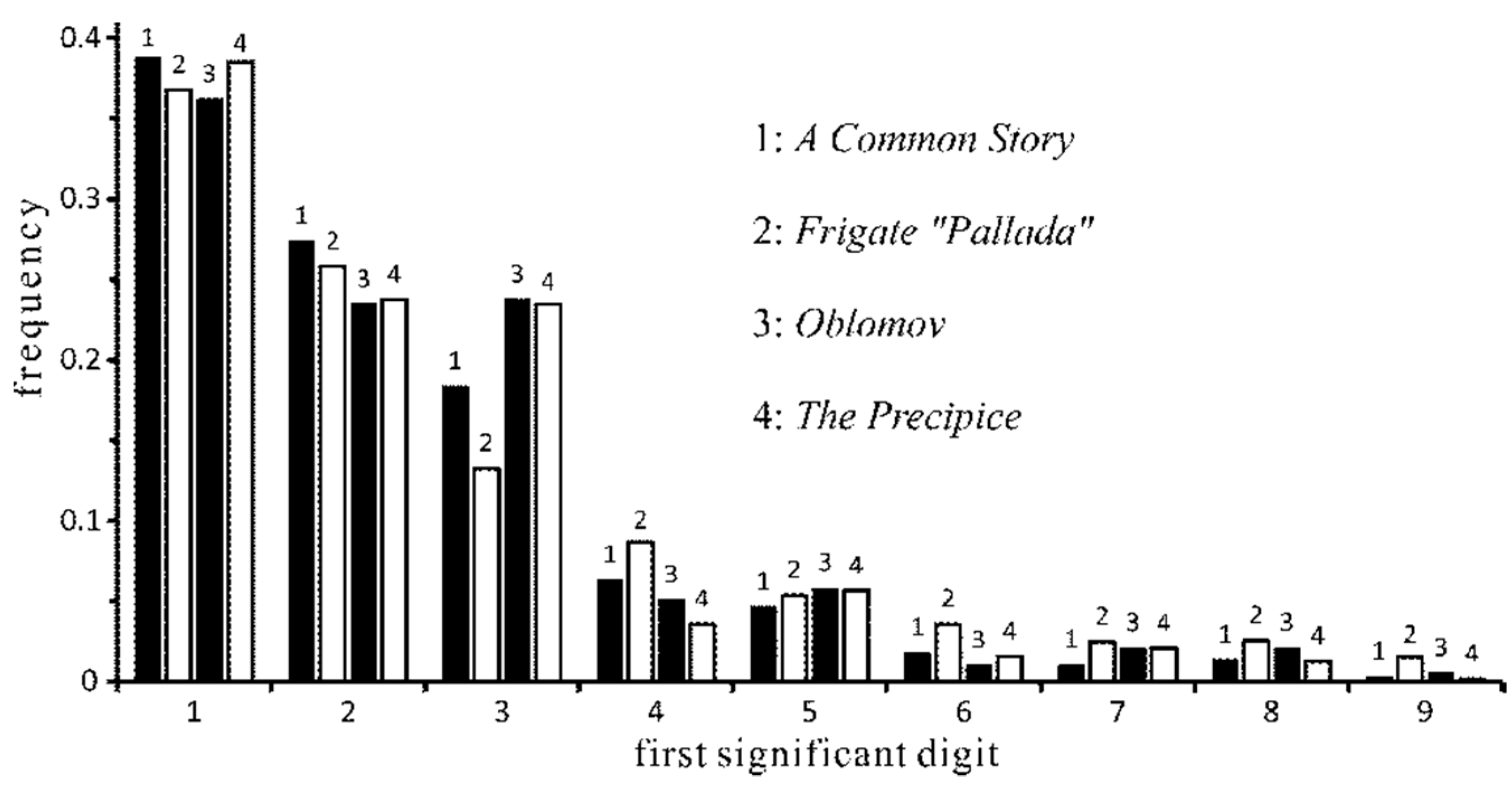
• It turned out that the share of the digit 1 is so much higher than prescribed by Benford’s Law (it varies from 38 to 45 percent instead of Benford’s 30 percent) that the distribution could be called ultra-Benfordian. As we later found out, this is typical for the coherent literary texts of most authors.

In the same paper [18], we analyzed the numerals occurrence in Julius Caesar’s Commentaries on the Gallic War (whose first seven books were written by Caesar, and the last, eighth, book by Hirtius) and Commentaries on the Civil War (written by Caesar alone). We started our research simply in the general direction of “putting yet another object to the test for Benfordness”, but the obtained results corrected our intentions and served as a starting point for stylometric research for several years:

Texts written by Caesar are characterized by a similar and abnormally low share of 1 as the first significant digit: it does not even reach Benford’s 30 percent (it later turned out that this phenomenon is not unique, although rare). In the part of the Commentaries on the Gallic War written by Hirtius, the share of one reaches 45 percent, more than twice Caesar’s value!

If the works by one author (Caesar), dedicated to different historical events, have similar distributions of first significant digits, and the text by another author (Hirtius) on the same topic as Caesar’s has a different distribution, then it becomes possible to distinguish the authorship of the texts by the features of the frequency distribution of first significant digits!

We summarized our first work with the following general conclusions:

• Benford’s Law approximately holds for coherent texts.
• Deviations from Benford’s Law are statistically significant author’s features that allow, under certain conditions, to distinguish between parts of the text with different authorship. The obvious requirements are the sufficient length of the text and the sufficient use of numerals in it, which, for example, is usually satisfied in historical literature.
• The distribution of the first significant digits at the end of the {1, 2,..., 7, 8, 9} row is subject to strong fluctuations (even in texts by the same author) and is not indicative.

In subsequent works, we refined and supplemented these conclusions [21].

• The frequencies of the first significant digits are stabilized for texts larger than 200 KB (the size of the txt file in UTF-8 encoding).
• We confirm the visual similarity/differences in the frequency distributions of the first significant digits by the Pearson chi-squared test; to apply it, we had to develop a special technique (for details, see [21]). Unfortunately, the standard procedure offered by statistical packages is not suitable here.

Below is an overview of some of our results that are simultaneously relevant to both Benford’s Law and stylometry. We deliberately have given our paper the horizontal structure, not a hierarchical one, since the topics discussed can hardly be subordinated.

When we analyze the texts of a particular author, we use all of his large texts for analysis. The texts of more than 40 authors in Russian, English, Czech, Lithuanian, and Turkish have already been analyzed within the framework of the presented methodology.

Benford’s Law and Texts: Overview of Results

2.1. Distribution of the First Significant Digits of the Numerals in Compiled Texts

The conditions of Hill’s theorem [4] are best fulfilled for compiled texts consisting of fragments by different authors. In this case, the authors’ peculiarities of the texts (see below) are averaged, and the distribution is obtained that resembles Benford’s one, but with a faster decrease in frequency; the occurrence of digit 1 is significantly higher than expected according to Benford’s Law. Starting with digit 3, the actual frequency usually decreases faster than the theoretical one.

In Figure 1, the results of the analysis of the compiled text of three collections of Russian-language literary prose are presented:

• “Russian Romantic Novel” [22];
• “Fascinated by the Book” [23];
• “Under Clear Stars” [24].

For each compilation, the frequency gradually decreases; patterns for different compilations are generally similar, the differences may be related to the peculiarities of the texts in each collection (for example, genre and time of creation, but this requires additional research).

In Figure 2, similar results for English-language compilations [25,26,27,28,29,30,31,32] are presented.

2.2. Coherent Literary Texts: The Author’s Peculiarities

As a rule, in texts written by one author, stable peculiarities in the statistics of the first significant digits are observed. We will limit ourselves to a few examples concerning Russian- and English-language literary works.

We present the results of the analysis of the most voluminous novels by L. Tolstoy (Figure 3), F. Dostoevsky (works Nos. 1–9 in Figure 4), and I. Goncharov (Figure 5).

Note the difference in the frequencies of occurrence of digit one in Figure 3, Figure 4 and Figure 5. The maximum frequency for Goncharov’s texts (Figure 5) is substantially less than for the texts by Tolstoy and Dostoevsky. Basically, in our approach, the digit 1 and sometimes (to a lesser extent) 2 and 3 define the author’s specificity of the text. (As can be seen from Figure 3, even the frequency of occurrence of the first significant digit 2 can be subject to strong fluctuations. Unfortunately, our stylometric method, which takes into account only the first significant digits of numerals, cannot explain the reasons for this (numbers 2, 20, 21,..., 200... fall into the general statistics.) The advanced method of analyzing the numerals themselves in the text (see below) would be able to reveal the causes of the maximum on 2 in Tolstoy’s “Youth”.). The digit one occurrence stability is characteristic for large texts of all researched authors. We tend to associate it with psychological peculiarities that, regardless of the author’s will and consciousness, influence his texts. The occurrence of subsequent digits {4, 5,…} is subject to strong fluctuations, which makes it hardly possible to extract useful information from their distribution.

For the statistical stability of frequency characteristics, the texts should be quite voluminous: a novel, a story, but, apparently, not a short story. Figure 4 comparatively shows the frequency characteristics of not only large texts but also a relatively short story A Little Hero; there is a marked difference from the corpus of the main works of Dostoevsky, which is also confirmed by Pearson’s test [21].

Statistical analysis of English-language coherent literary texts yielded similar results. In Figure 6, Figure 7 and Figure 8, some of them are presented.

For J. Joyce’s texts, the frequency of occurrence of the digit one is significantly less than for M. Twain’s texts (cf. Figure 6 and Figure 7).

Note two outliers, corresponding to the significant digit one, for texts not completely written by Stevenson (Figure 8).

The frequency of the first significant digit 1 can reach values twice as large according to Benford’s Law (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8).

2.3. First Significant Digits and Texts Authorship Attribution

We will restrict ourselves to one example that is often used as a touchstone to test the stylometric techniques. More examples can be found in [21,33,34].

The problem of “And Quiet Flows the Don”

A well-known problem of the text attribution is the question of the authorship of the novel And Quiet Flows the Don and, more broadly, of the entire M. Sholokhov’s literary heritage. There are strong arguments for and against plagiarism. The linguistic and statistical study of the novel revealed an extremely heterogeneous text. Many different candidates were put forward for the role of the true authors of its eight parts. There are also doubts about the authorship not only of And Quiet Flows the Don but also of the subsequent novels Virgin Soil Upturned and They Fought for Their Country [35,36].

Without going into detail in a philological review of the state of the problem, we present the results of a statistical study using our methodology.

First, we carried out a statistical analysis of the three novels by Sholokhov (Figure 9). The distribution of the first significant digits of the numerals in And Quiet Flows the Don, on the one hand, and Sholokhov’s two other novels (Virgin Soil Upturned, books I and II, They Fought for Their Country), on the other hand, are very different, although usually this distribution is stable for an author. Pearson’s test confirms the significance of these differences (between No. 1 and No. 2 at α = 0.05; between No. 1 and No. 4 even at α = 0.01).

This result necessitated the separate analysis of the eight parts of And Quiet Flows the Don. The analysis shows that Virgin Soil Upturned and They Fought for Their Country could have been written by one author, but, probably, And Quiet Flows the Don, firstly, has another authorship, and, secondly, the authorship does not pertain to a single person.

These conclusions are consistent with the results briefly described above, which were obtained by other (mostly philological) methods.

Thus, the statistical method, based on counting the occurrence of the first significant digits of the numerals, is able to answer the question about the text authorship.

2.4. Statistical Characteristics of Translated Texts

Our stylometric method has an obvious difficulty in applying to texts written in a language in which the numeral one coincides with an indefinite article, such as ein in German or un in French. (Hungerbühler [17] also pointed out this obstacle.) It turns out that after the translation into an intermediary language, in which there is no such problem, the basic statistical properties of the original source text are preserved. We made such a conclusion by analyzing a large amount of English-language literary texts and their Russian translations. Corpora used are Charles Dickens (The Pickwick Papers, Oliver Twist, Martin Chuzzlewit, Dombey and Son, David Copperfield, Little Dorrit, Great Expectations, Our Mutual Friend, The Mystery of Edwin Drood), M. Twain (The Adventures of Tom Sawyer, Adventures of Huckleberry Finn, The Prince and the Pauper, A Connecticut Yankee in King Arthur’s Court), H. G. Wells (The Food of the Gods, The Island of Doctor Moreau, The War in the Air, The War of the Worlds), J. Joyce (Dubliners, A Portrait of the Artist as a Young Man, Ulysses), F. Scott Fitzgerald (The Great Gatsby, Tender is the Night). For example, we give a bar chart for the novels of H. G. Wells in the English original version and in Russian translations (Figure 10).

The absolute values of occurrence frequencies of any first significant digit in the original and in the translation do not coincide, but the frequency ratio in different texts is preserved. It is noted down to digit 3 inclusive. (Due to differences in the structure of different languages, the requirement for the complete coincidence of frequency characteristics in texts in different languages would be excessive (this is noted in the pioneer book on quantitative linguistics by Herdan [37])).

Such an obvious conservatism greatly expands the possibilities of applying our method.

3. Beyond the Benford’s Law

Starting from the above analysis of statistics of the first significant digits of numerals, we now make a further step to the analysis of the use of the numerals themselves in the authorial texts. The first of the two approaches can be considered a convolution of the latter. (By the way, Nigrini [16] has also elaborated an express technique of Benford’s Law-based accounting fraud detection and an enlarged one.) Each approach has its advantages and disadvantages:

• The analysis of the statistics of the first significant digits is only applicable to the significant digit 1 and (sometimes) 2 and 3 since the occurrence of subsequent digits is subject to strong fluctuations even in the texts of the same author. Thus, only a small part of the statistical information on the numerals contained in the text is available for analysis.
• On the other hand, using the first significant digits is advantageous since the information here is presented in a generalized form: it can minimize the influence of numbers closely connected to the topic of the text (e.g., the year 1812 in L. Tolstoy’s War and Peace).
• Analysis of the use of the numerals themselves (and not the first significant digits) gives richer information about an author’s peculiarities of the text and, to a large extent, is not blocked by indistinguishability of the numeral one and the indefinite article.
• However, the analysis of numerals statistics is more difficult.

We now give a comparative example of the application of the original and advanced analysis methods.

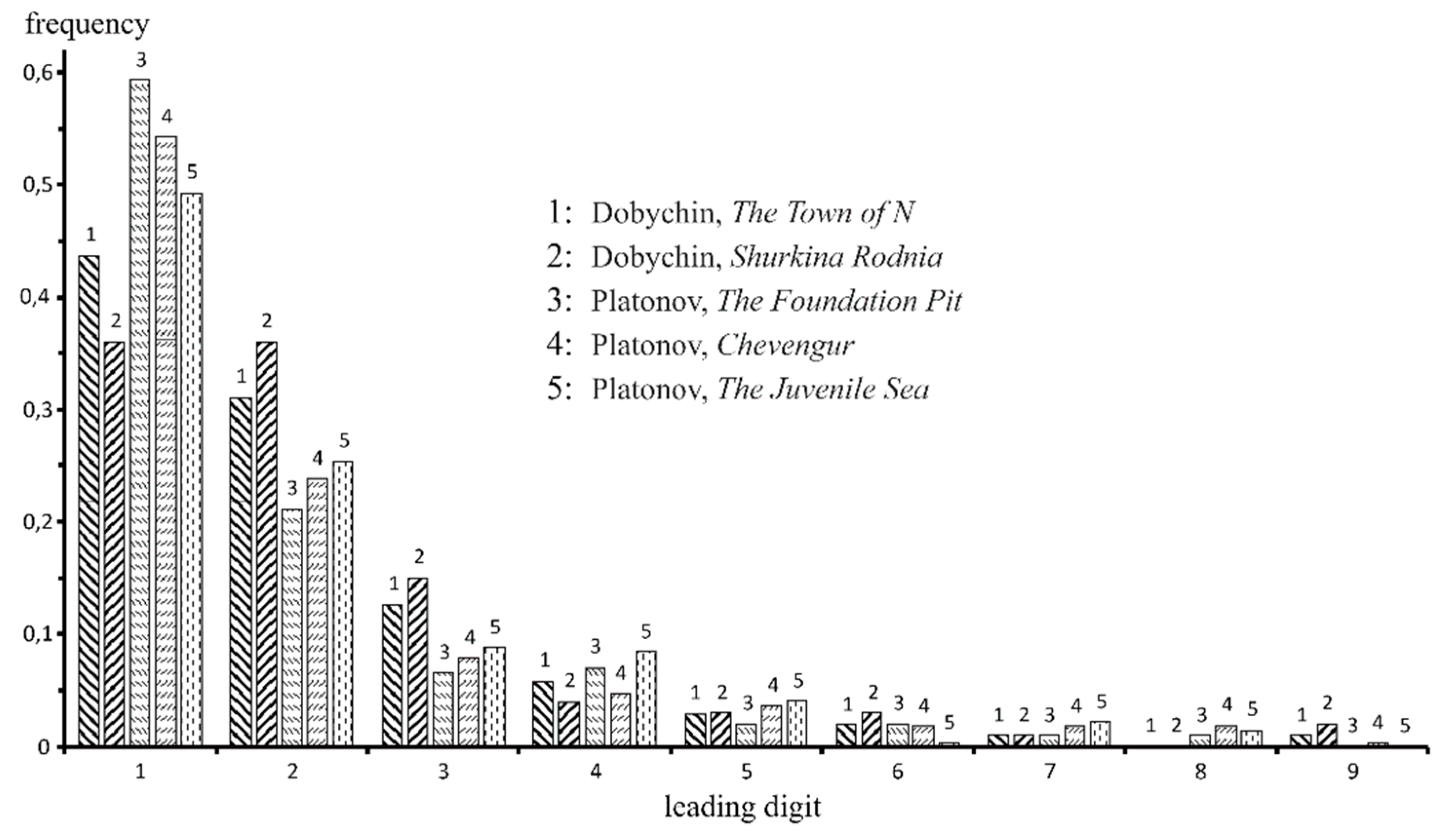
3.1. The Extension of the Numerals Analysis. Dobychin vs. Platonov

The literary texts of L.I. Dobychin and A.P. Platonov are distinguished by sharp stylistic originality; one finds common literary sources in Russian fiction and analogues in foreign literature [38]. Figure 11 shows the frequency distribution of the first significant digits of the numerals occurring in the most voluminous works by Dobychin and Platonov [39].

The first significant digits 1, 2, and 3 are characterized by a sharp difference in occurrence in the texts of Dobychin, on the one hand, and Platonov, on the other. This visual difference is confirmed by Pearson’s statistical test. Thus, the analysis of the distribution of the first significant digits indicates undoubted style differences in the texts of the two authors. The method is convenient for quickly checking whether a certain group of texts belongs to one author: in the case of significant differences in the statistical distributions, single authorship is doubtful.

The results of applying the advanced statistical method that analyzes the occurrence of the numerals themselves are incomparably richer. Figure 12 shows the absolute frequencies of numerals from the range [0, 100] in the same texts by Dobychin and Platonov. Since the analyzed texts have different sizes, correction coefficients were used to equalize the results on the occurrence of numerals.

Some of the results:

• Platonov, in his literary texts, more likely uses numerals than Dobychin.
• Platonov less often resorts to rounding of numerals (10, 20, 30...), which, in conjunction with item 1, can indirectly indicate a greater tendency to detail.
• The numeral one (in different word forms) is the undisputed leader among the numerals found in Platonov’s texts. In the texts by Dobychin, the numeral one is inferior in frequency to the numeral two!
• Note the psychologically understandable rarefaction of the series of numerals and a decrease in their occurrence as they increase, as well as a noticeable local maximum at the numeral 100, which, of course, plays the role of an indefinitely large number.

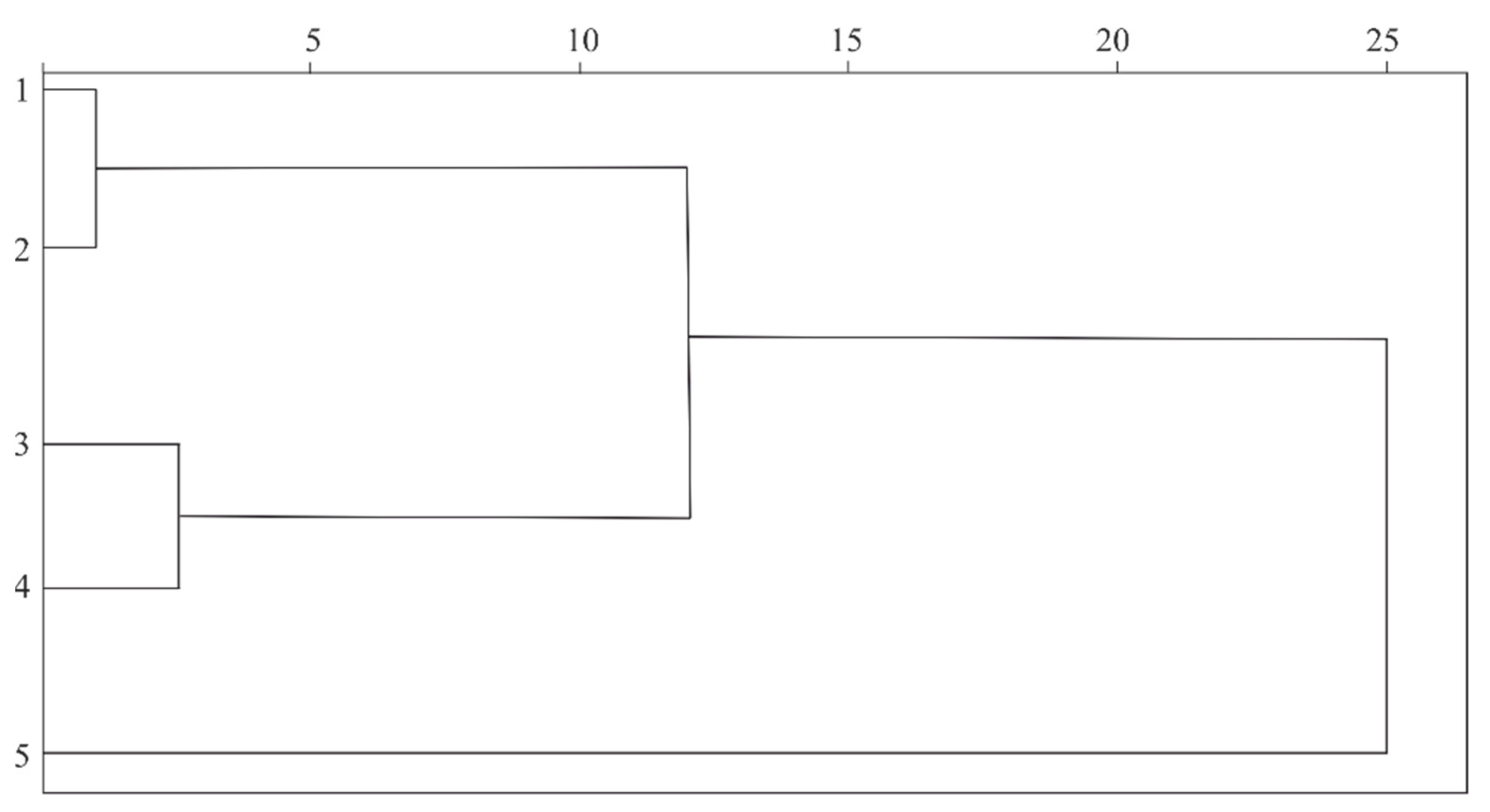
3.2. Who Wrote “The Twelve Chairs”?

The literary work of popular Soviet authors of the 1920s and 1930s I. Ilf and E. Petrov has repeatedly become the subject of discussion. The novels The Twelve Chairs and The Little Golden Calf are full of literary allusions; thematically and stylistically, they are related to the texts by V. Kataev, M. Bulgakov, Yu. Olesha, and others [40]. There is nothing comparable to these two works in the literary heritage of Ilf and Petrov. According to the radical point of view [41], Ilf and Petrov are the fake authors of The Twelve Chairs and The Little Golden Calf, and they were ghosted by Bulgakov. In this section, we will apply our methodology to a comparative analysis of the corpus of literary texts by Ilf and Petrov. Along the way, we study Kataev’s The Lord of Iron (1924) and The Embezzlers (1926), contemporary to The Twelve Chairs (1928) and The Little Golden Calf (1931), as well as Bulgakov’s The Master and Margarita.

The numerals extracted from the texts are displayed on frequency graphs [42], which allowed us to directly draw conclusions about the author’s style. Information about numerals found in texts was also systematized using the hierarchical cluster analysis [43]. The farthest neighbor clustering was used (which exaggerates differences yet provides clearly defined clusters).

The smaller the difference in the occurrence of the same numbers in two texts, the greater the similarity (the smaller the “distance” ρ) between these texts, so the Manhattan metric was used

$$\rho \left(\mathit{x},\mathit{y}\right)={\displaystyle \sum }_{i = 1}^n\left|x_i-y_i\right|$$

(1)

where x and y are n-dimensional vectors whose components are the absolute frequency of occurrence of the first n natural numbers found in both analyzed texts.

Figure 13 shows the frequency distribution of numerals in Ilf and Petrov’s The Twelve Chairs and The Little Golden Calf, as well as in Bulgakov’s The Master and Margarita, and Kataev’s The Embezzlers and The Lord of Iron. For clarity, we restrict the graph to the range [1, 50] on the horizontal axis; the conclusions formulated below are valid for the entire set of numerals found.

Some conclusions directly from the figure:

• For all the analyzed texts, there are peaks in the occurrence of round numbers 10, 20,..., 100, 200,…
• In the texts by Ilf and Petrov, as well as in Bulgakov’s The Master and Margarita, the numeral 1 has the highest frequency (which is consistent with Benford’s Law), but in Kataev’s texts, the number 2 leads.
• Between The Twelve Chairs and The Little Golden Calf, there is a conspicuous similarity in the numeral’s frequency (we will return to this later—see the conclusions to Figure 14 and Figure 15).
• These two texts are characterized by the greatest variety of numerals.
• On the contrary, Kataev’s texts are distinguished by the least variety of numerals.
• In terms of the variety of numerals, The Master and Margarita occupy an average position, but the frequencies of the numerals (after the initial frequent ones and twos) are usually lower than in other texts analyzed. In fact, many numbers occur once.

Based on the frequency distributions of numerals in the works by Ilf and Petrov included in their 5-volume collection of works [44], we performed clustering and built a dendrogram (Figure 14).

It turned out that all the analyzed texts contained natural numbers in the [1, 12] range; the frequencies of these numbers were used for clustering; n = 12 in Formula (1). The numbers to the left of the dendrogram refer to the following texts:

• The Twelve Chairs; a joint work by Ilf and Petrov, 1927–1928; vol. 1 [44];
• Joint works 1932–1937 (stories, feuilletons, articles, speeches, vaudevilles, screenplays) by Ilf and Petrov, included in vol. 3;
• The Little Golden Calf; a joint work by Ilf and Petrov, 1929–1930; vol. 2;
• Works (stories, essays, feuilletons) written individually by Petrov in 1924–1932 and included in vol. 5;
• Works (essays, articles, memoirs) written individually by Petrov in 1937–1942 and included in vol. 5;
• One-storied America (travel essays; sometimes translated as Little Golden America), 1936, vol. 4;
• Works (stories, essays, feuilletons) written solely by Ilf in 1923–1929, as well as his notebooks from 1925-37, included in vol. 5.

From the dendrogram, it is clear that the closest (in terms of the use of numerals) are Nos. 1 and 2: joint, mainly literary texts; to this initial cluster, No. 3 is soon added with the same characteristic. Nos. 5 and 6—late non-fiction works—form the next cluster, internally not as unified as the cluster {1, 2, 3}. At the last stage, No. 7 is added to the cluster—texts by Ilf.

Thus, from Figure 14, it follows that by the analysis of the use of numerals in texts, one can distinguish between genres and authors of texts.

Figure 15 shows the results of hierarchical cluster analysis of the occurrence of numerals (again from the range [1; 12], as in Figure 14) in the novels The Twelve Chairs (No. 1) and The Little Golden Calf (No. 2) by Ilf and Petrov, as well as in the works of writers who were named as possible true authors of these two novels—The Embezzlers (No. 3) and The Lord of Iron (No. 4) by Kataev, and Bulgakov’s The Master and Margarita (No. 5). Clustering took place in accordance with the generally accepted authorship of the texts. The distance between clusters {1, 2} and {3, 4}, not to mention the height of fusion with No. 5, is so great that it casts doubt on the hypothesis that Bulgakov or Kataev wrote The Twelve Chairs and The Little Golden Calf. Of course, taken separately, the results of Figure 15 do not confirm the authorship of Ilf and Petrov themselves, but the results of Figure 14 indirectly indicate their authorship.

The hypothesis [41] that M. Bulgakov is the author of The Twelve Chairs is not confirmed by our analysis.

Thus, the analysis of the use of numerals in texts can be used to test the authorship of texts.

4. Discussion

Our analysis of the numerals occurring in the texts shows that not only for a random combination of texts, but also for coherent texts, for which the conditions of Hill’s theorem [4] are not fulfilled, the frequency distribution of the first significant digits is similar to Benford’s one, but the quota of the digit 1 significantly exceeds the Benfordian 30 percent; the occurrence of subsequent digits usually decreases gradually. This is found directly for texts in Russian [18,21], Czech [34], Lithuanian [45], English [21,33], and Turkish [46] languages.

The digit one sharply prevails—at least because, formally being a numeral, the word one can actually play the role of an indefinite article. The common psychological propensity to round numbers also has an impact. (Example: “The era known in Japanese history as the Nara era...lasts a little less than a hundred years. It begins by the establishment of the capital of the state in the city of Heijō (Nara)—in 710, its end is considered at the capital transfer...to the city of Heian (Kyoto), which took place in 794” [47] (p. 45). Instead of eighty-four (with 8 as the first significant digit) appears one hundred (and, accordingly, the digit 1).).

Thus, the reasons for the frequent occurrence in the texts of the digit one as the first significant digit are partially clear, but why the numerals begin less and less often with each subsequent digit remains obscure. (Some insight is given by Burns [48], who coined the notion of a Benford bias of the human behavior: when people generate numbers, the first-digit distribution is distorted towards Benford’s Law).

In contrast to the traditional methodology of Benford’s Law application, which considers deviations from the law as an indication of possible falsifications (in a broad sense), we place the emphasis on comparing these deviations for texts by different authors. It is shown that these deviations are statistically stable author peculiarities, which makes it possible to distinguish texts by different authors. The frequencies of occurrence of the first significant digit 1, as well as digits 2 and 3 (to a lesser extent), are usually a characteristic peculiarity of the author’s style, consistently manifested in all (sufficiently long) literary texts of this author and were proven by statistical tests. (The frequencies of occurrence of subsequent digits are too variable even in the texts of one author to draw any conclusion from them).

Significant differences in these frequencies for given texts are an indication that the texts may have different authorship. Thus, the analysis of the frequencies of the first significant digits of the numerals can be used to solve the stylometric problems. Undoubtedly, frequencies similarity still does not prove the authorship identity. Our method is unlikely to deduce the actual authorship with absolute certainty except in cases where it can rule out all but one contender (and it is known or at least strongly suspected that the actual author is represented in the training data).

The translation into another language does not violate the ratio of the frequencies of the first significant digits 1, 2, and 3 (although it affects their absolute values). This expands the range of applicability of the proposed stylometric method to texts, in whose original language the indefinite article coincides with the numeral one: it is possible to analyze the translations of these texts into an intermediate language in which there is no such difficulty.

Taking into account the occurrence of numerals themselves (not the first significant digits) in literary texts can provide information about the authors and stylistic and genre features of texts. Sometimes, an analysis of the occurrence of numerals allows rejecting the hypothesis of the common authorship of texts.

Traditional stylometric practices include, for example, the analysis of the sentence and word length, of frequency of function words, and also of certain significant parts of speech, and even the analysis of frequencies of letter combinations [49]. Unfortunately, different methods do not always lead to consistent conclusions, and none of the existing methods of texts attribution (including the popular recent Burrows’s delta [50]) offers 100% reliability. Obviously, it is reasonable to use different methods and compare the results obtained. The use of neural networks can give impressive results, but the technique itself, unfortunately, is a black box: its results are often difficult to comprehend [51]. In this sense, our approach to the stylometric problems seems linguistically more informative and meaningful.

We believe that our methodology can be a useful addition to traditional stylometric practices.