Path Analysis of Sea-Level Rise and Its Impact
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Step 1: The Dynamic SEM Model
2.3. Step 2: A More Refined Vector Autoregression Model
2.4. STEP 3: The Generalized Additive Model
3. Results
3.1. Dynamic SEM Results
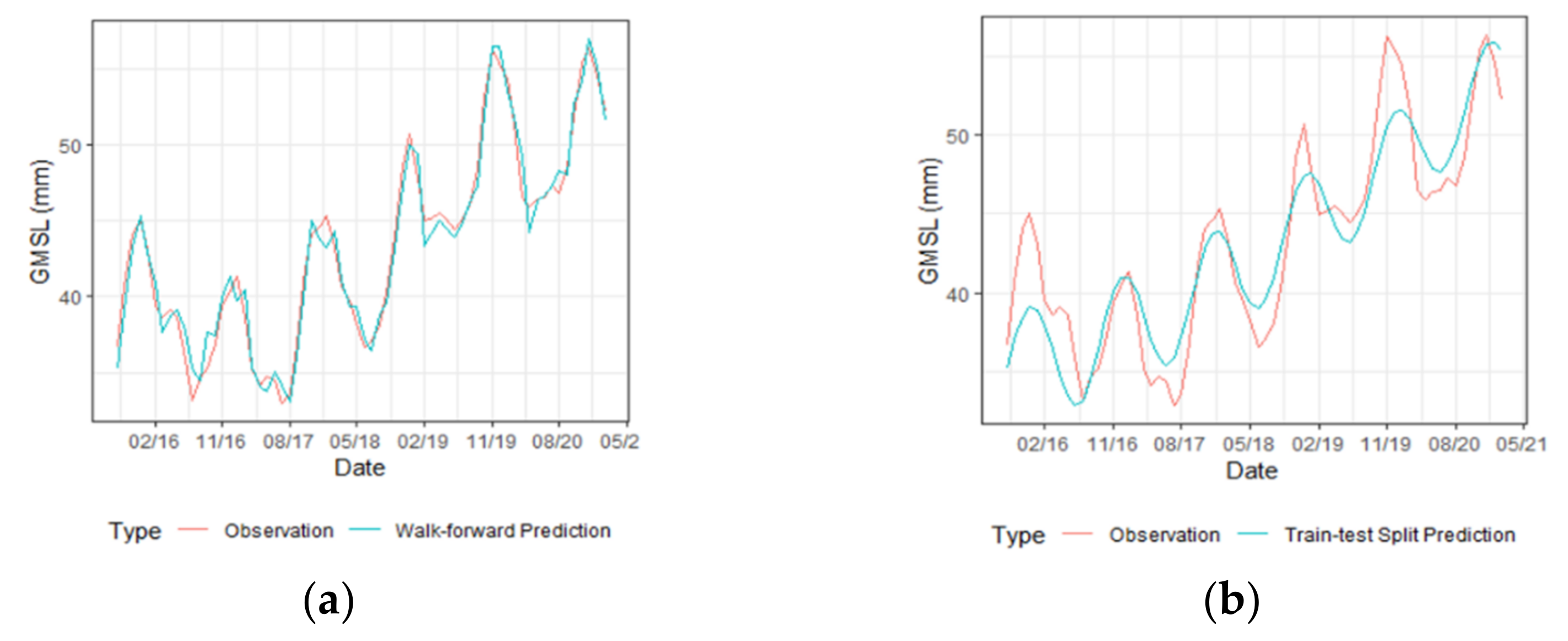
3.2. GMSL Projection with VAR(3)
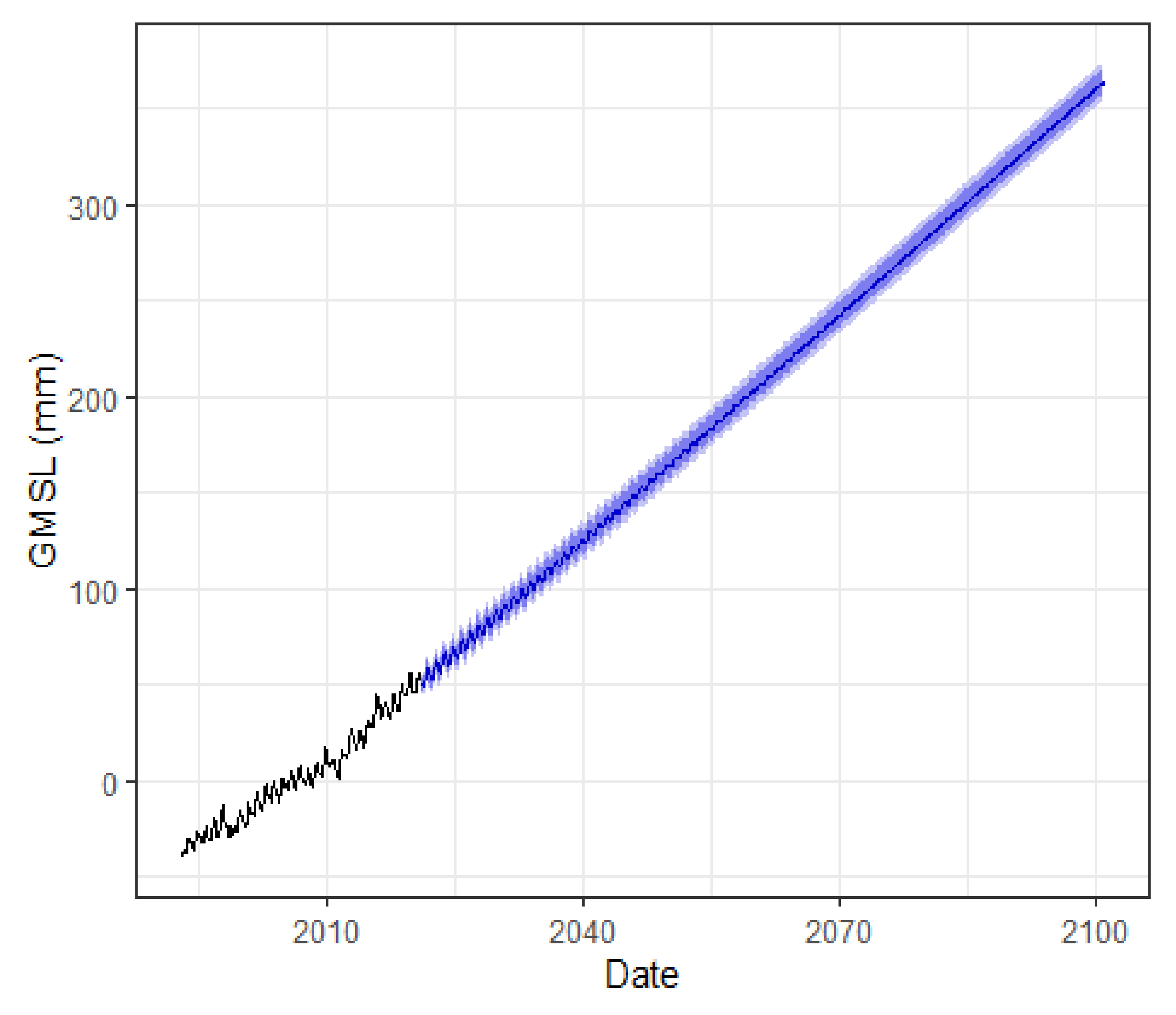
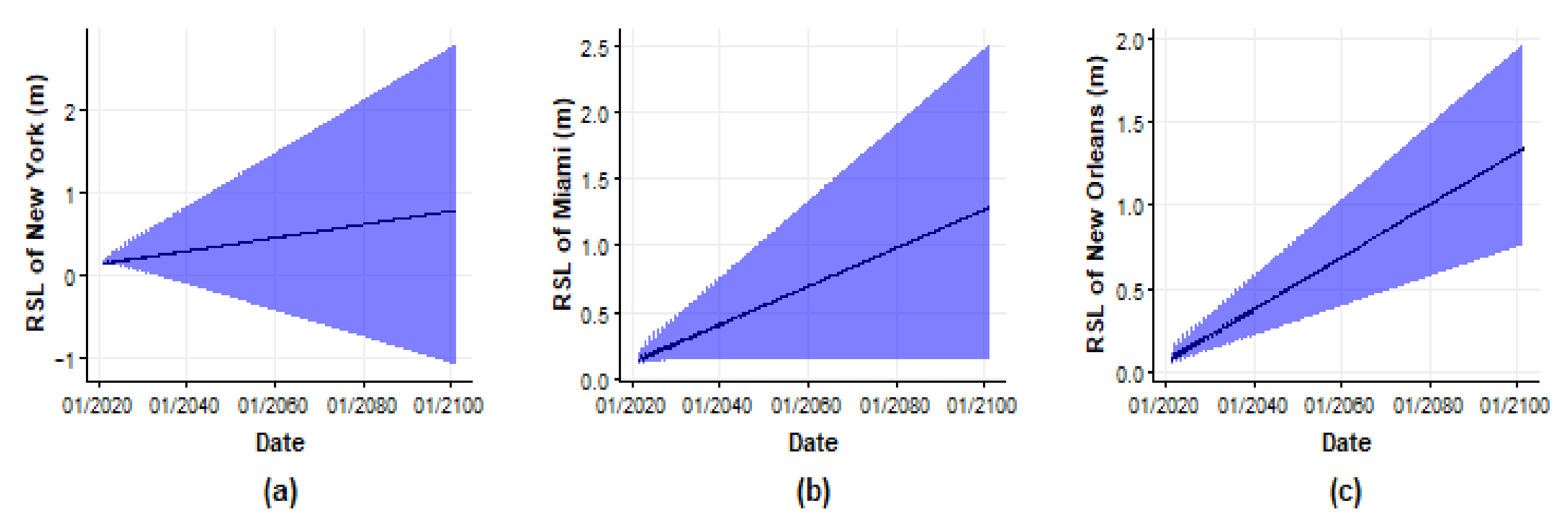
3.3. Projections of Coastal Regional Sea-Level Rise with GAM
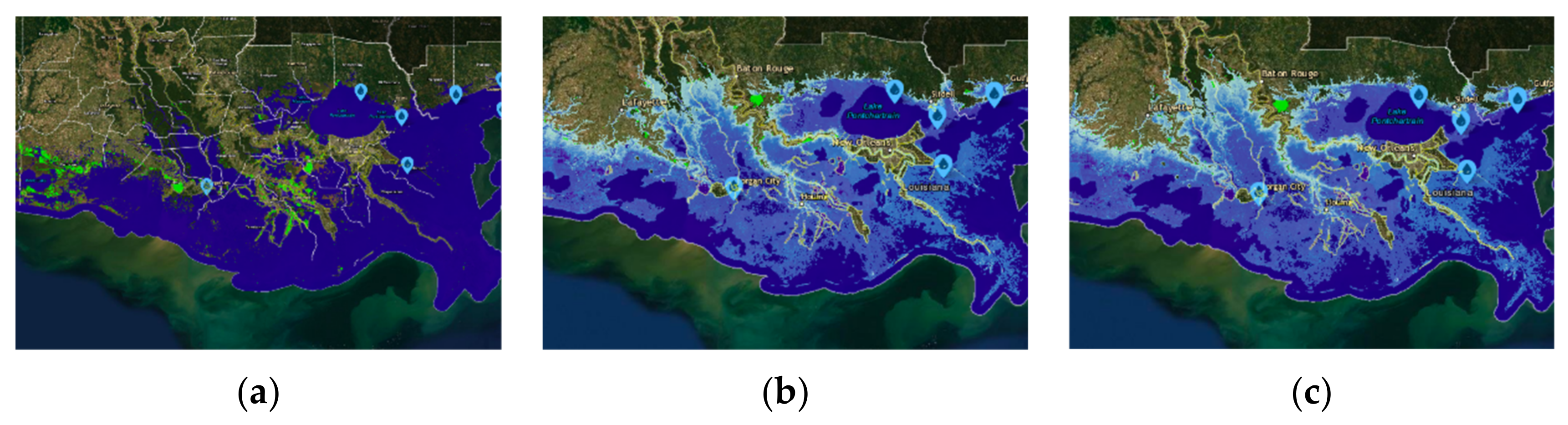
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability
Conflicts of Interest
References
- Climate.gov. Available online: https://www.climate.gov/news-features/understanding-climate/climate-change-global-sea-level (accessed on 8 October 2021).
- Schmith, T.; Johansen, S.; Thejll, P. Statistical analysis of global surface temperature and sea level using cointegration methods. J. Clim. 2012, 25, 7822–7833. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Glavovic, B.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; Deconto, R.M.; Ghosh, T.; et al. Sea Level Rise and Implications for Low Lying Islands, Coasts and Communities; The Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019. [Google Scholar]
- Sweet, W.W.V.; Dusek, G.; Obeysekera, J.T.B.; Marra, J.J. Patterns and Projections of High Tide Flooding along the US Coastline Using a Common Impact Threshold; NASA Technical Report NOS CO-OPS; National Oceanic and Atmospheric Administration: Washington, DC, USA, 2018. [Google Scholar]
- NPR. Available online: https://www.npr.org/templates/story/story.php?storyId=9162438#:~:text=Study%3A%20634%20Million%20People%20at%20Risk%20from%20Rising%20Seas%20A,related%20impacts%20of%20climate%20change (accessed on 8 October 2021).
- Balogun, A.-L.; Adebisi, N. Sea level prediction using ARIMA, SVR and LSTM neural network: Assessing the impact of ensemble Ocean-Atmospheric processes on models’ accuracy. Geomat. Nat. Hazards Risk 2021, 12, 653–674. [Google Scholar] [CrossRef]
- Johansen, S. The Analysis of Nonstationary Time Series Using Regression, Correlation and Cointegration with an Application to Annual mean Temperature and Sea Level; University of Copenhagen Department of Economics Discussion Papers No. 10–27; University of Copenhagen, Department of Economics: Copenhagen, Denmark, 2010. [Google Scholar]
- Aral, M.M.; Guan, J.; Chang, B. Dynamic system model to predict global sea-level rise and temperature change. J. Hydrol. Eng. 2012, 17, 237–242. [Google Scholar] [CrossRef]
- Aral, M.M.; Guan, J. Global sea surface temperature and sea level rise estimation with optimal historical time lag data. Water 2016, 8, 519. [Google Scholar] [CrossRef] [Green Version]
- Bâki İz, H.; Shum, C.K. Recent and future manifestations of a contingent global mean sea level acceleration. J. Geod. Sci. 2020, 10, 153–162. [Google Scholar]
- Beckley, B.; Zelensky, N.P.; Holmes, S.A.; Lemoine, F.G.; Ray, R.D.; Mitchum, G.T.; Desai, S.; Brown, S.T. Global Mean Sea Level Trend from Integrated Multi-Mission Ocean Altimeters TOPEX/Poseidon Jason-1 and OSTM/Jason-2 Version 4.2; NASA Physical Oceanography Distributed Active Archive Center: Pasadena, CA, USA, 2016. [Google Scholar]
- Sea Ice Data and Analysis Tools|Arctic Sea Ice News and Analysis. Available online: https://nsidc.org/arcticseaicenews/sea-ice-tools/ (accessed on 8 October 2021).
- IMBIE (Ice Sheet Mass Balance Inter-comparison Exercise). Available online: http://imbie.org/data-downloads/ (accessed on 8 September 2021).
- NASA (Ice Sheet. NASA). Available online: https://climate.nasa.gov/vital-signs/ice-sheets/ (accessed on 20 November 2021).
- Rohde, R.A.; Hausfather, Z. The Berkeley Earth land/ocean temperature record. Earth Syst. Sci. Data 2020, 12, 3469–3479. [Google Scholar] [CrossRef]
- Keeling, C.D.; Piper, S.C.; Bacastow, R.B.; Wahlen, M.; Whorf, T.P.; Heimann, M.; Meijer, H.A. Exchanges of Atmospheric CO2 and 13CO2 with the Terrestrial Biosphere and Oceans from 1978 to 2000. I. Global Aspects; Scripps Institution of Oceanography: San Diego, CA, USA, 2001. [Google Scholar]
- 2degreesinstitute. Available online: https://www.2degreesinstitute.org (accessed on 8 October 2021).
- NOAA Center for Operational Oceanographic Products and Services. Available online: https://tidesandcurrents.noaa.gov/sltrends/sltrends_global.html (accessed on 8 October 2021).
- Kline, R.B. Principles and Practice of Structural Equation Modeling; Guilford Publications: New York, NY, USA, 2015. [Google Scholar]
- Schumacker, R.E.; Lomax, R. A Beginner’s Guide to Structural Equation Modeling; Lawrence Erlbaum Associates: New Jersey, NJ, USA, 2004. [Google Scholar]
- Byrne, B.M. Structural Equation Modeling with Mplus: Basic Concepts, Applications, and Programming; Routledge: Oxfordshire, UK, 2013. [Google Scholar]
- Kim, J.; Zhu, W.; Chang, L.; Bentler, P.M.; Ernst, T. Unified structural equation modeling approach for the analysis of multisubject, multivariate functional MRI data. Hum. Brain Mapp. 2007, 28, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Di Narzo, A.F.; Aznarte, J.L.; Stigler, M.; Tsung-wu, H. tsDyn: Nonlinear Time Series Models with Regime Switching; R Package Version 10-1.2; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.r-project.org (accessed on 1 December 2021).
- Pfaff, B.; Stigler, M. Vars: VAR Modelling; R Package Version 1.5-3; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- MultiThreaded. Available online: https://multithreaded.stitchfix.com/blog/2015/07/30/gam/ (accessed on 8 October 2021).
- Wood, S. Mixed GAM Computation Vehicle with Automatic Smoothness Estimation; R Package Version 1.8-35; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Wood, S.N. Stable and efficient multiple smoothing parameter estimation for generalized additive models. J. Am. Stat. Assoc. 2004, 99, 673–686. [Google Scholar] [CrossRef] [Green Version]
- Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2011, 73, 3–36. [Google Scholar] [CrossRef] [Green Version]
- Marcy, D.; Brooks, W.; Draganov, K.; Hadley, B.; Haynes, C.; Herold, N.; McCombs, J.; Pendleton, M.; Ryan, S.; Schmid, K.; et al. New mapping tool and techniques for visualizing sea level rise and coastal flooding impacts. Solut. Coast. Disasters 2011, 2011, 474–490. [Google Scholar]
- National Oceanic and Atmospheric Administration U.S. Department of Commerce. Available online: https://oceanservice.noaa.gov/facts/sea-ice-climate.html (accessed on 8 October 2021).
- Sweet, W.; Park, J.; Marra, J.; Zervas, C.; Gill, S. Sea Level Rise and Nuisance Flood Frequency Changes around the United States; NOAA Technical Report NOS CO-OPS; National Oceanic and Atmospheric Administration: Washington, DC, USA, 2014. [Google Scholar]
- Sukop, M.C.; Rogers, M.; Guannel, G.; Infanti, J.M.; Hagemann, K. High temporal resolution modeling of the impact of rain, tides, and sea level rise on water table flooding in the Arch Creek basin, Miami-Dade County Florida USA. Sci. Total Environ. 2018, 616–617, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- New York Times. Available online: https://www.nytimes.com/2021/07/07/us/tropical-storm-elsa-florida.html (accessed on 9 October 2021).


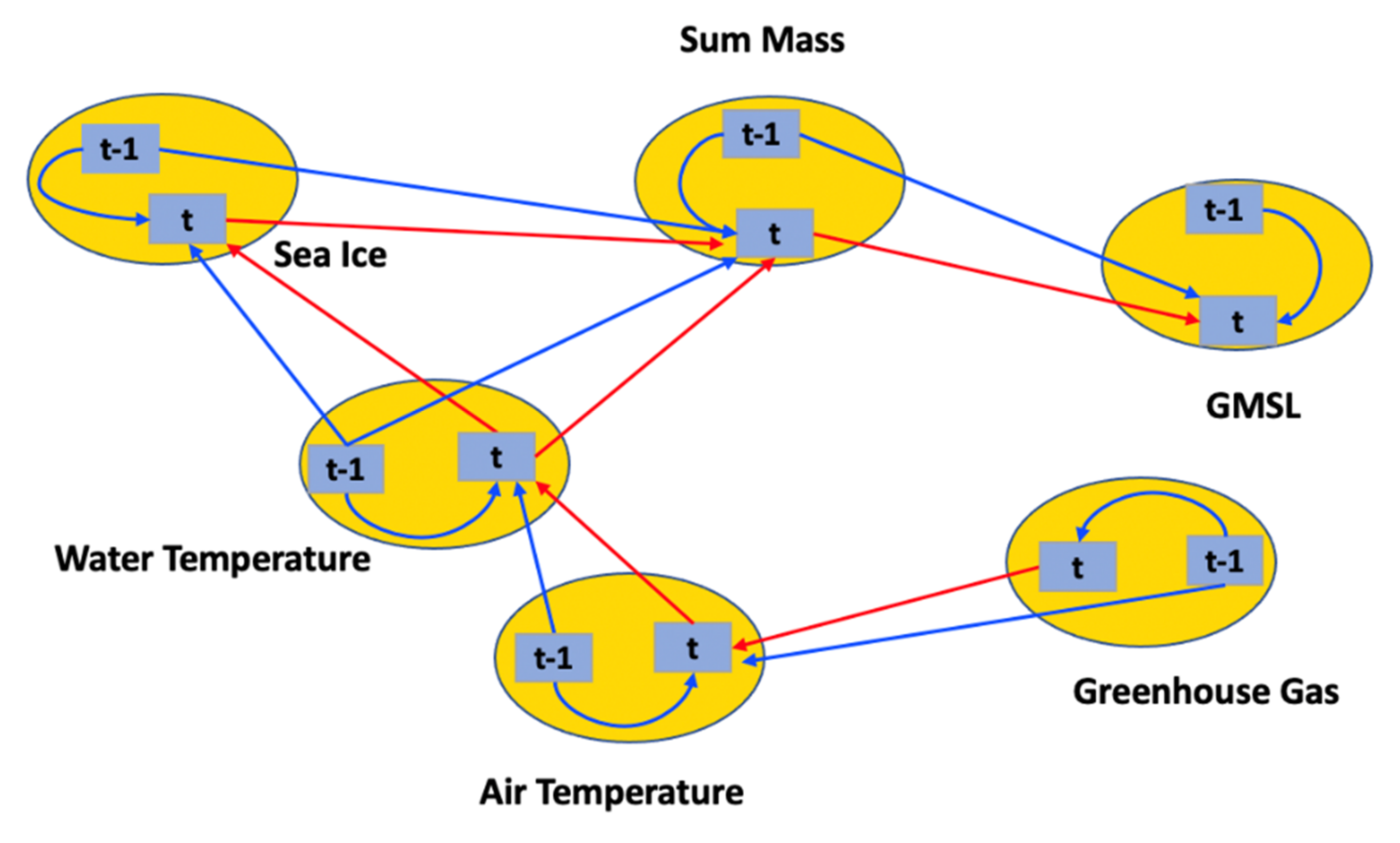


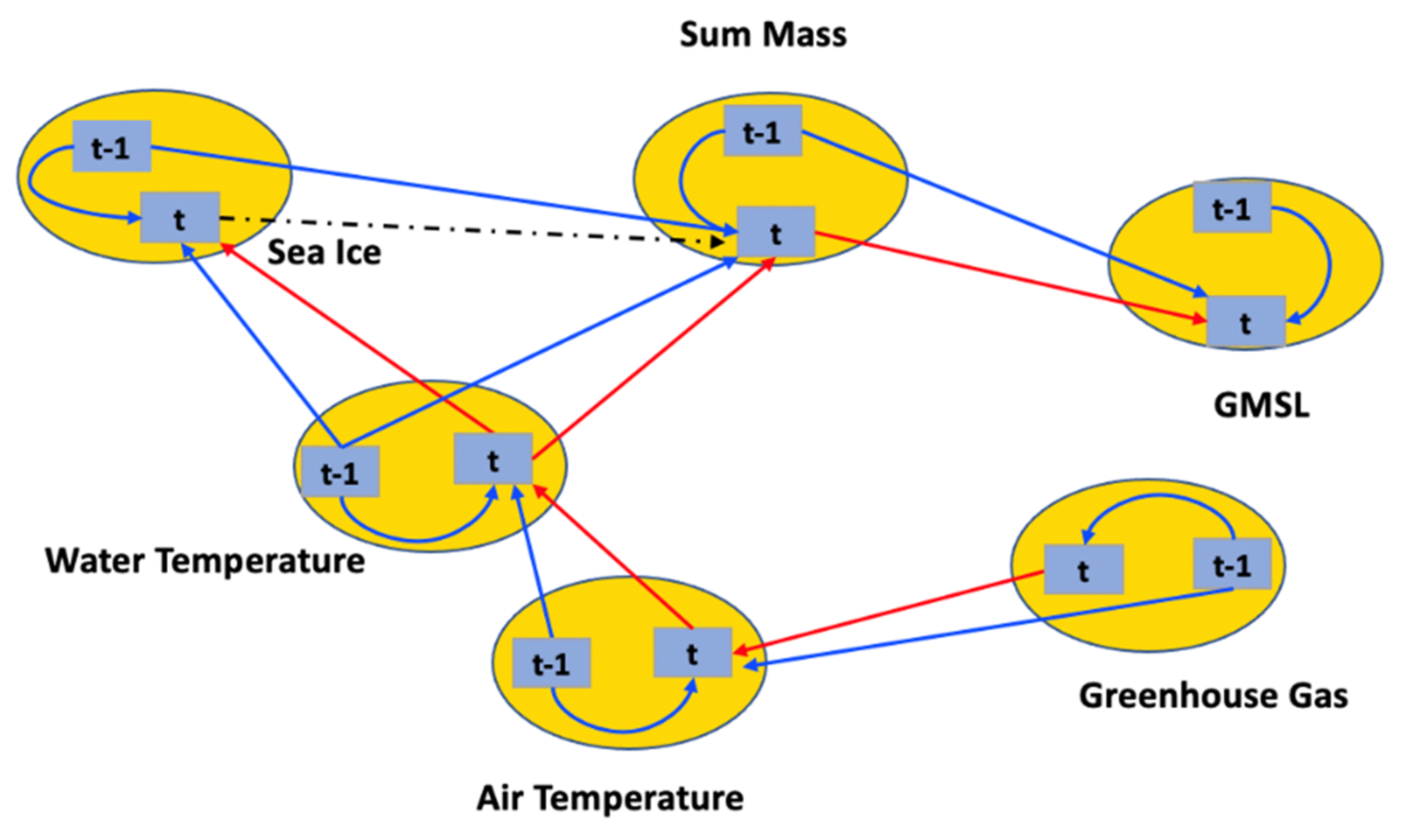


| Variable | Explanation |
|---|---|
| Air Temperature | Global average air temperature |
| GMSL | Global mean sea-level variation |
| Sum Mass | Summation of Greenland and Antarctic cumulative glacier mass change |
| Greenhouse Gas | The amount of CO2, N2O and CH4 in the air (parts per million) |
| Water Temperature | Global average water temperature |
| Sea Ice | Northern hemisphere sea ice extent |
| Significant Path Connection | Mean (SE) | t-Value (p-Value, 2-Sided) |
|---|---|---|
| Sum Mass(t) → GMSL(t) | 9.366 (4.528) | 2.068 (0.039) |
| Sum Mass(t − 1) → GMSL(t) | −10.242 (4.714) | −2.173 (0.030) |
| GMSL(t − 1) → GMSL(t) | 0.979 (0.009) | 107.188 (0.000) |
| Sum Mass(t − 1) → Sum M.(t) | 1.034 (0.001) | 817.450 (0.000) |
| Water T.(t) → Sum M.(t) | 0.021 (0.002) | 8.305 (0.000) |
| Water T.(t − 1) → Sum M.(t) | −0.024 (0.002) | −13.721 (0.000) |
| Sea Ice(t) → Sum M.(t) | 0.002 (0.002) | 0.944 (0.345) |
| Sea Ice(t − 1) → Sum M.(t) | −0.006 (0.001) | −4.727 (0.000) |
| Sea Ice(t − 1) → Sea Ice(t) | 0.697 (0.013) | 52.521 (0.000) |
| Water T.(t)→ Sea Ice(t) | −1.098 (0.052) | −20.924 (0.000) |
| Water T.(t − 1) → Sea Ice(t) | −0.328 (0.053) | −6.202 (0.000) |
| Air T.(t) → Water T.(t) | 0.951 (0.005) | 203.096 (0.000) |
| Air T.(t − 1) → Water T.(t) | −0.447 (0.040) | −11.039 (0.000) |
| Water T.(t − 1) → Water T.(t) | 0.447 (0.043) | 10.324 (0.000) |
| Greenhouse(t) → Air T.(t) | −0.118 (0.007) | −16.941 (0.000) |
| Greenhouse(t) → Air T.(t) | 0.123 (0.007) | 17.625 (0.000) |
| Air T.(t − 1) → Air T.(t) | 0.755 (0.020) | 37.435 (0.000) |
| Greenhouse(t − 1) → Greenhouse(t) | 0.979 (0.012) | 82.789 (0.000) |
| Method | Model | RMSE | MAE |
|---|---|---|---|
| Walk-forward | ARIMA(2,1,2) | 1.44 | 1.21 |
| Walk-forward | VAR(3) | 1.07 | 0.89 |
| Train-test split | ARIMA(2,1,2) | 6.67 | 5.55 |
| Train-test split | VAR(3) | 2.48 | 2.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, J.; Tong, G.; Chao, J.; Zhu, W. Path Analysis of Sea-Level Rise and Its Impact. Stats 2022, 5, 12-25. https://doi.org/10.3390/stats5010002
Chung J, Tong G, Chao J, Zhu W. Path Analysis of Sea-Level Rise and Its Impact. Stats. 2022; 5(1):12-25. https://doi.org/10.3390/stats5010002
Chicago/Turabian StyleChung, Jean, Guanchao Tong, Jiayou Chao, and Wei Zhu. 2022. "Path Analysis of Sea-Level Rise and Its Impact" Stats 5, no. 1: 12-25. https://doi.org/10.3390/stats5010002
APA StyleChung, J., Tong, G., Chao, J., & Zhu, W. (2022). Path Analysis of Sea-Level Rise and Its Impact. Stats, 5(1), 12-25. https://doi.org/10.3390/stats5010002








