Multiple Imputation of Composite Covariates in Survival Studies
Abstract
:1. Introduction
2. Background and Methods
2.1. Missingness Mechanisms
2.2. Multiple Imputation
Fully Conditional Specification (FCS)
- To obtain initial values, all incomplete values in a data set are replaced with a “placeholder”, such as the mean for that variable.
- Take one variable with placeholder values, , and set the placeholder values back to missing.
- Subset the data set to the complete case form.
- Fit a regression model where the outcome variable is . Choose which of the remaining variables in the data set to fit as covariates. This regression model is an Imputation Model, denoted by .
- Impute missing values in by using the estimated coefficients from the imputation model.
- Repeat steps 2–5 for any other variable that contains placeholder values.
- Repeat steps 2–6 until the estimate of the parameter of interest converges. This results in a complete data set.
2.3. Simulation Study Design
2.3.1. Generating the Data
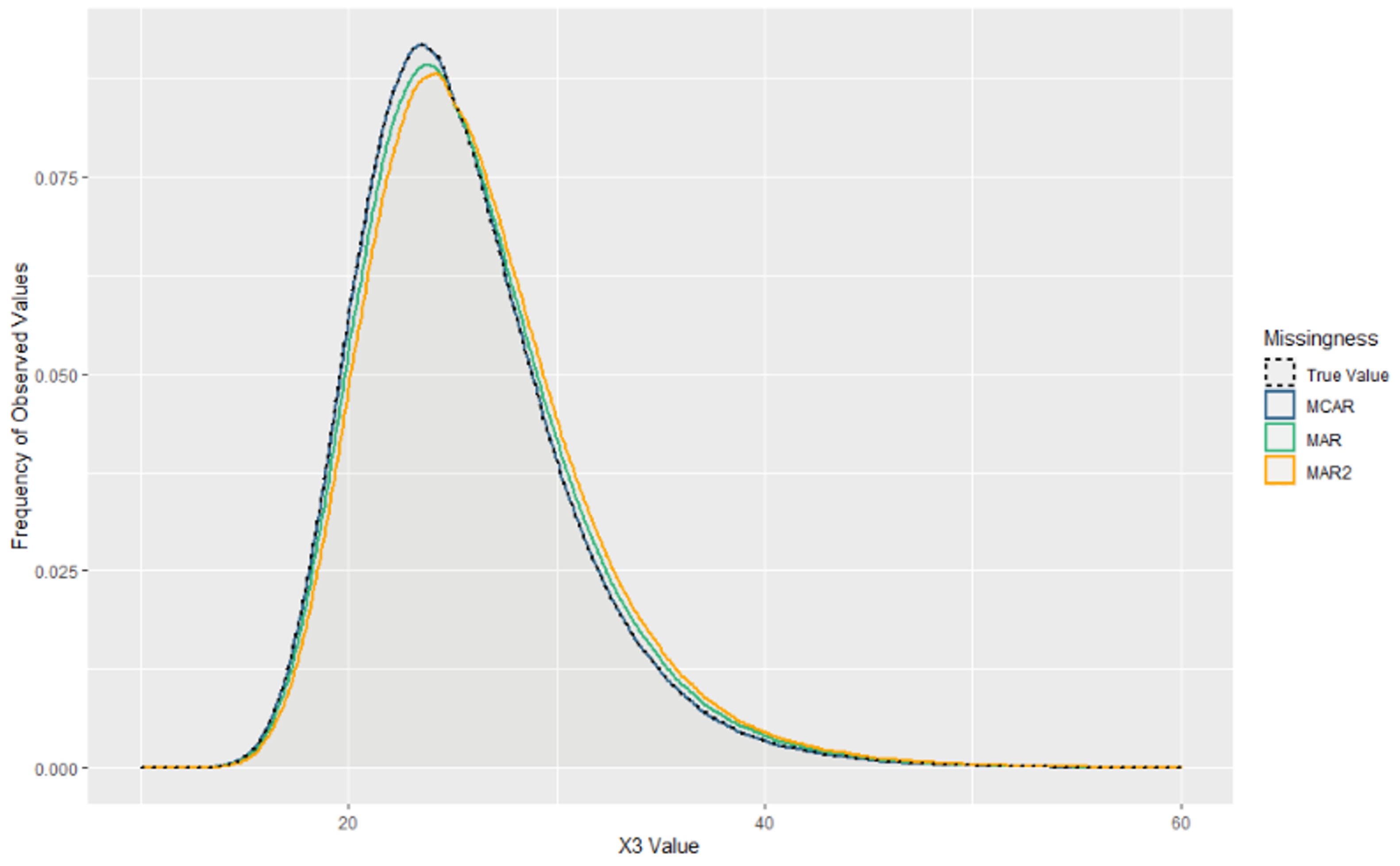
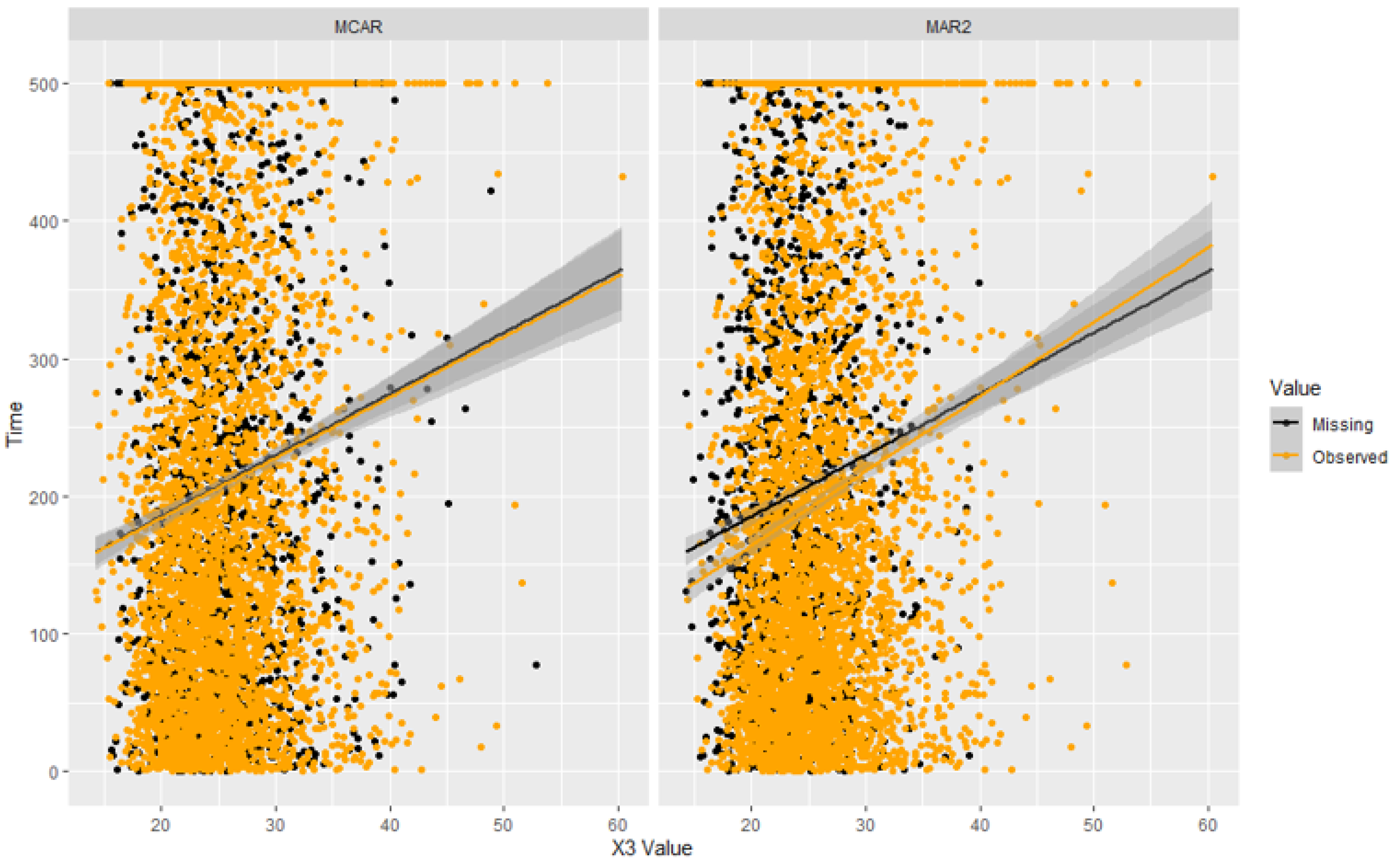
2.3.2. Generating Missing Values
2.3.3. Applying Multiple Imputation
- Active imputation without constituents present as predictors (AWO).
- Active imputation with constituents present as predictors (APA).
- Standard Passive Imputation (PNP).
- Log-Passive Imputation (LNP). In this imputation model, the constituents are first log-transformed before imputation takes place; :
2.3.4. Comparing Imputation Models
3. Results
3.1. MCAR
3.2. MAR1
3.3. MAR2
3.4. Imputation Methods
3.5. FCS-PMM
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BMI | Body Mass Index |
| MI | Multiple Imputation |
| FCS | Fully Conditional Specification |
| SMCFCS | Substantive Model Compatible Fully Conditional Specification |
| MCAR | Missing Completely at Random |
| MAR | Missing at Random |
| BLR | Bayesian Linear Regression |
| PMM | Predictive Mean Matching |
| MAR1 | First MAR structure used in the simulation study |
| MAR2 | Stricter MAR structure used in the simulation study |
| AWO | Active Imputation when the constituents are not predictors |
| APA | Active Imputation when the constituents are predictors |
| PNP | Standard Passive Imputation |
| LNP | Passive Imputation when the constituents are first log-transformed |
| PB | Percentage Bias |
| CR | Coverage Rate |
| AW | Average Width |
| FMI | Fraction of Missing Information |
| RIV | Relative Increase of Variance |
References
- Rubin, D.B. Multiple imputations in sample surveys—A phenomenological Bayesian approach to nonresponse. In Proceedings of the Survey Research Methods Section of the American Statistical Association, Alexandria, VA, USA, 2 January 1978; Volume 1, pp. 20–34. [Google Scholar]
- Pankhurst, L.; Mitra, R.; Kimber, A.C.; Collett, D. Multiply imputing missing values arising by design in transplant survival data. Biom. J. 2020, 62, 1192–1207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartlett, J.W.; Morris, T.P. Multiple imputation of covariates by substantive-model compatible fully conditional specification. Stata J. 2015, 15, 437–456. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, J.; Kenward, M. Multiple Imputation and Its Applications; Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Rubin, D.B. Multiple Imputation for Survey Nonresponse; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef]
- van Buuren, S. Flexible Imputation of Missing Data; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- White, I.R.; Royston, P.; Wood, A.M. Multiple imputation using chained equations: Issues and guidance for practice. Stat. Med. 2011, 30, 377–399. [Google Scholar] [CrossRef] [PubMed]
- Burton, A.; Altman, D.G.; Royston, P.; Holder, R.L. The design of simulation studies in medical statistics. Stat. Med. 2006, 25, 4279–4292. [Google Scholar] [CrossRef] [PubMed]
- van Buuren, S. Package ‘Mice’. Available online: https://github.com/cran/mice (accessed on 1 January 2022).
- Bartlett, J.; Keogh, R.; Bonneville, E.; Ekstrøm, C. Package ‘Smcfcs’. Available online: https://github.com/jwb133/smcfcs (accessed on 1 February 2021).
- Wagstaff, D.A.; Kranz, S.; Harel, O. A preliminary study of active compared with passive imputation of missing body mass index values among non-Hispanic white youths. Am. J. Clin. Nutr. 2009, 89, 1025–1030. [Google Scholar] [CrossRef] [PubMed]
- Morris, T.P.; White, I.R.; Royston, P.; Seaman, S.R.; Wood, A.M. Multiple imputation for an incomplete covariate that is a ratio. Stat. Med. 2014, 33, 88–104. [Google Scholar] [CrossRef] [Green Version]
- von Hippel, P.T. How to impute interactions, squares, and other transformed variables. Sociol. Methodol. 2009, 39, 265–291. [Google Scholar] [CrossRef]
- van Buuren, S. MICE: Passive Imputation and Post-Processing. Available online: https://www.gerkovink.com/miceVignettes/Passive_Post_processing/Passive_imputation_post_processing.html (accessed on 11 March 2019).
- Enders, C.K. Applied Missing Data Analysis; Guilford Press: New York, NY, USA, 2010. [Google Scholar]
- Eddings, W. A Note on How to Perform Multiple-Imputation Diagnostics in Stata. Available online: http://www.stata.com/users/ymarchenko/midiagnote.pdf (accessed on 20 May 2020).
- Brown, L.D.; Cai, T.T.; DasGupta, A. Interval estimation for a binomial proportion. Stat. Sci. 2001, 16, 101–133. [Google Scholar] [CrossRef]
| No Auxiliary Variables | One Auxiliary Variable | |||||||
|---|---|---|---|---|---|---|---|---|
| PB | CR (%) | AW | PB | CR (%) | AW | |||
| MCAR | FCS-BLR | AWO | 1.44 | 95.1 | 0.0239 | 0.88 | 96.2 | 0.0231 |
| APA | 1.28 | 96.3 | 0.0230 | 0.88 | 96.6 | 0.0224 | ||
| PNP | 3.12 | 95.1 | 0.0228 | 2.76 | 95.5 | 0.0223 | ||
| LNP | 0.26 | 95.7 | 0.0231 | 0.08 | 96.7 | 0.0226 | ||
| FCS-PMM | AWO | 1.92 | 94.3 | 0.0238 | 1.82 | 95.9 | 0.0229 | |
| APA | 1.14 | 96.0 | 0.0232 | 0.58 | 96.7 | 0.0222 | ||
| PNP | 0.86 | 95.6 | 0.0232 | 0.24 | 96.8 | 0.0221 | ||
| LNP | 0.60 | 95.8 | 0.0231 | 0.16 | 96.8 | 0.0224 | ||
| SMCFCS-BLR | PNP | 0.06 | 96.5 | 0.0228 | 0.02 | 96.2 | 0.0222 | |
| LNP | 0.54 | 96.4 | 0.0230 | 0.98 | 96.5 | 0.0224 | ||
| MAR1 | FCS-BLR | AWO | 1.66 | 95.1 | 0.0231 | 0.28 | 95.8 | 0.0224 |
| APA | 0.96 | 96.2 | 0.0223 | 0.20 | 96.1 | 0.0219 | ||
| PNP | 1.08 | 96.7 | 0.0222 | 1.84 | 95.6 | 0.0217 | ||
| LNP | 2.56 | 95.3 | 0.0224 | 1.74 | 96.0 | 0.0221 | ||
| FCS-PMM | AWO | 2.46 | 95.0 | 0.0232 | 1.54 | 96.2 | 0.0222 | |
| APA | 4.80 | 93.1 | 0.0226 | 2.96 | 95.1 | 0.0217 | ||
| PNP | 4.46 | 93.4 | 0.0226 | 2.46 | 95.9 | 0.0216 | ||
| LNP | 2.90 | 95.3 | 0.0225 | 1.94 | 96.1 | 0.0219 | ||
| SMCFCS-BLR | PNP | 0.12 | 96.8 | 0.0221 | 1.06 | 96.1 | 0.0216 | |
| LNP | 0.58 | 96.2 | 0.0223 | 0.34 | 96.0 | 0.0218 | ||
| MAR2 | FCS-BLR | AWO | 4.46 | 93.3 | 0.0224 | 1.32 | 94.8 | 0.0219 |
| APA | 2.56 | 95.1 | 0.0218 | 0.76 | 94.8 | 0.0215 | ||
| PNP | 0.32 | 95.2 | 0.0217 | 1.34 | 94.5 | 0.0213 | ||
| LNP | 4.64 | 92.4 | 0.0220 | 2.84 | 94.6 | 0.0217 | ||
| FCS-PMM | AWO | 0.64 | 76.7 | 0.0231 | 3.20 | 93.7 | 0.0216 | |
| APA | 7.12 | 88.4 | 0.0223 | 4.40 | 93.3 | 0.0213 | ||
| PNP | 6.88 | 88.8 | 0.0222 | 3.88 | 92.9 | 0.0212 | ||
| LNP | 5.24 | 91.2 | 0.0221 | 3.26 | 93.8 | 0.0216 | ||
| SMCFCS-BLR | PNP | 0.74 | 94.5 | 0.0212 | 2.44 | 94.2 | 0.0210 | |
| LNP | 0.10 | 95.4 | 0.0218 | 0.80 | 95.1 | 0.0214 | ||
| No Auxiliary Variables | One Auxiliary Variable | |||||
|---|---|---|---|---|---|---|
| FMI | RIV | FMI | RIV | |||
| MCAR | FCS-BLR | AWO | 0.304 | 0.436 | 0.256 | 0.344 |
| APA | 0.244 | 0.322 | 0.209 | 0.263 | ||
| PNP | 0.259 | 0.348 | 0.223 | 0.286 | ||
| LNP | 0.224 | 0.288 | 0.193 | 0.238 | ||
| FCS-PMM | AWO | 0.281 | 0.390 | 0.245 | 0.324 | |
| APA | 0.229 | 0.296 | 0.197 | 0.244 | ||
| PNP | 0.230 | 0.297 | 0.200 | 0.249 | ||
| LNP | 0.225 | 0.289 | 0.195 | 0.241 | ||
| SMCFCS-BLR | PNP | 0.242 | 0.326 | 0.204 | 0.260 | |
| LNP | 0.216 | 0.280 | 0.179 | 0.222 | ||
| MAR1 | FCS-BLR | AWO | 0.296 | 0.420 | 0.250 | 0.333 |
| APA | 0.231 | 0.300 | 0.204 | 0.255 | ||
| PNP | 0.249 | 0.331 | 0.218 | 0.278 | ||
| LNP | 0.202 | 0.252 | 0.175 | 0.211 | ||
| FCS-PMM | AWO | 0.247 | 0.328 | 0.210 | 0.264 | |
| APA | 0.208 | 0.262 | 0.179 | 0.217 | ||
| PNP | 0.207 | 0.260 | 0.180 | 0.218 | ||
| LNP | 0.199 | 0.248 | 0.174 | 0.210 | ||
| SMCFCS-BLR | PNP | 0.232 | 0.309 | 0.197 | 0.249 | |
| LNP | 0.191 | 0.240 | 0.158 | 0.190 | ||
| MAR2 | FCS-BLR | AWO | 0.286 | 0.400 | 0.243 | 0.320 |
| APA | 0.223 | 0.286 | 0.196 | 0.243 | ||
| PNP | 0.240 | 0.314 | 0.210 | 0.265 | ||
| LNP | 0.185 | 0.226 | 0.159 | 0.188 | ||
| FCS-PMM | AWO | 0.248 | 0.344 | 0.178 | 0.215 | |
| APA | 0.188 | 0.231 | 0.161 | 0.191 | ||
| PNP | 0.188 | 0.230 | 0.161 | 0.191 | ||
| LNP | 0.178 | 0.215 | 0.154 | 0.181 | ||
| SMCFCS-BLR | PNP | 0.222 | 0.289 | 0.189 | 0.236 | |
| LNP | 0.169 | 0.206 | 0.139 | 0.163 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clements, L.; Kimber, A.C.; Biedermann, S. Multiple Imputation of Composite Covariates in Survival Studies. Stats 2022, 5, 358-370. https://doi.org/10.3390/stats5020020
Clements L, Kimber AC, Biedermann S. Multiple Imputation of Composite Covariates in Survival Studies. Stats. 2022; 5(2):358-370. https://doi.org/10.3390/stats5020020
Chicago/Turabian StyleClements, Lily, Alan C. Kimber, and Stefanie Biedermann. 2022. "Multiple Imputation of Composite Covariates in Survival Studies" Stats 5, no. 2: 358-370. https://doi.org/10.3390/stats5020020
APA StyleClements, L., Kimber, A. C., & Biedermann, S. (2022). Multiple Imputation of Composite Covariates in Survival Studies. Stats, 5(2), 358-370. https://doi.org/10.3390/stats5020020






