Bayesian Semiparametric Regression Analysis of Multivariate Panel Count Data
Abstract
:1. Introduction
2. Model and Notation
2.1. Model Construction
2.2. Correlation Expression
3. The Proposed Bayesian Semiparametric Approach
3.1. Modeling with Monotone I-Splines
3.2. Likelihood Augmentation with Poisson Latent Variables
3.3. Prior Specification and Posterior Computation
- Sample (, …, ) from a multinomial distribution , for ; , where with , and
- Sample from a Gamma distribution , for , withand
- Sample from a Gamma distribution , for .
- Sample by using the adaptive rejection sampling (ARS) [28] method, for . The log full conditional distribution of each is proportional to
- Sample for , by using the ARS. The log full conditional distribution of each is proportional to
- Sample by using the ARMS, the log full conditional distribution of which is proportional to
- Sample , for , by using the ARMS, the log full conditional distribution of which is proportional toIn the R function arms(), we set the low bound of the support of as .
4. Simulation Studies
4.1. Data Generation
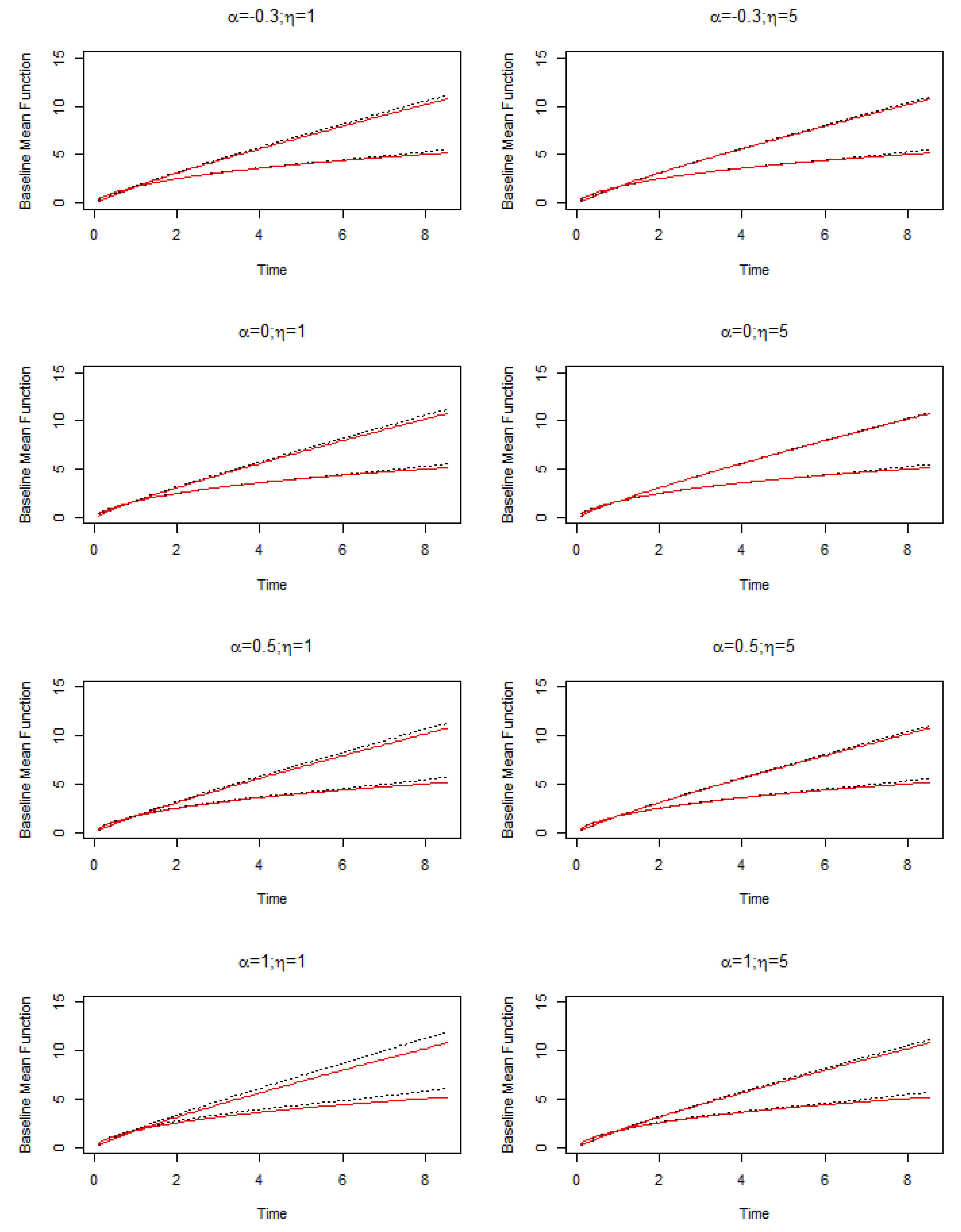
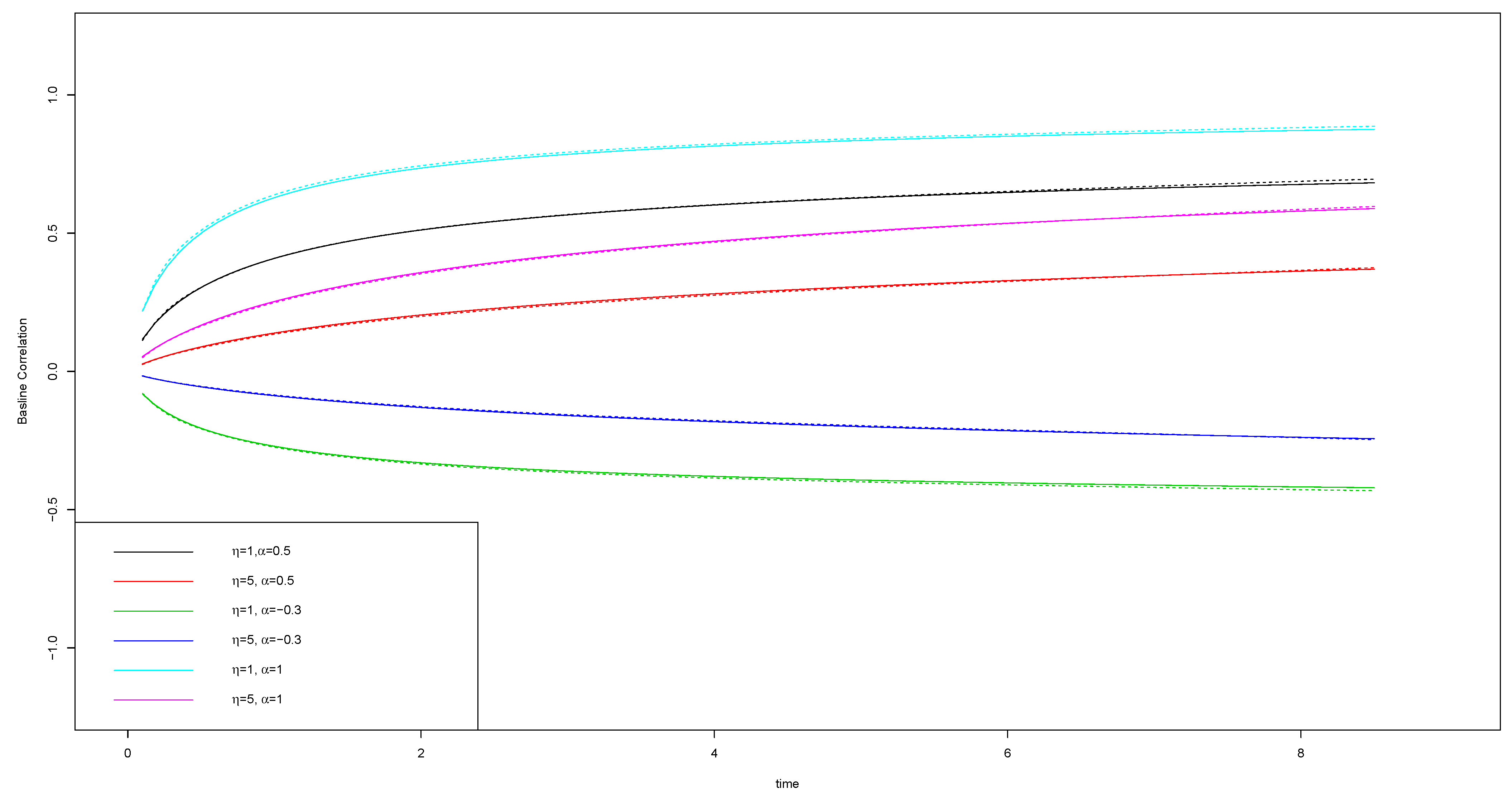
4.2. Simulation Results
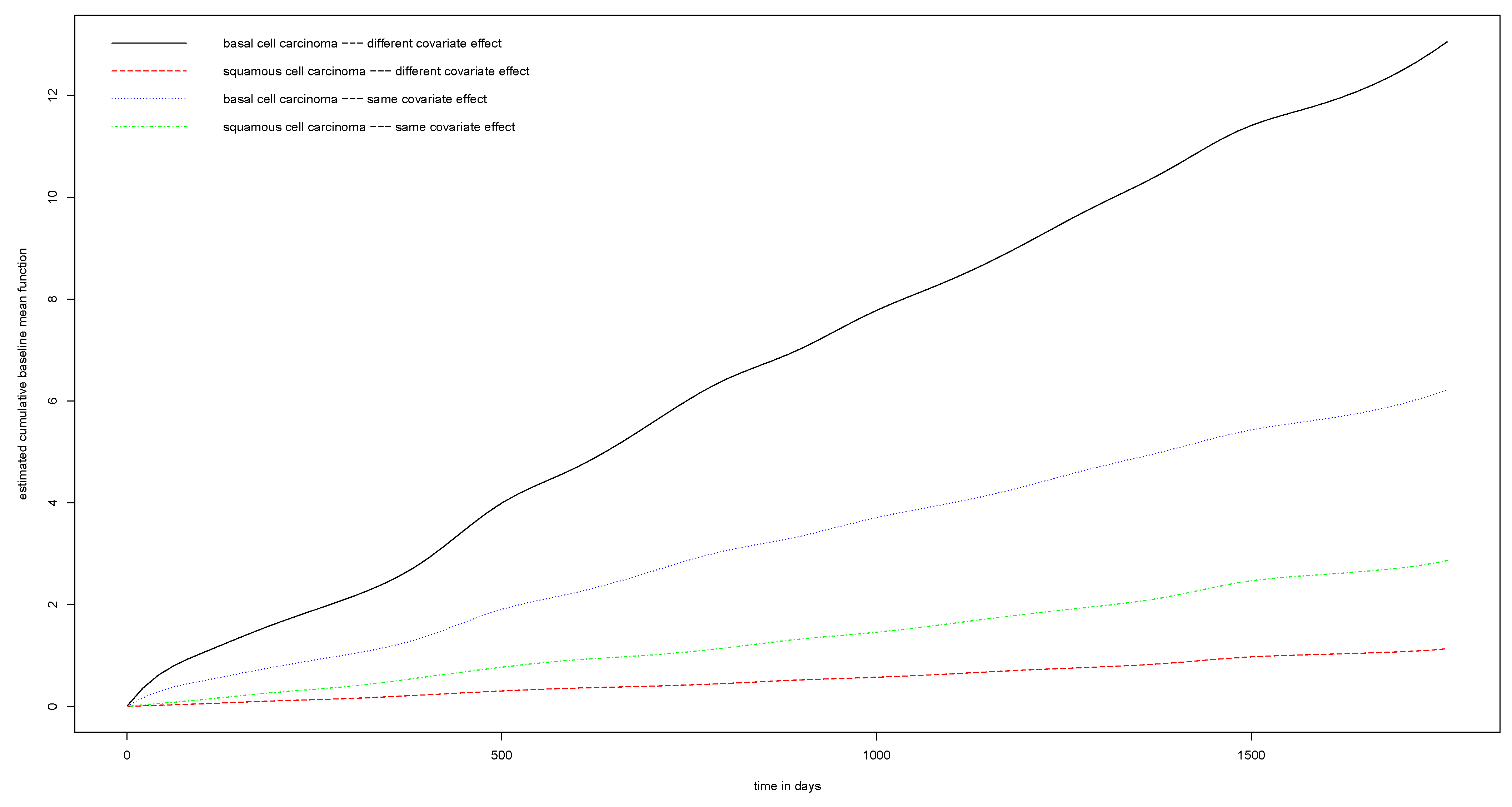
5. Real Data Analysis
6. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Cov(Ni(j), Ni(k) ), Var(Ni(j) ), and Var(Ni(k) ) for αj = 1
| Parameter | Truth | Bias | SD | SE | CP95 | Bias | SD | SE | CP95 |
| 0 | 0.0583 | 0.2238 | 0.1988 | 0.9520 | 0.0214 | 0.1287 | 0.1319 | 0.9400 | |
| 1 | 0.0004 | 0.1215 | 0.1223 | 0.9520 | 0.0015 | 0.0696 | 0.0722 | 0.9300 | |
| 1 | 0.0561 | 0.2225 | 0.1975 | 0.9700 | 0.0203 | 0.1291 | 0.1236 | 0.9600 | |
| 1 | −0.0002 | 0.1203 | 0.1220 | 0.9480 | 0.0004 | 0.0683 | 0.0689 | 0.9460 | |
| 0 | 0.0392 | 0.2294 | 0.2179 | 0.9580 | 0.0178 | 0.1303 | 0.1311 | 0.9520 | |
| 1 | −0.0053 | 0.1245 | 0.1228 | 0.9520 | −0.0008 | 0.0714 | 0.0709 | 0.9520 | |
| −1 | 0.0647 | 0.2523 | 0.2479 | 0.9560 | 0.0364 | 0.1651 | 0.1607 | 0.9500 | |
| 1 | −0.0109 | 0.1344 | 0.1297 | 0.9620 | −0.0001 | 0.0858 | 0.0824 | 0.9620 | |
| 1 | 0.0490 | 0.2198 | 0.2133 | 0.9500 | 0.0119 | 0.1203 | 0.1191 | 0.9540 | |
| 1 | −0.0078 | 0.1182 | 0.1202 | 0.9280 | −0.0017 | 0.0646 | 0.0653 | 0.9380 | |
| −1 | 0.0771 | 0.2497 | 0.2373 | 0.9440 | 0.0400 | 0.1629 | 0.1593 | 0.9500 | |
| 1 | −0.0127 | 0.1323 | 0.1335 | 0.9440 | −0.0026 | 0.0840 | 0.0825 | 0.9600 | |
| 1 | −0.0639 | 0.2152 | 0.2173 | 0.9320 | −0.0178 | 0.1192 | 0.1194 | 0.9392 | |
| −1 | 0.0025 | 0.1138 | 0.1121 | 0.9500 | 0.0051 | 0.0633 | 0.0678 | 0.9392 | |
| 1 | −0.0663 | 0.2202 | 0.2247 | 0.9300 | −0.0219 | 0.1280 | 0.1329 | 0.9196 | |
| 1 | 0.0031 | 0.1177 | 0.1156 | 0.9440 | 0.0046 | 0.0681 | 0.0786 | 0.9412 | |
| Parameter | Bias | SD | SE | CP95 | Bias | SD | SE | CP95 | |
| −0.0269 | 0.2190 | 0.2266 | 0.9300 | −0.0124 | 0.1216 | 0.1252 | 0.9360 | ||
| −0.0054 | 0.1168 | 0.1202 | 0.9460 | 0.0006 | 0.0652 | 0.0685 | 0.9460 | ||
| −0.0086 | 0.1048 | 0.1049 | 0.9440 | −0.0022 | 0.0829 | 0.0812 | 0.9540 | ||
| 0.0021 | 0.0548 | 0.0580 | 0.9400 | 0.0006 | 0.0421 | 0.0421 | 0.9600 | ||
| −0.0083 | 0.0423 | 0.0462 | 0.9200 | −0.0033 | 0.1010 | 0.1010 | 0.9400 | ||
| 0.0412 | 0.1699 | 0.1754 | 0.9440 | 0.2494 | 1.0231 | 0.8814 | 0.9740 | ||
| −0.0051 | 0.2229 | 0.2256 | 0.9400 | −0.0017 | 0.1208 | 0.1175 | 0.9588 | ||
| −0.0043 | 0.1195 | 0.1195 | 0.9460 | −0.0004 | 0.0654 | 0.0682 | 0.9294 | ||
| −0.0034 | 0.0758 | 0.0767 | 0.9460 | −0.0048 | 0.0770 | 0.0749 | 0.9608 | ||
| −0.0010 | 0.0370 | 0.0378 | 0.9580 | 0.0007 | 0.0377 | 0.0365 | 0.9627 | ||
| 0.0028 | 0.0344 | 0.0349 | 0.9420 | 0.0017 | 0.1152 | 0.1078 | 0.9784 | ||
| 0.0328 | 0.1790 | 0.1781 | 0.9560 | 0.6264 | 1.3301 | 1.3349 | 0.9588 | ||
| −0.0190 | 0.2194 | 0.2227 | 0.9360 | −0.0076 | 0.1213 | 0.1179 | 0.9588 | ||
| −0.0136 | 0.1162 | 0.1190 | 0.9340 | 0.0001 | 0.0647 | 0.0652 | 0.9490 | ||
| −0.0263 | 0.1372 | 0.1338 | 0.9400 | −0.0143 | 0.0958 | 0.0946 | 0.9549 | ||
| −0.0047 | 0.0719 | 0.0697 | 0.9600 | 0.0010 | 0.0497 | 0.0475 | 0.9588 | ||
| 0.0066 | 0.0589 | 0.0578 | 0.9480 | 0.0163 | 0.1213 | 0.1246 | 0.9471 | ||
| 0.0496 | 0.1729 | 0.1841 | 0.9500 | 0.4241 | 1.2655 | 1.2633 | 0.9569 | ||
| −0.0639 | 0.2152 | 0.2173 | 0.9320 | −0.0178 | 0.1192 | 0.1194 | 0.9392 | ||
| 0.0025 | 0.1138 | 0.1121 | 0.9500 | 0.0051 | 0.0633 | 0.0678 | 0.9392 | ||
| −0.0663 | 0.2202 | 0.2247 | 0.9300 | −0.0219 | 0.1280 | 0.1329 | 0.9196 | ||
| 0.0031 | 0.1177 | 0.1156 | 0.9440 | 0.0046 | 0.0681 | 0.0786 | 0.9412 | ||
| 0.0089 | 0.0804 | 0.0745 | 0.9760 | 0.0294 | 0.1529 | 0.1577 | 0.9392 | ||
| 0.0469 | 0.1684 | 0.1734 | 0.9540 | 0.3745 | 1.2136 | 1.2777 | 0.9490 | ||

| Parameter | Bias | SD | SE | CP95 | Bias | SD | SE | CP95 | |
| −0.0438 | 0.1344 | 0.2443 | 0.7220 | −0.0130 | 0.1016 | 0.1288 | 0.8640 | ||
| 0.0061 | 0.0710 | 0.1388 | 0.7080 | 0.0009 | 0.0536 | 0.0722 | 0.8500 | ||
| −0.0206 | 0.1353 | 0.1628 | 0.8880 | −0.0103 | 0.1085 | 0.0938 | 0.9800 | ||
| 0.0062 | 0.0715 | 0.0967 | 0.8540 | 0.0027 | 0.0574 | 0.0525 | 0.9720 | ||
| 2.6937 | 0.6275 | 0.9058 | 0.0000 | 3.9252 | 0.8115 | 0.3937 | 0.0060 | ||
| −0.0114 | 0.1459 | 0.2308 | 0.7820 | −0.0046 | 0.1021 | 0.1205 | 0.9080 | ||
| −0.0028 | 0.0770 | 0.1294 | 0.7700 | 0.0010 | 0.0544 | 0.0690 | 0.8760 | ||
| −0.0302 | 0.1513 | 0.1166 | 0.9800 | −0.0095 | 0.1106 | 0.0843 | 0.9900 | ||
| 0.0080 | 0.0802 | 0.0709 | 0.9820 | 0.0031 | 0.0587 | 0.0474 | 0.9780 | ||
| 1.9095 | 0.4903 | 0.6390 | 0.0000 | 3.6761 | 0.9184 | 0.5119 | 0.0320 | ||
| −0.0282 | 0.1826 | 0.2277 | 0.8840 | −0.0059 | 0.1073 | 0.1185 | 0.9160 | ||
| −0.0092 | 0.0962 | 0.1194 | 0.8780 | −0.0002 | 0.0568 | 0.0646 | 0.9220 | ||
| −0.0536 | 0.1893 | 0.1383 | 0.9760 | −0.0193 | 0.1162 | 0.0962 | 0.9780 | ||
| −0.0016 | 0.0997 | 0.0777 | 0.9880 | 0.0037 | 0.0617 | 0.0496 | 0.9920 | ||
| 0.5948 | 0.2502 | 0.2712 | 0.2160 | 2.3688 | 1.1662 | 0.9781 | 0.4600 | ||
| −0.0679 | 0.2161 | 0.2179 | 0.9320 | −0.0181 | 0.1196 | 0.1194 | 0.9420 | ||
| 0.0029 | 0.1136 | 0.1118 | 0.9500 | 0.0027 | 0.0631 | 0.0614 | 0.9500 | ||
| −0.0690 | 0.2202 | 0.2261 | 0.9380 | −0.0208 | 0.1276 | 0.1315 | 0.9280 | ||
| 0.0022 | 0.1170 | 0.1155 | 0.9520 | 0.0019 | 0.0673 | 0.0702 | 0.9440 | ||
| 0.0401 | 0.1552 | 0.1614 | 0.9400 | 0.1853 | 0.9692 | 0.9736 | 0.9600 | ||
| basal | −0.1902 | 0.1028 | −0.0376 | 0.0238 |
| 0.1500 | 0.0145 | 0.0055 | 0.1506 | |
| (−0.4894, 0.0987) | (0.0762, 0.1330) * | (−0.0487, −0.0273) * | (−0.2717, 0.3185) | |
| squamous | 0.1055 | 0.1451 | −0.0196 | 0.3053 |
| 0.2174 | 0.0213 | 0.0070 | 0.2142 | |
| (−0.3153, 0.5251) | (0.1051, 0.0.1894) * | ( −0.0333, −0.0060) * | (−0.1165, 0.7255) |
| Proposed | −0.1509 | 0.0810 | −0.0264 | 0.0636 |
| 0.1381 | 0.0122 | 0.0052 | 0.1409 | |
| (−0.4203, 0.1197) | (0.0599, 0.1087) * | (−0.0367, −0.0169) * | (−0.2098, 0.3369) | |
| He et al. | −0.0239 | 0.1440 | −0.0116 | 0.3807 |
| 0.1809 | 0.0212 | 0.0084 | 0.1778 | |
| (−0.3785, 0.3307) | (0.1024, 0.1856) * | (−0.0281, 0.0049) | (0.0322, 0.7292) * | |
| Zhang et al. | −0.2253 | 0.0784 | 0.0016 | 0.2534 |
| 0.1831 | 0.0090 | 0.0087 | 0.1942 | |
| (−0.5842, 0.1336) | (0.0608, 0.0960) * | (−0.0155, 0.0187) | (−0.1272, 0.06340) |

References
- Sun, J.; Zhao, X. Statistical Analysis of Panel Count Data; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sun, J.; Kalbfleisch, J. Estimation of the mean function of point processes based on panel count data. Stat. Sin. 1995, 5, 279–289. [Google Scholar]
- Wellner, J.A.; Zhang, Y. Two estimators of the mean of a counting process with panel count data. Ann. Stat. 2000, 28, 779–814. [Google Scholar] [CrossRef]
- Wellner, J.A.; Zhang, Y. Two likelihood-based semiparametric estimation methods for panel count data with covariates. Ann. Stat. 2007, 35, 2106–2142. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.; Zhang, Y.; Huang, J. Estimation of the mean function with panel count data using monotone polynomial splines. Biometrika 2007, 94, 705–718. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.; Zhang, Y.; Huang, J. Semiparametric estimation methods for panel count data using monotone B-splines. J. Am. Stat. Assoc. 2009, 104, 1060–1070. [Google Scholar] [CrossRef]
- Wang, J.; Lin, X. A Bayesian approach for semiparametric regression analysis of panel count data. Lifetime Data Anal. 2020, 26, 402–420. [Google Scholar] [CrossRef]
- He, X.; Tong, X.; Sun, J.; Cook, R.J. Regression analysis of multivariate panel count data. Biostatistics 2008, 9, 234–248. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, H.; Sun, J.; Wang, D.; Kim, K. Regression analysis of multivariate panel count data with an informative observation process. J. Multivar. Anal. 2013, 119, 71–80. [Google Scholar] [CrossRef]
- Li, N.; Park, D.H.; Sun, J.; Kim, K. Semiparametric transformation models for multivariate panel count data with dependent observation process. Can. J. Stat. 2010, 39, 458–474. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Li, Y.; Sun, J. Semiparametric analysis of multivariate panel count data with dependent observation processes and a terminal event. J. Nonparametr. Stat. 2013, 25, 379–394. [Google Scholar] [CrossRef]
- He, X.; Feng, X.; Tong, X.; Xingqiu, Z. Semiparametric partially linear varying coefficient models with panel count data. Lifetime Data Anal. 2017, 23, 439–466. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zhang, Y.; Zhao, X.; Yu, Z. A nonparametric regression model for panel count data analysis. Stat. Sin. 2019, 29, 809–826. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yu, Z. A kernel regression model for panel count data with time-varying coefficients. arXiv 2019, arXiv:1903.10233. [Google Scholar] [CrossRef]
- Li, Y.; He, X.; Wang, H.; Zhang, B.; Sun, J. Semiparametric regression of multivariate panel count data with informative observation times. J. Multivar. Anal. 2015, 140, 209–219. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z. A kernel regression model for panel count data with nonparametric covariate functions. Biometrics 2021. [Google Scholar] [CrossRef]
- Chib, S.; Greenberg, E.; Winkelmann, R. Posterior simulation and Bayes factors in panel count data models. J. Econom. 1998, 86, 33–54. [Google Scholar] [CrossRef] [Green Version]
- Ramsay, J. Monotone regression splines in action. Stat. Sci. 1988, 3, 425–441. [Google Scholar] [CrossRef]
- Dimitrakopoulos, S. Bayesian Estimation of Panel Count Data Models: Dynamics, Latent Heterogeneity, Serial Error Correlation, and Nonparametric Structures. Panel Data Econom. 2019, 6, 147–173. [Google Scholar]
- Liang, Y.; Li, Y.; Zhang, B. Bayesian nonparametric inference for panel count data with an informative observation process. Biom. J. 2018, 60, 583–596. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Tong, X.; He, X. Regression analysis of panel count data with dependent observation times. Biometrics 2007, 63, 1053–1059. [Google Scholar] [CrossRef]
- Sinha, D.; Maiti, T. A Bayesian approach for the analysis of panel-count data with dependent termination. Biometrics 2004, 60, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Cai, B.; Wang, L.; Zhang, Z. A Bayesian proportional hazards model for general interval-censored data. Lifetime Data Anal. 2015, 21, 470–490. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; Lin, X.; Wang, L. Bayesian proportional hazards model for current status data with monotone splines. Comput. Stat. Data Anal. 2011, 55, 2644–2651. [Google Scholar] [CrossRef]
- Wang, L.; Dunson, D.B. Semiparametric Bayes’ Proportional Odds Models for Current Status Data with Underreporting. Biometrics 2011, 67, 1111–1118. [Google Scholar] [CrossRef] [Green Version]
- Green, P.J. Reversible Jump Markov Chain Monte Carlo Computation and Bayesian Model Determination. Biometrika 1995, 82, 711–732. [Google Scholar] [CrossRef]
- Park, T.; Casella, G. The Bayeisan Lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Gilks, W.R.; Wild, P. Adaptive rejection sampling for Gibbs sampling. Appl. Stat. 1992, 41, 337–348. [Google Scholar] [CrossRef]
- Gilks, W.R.; Best, N.; Tan, K. Adaptive rejection Metropolis sampling within Gibbs sampling. Appl. Stat. 1995, 44, 455–472. [Google Scholar] [CrossRef] [Green Version]
- Petris, G.; Tardella, L. Original C code for ARMS by Wally Gilks. HI: Simulation from Distributions Supported by Nested Hyperplanes. R Package Version 0.4. 2013. Available online: https://rdrr.io/cran/HI/ (accessed on 10 January 2022).
- Plummer, M.; Best, N.; Cowles, K.; Vines, K. CODA: Convergence Diagnosis and Output Analysis for MCMC. R News 2006, 6, 7–11. [Google Scholar]
- Bedair, K.F.; Hong, Y.; Al-Khalidi, H.R. Copula-frailty models for recurrent event data based on Monte Carlo EM algorithm. J. Stat. Comput. Simul. 2021, 91, 3530–3548. [Google Scholar] [CrossRef]
- Balan, T.; Putter, H. A tutorial on frailty models. Stat. Methods Med. Res. 2020, 29, 3424–3452. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Lin, X. Bayesian Semiparametric Regression Analysis of Multivariate Panel Count Data. Stats 2022, 5, 477-493. https://doi.org/10.3390/stats5020028
Wang C, Lin X. Bayesian Semiparametric Regression Analysis of Multivariate Panel Count Data. Stats. 2022; 5(2):477-493. https://doi.org/10.3390/stats5020028
Chicago/Turabian StyleWang, Chunling, and Xiaoyan Lin. 2022. "Bayesian Semiparametric Regression Analysis of Multivariate Panel Count Data" Stats 5, no. 2: 477-493. https://doi.org/10.3390/stats5020028






