Newcomb–Benford’s Law in Neuromuscular Transmission: Validation in Hyperkalemic Conditions
Abstract
:1. Introduction
2. Mathematical Formulation of NBL
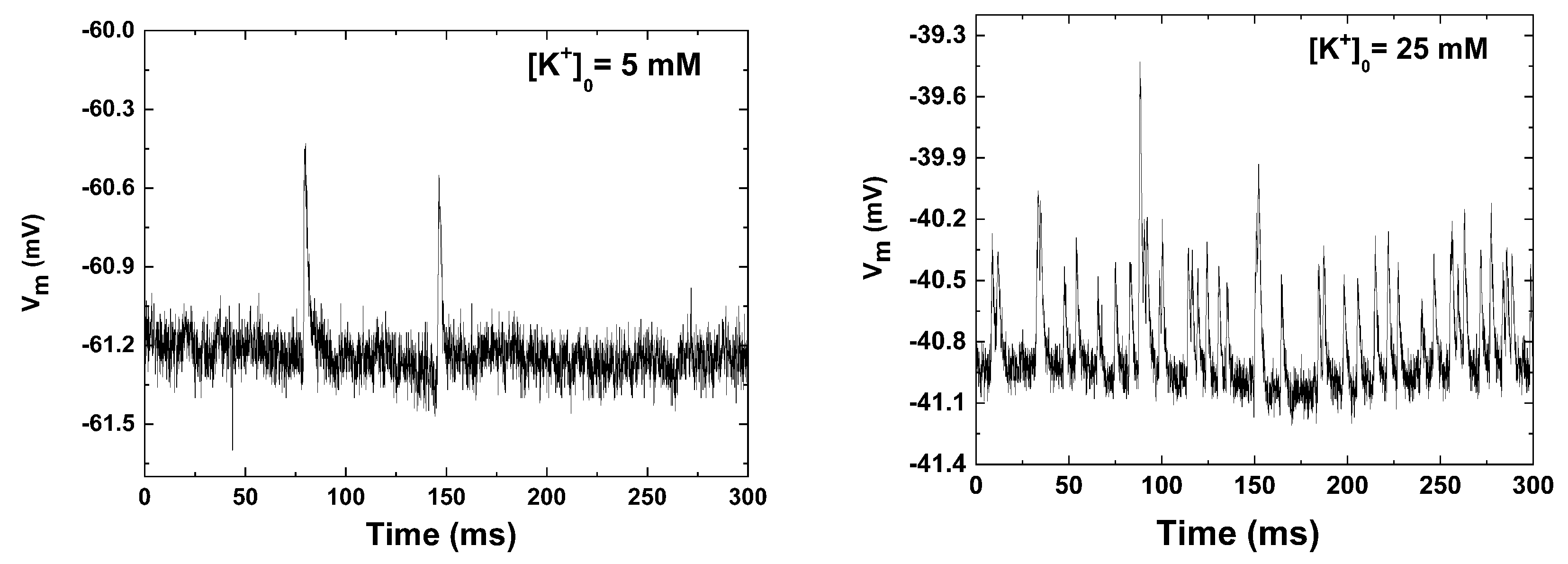
3. Electrophysiological Recordings
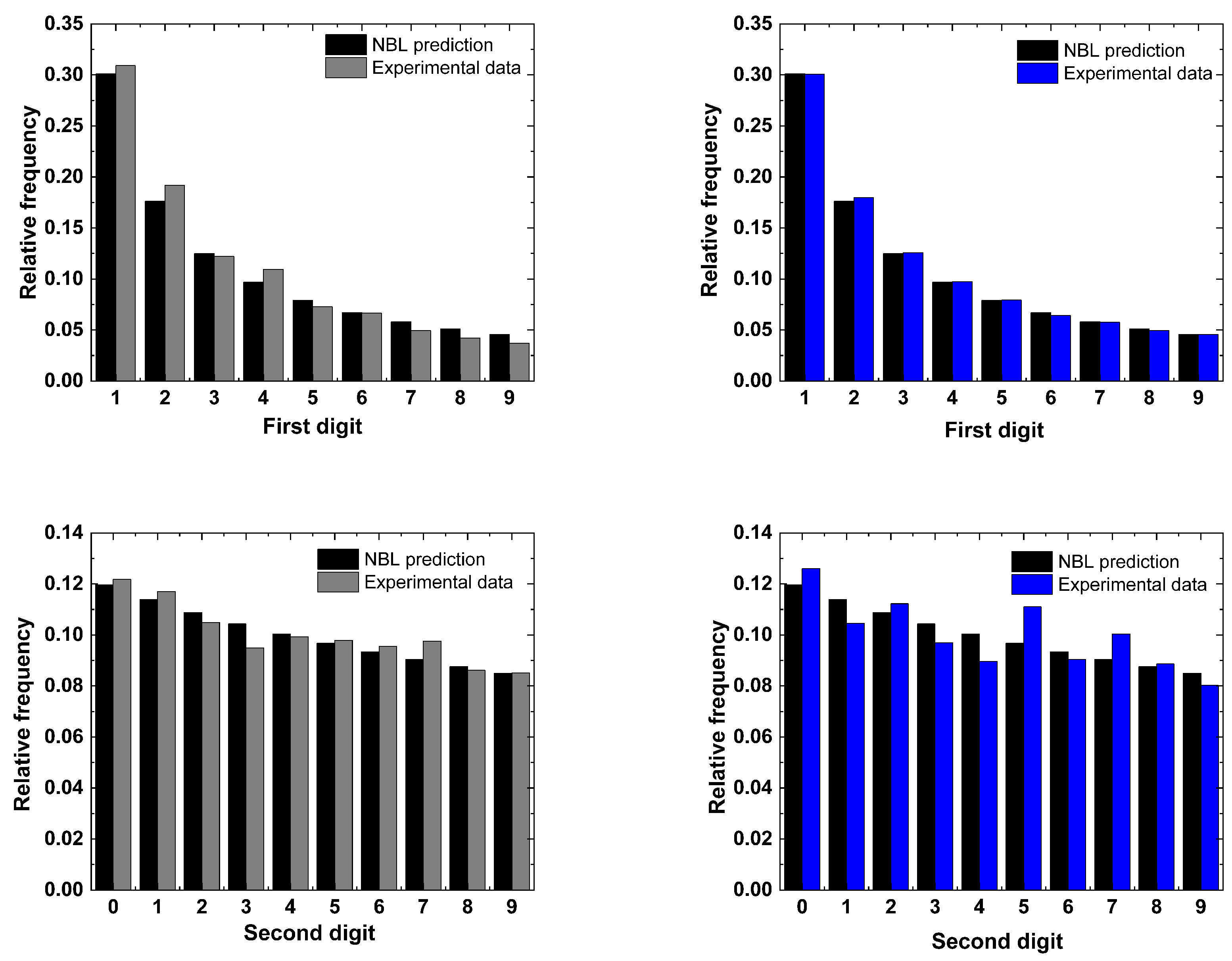
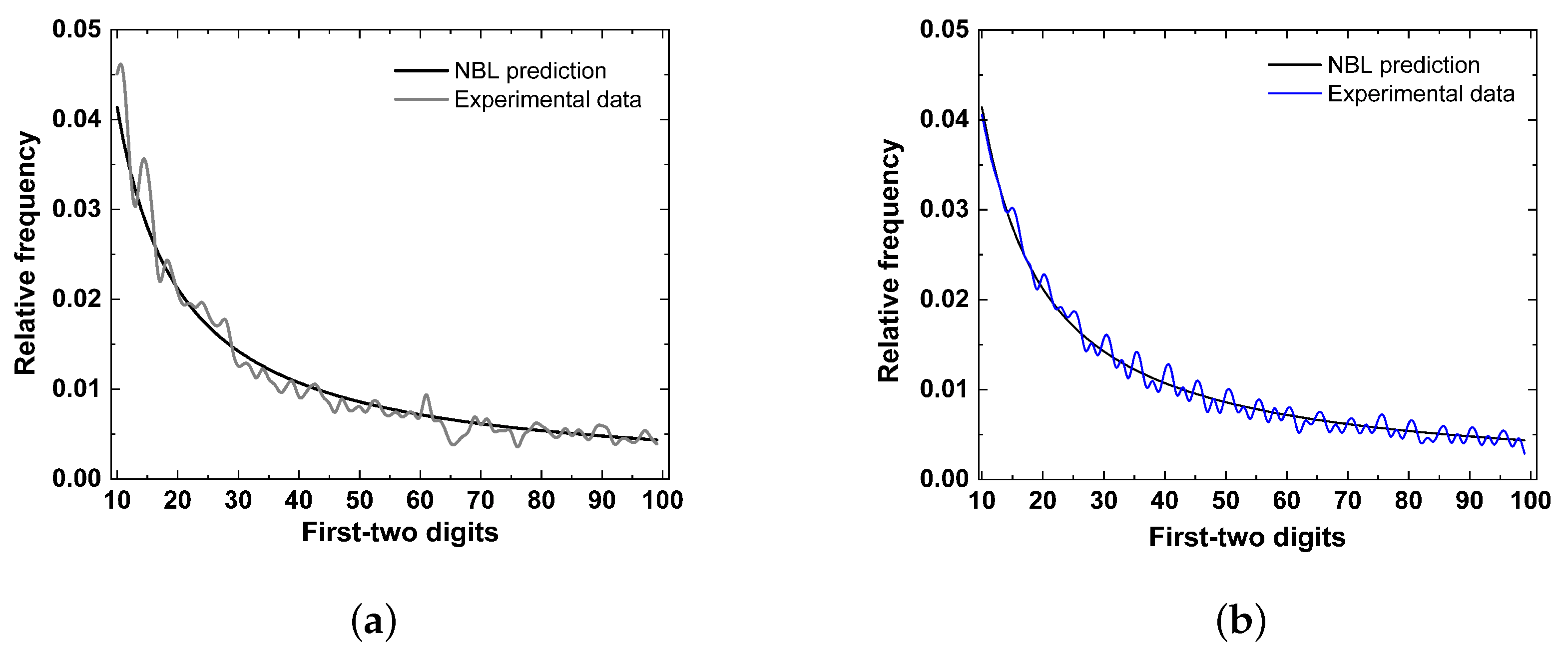
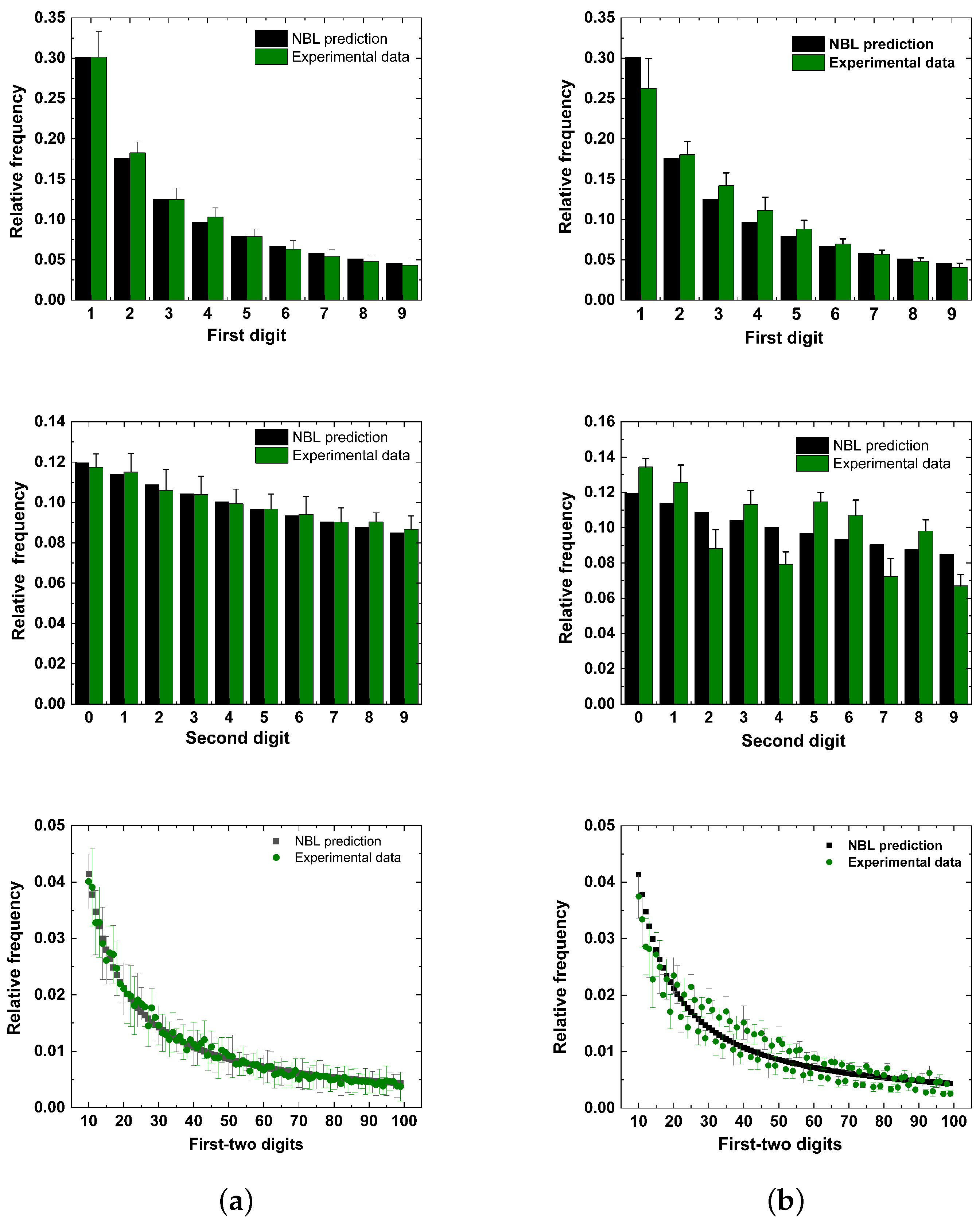
4. Conformity Analysis
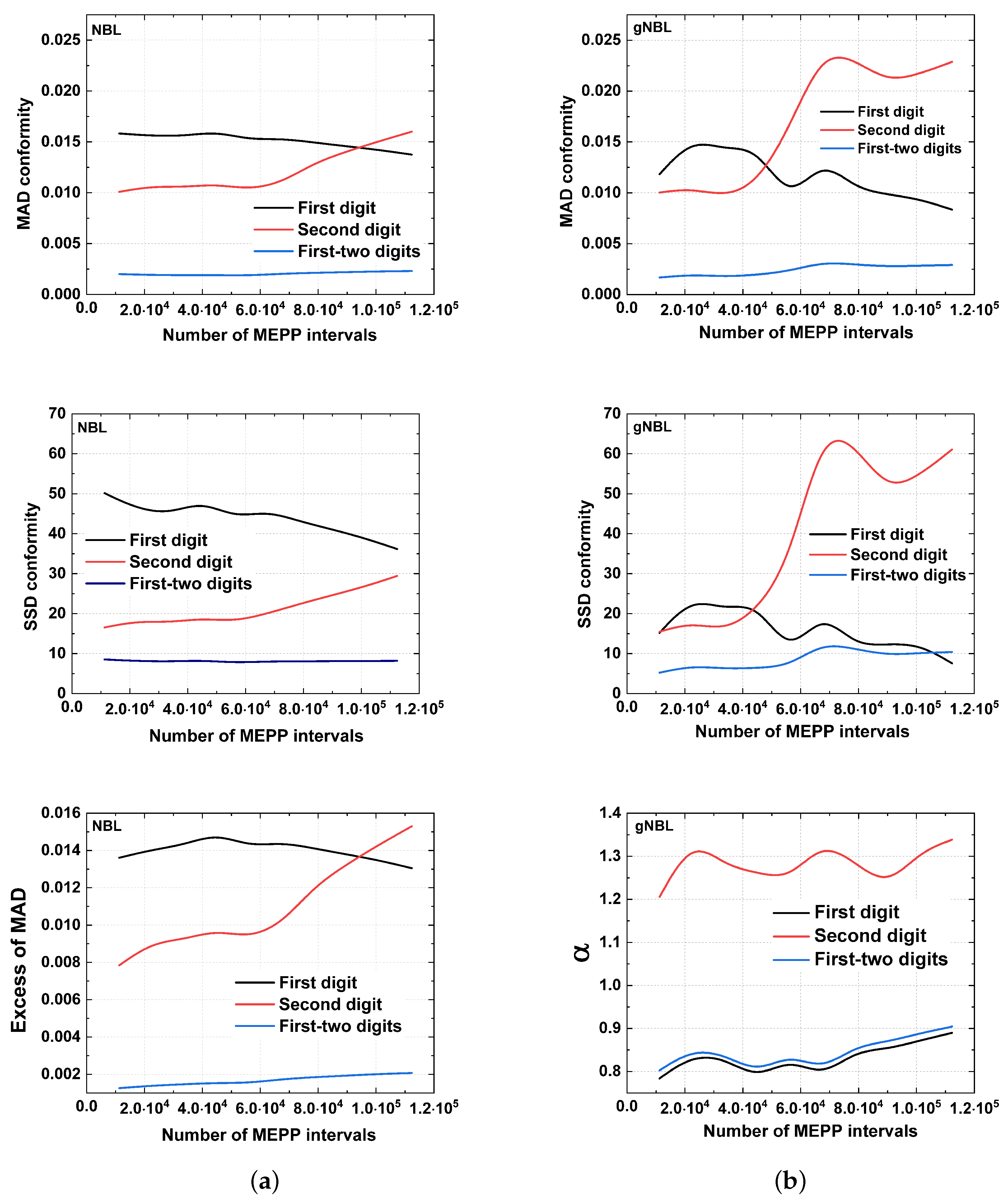
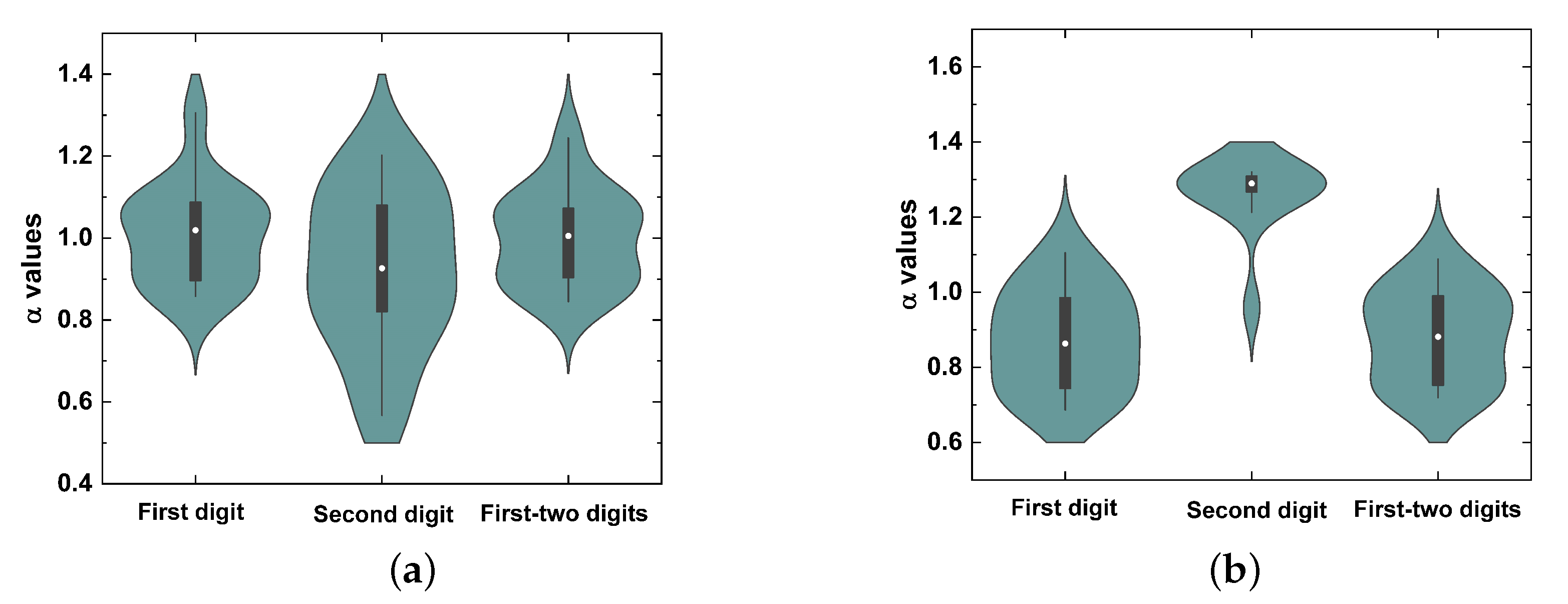
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van der Kloot, W. The regulation of quantal size. Prog. Neurobiol. 1991, 36, 93–130. [Google Scholar] [CrossRef]
- Katz, B. Quantal mechanism of neural transmitter release. Science 1971, 173, 123–126. [Google Scholar] [CrossRef]
- Bennett, M.R.; Kearns, J.L. Statistics of transmitter release at nerve terminals. Prog. Neurobiol. 2000, 60, 545–606. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J. Estimation of parameters for a model of transmitter release at synapses. Biometrics 1976, 32, 61–68. [Google Scholar] [CrossRef]
- Washio, H.M.; Inouye, S.T. The statistical analysis of spontaneous transmitter release at individual junctions on cockroach muscle. J. Exp. Biol. 1980, 87, 195–201. [Google Scholar] [CrossRef]
- Cohen, I.; Kita, H.; Van der Kloot, W. Miniature end-plate potentials: Evidence that the intervals are not fit by a Poisson distribution. Brain Res. 1973, 54, 318–323. [Google Scholar] [CrossRef]
- Lowen, S.B.; Cash, S.S.; Poo, M.; Teich, M.C. Quantal neurotransmitter secretion rate exhibits fractal behavior. J. Neurosci. 1997, 17, 5666–5677. [Google Scholar] [CrossRef] [PubMed]
- Takeda, T.; Sakata, A.; Matsuoka, T. Fractal dimensions in the occurrence of miniature end-plate potential in a vertebrate neuromuscular junction. Prog. Neuropsychopharmacol. Biol. Psychiatry. 1999, 23, 1157–1169. [Google Scholar] [CrossRef]
- da Silva, A.J.; Lima, R.F.; Moret, M.A. Nonextensivity and self-affinity in the mammalian neuromuscular junction. Phys. Rev. E 2011, 84, 041925. [Google Scholar] [CrossRef]
- Newcomb, S. Note on the Frequency of Use of the Different Digits in Natural Numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef]
- Benford, F. The Law of Anomalous Numbers. Benford. Proc. Am. Philos. Soc. 1938, 78, 551–572. Available online: https://www.jstor.org/stable/984802 (accessed on 4 September 2023).
- Kossovsky, A.E. Benford’s Law: Theory, the General Law of Relative Quantities, and Forensic Fraud Detection Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Berger, A.; Hill, T. An Introduction to Benford’s Law; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Hill, T.P. A Statistical Derivation of the Significant-Digit Law. Stat. Sci. 1995, 10, 354–363. Available online: https://www.jstor.org/stable/2246134 (accessed on 4 September 2023). [CrossRef]
- Hill, T.P. The Significant-Digit Phenomenon. Am. Math. Mon. 1995, 102, 322–327. [Google Scholar] [CrossRef]
- Hill, T.P. Base-Invariance Implies Benford’s Law. Proc. Am. Math. Soc. 1995, 123, 887–895. Available online: https://www.ams.org/journals/proc/1995-123-03/S0002-9939-1995-1233974-8/ (accessed on 4 September 2023).
- Burgos, A.; Santos, A. The Newcomb–Benford law: Scale invariance and a simple Markov process based on it. Am. J. Phys. 2021, 89, 851–861. [Google Scholar] [CrossRef]
- Morag, S.; Salmon-Divon, M. Characterizing Human Cell Types and Tissue Origin Using the Benford Law. Cells 2019, 8, 1004. [Google Scholar] [CrossRef] [PubMed]
- Crocetti, E.; Randi, G. Using the Benford’s Law as a First Step to Assess the Quality of the Cancer Registry Data. Front. Public Health 2016, 13, 225. [Google Scholar] [CrossRef]
- Yan, X.; Yang, S.; Kim, B.J.; Minnhagen, P. Benford’s law and first letter of words. Phys. A Stat. Mech. Appl. 2018, 512, 305–315. [Google Scholar] [CrossRef]
- Toledo, P.A.; Riquelme, S.R.; Campos, J.A. Earthquake source parameters that display the first digit phenomenon. Nonlin. Process. Geophys. 2015, 22, 625–632. [Google Scholar] [CrossRef]
- Bassingthwaighte, J.B.; Leibovitch, L.S.; West, B.J. Fractal Physiology; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Seenivasan, P.; Easwaran., S.; Sridhar, S.; Sinha, S. Using Skewness and the First-Digit Phenomenon to Identify Dynamical Transitions in Cardiac Models. Front. Physiol. 2015, 6, 390. [Google Scholar] [CrossRef]
- Tirunagari, S.; Abasolo, D.; Iorliam, A.; Ho, A.T.S.; Poh, N. Using Benford’s law to detect anomalies in electroencephalogram: An application to detecting Alzheimer’s disease. In Proceedings of the IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology, Manchester, UK, 23–25 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Silva, A.J.; Floquet, S.; Santos, D.O.C.; Lima, R.F. On the validation of Newcomb–Benford law and Weibull distribution in neuromuscular transmission. Phys. A Stat. Mech. Appl. 2020, 553, 124606. [Google Scholar] [CrossRef]
- Lindinger, M.I.; Cairns, S.P. Regulation of muscle potassium: Exercise performance, fatigue and health implications. Eur. J. Appl. Physiol. 2021, 121, 721–748. [Google Scholar] [CrossRef]
- Maljevic, S.; Lerche, H. Potassium channels: A review of broadening therapeutic possibilities for neurological diseases. J. Neurol. 2013, 260, 2201–2211. [Google Scholar] [CrossRef]
- Grohovaz, F.; Fesce, R.; Haimann, C. Dual effect of potassium on transmitter exocytosis. Cell Biol. Int. Rep. 1989, 12, 1085–1095. [Google Scholar] [CrossRef]
- Adrian, R.H. The effect of internal and external potassium concentration on the membrane potential of frog muscle. J. Physiol. 1956, 133, 631–658. [Google Scholar] [CrossRef]
- Ceccarelli, B.; Fesce, R.; Grohovaz, F.; Haimann, C. The effect of potassium on exocytosis of transmitter at the frog neuromuscular junction. J. Physiol. 1988, 401, 163–183. [Google Scholar] [CrossRef] [PubMed]
- Syková, E.; Nicholson, C. Diffusion in brain extracellular space. Physiol. Rev. 2008, 88, 1277–1340. [Google Scholar] [CrossRef]
- Diekmann, A. Not the First Digit! Using Benford’s Law to Detect Fraudulent Scientific Data. J. Appl. Stat. 2007, 34, 321–329. [Google Scholar] [CrossRef]
- Nigrini, M.J. Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Díaz, J.; Gallart, J.; Ruiz, M. On the Ability of the Benford’s Law to Detect Earthquakes and Discriminate Seismic Signals. Seismol. Res. Lett. 2014, 86, 192–201. [Google Scholar] [CrossRef]
- Gauvrit, N.G.; Houillon, J.C.; Delahaye, J.P. Generalized Benford’s Law as a Lie Detector. Adv. Cogn. Psychol. 2017, 13, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Pietronero, L.; Tosatti, E.; Tosatti, V.; Vespignani, A. Explaining the uneven distribution of numbers in nature: The laws of Benford and Zipf. Phys. A 2001, 293, 297–304. [Google Scholar] [CrossRef]
- Silva, A.J.; Trindade, M.A.; Santos, D.O.; Lima, R.F. Maximum-likelihood q-estimator uncovers the role of potassium at neuromuscular junctions. Biol. Cybern. 2016, 110, 31–40. [Google Scholar] [CrossRef]
- Lima, R.F.; Prado, V.F.; Prado, M.A.; Kushmerick, C. Quantal release of acetylcholine in mice with reduced levels of the vesicular acetylcholine transporter. J. Neurochem. 2010, 113, 943–951. [Google Scholar] [CrossRef] [PubMed]
- Cerqueti, R.; Maggi, M. Data validity and statistical conformity with Benford’s Law. Chaos Solit. Fract. 2021, 144, 110740. [Google Scholar] [CrossRef]
- Cerqueti, R.; Lupi, C. Severe testing of Benford’s law. Test 2023, 32, 677–694. [Google Scholar] [CrossRef]
- Nakanishi, T.; Norris, F.H. Effect of local temperature on resting membrane potential in rat muscle. Electroencephalogr. Clin. Neurophysiol. 1969, 718, 633–636. [Google Scholar] [CrossRef]
- Ward, D.; Crowley, W.J.; Johns, T.R. Effects of temperature at the neuromuscular junction. Am. J. Physiol. 1972, 222, 216–219. [Google Scholar] [CrossRef] [PubMed]
- White, R. Effects of high temperature and low calcium on neuromuscular transmission in frog. J. Therm. Biol. 1976, 1, 227–232. [Google Scholar] [CrossRef]
- Procopio, J.; Fornés, J.A. Fluctuation-dissipation theorem imposes high-voltage fluctuations in biological ionic channels. Phys. Rev. E. 1995, 51, 829–831. [Google Scholar] [CrossRef]
- Chame, A.; Mello, E.V.L. The fluctuation-dissipation theorem in the framework of the Tsallis statistics J. Phys. A Math. Gen. 1994, 27, 3663–3670. [Google Scholar] [CrossRef]
- Shao, L.; Ma, B.Q. First-digit law in nonextensive statistics. Phys. Rev. E 2010, 82, 041110. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.J.; Floquet, S.; Santos, D.O.C. Statistical crossover and nonextensive behavior of neuronal short-term depression. J. Biol. Phys. 2018, 44, 37–50. [Google Scholar] [CrossRef] [PubMed]

| Digit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | - | 0.30103 | 0.17609 | 0.12494 | 0.09691 | 0.07918 | 0.06695 | 0.05799 | 0.05115 | 0.04576 |
| 2nd | 0.11968 | 0.11389 | 0.10882 | 0.10433 | 0.10031 | 0.09668 | 0.09337 | 0.09035 | 0.08757 | 0.08500 |
| First Digit | Second Digit | First–Two Digits | ||||
|---|---|---|---|---|---|---|
| Range | Conformity | Range | Conformity | Range | Conformity | |
| MAD | 0.000 to 0.006 | Close | 0.000 to 0.008 | Close | 0.0000 to 0.0012 | Close |
| 0.006 to 0.012 | Acceptable | 0.008 to 0.010 | Acceptable | 0.0012 to 0.0018 | Acceptable | |
| 0.012 to 0.015 | Marginal | 0.010 to 0.012 | Marginal | 0.0018 to 0.0022 | Marginal | |
| Above 0.015 | Nonconformity | Above 0.012 | Nonconformity | Above 0.0022 | Nonconformity | |
| SSD | 0 to 2 | Close | 0 to 2 | Close | 0 to 2 | Close |
| 2 to 25 | Acceptable | 2 to 10 | Acceptable | 2 to 10 | Acceptable | |
| 25 to 100 | Marginal | 10 to 50 | Marginal | 10 to 50 | Marginal | |
| Above 100 | Nonconformity | Above 50 | Nonconformity | Above 50 | Nonconformity | |
| First Digit | ||||
|---|---|---|---|---|
| Data | n | MAD | Excess MAD | SSD |
| 1 | 730 | 0.00837 | −0.00032 | 12.28475 |
| 2 | 869 | 0.01995 | 0.01198 | 86.45288 |
| 3 | 2181 | 0.00989 | 0.00486 | 16.56178 |
| 4 | 928 | 0.00858 | 0.00087 | 10.08629 |
| 5 | 2973 | 0.01305 | 0.00874 | 21.54770 |
| 6 | 642 | 0.00986 | 0.00060 | 9.91123 |
| 7 | 1349 | 0.00887 | 0.00248 | 10.38188 |
| 8 | 1162 | 0.01270 | 0.00581 | 18.13111 |
| 9 | 1685 | 0.00845 | 0.00273 | 11.65409 |
| 10 | 1009 | 0.01137 | 0.00398 | 16.06490 |
| 11 | 2048 | 0.00807 | 0.00288 | 7.53752 |
| 12 | 3060 | 0.00722 | 0.00298 | 8.61009 |
| 13 | 1510 | 0.01192 | 0.00588 | 27.89886 |
| 14 | 2436 | 0.00916 | 0.00440 | 9.96616 |
| Second Digit | ||||
| Data | n | MAD | Excess MAD | SSD |
| 1 | 730 | 0.00683 | −0.00202 | 8.19079 |
| 2 | 869 | 0.00950 | 0.00139 | 12.32210 |
| 3 | 2181 | 0.00544 | 0.00033 | 4.28136 |
| 4 | 928 | 0.00851 | 0.00067 | 12.11295 |
| 5 | 2973 | 0.00318 | −0.00120 | 1.80299 |
| 6 | 642 | 0.00558 | −0.00385 | 4.44022 |
| 7 | 1349 | 0.00466 | −0.00184 | 3.15052 |
| 8 | 1162 | 0.00785 | 0.00084 | 8.96622 |
| 9 | 1685 | 0.00692 | 0.00110 | 7.73984 |
| 10 | 1009 | 0.00494 | −0.00258 | 3.72527 |
| 11 | 2048 | 0.00525 | −0.00003 | 3.96622 |
| 12 | 3060 | 0.00495 | 0.00063 | 3.65075 |
| 13 | 1510 | 0.00612 | −0.00003 | 5.18546 |
| 14 | 2436 | 0.00529 | 0.00045 | 4.44622 |
| First-Two Digits | ||||
| Data | n | MAD | Excess MAD | SSD |
| 1 | 730 | 0.00253 | −0.00040 | 10.83412 |
| 2 | 869 | 0.00366 | 0.00097 | 21.72249 |
| 3 | 2181 | 0.00232 | 0.00062 | 8.81407 |
| 4 | 928 | 0.00276 | 0.00016 | 12.93240 |
| 5 | 2973 | 0.00177 | 0.00031 | 5.02102 |
| 6 | 642 | 0.00268 | −0.00045 | 9.19816 |
| 7 | 1349 | 0.00225 | 0.00009 | 7.40826 |
| 8 | 1162 | 0.00244 | 0.00012 | 8.78088 |
| 9 | 1685 | 0.00225 | 0.00031 | 8.69891 |
| 10 | 1009 | 0.00240 | −0.00010 | 7.84890 |
| 11 | 2048 | 0.00169 | −0.00006 | 4.39289 |
| 12 | 3060 | 0.00141 | −0.00002 | 4.12983 |
| 13 | 1510 | 0.00263 | 0.00059 | 10.24864 |
| 14 | 2436 | 0.00167 | 0.00007 | 4.34060 |
| First Digit | ||||
|---|---|---|---|---|
| Data | n | MAD | Excess MAD | SSD |
| 1 | 56,853 | 0.02687 | 0.02589 | 117.77678 |
| 2 | 40,951 | 0.02383 | 0.02267 | 102.72734 |
| 3 | 72,519 | 0.01827 | 0.01740 | 69.91262 |
| 4 | 51,207 | 0.00910 | 0.00807 | 11.41064 |
| 5 | 112,330 | 0.01375 | 0.01305 | 36.17818 |
| 6 | 107,801 | 0.01952 | 0.01881 | 52.04470 |
| 7 | 36,330 | 0.00619 | 0.00496 | 4.52025 |
| 8 | 37,758 | 0.00117 | −0.00004 | 0.25865 |
| 9 | 37,703 | 0.00732 | 0.00611 | 7.98955 |
| 10 | 72,787 | 0.02064 | 0.01977 | 92.09016 |
| 11 | 34,833 | 0.01054 | 0.00928 | 19.34788 |
| 12 | 29,313 | 0.00318 | 0.00180 | 1.77512 |
| Second Digit | ||||
| Data | n | MAD | Excess MAD | SSD |
| 1 | 56,853 | 0.00995 | 0.00895 | 16.15754 |
| 2 | 40,951 | 0.00705 | 0.00586 | 6.48468 |
| 3 | 72,519 | 0.02088 | 0.02000 | 46.27171 |
| 4 | 51,207 | 0.01589 | 0.01484 | 26.70868 |
| 5 | 112,330 | 0.01601 | 0.01530 | 29.43487 |
| 6 | 107,801 | 0.02213 | 0.02140 | 52.58192 |
| 7 | 36,330 | 0.01576 | 0.01450 | 26.28400 |
| 8 | 37,758 | 0.01441 | 0.01318 | 21.98806 |
| 9 | 37,703 | 0.01253 | 0.01130 | 16.74141 |
| 10 | 72,787 | 0.02409 | 0.02320 | 61.55550 |
| 11 | 34,833 | 0.01854 | 0.01726 | 37.01945 |
| 12 | 29,313 | 0.01897 | 0.01757 | 38.09396 |
| First-Two Digits | ||||
| Data | n | MAD | Excess MAD | SSD |
| 1 | 56,853 | 0.00301 | 0.00268 | 15.60049 |
| 2 | 40,951 | 0.00249 | 0.00209 | 12.89166 |
| 3 | 72,519 | 0.00308 | 0.00278 | 13.89474 |
| 4 | 51,207 | 0.00181 | 0.00146 | 4.98217 |
| 5 | 112,330 | 0.00231 | 0.00207 | 8.19403 |
| 6 | 107,801 | 0.00318 | 0.00294 | 14.78929 |
| 7 | 36,330 | 0.00192 | 0.00150 | 3.94064 |
| 8 | 37,758 | 0.00163 | 0.00122 | 2.85762 |
| 9 | 37,703 | 0.00160 | 0.00119 | 3.65519 |
| 10 | 72,787 | 0.00349 | 0.00320 | 17.89426 |
| 11 | 34,833 | 0.00243 | 0.00200 | 6.71510 |
| 12 | 29,313 | 0.00217 | 0.00171 | 5.13421 |
| First Digit | ||||
|---|---|---|---|---|
| Data | n | Alpha | MAD | SSD |
| 1 | 730 | 1.09734 | 0.00636 | 5.35810 |
| 2 | 869 | 1.30536 | 0.01065 | 16.90700 |
| 3 | 2181 | 0.85783 | 0.00349 | 1.97250 |
| 4 | 928 | 0.98698 | 0.00828 | 9.96370 |
| 5 | 2973 | 0.87338 | 0.00851 | 9.87620 |
| 6 | 642 | 1.07180 | 0.00713 | 5.96820 |
| 7 | 1349 | 0.96904 | 0.00844 | 9.65490 |
| 8 | 1162 | 1.08773 | 0.01008 | 12.10020 |
| 9 | 1685 | 0.93251 | 0.00728 | 8.23990 |
| 10 | 1009 | 0.89552 | 0.00824 | 8.04460 |
| 11 | 2048 | 1.05146 | 0.00661 | 5.51620 |
| 12 | 3060 | 1.09466 | 0.00368 | 1.97250 |
| 13 | 1510 | 0.86705 | 0.01149 | 14.54340 |
| 14 | 2436 | 1.06165 | 0.00794 | 7.02810 |
| Second Digit | ||||
| Data | n | Alpha | MAD | SSD |
| 1 | 730 | 0.88315 | 0.00703 | 7.88420 |
| 2 | 869 | 1.20207 | 0.00977 | 11.27090 |
| 3 | 2181 | 0.76299 | 0.00480 | 3.19950 |
| 4 | 928 | 0.56741 | 0.00699 | 8.74690 |
| 5 | 2973 | 0.96940 | 0.00328 | 1.78210 |
| 6 | 642 | 0.82057 | 0.00565 | 3.79340 |
| 7 | 1349 | 0.83357 | 0.00431 | 2.57830 |
| 8 | 1162 | 1.14257 | 0.00794 | 8.44120 |
| 9 | 1685 | 1.14975 | 0.00653 | 7.19650 |
| 10 | 1009 | 1.04217 | 0.00485 | 3.68420 |
| 11 | 2048 | 0.82621 | 0.00465 | 3.33970 |
| 12 | 3060 | 1.08013 | 0.00531 | 3.49580 |
| 13 | 1510 | 0.61821 | 0.00425 | 2.57810 |
| 14 | 2436 | 0.98519 | 0.00538 | 4.44090 |
| First-Two Digits | ||||
| Data | n | Alpha | MAD | SSD |
| 1 | 730 | 1.11785 | 0.00241 | 9.63330 |
| 2 | 869 | 1.24452 | 0.00329 | 16.11180 |
| 3 | 2181 | 0.86327 | 0.00214 | 7.27660 |
| 4 | 928 | 0.97734 | 0.00276 | 12.88900 |
| 5 | 2973 | 0.87317 | 0.00157 | 3.66930 |
| 6 | 642 | 1.06433 | 0.00259 | 8.82400 |
| 7 | 1349 | 0.94217 | 0.00219 | 7.11010 |
| 8 | 1162 | 1.07238 | 0.00236 | 8.29090 |
| 9 | 1685 | 0.91808 | 0.00223 | 8.10760 |
| 10 | 1009 | 0.90327 | 0.00230 | 7.05690 |
| 11 | 2048 | 1.05125 | 0.00166 | 4.15790 |
| 12 | 3060 | 1.09810 | 0.00129 | 3.28490 |
| 13 | 1510 | 0.84443 | 0.00248 | 8.13420 |
| 14 | 2436 | 1.03307 | 0.00165 | 4.23940 |
| First Digit | ||||
|---|---|---|---|---|
| Data | n | Alpha | MAD | SSD |
| 1 | 56,853 | 0.68616 | 0.01982 | 45.09730 |
| 2 | 40,951 | 0.73411 | 0.02093 | 47.66000 |
| 3 | 72,519 | 0.75305 | 0.01487 | 23.73950 |
| 4 | 51,207 | 1.10501 | 0.00427 | 3.05230 |
| 5 | 112,330 | 0.83126 | 0.01152 | 14.63950 |
| 6 | 107,801 | 0.87603 | 0.01860 | 39.84270 |
| 7 | 36,330 | 0.92700 | 0.00228 | 0.68170 |
| 8 | 37,758 | 1.00437 | 0.00123 | 0.24450 |
| 9 | 37,703 | 1.02816 | 0.00712 | 7.37960 |
| 10 | 72,787 | 0.70165 | 0.01540 | 25.51630 |
| 11 | 34,833 | 0.84972 | 0.00475 | 2.89430 |
| 12 | 29,313 | 0.96620 | 0.00265 | 0.92750 |
| Second Digit | ||||
| Data | n | Alpha | MAD | SSD |
| 1 | 56,853 | 1.26913 | 0.00928 | 14.27730 |
| 2 | 40,951 | 0.95827 | 0.00709 | 6.44590 |
| 3 | 72,519 | 1.26304 | 0.01965 | 44.44780 |
| 4 | 51,207 | 1.30622 | 0.01444 | 24.16300 |
| 5 | 112,330 | 1.28374 | 0.01468 | 27.29740 |
| 6 | 107,801 | 1.32020 | 0.02061 | 49.80040 |
| 7 | 36,330 | 1.29637 | 0.01436 | 23.90470 |
| 8 | 37,758 | 1.27543 | 0.01312 | 19.94300 |
| 9 | 37,703 | 1.21247 | 0.01155 | 15.56480 |
| 10 | 72,787 | 1.29532 | 0.02269 | 59.22550 |
| 11 | 34,833 | 1.38829 | 0.01666 | 32.80310 |
| 12 | 29,313 | 1.31114 | 0.01749 | 35.45490 |
| First-Two Digits | ||||
| Data | n | Alpha | MAD | SSD |
| 1 | 56,853 | 0.71868 | 0.00249 | 9.14370 |
| 2 | 40,951 | 0.73705 | 0.00220 | 6.82500 |
| 3 | 72,519 | 0.76779 | 0.00272 | 9.27860 |
| 4 | 51,207 | 1.08779 | 0.00183 | 4.27770 |
| 5 | 112,330 | 0.84541 | 0.00215 | 6.12730 |
| 6 | 107,801 | 0.87479 | 0.00314 | 13.35130 |
| 7 | 36,330 | 0.95909 | 0.00189 | 3.80170 |
| 8 | 37,758 | 1.00499 | 0.00164 | 2.85540 |
| 9 | 37,703 | 1.00683 | 0.00160 | 3.65090 |
| 10 | 72,787 | 0.72606 | 0.00309 | 11.62400 |
| 11 | 34,833 | 0.88760 | 0.00224 | 5.66890 |
| 12 | 29,313 | 0.97453 | 0.00214 | 5.07780 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, A.; Floquet, S.; Lima, R. Newcomb–Benford’s Law in Neuromuscular Transmission: Validation in Hyperkalemic Conditions. Stats 2023, 6, 1053-1071. https://doi.org/10.3390/stats6040066
Silva A, Floquet S, Lima R. Newcomb–Benford’s Law in Neuromuscular Transmission: Validation in Hyperkalemic Conditions. Stats. 2023; 6(4):1053-1071. https://doi.org/10.3390/stats6040066
Chicago/Turabian StyleSilva, Adriano, Sergio Floquet, and Ricardo Lima. 2023. "Newcomb–Benford’s Law in Neuromuscular Transmission: Validation in Hyperkalemic Conditions" Stats 6, no. 4: 1053-1071. https://doi.org/10.3390/stats6040066
APA StyleSilva, A., Floquet, S., & Lima, R. (2023). Newcomb–Benford’s Law in Neuromuscular Transmission: Validation in Hyperkalemic Conditions. Stats, 6(4), 1053-1071. https://doi.org/10.3390/stats6040066






