An Archimedean Copulas-Based Approach for m-Consecutive-k-Out-of-n: F Systems with Exchangeable Components
Abstract
:1. Introduction
2. The Copulas-Based Framework for the Proposed Network Consisting of ξ m-Consecutive-k-Out-of-n: F Subsystems
- The Clayton family of n-copulas.
- The Gumbel–Hougaard family of n-copulas.
3. Main Results
- (i)
- Given that the ξ subsystems formulate a series network, then the MTTF of the resulting reliability scheme is given by
- (ii)
- Given that the ξ subsystems formulate a parallel network, then the MTTF of the resulting reliability scheme is given by
- (i)
- (ii)
- The MTTF of the parallel network NET(ξ,m,k,n) can be determined as
- (i)
- Given that the ξ subsystems formulate a series network, then the MTTF of the resulting reliability scheme is given by
- (ii)
- Given that the ξ subsystems formulate a parallel network, then the MTTF of the resulting reliability scheme is given by
- (i)
- The MTTF ( of the series network NET(ξ,m,k,n) can be computed with the aid of (13). We first replace the copula function of the Gumbel–Hougaard family (see Formula (6)) in the expression (16) and the following is readily observed
- (ii)
- The MTTF of the parallel network NET(ξ,m,k,n) can be determined via (20). Following a parallel argumentation with (i) partially implemented, we next substitute Formulas (12), (17) and (21) in (18) and the expression we are searching for is concluded after some straightforward manipulations. □
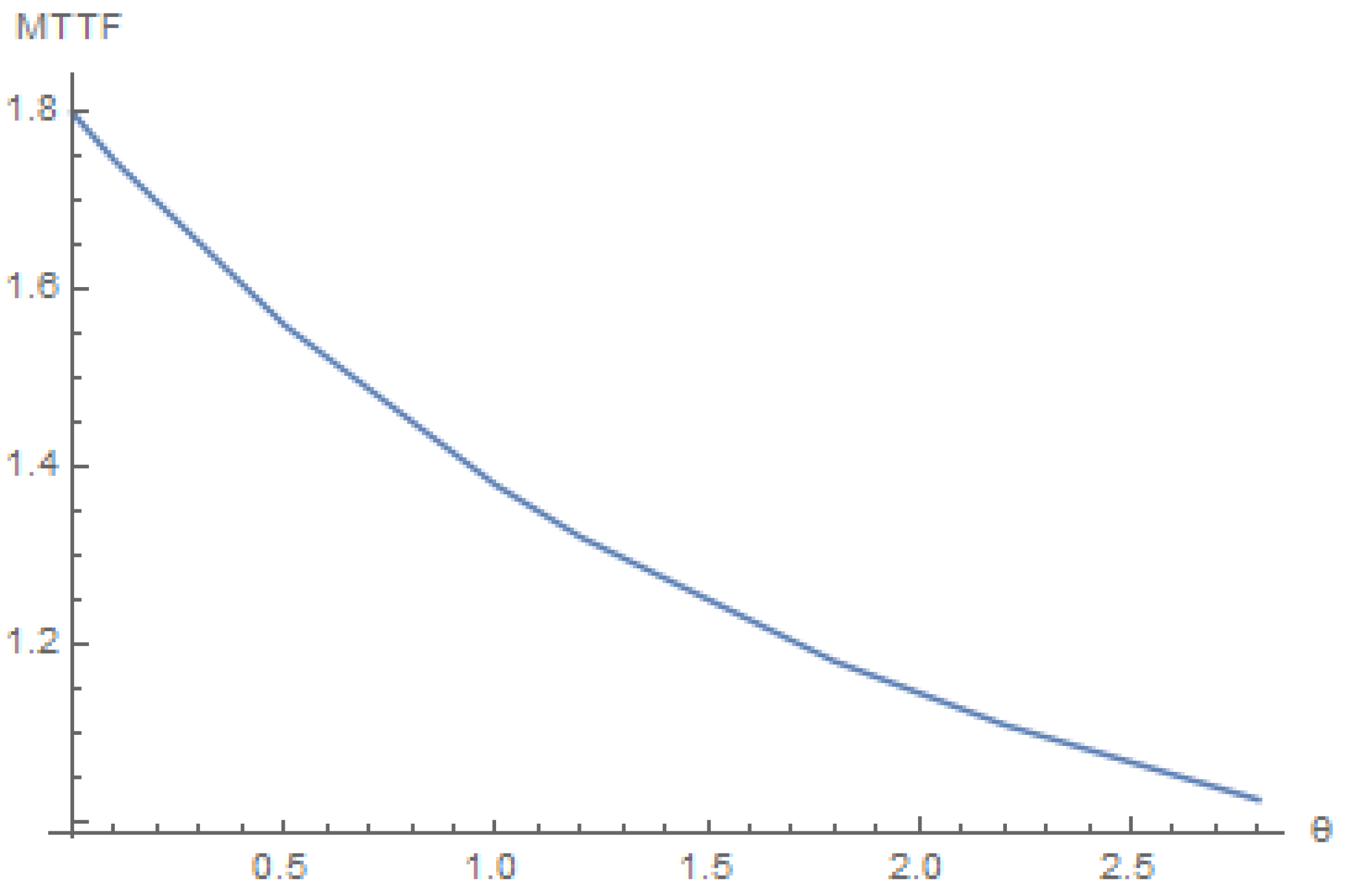
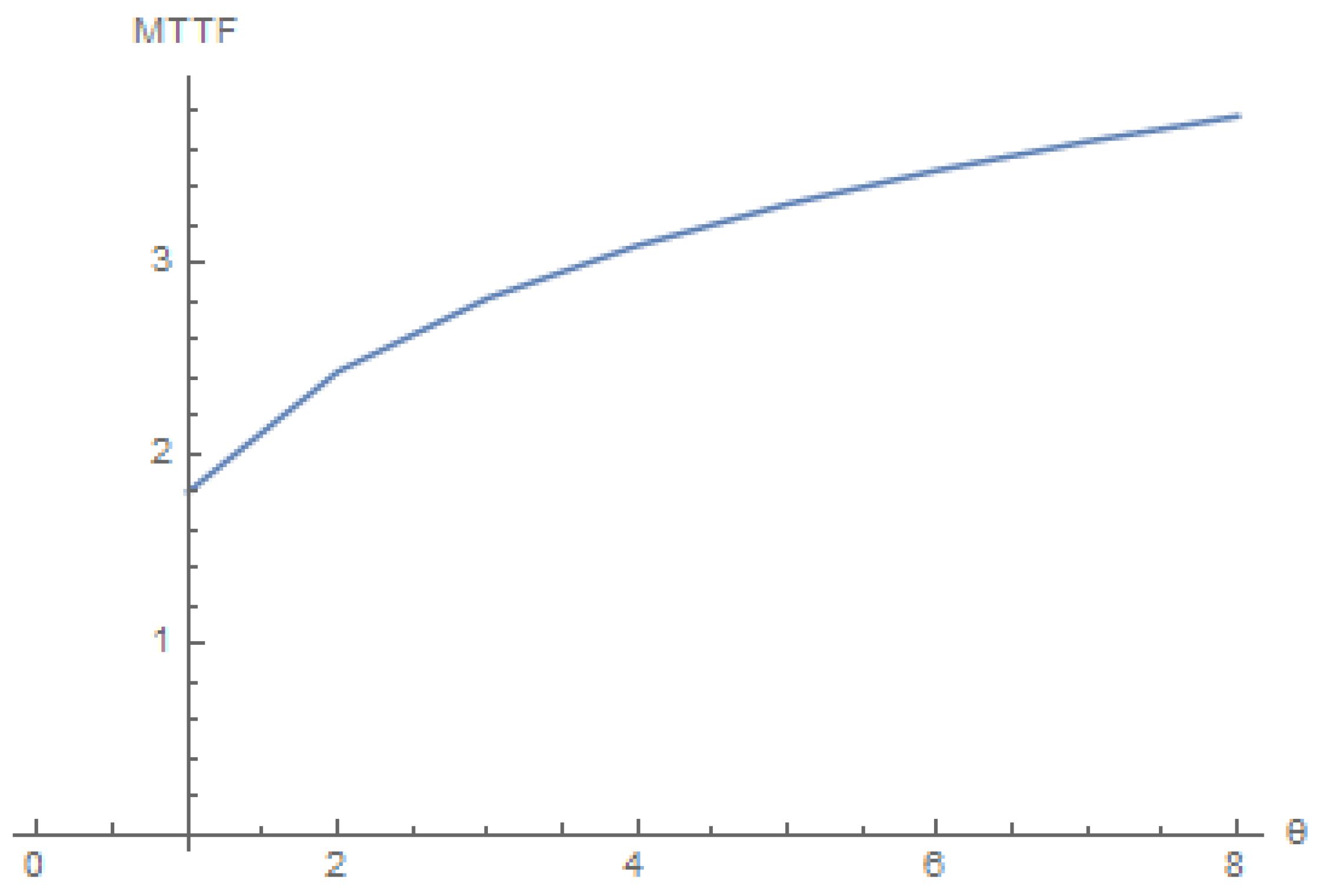
4. Numerical Results
- decreases as the parameter ξ increases
- decreases as the parameter n increases
- decreases as the parameter θ increases.
- The MTTF of the resulting network increases under the Clayton copula;
- The MTTF of the resulting network decreases under the Gumbel–Hougaard copula.
5. Symbols and Notations
- NET(ξ,m,k,n): The network that consists of ξ independent m-consecutive-k-out-of-
- n: F substructures.
- : The lifetimes of the components of the -th subsystem of the network
- NET(ξ,m,k,n).
- : The cumulative distribution function of the variable .
- : The joint distribution function of the lifetimes of the components of the -th subsystem.
- : The copula function related to .
- : The maximal signature of a coherent system with n components.
- : The lifetime of the network NET(ξ,m,k,n).
- : The corresponding subsystems’ lifetimes of the network NET(ξ,m,k,n). : Mean Time to Failure of the network NET(ξ,m,k,n).
6. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Derman, C.; Lieberman, G.J.; Ross, S.M. On the consecutive-k-out-of-n: F system. IEEE Trans. Reliab. 1982, 31, 57–63. [Google Scholar] [CrossRef]
- Chao, M.T.; Fu, J.C.; Koutras, M.V. Survey of reliability studies of consecutive-k-out-of-n: F and related systems. IEEE Trans. Rel. 1995, 44, 120–127. [Google Scholar] [CrossRef]
- Tong, Y.L. A rearrangement inequality for the longest run, with an application to network reliability. J. Appl. Probab. 1985, 22, 386–393. [Google Scholar] [CrossRef]
- Cui, L.; Kuo, W.; Li, J.; Xie, M. On the dual reliability systems of (n, f, k) and < n, f, k>. Stat. Probab. Lett. 2006, 76, 1081–1088. [Google Scholar]
- Eryilmaz, S.; Aksoy, T. Reliability of linear (n, f, k) systems with weighted components. J. Syst. Sci. Syst. Eng. 2010, 19, 277–284. [Google Scholar] [CrossRef]
- Eryilmaz, S.; Zuo, M.J. Constrained (k,d)-out-of-n systems. Int. J. Syst. Sci. 2010, 41, 679–685. [Google Scholar] [CrossRef]
- Triantafyllou, I.S. On the lifetime and signature of the constrained (k,d) out-of-n: F reliability systems. Int. J. Math. Eng. Manag. Sci. 2021, 6, 66–78. [Google Scholar] [CrossRef]
- Triantafyllou, I.S. On the consecutive- k1 and k2-out-of-n Reliability Systems. Mathematics 2020, 8, 630. [Google Scholar] [CrossRef]
- Coit, D.W. Cold-standby redundancy optimization for nonrepairable systems. IIE Trans. 2001, 33, 471–478. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Dai, Y. Optimal component loading in 1-out-of-N cold standby systems. Reliab. Eng. Syst. Saf. 2014, 127, 58–64. [Google Scholar] [CrossRef]
- Wang, W.; Xiong, J.; Xie, M. A study of interval analysis for cold-standby system reliability optimization under parameter uncertainty. Comput. Ind. Eng. 2016, 97, 93–100. [Google Scholar] [CrossRef]
- Eryilmaz, S.; Unlu, K.D. A new generalized δ-shock model and its application to 1-out-of-(m+1):G cold standby system. Reliab Eng Syst Saf. 2023, 234, 109203. [Google Scholar] [CrossRef]
- Shen, K.; Xie, M. The effectiveness of adding standby redundancy at system & component levels. IEEE Trans. Reliab. 1991, 40, 53–55. [Google Scholar]
- Boland, P.J.; El-Neweihi, E. Component redundancy vs system redundancy in the hazard rate ordering. IEEE Trans. Reliab 1995, 44, 614–619. [Google Scholar] [CrossRef]
- Eryilmaz, S. The effectiveness of adding cold standby redundancy to a coherent system at system and component levels. Reliab. Eng. Syst. Saf. 2017, 165, 331–335. [Google Scholar] [CrossRef]
- Triantafyllou, I.S. Combined m-Consecutive-k-Out-of-n: F and Consecutive kc-Out-of-n: F Structures with Cold Standby Redundancy. Mathematics 2023, 11, 2597. [Google Scholar] [CrossRef]
- Modibbo, U.M.; Arshad, M.; Abdalghani, O.; Ali, I. Optimization and estimation in system reliability allocation problem. Reliab Eng. Syst. Saf. 2021, 212, 107620. [Google Scholar] [CrossRef]
- Bhandari, A.S.; Kumar, A.; Ram, M. Reliability optimization and redundancy allocation for fire extinguisher drone using hybrid PSO–GWO. Soft Comput. 2023, 27, 14819–14833. [Google Scholar] [CrossRef]
- Kumar, A.; Pant, S.; Ram, M. Cost Optimization and Reliability Parameter Extraction of a Complex Engineering System. J. Reliab. Stat. Stud. 2023, 16, 99–116. [Google Scholar] [CrossRef]
- Ram, M.; Kumar, A.; Naaz, S. UGF-based signature reliability for solar panel k-out-of-n- multiplex systems. J. Qual. Mainten. Eng. 2023. ahead-of-print. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.B. Signature Reliability of Consecutive k-out-of-n: F System using Universal Generating Function. In Reliability and Risk Modeling of Engineering Systems; EAI/Springer Innovations in Communication and Computing; Panchal, D., Chatterjee, P., Pamucar, D., Tyagi, M., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Triantafyllou, I.S. Signature-Based Analysis of the Weighted-r-within-Consecutive-k-out-of-n: F Systems. Mathematics 2022, 10, 2254. [Google Scholar] [CrossRef]
- Kan, C.; Ozkut, M. Analysis of joint reliability importance in linear m-consecutive-k,l-out-of-n:F system. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2020, 69, 699–716. [Google Scholar] [CrossRef]
- Eryilmaz, S.; Tutuncu, G.Y. Reliability evaluation of linear consecutive-weighted-k-out-of-n: F. Asia-Pac. J. Oper. Res. 2009, 6, 805–816. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.B.; Ram, M. Reliability appraisal for consecutive-k-out-of-n: F system of non-identical components with intuitionistic fuzzy set. Int. J. Oper. Res. 2019, 36, 362–374. [Google Scholar] [CrossRef]
- Huang, J.; Zuo, M.J.; Fang, Z. Multi-State Consecutive-k-out-of-n Systems. IIE Trans. 2003, 6, 527–534. [Google Scholar] [CrossRef]
- Makri, F.S.; Philippou, A.N. Exact reliability formulas for linear and circular m-consecutive-k-out-of-n: F systems. Microelectron. Reliab. 1996, 36, 657–660. [Google Scholar] [CrossRef]
- Mohan, P.; Agarwal, M.; Sen, K. Combined m-Consecutive-k-Out-of-n:F & Consecutive kc-Out-of-n: F Systems. IEEE Trans. Reliab. 2009, 58, 328–337. [Google Scholar]
- Chang, Y.M.; Huang, T.H. Reliability of a 2-Dimensional k-Within-Consecutive-r×s-out-of-m×n: F System Using Finite Markov Chains. IEEE Trans. Reliab. 2010, 59, 725–733. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Ben-Haim, H.; Dai, Y. m/nCCS: Linear consecutively connected systems subject to combined gap constraints. Int. J. Gen. Syst. 2015, 44, 833–848. [Google Scholar] [CrossRef]
- Eryilmaz, S.; Ozkut, M. Optimization problems for a parallel system with multiple types of dependent components. Reliab. Eng. Syst. Saf. 2020, 199, 106911. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kolev, N. Copulas: A Review and Recent Developments. Stoch. Models 2006, 22, 617–660. [Google Scholar] [CrossRef]
- McNeil, A.J. Sampling nested Archimedean copulas. J. Stat. Comp. Sim. 2008, 78, 567–581. [Google Scholar] [CrossRef]
- Frahm, G.; Junker, M.; Szimayer, A. Elliptical copulas: Applicability and limitations. Stat. Prob. Let. 2003, 63, 275–286. [Google Scholar] [CrossRef]
- Smith, M.S. Implicit Copulas: An Overview. Econom. Stat. 2023, 28, 81–104. [Google Scholar] [CrossRef]
- Tyagi, V.; Arora, V.; Ram, M.; Triantafyllou, I.S. Copula based Measures of Repairable Parallel System with Fault Coverage. Int. J. Math. Eng. Manag. Sci. 2021, 6, 322–344. [Google Scholar] [CrossRef]
- Eryilmaz, S. Estimation in coherent reliability systems through copulas. Reliab. Eng. Syst. Saf. 2011, 96, 564–568. [Google Scholar] [CrossRef]
- Navarro, J.; Eryilmaz, S. Mean Residual Lifetimes of Consecutive k-out-of-n systems. J. Appl. Probab. 2007, 44, 82–98. [Google Scholar] [CrossRef]
- Navarro, J.; Ruiz, J.M.; Sandoval, C.J. Properties of coherent systems with dependent components. Commun. Stat. Theory Methods 2007, 36, 175–191. [Google Scholar] [CrossRef]
- Eryilmaz, S.; Koutras, M.V.; Triantafyllou, I.S. Signature based analysis of m-consecutive k-out-of-n: F systems with exchangeable components. Nav. Res. Logist. 2011, 58, 344–354. [Google Scholar] [CrossRef]

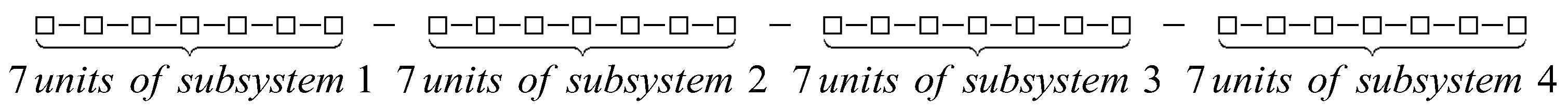

| Clayton Copula | Gumbel–Hougaard Copula | ||||
|---|---|---|---|---|---|
| n | ξ | θ | MTTF | θ | MTTF |
| 6 | 2 | 1 | 1.380130 | 1 | 1.796790 |
| 2 | 1.143790 | 2 | 2.430460 | ||
| 3 | 1 | 1.056160 | 1 | 1.535480 | |
| 2 | 0.813431 | 2 | 2.156320 | ||
| 4 | 1 | 0.867392 | 1 | 1.535480 | |
| 2 | 0.629722 | 2 | 2.156320 | ||
| 7 | 2 | 1 | 1.113730 | 1 | 1.450640 |
| 2 | 0.944208 | 2 | 2.062510 | ||
| 3 | 1 | 0.837676 | 1 | 1.231230 | |
| 2 | 0.664296 | 2 | 1.827570 | ||
| 4 | 1 | 0.679528 | 1 | 1.107220 | |
| 2 | 0.511124 | 2 | 1.692370 | ||
| 8 | 2 | 1 | 0.874650 | 1 | 1.156820 |
| 2 | 0.761105 | 2 | 1.745730 | ||
| 3 | 1 | 0.655515 | 1 | 0.998243 | |
| 2 | 0.535529 | 2 | 1.570740 | ||
| 4 | 1 | 0.528980 | 1 | 0.905478 | |
| 2 | 0.411793 | 2 | 1.466350 | ||
| 9 | 2 | 1 | 0.765576 | 1 | 1.003020 |
| 2 | 0.681833 | 2 | 1.574720 | ||
| 3 | 1 | 0.569664 | 1 | 0.867208 | |
| 2 | 0.478560 | 2 | 1.421680 | ||
| 4 | 1 | 0.457256 | 1 | 0.787787 | |
| 2 | 0.321452 | 2 | 1.330230 | ||
| 10 | 2 | 1 | 0.683293 | 1 | 0.887530 |
| 2 | 0.621696 | 2 | 1.443990 | ||
| 3 | 1 | 0.506140 | 1 | 0.770645 | |
| 2 | 0.425516 | 2 | 1.309540 | ||
| 4 | 1 | 0.362310 | 1 | 0.701700 | |
| 2 | 0.261182 | 2 | 1.228410 | ||
| Clayton Copula | Gumbel–Hougaard Copula | ||||
|---|---|---|---|---|---|
| n | ξ | θ | MTTF | θ | MTTF |
| 6 | 2 | 1 | 1.656160 | 1 | 2.156150 |
| 2 | 1.372550 | 2 | 2.916560 | ||
| 3 | 1 | 1.26739 | 1 | 1.842570 | |
| 2 | 0.976117 | 2 | 2.587580 | ||
| 4 | 1 | 1.040870 | 1 | 1.662250 | |
| 2 | 0.755646 | 2 | 2.395870 | ||
| 7 | 2 | 1 | 2.227470 | 1 | 1.740760 |
| 2 | 1.888420 | 2 | 2.475020 | ||
| 3 | 1 | 1.005121 | 1 | 1.477470 | |
| 2 | 0.797145 | 2 | 2.193220 | ||
| 4 | 1 | 0.815422 | 1 | 1.328660 | |
| 2 | 0.613488 | 2 | 1.992311 | ||
| 8 | 2 | 1 | 1.049580 | 1 | 1.388180 |
| 2 | 0.913326 | 2 | 2.094880 | ||
| 3 | 1 | 0.786618 | 1 | 1.197890 | |
| 2 | 0.642624 | 2 | 1.885100 | ||
| 4 | 1 | 0.634776 | 1 | 1.086570 | |
| 2 | 0.494148 | 2 | 1.576240 | ||
| 9 | 2 | 1 | 0.918691 | 1 | 1.203630 |
| 2 | 0.818196 | 2 | 1.889660 | ||
| 3 | 1 | 0.683592 | 1 | 1.040650 | |
| 2 | 0.574272 | 2 | 1.250000 | ||
| 4 | 1 | 0.548722 | 1 | 0.945345 | |
| 2 | 0.385740 | 2 | 0.998672 | ||
| 10 | 2 | 1 | 0.819952 | 1 | 1.065040 |
| 2 | 0.7460352 | 2 | 1.732830 | ||
| 3 | 1 | 0.607368 | 1 | 0.9247740 | |
| 2 | 0.510619 | 2 | 1.4429821 | ||
| 4 | 1 | 0.434772 | 1 | 0.8420390 | |
| 2 | 0.313418 | 2 | 1.2128762 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Triantafyllou, I.S. An Archimedean Copulas-Based Approach for m-Consecutive-k-Out-of-n: F Systems with Exchangeable Components. Stats 2023, 6, 1114-1125. https://doi.org/10.3390/stats6040070
Triantafyllou IS. An Archimedean Copulas-Based Approach for m-Consecutive-k-Out-of-n: F Systems with Exchangeable Components. Stats. 2023; 6(4):1114-1125. https://doi.org/10.3390/stats6040070
Chicago/Turabian StyleTriantafyllou, Ioannis S. 2023. "An Archimedean Copulas-Based Approach for m-Consecutive-k-Out-of-n: F Systems with Exchangeable Components" Stats 6, no. 4: 1114-1125. https://doi.org/10.3390/stats6040070





