Utility in Time Description in Priority Best–Worst Discrete Choice Models: An Empirical Evaluation Using Flynn’s Data
Abstract
:1. Introduction
2. Preliminary Results for Best–Worst Discrete Choice Modelling
2.1. Design of Experiment
2.1.1. Paired Model with Attribute and Level Variables
2.2. Utility Function–Attribute–Level Best–Worst Design
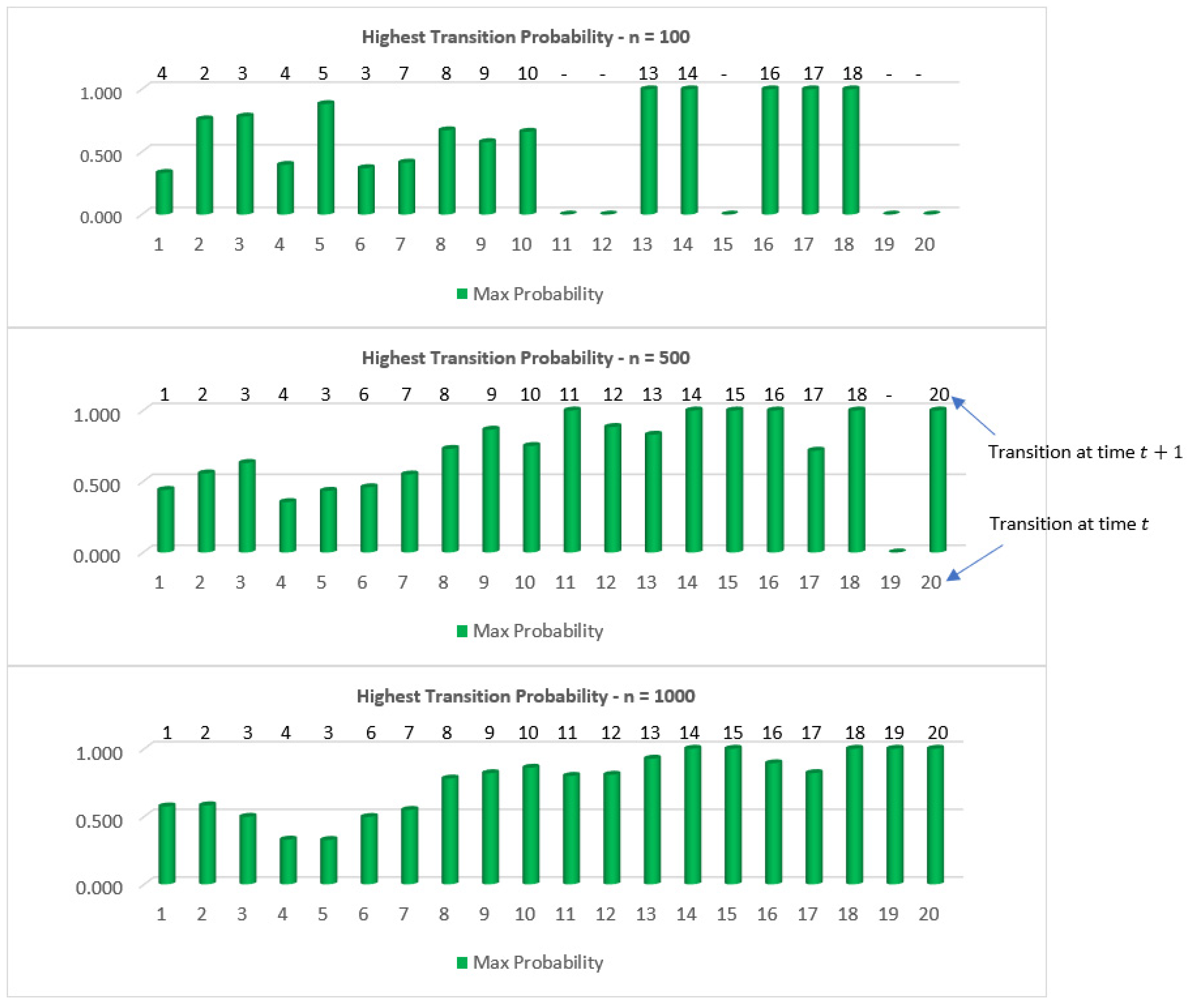
3. Transition Probability
3.1. Copula Methods
3.2. CUB Probability Model
3.3. The CO-CUB Model (Copula-Based CUB)
3.4. The CO-CUB Model with Plackett Copula without Covariates
3.5. Setting up the Transition Probability Matrix
4. Utility in Time with Dynamic Programming
5. Application and the Design of the Experiment
- Attachment: Attach_none, Attach_little, Attach_lot, Attach_all
- Security: Security_none, Security_little, Security_lot, Security_all
- Role: Enjoyment_none, Enjoyment_little, Enjoyment_lot, Enjoyment_all
- Enjoyment: Role_none, Role_few, Role_many, Role_all
- Control: Control_none, Control_few, Control_many, Control_all
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Louviere, J.J.; Woodworth, G.G. Best Worst Scaling: A Model for Largest Difference Judgments; Working Paper; Faculty of Business, University of Alberta: Edmonton, AB, Canada, 1990. [Google Scholar]
- Train, K.E. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Lancsar, E.; Louviere, J.; Donaldson, C.; Currie, G.; Burgess, L. Best worst discrete choice experiments in health: Methods and an application. Soc. Sci. Med. 2013, 76, 74–82. [Google Scholar] [CrossRef]
- Marley, A.A.; Louviere, J.J. Some probabilistic models of best, worst, and best–worst choices. J. Math. Psychol. 2005, 49, 464–480. [Google Scholar] [CrossRef]
- Marley, A.A.J.; Flynn, T.N.; Louviere, J.J. Probabilistic models of set-dependent and attribute-level best–worst choice. J. Math. Psychol. 2008, 52, 281–296. [Google Scholar] [CrossRef]
- Flynn, T.N.; Louviere, J.J.; Peters, T.J.; Coast, J. Best–worst scaling: What it can do for health care research and how to do it. J. Health Econ. 2007, 26, 171–189. [Google Scholar] [CrossRef]
- Street, D.J.; Knox, S.A. Designing for attribute-level best-worst choice experiments. J. Stat. Theory Pract. 2012, 6, 363–375. [Google Scholar] [CrossRef]
- Working, A.; Alqawba, M.; Diawara, N.; Li, L. Time Dependent Attribute-Level Best Worst Discrete Choice Modelling. Big Data Inf. Anal. 2018, 3, 55–72. [Google Scholar] [CrossRef]
- Potoglou, D.; Burge, P.; Flynn, T.; Netten, A.; Malley, J.; Forder, J.; Brazier, J.E. Best–worst scaling vs. discrete choice experiments: An empirical comparison using social care data. Soc. Sci. Med. 2011, 72, 1717–1727. [Google Scholar] [CrossRef]
- Sun, T.; Chen, H.; Gao, Y.; Xiang, Y.; Wang, F.; Ni, Z.; Wang, X.; Huang, X. Best-Worst Scaling Survey of Inpatients’ Preferences in Medical Decision-Making Participation in China. Healthcare 2023, 11, 323. [Google Scholar] [CrossRef] [PubMed]
- Aizaki, H.; Fogarty, J. An R package and tutorial for case 2 best–worst scaling. J. Choice Model. 2019, 32, 100171. [Google Scholar] [CrossRef]
- McFadden, D. Conditional logit analysis of qualitative choice behavior. Front. Econom. 2005, 1, 7–32. [Google Scholar]
- Flynn, T.N.; Louviere, J.J.; Peters, T.J.; Coast, J. Estimating preferences for a dermatology consultation using best-worst scaling: Comparison of various methods of analysis. BMC Med. Res. Methodol. 2008, 8, 76. [Google Scholar] [CrossRef] [PubMed]
- Louviere, J.J.; Street, D.; Burgess, L.; Wasi, N.; Islam, T.; Marley, A.A. Modeling the choices of individual decision-makers by combining efficient choice experiment designs with extra preference information. J. Choice Model. 2008, 1, 128–164. [Google Scholar] [CrossRef]
- Blanchet, J.; Gallego, G.; Goyal, V. A Markov chain approximation to choice modeling. Oper. Res. 2016, 64, 886–905. [Google Scholar] [CrossRef]
- Piccolo, D. On the moments of a mixture of uniform and shifted binomial random variables. Quad. Di Stat. 2003, 5, 85–104. [Google Scholar]
- Trivedi, P.K.; Zimmer, D.M. 2 copulas and dependence. Found. Trends Econom. 2005, 1, 7–32. [Google Scholar]
- Piccolo, D.; Simone, R.; Iannario, M. Cumulative and CUB models for rating data: A comparative analysis. Int. Stat. Rev. 2019, 87, 207–236. [Google Scholar] [CrossRef]
- D’Elia, A.; Piccolo, D. A mixture model for preferences data analysis. Comput. Stat. Data Anal. 2005, 49, 917–934. [Google Scholar] [CrossRef]
- Innario, M. CUBE models for interpreting ordered categorical data with overdispersion. CUBE Models Interpret. Ordered Categ. Data Overdispersion 2012, 14, 137–140. [Google Scholar]
- Iannario, M.; Piccolo, D. A new statistical model for the analysis of customer satisfaction. Qual. Technol. Quant. Manag. 2010, 7, 149–168. [Google Scholar] [CrossRef]
- Andreis, F.; Ferrari, P.A. On a copula model with CUB margins. Quad. Di Stat. 2013, 15, 33–51. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Genest, C.; Nešlehová, J. A primer on copulas for count data. ASTIN Bulletin J. IAA 2007, 37, 475–515. [Google Scholar] [CrossRef]
- Joe, H.; Xu, J.J. The Estimation Method of Inference Functions for Margins for Multivariate Models. 1996. Available online: https://open.library.ubc.ca/soa/cIRcle/collections/facultyresearchandpublications/52383/items/1.0225985 (accessed on 15 February 2024).
- Bellman, R. The theory of dynamic programming. Bull. Am. Math. Soc. 1954, 60, 503–515. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming and Lagrange multipliers. Proc. Natl. Acad. Sci. USA 1956, 42, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Rust, J. Structural estimation of Markov decision processes. Handb. Econom. 1994, 4, 3081–3143. [Google Scholar]
- Rust, J. Dynamic programming. New Palgrave Dict. Econ. 2008, 1, 8. [Google Scholar]
- Ellickson, P.B.; Misra, S. Structural workshop paper—Estimating discrete games. Mark. Sci. 2011, 30, 997–1010. [Google Scholar] [CrossRef]
- Feinberg, E.A.; Shwartz, A. Markov decision models with weighted discounted criteria. Math. Oper. Res. 1994, 19, 152–168. [Google Scholar] [CrossRef]
- Piccolo, D.; Simone, R. The class of CUB models: Statistical foundations, inferential issues and empirical evidence. Stat. Methods Appl. 2019, 28, 389–435. [Google Scholar] [CrossRef]




| B | W | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Constant | −0.3067 | 0.075 | * | * | Security All | 0.9511 | * | 0.8199 | * | |
| Attachment | 0.8105 | 0.0803 | 0.8655 | 0.0575 | Enjoyment None | −0.8888 | 0.1286 | −0.8327 | 0.0759 | |
| Security | * | * | * | * | Enjoyment Little | −0.3367 | 0.1632 | −0.3535 | 0.0773 | |
| Enjoyment | 0.2632 | 0.101 | 0.2684 | 0.0563 | Enjoyment Lot | 0.6561 | 0.1493 | 0.5862 | 0.0781 | |
| Role | 0.1908 | 0.0974 | 0.2294 | 0.0565 | Enjoyment All | 0.5695 | * | 0.60007 | * | |
| Control | 0.1076 | 0.0971 | 0.1217 | 0.0564 | Role None | −0.8956 | 0.1239 | −0.7697 | 0.0761 | |
| Attachment_None | −1.9678 | 0.1129 | −1.9633 | 0.0775 | Role Few | −0.0277 | 0.1532 | 0.1086 | 0.0776 | |
| Attachment_Little | 0.1694 | 0.1012 | 0.1811 | 0.0756 | Role Many | 0.4435 | 0.1363 | 0.2616 | 0.0784 | |
| Attachment_Lot | 0.9053 | 0.0905 | 1.0493 | 0.0811 | Role All | 0.4798 | * | 0.3995 | ||
| Attachment_All | 0.8932 | * | 0.7329 | * | Control None | −0.8085 | 0.1122 | −0.7149 | 0.0763 | |
| Security_None | −0.6123 | 0.118 | −0.6953 | 0.0764 | Control Few | 0.0835 | 0.1596 | 0.1505 | 0.0774 | |
| Security Little | −0.3761 | 0.1302 | −0.2449 | 0.077 | Control Many | 0.278 | 0.1376 | 0.2854 | 0.0785 | |
| Security Lot | 0.0373 | 0.1153 | 0.1203 | 0.0779 | Control All | 0.4471 | * | 0.2791 | * |
| Best Attribute | Worst Attribute | Best Level | Worst Level | No. of Picks | Rank |
|---|---|---|---|---|---|
| Attachment | Security | Attach_all | Security_none | 2629 | 1 |
| Attachment | Role | Attach_all | Role_few | 1204 | 2 |
| Enjoyment | Security | Enjoyment_all | Security_none | 1075 | 3 |
| Attachment | Control | Attach_all | Control_many | 994 | 4 |
| Control | Security | Control_many | Security_none | 700 | 5 |
| Attachment | Enjoyment | Attach_all | Enjoyment_all | 629 | 6 |
| Role | Security | Role_few | Security_none | 509 | 7 |
| Enjoyment | Role | Enjoyment_all | Role_few | 498 | 8 |
| Enjoyment | Control | Enjoyment_all | Control_many | 400 | 9 |
| Control | Role | Control_many | Role_few | 341 | 10 |
| Role | Control | Role_few | Control_many | 206 | 11 |
| Control | Enjoyment | Control_many | Enjoyment_all | 162 | 12 |
| Security | Role | Security_none | Role_few | 130 | 13 |
| Role | Enjoyment | Role_few | Enjoyment_all | 122 | 14 |
| Enjoyment | Attachment | Enjoyment_all | Attach_all | 117 | 15 |
| Security | Control | Security_none | Control_many | 89 | 16 |
| Control | Attachment | Control_many | Attach_all | 62 | 17 |
| Security | Enjoyment | Security_none | Enjoyment_all | 58 | 18 |
| Role | Attachment | Role_few | Attach_all | 51 | 19 |
| Security | Attachment | Security_none | Attach_all | 24 | 20 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.189 | 0.226 | 0.252 | 0.332 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 0.058 | 0.760 | 0.000 | 0.115 | 0.067 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 3 | 0.034 | 0.085 | 0.783 | 0.000 | 0.062 | 0.036 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 4 | 0.016 | 0.160 | 0.369 | 0.397 | 0.058 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5 | 0.000 | 0.000 | 0.000 | 0.000 | 0.882 | 0.000 | 0.000 | 0.118 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 6 | 0.000 | 0.000 | 0.371 | 0.000 | 0.177 | 0.311 | 0.000 | 0.142 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 7 | 0.000 | 0.000 | 0.000 | 0.269 | 0.159 | 0.093 | 0.415 | 0.064 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.327 | 0.000 | 0.673 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.421 | 0.000 | 0.000 | 0.579 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 10 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.661 | 0.339 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 17 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| 18 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| 19 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 20 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.441 | 0.266 | 0.178 | 0.116 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 0.101 | 0.557 | 0.197 | 0.112 | 0.033 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 3 | 0.113 | 0.171 | 0.631 | 0.046 | 0.012 | 0.026 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 4 | 0.189 | 0.191 | 0.219 | 0.355 | 0.022 | 0.016 | 0.007 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5 | 0.000 | 0.076 | 0.434 | 0.083 | 0.377 | 0.016 | 0.000 | 0.015 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 6 | 0.000 | 0.000 | 0.263 | 0.075 | 0.121 | 0.459 | 0.000 | 0.053 | 0.027 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 7 | 0.000 | 0.000 | 0.000 | 0.204 | 0.146 | 0.052 | 0.549 | 0.048 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.053 | 0.037 | 0.034 | 0.730 | 0.071 | 0.037 | 0.038 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.091 | 0.000 | 0.000 | 0.865 | 0.044 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 10 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.078 | 0.000 | 0.000 | 0.750 | 0.171 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.116 | 0.000 | 0.000 | 0.884 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.830 | 0.170 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 17 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.136 | 0.000 | 0.717 | 0.147 | 0.000 | 0.000 |
| 18 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| 19 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 20 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.574 | 0.217 | 0.123 | 0.086 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 0.131 | 0.583 | 0.161 | 0.085 | 0.040 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 3 | 0.197 | 0.217 | 0.498 | 0.052 | 0.017 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 4 | 0.236 | 0.217 | 0.127 | 0.329 | 0.050 | 0.029 | 0.012 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5 | 0.000 | 0.204 | 0.327 | 0.140 | 0.288 | 0.017 | 0.017 | 0.008 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 6 | 0.000 | 0.000 | 0.148 | 0.158 | 0.093 | 0.497 | 0.012 | 0.038 | 0.053 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 7 | 0.000 | 0.000 | 0.000 | 0.187 | 0.111 | 0.045 | 0.548 | 0.046 | 0.063 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.021 | 0.017 | 0.034 | 0.780 | 0.054 | 0.037 | 0.057 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.044 | 0.021 | 0.044 | 0.820 | 0.047 | 0.024 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 10 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.031 | 0.000 | 0.000 | 0.860 | 0.071 | 0.000 | 0.038 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.145 | 0.000 | 0.000 | 0.800 | 0.055 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.122 | 0.000 | 0.000 | 0.808 | 0.069 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.927 | 0.073 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.893 | 0.000 | 0.000 | 0.107 | 0.000 |
| 17 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.086 | 0.000 | 0.820 | 0.094 | 0.000 | 0.000 |
| 18 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| 19 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 |
| 20 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 |
| Choice | t = 1 | t = 2 | t = 3 | t = 4 | t = 5 | t = 6 | t = 7 | t = 8 | t = 9 | t = 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.2346 | 1.2613 | 1.3110 | 1.3983 | 1.5419 | 1.7660 | 2.1003 | 2.5814 | 3.2520 | 4.1576 |
| 2 | 0.9365 | 1.0047 | 1.1107 | 1.2680 | 1.4947 | 1.8143 | 2.2575 | 2.8627 | 3.6758 | 4.7452 |
| 3 | 0.8028 | 0.7827 | 0.7642 | 0.7572 | 0.7739 | 0.8287 | 0.9381 | 1.1201 | 1.3917 | 1.7638 |
| 4 | 1.2050 | 1.2500 | 1.3260 | 1.4446 | 1.6215 | 1.8769 | 2.2366 | 2.7325 | 3.4027 | 4.2880 |
| 5 | 0.5933 | 0.6260 | 0.6770 | 0.7530 | 0.8628 | 1.0178 | 1.2323 | 1.5241 | 1.9134 | 2.4200 |
| 6 | 0.9295 | 0.9248 | 0.9264 | 0.9418 | 0.9804 | 1.0536 | 1.1745 | 1.3574 | 1.6166 | 1.9616 |
| 7 | 0.9481 | 0.9799 | 1.0310 | 1.1087 | 1.2231 | 1.3867 | 1.6152 | 1.9276 | 2.3447 | 2.8856 |
| 8 | 1.0941 | 1.1007 | 1.1168 | 1.1484 | 1.2032 | 1.2902 | 1.4205 | 1.6063 | 1.8600 | 2.1914 |
| 9 | 1.1719 | 1.1818 | 1.2027 | 1.2404 | 1.3022 | 1.3971 | 1.5357 | 1.7300 | 1.9920 | 2.3310 |
| 10 | 0.7217 | 0.7911 | 0.8881 | 1.0144 | 1.1734 | 1.3711 | 1.6166 | 1.9242 | 2.3144 | 2.8145 |
| 11 | 0.3888 | 0.4186 | 0.4630 | 0.5224 | 0.5973 | 0.6890 | 0.8003 | 0.9358 | 1.1030 | 1.3135 |
| 12 | 0.1282 | 0.1306 | 0.1330 | 0.1335 | 0.1301 | 0.1200 | 0.0997 | 0.0648 | 0.0096 | −0.0736 |
| 13 | 0.4320 | 0.4390 | 0.4430 | 0.4389 | 0.4205 | 0.3802 | 0.3089 | 0.1959 | 0.0295 | −0.2022 |
| 14 | 0.7528 | 0.7431 | 0.7243 | 0.6911 | 0.6365 | 0.5516 | 0.4256 | 0.2452 | −0.0044 | −0.3383 |
| 15 | 0.3652 | 0.3564 | 0.3409 | 0.3160 | 0.2779 | 0.2214 | 0.1397 | 0.0234 | −0.1402 | −0.3686 |
| 16 | 1.4454 | 1.4596 | 1.4725 | 1.4786 | 1.4711 | 1.4417 | 1.3807 | 1.2765 | 1.1157 | 0.8841 |
| 17 | 0.8189 | 0.8620 | 0.9079 | 0.9462 | 0.9642 | 0.9469 | 0.8772 | 0.7351 | 0.4989 | 0.1469 |
| 18 | 1.5412 | 1.4548 | 1.3269 | 1.1446 | 0.8907 | 0.5427 | 0.0715 | −0.5588 | −1.3894 | −2.4609 |
| 19 | 1.0774 | 1.0947 | 1.1169 | 1.1398 | 1.1576 | 1.1636 | 1.1492 | 1.1046 | 1.0170 | 0.8699 |
| 20 | 1.2778 | 1.2731 | 1.2608 | 1.2341 | 1.1843 | 1.0997 | 0.9652 | 0.7611 | 0.4613 | 0.0295 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adikari, S.; Diawara, N. Utility in Time Description in Priority Best–Worst Discrete Choice Models: An Empirical Evaluation Using Flynn’s Data. Stats 2024, 7, 185-202. https://doi.org/10.3390/stats7010012
Adikari S, Diawara N. Utility in Time Description in Priority Best–Worst Discrete Choice Models: An Empirical Evaluation Using Flynn’s Data. Stats. 2024; 7(1):185-202. https://doi.org/10.3390/stats7010012
Chicago/Turabian StyleAdikari, Sasanka, and Norou Diawara. 2024. "Utility in Time Description in Priority Best–Worst Discrete Choice Models: An Empirical Evaluation Using Flynn’s Data" Stats 7, no. 1: 185-202. https://doi.org/10.3390/stats7010012








