New Goodness-of-Fit Tests for the Kumaraswamy Distribution
Abstract
:1. Introduction
2. Raschke’s “Biased Transformation” Testing
- (i)
- (ii)
- Using these parameter estimates, generate a sample of Y, where , is the distribution function for the standard normal distribution, and is given in (1);
- (iii)
- Obtain the ML estimates of the parameters of the normal distribution for Y;
- (iv)
- Apply an EDF test for normality to the Y data;
- (v)
- For a chosen significance level, α, reject “X is Kumaraswamy” if “Y is Normal” is rejected.
3. A Simulation Study
4. Empirical Applications
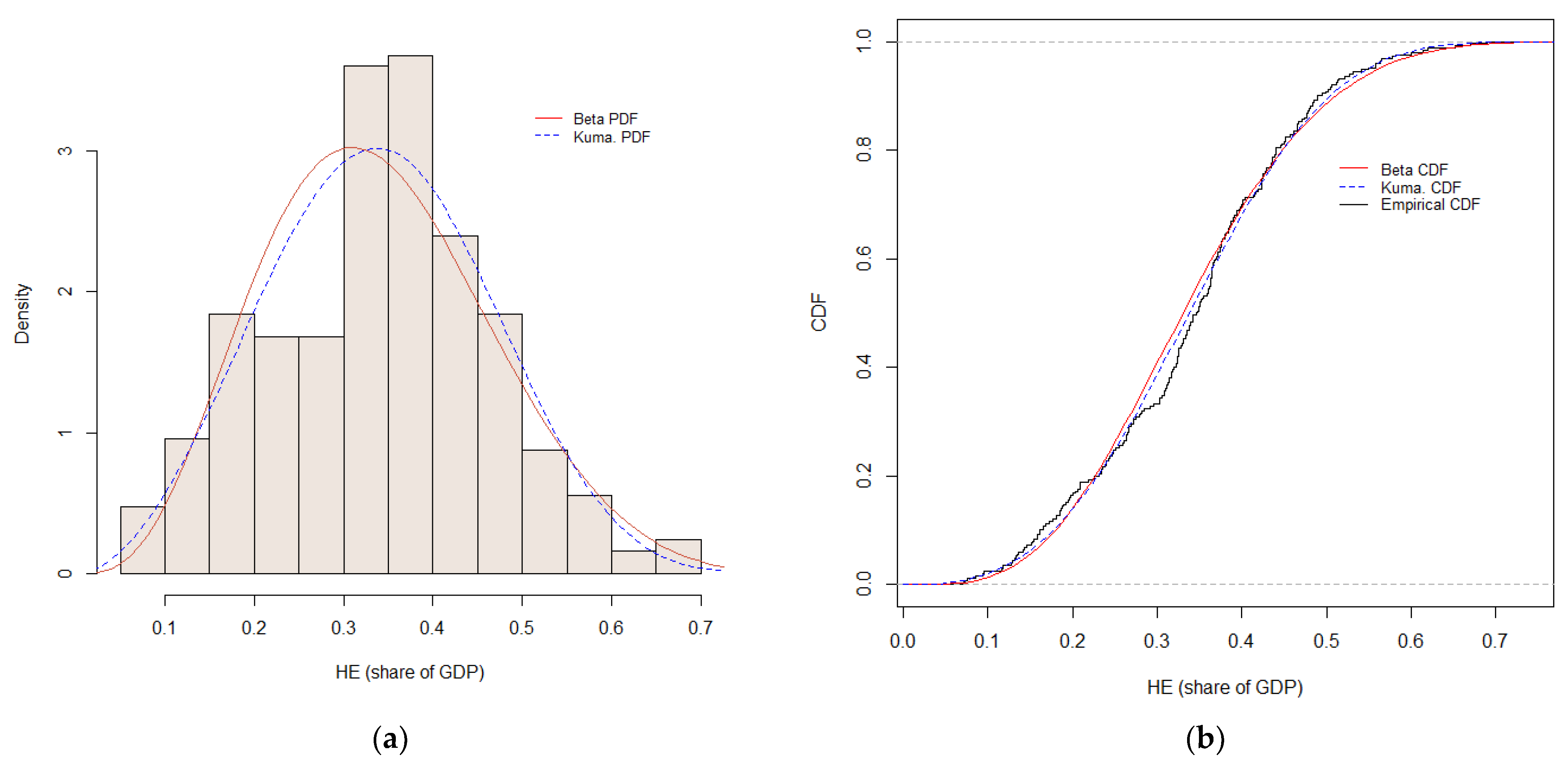
4.1. The Hidden Economy
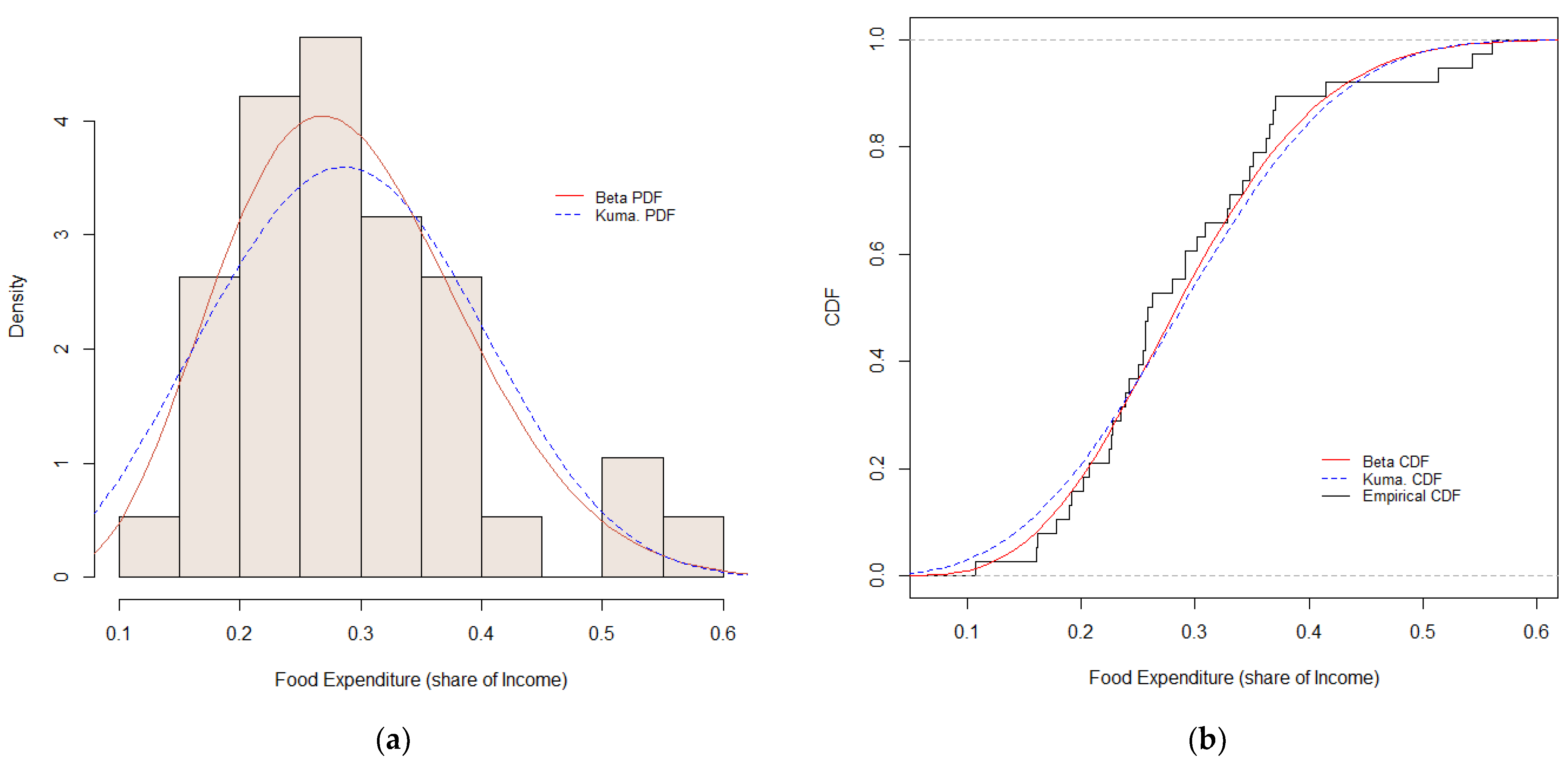
4.2. Food Expenditure
5. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Sundar, V.; Subbiah, K. Application of double bounded probability density function for analysis of ocean waves. Ocean Eng. 1989, 16, 193–200. [Google Scholar] [CrossRef]
- Seifi, A.; Ponnambalam, K.; Vlach, J. Maximization of Manufacturing Yield of Systems with Arbitrary Distributions of Component Values. Ann. Oper. Res. 2000, 99, 373–383. [Google Scholar] [CrossRef]
- Ponnambalam, K.; Seifi, A.; Vlach, J. Probabilistic design of systems with general distributions of parameters. Int. J. Circuit Theory Appl. 2001, 29, 527–536. [Google Scholar] [CrossRef]
- Ganji, A.; Ponnambalam, K.; Khalili, D.; Karamouz, M. Grain yield reliability analysis with crop water demand uncertainty. Stoch. Environ. Res. Risk Assess. 2006, 20, 259–277. [Google Scholar] [CrossRef]
- Courard-Hauri, D. Using Monte Carlo analysis to investigate the relationship between overconsumption and uncertain access to one’s personal utility function. Ecol. Econ. 2007, 64, 152–162. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2010, 81, 883–898. [Google Scholar] [CrossRef]
- Bayer, F.M.; Bayer, D.M.; Pumi, G. Kumaraswamy autoregressive moving average models for double bounded environmental data. J. Hydrol. 2017, 555, 385–396. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Machado, E.C.; Botter, D.A.; Sandoval, M.C. The Kumaraswamy normal linear regression model with applications. Commun. Stat.-Simul. Comput. 2018, 47, 3062–3082. [Google Scholar] [CrossRef]
- Nadarajah, S. On the distribution of Kumaraswamy. J. Hydrol. 2008, 348, 568–569. [Google Scholar] [CrossRef]
- McDonald, J.B. Some Generalized Functions for the Size Distribution of Income. Econometrica 1984, 52, 647. [Google Scholar] [CrossRef]
- Jones, M. Kumaraswamy’s distribution: A beta-type distribution with some tractability advantages. Stat. Methodol. 2009, 6, 70–81. [Google Scholar] [CrossRef]
- Garg, M. On Distribution of Order Statistics from Kumaraswamy Distribution. Kyungpook Math. J. 2008, 48, 411–417. [Google Scholar] [CrossRef]
- Mitnik, P.A. New properties of the Kumaraswamy distribution. Commun. Stat.-Theory Methods 2013, 42, 741–755. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta Regression for Modelling Rates and Proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Mitnik, P.A.; Baek, S. The Kumaraswamy distribution: Median-dispersion re-parameterizations for regression modeling and simulation-based estimation. Stat. Pap. 2013, 54, 177–192. [Google Scholar] [CrossRef]
- Hamedi-Shahraki, S.; Rasekhi, A.; Yekaninejad, M.S.; Eshraghian, M.R.; Pakpour, A.H. Kumaraswamy regression modeling for Bounded Outcome Scores. Pak. J. Stat. Oper. Res. 2021, 17, 79–88. [Google Scholar] [CrossRef]
- Raschke, M. The Biased Transformation and Its Application in Goodness-of-Fit Tests for the Beta and Gamma Distribution. Commun. Stat.-Simul. Comput. 2009, 38, 1870–1890. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain “goodness of fit” criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test for goodness of fit. J. Am. Stat. Assoc. 1954, 49, 300–310. [Google Scholar] [CrossRef]
- Raschke, M. Empirical behaviour of tests for the beta distribution and their application in environmental research. Stoch. Environ. Res. Risk Assess. 2011, 25, 79–89. [Google Scholar] [CrossRef]
- Kuiper, N.H. Tests concerning random points on a circle. Proc. K. Ned. Akad. Wet. A 1962, 63, 38–47. [Google Scholar] [CrossRef]
- Watson, G.S. Goodness-of-fit tests on a circle. I. Biometrika 1961, 48, 109–114. [Google Scholar] [CrossRef]
- Cramér, H. On the composition of elementary errors. Scand. Actuar. J. 1928, 1928, 13–74. [Google Scholar] [CrossRef]
- von Mises, R.E. Wahrscheinlichkeit, Statistik und Wahrheit; Julius Springer: Vienna, Austria, 1928. [Google Scholar]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. G. dell’Ist. Ital. Attuari 1933, 4, 83–91. [Google Scholar]
- Smirnov, N. Table for Estimating the Goodness of Fit of Empirical Distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Lemonte, A.J. Improved point estimation for the Kumaraswamy distribution. J. Stat. Comput. Simul. 2011, 81, 1971–1982. [Google Scholar] [CrossRef]
- Stephens, M.A. Tests based on EDF statistics. In Goodness-of-Fit Techniques; D’Augustino, R.B., Stephens, M.A., Eds.; Marcel Dekker: New York, NY, USA, 1986; pp. 97–194. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 5 March 2024).
- Moss, J.; Nagler, T. Package ‘univariateML’. 2022. Available online: https://cran.r-project.org/web/packages/univariateML/univariateML.pdf (accessed on 5 March 2024).
- Pavia, J.M. Package ‘GoFKernel’. 2022. Available online: https://cran.r-project.org/web/packages/GoFKernel/GoFKernel.pdf (accessed on 5 March 2024).
- Millard, S.P.; Kowarik, A. Package ‘EnvStats’. 2023. Available online: https://cran.r-project.org/web/packages/EnvStats/EnvStats.pdf (accessed on 5 March 2024).
- Yee, T. Package ‘VGAM’. 2023. Available online: https://cran.r-project.org/web/packages/VGAM/VGAM.pdf (accessed on 5 March 2024).
- Hetzel, J.T. Package ‘trapezoid’. 2022. Available online: https://cran.r-project.org/web/packages/trapezoid/trapezoid.pdf (accessed on 5 March 2024).
- Mersmann, O.; Trautmann, H.; Steuer, D.; Bornkamp, B. Package ‘Truncnorm’. 2023. Available online: https://cran.r-project.org/web/packages/truncnorm/truncnorm.pdf (accessed on 5 March 2024).
- Bear, R.; Shang, K.; You, H.; Fannin, B. Package ‘Cascsim’. 2022. Available online: https://cran.r-project.org/web/packages/cascsim/cascsim.pdf (accessed on 5 March 2024).
- Reynkens, T. Package ‘ReIns’. 2023. Available online: https://cran.r-project.org/web/packages/ReIns/ReIns.pdf (accessed on 5 March 2024).
- Medina, L.; Schneider, H. Shedding Light on the Shadow Economy: A Global Database and the Interaction with the Official One; CESifo Working Paper No. 7981; Ludwig Maximilian University of Munich: Munich, Germany, 2019. [Google Scholar] [CrossRef]
- Zeileis, A.; Cribari-Neto, F.; Gruen, B.; Kosmidis, I.; Simas, A.B.; Rocha, A.V. Package ‘betareg’. 2022. Available online: https://cran.r-project.org/web/packages/betareg/betareg.pdf (accessed on 5 March 2024).
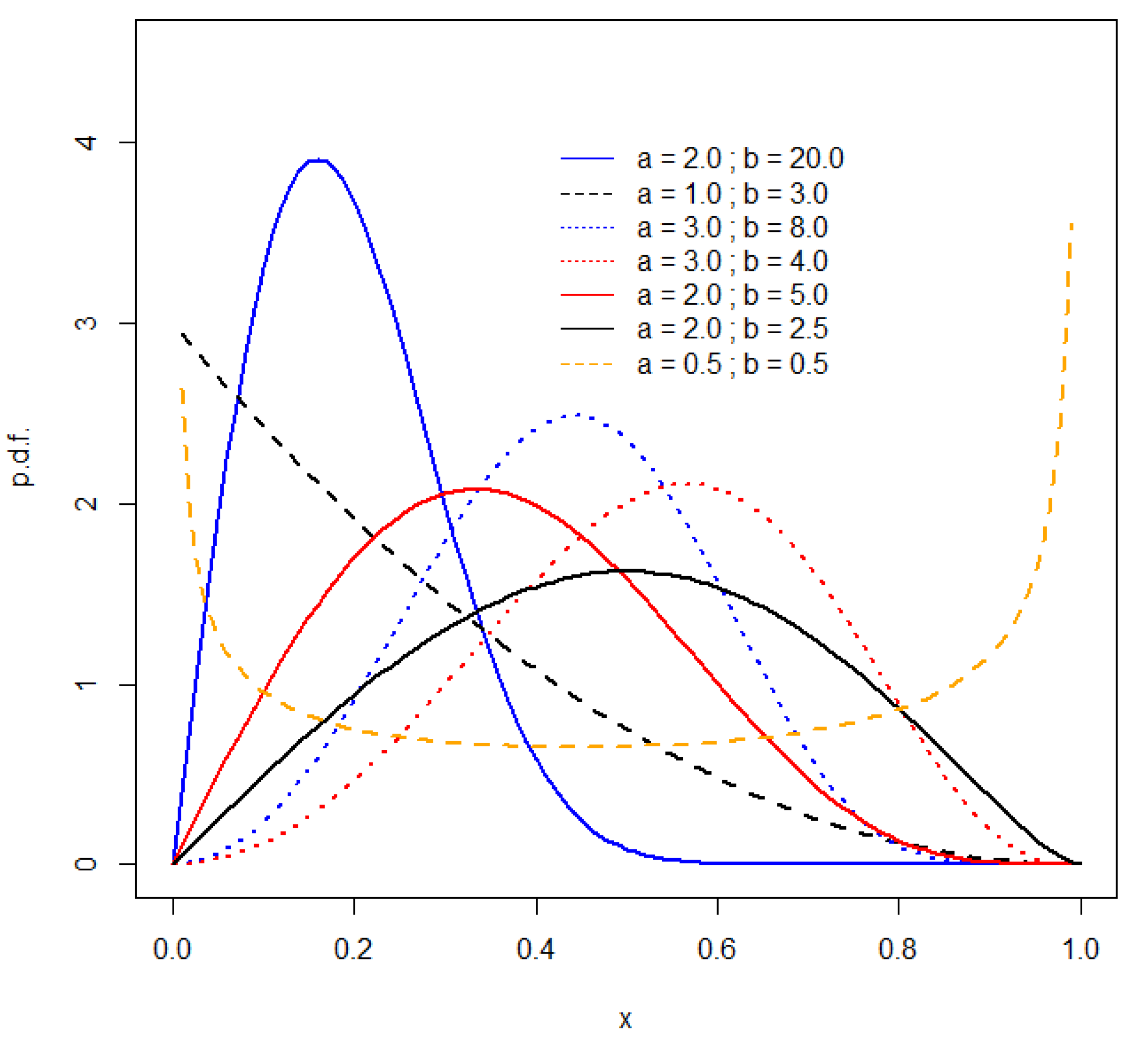
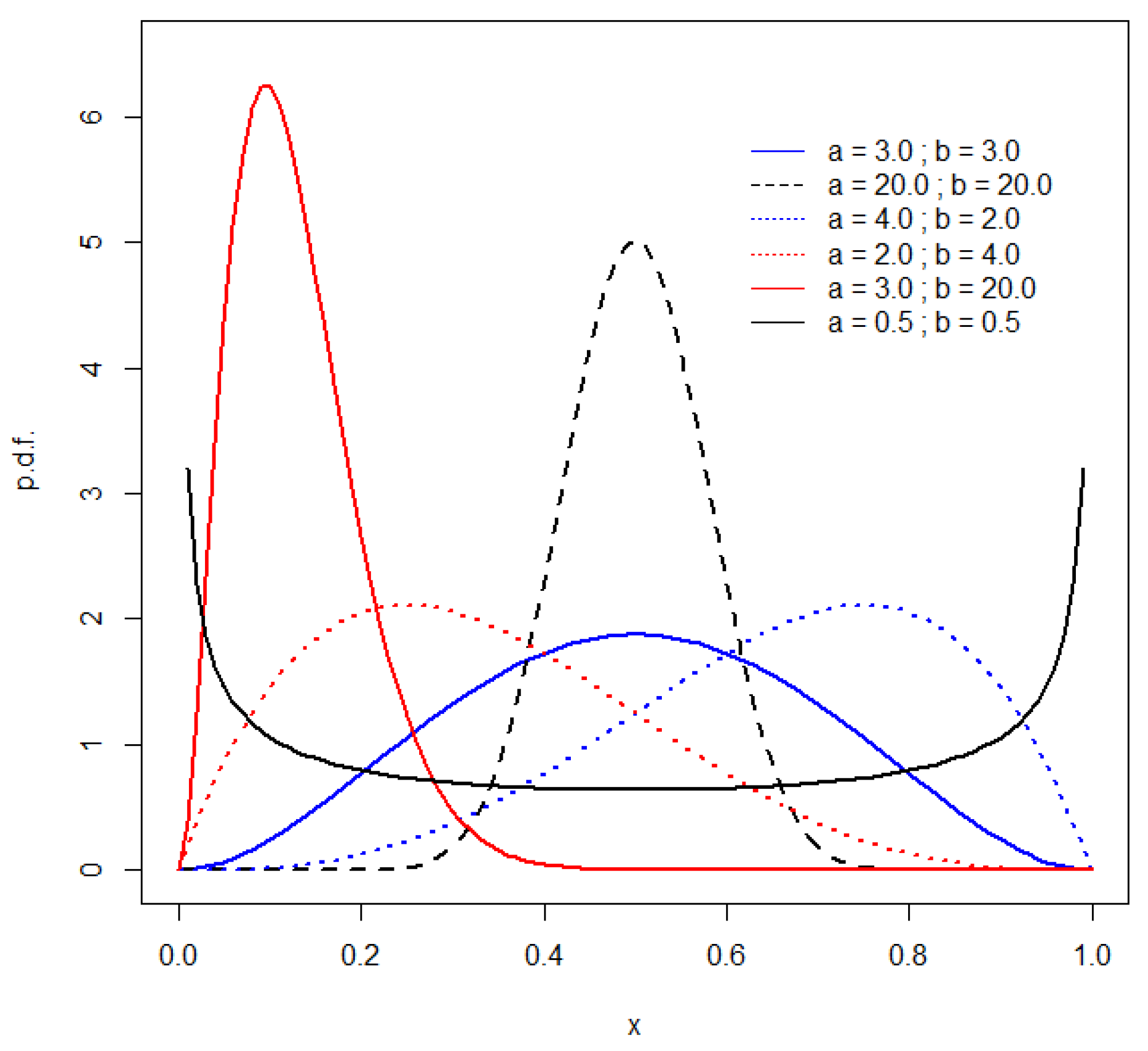
| n | K-S | Kuiper | C-M | Watson | A-D | K-S | Kuiper | C-M | Watson | A-D |
|---|---|---|---|---|---|---|---|---|---|---|
| a = 3, b = 4 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0585 | 0.0597 | 0.0561 | 0.0550 | 0.0638 | 0.1193 | 0.1210 | 0.1133 | 0.1189 | 0.1277 |
| 25 | 0.0492 | 0.0464 | 0.0482 | 0.0486 | 0.0487 | 0.1053 | 0.0978 | 0.0990 | 0.1015 | 0.1037 |
| 50 | 0.0505 | 0.0475 | 0.0459 | 0.0451 | 0.0472 | 0.1007 | 0.0981 | 0.0941 | 0.0977 | 0.0982 |
| 100 | 0.0497 | 0.0467 | 0.0488 | 0.0480 | 0.0486 | 0.1002 | 0.0925 | 0.0932 | 0.0967 | 0.0949 |
| a = 3, b = 8 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0577 | 0.0593 | 0.0559 | 0.0551 | 0.0628 | 0.1174 | 0.1209 | 0.1130 | 0.1178 | 0.1255 |
| 25 | 0.0479 | 0.0460 | 0.0474 | 0.0481 | 0.0485 | 0.1040 | 0.0972 | 0.0978 | 0.1013 | 0.1033 |
| 50 | 0.0498 | 0.0470 | 0.0447 | 0.0434 | 0.0463 | 0.1002 | 0.0969 | 0.0924 | 0.0976 | 0.0972 |
| 100 | 0.0494 | 0.0462 | 0.0481 | 0.0475 | 0.0475 | 0.0986 | 0.0926 | 0.0922 | 0.0956 | 0.0927 |
| a = 2, b = 2.5 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0598 | 0.0590 | 0.0570 | 0.0560 | 0.0642 | 0.1184 | 0.1214 | 0.1133 | 0.1192 | 0.1267 |
| 25 | 0.0500 | 0.0470 | 0.0486 | 0.0486 | 0.0496 | 0.1048 | 0.0981 | 0.0991 | 0.1019 | 0.1034 |
| 50 | 0.0515 | 0.0479 | 0.0460 | 0.0460 | 0.0479 | 0.1021 | 0.0988 | 0.0951 | 0.0986 | 0.0985 |
| 100 | 0.0489 | 0.0468 | 0.0496 | 0.0494 | 0.0492 | 0.1010 | 0.0929 | 0.0946 | 0.0974 | 0.0957 |
| a = 2.0, b = 5.0 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0586 | 0.0597 | 0.0557 | 0.0550 | 0.0630 | 0.1184 | 0.1208 | 0.1130 | 0.1184 | 0.1269 |
| 25 | 0.0491 | 0.0463 | 0.0478 | 0.0486 | 0.0489 | 0.1055 | 0.0977 | 0.0983 | 0.1015 | 0.1032 |
| 50 | 0.0503 | 0.0472 | 0.0457 | 0.0445 | 0.0468 | 0.1003 | 0.0973 | 0.0931 | 0.0976 | 0.0976 |
| 100 | 0.0496 | 0.0464 | 0.0488 | 0.0474 | 0.0485 | 0.1000 | 0.0923 | 0.0930 | 0.0959 | 0.0941 |
| a = 2.0, b = 20.0 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0576 | 0.0593 | 0.0550 | 0.0550 | 0.0620 | 0.1170 | 0.1205 | 0.1106 | 0.1172 | 0.1248 |
| 25 | 0.0473 | 0.0455 | 0.0474 | 0.0481 | 0.0476 | 0.1034 | 0.0969 | 0.0978 | 0.1018 | 0.1022 |
| 50 | 0.0492 | 0.0464 | 0.0442 | 0.0430 | 0.0456 | 0.0999 | 0.0963 | 0.0911 | 0.0974 | 0.0964 |
| 100 | 0.0485 | 0.0463 | 0.0469 | 0.0466 | 0.0459 | 0.0978 | 0.0923 | 0.0913 | 0.0943 | 0.0923 |
| a = 1.0, b = 3.0 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0589 | 0.0592 | 0.0560 | 0.0553 | 0.0642 | 0.1189 | 0.1209 | 0.1131 | 0.1192 | 0.1273 |
| 25 | 0.0497 | 0.0464 | 0.0486 | 0.0486 | 0.0493 | 0.1051 | 0.0980 | 0.0993 | 0.1021 | 0.1037 |
| 50 | 0.0512 | 0.0477 | 0.0460 | 0.0455 | 0.0474 | 0.1014 | 0.0986 | 0.0948 | 0.0981 | 0.0985 |
| 100 | 0.0495 | 0.0470 | 0.0493 | 0.0487 | 0.0487 | 0.1002 | 0.0926 | 0.0940 | 0.0968 | 0.0955 |
| a = 0.5, b = 0.5 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0625 | 0.0603 | 0.0574 | 0.0582 | 0.0679 | 0.1260 | 0.1199 | 0.1179 | 0.1203 | 0.1346 |
| 25 | 0.0592 | 0.0527 | 0.0619 | 0.0590 | 0.0643 | 0.1154 | 0.1071 | 0.1158 | 0.1168 | 0.1235 |
| 50 | 0.0650 | 0.0571 | 0.0689 | 0.0624 | 0.0742 | 0.1267 | 0.1165 | 0.1285 | 0.1238 | 0.1366 |
| 100 | 0.0864 | 0.0730 | 0.0940 | 0.0819 | 0.1017 | 0.1563 | 0.1356 | 0.1605 | 0.1509 | 0.1706 |
| Crit. | 0.895 | 1.489 | 0.126 | 0.117 | 0.752 | 0.819 | 1.386 | 0.104 | 0.096 | 0.631 |
| n | K-S | Kuiper | C-M | Watson | A-D | K-S | Kuiper | C-M | Watson | A-D |
|---|---|---|---|---|---|---|---|---|---|---|
| Triangular (mode = 1/4) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0784 | 0.0752 | 0.0765 | 0.0754 | 0.0878 | 0.1439 | 0.1409 | 0.1426 | 0.1463 | 0.1604 |
| 25 | 0.0978 | 0.0868 | 0.1097 | 0.0987 | 0.1175 | 0.1766 | 0.1550 | 0.1857 | 0.1785 | 0.1988 |
| 50 | 0.1422 | 0.1218 | 0.1707 | 0.1498 | 0.1806 | 0.2397 | 0.2061 | 0.2597 | 0.2422 | 0.2742 |
| 100 | 0.2470 | 0.2121 | 0.3051 | 0.2639 | 0.3160 | 0.3740 | 0.3182 | 0.4157 | 0.3773 | 0.4333 |
| 250 | 0.5491 | 0.4885 | 0.6490 | 0.5831 | 0.6723 | 0.6762 | 0.6224 | 0.7564 | 0.703 | 0.7712 |
| 500 | 0.8529 | 0.8178 | 0.9246 | 0.8865 | 0.9347 | 0.9196 | 0.8940 | 0.9573 | 0.9351 | 0.9637 |
| 1000 | 0.9929 | 0.9909 | 0.9978 | 0.9961 | 0.9986 | 0.9975 | 0.9963 | 0.9992 | 0.9986 | 0.9994 |
| Triangular (mode = 7/8) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0676 | 0.0711 | 0.0660 | 0.0644 | 0.0755 | 0.1314 | 0.1330 | 0.1283 | 0.1353 | 0.1446 |
| 25 | 0.0736 | 0.0680 | 0.0822 | 0.0768 | 0.0866 | 0.1422 | 0.1294 | 0.1455 | 0.1462 | 0.1538 |
| 50 | 0.0969 | 0.0884 | 0.1144 | 0.1052 | 0.1233 | 0.1797 | 0.1626 | 0.1966 | 0.1854 | 0.2124 |
| 100 | 0.1575 | 0.1336 | 0.1928 | 0.1659 | 0.2191 | 0.2561 | 0.2294 | 0.2964 | 0.2703 | 0.3264 |
| 250 | 0.3588 | 0.3192 | 0.4530 | 0.3883 | 0.5122 | 0.5053 | 0.4532 | 0.5853 | 0.5231 | 0.6366 |
| 500 | 0.6568 | 0.6198 | 0.7771 | 0.6994 | 0.8386 | 0.7845 | 0.7446 | 0.8622 | 0.8127 | 0.9001 |
| 1000 | 0.9364 | 0.9310 | 0.9789 | 0.9603 | 0.9890 | 0.9730 | 0.9671 | 0.9904 | 0.9815 | 0.9954 |
| Truncated Log-Normal (meanlog = 0, sdlog = 1) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0774 | 0.0758 | 0.0762 | 0.0738 | 0.0883 | 0.1458 | 0.1409 | 0.1420 | 0.1452 | 0.1614 |
| 25 | 0.1011 | 0.0862 | 0.1147 | 0.1003 | 0.1260 | 0.1836 | 0.1560 | 0.1918 | 0.1796 | 0.2139 |
| 50 | 0.1536 | 0.1212 | 0.1836 | 0.1548 | 0.2073 | 0.2533 | 0.2037 | 0.2842 | 0.2528 | 0.3148 |
| 100 | 0.2778 | 0.2193 | 0.3431 | 0.2785 | 0.3907 | 0.4153 | 0.3310 | 0.4672 | 0.4035 | 0.5182 |
| 250 | 0.6143 | 0.5376 | 0.7436 | 0.6318 | 0.8054 | 0.7399 | 0.6646 | 0.8319 | 0.7519 | 0.8795 |
| 500 | 0.9105 | 0.8815 | 0.9713 | 0.9290 | 0.9867 | 0.9600 | 0.9397 | 0.9870 | 0.9657 | 0.9936 |
| 1000 | 0.9981 | 0.9975 | 1.0000 | 0.9992 | 1.0000 | 0.9996 | 0.9994 | 1.0000 | 0.9999 | 1.0000 |
| Truncated Log-Normal (meanlog= 0.5, sdlog = 0.5) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0398 | 0.0400 | 0.0375 | 0.0382 | 0.0432 | 0.0786 | 0.0757 | 0.0751 | 0.0765 | 0.0841 |
| 25 | 0.0653 | 0.0589 | 0.0672 | 0.0635 | 0.0718 | 0.1303 | 0.1167 | 0.1313 | 0.1272 | 0.1382 |
| 50 | 0.0798 | 0.0671 | 0.0868 | 0.0760 | 0.0956 | 0.1503 | 0.1290 | 0.1539 | 0.1459 | 0.1673 |
| 100 | 0.1164 | 0.0924 | 0.1349 | 0.1106 | 0.1474 | 0.1997 | 0.1679 | 0.2168 | 0.1946 | 0.2374 |
| 250 | 0.2427 | 0.1834 | 0.2966 | 0.2365 | 0.3371 | 0.3668 | 0.2937 | 0.4120 | 0.354 | 0.4568 |
| 500 | 0.4474 | 0.3538 | 0.5422 | 0.4401 | 0.6156 | 0.5861 | 0.4880 | 0.6661 | 0.5742 | 0.7337 |
| 1000 | 0.7557 | 0.6784 | 0.8670 | 0.7678 | 0.9163 | 0.8594 | 0.7980 | 0.9255 | 0.8623 | 0.9582 |
| Truncated Normal (mean = 0.5, sd = 0.1) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0704 | 0.0648 | 0.0686 | 0.0629 | 0.0799 | 0.1348 | 0.1253 | 0.1260 | 0.1287 | 0.1476 |
| 25 | 0.0839 | 0.0770 | 0.0952 | 0.0856 | 0.1076 | 0.1540 | 0.1368 | 0.1644 | 0.1517 | 0.1798 |
| 50 | 0.1188 | 0.0986 | 0.1395 | 0.1166 | 0.1607 | 0.2031 | 0.1698 | 0.2209 | 0.1991 | 0.2457 |
| 100 | 0.1928 | 0.1506 | 0.2309 | 0.1868 | 0.2682 | 0.3029 | 0.2497 | 0.3393 | 0.2945 | 0.3834 |
| 250 | 0.4263 | 0.3493 | 0.5179 | 0.4206 | 0.5840 | 0.5625 | 0.4782 | 0.6409 | 0.5542 | 0.6987 |
| 500 | 0.7151 | 0.6509 | 0.8345 | 0.7321 | 0.8822 | 0.8227 | 0.7661 | 0.8988 | 0.8336 | 0.9310 |
| 1000 | 0.9516 | 0.9408 | 0.9891 | 0.9675 | 0.9957 | 0.9813 | 0.9723 | 0.9954 | 0.9857 | 0.9984 |
| Truncated Normal (mean = 0.8, sd = 0.8) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0577 | 0.0586 | 0.0547 | 0.0559 | 0.0647 | 0.1170 | 0.1166 | 0.1137 | 0.1163 | 0.1306 |
| 25 | 0.0519 | 0.0500 | 0.0529 | 0.0517 | 0.0540 | 0.1040 | 0.0981 | 0.1045 | 0.1080 | 0.1096 |
| 50 | 0.0544 | 0.0507 | 0.0584 | 0.0559 | 0.0573 | 0.1081 | 0.1003 | 0.1044 | 0.1063 | 0.1088 |
| 100 | 0.0558 | 0.0544 | 0.0558 | 0.0552 | 0.0574 | 0.1193 | 0.1075 | 0.1115 | 0.1126 | 0.1154 |
| 250 | 0.0681 | 0.0657 | 0.0720 | 0.0692 | 0.0765 | 0.1293 | 0.1244 | 0.1284 | 0.1241 | 0.1349 |
| 500 | 0.0873 | 0.0867 | 0.0999 | 0.0904 | 0.1099 | 0.1648 | 0.1578 | 0.1696 | 0.1628 | 0.1790 |
| 1000 | 0.1404 | 0.1300 | 0.1566 | 0.1410 | 0.1717 | 0.2318 | 0.2196 | 0.2476 | 0.2374 | 0.2695 |
| Trapezoidal (m1 = 1/8, m2 = 3/8; n1 = n3 = 2) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0636 | 0.0652 | 0.0606 | 0.0605 | 0.0691 | 0.1250 | 0.1249 | 0.1193 | 0.1254 | 0.1372 |
| 25 | 0.0632 | 0.0570 | 0.0651 | 0.0620 | 0.0730 | 0.1282 | 0.1169 | 0.1293 | 0.1261 | 0.1400 |
| 50 | 0.0771 | 0.0652 | 0.0830 | 0.0703 | 0.0968 | 0.1473 | 0.1275 | 0.1537 | 0.1417 | 0.1704 |
| 100 | 0.1124 | 0.0877 | 0.1292 | 0.1054 | 0.1531 | 0.1934 | 0.1616 | 0.2146 | 0.1889 | 0.2477 |
| 250 | 0.2306 | 0.1772 | 0.2885 | 0.2196 | 0.3537 | 0.3521 | 0.2873 | 0.4103 | 0.3433 | 0.4821 |
| 500 | 0.4214 | 0.3613 | 0.5405 | 0.4248 | 0.6512 | 0.5705 | 0.4937 | 0.6686 | 0.5650 | 0.7640 |
| 1000 | 0.7258 | 0.7011 | 0.8737 | 0.7625 | 0.9371 | 0.8409 | 0.8148 | 0.9322 | 0.8639 | 0.9694 |
| Trapezoidal (m1 = 5/8, m2 = 7/8; n1 = n3 = 2) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0587 | 0.0618 | 0.0570 | 0.0575 | 0.0678 | 0.1221 | 0.1241 | 0.1172 | 0.1232 | 0.1331 |
| 25 | 0.0553 | 0.0518 | 0.0570 | 0.0572 | 0.0603 | 0.1136 | 0.1040 | 0.1121 | 0.1151 | 0.1176 |
| 50 | 0.0628 | 0.0577 | 0.0622 | 0.0580 | 0.0681 | 0.1185 | 0.1102 | 0.1231 | 0.1201 | 0.1309 |
| 100 | 0.0726 | 0.0637 | 0.0822 | 0.0740 | 0.0936 | 0.1439 | 0.1222 | 0.1477 | 0.1390 | 0.1635 |
| 250 | 0.1270 | 0.1021 | 0.1473 | 0.1203 | 0.1781 | 0.2181 | 0.1827 | 0.2343 | 0.2051 | 0.2822 |
| 500 | 0.2183 | 0.1782 | 0.2735 | 0.2157 | 0.3452 | 0.3429 | 0.2856 | 0.3934 | 0.3329 | 0.4788 |
| 1000 | 0.3973 | 0.3560 | 0.5320 | 0.4180 | 0.6536 | 0.5543 | 0.5058 | 0.6674 | 0.5676 | 0.7692 |
| Trapezoidal (m1 = 1/4, m2 = 3/4; n1 =n3 = 3) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0626 | 0.0732 | 0.0637 | 0.0687 | 0.0719 | 0.1271 | 0.1389 | 0.1291 | 0.1395 | 0.1439 |
| 25 | 0.0711 | 0.0862 | 0.0781 | 0.0858 | 0.0809 | 0.1402 | 0.1560 | 0.1517 | 0.1663 | 0.1576 |
| 50 | 0.0973 | 0.1285 | 0.1224 | 0.1313 | 0.1274 | 0.1860 | 0.2172 | 0.2143 | 0.2302 | 0.2213 |
| 100 | 0.1543 | 0.2168 | 0.2118 | 0.2317 | 0.2272 | 0.2707 | 0.3330 | 0.3306 | 0.3574 | 0.3496 |
| 250 | 0.3816 | 0.5086 | 0.5225 | 0.5503 | 0.5607 | 0.5477 | 0.6386 | 0.6588 | 0.6863 | 0.6912 |
| 500 | 0.7178 | 0.8402 | 0.8635 | 0.8791 | 0.8885 | 0.8447 | 0.9095 | 0.9238 | 0.9322 | 0.9389 |
| 1000 | 0.9719 | 0.9914 | 0.9938 | 0.9953 | 0.9969 | 0.9905 | 0.9971 | 0.9983 | 0.9989 | 0.9991 |
| Truncated Gamma (2,3) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.2211 | 0.2728 | 0.2364 | 0.2498 | 0.3155 | 0.3266 | 0.3958 | 0.3626 | 0.3759 | 0.4511 |
| 25 | 0.5018 | 0.6293 | 0.5807 | 0.5813 | 0.7294 | 0.6489 | 0.7385 | 0.7025 | 0.7058 | 0.8269 |
| 50 | 0.8745 | 0.9442 | 0.9062 | 0.9023 | 0.9748 | 0.9391 | 0.9708 | 0.9516 | 0.9507 | 0.9890 |
| 100 | 0.9985 | 0.9998 | 0.9989 | 0.9983 | 1.0000 | 0.9997 | 0.9999 | 0.9996 | 0.9996 | 1.0000 |
| 250 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Truncated Gamma (2,6) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.1423 | 0.1321 | 0.1550 | 0.1423 | 0.1834 | 0.2234 | 0.2082 | 0.2346 | 0.2222 | 0.2713 |
| 25 | 0.2556 | 0.2388 | 0.3222 | 0.2818 | 0.3717 | 0.3662 | 0.3426 | 0.4142 | 0.3788 | 0.4710 |
| 50 | 0.4407 | 0.4211 | 0.5428 | 0.4775 | 0.6116 | 0.5646 | 0.5251 | 0.6368 | 0.5872 | 0.7005 |
| 100 | 0.7104 | 0.6954 | 0.8124 | 0.7516 | 0.8649 | 0.8072 | 0.7799 | 0.8703 | 0.8268 | 0.9083 |
| 250 | 0.9740 | 0.9743 | 0.9910 | 0.9830 | 0.9958 | 0.9878 | 0.9860 | 0.9956 | 0.9906 | 0.9977 |
| 500 | 0.9998 | 0.9997 | 1.0000 | 0.9997 | 1.0000 | 1.0000 | 0.9999 | 1.0000 | 0.9999 | 1.0000 |
| 1000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Truncated Weibull (shape = 2, scale = 1) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0569 | 0.0553 | 0.0508 | 0.0524 | 0.0540 | 0.1138 | 0.112 | 0.1052 | 0.1099 | 0.1086 |
| 25 | 0.0587 | 0.0537 | 0.0608 | 0.0588 | 0.0630 | 0.1192 | 0.1084 | 0.1156 | 0.1148 | 0.1266 |
| 50 | 0.0643 | 0.0580 | 0.0696 | 0.0644 | 0.0745 | 0.1243 | 0.1168 | 0.1275 | 0.1243 | 0.1345 |
| 100 | 0.0852 | 0.0702 | 0.0935 | 0.0807 | 0.1004 | 0.1508 | 0.1306 | 0.1563 | 0.1455 | 0.1701 |
| 250 | 0.1450 | 0.1108 | 0.1607 | 0.1345 | 0.1739 | 0.2354 | 0.1943 | 0.2535 | 0.2244 | 0.2744 |
| 500 | 0.2478 | 0.1900 | 0.2874 | 0.2381 | 0.3143 | 0.3634 | 0.2943 | 0.3938 | 0.3456 | 0.4239 |
| 1000 | 0.4308 | 0.3457 | 0.5167 | 0.4260 | 0.5630 | 0.5717 | 0.4757 | 0.6333 | 0.5563 | 0.6767 |
| Beta (3,3) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0545 | 0.0573 | 0.0539 | 0.0528 | 0.0606 | 0.1128 | 0.1115 | 0.1065 | 0.1105 | 0.1215 |
| 25 | 0.0506 | 0.0484 | 0.0534 | 0.0513 | 0.0542 | 0.1047 | 0.0982 | 0.1036 | 0.1054 | 0.1088 |
| 50 | 0.0527 | 0.0501 | 0.0565 | 0.0542 | 0.0569 | 0.1114 | 0.0975 | 0.1075 | 0.1073 | 0.1149 |
| 100 | 0.0577 | 0.0532 | 0.0600 | 0.0586 | 0.0629 | 0.1215 | 0.1112 | 0.1186 | 0.116 | 0.1232 |
| 250 | 0.0790 | 0.0641 | 0.0821 | 0.0706 | 0.0897 | 0.1492 | 0.1266 | 0.1492 | 0.1369 | 0.1571 |
| 500 | 0.1151 | 0.0863 | 0.1148 | 0.0964 | 0.1302 | 0.1939 | 0.1603 | 0.1947 | 0.1714 | 0.2145 |
| 1000 | 0.1847 | 0.1339 | 0.2065 | 0.1586 | 0.2340 | 0.2919 | 0.2257 | 0.3078 | 0.2603 | 0.3401 |
| Beta (20,20) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0710 | 0.0670 | 0.0689 | 0.0664 | 0.0790 | 0.1344 | 0.1288 | 0.1296 | 0.1325 | 0.1493 |
| 25 | 0.0892 | 0.0765 | 0.0974 | 0.0858 | 0.1100 | 0.1608 | 0.1397 | 0.1738 | 0.1610 | 0.1941 |
| 50 | 0.1340 | 0.1048 | 0.1629 | 0.1347 | 0.1808 | 0.2313 | 0.1871 | 0.2501 | 0.2235 | 0.281 |
| 100 | 0.2395 | 0.1784 | 0.2922 | 0.2287 | 0.3373 | 0.3682 | 0.2842 | 0.4157 | 0.3494 | 0.4655 |
| 250 | 0.5380 | 0.4486 | 0.6598 | 0.5398 | 0.7355 | 0.6814 | 0.5858 | 0.7703 | 0.6677 | 0.8338 |
| 500 | 0.8580 | 0.8040 | 0.9427 | 0.8691 | 0.9692 | 0.9295 | 0.8896 | 0.9719 | 0.9291 | 0.9875 |
| 1000 | 0.9925 | 0.9904 | 0.9995 | 0.9953 | 0.9999 | 0.9981 | 0.9968 | 0.9997 | 0.9987 | 0.9999 |
| Beta (4,2) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0562 | 0.0588 | 0.0562 | 0.0578 | 0.0630 | 0.1155 | 0.1153 | 0.1102 | 0.1138 | 0.1229 |
| 25 | 0.0509 | 0.0532 | 0.0507 | 0.0503 | 0.0522 | 0.1003 | 0.1019 | 0.1009 | 0.1046 | 0.1072 |
| 50 | 0.0542 | 0.0516 | 0.0555 | 0.0544 | 0.0574 | 0.1080 | 0.0982 | 0.1050 | 0.1071 | 0.1100 |
| 100 | 0.0549 | 0.0540 | 0.0562 | 0.0545 | 0.0559 | 0.1079 | 0.1038 | 0.1074 | 0.1076 | 0.1076 |
| 250 | 0.0672 | 0.0613 | 0.0641 | 0.0579 | 0.0649 | 0.1237 | 0.1134 | 0.1186 | 0.1156 | 0.1232 |
| 500 | 0.0740 | 0.0647 | 0.0761 | 0.0674 | 0.0795 | 0.1414 | 0.1245 | 0.1346 | 0.1283 | 0.1433 |
| 1000 | 0.1048 | 0.0787 | 0.1085 | 0.0905 | 0.1167 | 0.1866 | 0.1489 | 0.1808 | 0.1635 | 0.1956 |
| Beta (2,4) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0567 | 0.0584 | 0.0533 | 0.0557 | 0.0601 | 0.1118 | 0.1127 | 0.1075 | 0.1131 | 0.1194 |
| 25 | 0.0521 | 0.0544 | 0.0553 | 0.0539 | 0.0575 | 0.1053 | 0.1032 | 0.1066 | 0.1069 | 0.1120 |
| 50 | 0.0571 | 0.0539 | 0.0579 | 0.0534 | 0.0587 | 0.1108 | 0.1036 | 0.1121 | 0.1117 | 0.1180 |
| 100 | 0.0599 | 0.0563 | 0.0631 | 0.0599 | 0.0674 | 0.1168 | 0.1057 | 0.1164 | 0.1116 | 0.1238 |
| 250 | 0.0799 | 0.0671 | 0.0782 | 0.0689 | 0.0840 | 0.1455 | 0.1262 | 0.1436 | 0.1335 | 0.1569 |
| 500 | 0.1066 | 0.0835 | 0.1156 | 0.0973 | 0.1254 | 0.1896 | 0.1540 | 0.1897 | 0.1686 | 0.2060 |
| 1000 | 0.1720 | 0.1248 | 0.1855 | 0.1498 | 0.2118 | 0.2744 | 0.2068 | 0.2879 | 0.2426 | 0.3124 |
| Beta (3,20) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0580 | 0.0585 | 0.0562 | 0.0550 | 0.0651 | 0.1180 | 0.1170 | 0.1125 | 0.1147 | 0.1297 |
| 25 | 0.0662 | 0.0581 | 0.0688 | 0.0640 | 0.0738 | 0.1270 | 0.1182 | 0.1287 | 0.1243 | 0.1413 |
| 50 | 0.0833 | 0.0678 | 0.0879 | 0.0781 | 0.0953 | 0.1516 | 0.1291 | 0.1574 | 0.1452 | 0.1677 |
| 100 | 0.1182 | 0.0932 | 0.1374 | 0.1117 | 0.1504 | 0.2104 | 0.1643 | 0.2211 | 0.1936 | 0.2384 |
| 250 | 0.2426 | 0.1747 | 0.2923 | 0.2226 | 0.3365 | 0.3674 | 0.2825 | 0.4119 | 0.3431 | 0.4621 |
| 500 | 0.4480 | 0.3450 | 0.5458 | 0.4331 | 0.6145 | 0.5923 | 0.4819 | 0.6718 | 0.5656 | 0.7343 |
| 1000 | 0.7586 | 0.6753 | 0.8664 | 0.7577 | 0.9139 | 0.8600 | 0.7928 | 0.9258 | 0.8546 | 0.9548 |
| Beta (0.5,0.5) | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0547 | 0.0557 | 0.0482 | 0.0491 | 0.0577 | 0.1154 | 0.1121 | 0.1053 | 0.1129 | 0.1224 |
| 25 | 0.0500 | 0.0506 | 0.0529 | 0.0531 | 0.0542 | 0.1067 | 0.0997 | 0.1073 | 0.1120 | 0.1131 |
| 50 | 0.0500 | 0.0501 | 0.0532 | 0.0505 | 0.0541 | 0.1048 | 0.1042 | 0.1052 | 0.1102 | 0.1070 |
| 100 | 0.0538 | 0.0533 | 0.0553 | 0.0542 | 0.0585 | 0.1064 | 0.1056 | 0.1070 | 0.1069 | 0.1086 |
| 250 | 0.0663 | 0.0615 | 0.0675 | 0.0631 | 0.0702 | 0.1263 | 0.1165 | 0.1235 | 0.1210 | 0.1259 |
| 500 | 0.0834 | 0.0726 | 0.0853 | 0.0772 | 0.0898 | 0.1551 | 0.1363 | 0.1530 | 0.1457 | 0.1600 |
| 1000 | 0.1192 | 0.0993 | 0.1275 | 0.1137 | 0.1363 | 0.1983 | 0.1750 | 0.2071 | 0.1895 | 0.2232 |
| n | K-S | Kuiper | C-M | Watson | A-D | K-S | Kuiper | C-M | Watson | A-D |
|---|---|---|---|---|---|---|---|---|---|---|
| Triangular (mode = ¼); a = 2, b = 20 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0649 | 0.0612 | 0.0647 | 0.0638 | 0.0662 | 0.1227 | 0.1124 | 0.1206 | 0.1162 | 0.1251 |
| 25 | 0.0912 | 0.0829 | 0.0482 | 0.1001 | 0.1021 | 0.1531 | 0.1443 | 0.1715 | 0.1606 | 0.1729 |
| 50 | 0.1243 | 0.1171 | 0.1527 | 0.1398 | 0.1535 | 0.2146 | 0.1931 | 0.2421 | 0.2224 | 0.2410 |
| 100 | 0.2078 | 0.1914 | 0.2537 | 0.2269 | 0.2600 | 0.3197 | 0.2906 | 0.3594 | 0.3308 | 0.3644 |
| Truncated-Log-Normal (meanlog = sdlog = 0.5); a= 2, b = 20 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0507 | 0.0508 | 0.0502 | 0.0496 | 0.0511 | 0.1005 | 0.1015 | 0.1010 | 0.0098 | 0.1001 |
| 25 | 0.0691 | 0.0617 | 0.0729 | 0.0655 | 0.0757 | 0.1204 | 0.1177 | 0.1334 | 0.1281 | 0.1328 |
| 50 | 0.0817 | 0.0974 | 0.0970 | 0.0877 | 0.1009 | 0.1494 | 0.1364 | 0.1672 | 0.1531 | 0.1730 |
| 100 | 0.1253 | 0.1078 | 0.1454 | 0.1274 | 0.1603 | 0.2132 | 0.1856 | 0.2379 | 0.2108 | 0.2600 |
| Trapezoidal (m1 = ¼, m2 = ¾, n1 = n2 = 3); a = 3, b = 8 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0505 | 0.0574 | 0.0527 | 0.0552 | 0.0514 | 0.1073 | 0.1158 | 0.1045 | 0.1114 | 0.1049 |
| 25 | 0.0697 | 0.0882 | 0.0817 | 0.0874 | 0.0818 | 0.1330 | 0.1562 | 0.1507 | 0.1573 | 0.1530 |
| 50 | 0.0959 | 0.1328 | 0.1266 | 0.1415 | 0.1311 | 0.1796 | 0.2183 | 0.2218 | 0.2325 | 0.2254 |
| 100 | 0.1263 | 0.2346 | 0.2299 | 0.2503 | 0.2454 | 0.2820 | 0.3522 | 0.3567 | 0.3770 | 0.3742 |
| Truncated Gamma (2,3); a = 3, b = 4 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.1924 | 0.2435 | 0.2263 | 0.2353 | 0.2767 | 0.3011 | 0.3435 | 0.3351 | 0.3425 | 0.4010 |
| 25 | 0.5145 | 0.6463 | 0.5869 | 0.5889 | 0.7374 | 0.6464 | 0.7506 | 0.7104 | 0.7113 | 0.8297 |
| 50 | 0.8733 | 0.9454 | 0.9143 | 0.9236 | 0.9756 | 0.9392 | 0.9706 | 0.9570 | 0.9528 | 0.9888 |
| 100 | 0.9978 | 0.9998 | 0.9986 | 0.9979 | 1.0000 | 0.9993 | 0.9999 | 0.9999 | 0.9998 | 1.0000 |
| Beta (20,20); a = 3, b = 8 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0623 | 0.0603 | 0.0651 | 0.0616 | 0.0678 | 0.1201 | 0.1127 | 0.1225 | 0.1201 | 0.1257 |
| 25 | 0.0942 | 0.0824 | 0.1033 | 0.0907 | 0.1154 | 0.1574 | 0.1457 | 0.1806 | 0.1647 | 0.1921 |
| 50 | 0.1357 | 0.1126 | 0.1692 | 0.1461 | 0.1934 | 0.2273 | 0.1908 | 0.2704 | 0.2272 | 0.2892 |
| 100 | 0.2399 | 0.1916 | 0.3063 | 0.2455 | 0.3511 | 0.3659 | 0.3040 | 0.4326 | 0.3610 | 0.4767 |
| Beta (3,20); a = 2, b = 20 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0572 | 0.0544 | 0.0568 | 0.0568 | 0.0565 | 0.1083 | 0.1073 | 0.1093 | 0.1072 | 0.1100 |
| 25 | 0.0692 | 0.0679 | 0.0755 | 0.0711 | 0.0777 | 0.1242 | 0.1239 | 0.1340 | 0.1254 | 0.1363 |
| 50 | 0.0822 | 0.0689 | 0.0940 | 0.0846 | 0.1015 | 0.1507 | 0.1312 | 0.1661 | 0.1474 | 0.1738 |
| 100 | 0.1209 | 0.0993 | 0.1425 | 0.1193 | 0.1595 | 0.2078 | 0.1778 | 0.2329 | 0.2002 | 0.2539 |
| Beta (0.5,0.5); a = b = 0.5 | ||||||||||
| α = 5% | α = 10% | |||||||||
| 10 | 0.0442 | 0.0491 | 0.0498 | 0.0501 | 0.0499 | 0.0954 | 0.0966 | 0.0958 | 0.0974 | 0.0938 |
| 25 | 0.0534 | 0.0552 | 0.0569 | 0.0562 | 0.0546 | 0.1002 | 0.1037 | 0.1026 | 0.1032 | 0.1048 |
| 50 | 0.0478 | 0.0529 | 0.0524 | 0.0519 | 0.0510 | 0.0965 | 0.0997 | 0.1074 | 0.1092 | 0.1058 |
| 100 | 0.0549 | 0.0539 | 0.0546 | 0.0532 | 0.0563 | 0.1099 | 0.1100 | 0.1114 | 0.1121 | 0.1141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giles, D.E. New Goodness-of-Fit Tests for the Kumaraswamy Distribution. Stats 2024, 7, 373-388. https://doi.org/10.3390/stats7020023
Giles DE. New Goodness-of-Fit Tests for the Kumaraswamy Distribution. Stats. 2024; 7(2):373-388. https://doi.org/10.3390/stats7020023
Chicago/Turabian StyleGiles, David E. 2024. "New Goodness-of-Fit Tests for the Kumaraswamy Distribution" Stats 7, no. 2: 373-388. https://doi.org/10.3390/stats7020023
APA StyleGiles, D. E. (2024). New Goodness-of-Fit Tests for the Kumaraswamy Distribution. Stats, 7(2), 373-388. https://doi.org/10.3390/stats7020023





