Limits of Agreement Based on Transformed Measurements
Abstract
1. Introduction
2. Method
2.1. Standard Limits of Agreement
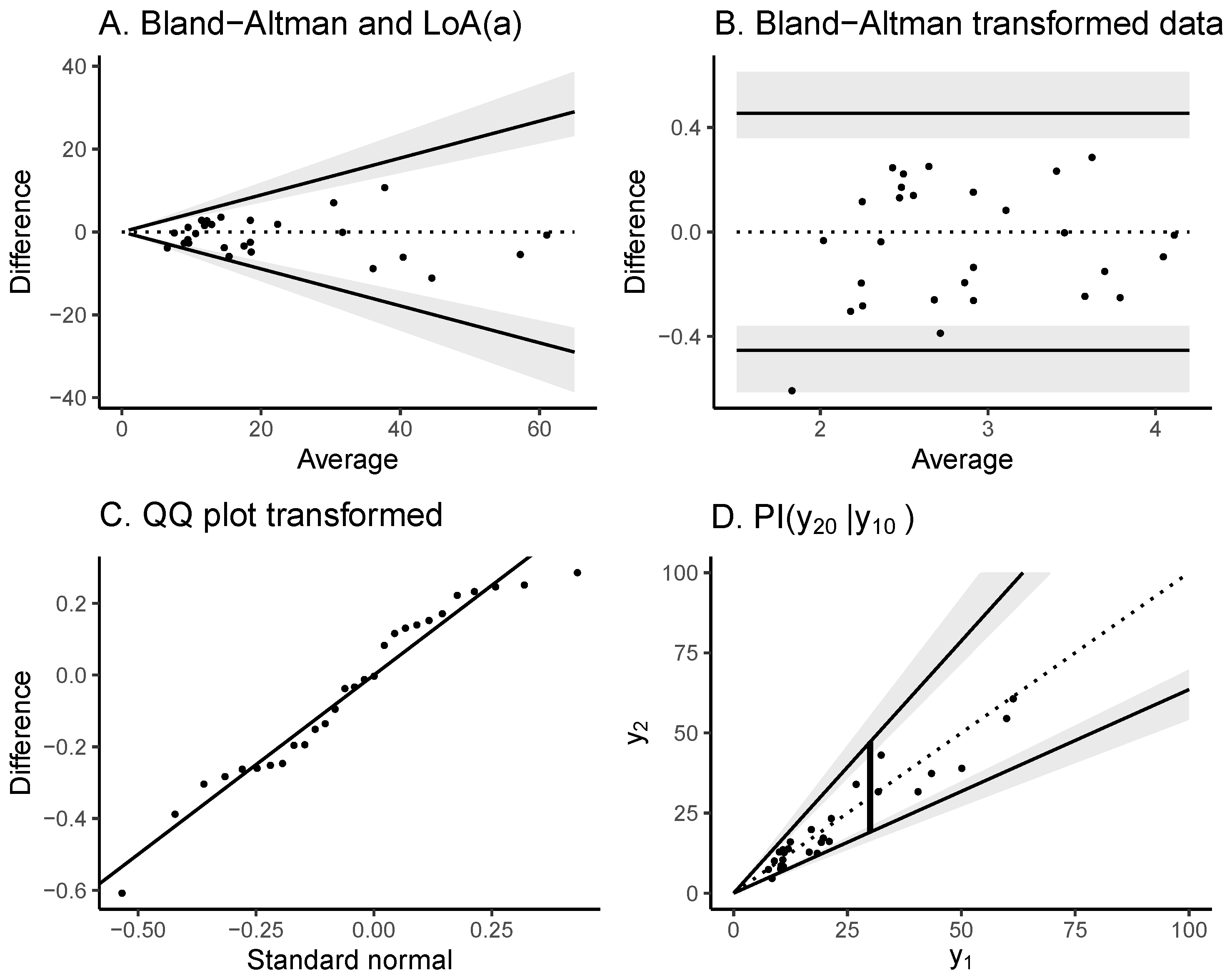
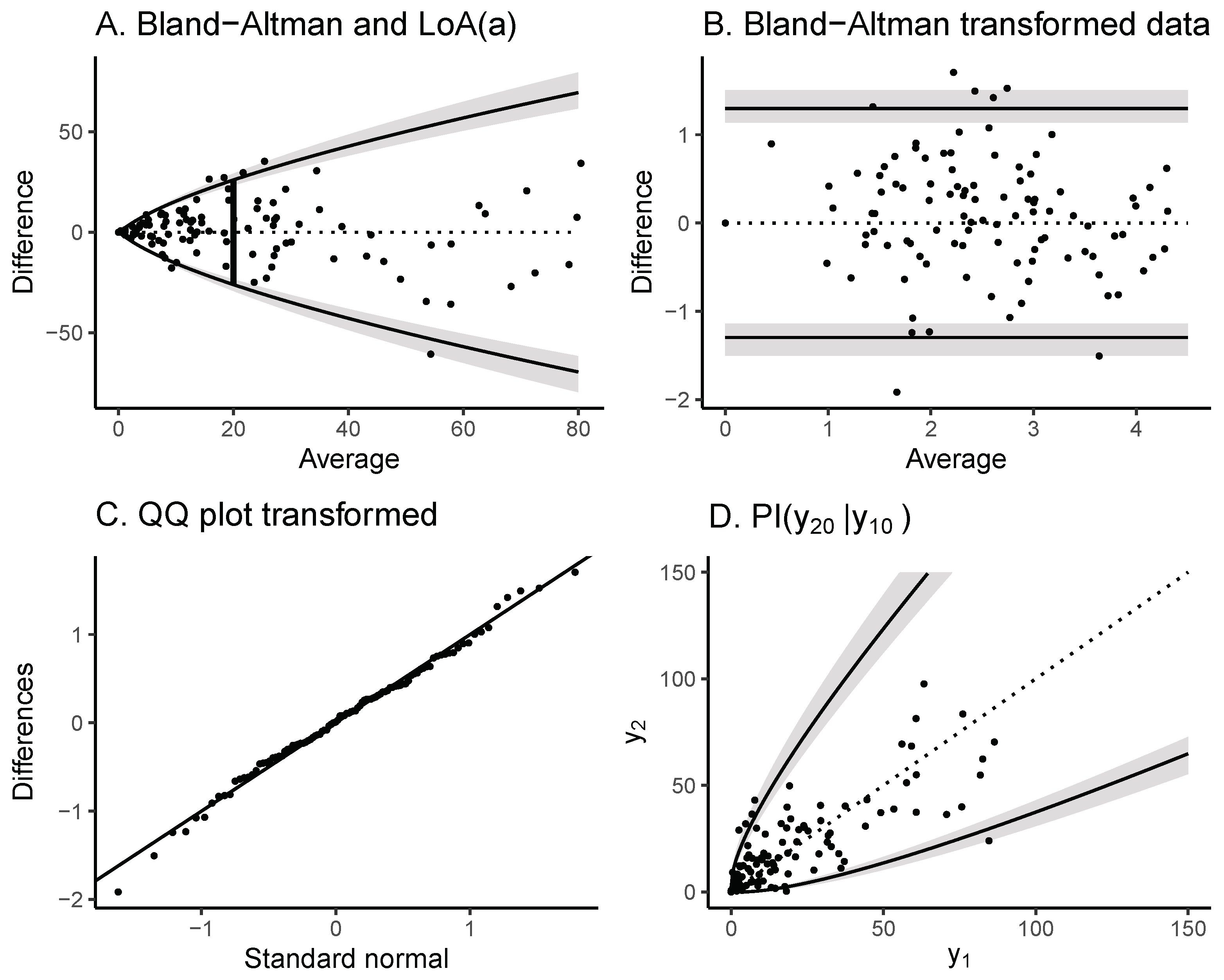
2.2. Limits of Agreement Based on Transformed Measurements
3. Simulations
The Bland–Altman Regression Model
4. Applications
4.1. Sperm DNA Fragmentation Index
4.2. Coronary Plaque Volume Measurements
5. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CI | Confidence interval |
| LoA | Limits of agreement |
| PI | Prediction interval |
| Quantile–quantile | |
| s.d. | Standard deviation |
References
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Paixao, A.R.; Neeland, I.J.; Ayers, C.R.; Xing, F.; Berry, J.D.; de Lemos, J.A.; Abbara, S.; Peshock, R.M.; Khera, A. Defining coronary artery calcium concordance and repeatability-Implications for development and change: The Dallas Heart Study. J. Cardiovasc. Comput. Tomogr. 2017, 11, 347–353. [Google Scholar] [CrossRef] [PubMed]
- Sevrukov, A.B.; Bland, J.M.; Kondos, G.T. Serial electron beam CT measurements of coronary artery calcium: Has your patient’s calcium score actually changed? Am. J. Roentgenol. 2005, 185, 1546–1553. [Google Scholar] [CrossRef] [PubMed]
- Andersen, K.P.; Gerke, O. Assessing Agreement When Agreement Is Hard to Assess—The Agatston Score for Coronary Calcification. Diagnostics 2022, 12, 2993. [Google Scholar] [CrossRef]
- Brøndsted, L. Quantification of Agreement. Ph.D. Thesis, Department of Biostatistics, University of Copenhagen, Copenhagen, Denmark, 2002. [Google Scholar]
- Carstensen, B. Comparing Clinical Measurement Methods: A Practical Guide; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Harrell, F. Biostatistics for Biomedical Research. 2024. Available online: https://hbiostat.org/bbr/ (accessed on 26 March 2024).
- Box, G.E.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Stat. Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Comparing methods of measurement: Why plotting difference against standard method is misleading. Lancet 1995, 346, 1085–1087. [Google Scholar] [CrossRef] [PubMed]
- Mansournia, M.A.; Waters, R.; Nazemipour, M.; Bland, M.; Altman, D.G. Bland-Altman methods for comparing methods of measurement and response to criticisms. Glob. Epidemiol. 2021, 3, 100045. [Google Scholar] [CrossRef] [PubMed]
- Shieh, G. The appropriateness of Bland-Altman’s approximate confidence intervals for limits of agreement. BMC Med. Res. Methodol. 2018, 18, 45. [Google Scholar] [CrossRef] [PubMed]
- Carstensen, B. Comparing methods of measurement: Extending the LoA by regression. Stat. Med. 2010, 29, 401–410. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, C.E.; Neuhaus, J.M. Misspecifying the shape of a random effects distribution: Why getting it wrong may not matter. Statist. Sci. 2011, 26, 388–402. [Google Scholar] [CrossRef]
- Carstensen, B. Comparing and predicting between several methods of measurement. Biostatistics 2004, 5, 399–413. [Google Scholar] [CrossRef]
- Ludbrook, J. Confidence in Altman–Bland plots: A critical review of the method of differences. Clin. Exp. Pharmacol. Physiol. 2010, 37, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Francq, B.G.; Govaerts, B. How to regress and predict in a Bland–Altman plot? Review and contribution based on tolerance intervals and correlated-errors-in-variables models. Stat. Med. 2016, 35, 2328–2358. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W. Bias in Bland-Altman but not regression validity analyses. Sportscience 2004, 8, 42–47. [Google Scholar]
- Krouwer, J.S. Why Bland–Altman plots should use X, not (Y + X)/2 when X is a reference method. Stat. Med. 2008, 27, 778–780. [Google Scholar] [CrossRef]
- Alahmar, A.T.; Singh, R.; Palani, A. Sperm DNA fragmentation in reproductive medicine: A review. J. Hum. Reprod. Sci. 2022, 15, 206–218. [Google Scholar] [CrossRef]
- Christensen, P.; Fischer, R.; Schulze, W.; Baukloh, V.; Kienast, K.; Coull, G.; Parner, E.T. Role of intra-individual variation in the detection of thresholds for DFI and for misclassification rates: A retrospective analysis of 14,775 SCSA® tests. Andrology 2024, early view. [Google Scholar] [CrossRef]
- Iraqi, N.; Mortensen, M.; Sand, N.; Busk, M.; Grove, E.; Dey, D.; Pedersen, K.; Kanstrup, H.; Madsen, K.; Parner, E.; et al. Interscan reproducibility of computed tomography derived coronary plaque volume measurements using a semi-automated analysis software. Eur. Heart J. 2024, 45, ehae666.175. [Google Scholar] [CrossRef]
- Stevens, N.T.; Steiner, S.H.; MacKay, R.J. Assessing agreement between two measurement systems: An alternative to the limits of agreement approach. Stat. Methods Med. Res. 2017, 26, 2487–2504. [Google Scholar] [CrossRef] [PubMed]

| Coverage | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| LoA | |||||||||
| Ratio | CI (Lower) | CI (Upper) | LoA | CI (Lower) | CI (Upper) | ||||
| 50 | 0.25 | 0.62 | 0.16 | 0.905 | 0.936 | 0.937 | 0.905 | 0.936 | 0.937 |
| 50 | 0.50 | 0.62 | 0.31 | 0.903 | 0.939 | 0.946 | 0.898 | 0.939 | 0.946 |
| 50 | 1.00 | 0.62 | 0.62 | 0.952 | 0.942 | 0.937 | 0.959 | 0.942 | 0.937 |
| 100 | 0.25 | 0.62 | 0.16 | 0.964 | 0.944 | 0.945 | 0.961 | 0.944 | 0.945 |
| 100 | 0.50 | 0.62 | 0.31 | 0.938 | 0.951 | 0.947 | 0.941 | 0.951 | 0.947 |
| 100 | 1.00 | 0.62 | 0.62 | 0.941 | 0.948 | 0.947 | 0.946 | 0.948 | 0.947 |
| 200 | 0.25 | 0.62 | 0.16 | 0.925 | 0.948 | 0.950 | 0.924 | 0.948 | 0.950 |
| 200 | 0.50 | 0.62 | 0.31 | 0.947 | 0.946 | 0.947 | 0.944 | 0.946 | 0.947 |
| 200 | 1.00 | 0.62 | 0.62 | 0.918 | 0.947 | 0.946 | 0.922 | 0.947 | 0.946 |
| 500 | 0.25 | 0.62 | 0.16 | 0.963 | 0.952 | 0.949 | 0.959 | 0.952 | 0.949 |
| 500 | 0.50 | 0.62 | 0.31 | 0.955 | 0.950 | 0.949 | 0.958 | 0.950 | 0.949 |
| 500 | 1.00 | 0.62 | 0.62 | 0.949 | 0.951 | 0.952 | 0.952 | 0.951 | 0.952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parner, E.T. Limits of Agreement Based on Transformed Measurements. Stats 2025, 8, 17. https://doi.org/10.3390/stats8010017
Parner ET. Limits of Agreement Based on Transformed Measurements. Stats. 2025; 8(1):17. https://doi.org/10.3390/stats8010017
Chicago/Turabian StyleParner, Erik Thorlund. 2025. "Limits of Agreement Based on Transformed Measurements" Stats 8, no. 1: 17. https://doi.org/10.3390/stats8010017
APA StyleParner, E. T. (2025). Limits of Agreement Based on Transformed Measurements. Stats, 8(1), 17. https://doi.org/10.3390/stats8010017






