Cosmological Formation of (2 + 1)-Dimensional Soliton Structures in Models Possessing Potentials with Local Peaks
Abstract
:1. Introduction
2. Model
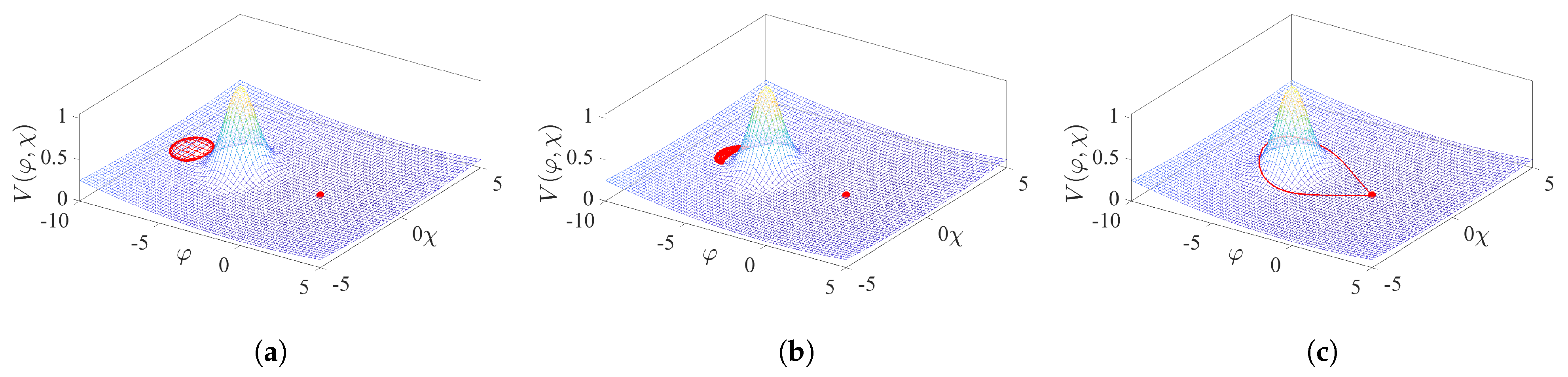
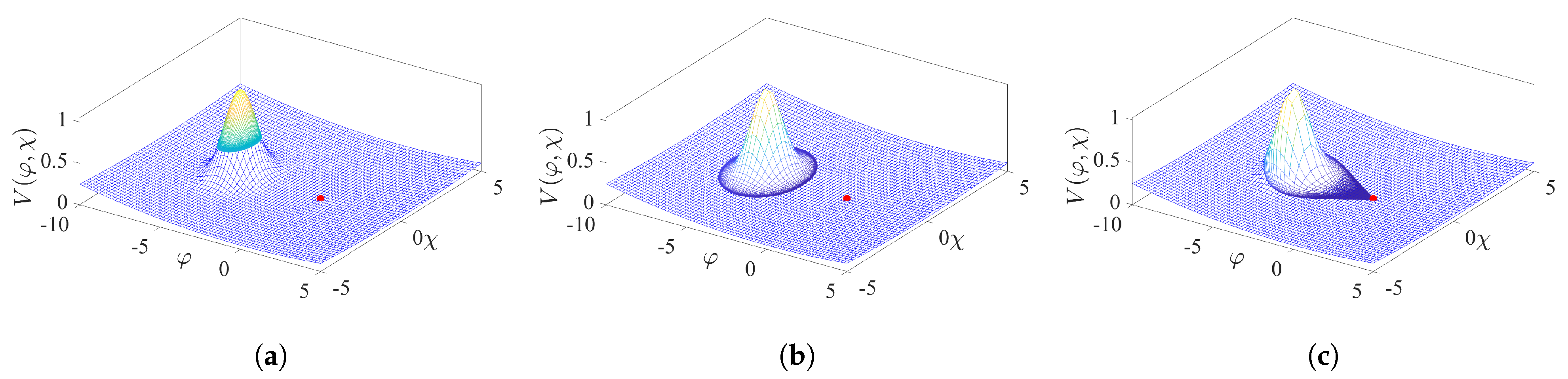
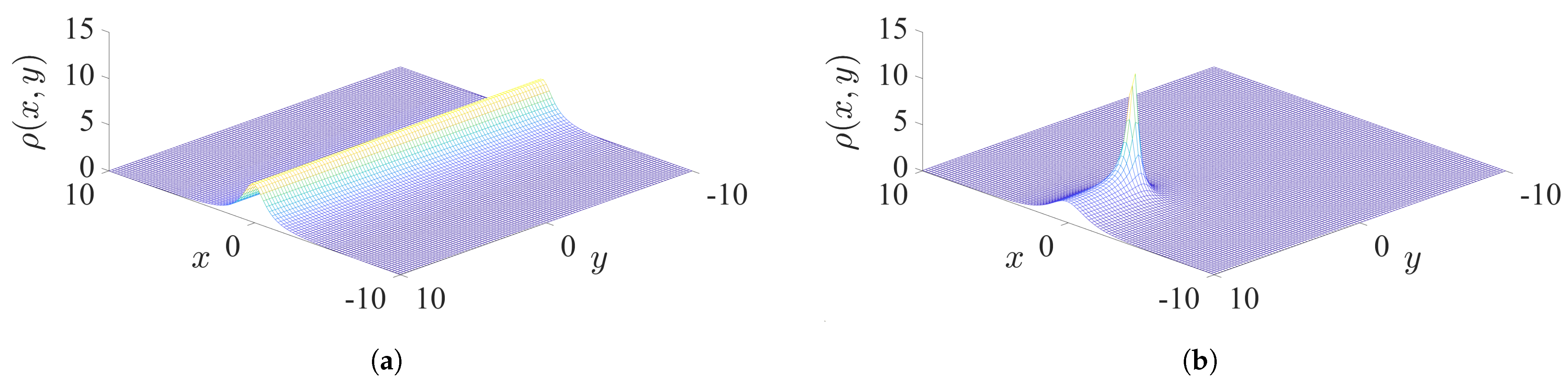
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adams, F.C.; Bond, J.R.; Freese, K.; Frieman, J.A.; Olinto, A.V. Natural inflation: Particle physics models, power-law spectra for large-scale structure, and constraints from the Cosmic Background Explorer. Phys. Rev. D 1993, 47, 426–455. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linde, A. Hybrid inflation. Phys. Rev. D 1994, 49, 748–754. [Google Scholar] [CrossRef] [PubMed]
- Liddle, A.R.; Mazumdar, A.; Schunck, F.E. Assisted inflation. Phys. Rev. D 1998, 58, 061301. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.E.; Nilles, H.P.; Peloso, M. Completing natural inflation. J. Cosmol. Astropart. Phys. 2005, 2005, 005. [Google Scholar] [CrossRef] [Green Version]
- Battefeld, D.; Battefeld, T. A smooth landscape: Ending saddle point inflation requires features to be shallow. J. Cosmol. Astropart. Phys. 2013, 2013, 038. [Google Scholar] [CrossRef]
- Peloso, M.; Unal, C. Trajectories with suppressed tensor-to-scalar ratio in aligned natural inflation. J. Cosmol. Astropart. Phys. 2015, 2015, 040. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.L.; Gherghetta, T.; Peloso, M. Affleck-Dine sneutrino inflation. Phys. Rev. D 2015, 92, 021303. [Google Scholar] [CrossRef] [Green Version]
- Susskind, L. The Anthropic landscape of string theory. In Proceedings of the Davis Meeting on Cosmic Inflation, Davis, CA, USA, 22–25 March 2003; p. 26. Available online: https://arxiv.org/abs/hep-th/0302219 (accessed on 20 July 2021).
- Basu, R.; Guth, A.H.; Vilenkin, A. Quantum creation of topological defects during inflation. Phys. Rev. D 1991, 44, 340–351. [Google Scholar] [CrossRef] [PubMed]
- Garriga, J.; Vilenkin, A.; Zhang, J. Black holes and the multiverse. J. Cosmol. Astropart. Phys. 2016, 2016, 064. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Garriga, J.; Vilenkin, A. Primordial black hole and wormhole formation by domain walls. J. Cosmol. Astropart. Phys. 2017, 2017, 050. [Google Scholar] [CrossRef]
- Deng, H.; Vilenkin, A. Primordial black hole formation by vacuum bubbles. J. Cosmol. Astropart. Phys. 2017, 2017, 044. [Google Scholar] [CrossRef] [Green Version]
- Vilenkin, A. Cosmic strings and domain walls. Phys. Rep. 1985, 121, 263–315. [Google Scholar] [CrossRef]
- Vilenkin, A.; Shellard, E. Cosmic Strings and Other Topological Defects; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Garriga, J.; Vilenkin, A. Black holes from nucleating strings. Phys. Rev. D 1993, 47, 3265–3274. [Google Scholar] [CrossRef] [Green Version]
- Hansen, R.N.; Christensen, M.; Larsen, A.L. Cosmic string loops collapsing to black holes. Int. J. Mod. Phys. A 2000, 15, 4433–4445. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K. Gravitational waves from collapsing domain walls. J. Cosmol. Astropart. Phys. 2010, 2010, 032. [Google Scholar] [CrossRef] [Green Version]
- Vilenkin, A.; Levin, Y.; Gruzinov, A. Cosmic strings and primordial black holes. J. Cosmol. Astropart. Phys. 2018, 2018, 008. [Google Scholar] [CrossRef] [Green Version]
- Helfer, T.; Aurrekoetxea, J.C.; Lim, E.A. Cosmic string loop collapse in full general relativity. Phys. Rev. D 2019, 99, 104028. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Guo, Z.K.; Cai, R.G. Primordial black holes from cosmic domain walls. Phys. Rev. D 2020, 101, 023513. [Google Scholar] [CrossRef] [Green Version]
- Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Y. The formation of primary galactic nuclei during phase transitions in the early Universe. J. Exp. Theor. Phys. 2001, 92, 921–929. [Google Scholar] [CrossRef] [Green Version]
- Belotsky, K.M.; Dokuchaev, V.I.; Eroshenko, Y.N.; Esipova, E.A.; Khlopov, M.Y.; Khromykh, L.A.; Kirillov, A.A.; Nikulin, V.V.; Rubin, S.G.; Svadkovsky, I.V. Clusters of primordial black holes. Eur. Phys. J. C 2019, 79, 246. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.; Kühnel, F. Primordial black holes as dark matter: Recent developments. Annu. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Rubin, S.G. Abilities of multidimensional gravity. Grav. Cosmol. 2007, 13, 253–258. Available online: https://arxiv.org/abs/0712.0888 (accessed on 20 July 2021).
- Ketov, S.V. Multi-field versus single-field in the supergravity models of inflation and primordial black holes. Universe 2021, 7, 115. [Google Scholar] [CrossRef]
- Gani, V.A.; Kirillov, A.A.; Rubin, S.G. Transitions between topologically non-trivial configurations. J. Phys. Conf. Ser. 2017, 934, 012046. [Google Scholar] [CrossRef]
- Gani, V.A.; Kirillov, A.A.; Rubin, S.G. Classical transitions with the topological number changing in the early Universe. J. Cosmol. Astropart. Phys. 2018, 2018, 042. [Google Scholar] [CrossRef] [Green Version]
- Kirillov, A.A.; Murygin, B.S. Domain walls and strings formation in the early Universe. Bled Workshop Phys. 2020, 21, 128–133. Available online: http://bsm.fmf.uni-lj.si/bled2020bsm/talks/BledVol21No2Proceedings-proc20Vol2.pdf (accessed on 20 July 2021).
- Kirillov, A.A.; Murygin, B.S. The mechanism of domain walls and strings formation in the early Universe. J. Phys. Conf. Ser. 2020, 1690. [Google Scholar] [CrossRef]
- Chang, S.; Hagmann, C.; Sikivie, P. Studies of the motion and decay of axion walls bounded by strings. Phys. Rev. D 1998, 59, 023505. [Google Scholar] [CrossRef] [Green Version]
- Hindmarsh, M.B.; Kibble, T.W.B. Cosmic strings. Rep. Prog. Phys. 1995, 58, 477–562. [Google Scholar] [CrossRef]
- Linde, A.D. Scalar field fluctuations in the expanding universe and the new inflationary universe scenario. Phys. Lett. B 1982, 116, 335–339. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murygin, B.S.; Kirillov, A.A.; Nikulin, V.V. Cosmological Formation of (2 + 1)-Dimensional Soliton Structures in Models Possessing Potentials with Local Peaks. Physics 2021, 3, 563-568. https://doi.org/10.3390/physics3030035
Murygin BS, Kirillov AA, Nikulin VV. Cosmological Formation of (2 + 1)-Dimensional Soliton Structures in Models Possessing Potentials with Local Peaks. Physics. 2021; 3(3):563-568. https://doi.org/10.3390/physics3030035
Chicago/Turabian StyleMurygin, Boris S., Alexander A. Kirillov, and Valery V. Nikulin. 2021. "Cosmological Formation of (2 + 1)-Dimensional Soliton Structures in Models Possessing Potentials with Local Peaks" Physics 3, no. 3: 563-568. https://doi.org/10.3390/physics3030035
APA StyleMurygin, B. S., Kirillov, A. A., & Nikulin, V. V. (2021). Cosmological Formation of (2 + 1)-Dimensional Soliton Structures in Models Possessing Potentials with Local Peaks. Physics, 3(3), 563-568. https://doi.org/10.3390/physics3030035




