A Review on Scene Prediction for Automated Driving
Abstract
:1. Introduction
2. The Context of Scene Prediction for Automated Driving
2.1. Sensors
2.2. Evolutionary versus Revolutionary Approach
2.3. Scene Prediction and Its Challenges
3. Methods for Scene Prediction
3.1. Model-Driven Approaches for Scene Prediction
3.1.1. Kinematic Models
3.1.2. Dynamic Models
3.1.3. Adding Uncertainties to the Model
3.2. Data-Driven Approaches for Scene Prediction
3.2.1. Classic Methods
Hidden Markov Models
Regression Models
3.2.2. Neural Networks
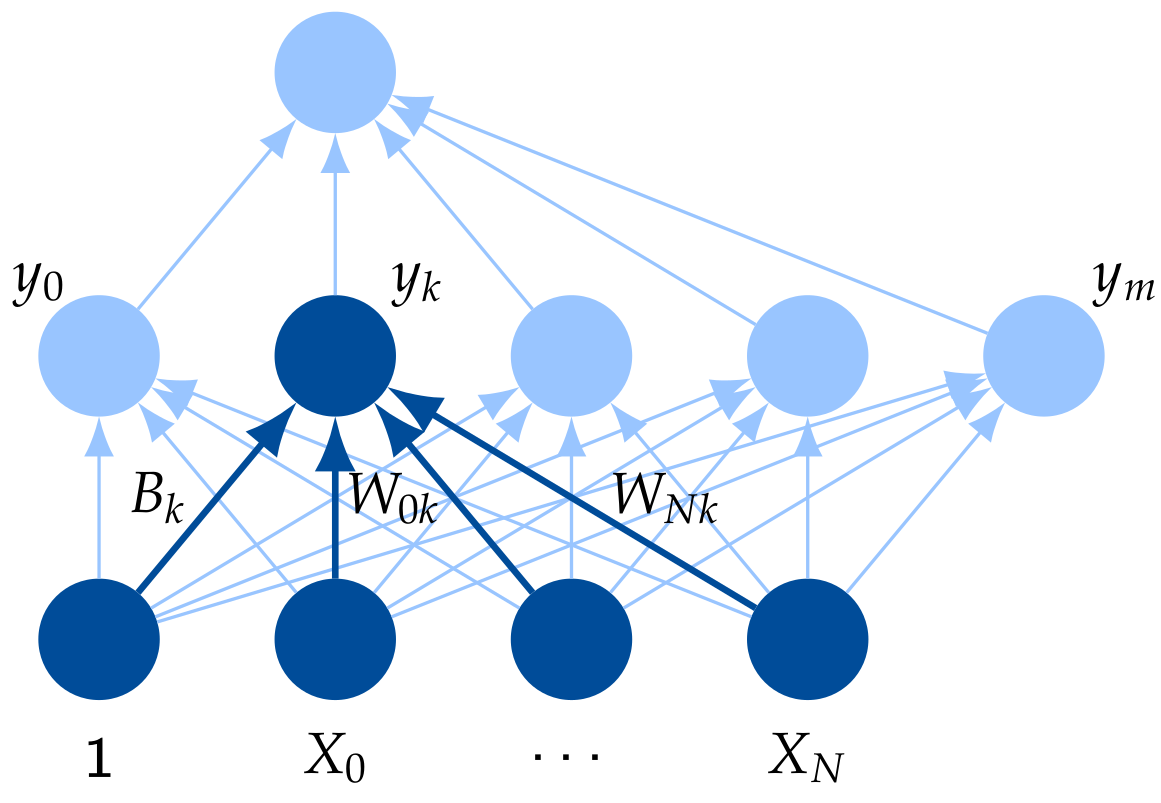
Feed-Forward Neural Network
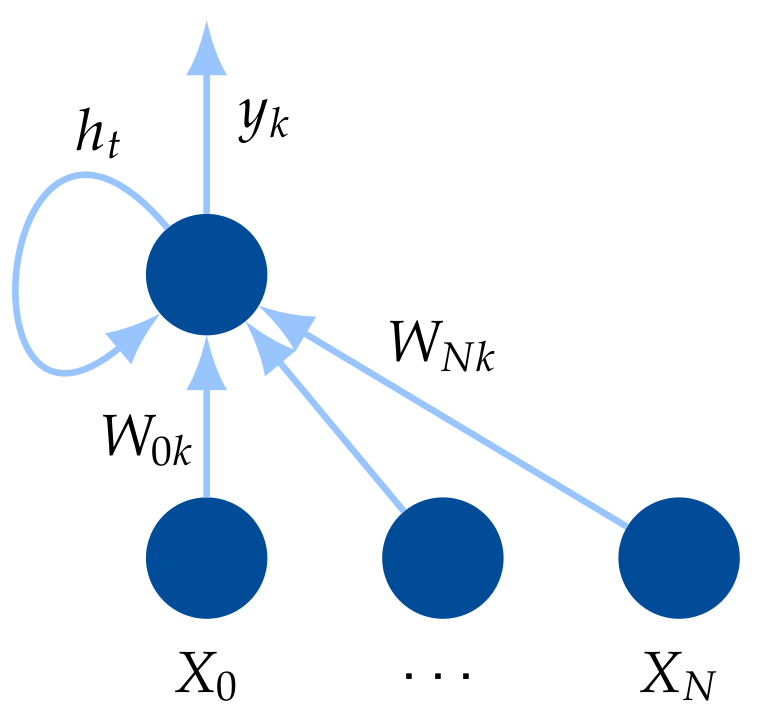
Recurrent Neural Network
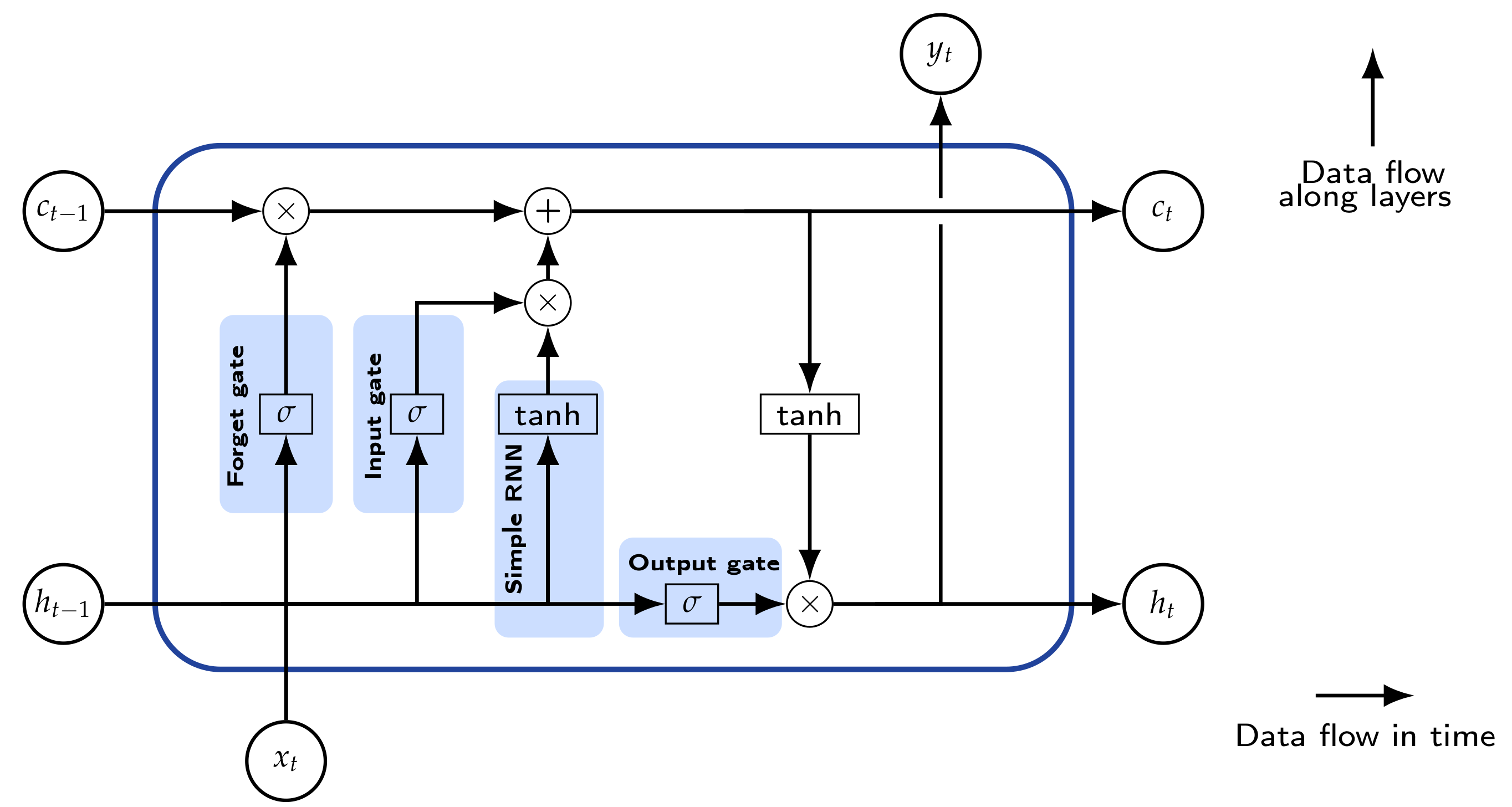
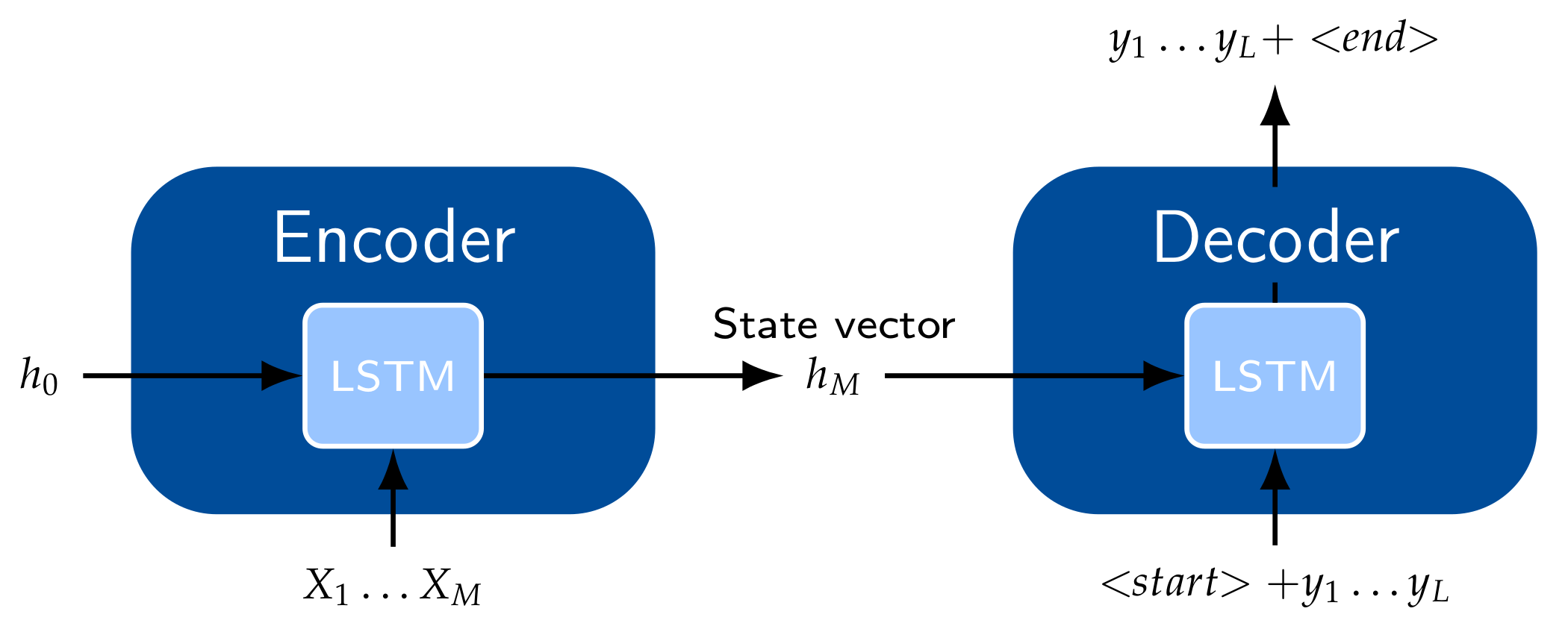
Long Short-Term Memory
3.2.3. Encoder–Decoder Models and Attention Mechanism
Variational Autoencoder
Convolutional Neural Network Models
Transformer Models
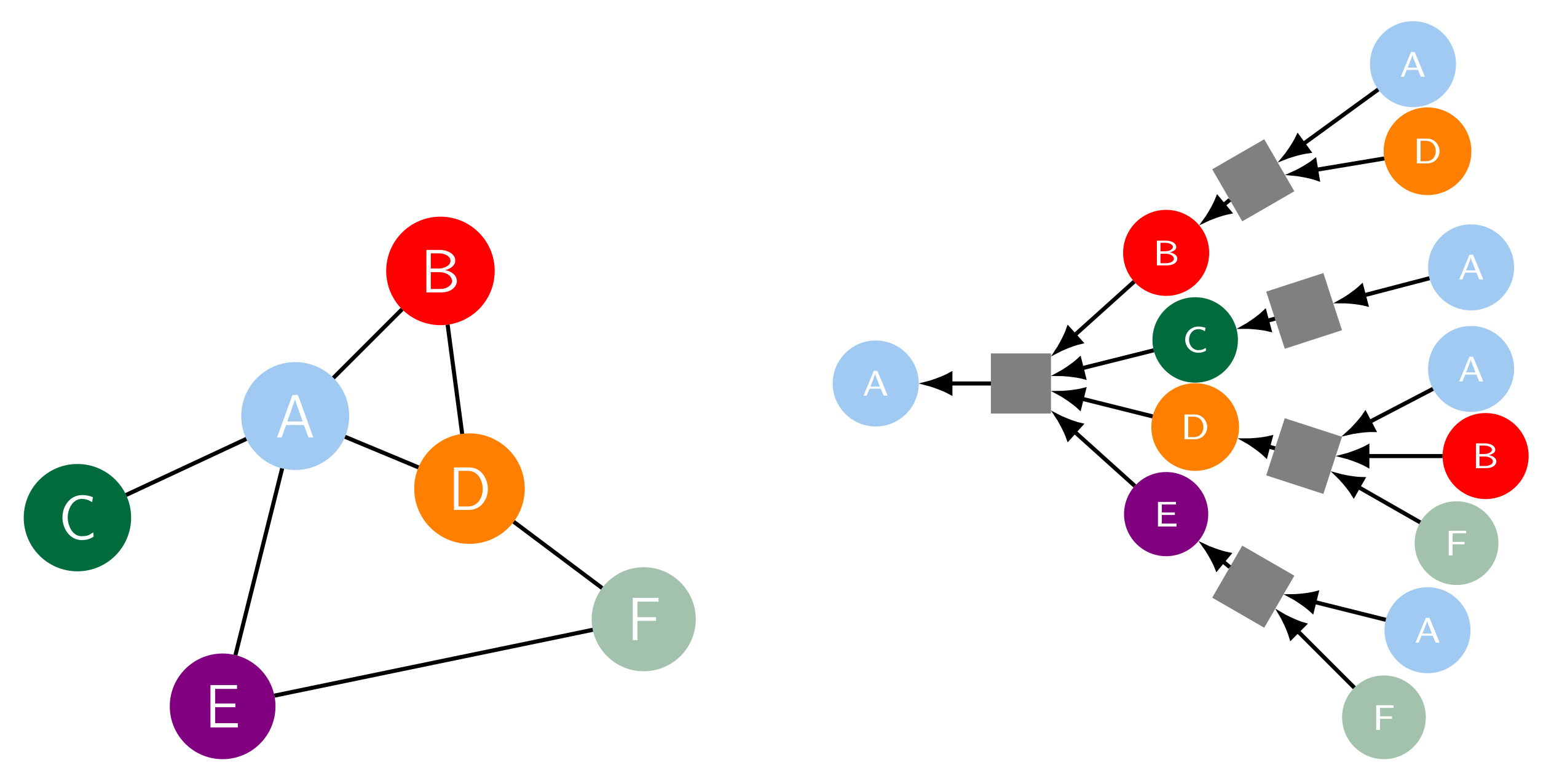
Graph Neural Network Models
4. Historical Review of Relevant Work
4.1. Recognition of Other Drivers’ Intentions
4.1.1. Lane Change Prediction
4.1.2. Car-Following
4.2. Full Trajectory Prediction
4.2.1. 1980s–2015
4.2.2. 2016: The Rise of Deep Learning Techniques
4.2.3. GNNs, Attention and New Use Cases
5. Public Datasets
6. Discussion
7. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Automated Driving |
| ADAS | Advanced Driver Assistance System |
| ADE | Average Displacement Error |
| API | Application Programming Interface |
| CNN | Convolutional Neural Network |
| CVAE | Conditional Variational Auto Encoder |
| CYRA | Constant Yaw Rate and Acceleration |
| ELBO | Evidence Lower Bound |
| FDE | Final Displacement Error |
| FFNN | Feed-Forward Neural Network |
| GNN | Graph Neural Network |
| GPS | Global Positioning System |
| GRU | Gated Recurrent Unit |
| HD | High Density |
| HMM | Hidden Markov Model |
| IMU | Integrated Motion Unit |
| LSTM | Long Short-Term Memory Network |
| MAE | Mean Absolute Error |
| NLP | Natural Language Processing |
| OEM | Original Equipment Manufacture |
| RNN | Recurrent Neural Network |
| RMSE | Root Mean Squared Error |
| SAE | Society of Automotive Engineers |
Appendix A. Long Short-Term Memory Networks
Appendix B. Gated Recurrent Unit
References
- Autopilot and Full Self-Driving Capability. Available online: https://www.tesla.com/support/autopilot/ (accessed on 31 October 2021).
- The Society of Automotive Engineers (AES). Available online: https://www.sae.org (accessed on 31 October 2021).
- Available online: https://twitter.com/elonmusk/status/1148070210412265473 (accessed on 31 October 2021).
- Scanlon, J.M.; Kusano, K.D.; Daniel, T.; Alderson, C.; Ogle, A.; Victor, T. Waymo Simulated Driving Behavior in Reconstructed Fatal Crashes within an Autonomous Vehicle Operating Domain. 2021. Available online: http://bit.ly/3bu5VcM (accessed on 31 October 2021).
- Jiang, R.; Hu, M.B.; Jia, B.; Wang, R.L.; Wu, Q.S. The effects of reaction delay in the Nagel-Schreckenberg traffic flow model. Eur. Phys. J. B 2006, 54, 267–273. [Google Scholar] [CrossRef]
- Preliminary Regularoty Impact Analysis. Available online: https://www.nhtsa.gov/sites/nhtsa.gov/files/documents/v2v_pria_12-12-16_clean.pdf (accessed on 31 October 2021).
- Huang, X.; Kroening, D.; Ruan, W.; Sharp, J.; Sun, Y.; Thamo, E.; Wu, M.; Yi, X. A survey of safety and trustworthiness of deep neural networks: Verification, testing, adversarial attack and defence, and interpretability. Comput. Sci. Rev. 2020, 37, 100270. [Google Scholar] [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Marti, E.; de Miguel, M.A.; Garcia, F.; Perez, J. A Review of sensor technologies for perception in automated driving. IEEE Intell. Transp. Syst. Mag. 2019, 11, 94–108. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wu, Y.; Niu, Q. Multi-sensor fusion in automated driving: A survey. IEEE Access 2020, 8, 2847–2868. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A Survey of autonomous driving: Common practices and emerging technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Lu, Z.; Happee, R.; Cabrall, C.D.D.; Kyriakidis, M.; de Winter, J.C.F. Human factors of transitions in automated driving: A general framework and literature survey. Transp. Res. Part F Traffic Psychol. Behav. 2016, 43, 183–198. [Google Scholar] [CrossRef] [Green Version]
- Petermeijer, S.M.; de Winter, J.C.F.; Bengler, K.J. Vibrotactile displays: A survey with a view on highly automated driving. IEEE Trans. Intell. Transp. Syst. 2016, 17, 897–907. [Google Scholar] [CrossRef] [Green Version]
- Pfleging, B.; Rang, M. Investigating user needs for non-driving-related activities during automated driving. In Proceedings of the 15th International Conference on Mobile and Ubiquitous Multimedia MUM ’16, Rovaniemi, Finland, 12–15 December 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 91–99. [Google Scholar] [CrossRef]
- Lefèvre, S.; Vasquez, D.; Laugier, C. A survey on motion prediction and risk assessment for intelligent vehicle. Robomech J. 2014, 1, 1. [Google Scholar] [CrossRef] [Green Version]
- Toledo, T. Driving behaviour: Models and challenges. Transp. Rev. 2007, 27, 65–84. [Google Scholar] [CrossRef]
- Xue, J.R.; Fang, J.W.; Zhang, P.A. Survey of scene understanding by event reasoning in autonomous driving. Int. J. Autom. Comput. 2018, 15, 249–266. [Google Scholar] [CrossRef]
- The Web of Science. Available online: https://www.webofscience.com/ (accessed on 5 May 2021).
- Hirakawa, T.; Yamashita, T.; Tamaki, T.; Fujiyoshi, H. Survey on vision-based path prediction. In Proceedings of the 6th International Conference on Distributed, Ambient, and Pervasive Interactions: Technologies and Contexts (DAPI 2018), Las Vegas, NV, USA, 15–20 July 2018; Springer: Cham, Switzerland, 2018; pp. 48–64. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Abdul-Rashid, H.; Li, B. A survey of recent 3D scene analysis and processing methods. Multimed. Tools Appl. 2021, 80, 19491–19511. [Google Scholar] [CrossRef]
- Yin, X.; Wu, G.; Wei, J.; Shen, Y.; Qi, H.; Yin, B. Deep learning on traffic prediction: Methods, analysis and future directions. IEEE Trans. Intell. Transp. Syst. 2021, in press. [Google Scholar] [CrossRef]
- Tedjopurnomo, D.A.; Bao, Z.; Zheng, B.; Choudhury, F.; Qin, A.K. A Survey on Modern Deep Neural Network for Traffic Prediction: Trends, Methods and Challenges. IEEE Trans. Knowl. Data Eng. 2020, 1, 1. [Google Scholar] [CrossRef]
- Rasouli, A. Deep learning for Vision-based prediction: A survey. arXiv 2020, arXiv:2007.00095. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME-J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Dellaert, F.; Fox, D.; Burgard, W.; Thrun, S. Monte Carlo localization for mobile robots. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; pp. 1322–1328. [Google Scholar] [CrossRef] [Green Version]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef] [Green Version]
- Rumelhart, D.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, J. Untersuchungen zu Dynamischen Neuronalen Netzen. Master’s Thesis, Universität München, München, Germany, 1991. (In Germany). [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning (ICML’13), Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 1310–1318. Available online: http://proceedings.mlr.press/v28/pascanu13.pdf (accessed on 31 October 2021).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder–decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.H.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Karras, T.; Laine, S.; Aittala, M.; Hellsten, J.; Lehtinen, J.; Aila, T. Analyzing and improving the image quality of StyleGAN. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar] [CrossRef] [Green Version]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Gipps, P.G. A model for the structure of lane-changing decisions. Transp. Res. Part B Methodol. 1986, 20B, 403–414. [Google Scholar] [CrossRef]
- Toledo, T.; Koutsopoulos, H.N.; Ben-Akiva, M.E. Modeling integrated Lane-changing behavior. Transp. Res. Rec. J. Transp. Res. Board 2003, 1857, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Hunt, J.G.; Lyons, G.D. Modelling dual carriageway lane changing using neural networks. Transp. Res. Part C Emerg. Technol. 1994, 2, 231–245. [Google Scholar] [CrossRef]
- Salvucci, D.D.; Liu, A. The time course of a lane change: Driver control and eye-movement behavior. Transp. Res. Part F Traffic Psychol. Behav. 2002, 5, 123–132. [Google Scholar] [CrossRef]
- Oliver, N.; Pentland, A.P. Graphical models for driver behavior recognition in a SmartCar. In Proceedings of the IEEE Intelligent Vehicles Symposium 2000, Dearborn, MI, USA, 3–5 October 2000; pp. 7–12. [Google Scholar] [CrossRef]
- Toledo-Moreo, R.; Zamora-Izquierdo, M.A. IMM-based lane-change prediction in highways with low-cost GPS/INS. IEEE Trans. Intell. Transp. Syst. 2009, 10, 180–185. [Google Scholar] [CrossRef] [Green Version]
- Kasper, D.; Weidl, G.; Dang, T.; Breuel, G.; Tamke, A.; Wedel, A.; Rosenstiel, W. Object-oriented Bayesian networks for detection of lane change maneuvers. IEEE Intell. Transp. Syst. Mag. 2012, 4, 19–31. [Google Scholar] [CrossRef]
- Lefèvre, S.; Laugier, C.; Ibañez-Guzmán, J. Exploiting map information for driver intention estimation at road intersections. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 583–588. [Google Scholar] [CrossRef] [Green Version]
- Liebner, M.; Baumann, M.; Klanner, F.; Stiller, C. Driver intent inference at urban intersections using the intelligent driver model. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012; pp. 1162–1167. [Google Scholar] [CrossRef]
- Schlechtriemen, J.; Wedel, A.; Hillenbrand, J.; Breuel, G.; Kuhnert, K. A lane change detection approach using feature ranking with maximized predictive power. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 108–114. [Google Scholar] [CrossRef]
- Laval, J.A.; Daganzo, C.F. Lane-changing in traffic streams. Transp. Res. Part B Methodol. 2006, 40, 251–264. [Google Scholar] [CrossRef]
- Aoude, G.S.; Desaraju, V.R.; Stephens, L.H.; How, J.P. Driver behavior classification at intersections and validation on large naturalistic data set. IEEE Trans. Intell. Transp. Syst. 2012, 13, 724–736. [Google Scholar] [CrossRef]
- Kumar, P.; Perrollaz, M.; Lefèvre, S.; Laugier, C. Learning-based approach for online lane change intention prediction. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast City, Australia, 23 June 2013; pp. 797–802. [Google Scholar] [CrossRef] [Green Version]
- Mandalia, H.M.; Salvucci, M.D.D. Using support vector machines for lane change detection. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; SAGE Publications: Los Angeles, CA, USA, 2005; Volume 49, pp. 1965–1969. [Google Scholar] [CrossRef]
- Bahram, M.; Hubmann, C.; Lawitzky, A.; Aeberhard, M.; Wollherr, D. A Combined Model- and Learning-Based Framework for Interaction-Aware Maneuver Prediction. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1538–1550. [Google Scholar] [CrossRef]
- Khosroshahi, A.; Ohn-Bar, E.; Trivedi, M.M. Surround vehicles trajectory analysis with recurrent neural networks. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 2267–2272. [Google Scholar] [CrossRef]
- Mammar, S.; Glaser, S.; Netto, M. Time to line crossing for lane departure avoidance: A theoretical study and an experimental setting. IEEE Trans. Intell. Transp. Syst. 2006, 7, 226–241. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, K.I. Modeling Drivers’ Acceleration and Lane Changing Behavior. Sc.D. Thesis, Massachusetts Institute of Technology, Department of Civil and Environmental Engineering, Cambridge, MA, USA, 1999. Available online: https://dspace.mit.edu/handle/1721.1/9662 (accessed on 31 October 2021).
- Helbing, D.; Tilch, B. Generalized force model of traffic dynamics. Phys. Rev. E 1998, 58, 133. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://paperswithcode.com/ (accessed on 31 October 2021).
- Hermes, C.; Wohler, C.; Schenk, K.; Kummert, F. Long-term vehicle motion prediction. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 652–657. [Google Scholar] [CrossRef]
- Houenou, A.; Bonnifait, P.; Cherfaoui, V.; Yao, W. Vehicle trajectory prediction based on motion model and maneuver recognition. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4363–4369. [Google Scholar] [CrossRef] [Green Version]
- Deo, N.; Rangesh, A.; Trivedi, M.M. How would surround vehicles move? A unified framework for maneuver classification and motion prediction. IEEE Trans. Intell. Veh. 2018, 3, 129–140. [Google Scholar] [CrossRef] [Green Version]
- Casas, S.; Luo, W.; Urtasun, R. IntentNet: Learning to predict intention from raw sensor data. In Proceedings of the 2nd Conference on Robot Learning (CoRL 2018), Zürich, Switzerland, 29–31 October 2018; pp. 947–956. Available online: http://proceedings.mlr.press/v87/casas18a/casas18a.pdf (accessed on 31 October 2021).
- Park, S.H.; Kim, B.; Kang, C.M.; Chung, C.C.; Choi, J.W. Sequence-to-sequence prediction of vehicle trajectory via LSTM encoder-decoder architecture. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Suzhou, China, 26–30 June 2018; pp. 1672–1678. [Google Scholar] [CrossRef] [Green Version]
- Cui, H.; Radosavljevic, F.; Chou, F.-C.; Lin, T.-H.; Nguyen, T.; Huang, T.-K.; Schneider, J.; Djuric, N. Multimodal trajectory predictions for autonomous driving using deep convolutional networks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2090–2096. [Google Scholar] [CrossRef] [Green Version]
- Altché, F.; de la Fortelle, A. An LSTM network for highway trajectory prediction. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Las Vegas, NV, USA, 27–30 June 2016; pp. 353–359. [Google Scholar] [CrossRef] [Green Version]
- Deo, N.; Trivedi, M.M. Convolutional social pooling for vehicle trajectory prediction. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1549–15498. [Google Scholar] [CrossRef] [Green Version]
- Chandra, R.; Bhattacharya, U.; Bera, A.; Manocha, D. TraPHic: Trajectory prediction in dense and heterogeneous traffic using weighted interactions. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8475–8484. [Google Scholar] [CrossRef] [Green Version]
- Zhao, T.; Xu, Y.; Monfort, M.; Choi, W.; Baker, C.; Zhao, Y.; Wang, Y.; Wu, Y.N. Multi-agent tensor fusion for contextual trajectorypPrediction. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12118–12126. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.C.; Salakhutdinov, R. Multiple futures prediction. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Song, H.; Ding, W.; Chen, Y.; Shen, S.; Wang, M.Y.; Chen, Q. PiP Planning-informed trajectory prediction for autonomous driving. In European Conference on Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 598–614. [Google Scholar] [CrossRef]
- Chandra, R.; Guan, T.; Panuganti, S. Forecasting trajectory and behavior of road-agents using spectral clustering in graph-LSTMs. IEEE Robot. Autom. Lett. 2020, 5, 4882–4890. [Google Scholar] [CrossRef]
- Lee, N.; Choi, W.; Vernaza, P.; Choy, C.B.; Torr, P.H.S.; Chandraker, M. DESIRE: Distant future prediction in dynamic scenes with interacting agents. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2165–2174. [Google Scholar] [CrossRef] [Green Version]
- Choi, C.; Choi, J.H.; Li, J.; Malla, S. Shared cross-modal trajectory prediction for autonomous driving. arXiv 2020, arXiv:2004.00202. [Google Scholar]
- Chai, Y.; Sapp, B.; Bansal, M.; Anguelov, D. MultiPath: Multiple probabilistic anchor trajectory hypotheses for behavior prediction. In Conference on Robot Learning; PMLR: New York, NY, USA, 2020; Volume 100, pp. 86–99. [Google Scholar]
- Mangalam, K.; Girase, H.; Agarwal, S.; Lee, K.H.; Adeli, E.; Malik, J.; Gaidon, A. It is not the journey but the destination: Endpoint conditioned trajectory prediction. In Proceedings of the European Conference on Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, G.; Seo, J.; Bhat, M.; Kang, M.; Francis, J.; Jadhav, A.; Liang, P.P.; Morency, L.P. Diverse and admissible trajectory forecasting through multimodal context understanding. In Proceedings of the European Conference on Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 282–298. [Google Scholar] [CrossRef]
- Song, H.; Luan, D.; Ding, W.; Wang, M.Y.; Chen, Q. Learning to predict vehicle trajectories with model-based planning. arXiv 2021, arXiv:2103.04027. [Google Scholar]
- Zeng, W.; Liang, M.; Liao, R.; Urtasun, R. LaneRCNN: Distributed representations for graph-centric motion forecasting. arXiv 2021, arXiv:2101.06653. [Google Scholar]
- Casas, S.; Gulino, C.; Liao, R.; Urtasun, R. SpAGNN: Spatially-Aware Graph Neural Networks for relational behavior forecasting from sensor data. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9491–9497. [Google Scholar] [CrossRef]
- Phan-Minh, T.; Grigore, E.C.; Boulton, F.A.; Beijbom, O.; Wolff, E.M. CoverNet: Multimodal behavior prediction using trajectory sets. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 14062–14071. [Google Scholar] [CrossRef]
- Liang, M.; Yang, B.; Zeng, W.; Chen, Y.; Hu, R.; Casas, S.; Urtasun, R. PnPNet: End-to-end perception and prediction with tracking in thelLoop. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11550–11559. [Google Scholar] [CrossRef]
- Narayanan, S.; Moslemi, R.; Pittaluga, F.; Liu, B.; Chandraker, M. Divide-and-conquer for lane-aware diverse trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar] [CrossRef]
- Li, J.; Ma, H.; Zhang, Z.; Tomizuka, M. Social-WaGDAT interaction-aware trajectory prediction via Wasserstein graph double-attention network. arXiv 2020, arXiv:2002.06241. [Google Scholar]
- Mohta, A.; Chou, F.C.; Becker, B.C.; Vallespi-Gonzalez, C.; Djuric, N. Investigating the effect of sensor modalities in multi-sensor detection-prediction models. arXiv 2021, arXiv:2101.03279. [Google Scholar]
- Pomerleau, D.A. ALVINN: An autonomous land vehicle in a neural network. Adv. Neural Inf. Process. Syst. 1989, 1, 305–313. [Google Scholar]
- Fix, E.; Armstrong, H.G. Modeling human performance with neural networks. Int. Jt. Conf. Neural Netw. 1990, 1, 247–252. [Google Scholar]
- Vasquez, D.; Fraichard, T. Motion prediction for moving objects: A statistical approach. Proc. IEEE Int. Conf. Robot. Autom. 2004, 4, 3931–3936. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Hu, W.; Hu, W. A coarse-to-fine strategy for vehicle motion trajectory clustering. In Proceedings of the 18th International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; 2006; Volume 1, pp. 591–594. [Google Scholar] [CrossRef]
- Vasquez, D.; Fraichard, T.; Laugier, C. Incremental learning of statistical motion patterns with growing hidden Markov models. IEEE Trans. Intell. Transp. Syst. 2009, 10, 403–416. [Google Scholar] [CrossRef]
- Morton, J.; Wheeler, T.A.; Kochenderfer, M.J. Analysis of recurrent neural networks for probabilistic modeling of driver behavior. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1289–1298. [Google Scholar] [CrossRef]
- Kim, B.; Kang, C.M.; Kim, J.; Lee, S.H.; Chung, C.C.; Choi, J.W. Probabilistic vehicle trajectory prediction over occupancy grid map via recurrent neural network. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 399–404. [Google Scholar] [CrossRef] [Green Version]
- Krüger, M.; Stockem Novo, A.; Nattermann, T.; Bertram, T. Interaction-aware trajectory prediction based on a 3D spatio-temporal tensor representation using convolutional–recurrent neural networks. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1122–1127. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social LSTM: Human trajectory prediction in crowded spaces. In Proceedings of the 29th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar] [CrossRef] [Green Version]
- Robicquet, A.; Sadeghian, A.; Alahi, A.; Savarese, S. Learning social etiquette: Human trajectory understanding in crowded scenes. In Proceedings of the Computer Vision—ECCV 2016, Glasgow, UK, 23–28 August 2020; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 549–565. [Google Scholar] [CrossRef] [Green Version]
- Rudenko, A.; Palmieri, L.; Herman, M.; Kitani, K.M.; Gavrila, D.; Arras, K. Human motion trajectory prediction: A survey. Int. J. Robot. Res. 2020, 39, 895–935. [Google Scholar] [CrossRef]
- Li, X.; Ying, X.; Chuah, M.C. GRIP: Graph-based interaction-aware trajectory prediction. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3960–3966. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Su, P.-H.; Hoang, J.; Haynes, G.C.; Marchetti-Bowick, M. Map-adaptive goal-based trajectory prediction. arXiv 2020, arXiv:2009.04450. [Google Scholar]
- Xu, H.; Gao, Y.; Yu, F.; Darrell, T. End-to-end learning of driving models from large-scale video datasets. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3530–3538. [Google Scholar] [CrossRef] [Green Version]
- Deo, N.; Trivedi, M.M. Multi-modal trajectory prediction of surrounding vehicles with maneuver based LSTMs. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Suzhou, China, 26–30 June 2018; pp. 1179–1184. [Google Scholar] [CrossRef] [Green Version]
- Hoermann, S.; Bach, M.; Dietmayer, K. Dynamic occupancy grid prediction for urban autonomous driving: A deep learning approach with fully automatic labeling. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2056–2063. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Yang, B.; Urtasun, R. Fast and furious: Real time end-to-end 3D detection, tracking and motion forecasting with a single convolutional net. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 3569–3577. [Google Scholar] [CrossRef]
- Choi, C.; Malla, S.; Patil, A.; Choi, J.H. DROGON: A trajectory prediction model based on intention-conditioned behavior reasoning. arXiv 2020, arXiv:1908.00024. [Google Scholar]
- Gao, J.; Sun, C.; Zhao, H. VectorNet: Encoding HD maps and agent dynamics from vectorized representation. arXiv 2020, arXiv:2005.04259. [Google Scholar]
- Gomez-Gonzalez, S.; Prokudin, S.; Schölkopf, B.; Peters, J. Real time trajectory prediction using deep conditional generative models. IEEE Robot. Autom. Lett. 2020, 5, 970–976. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Chen, S.; Zhang, Y.; Gu, X. Collaborative motion prediction via neural motion message passing. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 6318–6327. [Google Scholar] [CrossRef]
- Mohamed, A.; Qian, K.; Elhoseiny, M.; Claudel, C. Social-STGCNN: A social spatio-temporal graph convolutional neural network for human trajectory prediction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 14412–14420. [Google Scholar] [CrossRef]
- Pareja, A.; Domeniconi, G.; Chen, J.; Ma, T.; Suzumura, T.; Kanezashi, H.; Kaler, T.; Schardl, T.B.; Leiserson, C.E. EvolveGCN: Evolving Graph Convolutional Networks for dynamic graphs. arXiv 2019, arXiv:1902.10191. [Google Scholar] [CrossRef]
- Roh, J.; Mavrogiannis, C.; Madan, R.; Fox, D.; Srinivasa, S.S. Multimodal trajectory prediction via yopological nvariance for navigation at uncontrolled intersections. arXiv 2011, arXiv:2011.03894. [Google Scholar]
- Zhang, Z.; Gao, J.; Mao, J.; Liu, Y.; Anguelov, D.; Li, C. STINet: Spatio-Temporal-Interactive Network for Pedestrian Detection and Trajectory Prediction. arXiv 2020, arXiv:2005.04255. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. IJCAI-19 2019, 33, 922–929. [Google Scholar] [CrossRef] [Green Version]
- Diehl, F.; Brunner, T.; Le, M.T.; Knoll, A. Graph neural networks for modelling traffic participant interaction. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 695–701. [Google Scholar]
- Ivanovic, B.; Pavone, M. The Trajectron: Probabilistic multi-agent trajectory modeling with dynamic spatiotemporal graphs. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 2375–2384. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Bi, H.; Li, Z.; Mao, T.; Wang, Z. STGAT: Modeling spatial-temporal interactions for human trajectory prediction. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 6271–6280. [Google Scholar] [CrossRef]
- Khandelwal, S.; Qi, W.; Sing, J.; Hartnett, A.; Ramanan, D. What-if motion prediction for autonomous driving. arXiv 2020, arXiv:2008.10587. [Google Scholar]
- Kosaraju, V.; Sadeghian, A.; Martin-Martin, R. Social-BiGAT: Multimodal trajectory forecasting using bicycle-GAN and graph attention networks. arXiv 2019, arXiv:1907.03395. [Google Scholar]
- Liang, M.; Yang, B.; Hu, R. Learning lane graph representations for motion forecasting. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; Volume 12347, pp. 541–556. [Google Scholar]
- Messaoud, K.; Yahiaoui, I.; Verroust-Blondet, A.; Nashashibi, F. Attention based vehicle trajectory prediction. IEEE Trans. Intell. Veh. 2021, 6, 175–185. [Google Scholar] [CrossRef]
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Multi-agent generative trajectory forecasting with heterogeneous data for control. arXiv 2020, arXiv:2001.03093. [Google Scholar]
- Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Transformer networks for trajectory forecasting. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 10335–10342. [Google Scholar] [CrossRef]
- Xue, H.; Salim, F.D. TERMCast: Temporal relation modeling for effective urban flow forecasting. In Advances in Knowledge Discovery and Data Mining, Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining 2021 (PAKDD 2021), Virtual Event, 11–14 May 2021; Karlapalem, K., Cheng, H., Ramakrishnan, N., Agrawal, R.K., Krishna Reddy, P., Srivastava, J., Chakraborty, T., Eds.; Springer: Cham, Switzerland, 2021; pp. 741–753. [Google Scholar] [CrossRef]
- Cai, L.; Janowicz, K.; Mai, G.; Yan, B.; Zhu, R. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting. Trans. GIS 2020, 24, 736–755. [Google Scholar] [CrossRef]
- Bogaerts, T.; Masegosa, A.; Angarita-Zapata, J.S.; Onieva, E.; Hellinckx, P. A graph CNN-LSTM neural network for short and long-term traffic forecasting based on trajectory data. Transp. Res. Part C Emerg. Technol. 2020, 112, 62–77. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, J.; Lan, T.; Sun, C.; Sapp, B.; Varadarajan, B.; Shen, Y.; Chai, Y.; Schmid, C.; Congcong, L.; et al. TNT: Target-driveN Trajectory prediction. arXiv 2020, arXiv:2008.08294. [Google Scholar]
- Ma, Y.; Zhu, X.; Zhang, S.; Yang, R.; Wang, W.; Manocha, D. TrafficPredict: Trajectory prediction for heterogeneous traffic-agents. arXiv 2019, arXiv:1811.02146. [Google Scholar] [CrossRef] [Green Version]
- Kuefler, A.; Morton, J.; Wheeler, T.; Kochenderfer, M. Imitating driver behavior with generative adversarial networks. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 204–211. [Google Scholar] [CrossRef] [Green Version]
- Rhinehart, N.; Kitani, K.M.; Vernaza, P. r2p2: A Reparameterized pushforward policy for diverse, precise generative path forecasting. In Proceedings of the European Conference on Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- FHWA, U.S. Department of Transportation. NGSIMNext Generation SIMulation. Available online: http://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm (accessed on 31 October 2021).
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar] [CrossRef]
- Chang, M.-F.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; Lucey, S.; Ramanan, D.; et al. Argoverse: 3D tracking and forecasting with rich maps. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8748–8757. [Google Scholar] [CrossRef] [Green Version]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Lion, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A multimodal dataset for autonomous driving. arXiv 2020, arXiv:1903.11027. [Google Scholar]
- Argoverse Motion Forecasting Competition Leaderboard. Available online: https://eval.ai/web/challenges/challenge-page/454/leaderboard/1279 (accessed on 31 October 2021).
- Zhuang, F.; Qi, Z.; Duan, K. A Comprehensive survey on transfer learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Mahapatra, D.; Bozorgtabar, B.; Thiran, J.P.; Reyes, M. Efficient active learning for image classification and segmentation using a sample selection and conditional generative adversarial network. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2018; Frangi, A., Schnabel, J., Davatzikos, C., Alberola-López, C., Fichtinger, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 580–588. [Google Scholar] [CrossRef] [Green Version]
- Louizos, C.; Reisser, M.; Blankevoort, T.; Gavves, E.; Welling, M. Relaxed Quantization for discretized neural networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wu, S.; Li, G.; Chen, F.; Shi, L. Training and inference with integers in deep neural networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; Available online: https://openreview.net/forum?id=HJGXzmspb (accessed on 31 October 2021).
- Baker, C.L.; Jara-Ettinger, J.; Saxe, R.; Tenenbaum, J.B. Rational quantitative attribution of beliefs, desires and percepts in human mentalizing. Nat. Hum. Behav. 2017, 1, 0064. [Google Scholar] [CrossRef]
- Look, A.; Doneva, S.; Kandemir, M.; Gemulla, R.; Peters, J. Differentiable implicit layers. arXiv 2020, arXiv:2010.07078. [Google Scholar]

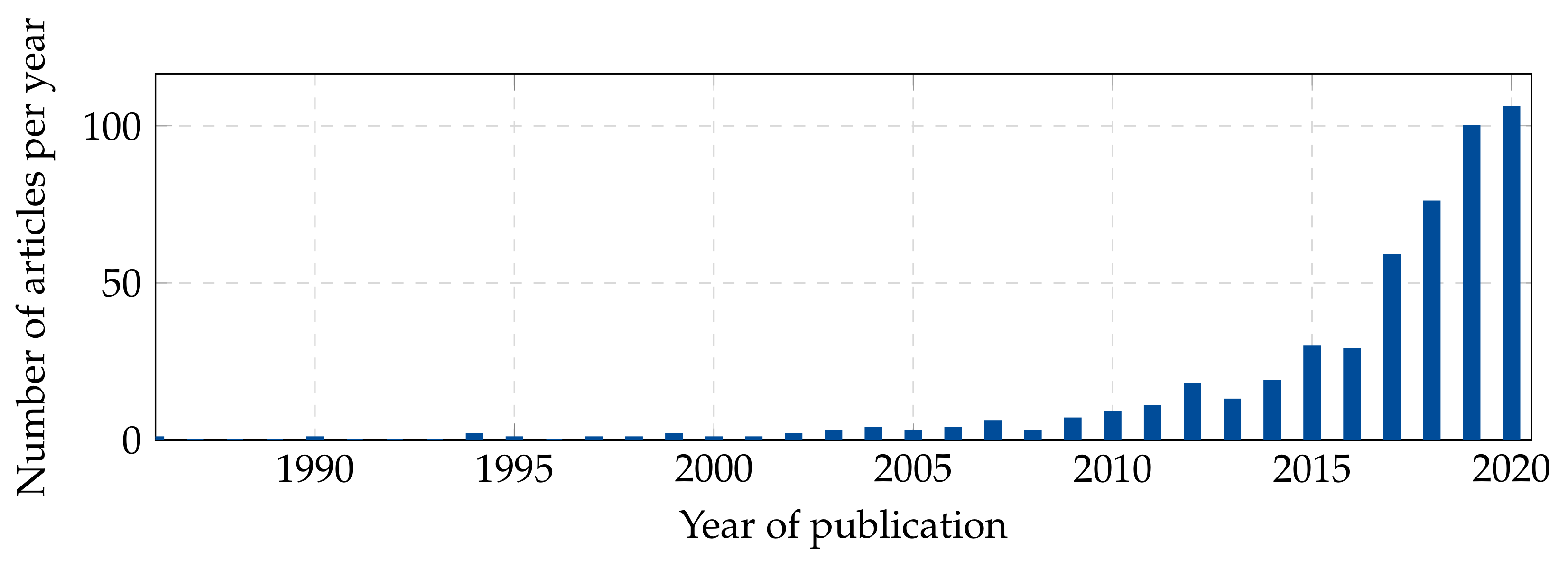



| Authors | Data | Year | Method | Horizon [s] | Metrics | Error [m] |
|---|---|---|---|---|---|---|
| Hermes et al. [59] | real | 2009 | Clustering | 3 | RMSE | |
| Houenou et al. [60] | real | 2013 | CYRA | 4 | RMSE | 0.45 |
| Deo et al. [61] | real | 2018 | VGMM | 5 | MAE | 2.18 |
| Casas et al. [62] | real | 2018 | C | 3 | MAE | 1.61 |
| Park et al. [63] | real | 2018 | L | 2 | MAE | 0.93 () |
| Cui et al. [64] | real | 2019 | C | 6 | ADE | 2.31 () |
| Altche et al. [65] | NGSIM | 2017 | L | 10 | RMSE | 0.65 1 |
| Deo et al. [66] | NGSIM | 2018 | L+C | 5 | RMSE | 4.37 |
| Chandra et al. [67] | NGSIM | 2019 | L+C | 5 | ADE/FDE | 5.63/9.91 |
| Zhao et al. [68] | NGSIM | 2019 | L+C | 5 | RMSE | 4.13 |
| Tang et al. [69] | NGSIM | 2019 | G+A | 5 | RMSE | 3.80 () |
| Song et al. [70] | NGSIM | 2020 | L+C | 5 | RMSE | 4.04 |
| Chandra et al. [71] | NGSIM | 2020 | G+L | 5 | ADE/FDE | 0.40/1.08 |
| Lee et al. [72] | KITTI | 2017 | L+C | 4 | RMSE | 2.06 |
| Choi et al. [73] | KITTI | 2020 | G+L+C | 4 | ADE/FDE | 0.75/1.99 () |
| Lee et al. [72] | SDD | 2017 | L+C | 4 | RMSE | 5.33 |
| Chai et al. [74] | SDD | 2019 | C | 5 | ADE | 3.50 () |
| Mangalam et al. [75] | SDD | 2020 | A | 5 | ADE/FDE | 0.18/0.29 () |
| Tang et al. [69] | Argoverse | 2019 | G+A | 3 | ADE | 1.40 () |
| Chandra et al. [71] | Argoverse | 2020 | G+L | 5 | ADE/FDE | 0.99/1.87 |
| Park et al. [76] | Argoverse | 2020 | L+A | 3 | ADE/FDE | 0.73/1.12 () |
| Song et al. [77] | Argoverse | 2021 | L+C+A | 3 | ADE/FDE | 1.22/1.56 () |
| Zeng et al. [78] | Argoverse | 2021 | G+C | 3 | ADE/FDE | 0.9/1.45 () |
| Casas et al. [79] | nuScenes | 2020 | G+C | 3 | RMSE | 1.45 |
| Phan-Minh et al. [80] | nuScenes | 2020 | C | 6 | ADE/FDE | 1.96/9.26 () |
| Liang et al. [81] | nuScenes | 2020 | L+C | 3 | ADE/FDE | 0.65/1.03 |
| Park et al. [76] | nuScenes | 2020 | L+A | 3 | ADE/FDE | 0.64/1.17 () |
| Narayanan et al. [82] | nuScenes | 2021 | C+L | 4 | ADE/FDE | 1.10/1.66 () |
| Casas et al. [79] | ATG4D | 2020 | G+C | 3 | RMSE | 0.96 |
| Liang [81] | ATG4D | 2020 | L+C | 3 | ADE/FDE | 0.68/1.04 |
| Chandra et al. [71] | Lyft | 2020 | G+L | 5 | ADE/FDE | 2.65/2.99 |
| Chandra et al. [71] | Apolloscape | 2020 | G+L | 3 | ADE/FDE | 1.12/2.05 |
| Li et al. [83] | INTERACTION | 2020 | G+C+A | 5 | ADE/FDE | 1.31/3.34 |
| Choi et al. [73] | H3D | 2020 | G+L+C | 4 | ADE/FDE | 0.42/0.96 () |
| Song et al. [70] | HighD | 2020 | L+C | 5 | RMSE | 2.63 |
| Mohta et al. [84] | X17k | 2021 | C | 3 | FDE | 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stockem Novo, A.; Krüger, M.; Stolpe, M.; Bertram, T. A Review on Scene Prediction for Automated Driving. Physics 2022, 4, 132-159. https://doi.org/10.3390/physics4010011
Stockem Novo A, Krüger M, Stolpe M, Bertram T. A Review on Scene Prediction for Automated Driving. Physics. 2022; 4(1):132-159. https://doi.org/10.3390/physics4010011
Chicago/Turabian StyleStockem Novo, Anne, Martin Krüger, Marco Stolpe, and Torsten Bertram. 2022. "A Review on Scene Prediction for Automated Driving" Physics 4, no. 1: 132-159. https://doi.org/10.3390/physics4010011
APA StyleStockem Novo, A., Krüger, M., Stolpe, M., & Bertram, T. (2022). A Review on Scene Prediction for Automated Driving. Physics, 4(1), 132-159. https://doi.org/10.3390/physics4010011





