Recent Progress on the Sum over Paths Approach in Quantum Mechanics Education

Abstract

In this paper, we present an overview of recent developments in the Feynman sum over paths approach for teaching introductory quantum mechanics to high school students and university undergraduates. A turning point in recent research is identified in the clarification of the distinction between the time-dependent and time-independent approaches, and it is shown how the adoption of the latter has allowed new educational reconstructions to proceed much farther beyond what had previously been achieved. It is argued that sum over paths has now reached full maturity as an educational reconstruction of quantum physics and offers several advantages with respect to other approaches in terms of leading students to develop consistent mental models of quantum phenomena, achieving better conceptual understanding and a higher degree of longitudinal integration of knowledge.

1. Introduction

The sum over paths approach in physics education originates mainly from two sources: Feynman’s path integral formulation of quantum physics [1] and his own divulgation book QED: the Strange Theory of Light and Matter [2] (‘’QED’’ stays for Quantum Electro-Dynamics). The latter, in fact, constitutes the first, fundamental sketch of an educational reconstruction of quantum physics based on the path integral formulation. Among the milestones for the development of the approach, one can trace the undergraduate course Demystifying Quantum Mechanics on quantum physics held by E.F. Taylor at MIT (Massachusetts Institute of Technology, USA) [3], which had a profound impact in the international physics education research community, and the Advancing Physics project [4] of the British Institute of Physics, an advanced physics course for high schools, designed to attract students to physics, and to give them a good basis for their future progression in the subject at university level, in which J. Ogborn, A. Dobson and collaborators [5] proposed an innovative presentation of quantum physics based on sum over paths. After the turn of the millennium, interest in the sum over paths approach has grown, with several works of great interest, both empirical [6,7] and theoretical [8,9].

Sum over paths has been considered right from the beginning of its history in education as a promising route for teaching the conceptual core of quantum physics to secondary school students and non-physicists. However, some critical points in the approach were also highlighted by some authors (e.g., [10]). These questions and critical remarks can be summarized as follows:

• Is it possible that using the sum over paths approach may encourage students to retain the classical concept of trajectory, as they may misinterpret Feynman paths as trajectories that are taken alternatively according to some probability rule?
• The treatment of simple one-dimensional time independent systems may be much more complicated using Feynman’s approach than using a standard formulation (i.e., a wavefunction approach).
• Can the approach be integrated to provide at least an elementary introduction to concepts, related to spin?

2. A summary of Recent Developments

Recent educational research has addressed many of the open issues standing on the sum over paths approach [11], including devising effective educational strategies for discussing time-independent problems such as bound states and tunneling [12,13]; improving the treatment of the uncertainty principle [14]; establishing connections with two state approaches based on spin or light polarization [15]; designing and realizing tools such as interactive simulations and tutorials to sustain students’ learning [16,17]. Many of these advances were stimulated or facilitated by the complete clarification of the distinction between a time-dependent and a time-independent sum over paths approach in education [13]. Further improvements included pinpointing and clarifying the educational advantages of sum over paths, including reliable measures of conceptual learning outcomes [18,19] and highlighting the importance of concepts such as path distinguishability, which were not central in the initial educational tests of the approach, but have demonstrated extremely fecund in leading to conceptual understanding of wave particle duality, and allowing modern experimental settings and technologies to be introduced [20].

In the last 10 years, interest in the sum over paths approach has remained high, although research has been led by a few groups, such as the physics education groups at the Universities of Pavia and Trento in Italy and the physics education group at CONICET (Consejo Nacional de Investigaciones Científicas y Técnicas) and the National University of La Plata in Argentina. There has also been related research into the use of Feynman diagrams in education (e.g., Ref. [21]), which can be considered, given the shared underlying philosophy, a ‘‘natural’’ prosecution of quantum instruction in the perspective of sum over paths.

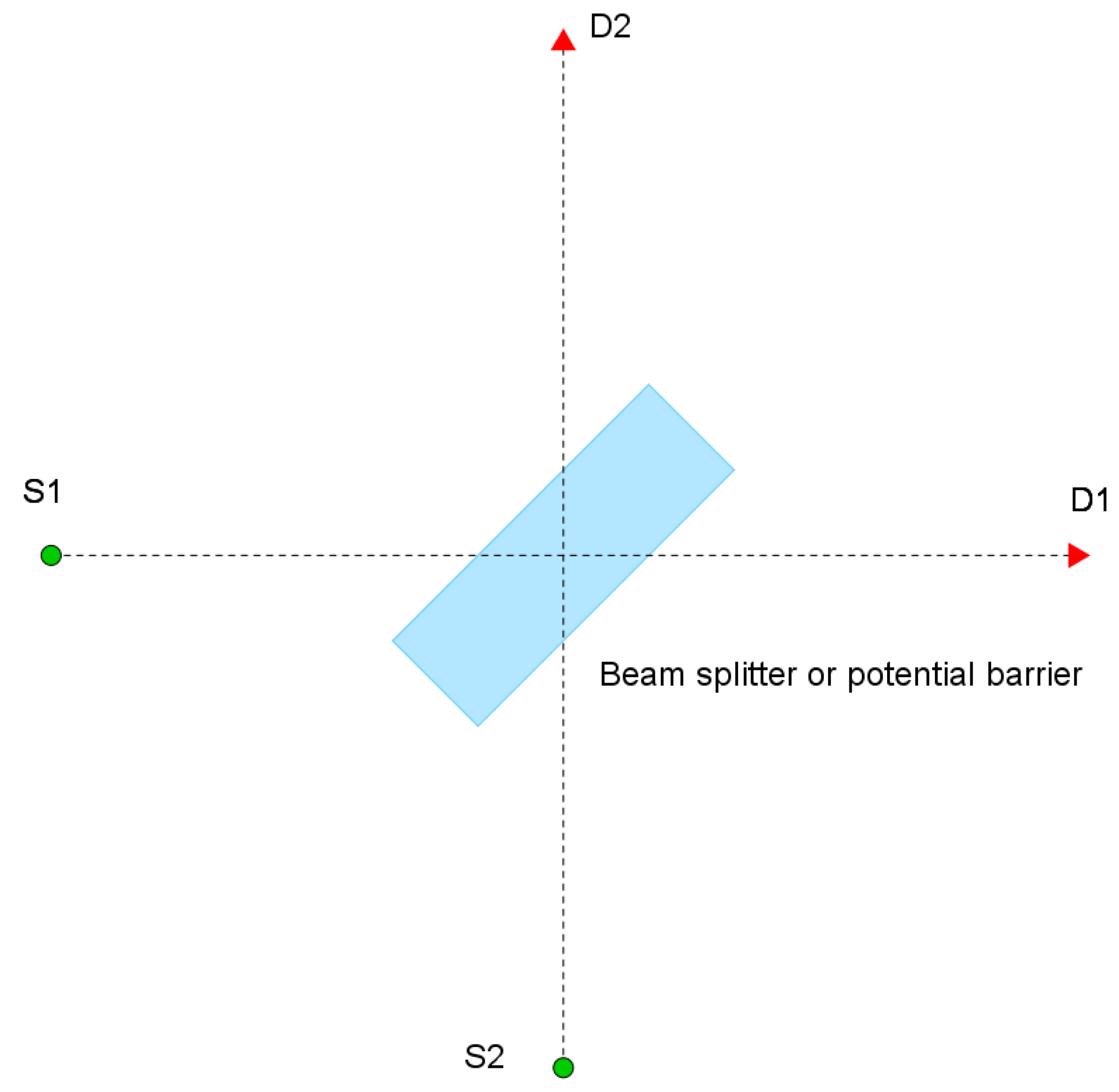
3. Time Dependent vs. Time Independent Sum over Paths Approach

To some degree, the disagreement about the educational usefulness of sum over paths in the last 20 years has been due to a confusion surrounding the role of time in the algorithm for computing detection probabilities. In the 10 years, our group took significant efforts to clarify the situation and show that it is actually possible to use two sum over paths approaches, with a similar general structure but a different identification of physical variables involved in the algorithm of summing over all possible paths. In order to clarify the problem concerning the stationary or time-dependent phenomena, one can analyze the case of the two slit interference of an individual electron.

This problem can be treated in the sum over paths perspective in two ways:

• Considering an initial wavefunction (a “wavepacket”) and evolving all the points belonging to it using Feynman’s path integral propagator.
• Considering the time-independent problem (at fixed energy) of the propagation of a quantum object from the source to the detector, and using the time-independent propagator (Green function), which basically (apart from a prefactor) reduces to $e^{ikx}$ with x denoting the path length. This approach draws, in addition to Feynman’s original works, from more recent research in the area of semiclassical path integrals [22].

The latter approach may be called “stationary” or “time-independent” path integral and the results of the two methods agree, if the energy of the time-dependent wavepacket in the former of the two approaches above is defined with sufficiently small uncertainty (see e.g., Ref. [23]).

In both the following expositions of the time-dependent and time-independent approaches, the concept of action is used. However, secondary school students are rarely exposed to either the full or abbreviated action in the study of classical mechanics. Typically, in both kinds of approaches a rule is given for computing the phase of path amplitudes, and then, if desired, the concept of action is introduced, and the principles of stationary action are derived, after recovering the classical from quantum behavior (correspondence principle) in the short wavelength limit [8].

3.1. The Time-Dependent Sum over Paths Approach

The time-dependent version of the sum over paths approach, derived directly from Feynman’s path integral formulation, can be summarized as follows [3,24,25,26]:

• The quantum object goes through all possible paths from an initial space–time point (x_i, t_i) to a final space–time point (x_f, t_f).
• A complex number, often represented by a conventional rotating vector, is associated with each of the paths; its phase angle is proportional to the classical action, R = ∫$\mathcal{L}$(t)dt, calculated along the path. Here, $\mathcal{L}$ denotes the Lagrangian.
• The (normalized) sum of all contributions from the possible paths starting at (x_i, t_i) and ending at (x_f, t_f) gives the time-dependent propagator, which can be understood as the probability amplitude of finding at (x_f, t_f) a quantum object that was initially at (x_i, t_i).
• The probability, P, of detecting the quantum object at (x_f, t_f) is then computed by taking the square modulus of the propagator.

Authors have proposed and experimented with several versions of this approach, especially in university education for non-specialists [3,27] and in secondary school [26], but also in introductory courses for first year physics students [28]. These settings are typical of research on sum over paths, as the use of less advanced mathematics is normally in order, and the ability to solve problems may be partly sacrificed in favor of a conceptual understanding of a deep and productive reconstruction of quantum theory. The approach was in general judged promising by physics education researchers although some difficulties were highlighted already from the initial paper by Taylor [3], among which in particular:

• A time-dependent formulation may increase students’ confusion about the concepts of quantum paths and classical trajectories.
• The time-dependent treatment obscures the fact that many of the most important predictions of quantum physics are actually time-independent statistics. For example, finding the eigenfunctions for confining potentials usually requires computing the time-dependent propagator and then determining the initial amplitudes that, for the given propagator, are stationary in time, a procedure which appears intricated to students even in the presence of technological aids such as tailored simulation software.

3.2. The Time Independent Sum over Paths Approach

In this approach, the behavior of quantum objects is modelled using a sum-over-paths approach at fixed energy, independent of time. More explicitly, the sum over paths approach at fixed energy, for time-independent problems, can be compactly described as follows:

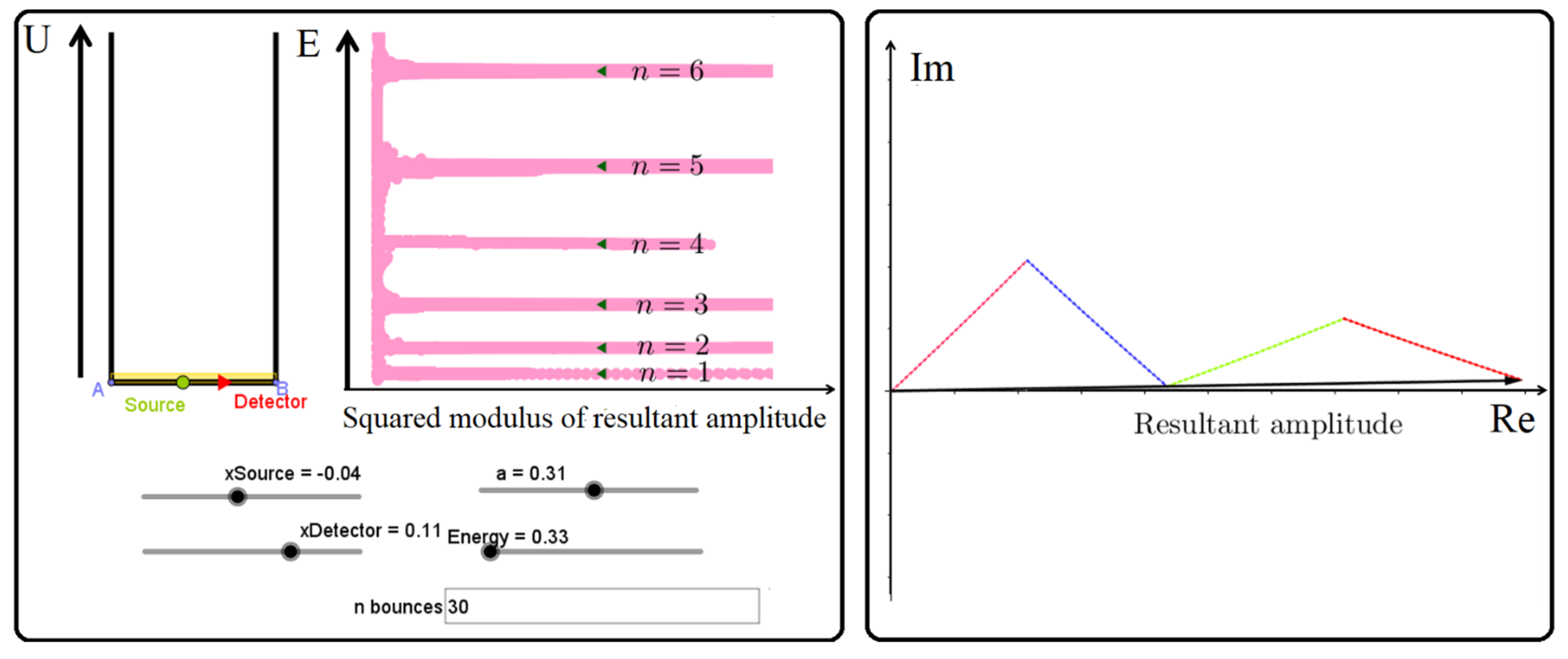
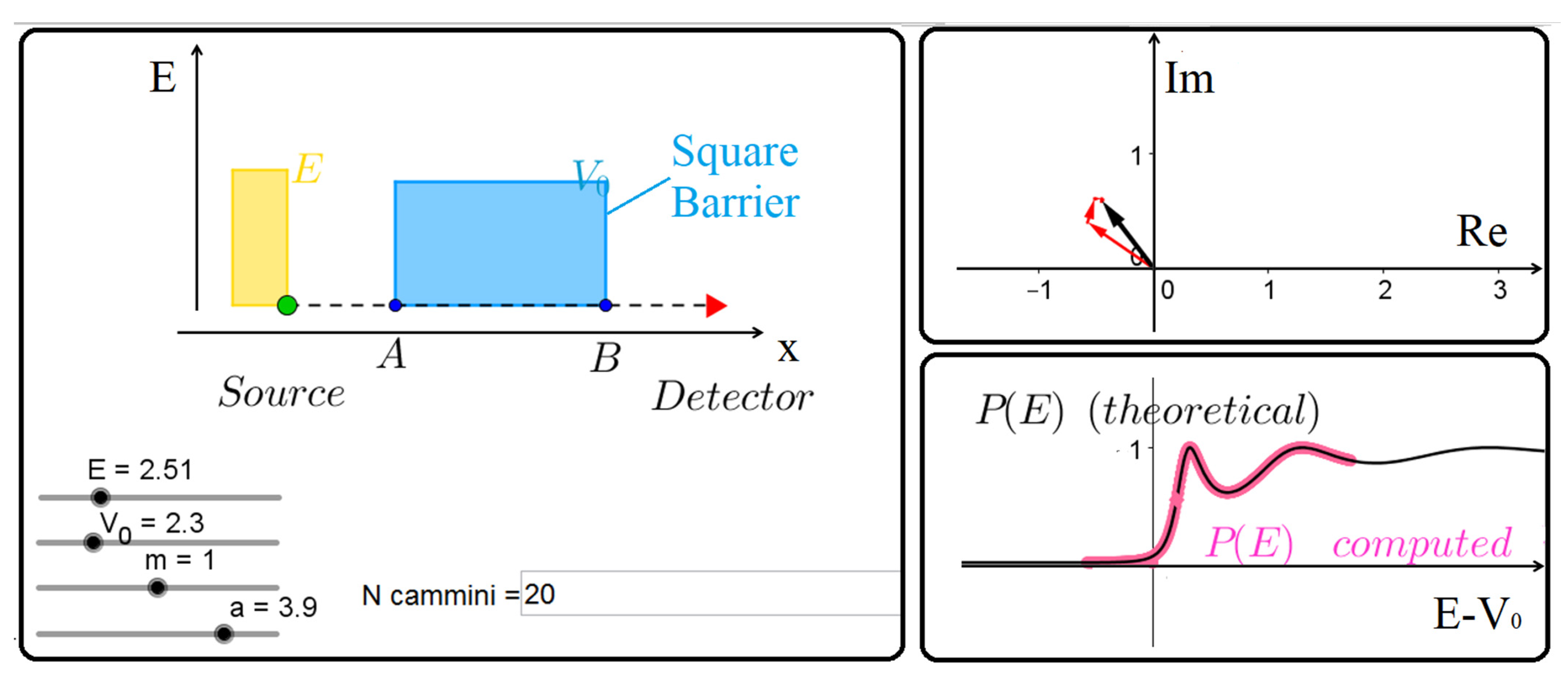
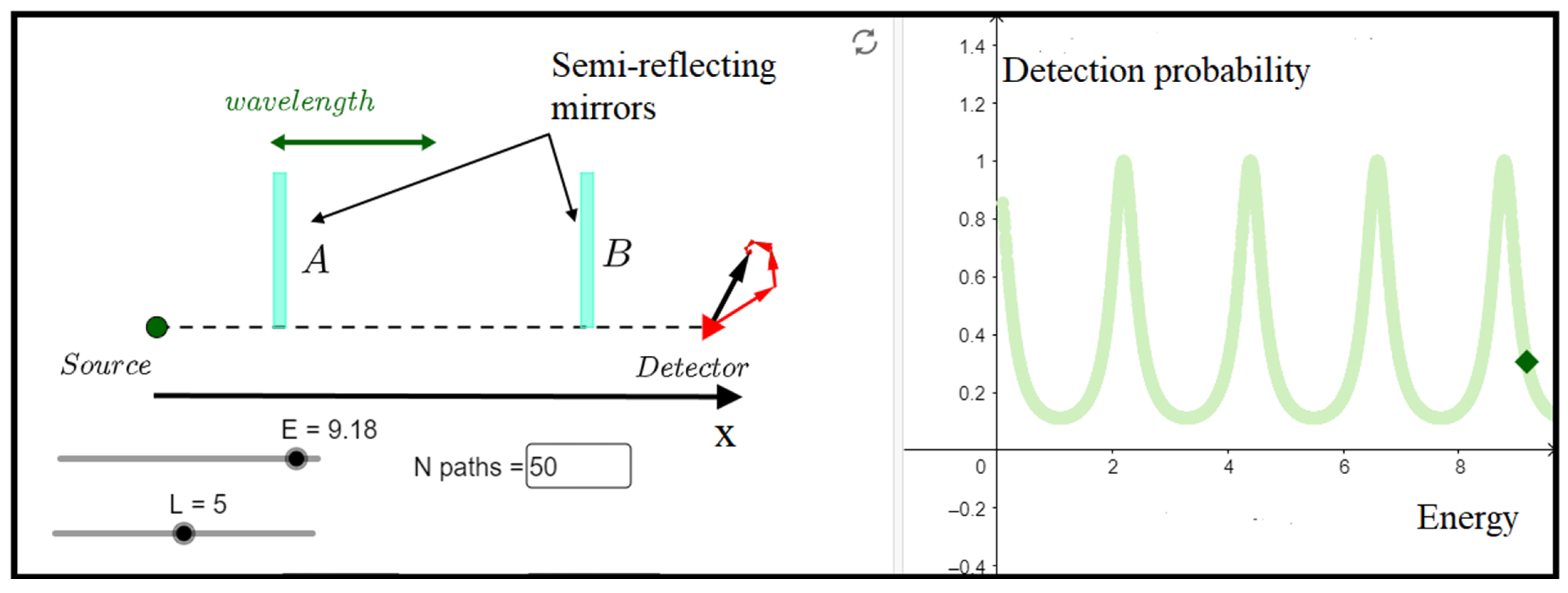
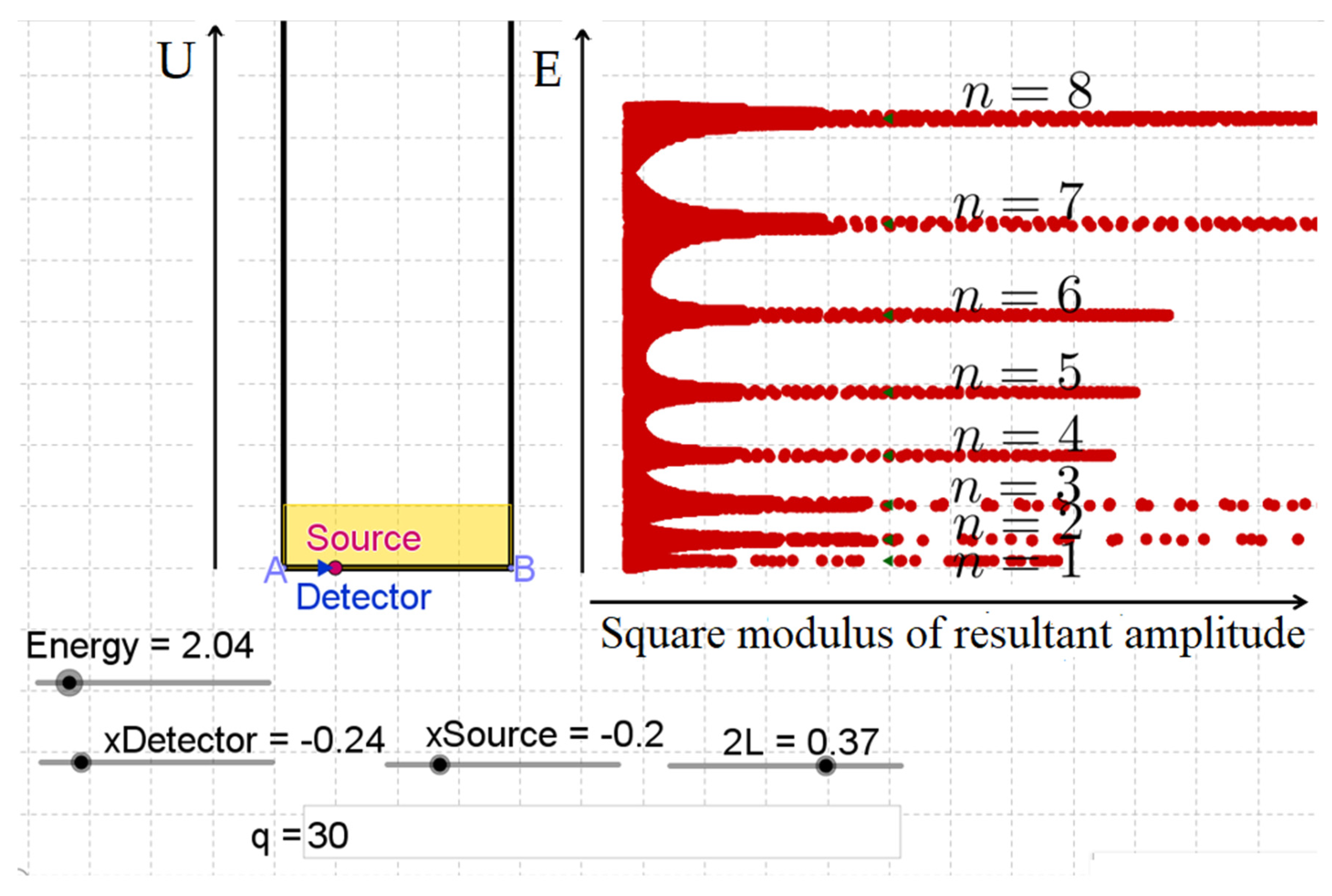
• The quantum object goes through all possible paths at fixed energy, E, from an initial point in space, x_i (the source), to a final one, x_f (the detector).
• A complex number, often represented by a conventional rotating vector, is associated with each of the paths; its phase angle is proportional to the classical abbreviated action, S = ∫p(x) dx, calculated along the path, where p(x) is the particle momentum at point x.
• The sum of all contributions from the possible paths at fixed energy starting at x_i and ending at x_f gives the energy-dependent propagator, or Green function, which can be understood as the probability amplitude of finding at x_f, independently of arrival time, a particle with defined energy whose source is at x_i.
• The probability P of detecting the quantum object at x_f is then proportional to the square modulus of the Green function. For bound systems, the probability is nonvanishing only when the energy E corresponds to an allowed energy level.

In this way, the conceptual structure of Feynman’s formulation is entirely preserved, with two main modifications:

• The action R is replaced by the abbreviated action S;
• All paths connecting x_i and x_f, regardless of travel time, are considered.

The “disappearance of time” allows the idea (of educational value in itself) to be introduced that when energy is fixed, time must be completely unknown. This also enables an interesting connection with the time–energy uncertainty to be constructed, which is explored in more detail in Section 5.

The time-independent path integral can be considered a partially different educational reconstruction of quantum mechanics, which in addition to the works of Feynman, also draws from the research on the semiclassical path integral, especially by M.C. Gutzwiller [29] and L.S. Schulman [30]. Within this new perspective, it was possible for researchers to address in a more educationally constructive way several problems of interest in introductory quantum mechanics, such as confined systems with discrete energy levels, as well as the important case of tunnelling [11] with the same elementary mathematical tools used in Feynman’s QED [2]. Furthermore, educational advantages in using the time-independent sum over paths approach were found also in the case of open systems: for example, the issue sometimes brought up by students in the treatment of the two slit interference [8], of why it is it that paths of different length are allowed to interfere, since the photon goes through them in different times, is answered right from the beginning in this picture. Paths are independent of time, as they represent the corpuscular equivalent of a plane wave, i.e., a quantum object emitted with infinite uncertainty on emission time, so that paths of different length are actually not distinguishable and the sum of their amplitudes must be considered. The focus, right on the beginning, on the importance of path indistinguishability for producing interference (see Section 7) allows students to construct a more consistent idea of wave particle duality. In the following Section, we provide some recent results deriving from the adoption of a time-independent sum over paths approach.

4. Treatment of Stationary Problems

4.1. Infinite Square Well

The ‘’particle in a box’’ problem is the paradigmatic example for the treatment of bound systems in the sum over paths approach. A quantum object is confined in a square potential well with infinite depth and width L. For a fixed energy E, the particle can reach the detector x_f starting from a source at x_i through one of four families of paths, depicted in Figure 1. The phasor corresponding to each path is computed by the usual rules, with each reflection contributing a π phase loss, and the result is that amplitudes associated with all possible paths interfere constructively when the value of energy corresponds to an allowed energy level (Figure 2; the computed amplitude sum is in the right window) and destructively otherwise.

Analytically, the allowed energy levels (the poles of the energy dependent Green function) can be determined uniquely from the condition that two paths differing for a full back and forth round trip in the well are in phase. Thus, the full Green function can be determined and the stationary wave functions (eigenfunctions) can be also evaluated. The set of GeoGebra tutorials [31], created to support student understanding of quantum concepts within the sum over paths approach [16,17], have been tested with both secondary school students and pre-service and in-service teachers in several courses. Since the simulations are available for free on the GeoGebra website [31], they have also occasionally been modified by teachers to produce simulations of different physical situations or more suitable to the needs [32], or considered in other research [33].

In a similar fashion to the square well potential, other confined systems of interest (e.g., the harmonic oscillator, the finite square well [12], the particle confined on a circumference [14]) can be discussed with students in a conceptually consistent way, using the same simple mathematical tools (vector amplitudes) used in the treatment of open systems, such as the two slit interference.

Despite the conceptual simplicity of the treatment of one-dimensional systems, it has to be remembered that there have been technical difficulties in extending path integral techniques to radial coordinates beyond the simplest cases [30,34], and progress in obtaining path integral solutions to three dimensional problems in radial coordinates, including the hydrogen atom, has been slow [35,36]. Correspondingly, a sum over paths approach may not be the most suitable way to deal with these problems, which typically appear at advanced undergraduate and graduate levels.

4.2. Tunneling from a Square Barrier

In the context of the time-independent sum over paths approach, the problem of tunneling from a square barrier can also be solved analytically, and the main conceptual elements of the solution can be shown to students through a simulation (Figure 3). Transmission and reflection coefficients at the barrier borders are computed by the simulation through the equivalent for massive particles of Fresnel coefficients [12], but like in the case of the square well potential, important features of the solution, such as the formation of energy-dependent resonances in the transmitted amplitude, are due to constructive interference between paths, which undergo multiple reflections within the barrier.

In the typical structure of a teaching-learning sequence based on the sum over paths approach (e.g., Ref. [18]), the topic of tunneling is treated before bound systems and energy quantization, with the case of the resonant scattering of a photon between two semi-reflecting mirrors (Figure 4) playing the role of a transition case between open and bound systems.

5. Stationary Sum over Paths Approach and the Time-Energy Uncertainty Relationship

In the fixed-energy sum over paths approach, the uncertainty in the travel time of the quantum object from source to detector is considered infinite. Thus, for bound systems, infinitely many paths, going through an arbitrary number of back and forth roundabouts within the confining potential, need to be considered in order to obtain the allowed energy levels. On the other hand, it was shown recently [14] that, if the assumption of infinite uncertainty in travel time is weakened, considering only a finite, though large, uncertainty in time, it is possible to derive from the time-independent sum over paths approach, through geometrical considerations and simple algebra, a time-energy indeterminacy relationship of the form $\Delta E\cdot \Delta t\approx \hslash$, where ħ is the reduced Planck’s constant. In fact, if only a finite number of paths are considered, namely those whose travel times differ by less than the time uncertainty, the resulting approximate Green function will not have sharp divergences, but widened peaks, whose width in energy can be described such relationship.

The derivation is not valid only for the infinite square well shown in Figure 5, but for any confined system (in Ref. [14] the particle on a ring is treated). The time indeterminacy, Δt, thus derived can be given different interpretations [14]: (a) upper limit on the time the quantum object can have spent in the confined system before measurement, which is the most literal interpretation within the sum over paths approach: (b) coherence time for paths of different length, i.e., timescale over which they can still considered indistinguishable; and (c) lifetime of the quantum state, due to external, unspecified reasons, which make it an unstable state. Among the interpretations proposed by the authors, the third one seems the most promising in education, given the relevance of the lifetime–linewidth relationship in the elementary treatment of the time-energy uncertainty principle. Thus, it may be worth explaining the terms of such interpretation in some more detail. The lifetime–linewidth relationship, originally derived by G. Gamow in the context of alpha decay [37] but valid in a wide range of different contexts, applies to quasi-bound states, which are resonances in the continuous spectrum of object temporarily confined by a potential barrier, which nonetheless possess a positive total energy. Gamow’s derivation made use of a semiclassical picture, in which the quantum object, bounced within the walls of the potential an indeterminate number of times, each time with a finite probability of escaping the well. In this picture, the time indeterminacy Δt is the expected value of the time the quantum object remains in the confined state. Thus, the derivation proposed in Ref. [14] can be seen as a simplified (at a level accessible also to advanced high school students) treatment of Gamow’s analysis, in which rather than assigning a finite probability to the escape of the quantum object from the potential at each bounce, a hard limit is imposed on the dwell time. Note that a rigorous analysis of Alpha decay in terms of the semiclassical path integral (which involves assigning progressively decreasing amplitudes to paths) was given in Ref. [38], where its results are compared to those of Gamow’s original treatment.

6. Connections with Spin: From the Hong-Ou-Mandel Experiment to Quantum Computing

The Hong-Ou-Mandel (HOM) experiment [39] demonstrates interference between indistinguishable processes, and its generalized version [15] using electrons can be used to explain the properties of bosons and fermions. The general setup of the HOM experiment is depicted in Figure 6. The experiment is known in its original version performed with photons, as it demonstrates the possibility of two photon interference due to perfect time overlap and consequent indistinguishability. A less known version of the experiment with electrons was also performed [40].

Discussing this experiment with students involves first of all a change of perspective, from performing the sum over all possible paths, to performing a sum over all possible processes or histories for a given setup. The crucial step in such direction is to explain that, for processes involving more than one quantum object, amplitudes of histories can be derived from the amplitudes of single particles paths through a multiplicative operation (mirroring the multiplication between complex numbers): the result, in the language of Feynman’s QED, is an arrow whose length is the product of the lengths of the single-particle arrows, and whose phase is the sum of their phases [2]. At this point, the three possible distinct outcomes of the experiment (two particles found at D1, two particles at D2, or one particle in each, referring to Figure 6) can each be represented by two diagrams differing by the exchange of identical particles (see Figure 3 in Ref. [15] and the text there). Next, the outcomes of the real experiment are considered. With perfect time coherence, and so perfect indistinguishability of the two quantum objects, photons are always detected either both at D1, or both at D2. On the other hand, in the same conditions, electrons are always found at different detectors. Considering also the phase shift properties of beam splitters, the only way to solve such a puzzle is to postulate different exchange rules for the two types of quantum objects: for indistinguishable fermions, a change of sign for the global amplitude is involved for diagrams, which only differ by the exchange of two particles; while for indistinguishable bosons, no such change of sign is involved. The possibility to introduce, starting from the phenomenology of outcomes of modern experiments, a key element of the spin-statistics connection, namely the different rules related to indistinguishability for bosons and fermions, on the one hand reinforces the centrality of the concept of indistinguishability in quantum mechanics (which is a key idea of the HOM experiment), and on the other hand provides a first connection of the sum over paths approach with topics related to spin.

Furthermore, there is currently ongoing research on the integration of sum over paths with two state approaches [41], especially in the context of teaching introductory elements of quantum computation and communication. In fact, in this context, in order to show students applications of quantum computing that are not entirely trivial (e.g., the Deutsch and Grover algorithms), it is necessary to code more than just a single qubit (often at least two). The educational issue in choosing, as the physical realization of such qubits, different quantum objects (e.g., two or more electrons) is that by doing so the quantum gates become very difficult to interpret as physical systems within the reach of secondary school students. The consequence is that at that point the treatment of quantum algorithms becomes completely symbolic and algebraic, disconnected by any concrete physical representation. One alternative that is being explored [42], which allows two qubit quantum logical circuits using simple optical devices to be constructed, is to use photons and code one qubit as the polarization state, the second qubit as the choice between possible paths (typically at a beam splitter). Of course, for the second qubit, all the rules typically introduced in sum over paths concerning, for example, phase displacements at reflection and transmission are valid. This approach can be considered a prosecution of the one pioneered by Daniel F. Styer in his book The Strange World of Quantum Mechanics [27].

7. Path Indistinguishability and the Zhou–Wang–Mandel Experiment

The HOM experiment is only one example of the fecundity of the concept of path distinguishability/indistinguishability in education [20]. Another experimental result that has proven highly useful in education is the Zhou–Wang–Mandel (ZWM) experiment [43], which highlights in a peculiarly sharp way the loss of interference resulting from rendering quantum processes experimentally distinguishable. The ZWM experiment is conceptually a concrete realization of a two slit interference experiment with which-way detectors; but which way information is obtained not by physical detection of the photon passing through a slit, but by detection of a secondary photon that is emitted by a non-linear crystal at the same time as the primary one. Discussion of this experiment is highly instructive for students, as they are introduced to a case in which interference can be made to appear or disappear, without physically touching the quantum object, which is (supposedly) only responsible for the appearance of interference fringes, i.e., the ‘‘signal’’ photon arriving at the primary detector. While the initial reaction of many students is to declare that the experiment works by way of magic, a more thorough discussion leads to a deeper understanding of the modern meaning of wave particle duality in quantum mechanics as a relationship of complementarity between interference fringe visibility and path distinguishability [44].

8. Educational Outcomes

Several tests of the educational effectiveness of the sum over paths approach were performed in recent years. In Ref. [18], based on an experimentation in a class of final year secondary school students, the authors found that Feynman’s approach could lead students to build consistent, detailed, and integrated mental models of wave particle duality, as tested within Knowledge Integration theory [45]. Furthermore, the approach could also help overcome some other integration issues in teaching–learning quantum mechanics, such as students building completely different mental models for the photon and the electron. In this study, specific strategies are adopted in order to reduce the possibility that students interpret paths as classical trajectories. They emphasized that the sum over possible paths has to be considered a representation of the mathematical model of quantum theory, and not of the actual physical reality. Moreover, students were guided through a detailed analysis, in the context of the two slit and Mach Zehnder settings, of the inconsistency of considering paths as mutually exclusive classical trajectories (e.g., that the quantum object passed through one or the other slit, or one or the other arm of the interferometer). In the teaching experiment of Ref. [18], the issue of students appearing to reason as if paths were alternative classical trajectories was limited to one student. The incidence of other deterministic and hybrid conceptions was also reportedly low or non-existent. Advantages in terms of consistence between students’ mental models of the photon and electron were also reported in Ref. [19], which discusses an experimentation in a class of 16–17-year-old students. In Ref. [46], which is based on an experimentation with four classes of 16–17-year-old secondary school students, the authors report advantages in helping students form consistent and integrated models of light, by connecting in a unified perspective phenomena related to ray optics, wave optics, and the quantum theory of light. These results, which echo the findings reported in Ref. [47], appear especially important in view of the extremely fragmented character of the topic of light within the secondary school curriculum in many countries. Convincing results were obtained in the context of teacher education in several studies [16,17] and it was highlighted that the deep conceptual understanding provided by the sum over paths approach in in-service courses can render a teacher confident enough to undertake the enterprise of treating quantum physics in the classroom, even in contexts (such as the Italian system) in which it is possible, and quite frequent, that secondary school physics teachers have no formal instruction on the topic at all (for example, having a degree in mathematics or engineering).

9. Discussion and Recapitulation of Educational Perspectives

Based on the results of research literature, and several years of direct experience with using the sum over paths approach in teacher education, let us summarize the main educational advantages offered by in the following way:

• On the mathematical level, the sum over paths approach allows quantum phenomena to be discussed using quite a simple formal language. At its heart, such a possibility is due to the fact that, rather than finding solutions to the Schrödinger equation, Feynman’s method constructs the Green function for the same equation, representing it as a sum of complex amplitudes computed over all possible paths. In educational practice, complex amplitudes associated with paths can be represented and added up as vectors or “little arrows”, a strategy directly derived from the one used by Feynman himself, which greatly reduces the stress on student’s cognitive resources while learning the basics of quantum theory. The recent advances in the design of teaching–learning sequences based on sum over paths, mostly due to a significant clarification of the subject matter and the adoption of the time-independent version of the approach, allow the same simple mathematical machinery essentially to be treated with all problems, which are typically solved with the one-dimensional time-independent Schrodinger equation. Thus, sum over paths can be considered an attractive option not only for secondary education, but also for the introduction of elements of quantum physics to non-physicists.
• On the conceptual level, sum over paths has the unique peculiarity of offering students a clear and unambiguous representation of one of the most profound quantum mysteries, namely wave particle duality. There are two basic ingredients that contribute to forming such conceptual understanding. The first one consists of the distinction between classical and quantum ways of computing probabilities, which is at the heart of the approach, and allows what is always “corpuscular” in quantum objects’ behaviour (they are always revealed as discrete entities at detectors) and what may, or may not, be “wave-like” (the statistics of their detection events) to be clearly distinguished. The second ingredient is the focus on path distinguishability/indistinguishability, which allows a modern understanding of duality to be constructed in which an either/or (particle or wave) idea of the quantum object is replaced by a continuum of wave-like and particle-like behaviours, regulated by the respective weight of path distinguishability and fringe visibility. Furthermore, while going through this educational path, students generalize the concept of ‘sum over paths’ to ‘sum over histories’, and by doing so they construct a language capable to discuss modern experiments and technologies based on quantum optics, and in principle, to understand the conceptual meaning of simpler Feynman diagrams [15]. Finally, modern educational reconstructions based on sum over paths can offer deep insight into the origin of energy quantization for bound systems, and help clarify the meaning of the time-energy uncertainty principle.
• At the level of knowledge integration, the sum over paths formulation can make the classical limit (correspondence principle) completely transparent [8], and provide a unifying perspective on the nature of light, connecting ray optics, wave optics, and the quantum behaviour of photons. The approach allows students to build consistent mental models for photons and electrons, in which differences (the dispersion relation, the exchange rule) are highlighted that build on a common basic model of the quantum object. Rather than presenting quantum theory as a set of disconnected formulas for different situations, as it appears in many secondary school textbooks, in sum over paths the subject matter is presented as an organic theory, with the additional advantage of offering the possibility to teachers to develop their own exercises and problems, applying the computational rules to new situations.

10. Conclusions

In this overview of research on the sum over paths approach for teaching introductory quantum physics, we have argued that such an approach, whose history started in the late 1980s, has reached full maturity in the second decade of the XXI century. Research has addressed most of the critical points enumerated in Section 1, and while there may not be a consensus as to whether they have been fully resolved (especially concerning the first of the three issues, on which data, while encouraging, is rather scarce), progress has been significant, and can be considered decisive especially concerning the treatment of bound systems. Furthermore, new experimentations have reinforced evidence on the educational advantages of sum over paths, demonstrating that the approach can help researchers and educators improve educational outcomes in terms of conceptual understanding and knowledge integration, and be an invaluable aid in the introduction of quantum technologies, an issue which is increasingly felt as central and urgent.