An Approach to Quantum Physics Teaching through Analog Experiments

Abstract

With quantum physics being a particularly difficult subject to teach because of its contextual distance from everyday life, the need for multiperspective teaching material arises. Quantum physics education aims at exploring these methods but often lacks physical models and haptic components. In this paper, we provide two analog models and corresponding teaching concepts that present analogies to quantum phenomena for implementation in secondary school and university classrooms: While the first model focuses on the polarization of single photons and the deduction of reasoning tools for elementary comprehension of quantum theory, the second model investigates analog Hardy experiments as an alternative to Bell’s theorem. We show how working with physical models to compare classical and quantum perspectives has proven helpful for novice learners to grasp the abstract nature of quantum experiments and discuss our findings as an addition to existing quantum physics teaching concepts.

1. Introduction

Due to its inherently unintuitive nature, quantum theory has been met with disbelief and partly even resentment since its conception in the early twentieth century. Accordingly, most physicists have been struggling with overcoming the established concepts of the deterministic and local worldview—seasoned experts maybe even more so than novice learners. One of the most known examples is the classic Einstein–Podolsky–Rosen (EPR) paradox [1]. However, even for younger minds, it is often challenging to accept the results provided by modern quantum experiments and the implications that arise thereof [2], even though modern views on quantum physics that emphasize its comprehensibility and help with the interpretation are now widespread and have found their way into standard textbooks [3,4,5]. For that reason, educators have since been trying to enrich their teaching with thought experiments, mental models, and analogies [6] to allow their audience to develop an understanding from multiple perspectives. Luckily, with the growing importance of quantum physics for modern society and industry [7], research in the field of quantum physics education has progressed to explore a variety of options bringing advanced topics and methods into secondary school and university classrooms: quantum computing [8], quantum randomness [9,10], quantum sensing, and new concepts applying quantum technologies to a changing educational framework [11,12,13,14]. Recent empirical studies play an equally important role in evaluating the overall progress of the field [7,15,16]. In addition, the growing field of edutainment, combining modern multimedia technologies such as augmented and virtual reality with learning experiences, has been explored for quantum education [17,18,19].

Education psychology attributes validity to all of these approaches by emphasizing the importance of multisensory learning materials: cognitive-affective theory of learning with media (CATLM) suggests consideration of not just auditory and visual sources but tactile and haptic elements as well [20,21,22,23], and object-based learning (OBL) claims “that haptic interaction with real tangible objects can serve important roles in the learning process and encourages students to link these experiences to abstract ideas and concepts” [20]—an idea that extends through education ever since physical models, exemplary specimens, and other display items decorated walls, shelves, and school supply rooms waiting for their deployment in a lesson period.

On the same level, especially considering physics education, the use of analogies becomes an undeniably important factor since most physics teaching is based on the simplification and idealization of complex processes. The use of models and analogies appears inevitable, bridging the gap between empirical and theoretical entities through “familiarity” [20]. In that way, quantum physics teaching often lacks the ability to build on familiarity just because the subject matter does not allow comparison to the macroscopic world. Nevertheless, we are aiming to fill the gap of missing analog models and add to the already existing representations of quantum phenomena.

In what follows, we present two applications of analog experiments of quantum phenomena for teaching scenarios. The first application addresses the polarization of single photons in Section 2 and showcases a model based on near-field communication (NFC) technology, Arduino microcontrollers, and 3-dimensional (3D) printing. The corresponding teaching concept focuses on a multiperspective approach, comparing classical and quantum explanations of polarization through Section 2.1 while following the study of Müller and Küblbeck [24], who laid most accepted foundations for modern quantum physics teaching. All technical aspects of the polarization analogy modules are mapped out in Section 2.2 before their implementation into quantum physics teaching is featured in Section 2.3. The second application (Section 3) employs a different analog architecture based on mechanical rather than electronic components: combining clear formalism of quantum mechanics with a local representation, we propose a model to disprove the local hidden variable theory, following the argumentation of Lucien Hardy [25]. Section 3.1. summarizes these considerations about nonlocality regarding entangled spin-states of electrons in a Stern–Gerlach experiment [6]. while Section 3.2. motivates its usage in a (higher) education context. Conclusions are drawn in Section 4.

2. Analog Experiment: Polarization Modules

2.1. Comparison of Quantum and Classical Polarization from a Teaching Perspective

Talking about polarization in a secondary school classroom is usually conducted within a unit about mechanical oscillations and waves and again at an advanced stage when talking about the properties of light [26]. Especially the latter leads to a dilemma, which is conventionally used as a stepping stone into the field of modern physics and quantum mechanics: What is light? At that point, students have seen light behave as a ray, a wave, or a particle, depending on the examined experiment and context. They learn that light may exhibit all of these characteristics, but the individual photon is, in fact, something entirely new: an object called a quantum object. The common narrative then explains the quantum object to be governed by a set of peculiar, unintuitive rules, fully unfathomable to the human mind. However, through experimentation, a set of “reasoning tools” [27] can be found, which then help create a conceptual approach to quantum physics. The following Sections compare quantum and classical explanations of polarization and show how the analog model mediates between both perspectives. The quantum aspects are only discussed on the level of clearly defined photon number states, i.e., we do not take states with undefined photon numbers into account. While there are reasons, even in a school context, to discuss the existence of quantum states of light, in which the photon number is not well defined [28], this is not required for the educational purpose of this work.

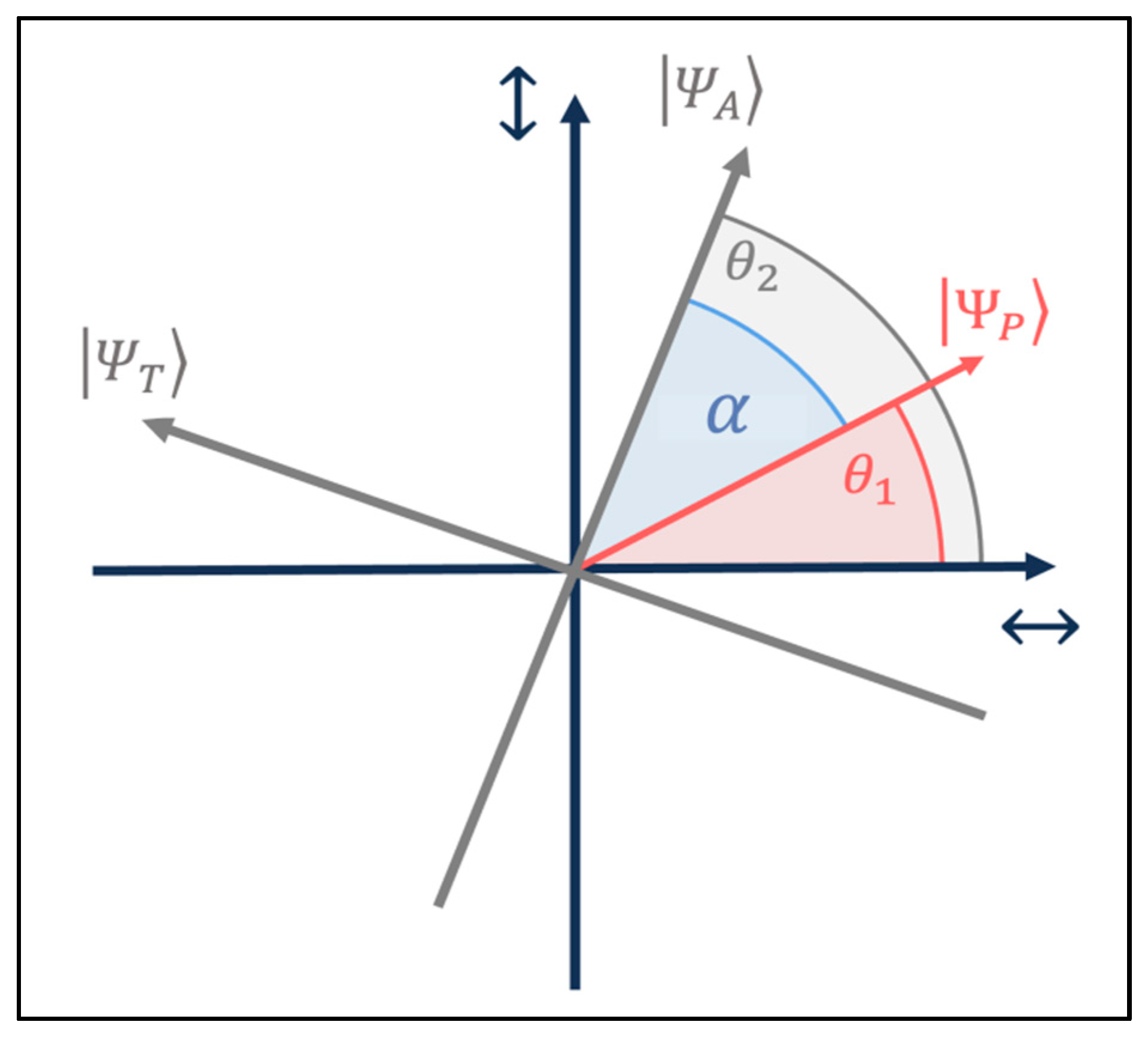
2.1.1. Classical Perspective

Most curricula introduce light as a wave by referring to mechanical transverse waves. As such, it shares its most common features, such as diffraction behaviors and the ability to create interference and be polarized. A linear polarizer filters out any part of the wave that does not match the polarization axis of the filter, thus diminishing light intensity. The remainder is transmitted and oriented along that axis—hence polarized. What happens when this transmitted, polarized portion meets a second polarizer is expressed by Malus’ law of the light intensity [3],

$$I=I_0·{\cos }^2\left(\alpha \right).$$

(1)

Light as an electromagnetic wave is thought to pass a linear polarizer partially: Its oscillating vector (result of electric and magnetic field vector, respectively) is split into components vertical and horizontal to the polarization axis of the filter—one part being transmitted and the other being absorbed. The angle α between the first and second polarization affects how much of the initial intensity, $I_0,$ will be measured behind the second filter.

The cosine dependency of Malus’ law (1) can be tested qualitatively and even quantitatively in most classroom settings. A light meter is sufficient.

2.1.2. Quantum Perspective

One conclusion that is carried over from a physics curriculum’s explanation of the photoelectric effect and the black body radiation problem to this polarization case is the quantization of photon energy. Thinking of light as discrete packages of energy called photons leads to the idea that light cannot pass a polarizer just partially. The individual photon may only be transmitted entirely or not at all [29]. A detector behind a polarizing filter will—within a certain time interval—either detect the photon or not. It is impossible to make a statement about the behavior of a single photon until we measure its presence (or absence) at the output of the experiment. In other words: quantum objects are inherently governed by randomness. Students may arrive at this profound conclusion with the help of a teacher guiding their train of thought or possibly even on their own. Either way, abandoning classical determinism is key to engaging with quantum phenomena.

Nevertheless, experiments on quantum systems show that statistical predictions about results are possible. For polarization problems, this means there is a certain probability for the photon to be transmitted, to be in a transmission state, $|{\Psi }_T\rangle$, and pass the filter or to be absorbed and be in an absorption state, $|{\Psi }_A\rangle ,$ when it interacts with the filter. To calculate these probabilities (see Figure 1), we define the photon’s polarization state before the filter,

$$|{\Psi }_P\rangle =\cos {\theta }_1|\leftrightarrow \rangle +\sin {\theta }_1|\updownarrow \rangle ,$$

(2)

as a combination of vertical, $|\updownarrow \rangle ,$ and horizontal, $|\leftrightarrow \rangle ,$ vectors in a reference basis. ${\theta }_1$ is the angle the polarization state is rotated from $|\leftrightarrow \rangle$. Let us further define a measurement basis representing the second polarizer. This second polarizer will either transmit or absorb—in other words, measure—the photon. It is rotated by an angle ${\theta }_2$ to the reference basis and holds the transmission and absorption states, $|{\Psi }_T\rangle$ and $|{\Psi }_A\rangle$, which we define in relation to the reference vectors:

$$|{\Psi }_T\rangle =-\sin {\theta }_2|\leftrightarrow \rangle +\cos {\theta }_2|\updownarrow \rangle ,$$

(3)

$$|{\Psi }_A\rangle =\cos {\theta }_2|\leftrightarrow \rangle +\sin {\theta }_2|\updownarrow \rangle .$$

(4)

One is now ready to calculate the probabilities, $P_T$ and $P_A$, respectively, of transmitting or absorbing the photon at the second filter by projecting the polarization state onto the measurement basis, which leads to:

$$P_T={|\langle {\Psi }_T|{\Psi }_P\rangle |}^2={\cos }^2\left({\theta }_1-{\theta }_2\right),$$

(5)

$$P_A={|\langle {\Psi }_A|{\Psi }_P\rangle |}^2={\sin }^2\left({\theta }_1-{\theta }_2\right).$$

(6)

As it turns out, the same cosine dependency of the angle $\alpha =\left({\theta }_1-{\theta }_2\right)$ is found between the two polarizers, as Malus’ law (1) states for classical light intensity: what defines the transmission probability of the single photon in a quantum state of a well-defined photon number manifests itself as statistical evidence on a macroscopic level.

Using Dirac’s bra–ket notation, <…>, simplifies the quantum mechanical calculation and could, for that reason, be used even in secondary school classrooms. However, in the next Section we show that the understanding been derived from this calculation may also be reached experimentally using the analog model.

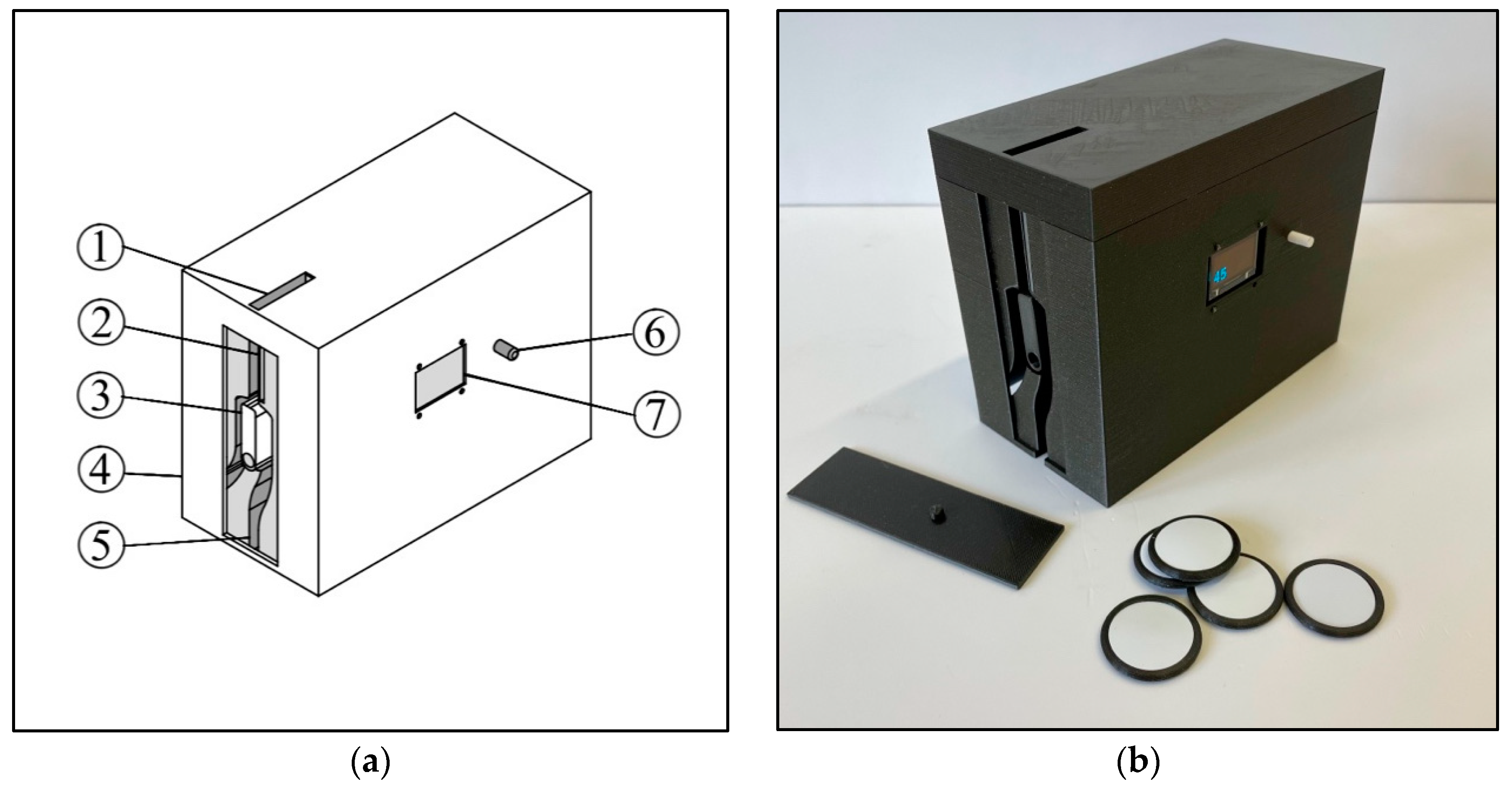
2.2. Polarization Analogy Module

After considering a number of different methods to implement the extraordinary phenomena of quantum physics into a physical model, a hybrid approach of mechanical and electronic elements was settled on: The current iteration of the project takes the shape of a black box that reads, writes, and redirects incoming NFC chips through utilizing servo motors and an Arduino microcontroller. NFC chips are able to store and carry information passively without the need for additional battery power. They are activated through a radio frequency identification (RFID) module controlled by the Arduino. An Arduino can connect and control several different input and output components, such as potentiometers, sensors, motors, displays, and buttons, at the same time. The combination of all these electronic parts with physical elements such as ducts, switches, and flaps, all within a suitable enclosure, guide the NFC chips within a physical model representing quantum measurements and results. We find this hybrid approach to be the most flexible and best-suited platform for creating analogies for a variety of real-world experiments on quantum systems. Figure 2 shows images of the current prototyping state of the model.

Functionally, this model resembles the “behavior” of single photons at a polarizing filter. Though one cannot speak of what the photon actually does, one can conduct experiments and take measurements that lead to definite results and tangible interpretations. Specifically, one knows that the photon as a quantum object will either be fully transmitted or fully absorbed by the filter. Furthermore, we know that the probability of either of those events is dependent on the polarization state of the photon in relation to the polarization axis of the filter. These results are replicated by the model relating to the following analogy:

Single photons passing a polarizer are represented by individual NFC chips passing through the black box in the following, called the polarization module (Figure 2). Similar to photons, these chips will either be transmitted (leaving through the bottom exit slit) or absorbed (leaving through the back exit slit). Additionally, they are given a polarization state, corresponding to the polarization axis of the filter, that is written onto the chip and saved as an integer value. This value is displayed at the front of the module and can be set between 0 degrees and 90 degrees by turning the control knob. Adjusting this value is equivalent to rotating the orientation of a physical polarizer when light is passed through. Which path the chips take within the polarization module is determined by the Arduino microcontroller. First, it reads the polarization state of an incoming chip and compares this value with the setting on the display, i.e., the orientation of the polarization axis of the filter. Second, it calculates the difference between the two angles and the resulting transmission and absorption probability, respectively. Third, it uses a pseudorandom number with respect to that probability to choose the path in which the chip will be redirected.

Polarization phenomena may not be the prime example to emphasize the fundamental differences between classical and quantum physics (that may be the double slit experiment); however, it may serve as yet another case in which to derive and discuss these differences. As shown in the following, for the early stages, this can be done even without a deep understanding of the concept of interference (as is required for the double slit).

2.3. Polarization Analogy and Reasoning Tools

Comparing the classical and quantum perspectives of the same phenomena allow learners to identify key differences between the classical and the modern worldview. They are enabled to generalize their findings, define a set of rules—or rather reasoning tools—and make predictions about the outcome of experiments. So far, it has been explained what this comparison yields theoretically. The following describes what this multiple perspective approach, supported by physical analog models, looks like when practiced with a group of students entirely new to the field of quantum physics.

2.3.1. Conceptualization of a Students’ Laboratory

The polarization analogy modules (Section 2.2) have been designed as a platform to be introduced in physics classrooms and student labs in a variety of different use cases. Their hardware, software, and lesson integration can be altered in any way to fit different preconditions, learner types, time frames, and classroom layouts. Even their contextual setting as “polarization filters” might, at some point, be changed to suit another narrative. Therefore, the scenario presented here, which describes a first learning setup, may be understood as a promising yet preliminary result. The concept at hand was developed with a certain one-size-fits-all mentality in mind, with the purpose of accommodating student groups at different learning stages as follows:

A visiting group of students at our laboratory is separated into small peer groups of two to three learners (11 students in total). Depending on their knowledge prior to the lesson, they receive a short theoretical introduction (in part, a revision of wave optics) to particle–wave duality of light, leading up to the question: What is a quantum object, and how does it behave? Afterward, the main goal of their 2-h-visit is to answer that question and to find out how photons behave as quantum objects. The peer groups are then asked to work at four stations simultaneously, switch after a certain amount of time, and discuss and compare their findings with the rest of the class at the end of the lesson. Three of the four stations are set up with a number of polarization analogy modules, while the fourth station allows the learners to experiment with actual polarizers and lasers on an optical bench. Throughout the entire lesson, students are guided by supervisors.

Thematically, the first two stations form a unit regarding the statistical behavior of quantum objects. Having arrays of two to three analog modules (representing two to three polarizers in a row) available at each table, students are tasked to drop NFC chips (photons) into their models and make predictions about each individual outcome. Station 1 consists of two of the modules introduced in Section 2.2. The first module prepares the state of the photon, writing a value onto the chips. The second module then measures the state of the photon by reading the value off of the chip. It is then to be determined what effect the angle $\alpha$ between the two polarization axes has (especially considering special case angles of 0 and 90 degrees). After adding a third module to the array (station 2), the experiment can be altered to check if the same findings remain true when a third polarization axis is added to the system. Meanwhile, the students take notes of the results, list occurrences of each possibility, and calculate percentages of transmission events with respect to the angle between two polarizers. They draw conclusions and make generalizations about what would affect the “behavior” of single photons and about how their choice of polarization angles would influence those results. Finally—though not as abstract and generalized, but in conversation with supervisors and peers—the learners are then aiming to summarize what Küblbeck and Müller called “Wesenszüge” [24] and Müller and Mishina translated as “reasoning tools” [27]: a set of rules allowing to axiomatically describe the essence of quantum physical phenomena.

• Rule 1—Statistical Behavior. Single events are not predictable; they are random. Only statistical predictions (for many repetitions) are possible in quantum physics.
• Rule 2—Unique Measurement Results. Even if quantum objects in a superposition state need not have a fixed value of the measured quantity, one always finds a unique result upon measurement.

Similarly, stations 3 and 4 are united by their subject matter. These stations are used to strengthen the understanding reached so far by linking the behavior of single photons to the statistical result observed with a classical light wave. At station 3, the findings of the first two stations are to be built upon by extending the array of polarizers by another pair, such that the students now examine the statistics of photons passing through four or five successive filters. Additionally, while the first and last filters are oriented 90 degrees apart from each other, the polarizers in between are to be adjusted to transmit as much light as possible. This task is then replicated at station four using classical light, actual polarizers, and an optical bench. The resulting intensity after the last polarizer is measured with a light meter and placed in relation to the original intensity of the laser. The ratio of these two intensities is then compared with the statistics observed in station 3. In addition, station 4 allows the students to test Malus’ law (1) qualitatively.

The study at hand only includes student tasks to find Rules 1 and 2 of the reasoning tools. However, the original set comprises four Rules. Let us list here the remaining two Rules for completeness:

• Rule 3—Ability to Interfere. Interference occurs if there are two or more “paths” leading to the same experimental result. Even if these alternatives are mutually exclusive in classical physics, none of them will be “realized” in a classical sense.
• Rule 4—Complementarity. Exemplary formulations are: “which path information and interference pattern are mutually exclusive” or “quantum objects cannot be prepared for position and momentum simultaneously”.

A reasonable discussion of interference should include interference patterns, which need some spatial resolution to be clearly observed. Naturally, such resolution cannot be implemented with the two-way output of the analog modules: the binary output information is not sufficient. However, the Arduino platform is highly flexible, and a multiple-output setup is possible. In the future, this will be used to extend the teaching concept with analog modules to complete the set of reasoning tools.

2.3.2. Results and Students’ Evaluation

As mentioned before, so far, we have been able to test this teaching concept with a group of secondary school students. The participating group arrived in our laboratory without a prior introduction to quantum physics. However, in preparation for their visit, they had been reviewing topics of wave optics, such as interference, polarization of light, and even particle–wave duality. Though the sample size is too small to extrapolate actual empirical evidence, we were able to register a significant increase in content knowledge, which can be described as follows.

Primarily, for internal review, the students were asked to participate not just in the testing of the analog polarization modules but in a contextual pre-test and post-test designed to evaluate their general understanding of the subject matter (see

Table 1. Comparison of pre-test and post-test results. A total of 110 comprehension items—10 items per person—was answered by 11 students before and after their lesson to track comprehension. Correct answers increased from 51% to 68%.

	Pre-Test		Post-Test
	Absolute	Percentage	Absolute	Percentage
Correct Answers	56/110	51%	75/110	68%
Incorrect Answers	54/110	49%	35/110	32%

). Before and after their laboratory visit, all of the 11 students answered a set of comprehension items, deciding whether they were true or false. The increase in understanding was expressed in the following items: “A photon at a polarization filter can be absorbed partially” (pre-test: 2 correct answers, post-test: 9); “The measurement of the state of a quantum object does not affect that state” (pre-test: 4 correct answers, post-test: 6); “Compared to classical experiments, the results of quantum experiments are governed by randomness” (pre-test: 8 correct answers, post-test: 11). Hence, in the second run after the lesson, the rate of correctly answered items was significantly higher. Surprisingly, one item did not follow that trend and triggered more incorrect answers in the second round: “Quantum phenomena can only be verified through thought experiments and analogies, not real experiments” (pre-test: 5 correct answers, post-test: 2). In the future, more attention to be paid to this result to avoid misconceptions from only focusing on analog experiments. One possible solution might lie in expanding this setup through an actual quantum experiment.

Overall, the students were able to gain a deeper understanding of how quantum objects “behave” while being introduced to concepts that will help shape an easier transition into learning about quantum physics. We were able to convey the gist of Section 2.1.2. in a student-centered approach, implementing different perspectives and experiments—rather untypical for quantum physics teaching.

3. A Hidden Parameter and Hardy’s Experiment

The nonlocal nature of quantum mechanics is hard to believe since it contradicts the experience we obtained in the classical world. This is, in particular, true for novice learners. When they first hear about entanglement, the concept of hidden parameters seems to be appealing. With the following second analog experiment, we address this point and introduce a possibility to disprove one (at first glance) attractive idea to avoid nonlocality. This is performed with a non-complicated choice of a (local) hidden parameter. It might seem to be quite critical to place so much emphasis on hidden parameters since this could lead to misunderstandings (which happens often enough in this context [30,31]). The use of hidden parameters could distract from the importance of nonlocality. This should be discussed in any teaching concept.

Analogous experiments that imitate entanglement already possess hidden parameters since they are based on classical objects. Certain material properties such as weight, shape, magnetism, or a digital number on a chip can be such hidden parameters. We see great potential for teaching with analog experiments to first illustrate and discuss relevant terms and concepts (such as reality and locality). Afterward, a quantum mechanical experiment can be thought through/played out with a hidden parameter until a contradiction to the real experiment occurs, and, thus, a conceptual change, showing that the first appealing concept of local hidden parameters is not a good choice, can be triggered. This, certainly does not clarify that nonlocality is the only required assumption for the correct prediction of quantum physics. However, it provides a relevant step in the discussion with learners.

Actually, Bell’s inequalities are used to disprove a hidden parameter in the experiment [32]. However, we present here an experiment proposed by Lucien Hardy [25]. This experiment was chosen as soon as its hidden parameter variant is not too complicate to be reproduced with an analog experiment, and the chain of reasoning to contradict quantum physics with a hidden parameter is quite straightforward and, therefore, more accessible for students.

3.1. Nonlocality for Two Particles without Inequalities for Almost All Entangled States

The experiment starts with a system of two entangled particles, where α and β are two real constants with ${\alpha }^2+{\beta }^2=1:$

$$|\Psi \rangle =\mathsf{\alpha }{|\uparrow \rangle }_1{|\uparrow \rangle }_2-\mathsf{\beta }{|\downarrow \rangle }_1{|\downarrow \rangle }_2.$$

(7)

The arrows in this notation represent orientations of electron spins in the z-direction, which can be measured in a Stern–Gerlach experiment. The two particles are sent to two different researchers (Alice and Bob) with different Stern–Gerlach experiments. Alice and Bob can measure the spin orientation in the z-direction and two other directions tilted by the angles ${\theta }_1$ and ${\theta }_2$, where $\tan \left({\theta }_1/2\right)=\sqrt{\mathsf{\alpha }/\mathsf{\beta }}$ and $\tan \left({\theta }_2/2\right)=-{\left(\alpha /\beta \right)}^{3/2}$. These tilted measurements can be expressed in new bases. There is the skewed ${\theta }_1$-basis with basis states “up”, $|\nearrow \rangle ,$ and “down”, $|\swarrow \rangle$, and the horizontal ${\theta }_2$-basis with the basis states “right”, $|\to \rangle ,$ and “left”, $|\leftarrow \rangle$. The initial state can now, according to quantum theory, be expressed for four different measurement cases.

Alice and Bob both decide to measure the spin in ${\theta }_1$-direction:

$$|\Psi \rangle =\mathrm{N}\left(AB{|\nearrow \rangle }_1{|\swarrow \rangle }_2+AB{|\swarrow \rangle }_1{|\nearrow \rangle }_2+B^2{|\swarrow \rangle }_1{|\swarrow \rangle }_2\right).$$

(8)

Alice measures the spin in ${\theta }_2$ direction and Bob in ${\theta }_1$-direction:

$$|\Psi \rangle =\mathrm{N}\left(\left(A-A^2{A}^{*}\right){|\to \rangle }_1{|\nearrow \rangle }_2+B{|\to \rangle }_1{|\swarrow \rangle }_2-A^{2}B{|\leftarrow \rangle }_1{|\nearrow \rangle }_2\right).$$

(9)

Alice measures the spin in ${\theta }_1$ direction and Bob in ${\theta }_2$-direction:

$$|\Psi \rangle =\mathrm{N}\left(\left(A-A^2{A}^{*}\right){|\nearrow \rangle }_1{|\to \rangle }_2+B{|\swarrow \rangle }_1{|\to \rangle }_2-A^{2}B{|\nearrow \rangle }_1{|\leftarrow \rangle }_2\right).$$

(10)

Alice and Bob both decide to measure the spin in ${\theta }_2$-direction:

$$\begin{gathered} |\Psi \rangle =\mathrm{N}\left(\left(1-{\left|A\right|}^4\right){|\to \rangle }_1{|\to \rangle }_2+A^2{A}^{*}B{|\leftarrow \rangle }_1{|\to \rangle }_2+A^2{A}^{*}B{|\to \rangle }_1{|\leftarrow \rangle }_2 \\ -A^2{B}^2{|\leftarrow \rangle }_1{|\leftarrow \rangle }_2\right). \end{gathered}$$

(11)

Here, $N=\frac{1-\left|\alpha \beta \right|}{\left|\alpha \right|-\left|\beta \right|},A=\frac{\sqrt{\alpha \beta }}{\sqrt{1-\left|\alpha \beta \right|}}\mathrm{and}B=\frac{\left|\alpha \right|-\left|\beta \right|}{\sqrt{1-\left|\alpha \beta \right|}}$ are prefactors.

Equation (11) clearly states that in some cases, Alice and Bob can both measure spin “left”, ${|\leftarrow \rangle }_2,$ in the horizontal, i.e., ${\theta }_2$-basis. If the measurement result is predetermined by a hidden parameter, then in such an experiment, the two particles must be prepared in such a way that if Alice and Bob measure in the ${\theta }_2$-basis, both get spin “left” as a result.

If just such a spin pair were underway, but Bob had chosen to measure in the oblique ${\theta }_1$-base, his result would also be predetermined according to Equation (9), as Bob must measure spin “up” in the ${\theta }_1$-base because there is no other possibility in which the predetermined result “left” for Alice is preserved. When Bob chooses the skewed ${\theta }_1$-basis so late that his measurement cannot affect Alice’s measurement according to the laws of realism and locality, then a hidden parameter λ, which is still unknown but is supposed to fully describe quantum mechanics, must account for the result of Equation (9). The same is true in case Bob remains in the ${\theta }_2$-basis and Alice chooses the skewed ${\theta }_1$-basis according to Equation (10). Here, the only possibility for Alice is to obtain the value “up” in the ${\theta }_1$-basis.

Finally, if both chose the Stern–Gerlach experiment in the ${\theta }_1$-direction, the two cases with a hidden parameter λ discussed above indicate that both Alice and Bob must measure spin “up” since no setup knows the orientation of the other. However, such a measurement result is forbidden according to quantum theory, cf. Equation (8). Here lies the contradiction, which can be checked experimentally.

3.2. Didactical Framework

Our experience shows that students can have difficulties even with this simplified chain of reasoning. In order to support this graphically and haptically, we offer an analog experiment according to the following structure. The hidden parameter is the magnetizability of balls, which pass through a box with two-way junctions (see Figure 3). Magnetizable balls are deflected, and the others are not. Two Stern–Gerlach experiments each can now be selected by Alice and Bob, each representing a measurement in the ${\theta }_1$ or ${\theta }_2$ direction. The setup can be built to reproduce all the cases discussed above for a ${|\leftarrow \rangle }_1{|\leftarrow \rangle }_2$ pair. Thus, the hidden parameter setup provides the theoretical result for a hidden parameter quantum physics, i.e., one possible local description of quantum physics.

The setup is designed in a way that an electron pair with the hidden parameter “magnetizable” will reproduce the measurement result spin “left” for Alice and Bob when they decide to use the horizontal ${\theta }_2$-orientated Stern–Gerlach experiment. The red handle is pointing to the right (thus choosing the θ₂-basis) and the ball takes, in both cases, the left path. Due to the magnet at the bifurcation, both balls will go the left path, resulting in a measurement spin left, $|\leftarrow \rangle$. If one chooses the right path, which stands for a Stern–Gerlach experiment in the ${\theta }_1$-orientation, the magnet on the right-hand side guarantees a measurement outcome of spin “up”, $|\nearrow \rangle$, in the ${\theta }_1$-direction, as is demanded in Equations (9) and (10). Without communication at the bifurcation points, Alice and Bob will both measure spin “up”, $|\nearrow \rangle ,$ when they chose the ${\theta }_1$-orientated Stern–Gerlach experiment, which is forbidden in quantum mechanics.

Thus, the case distinction can be set up and experimentally performed by learners themselves. Afterward, the real quantum mechanical experiments and their results have to be shown and discussed so that the intuitive notion does not take root. Nevertheless, we consider this procedure to be useful because it shows clearly enough that the intuitive ideas reach their limits in quantum mechanics, but that the theory and the formalism provide us with tools that can describe quantum mechanical experiments exactly.

4. Conclusions

Quantum physics is generally perceived as one of the most difficult fields of physics, not because of an especially complex mathematical formalism but because of the rules that inherently govern quantum phenomena—rules that go directly against the intuition of how natural world works. Certainly, it is known that meaning can be brought to this formalism even for novices. However, this meaning still has to be explained to learners. For that reason, educators who have since been trying to help their students wrap their heads around these concepts often resorted to a multitude of representations, analogies, and thought experiments. Despite real experimental data of empirical evidence, quantum theory often seems out of reach—even more so in physics classrooms. This is why we have presented an approach to add to the multitude of representations by providing analog experiments as a platform for quantum physics education—yet another perspective to make experimental results more graspable.

Analog polarization modules bear the potential to adapt to various teaching scenarios and have already proven helpful in reconstructing fundamental principles of thinking about quantum objects. While expanding the methods and ways in which the models can be used, prototypes were already tested under real-world conditions: we collected feedback from students who showed keen interest in working with the physical simulations mimicking quantum physics experiments and started to have fun learning about the subject.

On the same level, in a different context, the analog Hardy experiment [25] achieves similarly promising results: disproving the existence of a local hidden parameter by simple means of comparison. The contradiction of quantum theoretical formalism and forbidden measurement is inherent to this classical (thus, local) experiment and is, therefore, predestined to be used in analogy-driven teaching. This model, too, has already received great acceptance in a physics classroom, albeit within a higher education setting in a course for advanced learners.

The next step is to build upon the results gained from testing the analog models, expand the corresponding teaching concept with further modules, and implement the findings into physics teaching by offering the materials we developed open source.