The Barbero–Immirzi Parameter: An Enigmatic Parameter of Loop Quantum Gravity

Abstract

The Barbero–Immirzi parameter, (γ), is introduced in loop quantum gravity (LQG), whose physical significance is still the biggest open question because of its profound traits. In some cases, it is real valued, while it is complex valued in other cases. This parameter emerges in the process of denoting a Lorentz connection with a non-compact group SO(3,1) in the form of a complex connection with values in a compact group of rotations, either SO(3) or SU(2). Initially, it appeared in the Ashtekar variables. Fernando Barbero proposed its possibility for inclusion within formalism. Its present value is fixed by counting micro states in loop quantum gravity and matching with the semi-classical black hole entropy computed by Stephen Hawking. This parameter is used to count the size of the quantum of area in Planck units. Until the discovery of the spectrum of the area operator in LQG, its significance remained unknown. However, its complete physical significance is yet to be explored. In the present paper, an introduction to the Barbero–Immirzi parameter in LQG, a timeline of this research area, and various proposals regarding its physical significance are given.

1. Introduction

Loop quantum gravity (LQG) is one of the supposed candidates of the theory of quantum gravity. It can unify general relativity (GR) with quantum field theory (QFT). It is a non-perturbative and background independent approach to quantum gravity theory. LQG begins with GR; thereafter, it takes some conceptual basis from QFTs to deliver a quantum theory of gravity. LQG is a theory of constraints, in which various constraints such as Hamiltonian, diffeomorphism and Gauss constraints are converted into operators. In the canonical quantization approach of LQG (ADM formalism), 3 + 1 decomposition of spacetime is necessary to quantize gravity; however, the covariant approach (sum over geometry) follows a different strategy. Here, due to limited space, basics of LQG are not given. There are many classic texts [1,2,3,4,5,6,7,8,9,10] and papers [11,12,13,14,15,16,17,18,19,20,21,22,23] that explain LQG lucidly.

In 1986, Abhay Ashtekar [24] found new kind of variables (Ashtekar’s variable) in classical and quantum gravity. In Ashtekar’s formulations, the constraints are simplified by considering a complex valued form for the connection and tetrad variables, and these are known as Ashtekar’s variables [1,2,3,4,5].

While dealing with the reality condition of the formalism of Ashtekar’s variable, Barbero [25,26] firstly introduced a free parameter in the expression of Ashtekar’s variable and then in the expression of constraints. Thereafter, Immirzi [27,28] used various possibilities of this free parameter in the expression of LQG. This free parameter is nowadays known as the Barbero–Immirzi (BI) parameter, $\gamma$. Given $\gamma$ is complex or real, it provides a number of results in LQG. In some cases, the real valued BI parameter is required, while in the other cases, the complex valued BI parameter is necessary [1,2,3,4,5].

The physical significance of the area operator in LQG with the complex BI parameter becomes ambiguous. The LQG kinematics, i.e., kinematical Hilbert space can only be comprehended if the $\gamma$ is a real number. The $SU\left(2\right)$ spin network of LQG can only be created with the real value of the BI parameter [1,2,3,4,5].

With the complex value of the BI parameter ($\gamma =i$), the spatial connection can be seen as spacetime connection, since it transforms under diffeomorphism in the right way. There are also some cases that show that the complex valued BI parameter is also crucial in LQG formalism. For instance, the form of Hamiltonian constraints becomes simpler if $\gamma =i$ is taken [1,2,3,4,5].

In the next Section, various proposals regarding the BI parameter are briefly reviewed in which some proposals advocate the real valued BI parameter, while the other advocates the complex valued BI parameter.

1.1. Ashtekar’s Formalism

Before the discovery of Ashtekar’s variables, the Palatini action, i.e., the first-order formulation, was incomplete. However, Ashtekar formalism made it complete. In the Palatini action, the tetrad, $e_J^{\mu }$, and the spin connection, ${\omega }_{\mu }^{JK}$, are used as independent variables. In GR, the Palatini action is written as [1,2,3,4,5]

$$S_P=\int d^{4}xe{e}_J^{\mu }{e}_K^{\eta }{\Omega }_{\mu \eta }^{JK}\left[\omega \right],$$

(1)

where $e=\sqrt{-g}$, where g is the determinant of the 4-dimensional metric, $g_{\mu \nu }$, and ${\Omega }_{\mu \eta }^{JK}$ is the curvature. The capital Latin letters are the internal indices, the Greek and lower-case Latin letters denote the time (0) and space coordinates. The $\left[\omega \right]$ denotes the spin connection. Using the Palatini action, the Einstein field equation could be derived, but the form of equation of constraints within this formalism is mathematically complicated [1,2,3,4,5,12,15,17]. The generalization of the Palatini action is equivalent to the Ashtekar formalism, and it is achieved by the Holst action [29].

In the Ashtekar formalism, by converting tetrads into triads, i.e., three-dimensional hypersurfaces ${\Sigma }_t$, one gets $e_{\mu }^J\to e_c^j$, where $\mu \to c\in \{1,2,3\}$, $J\to j\in \{1,2,3\}$ and the spin connection is also transformed as ${\Gamma }_c^j={\omega }_{ckl}{\epsilon }^{klj}$, where ${\epsilon }^{klj}$ is the Levi-Civita tensor [1,2,3,4,5,12,15,17].

The Hamiltonian constraint is a complicated non-polynomial function in Palatini formulation; thus, canonical quantization is not easy within this formalism. In Palatini formulation, the variables of phase space are $(e_c^j,{\Gamma }_c^j)$, where $e_c^j$ is the intrinsic metric of the spacelike manifold $\Sigma$ and ${\Gamma }_c^j$ is a function of its extrinsic curvature [1,2,3,4,5,12,15,17].

In the Ashtekar’s formalism, complex valued connection ${\Gamma }_c^j$ replaces the real connection ${\omega }_{\mu }^{JK}$ with duality (either self (+1) or anti-self (−1)) [1,2,3,4,5,12,15,17],

$${\tilde{E}}_j^c\to \frac{1}{i}{\tilde{E}}_j^c,K_c^j\to A_c^j={\Gamma }_c^j-i{K}_c^j,$$

(2)

where ${\tilde{E}}_j^c$ is the scalar density or triad electric field, $A_c^j$ is the Ashtekar–Barbero connection or spatial connection, $K_c^j=k_{cd}{e}^{dj}$ with $k_{cd}$ the extrinsic curvature of $\Sigma$. Thus, there are two phase space variables, i.e., $A_c^j$ and ${\tilde{E}}_j^c$ [1,2,3,4,5,12,15,17].

Since the Ashtekar’s connection formulation variables, i.e., $A_c^j$ and ${\tilde{E}}_j^c$, follow rotation of $SU\left(2\right)$ symmetry with respect to the internal indices, the Ashtekar’s formalism plays the role of $SU\left(2\right)$ gauge theory, and this $SU\left(2\right)$ group is a subgroup of $SL(2,\mathbb{C})$ [1,2,3,4,5,12,15,17].

All three constraints are simplified in Ashtekar’s variables, and their expressions are [1,2,3,4,5,12,15,17]:

$${\mathcal{G}}_j=D_c{\tilde{E}}_j^c,$$

(3)

$${\mathcal{C}}_c={\tilde{E}}_j^d{F}_{cd}^j-A_c^j{\mathcal{G}}_j,$$

(4)

$$\mathcal{H}={\epsilon }_l^{jk}{\tilde{E}}_j^c{\tilde{E}}_k^d{F}_{cd}^l.$$

(5)

Here, $D_c$ is the covariant derivative.

Equations (3), (4), and (5) are Gauss, diffeomorphism, and Hamiltonian constraints, respectively. In Ashtekar’s formalism, the Einstein–Hilbert–Ashtekar (EHA) Hamiltonian of GR reads [1,2,3,4,5,12,15,17]:

$${\mathcal{H}}_{\mathrm{EHA}}=N^c{\mathcal{C}}_c+N\mathcal{H}+T^j{\mathcal{G}}_j=0$$

(6)

where ${\mathcal{C}}_c,\mathcal{H},{\mathcal{G}}_j,N^c$, and N are the vector constraint, the scalar constraint, the Gauss constraints, the shift, and the lapse, respectively. The $T^j$ is a Lie algebra valued function over spatial surface [1,2,3,4,5,12,15,17].

The unit imaginary, i.e., $i=\sqrt{-1}$, which appears in Equation (2), makes the formalism complex valued. Therefore, some restrictions in terms of reality conditional on the possible solutions of the theory must be applied to achieve tangible physical results relevant to a metric valued in $\mathbb{R}$ instead of in $\mathbb{C}$ [1,2,3,4,5,12,15,17].

For example, if $\dot{Z}$ is used to represent the time derivative of Z, then the reality condition and constraints, i.e., ${\mathcal{G}}_j=D_c{\tilde{E}}_j^c$ must be satisfied by solutions. In this case, there are two reality conditions, and the second condition is the time derivative of the first condition; thus [1,2,3,4,5,12,15,17],

$${\tilde{E}}_j^c{\tilde{E}}_k^d{\delta }^{jk}\in \mathbb{R},$$

(7)

$${\left\{{\tilde{E}}_j^c{\tilde{E}}_k^d{\delta }^{jk}\right\}}^{•}\in \mathbb{R}.$$

(8)

with ${\delta }^{jk}$ being the Kronecker delta.

In a standard form, the Ashtekar variables are given as [1,2,3,4,5,12,15,17]

$${\tilde{E}}_j^c\to \frac{1}{\gamma }{\tilde{E}}_j^c,K_c^j\to A_c^j={\Gamma }_c^j-\gamma K_c^j.$$

(9)

If $\gamma =i$, then the equation takes the original form.

The Poisson brackets are written as [1,2,3,4,5,12,15,17]

$$\{K_c^j\left(x\right),{\tilde{E}}_k^d\left(y\right)\}=\{A_c^j\left(x\right),{\tilde{E}}_k^d\left(y\right)\}=k{\delta }_k^j{\delta }_c^d\delta (x,y),$$

(10)

where $k=8\pi G\gamma$ with G the gravitational constant.

In a standard form [1,2,3,4,5,12,15,17],

$$\{A_c^j\left(x\right),{\tilde{E}}_k^d\left(y\right)\}=8\pi G\gamma {\delta }_k^j{\delta }_c^d{\delta }^3(x,y).$$

(11)

The reality condition is not necessary for a real value, and as a result, new variables and constraints are also real [1,2,3,4,5,12,15,17].

The form of the Hamiltonian constraint becomes complicated with the real value of the $\gamma$, i.e.,

$$\mathcal{H}={\epsilon }_l^{jk}{\tilde{E}}_j^c{\tilde{E}}_k^d{F}_{cd}^l-2(1+{\gamma }^2){\tilde{E}}_j^{[c}{\tilde{E}}_k^{d]}{K}_c^j{K}_d^k\approx 0.$$

(12)

If, $\gamma =i$; then the form of Hamitonian constraints simplifies [1,2,3,4,5,12,15,17].

1.2. Why the BI Parameter Was Introduced in LQG?

As mentioned, the complex valued Ashtakar’s variables simplified constraints of quantum gravity based on canonical quantization, i.e., LQG. Thereafter, Barbero [25,26] came up with a new strategy to tackle Ashtekar’s variable with real value for Lorentzian signature space-times. In [25,26] Barbero wrote down Ashtekar’s variable with a free parameter (Equation (9)); namely, $\gamma$ (denoted $\beta$ there). Ashtekar used $SU\left(2\right)$ and $SL(2,\mathbb{C})$ groups of Yang–Mill theory to deliver complex valued constraints, i.e., Ashtekar’s variables. Meanwhile, Barbero showed that one can use $SO\left(3\right)$ Yang–Mill phase space to expressthe modified Hamiltonian constraint with Lorentz signatures without complex variables to elaborate space-times without losing the features of Ashtekar’s variables [1,2,3,4,5,25].

Barbero [25,26] also showed that for simple forms of a Hamiltonian constraint, complex variable is required, while for a complicated form, this constraint could be written with real variables; for instance, a loop variable of LQG. Barbero derived a Hamiltonian constraint with ${\gamma }^2=1$ (real valued and Euclidean signature). Meanwhile, the Lorentzian signature again yields a complex valued form of the equation. Barbero also derived a Hamiltonian constraint with $\gamma =-1$. The Hamiltonian constraint could also be written with real Ashtekar variables for Lorentzian general relativity with $SO\left(3\right)$ ADM formalism [25].

Thereafter, Immirzi [27,28] further clarified on the importance of this parameter. In these papers, Immirzi explained canonical quantization of gravity, i.e., LQG with the Regge calculus. In Immirzi elaborated the basics of LQG with the discussion on the $\gamma$. Immirzi discussed various possibilities of the value of the $\gamma$ and named this arbitrariness of the $\gamma$ the $\gamma$ crisis [27,28].

Since Barbero introduced this free parameter and Immirzi used it to explain the canonical quantization method along with Regge calculus, the $\gamma$ is known as the Barbero–Immirzi parameter. In short, Barbero used one-parameter scale transformation to generalize the Ashtekar canonical transformation to a $U\left(\gamma \right)$. Meanwhile, Immirzi observed that such a transformation modifies the spectra of geometrical quantities of LQG [1,2,3,4,5,27,28].

1.3. The Holst Action and the BI Parameter

Today, there are two types of version for the connection variables: $SL(2,\mathbb{C})$ with a self duality of Yang–Mills type of connection i.e., the Ashtekar connection, and the connection with a real $SU\left(2\right)$ the Barbero connection. In the latter type of connection, the issue of the reality condition is not present. With the aid of the Holst action, both of the connections can be obtained. The $\gamma$ is introduced in the Holst action as a multiplicative constant that governs the strength of the dual curvature correction.

The Holst action generalizes the Hilbert–Palatini action using the $\gamma$. The Holst action can be derived in the following way using the Einstein–Hilbert action (EH). In GR, the EH action is written as [1,2,3,4,5,15,29]

$$S_{\mathrm{EH}}\left(g_{\mu \nu }\right)=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}{g}^{\mu \nu }{R}_{\mu \nu },$$

(13)

where $R_{\mu \nu }$ is the Ricci tensor.

If $e=\sqrt{-g}$ and $8\pi G=1$ are taken; then [1,2,3,4,5,15,29],

$$\begin{array}{c}{S}_{\mathrm{EH}}\left(g_{\mu \nu }\left(e\right)\right)=\int d^{4}xe{e}_J^{\mu }{e}^{\nu J}{R}_{\mu \nu \eta \tau }{e}_K^{\eta }{e}^{\tau K}\\ =\int d^{4}xe{e}_J^{\mu }{e}_K^{\eta }{F}_{\mu \eta }^{JK}\left(\omega \left(e\right)\right),\end{array}$$

where $F_{\mu \eta }^{JK}\left(\omega \left(e\right)\right)=e^{J\mu }{e}^{\eta K}{R}_{\mu \nu \eta \tau }\left(e\right)$,

$$S_{\mathrm{EH}}\left(g_{\mu \nu }\left(e\right)\right)=\int d^{4}x\frac{1}{4}{ϵ}_{JKLM}{ϵ}^{\mu \eta \alpha \beta }{e}_{\alpha }^L{e}_{\beta }^M{F}_{\mu \eta }^{JK}\left(\omega \left(e\right)\right).$$

Hence, as a functional of a densitized triad, the Einstein–Hilbert action takes the form [1,2,3,4,5,15,29],

$$\therefore S\left(e_{\mu }^J,{\omega }_{\mu }^{JK}\right)=\frac{1}{2}{ϵ}_{JKLM}\int e^J\wedge e^K\wedge F^{LM}\left(\omega \right).$$

(14)

By considering the Palatini identity, i.e., ${\delta }_{\omega }=F^{LM}\left(\omega \right)=d_{\omega }{\delta }_{\omega }^{LM}$ where $d_{\omega }$ denotes derivative with respect to $\omega$, and taking the variation of Equation (14), one gets [1,2,3,4,5,15,29]:

$${\delta }_{\omega }S\left(e_{\mu }^J,{\omega }_{\mu }^{JK}\right)=\frac{1}{2}{ϵ}_{JKLM}\int e^J\wedge e^K{d}_{\omega }{\delta }_{\omega }^{LM},$$

$$\therefore {\delta }_{\omega }S\left(e_{\mu }^J,{\omega }_{\mu }^{JK}\right)=-\frac{1}{2}{ϵ}_{JKLM}\int d_{\omega }\left(e^J\wedge e^K\right)\wedge {\delta }_{\omega }^{LM}.$$

(15)

If the coupling constant, $1/\gamma$, is added in Equation (14), then one gets the Holst action [1,2,3,4,5,15,29], i.e,

$$S(e,\omega )=\left(\frac{1}{2}{ϵ}_{JKLM}+\frac{1}{\gamma }{\delta }_{JKLM}\right)\int e^J\wedge e^K\wedge F^{LM}\left(\omega \right).$$

(16)

The Holst action is equivalent to the Ashtekar Hamiltonian if $\gamma =i$ is set in Equation (16) [1,2,3,4,5,15,29].

In general, the Holst action is written as [1,2,3,4,5,15,29]

$$S[e,A]=\frac{1}{8\pi G}\left(\int d^{4}xe{e}_J^{\mu }{e}_K^{\nu }{F}_{\mu \nu }^{JK}-\frac{1}{\gamma }\int d^{4}xe{e}_J^{\mu }{e}_K^{\nu }\ast F_{\mu \nu }^{JK}\right)$$

(17)

where the symbol “∗“ denotes the self-duality in Equation (17) in the presence of the BI parameter.

2. Various Proposals on the Physical Significance of the BI Parameter

In this Section, the historical time line of the research in the BI parameter and various proposals on the physical significance of the BI parameter are briefly discussed. After introducing each of the proposals, pros and cons of a proposal are given and the role of the BI parameter is explained. Here, all proposals are explained only in the context of the BI parameter to an extent relevant to the necessary mathematical treatment.

2.1. Historical Timeline

Table 1. Timeline of research on the Barbero–Immirzi parameter.

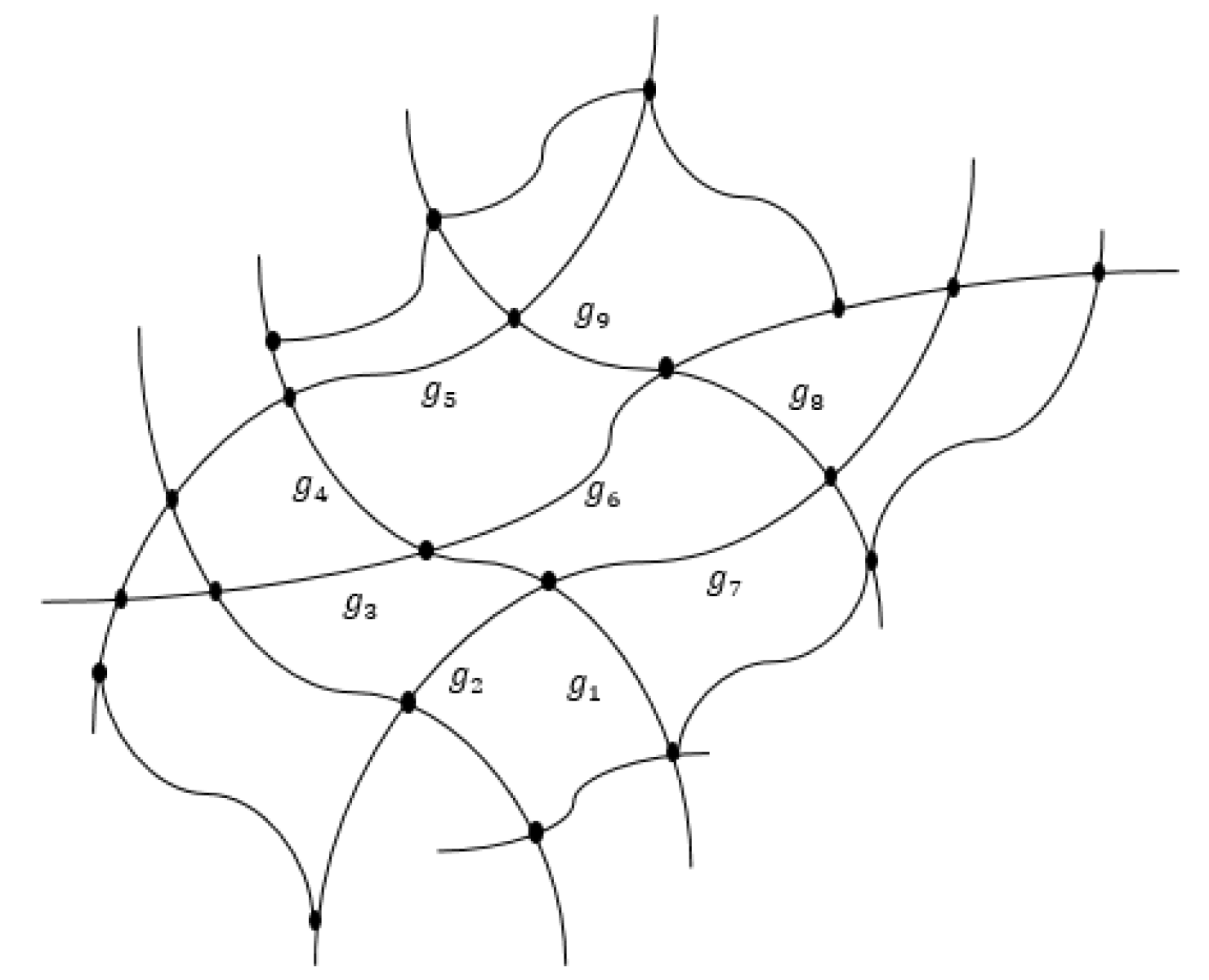
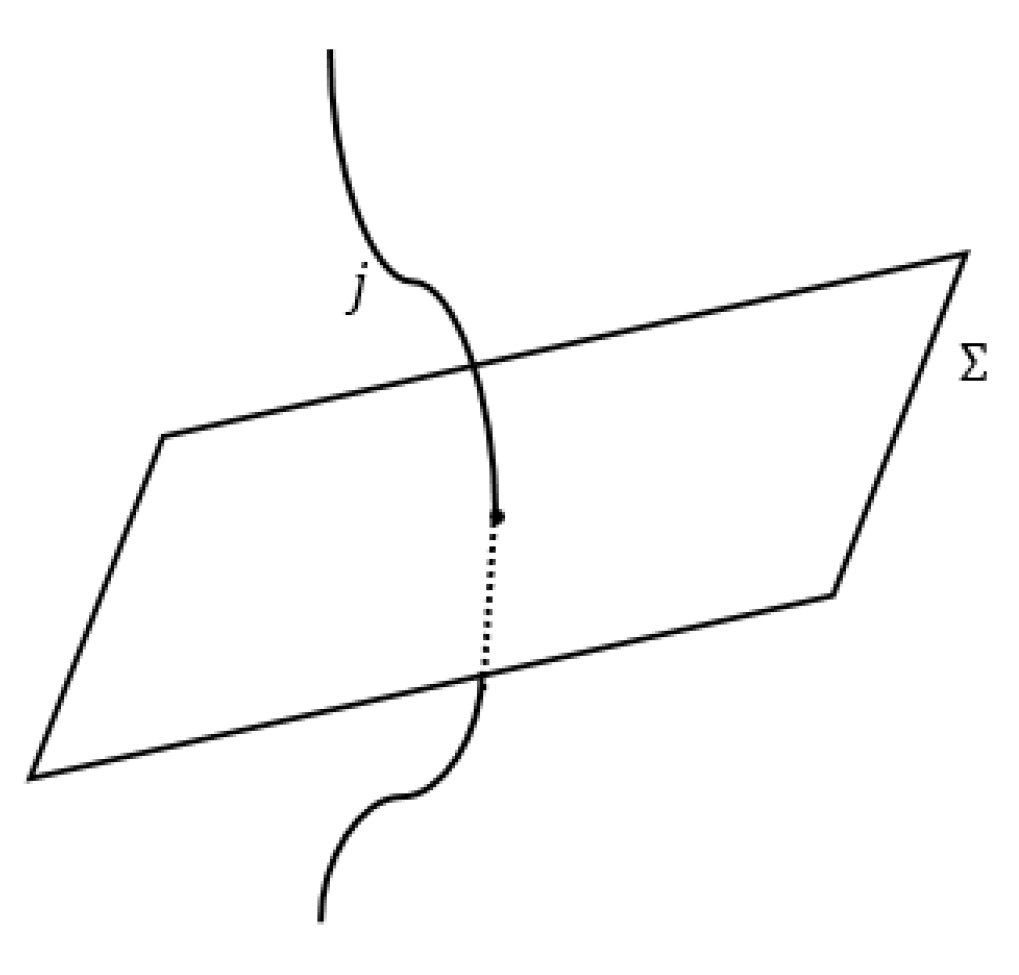
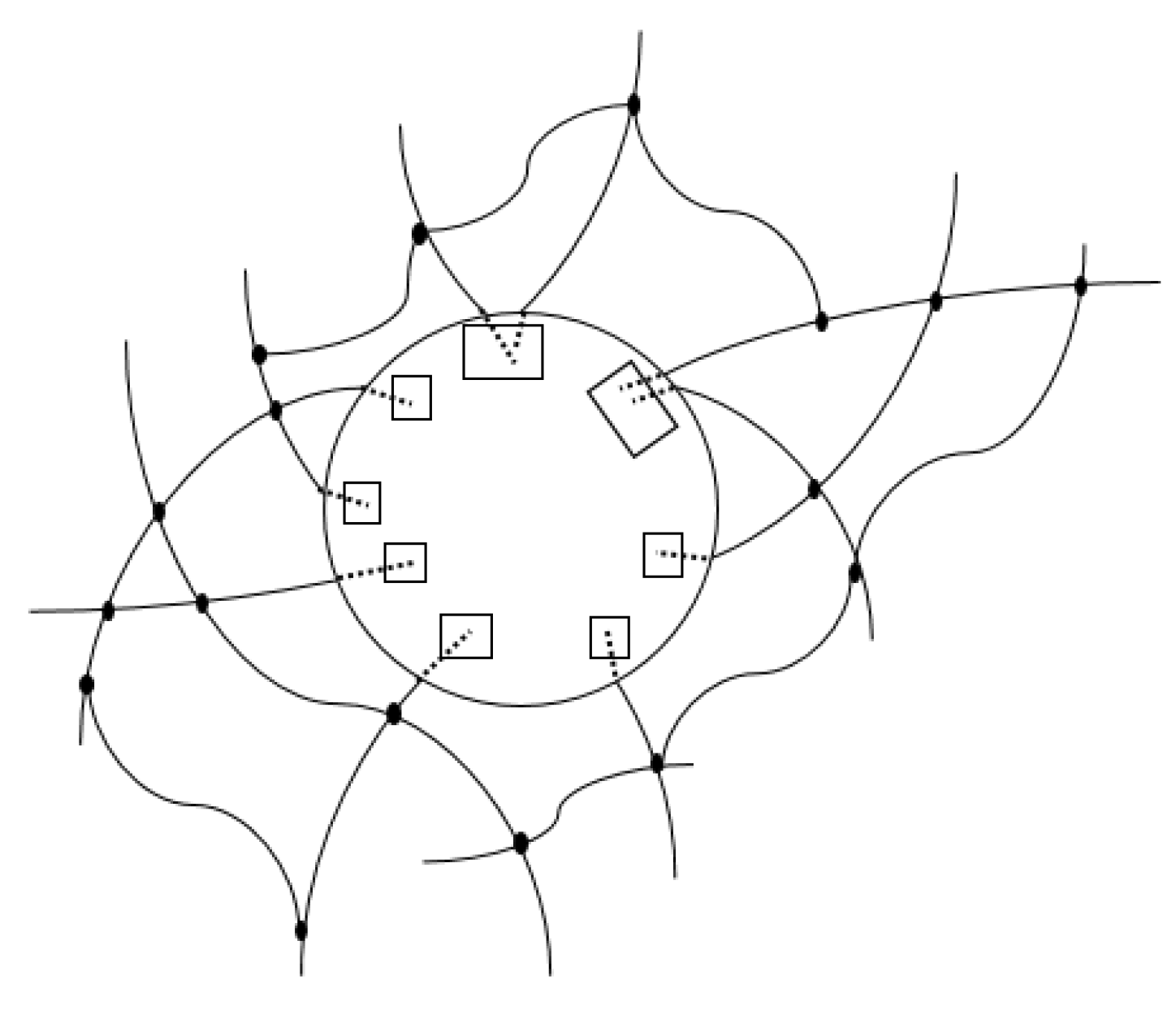
Year	Research on the BI Parameter and Its Significance
1986	Discovery of the Ashtekar variables
1995	Real Ashtekar variables for Lorentzian signature space–times
1996	Barbero’s Hamiltonian derived from a generalized Hilbert–Palatini action
1996	Black hole entropy from loop quantum gravity
1996	From Euclidean to Lorentzian general relativity: the real way
1996	Real and complex connections for canonical gravity
1997	Quantum gravity and Regge calculus
1997	Counting surface states in loop quantum gravity (LQG)
1997	Immirzi parameter in quantum general relativity
1997	On the constant that fixes the area spectrum in canonical quantum gravity
1998	Quantum geometry and black hole entropy
2000	Is Barbero’s Hamiltonian formulation a gauge theory of Lorentzian gravity?
2001	Comment on “Immirzi parameter in quantum general relativity“
2003	Quasinormal modes, the area spectrum, and black hole entropy
2004	Black-hole entropy in loop quantum gravity
2004	Black-hole entropy from quantum geometry
2005	Origin of the Immirzi parameter
2005	Physical effects of the Immirzi parameter
2005	On choice of connection in LQG
2007	On a covariant formulation of the Barbero–Immirzi connection
2007	Renormalization and black hole entropy in Loop Quantum Gravity
2008	From the Einstein–Cartan to the Ashtekar–Barbero canonical constraints, passing through the Nieh–Yan functional
2008	The Barbero–Immirzi parameter as a scalar field: K-inflation from LQG?
2008	Topological interpretation of Barbero–Immirzi parameter
2009	Peccei–Quinn mechanism in gravity and the nature of the Barbero–Immirzi parameter
2010	A relation between the Barbero–Immirzi parameter and the standard model
2011	Complex Ashtekar variables, the Kodama state and spinfoam gravity
2012	The quantum gravity Immirzi parameter—A general physical and topological interpretation
2012	Complex Ashtekar variables and realitycConditions for Holst’s action
2013	Black Hole Entropy from complex Ashtekar variables
2014	Geometric temperature and entropy of quantum isolated horizons
2014	A Correction to the Immirizi Parameter of SU(2) Spin Networks
2014	The Microcanonical Entropy of quantum isolated horizon, “quantum hair” N and the Barbero–Immirzi parameter fixation
2015	The holographic principle and the Immirzi parameter of loop quantum gravity
2017	Immirzi parameter without Immirzi ambiguity: conformal loop quantization of scalar-tensor gravity
2018	Horizon entropy with loop quantum gravity methods
2018	Generalizing the Kodama state. I: construction
2018	Generalizing the Kodama state. II: properties and physical interpretation
2018	Chiral vacuum fluctuations in quantum gravity
2018	Black hole entropy from the SU(2)-invariant formulation of Type I isolated horizons
2018	Black hole entropy and SU(2) Chern–Simons theory
2020	On the value of the Immirzi parameter and the horizon entropy

shows the historical timeline of research on the BI parameter in LQG in a chronological order. The table lists the enriched literature of the BI parameter and clarifies on the importance of the study of the BI parameter in LQG. The listing implies that the BI parameter is itself a crucial research area in LQG.

2.2. The Area Operator and the BI Parameter

In LQG, the loop states as a graph or network $\Theta$ with edges $e_i$ denoted by elements of some gauge group. In general, this gauge group can be $SU\left(2\right)$ or $SL(2,\mathbb{C})$ [1,2,3,4,5,12,15,17],

$${\psi }_{\Theta }=\psi (g_1,g_2,\dots ,g_k),$$

(18)

where $k=0,1,2,\dots ,n$ and $g_k$ is the holonomy (group element) of connection A on the kth edge; see Figure 1. In LQG, the spin network is used to describe these loop states. Penrose [30,31] gave the notion of the spin network. In the spin network, the combinatorial principle of angular momentum is used, and it defines the space–time in discrete way. In LQG, the spin network is essential for representing the loop state [1,2,3,4,5,12,15,17].

The area of a two-dimensional (2D) surface, S, that is embedded in any manifold, $\Sigma$, is defined as [1,2,3,4,5,12,15,17]

$${\mathcal{A}}_S=\int d^{2}x\sqrt{{}^{\left(2\right)}m},$$

(19)

where ${}^{\left(2\right)}m$ is the determinant of the metric ${}^{\left(2\right)}{m}_{EF}$. The area is 2D; hence, the components of the 2D metric ${}^{\left(2\right)}{m}_{EF}$ can be denoted as the dyad basis, $e_E^J$, and $E,F\in \{x,y\}$ here are spatial indices

$${}^2{m}_{EF}=e_E^J{e}_F^K{\delta }_{JK}.$$

(20)

The determinant of ${}^2{m}_{EF}$ can be written as [1,2,3,4,5,12,15,17]

$$\det \left({}^2{m}_{EF}\right)=m_{11}{m}_{22}-m_{12}{m}_{21}={\overrightarrow{e}}_z·{\overrightarrow{e}}_z.$$

(21)

Hence, Equation (19) becomes [1,2,3,4,5,12,15,17]:

$$A_S=\int d^{2}x\sqrt{{\overrightarrow{e}}_z·{\overrightarrow{e}}_z}.$$

(22)

In LQG, the frame field $e_E^k$ and the connection $A_k^E$ are conjugates. For instance, $e_E^k\to -i\hslash \frac{\delta }{\delta A_k^E}$, where ℏ is the reduced Planck’s constant. Inserting the latter into Equation (22) [1,2,3,4,5,12,15,17],

$${\widehat{A}}_S=\int d^{2}x\sqrt{{\delta }_{JK}\frac{\delta }{\delta A_J^z}\frac{\delta }{\delta A_K^z}}.$$

(23)

In LQG, $e_E^J{e}_F^K=\frac{\delta }{\delta A_J^E}\frac{\delta }{\delta A_K^F}=n_E{n}_F{J}^J{J}^K$. For $SO\left(3\right)$ group, the generator is the angular momentum operator, $J^J$. Here, $n_E$ and $n_F$ are unit tangent vectors. Therefore, the equation of the area operator becomes [1,2,3,4,5,12,15,17]

$${\widehat{A}}_S={\Sigma }_p\sqrt{{\delta }^{JK}{n}_E{n}_F{J}^J{J}^K}={\Sigma }_p\sqrt{{\delta }^{JK}{\widehat{J}}_J{\widehat{J}}_K}{\Psi }_{\Theta }(\because n^c{n}_c=1),$$

(24)

$$\therefore {\widehat{A}}_S={\Sigma }_p\sqrt{{\mathbf{J}}^{\mathbf{2}}}.$$

(25)

However, the quantum state of J is ${\mathbf{J}}^{\mathbf{2}}|j\rangle ={\hslash }^{2}j(j+1)|j\rangle$, where j represents the value of the quantum spin; hence, the equation is [1,2,3,4,5,12,15,17]:

$${\widehat{A}}_S{\Psi }_{\Theta }=l_P^2{\Psi }_p\sqrt{j_p(j_p+1)}{\Psi }_{\Theta },$$

(26)

where $l_P^2=G\hslash /c^3$ is the Planck area with c the speed of light.

In LQG, lines of the spin network can intersect. Any surface $\Sigma$ acquires area through the puncture of these lines [1,2,3,4,5,12,15,17]; see Figure 2.

In standard form, the area operator with the $\gamma$ can also be written as [1,2,3,4,5,12,15,17]

$$\therefore {\widehat{A}}_S=\gamma l_P^2{\Sigma }_p\sqrt{j_p(j_p+1)}.$$

(27)

The proportionality coefficient in the formula of area operator in LQG includes the $\gamma$ [1,2,3,4,5,23]. In 1998, Krasnov [32] found that the multiplicative factor of the area operator is $8\pi \gamma$. Hence, the equation is [1,2,3,4,5,12,15,17]

$$A=8\pi \gamma l_P^2\sqrt{j(j+1)}.$$

(28)

Similar to the area operator, the BI parameter also appears in the volume operator. The spectrum of volume operator can only be understood; if the $\gamma$ is real valued [1,2,3,4,5].

Pros and Cons of the Area Operator and the BI Parameter

The spectrum of the area and the volume operator and its eigenvalue can only be understood with the real valued $\gamma$. As mentioned, the complex valued $\gamma$ makes these operators complex valued and the significance of these complex valued operators is ambiguous. Is there any valid significance of the area operator and the volume operator with the complex valued $\gamma$? This question is still unresolved.

In short, there are two difficulties for the complex valued $\gamma$ for these geometrical operators. (1) The physical significance of the complex valued geometrical operators such as the area and the volume operator is yet to be found. (2) The mathematical structure of the complex valued geometrical operators is not yet clear and complete.

2.3. The BI Parameter and Black Hole Entropy Calculation in LQG

The expression of entropy of a black hole in Planck units calculated semi-classically by Hawking is written as [1,2,3,4,5,23]

$$S=A/4.$$

(29)

In 1996, Rovelli [33] calculated black hole entropy within LQG using the statistical framework.

In LQG, any surface obtains area when the link of the spin network punctures that surface. One can allot micro states to each surface puncture. Thus, the micro states are associated with the discrete pieces of the surface, which provide the value of area spectrum by puncturing. So, the entropy, S, is proportional to the log of the number of ways in which the sphere can be punctured that provides an area within each macroscopic interval (see Figure 3) [33].

If the eigenvalue, $A_p$, of the area operator is expressed via the $j_p$ of the form $m_p/2$ ($m_p\in Z$), then [33]

$$A_p=4\pi \gamma l_P^2\sqrt{m_p(m_p+2)}.$$

(30)

For an interval $[A+\delta A,A-\delta A]$, where $\delta A$ is some small interval $(\delta A/A\ll 1)$, A is a macroscopic value of area. The allowed number $N\left(M\right)$ of sequences of integers $\{m_p,\dots ,m_N\}$, $p=1,2,3,\dots ,N$, is determined by the number N of edges that puncture the surface, so that the determined value for the total area lies within the given interval, $M=A/\left(4\pi \gamma l_P^2\right)$ [33].

The number of sequences $N\left(M\right)$, in which each sequence is $\left\{m_p\right\}$, can be given as [33]

$$M=\frac{A}{4\pi \gamma l_P^2}={\Sigma }_p\sqrt{m_p(m_p+2)}.$$

(31)

The number of sequences is indicated by $N_{+}\left(M\right)$, such that ${\Sigma }_p{m}_p=M$ and the number of sequences is indicated by $N_{-}\left(M\right)$, such that ${\Sigma }_p(m_p+1)=M$. Hence, the given set of inequalities implies that [33]

$$N_{-}\left(M\right)<N\left(M\right)<N_{+}\left(M\right).$$

(32)

From calculation, $ln{N}_{+}\left(M\right)=ln2$, $ln{N}_{-}\left(M\right)=ln\frac{1+\sqrt{5}}{2}$ and $lnN\left(M\right)=dM$. From Equation (32), the inequalities are now given as [33]

$$\begin{array}{c}ln\frac{1+\sqrt{5}}{2}<d<ln2,\\ 0.48<d<0.69.\end{array}$$

(33)

By taking $M=A/(8\pi \hslash G)$, one gets

$$\begin{array}{ccc}\hfill lnN\left(A\right)& =\hfill & d\frac{A}{8\pi \hslash G},\hfill \\ \hfill S\left(A\right)& =\hfill & klnN\left(A\right),\hfill \end{array}$$

(34)

$$\therefore S\left(A\right)=c\frac{k}{\hslash G}A,$$

(35)

where $c=d/\left(8\pi \right)=1/4$ is constant.

In 1997, Ashtekar et al. [34] showed that spin networks explains spacetime geometry outside a black hole. Some edges of this spin network puncture the event horizon and provide the value of area through this contribution. The $U\left(1\right)$ Chern–Simons theory explains the quantum geometry of the horizon. In this formalism, the rotation of $SO\left(2\right)$ describes 2D geometry, which is isomorphic to $U\left(1\right)$. The entropy of a black hole is calculated by counting the spin network states relevant to an event horizon. Thus, the expression of black hole entropy in LQG is [1,2,3,4,5,34],

$$S=\frac{{\gamma }_{0}A}{4\gamma }.$$

(36)

There are two possibilities for the value of ${\gamma }_0$ [1,2,3,4,5,34], i.e.,

$${\gamma }_0=\frac{ln2}{\sqrt{3}\pi }$$

(37)

or

$${\gamma }_0=\frac{ln3}{\sqrt{8}\pi }.$$

(38)

The value of ${\gamma }_0$ relies on the choice of the gauge group. By taking ${\gamma }_0=\gamma$, one gets actual black hole entropy formula, calculated by Hawking [1,2,3,4,5,34], i.e.,

$$S=\frac{{\gamma }_{0}A}{4{\gamma }_0}=\frac{A}{4}.$$

(39)

This calculation is true for each sort of black hole. The black hole entropy calculation in LQG is a quite enriched research area. The value of the $\gamma$ and black hole entropy formula in LQG is a topic whose implications are far-reaching [1,2,3,4,5,34].

In 2002, Dreyer [35] fixed the value of the $\gamma$ using classical quasinormal mode spectrum of a black hole and gave black hole entropy formula in LQG with $SO\left(3\right)$ group instead of $SU\left(2\right)$. Instead of $j_{\min }=1/2$, the value of $j_{\min }=1$ is taken in the expression of the area operator, i.e.,

$$\Delta A=A\left(j_{\min }\right)=8\pi \gamma l_P^2\sqrt{j_{\min }(j_{\min }+1)}.$$

(40)

In this case, the change in the mass due to the frequency of the quasinormal modes (QNM) is [35]

$$\Delta M=\hslash {\omega }_{\mathrm{QNM}}=\frac{\hslash ln3}{8\pi M}.$$

(41)

For a Schwarzschild black hole, the area and the mass are related to each other by the relation $A=16\pi M^2$. A change in the area corresponding to the mass change is given as [35]

$$\Delta A=4ln3l_P^2.$$

(42)

The expression for the $\gamma$ is obtained through comparison between Equations (40) and (42) [35],

$$\gamma =\frac{ln3}{2\pi \sqrt{j_{\min }(j_{\min }+1)}}.$$

(43)

If $j_{\min }=1$ is taken in Equation (43), then the fixed value of the BI parameter is [35]

$$\gamma =\frac{ln3}{2\pi \sqrt{2}}.$$

(44)

Thereafter, Meissner [36] fixed the value of the area in LQG by fixing ${\gamma }_M$ and $\gamma$ by comparing the Bekenstein–Hawking entropy formula with the derived formula. The Bekenstein–Hawking entropy formula reads:

$$S=\frac{1}{4}\frac{A}{l_P^2}.$$

(45)

In [36], the derived expression of the black hole entropy formula is:

$$S=lnN\left(a\right)=\frac{{\gamma }_M}{4\gamma }\frac{A}{l_P^2}+\mathcal{O}(lnA).$$

(46)

Here, by comparing the derived black hole entropy Formula (46) with the Bekenstein–Hawking Formula (45), one gets [1,2,3,4,5,36].

$$\gamma ={\gamma }_M.$$

(47)

The calculated value of ${\gamma }_M$ is [36]

$${\gamma }_M=0.2375\dots$$

(48)

or

$${\gamma }_M=0.2739\dots$$

(49)

In 2004, Domagala and Lewandowski [37] defined microscopic degrees of freedom to count the black-hole entropy. On the basis of a ratio, i.e., $ln\left(N\right(a\left)\right)/a$, for large a, the value of entropy (the eigen value of area operator is equal to or less than a that is a number; for quantum states of black holes) is

$$\frac{ln2}{4\pi \gamma l_P^2}a\le lnN\left(a\right)\le \frac{ln3}{4\pi \gamma l_P^2}a.$$

(50)

Hence, the upper and lower bounds value for $\gamma$ are [37]

$$\frac{ln2}{\pi }\le \gamma \le \frac{ln3}{\pi }.$$

(51)

Since the spin greater than $1/2$ also contributes to the entropy, this contribution is also considered here [37].

In 2007, Jacobson [38] studied the renormalization and the black hole entropy in LQG. For black holes, he found that the microscopic state counting is related to Newton’s universal constant

G:

$$S_{\mathrm{LQG}}=\frac{b}{\gamma }\frac{A}{\hslash G},$$

(52)

where b is a numerical constant. In LQG, from Equation (52), one can see that the entropy is related to the area of the horizon A$(S_{\mathrm{LQG}}\propto A)$ and the gravitational constant G$(S_{\mathrm{LQG}}\propto 1/G)$ [38].

Jacobson found that one should compare this formula with the actual Bekenstein–Hawking entropy formula after accounting the scale dependence of Newton’s constant and area. For any value of the $\gamma$, if some property of the renormalization is followed, then one can compare both entropy formulas. The BI parameter to be $\gamma =4b$ to match the black hole entropy in LQG with the Bekenstein–Hawking Formula (45) [38].

In 2013, Frodden et al. [39] found that by taking complex valued Ashtekar variables, the black hole entropy formula is achieved in certain conditions. In this case, the BI parameter can be complex valued $(\gamma =\pm i)$. Ref. [39] shows that the number of micro states $N_{\Gamma }\left(A,\gamma \to \pm i\right)$ acts as $exp\left(A/\left(4l_P^2\right)\right)$ for certain case, i.e., for large area A in the large spin semi-classical limit. With respect to the complex self-dual Ashtekar connections, $N_{\Gamma }\left(A,\pm i\right)$ is the number of states for a theory to be defined.

The $SU\left(2\right)$ Chern–Simons theory is related to the study of the black hole entropy in LQG. From $SU\left(2\right)$ to $SL(2,\mathbb{C})$ representation, the formula for the Hilbert space of $SU\left(2\right)$ Chern–Simons theory follows a specific analytic continuation with constraints of self-duality. The complex formulation (with the Ashtekar variables) within this proposal gives the derivation of the black hole entropy within LQG formalism for a large spin asymptotic domain which is semi classical in nature [39]. Hence,

$$log\left(N_{\Gamma }(A,\pm i)\right)\sim \frac{A}{4l_P^2}.$$

(53)

One can list more papers on black hole entropy in LQG [40,41,42,43,44,45,46,47,48].

Pros and Cons of the BI Parameter and Black Hole Entropy Calculation in LQG

On the basis of the black hole entropy calculation in LQG, one gets various expressions for the real valued $\gamma$, such as ${\gamma }_0=\frac{ln2}{\sqrt{3}\pi }$, ${\gamma }_0=\frac{ln3}{\sqrt{8}\pi }$ and $\gamma =\frac{ln3}{2\pi \sqrt{2}}$. The numerical value for the $\gamma$ is either $0.2375\dots$ or $0.2739\dots$ based on the calculation. The BI parameter is also expressed in terms of a numerical constant b, i.e., $\gamma =4b$. With the complex valued $\gamma$, the black hole entropy can also be calculated using $SU\left(2\right)$ Chern–Simons theory. Whether it is the real valued or the complex valued $\gamma$; the black hole entropy can be calculated in LQG. However, the interpretation of the complex valued BI parameter within the black hole entropy formula in LQG is difficult to comprehend.

One criticism for the black hole entropy calculation in LQG is regarding the different value of the $\gamma$. However, this criticism is easy to address, because a value of the real valued $\gamma$ can be applied to all kinds of black holes. The $\gamma$ is a free parameter; its same value is applied to all kinds of black hole.

2.4. The BI Parameter as Immirzi Ambiguity

In LQG, the geometrical observables, such as the area and the volume, are quantized and exhibit a discrete spectrum. In 1996, Immirzi noticed that LQG does not determine the complete scale of these spectra [27]. Immrizi also observed that one can have different spectra for the same geometrical quantities, if starting with the scaled elementary variables. The algebra of holonomy relies on a free parameter that gives the family of one parameter of quantum theories with inequivalence. The $\gamma$ represents this family of one parameter [49].

There is a certain symmetry under study, according to which classical theory is identified as a canonical transformation; however, one cannot identify it as a unitary transformation of quantum theory. Since the holonomy is the operator of LQG and because of weird sort of representation of LQG, one has to consider the $\gamma$ as an ambiguity [49].

In LQG, there are two connections, i.e., A and $\Gamma$. Therefore, one has to create the $\gamma$-scaled connection, namely, $A_{\gamma }$, via interpolation between different connections. Thus, the elementary excitation of LQG—namely the Wilson loop of $A_{\gamma }$—has different results for various value of the $\gamma$. Therefore, some physical spectrum of quantity of LQG relies on the $\gamma$ [49].

Additionally, the metric information resides in the E (conjugate variable). Since E is a conjugate for connection, in quantum formalism, it is written as a derivative operator that acts on functions over the group. Over the group manifold, any geometrical quantity that is a function of E behaves as an elliptic operator that results in the discrete spectrum. Such elliptic operators possess non-vanishing scalar dimension relative to the affine scaling of the connection. Hence, in the elliptic geometric operators spectrum, ambiguity is introduced, i.e., the Immirzi ambiguity. This ambiguity influences the discreteness of the space in LQG. In [49], the The authors also described that various interpretations regarding the $\gamma$ are incorrect in context with the Immirzi ambiguity. The authors also gave various models such as harmonic oscillator with no Immirzi ambiguity, a particle on a circle with no Immirzi ambiguity, and a simple model with $\gamma$ as a free parameter. Due to lack of space, here, only the cause of the Immirzi ambiguity and its effect in LQG are given [49].

In the year 2001, Samual [50] commented that interpretations of the Immirzi ambiguity are unclear and do not give any agreement on its origin and significance. All interpretations of the BI parameter as Immirzi ambiguity seem unclear, and do not give any satisfactory explanation about the origin and significance of it. Moreover, the examples of the Immirzi ambiguity are not real, but are artificially generated through the compactification of the configuration space.

In 2017, Veraguth and Wang [51] gave a proposal in which they explained LQG without Immirzi ambiguity using conformal LQG. The conformal LQG provides a way to achieve loop quantization through a conformally equivalent class of metrics. The conformal geometry gives an extended symmetry to permit a reformulated BI parameter. In scalar–tensor gravity, this can be achieved via conformal frame transformations. In this proposal, the authors showed that the LQG, along with a conformally transformed Einstein metric which has dissimilar values of the relevant BI parameter, are connected by a conformal frame with global change. The conformal LQG is free from the Immirzi ambiguity. They defined the Ashtekar variables in the following way [51]:

$$A_c^{{}^{\prime }j}={\Gamma }_c^j+\gamma \kappa K_c^j,\frac{1}{\gamma \kappa }{E}_c^j.$$

(54)

Pros and Cons of the BI Parameter as Immirzi Ambiguity

Research on the Immirzi ambiguity is still incomplete. As mentioned, there is a specific symmetry under study, according to which classical theory is identified as a canonical transformation, but one cannot identify it as a unitary transformation of quantum theory. This is the reason behind the Immirzi ambiguity. One-parameter family of the BI parameter is another reason. The $\gamma$-scaled connection, namely $A_{\gamma }$ for various values of the BI parameter, is also different. The elliptic nature of the geometric operator due to the frame field E that is a conjugate to the connection A is also responsible for the Immirzi ambiguity. However, the conformal formalism of LQG may remove the Immirzi ambiguity.

The BI parameter was added into the LQG framework to remove mathematical complexities (in the connection formalism, constraints equations, geometrical operators equations and many other important equations); however, it emerged as ambiguity because of the above-mentioned causes.

2.5. Origin of the BI Parameter

In 2005, Chou et al. [52] found a technique, through which a ratio which equals the $\gamma$ is obtained. They used quadratic spinor techniques, in which the physical significance and effect of the $\gamma$ become obvious in GR. The authors also inferred that without other matter fields in GR, the $\gamma$ as a observable is a physical property of the sector of gravity.

Firstly, the Holst action is defined in a novel way [52], i.e.,

$$S[\mathbf{e},\omega ]=\alpha \int \ast \left({\mathbf{e}}^c\wedge {\mathbf{e}}^d\right)\wedge R_{cd}\left(\omega \right)+\gamma \left({\mathbf{e}}^c\wedge {\mathbf{e}}^d\right)\wedge R_{cd}\left(\omega \right),$$

(55)

where the $\gamma$ is a ratio, i.e., $\gamma =\alpha /\beta$, $c,d,\dots =0,1,2,3$, and “∗“ denotes duality. Thereafter, the authors compared the Equation (55) with the quadratic spinor Lagrangian [52], i.e.,

$${\mathcal{L}}_{\psi }=2D\left(\overline{\psi }\mathbf{e}\right){\gamma }_{5}D\left(\psi \mathbf{e}\right),$$

(56)

where $\psi$ is auxiliary spinor field, $\mathbf{e}$ is $\mathbf{e}={\mathbf{e}}^c{\gamma }_c$, D is the covariant derivative, and ${\gamma }_c$ is the Dirac gamma matrix.

By defining the spinor curvature identity [52],

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 2D\left(\overline{\psi }\mathbf{e}\right){\gamma }_{5}D\left(\mathbf{e}\psi \right)=& \overline{\psi }\psi R_{cd}\wedge \ast \left({\mathbf{e}}^c\wedge {\mathbf{e}}^d\right)\hfill \\ & +\overline{\psi }{\gamma }_5\psi R_{cd}\wedge {\mathbf{e}}^c\wedge {\mathbf{e}}^d+d[D\left(\overline{\psi }\mathbf{e}\right){\gamma }_5\mathbf{e}\psi +\overline{\psi }\mathbf{e}{\gamma }_{5}D\left(\mathbf{e}\psi \right)].\hfill \end{array}\end{array}$$

(57)

For $\omega \left[e\right]$, the equation of motion is [52]:

$$D[\overline{\psi }\psi \ast \left({\mathbf{e}}^c\wedge {\mathbf{e}}^d\right)+\overline{\psi }{\gamma }_5\psi \left({\mathbf{e}}^c\wedge {\mathbf{e}}^d\right)]=0.$$

(58)

It was found that the $\gamma$ can be written as a ratio of scalar and pseudoscalar contributions in the theory [52], i.e.,

$$\gamma =\frac{\langle \overline{\psi }\psi \rangle }{\langle \overline{\psi }{\gamma }_5\psi \rangle }.$$

(59)

If $\overline{\psi }\psi =1$ and $\overline{\psi }{\gamma }_5\psi =0$, then $\gamma =\infty$. The BI parameter $\gamma =i$ corresponds to Ashtekar formalism with self duality; meanwhile, $\gamma =1$ satisfies the action of the Hamiltonian given by Barbero. Therefore, the $\gamma$ implies that Einstein gravity can be distinguished from the other gravitation theories via general covariance. In other words, this ratio the ratio (59) can be seen as a measure of how gravity differs from covariant gravity. Such a technique permits the renormalization scale, $\mu$, regarding the $\gamma$ via spinor’s expectation value in quantization process $(\therefore {\langle \overline{\psi }\psi \rangle }_{\mu },{\langle \overline{\psi }{\gamma }_5\psi \rangle }_{\mu })$. Here, $\overline{\psi }{\gamma }_5\psi$ is not a real function. To get $\overline{\psi }{\gamma }_5\psi$ to be real, one has to use an anti-commuting spinor to achieve the real Ashtekar variables [52].

Pros and Cons of Origin of the BI Parameter

This proposal gives the origin of the $\gamma$ using quadratic spinor techniques in which a ratio of scalar and pseudoscalar contributions is defined as the $\gamma$. In essence, in this proposal, the $\gamma$ can be real as well as complex valued under different condition. The anti-commuting spinor is necessary to get real valued $\overline{\psi }{\gamma }_5\psi$ and the Ashtekar variables.

2.6. On a Covariant Formulation of the BI Connection

In 2007, Fatibene et al. [53] gave a proposal on covariant formulation of the BI connection in which they defined a global covariant $SU\left(2\right)$-connection over whole spacetime that limits generalizations of the Barbero–Immirzi connection on a given slice of space. The BI connection is a collective $SU\left(2\right)$ gauge connection on a 3D surface $S\subset \mathcal{M}$ in 4D spacetime $\mathcal{M}$. On the basis of groups and spacetime involved in the theory, the BI connection is global. However, the $SU\left(2\right)$ principal bundles ${}^{+}\Sigma$ over one 3D base S should be trivial. In this paper, the global aspects of the BI connection, the covariant formulation of the BI connection with its spacetime interpretation and the Lorentzian case are investigated. Here, the point of study is the BI connection. The $\gamma$ is less emphasized in this study. Thus, this investigation is covered with the necessary details.

Pros and Cons of a Covariant Formulation of the BI Connection

This proposal advocates the usual interpretation of the $\gamma$ (real valued) on the basis of the black hole entropy calculation in LQG. In this proposal, the complex valued $\gamma$ is also less emphasized due to its obscured significance.

2.7. The BI Parameter as a Scalar Field

In 2008, Taveras and Yunes [54] (see also [55]) gave a proposal on the $\gamma$ as a scalar field. They studied the LQG-based generalization of GR, in which they modified the Holst action was modifeid.

The authors scalarized the $\gamma$ in the Holst action. This meant that the $\gamma$ was promoted as a field under the integral of the dual curvature term. In this formalism, the $\gamma$ acts as a dynamical scalar field. This formalism gives a non-zero torsion tensor which modifies the field equations through quadratic first derivatives of the BI field. Such a modification is similar to the general theory of relativity with non-trivial kinetic energy in the presence of a scalar field [54].

Before promoting the the authors firstly modified the Holst action [54], i.e.,

$$S=\frac{1}{4\kappa }\int {ϵ}_{JKLM}{e}^J\wedge e^K\wedge F^{LM}+\frac{1}{2\kappa }\int \overline{\gamma }{e}^J\wedge e^K\wedge F_{LM}+S_{\mathrm{mat}},$$

(60)

where $\kappa =8\pi G$, the coupling field $\overline{\gamma }$ is $\overline{\gamma }=1/\gamma$, and $S_{\mathrm{mat}}$ is the action for additional matter degrees of freedom. To introduce torsion and contorsion in Equation (60) one can simplify the Holst action as follows [54]:

$$\begin{array}{c}S=\frac{1}{4\kappa }\int {ϵ}_{JKLM}{e}^J\wedge e^K\wedge e^Q\wedge e^R\frac{1}{2}{F}_{QR}^{LM}+\frac{1}{2\kappa }\int \overline{\gamma }{e}^J\wedge e^K\wedge e^L\wedge e^M\frac{1}{2}{F}_{JKLM}+S_{\mathrm{mat}}\\ =\frac{1}{8\kappa }\int {ϵ}_{JKLM}(-\tilde{\sigma }){ϵ}^{JKQR}{F}_{QR}^{LM}+\frac{1}{4\kappa }\int \overline{\gamma }(-\tilde{\sigma }){ϵ}^{JKLM}{F}_{JKLM}+S_{\mathrm{mat}}.\end{array}$$

(61)

Through simplification, one gets [54]

$$\therefore S=\frac{1}{2\kappa }\int \tilde{\sigma }\left[{\delta }_{LM}^{\left[QR\right]}{F}_{QR}^{LM}-\frac{\overline{\gamma }}{2}{ϵ}^{JKLM}{F}_{JKLM}\right]+S_{\mathrm{mat}},$$

(62)

where $\tilde{\sigma }=d^{4}xe=d^{4}x\sqrt{-g}$, and $e^J\wedge e^K\wedge e^L\wedge e^M=-\tilde{\sigma }{ϵ}^{JKLM}$.

In the simpler form, the modified form of the Holst action is [54]

$$S=\frac{1}{2\kappa }\int d^{4}xe{p}_{LM}^{JK}{e}_J^{\mu }{e}_K^{\nu }{F}_{\mu \nu }^{LM}$$

(63)

where $p_{LM}^{JK}={\delta }_J^{[L}{\delta }_K^{M]}-\frac{\overline{\gamma }}{2}{ϵ}_{JK}^{LM}$.

Thereafter, the authors gave field equations with the modified Holst action and its solutions. They also gave effective action and the inflation with the $\gamma$ as a dynamical scalar field [54].

In 2009, Calcagni and Mercuri [54] also promoted the $\gamma$ as a field in the canonical formalism of pure gravity. In this paper, the authors investigated the parity properties of the field of the $\gamma$ by performing the decomposition of torsion into irreducible components. Under a local Lorentz group, they suggested that the $\gamma$ ought to be pseudoscalar to conserve the transformation properties of these components.

To understand the Riemann–Cartan space–time, one has to generalize the Holst formalism. This can be achieved by adding a torsion part in the Holst action. It gives net coupling with the $\gamma$, which gives rise to Nieh–Yan density [54].

The field of the $\gamma$ is a real canonical pseudoscalar field for $\gamma =\gamma \left(x\right)$ coupled with the Nieh–Yan invariant. The $\gamma$ is pseudoscalar in nature because of the axial component of torsion, which is proportional to the partial derivative of the In the absence of matter, the field of the was studied in the first-order Hamiltonian formalism. Here, the derivation of the action in the Lagrangian formalism is avoided, since the subject of study is the field of the BI parameter in the Hamiltonian formalism (canonical). The authors also compared the Holst case with the Nieh–Yan case. The total Hamiltonian in the form of the action in the Holst case is expressed as [54]

$$H_D=\int d^{3}x\left({\Lambda }^j{\mathcal{R}}_j+N^{\beta }{\mathcal{H}}_{\beta }+N\mathcal{H}\right),$$

(64)

where ${\Lambda }^j$, $N^{\beta }$ and N are Lagrange-undetermined multipliers. ${\mathcal{R}}_j$, $H_{\beta }$ and $\mathcal{H}$ are the rotation, super momentum and super Hamiltonian constraints, respectively.

The expression of all constraints is written as [54],

$${\mathcal{R}}_j\equiv {ϵ}_{jk}^l{K}_{\beta }^k{E}_l^{\beta },$$

(65)

$${\mathcal{H}}_{\beta }\equiv E_j^{\eta }{D}_{[\beta }{K}_{\eta ]}^j+\Pi {\partial }_{\beta }\gamma \approx 0,$$

(66)

$$\begin{array}{cc}\hfill \mathcal{H}\equiv & -\frac{1}{2e}{E}_j^{\beta }{E}_k^{\eta }\left({ϵ}_l^{jk}{R}_{\beta \eta }^l+2K_{[\beta }^j{K}_{\eta ]}^k\right)+\frac{1+{\gamma }^2}{3e}{\Pi }^2-\frac{3}{4}\frac{e}{1+{\gamma }^2}{\partial }_{\beta }\gamma {\partial }^{\beta }\gamma \approx 0.\hfill \end{array}$$

(67)

Here, ${\partial }_{\beta }$ denotes the coordinate derivative.

For the Nieh–Yan case, the super Hamiltonian is denoted as [54] $\mathcal{H}$, i.e.,

$$\begin{array}{cc}\hfill \mathcal{H}\equiv & -\frac{1}{2e}{E}_j^{\beta }{E}_k^{\eta }\left({ϵ}_l^{jk}{R}_{\beta \eta }^l+2K_{[\beta }^j{K}_{\eta ]}^k\right)+\frac{1}{3e}{\Pi }^2-\frac{3}{4}e{\partial }_{\beta }\gamma {\partial }^{\beta }\gamma \approx 0.\hfill \end{array}$$

(68)

Here, in the canonical formalism, the factor $\left(1+{\gamma }^2\right)$ disappears in the contribution of the pseudo-scalar field for the Nieh–Yan term. The Nieh–Yan term exhibits a shift symmetry, i.e., $\gamma \to \gamma +{\gamma }_0$ [54].

Pros and Cons of the BI Parameter as a Scalar Field

Taveras and Yunes defined the $\gamma$ as a dynamical scale field in the Holst action with non zero torsion tensor, while Calcagni and Mercuri defined the $\gamma$ as a field in the canonical formalism. These proposals provide new significance of the BI parameter; however, the $\gamma$, which is sometimes complex valued, is still unclear.

2.8. Topological Interpretation of the BI Parameter

In 2008, Date et al. [56] gave a proposal on the topological interpretation of the $\gamma$.

In terms of the Holst formalism, the Hilbert–Palatini Lagrangian as the Lagrangian density can be written as [56]

$$\mathcal{L}=\frac{1}{2}e{\Sigma }_{JK}^{\mu \nu }{R}_{\mu \nu }^{JK}\left(\omega \right)+\frac{\gamma }{2}e{\Sigma }_{JK}^{\mu \nu }{\tilde{R}}_{\mu \nu }^{JK}\left(\omega \right)$$

(69)

where ${\Sigma }_{JK}^{\mu \nu }:=\frac{1}{2}\left(e_J^{\mu }{e}_K^{\nu }-e_K^{\mu }{e}_J^{\nu }\right)$, $R_{\mu \nu }^{JK}\left(\omega \right):={\partial }_{[\mu }{\omega }_{\nu ]}^{JK}+{\omega }_{[\mu }^{JK}{\omega }_{\nu ]L}^J$ and ${\tilde{R}}_{\mu \nu }^{JK}\left(\omega \right):=\frac{1}{2}{ϵ}_{JKLM}{R}_{\mu \nu LM}\left(\omega \right)$.

Here, with ${\gamma }^{-1}$, the second term is the Holst term, while with $\gamma =-i$, this Lagrangian density gives the complex value $SU\left(2\right)$ Ashtekar connection. For $\gamma =1$, one gets the real valued $SU\left(2\right)$ Barbero connection [56]. This has been already discussed in the introduction.

The expression of the Nieh–Yan (NY) density is given as [56]

$$I_{\mathrm{NY}}={ϵ}^{\mu \nu \beta \eta }\left[D_{\mu }\left(\omega \right)e_{\nu }^J{D}_{\beta }\left(\omega \right)e_{J\beta }-\frac{1}{2}{\Sigma }_{\mu \nu }^{JK}{R}_{\beta \eta JK}\left(\omega \right)\right],$$

(70)

where $D_{\mu }\left(\omega \right)e_{\nu }^J={\partial }_{\mu }{e}_{\nu }^J+{\omega }_{\mu K}^J{e}_{\nu }^K$. For a torsion-free connection, the Nieh–Yan density disappears.

In this proposal, in the time gauge, Nieh–Yan topological density of a theory of gravity permits us to explain gravity as a real $SU\left(2\right)$ connection. For $\gamma =1$, the set of constraints for both the Hamiltonian and the Barbero formalism are the same. For the rest of the values of the $\gamma$, the Immirzi formulation exhibits $\frac{1}{\gamma }$. The parameter $\gamma$ is analogous to the $\theta$ parameter of the quantum chromodynamics. This parameter ($\gamma$) implies an enriched vacuum structure of gravity. The Nieh–Yan density is fully constructed from geometric quantities, while the modified Holst terms exhibit fields of matter. With the aid of connection equation of motion, both are connected [56].

Pros and Cons of Topological Interpretation of the BI Parameter

In this proposal, the authors gave the interpretation of the $\gamma$ topologically using the Nieh–Yan density with the real valued $SU\left(2\right)$ connection. From this proposal, the $\gamma$ can be compared to the $\theta$ parameter of the quantum chromodynamics. The complex valued $\gamma$ is also less emphasized in this proposal.

2.9. The Peccei–Quinn Mechanism in Gravity and the Nature of the BI Parameter

Promoting the $\gamma$ as a field was an active research area between 2007 and 2011; that added new physical significance for the $\gamma$ with the topological perspective in LQG.

In 2009, Mercuri [57] gave a proposal on the nature of the $\gamma$ using the Peccei–Quinn mechanism in gravity, in which the $\gamma$ is taken as a field. Using the Holst formalism, the modified Hilbert–Palatini (HP) action is obtained. This modified (total) action with the Nieh–Yan invariant (spacetime with the torsion) and the matter coupling is given as $S_{\mathrm{tot}}=S_{\mathrm{HP}}[e,\omega ]+S_{\mathrm{NY}}[e,\omega ]+S_{\mathrm{mat}}$. Hence,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill S_{\mathrm{tot}}=& -\frac{1}{16\pi G}\int e_c\wedge e_d\wedge \star R^{cd}+\frac{\gamma }{16\pi G}\int \left(T^c\wedge T_c-e_c\wedge e_d\wedge R^{cd}\right)\hfill \\ & +\frac{i}{2}\int \star e_c\wedge \left(\overline{\psi }{\gamma }^{c}D\psi -\overline{D\psi }{\gamma }^c\psi +\frac{i}{2}m{e}^c\overline{\psi }\psi \right),\hfill \end{array}\end{array}$$

(71)

where $T_c$ denotes the torsion two-form. The author suggested promoting $\gamma$ as a field, the contribution from divergence to the chiral anomaly must be reabsorbed [57].

The author also implied that the Peccei–Quinn mechanism (this mechanism is used for charge-parity (CP) conservation for a strong force, in which pseudo-particle effects are considered with a scalar field) permits one to connect the constant value of the $\gamma$ to the other certain topological ambiguities. This connection creates an interaction between gravity and the field of the BI parameter [57].

From the spontaneous symmetry breaking ($SU\left(2\right)\times U\left(1\right)$), the obtained quark mass matrices M is not diagonal and Hermitian. A chiral rotation is needed to diagonalize it. Similar to this, the chiral rotation of the fermionic measure in the Euclidean path integral produces a NY term with Pontryagin class in space–time with torsion that is diverged as the square of the regulator [57].

The following equation is a part of regularization procedure when $\gamma$ is considered as a field:

$$\delta \psi \delta \overline{\psi }\to \delta \psi \delta \overline{\psi }exp\left\{\frac{i}{8{\pi }^2}\int \beta \left[R_{cd}\wedge R^{cd}+2{\Lambda }^2\left(T_c\wedge T^c-e_c\wedge e_d\wedge R^{cd}\right)\right]\right\},$$

(72)

where $\beta$ is the transformation parameter and $\Lambda$ is a regulator. In short, Equation (72) shows the regularization. Hence, the effective action after the regularization procedure in Equation (72) reads:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill S_{\mathrm{eff}}=& S_{\mathrm{HP}}[e,\omega ]+S_D[e,\omega ,\psi ,\overline{\psi }]+\frac{1}{8{\pi }^2}\beta \int R_{cd}\wedge R^{cd}+\frac{1}{16\pi G}\left(\gamma +\frac{4G}{\pi }\beta {\Lambda }^2\right)\hfill \\ & \times \int \left(T^c\wedge T_c-e_c\wedge e_d\wedge R^{cd}\right).\hfill \end{array}\end{array}$$

(73)

Any attempt at removal of the regulator results in the divergence of $\beta$. By promoting $\gamma$ as a field, this divergence is reabsorbed [57]. Hence,

$$\begin{array}{cc}\hfill S_{\mathrm{eff}}=& S_{\mathrm{HP}}[e,\omega ]+S_D[e,\omega ,\psi ,\overline{\psi }]+\frac{1}{16\pi G}\times \int {\gamma }^{{}^{\prime }}\left(x\right)\left(T^c\wedge T_c-e_c\wedge e_d\wedge R^{cd}\right),\hfill \end{array}$$

(74)

where ${\gamma }^{{}^{\prime }}\left(x\right)=\gamma \left(x\right)+\frac{4G}{\pi }\beta {\Lambda }^2$.

Pros and Cons of the Peccei–Quinn Mechanism in Gravity and the Nature of the BI Parameter

In this proposal, the $\gamma$ is promoted as a field using the Peccei–Quinn mechanism in LQG. This notion is essential, since it removes divergence from the total effective action. However, the origin of the complex valued $\gamma$ is still open for exploration.

2.10. The Kodama State and the BI Parameter

In year 2006, suggested Randono [58,59] the generalization of Kodama states, in which the real valued $\gamma$ was used to generalize these states and derived physical interpretation of these states. The Kodama state is special, providing an exact solution to all the normal constraints of canonical quantum gravity.

The Kodama state has an unambiguous semi-classical interpretation as a quantum sort of classical spacetime (anti-de Sitter space). However, the structure of the phase space is complex. Therefore, a generalization of the real valued $\gamma$ state is needed [58].

The state of Lorentzian Kodama is a solution to the quantum constraints in the Ashtekar formalism, in which the connection is complex valued. However, to get the classical GR, one has to execute the reality conditions ensuring the reality of the metric [58].

In the Euclidean framework formalism, the $SO\left(4\right)$ group is divided into two left and right parts, as in the complex framework. The Ashtekar variables exhibit a real valued $SO\left(3\right)$ connection, and its real valued momentum conjugate for the left-handed part of the group. The corresponding state in the Euclidean framework is a pure phase, because the connection is real. Thus, the state is written as [58],

$$\Psi \left[A\right]=\mathcal{N}{e}^{-\frac{3}{4\kappa \lambda }}\int Y_{\mathrm{CS}}\left[A\right],$$

(75)

where $\int Y_{\mathrm{CS}}\left[A\right]$ is the Chern–Simon term, $\lambda =G\hslash \Lambda$ with $\Lambda$ the cosmological constant, and $\mathcal{N}$ being topology dependent normalization.

For this result, no reality condition is required, since the structure of the phase space of the Euclidean framework is simple. Hence, the complexification of the phase space (in which the $\gamma$ is the complex valued $\gamma =i$) is the main reason for the requirement of the reality conditions [58].

The Kodama state beginning with the Holst action with the cosmological constant is given as [58],

$$S_{\mathrm{H}}=\frac{1}{\kappa }{\int }_{\mathcal{M}}\star e\wedge e\wedge R+\frac{1}{\gamma }e\wedge e\wedge R-\frac{\lambda }{3}\star e\wedge e\wedge e\wedge e,$$

(76)

where $e=\frac{1}{2}{\gamma }_J{e}^J$, $R=\frac{1}{4}{\gamma }_{[J}{\gamma }_{K]}{\omega }^{JK}$, $\star =-i{\gamma }^5={\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3$, and $\mathcal{M}$ is the manifold.

The chiral symmetric Holst action is written as [58]

$$\begin{array}{c}S=\frac{1}{\kappa }{\int }_{\mathcal{M}}2\left({\alpha }_L{P}_L+{\alpha }_R{P}_R\right)\star \Sigma \wedge \left(R-\frac{\lambda }{6}\right)\\ =\frac{2}{\kappa }{\int }_{\mathcal{M}}{\alpha }_L\star {\Sigma }_L\wedge \left(R_L-\frac{\lambda }{6}{\Sigma }_L\right)+{\alpha }_R\star {\Sigma }_R\wedge \left(R_R-\frac{\lambda }{6}{\Sigma }_R\right).\end{array}$$

Here, ${\Sigma }_R={(e\wedge e)}_R$, $P_L$ and $P_R$ are left-handed and right-handed chiral projection operators, $R_L$ and $R_R$ are the left-handed and right-handed chiral curvatures for $spin(3,1)$ connection.

If ${\alpha }_L+{\alpha }_R=1$ and $\gamma =\frac{-i}{{\alpha }_L-{\alpha }_R}$, the equation becomes [58]

$$S=\frac{1}{\kappa }{\int }_{\mathcal{M}}\left({\alpha }_L+{\alpha }_R\right)\star \Sigma \wedge \left(R-\frac{\lambda }{6}\Sigma \right)+i\left({\alpha }_L-{\alpha }_R\right)\Sigma \wedge R.$$

(77)

In year 2011, Wieland [60] gave a proposal, namely complex Ashtekar variables, the Kodama state and spinfoam gravity, in which the complex valued Ashtekar variable and the real valued $\gamma$ were used. In Ref. [60], the author used $SL(2,\mathbb{C})$ Kodama state and proposed a spinfoam vertex amplitude.

As per the usual method, it also started with the Holst action with the cosmological constant, $\Lambda$ [60], i.e.,

$$S[e,\omega ]=\frac{\hslash }{4l_P^2}{\int }_{\mathcal{M}}{e}^J\wedge e^K\wedge \left({ϵ}_{JKLM}{R}^{LM}\left[\omega \right]-\frac{2}{\gamma }{R}_{JK}\left[\omega \right]-\frac{\Lambda }{6}{ϵ}_{JKLM}{e}^L\wedge e^M\right).$$

(78)

where $\gamma \in \mathbb{R}$.

As mentioned, in this proposal, the real valued $\gamma$ and the complex valued Ashtekar variable are considered [60].

Pros and Cons of the Kodama State and the BI Parameter

The generalization of the Kodama state can only be achieved with the real valued $\gamma$, since, the $\gamma$ with the complex value makes the state complex and ambiguous. Here, the significance of the complex valued BI parameter is also unclear.

2.11. The Quantum Gravity BI Parameter—A General Physical and Topological Interpretation

In the year 2013, El Naschie [61] gave a proposal on general physical and topological interpretation of the $\gamma$. This proposal is not directly related to LQG. In this paper, the $\gamma$ of LQG is considered as a definite quantum entanglement correction.

According to this proposal, the $\gamma$ is not only a free basic parameter of LQG; it is also an exact sort of a basic constant of the micro-spacetime topology [61].

As mentioned in Section 2.3, one of the fixed values of the $\gamma$ from black hole entropy calculation in LQG is given as [61]

$$\gamma =\frac{log2}{\pi \sqrt{3}}=0.055322.$$

(79)

From Hardy’s quantum entanglement, the author proposed that the value of the $\gamma$ is same as that obtained from quantum entanglement correction [61], i.e.,

$$\gamma ={\varphi }^6={\left(\frac{\sqrt{5}-1}{2}\right)}^6=0.055728.$$

(80)

Pros and Cons of the Quantum Gravity BI Parameter—A General Physical and Topological Interpretation

This proposal advocates the real valued $\gamma$. It does not explain the physical significance of the $\gamma$ in LQG.

2.12. A Correction to the BI Parameter of SU(2) Spin Networks

In year 2014, Sadiq [62] gave a correction to the $\gamma$ of $SU\left(2\right)$ spin networks. In this paper, by taking $j=1$ and to preserve the $SU\left(2\right)$ symmetry of theory, twice the value of the $\gamma$ is proposed. Previously in LQG, the $\gamma$ was fixed by $j=1$ transitions of spin networks as the dominant processes instead of $j=1/2$ transitions. This means $SO\left(3\right)$ should be a gauge group instead of $SU\left(2\right)$.

This proposal begins with [35] (see Section 2.3) and gave a correction to the $\gamma$. The author investigated that if $SU\left(2\right)$ is the compatible gauge group and $j_{\min }=1$ process governs, then the change in the mass of the black hole during the transition is [62]

$$\Delta M=2\hslash {\omega }_{\mathrm{QNM}}.$$

(81)

Since the value of ${\omega }_{\mathrm{QNM}}$ is ${\omega }_{\mathrm{QNM}}=ln3/\left(8\pi M\right)$, the change in the mass is [62]

$$\Delta M=\frac{2\hslash ln3}{8\pi M}.$$

(82)

Therefore, the fixed value of $\gamma$ for $j_{\min }=1$ is [62]

$$\gamma =\frac{ln3}{\pi \sqrt{2}}.$$

(83)

Pros and Cons of a Correction to the BI Parameter of $SU\left(2\right)$ Spin Networks

In this proposal, the author modified the fixed value of the $\gamma$; that was proposed in [35]. This proposal advocates the real valued $\gamma$. The physical significance is based on the black hole entropy calculation in LQG.

2.13. Physical Effect of the Immirzi Parameter in LQG

In this proposal, Perez and Rovelli [63] proposed that the BI term in the (Holst) action does not disappear on the shell when fermions are there. The BI term is also present in the equations of motion. The $\gamma$ governs the coupling constant of a four-fermion interaction (it is mediated by a torsion). In other words, the $\gamma$ is a coupling constant that governs the strength of a four-fermion interaction. Thus, the $\gamma$ may show physical effects that can be observed independently from LQG.

The Holst action with the fermionic field is expressed as [63]

$$S[e,A,\psi ]=S[e,A]+\frac{i}{2}\int d^{4}xe\left(\overline{\psi }{\gamma }^J{e}_J^c{D}_c\psi -\overline{D_c\psi }{\gamma }^J{e}_J^c\psi \right),$$

(84)

where $S[e,A]=\frac{1}{16\pi G}\left(\int d^{4}xe{e}_J^c{e}_K^d{F}_{cd}^{JK}-\frac{1}{\gamma }\int d^{4}xe{e}_J^c{e}_K^d\ast F_{cd}^{JK}\right)$, $D_c$ is a covariant derivative, and ${\gamma }^J$ is the Dirac matrix. In this proposal, $D_{[c}{e}_{d]}^J$ is the fermionic current. In the connection, the fermion current behaves as a source for a torsion component [63].

In the fermionic current, the linear terms are total derivative; hence, the resulting action is

$$S[e,\psi ]=S\left[e\right]+S_f[e,\psi ]+S_{int}[e,\psi ],$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \therefore S[e,\psi ]=& \frac{1}{16\pi G}\int d^{4}xe{e}_J^c{e}_K^d{F}_{cd}^{JK}\left[\omega \left[e\right]\right]+i\int d^{4}xe\overline{\psi }{\gamma }^J{e}_J^c{D}_c\left[\omega \left[e\right]\right]\psi \hfill \\ & -\frac{3}{2}\pi G\frac{{\gamma }^2}{{\gamma }^2+1}\int d^{4}xe\left(\overline{\psi }{\gamma }_5{\gamma }_A\psi \right)\left(\overline{\psi }{\gamma }_5{\gamma }^A\psi \right).\hfill \end{array}\end{array}$$

(85)

The standard coupling of the Einstein–Cartan theory is recovered in the third term with the limit $\gamma \to \infty$ [63].

Pros and Cons of Physical Effect of the Immirzi Parameter in LQG

In this proposal, the $\gamma$ is a coupling constant that governs the strength of a four-fermion interaction. Here, the $\gamma$ is indeed free parameter. $\gamma =i$ gives the self-dual Ashtekar canonical formalism and $\gamma =1$ (real valued) gives the $SU\left(2\right)$ Barbero connection.

2.14. A Relation between the BI Parameter and the Standard Model

In the year 2010, Broda and Szanecki [64] established the relationship between the $\gamma$ and the standard model.

In this proposal, Sakharov’s method was used with the Nieh–Yan term (in the Holst action) that fixed the $\gamma$ by considering the Lagrangian density [64], i.e.,

$$\mathcal{L}=\alpha \star \left(e^c\wedge e^d\right)\wedge R_{cd}-\beta \left(T^c\wedge T_d-e^c\wedge e^d\wedge R_{cd}\right),$$

(86)

where $\gamma =\alpha /\beta$.

The Einstein–Hilbert Lagrangian is written as [64]

$${\mathcal{L}}_{\mathrm{EH}}=-\frac{1}{12}{\left(\frac{M}{4\pi }\right)}^2\left(N_0+N_{\frac{1}{2}}-4N_1\right)\star \left(e^c\wedge e^d\right)\wedge R_{cd},$$

(87)

where $N_1$ is the gauge fields number, $N_{\frac{1}{2}}$ the two-component fermion fields number, and $N_0$ is the minimal scalar degrees of freedom number. Here, the $\gamma$ is defined as [64]

$$\gamma =\frac{-\frac{1}{12}\left(N_0+N_{\frac{1}{2}}-4N_1\right)}{-\frac{1}{4}{N}_L}=\frac{1}{9}\approx 0.11.$$

(88)

Here, $N_L$ is the number of the chiral left-handed modes. By taking $N_0=4$ (for Higgs), $N_1=12$, $N_{\frac{1}{2}}=45$ and $N_L=3$ (3 neutrinos) [64].

This is approximately equal to one of the values of the BI parameter in black hole entropy calculation in LQG [64],

$$\gamma =\frac{ln2}{\pi \sqrt{3}}\approx 0.13.$$

(89)

Pros and Cons of a Relationship between the BIParameter and the Standard Model

This proposal established a relationship between the $\gamma$ and the standard model. It advocates the real valued $\gamma$ by comparing the results with the black hole entropy calculation in LQG. Similar to other proposals, the significance of the complex valued $\gamma$ is less emphasized.

2.15. The Holographic Principle and the BI Parameter of LQG

In the year 2015, Sadiq [65] gave a proposal that correlates the $\gamma$ in LQG and the holographic principle. In this proposal, the $\gamma$ is fixed using the equipartition theorem based on LQG at holographic boundary in such a way that the Unruh–Hawking law of temperature holds and follows. Such derived value of the $\gamma$ exhibits validity universally. In this way, this approach correlates the value of the $\gamma$ in LQG and the holographic principle. In this proposal, the real valued BI parameter is considered. Since the relation between the holographic principle and LQG demands more research, this proposal is given in brief.

Pros and Cons of the Holographic Principle and the BI Parameter of LQG

Similar to majority of the proposals, this proposal also advocates the real valued BI parameter.

2.16. Discussion

The $\gamma$ is a free parameter as well as an enigmatic parameter of LQG. It is a free parameter because it can be real valued as well as complex valued. It is enigmatic parameter because its significance for either the real value or with the complex value is still obscure.

As mentioned, there are two kinds of version for the connection variables: $SL(2,\mathbb{C})$, with a self-duality of Ashtekar formalism, $\gamma =i$, and the connection with a real $SU\left(2\right)$ Barbero connection, $\gamma =1$.

If LQG is compared with the other quantum gravity theory, it has only one free parameter in its formalism. Here, several proposals on the physical significance of the $\gamma$ are discussed. Some argue in favor of the real valued BI parameter, while the others argue in favor of the complex valued BI parameter. The real valued proposals on BI parameter are more tangible. The value of the BI parameter found from the Black hole entropy calculation in LQG has more consent than other proposals because the same value is applied for all sorts of black holes.

Still, the exact physical significance of the $\gamma$ is yet to be found. There are several questions regarding the choice of the BI parameter, which are discussed via various proposals. The most important question is regarding the physical significance of the area operator and the volume operator spectrum with the complex valued BI parameter. The complex valued BI parameter is also important because it removes the mathematical complexities from the equations of the constraints, especially from the Hamiltonian constraint. Research on the physical significance of the complex valued BI parameter $\gamma =i$ will open up a new direction in the field of quantum gravity. Time will shed light on these mysteries.

3. Concluding Remarks

• In this paper, initially, a short introduction of the Barbero–Immirzi (BI) parameter, $\gamma$, along with the introduction to the Ashtekar formalism, the origin of the BI parameter, the Holst action and a historical timeline of research on the physical significance of the $\gamma$ in LQG are given.
• The value of the $\gamma$ and its implication are very important, especially in the area operator spectrum and the black hole entropy calculation in LQG; afterwards, these are elaborated on.
• Thereafter, various proposals on the physical significance of the $\gamma$ in LQG are given in brief with their pros and cons.
• Most of the proposals advocate the real valued BI parameter $\gamma$, since the significance of the complex valued BI parameter $\gamma$ is not yet clear. However, the complex valued $\gamma$ is also important, as it removes mathematical complexities from the LQG framework. Research on the complex valued BI parameter will shed light on its physical significance in future.
• Hence, the $\gamma$, whether it is complex valued or the real valued, is a crucial free parameter of LQG.