The Impact of Radio Frequency Waves on the Plasma Density in the Tokamak Edge
Abstract
:1. Introduction
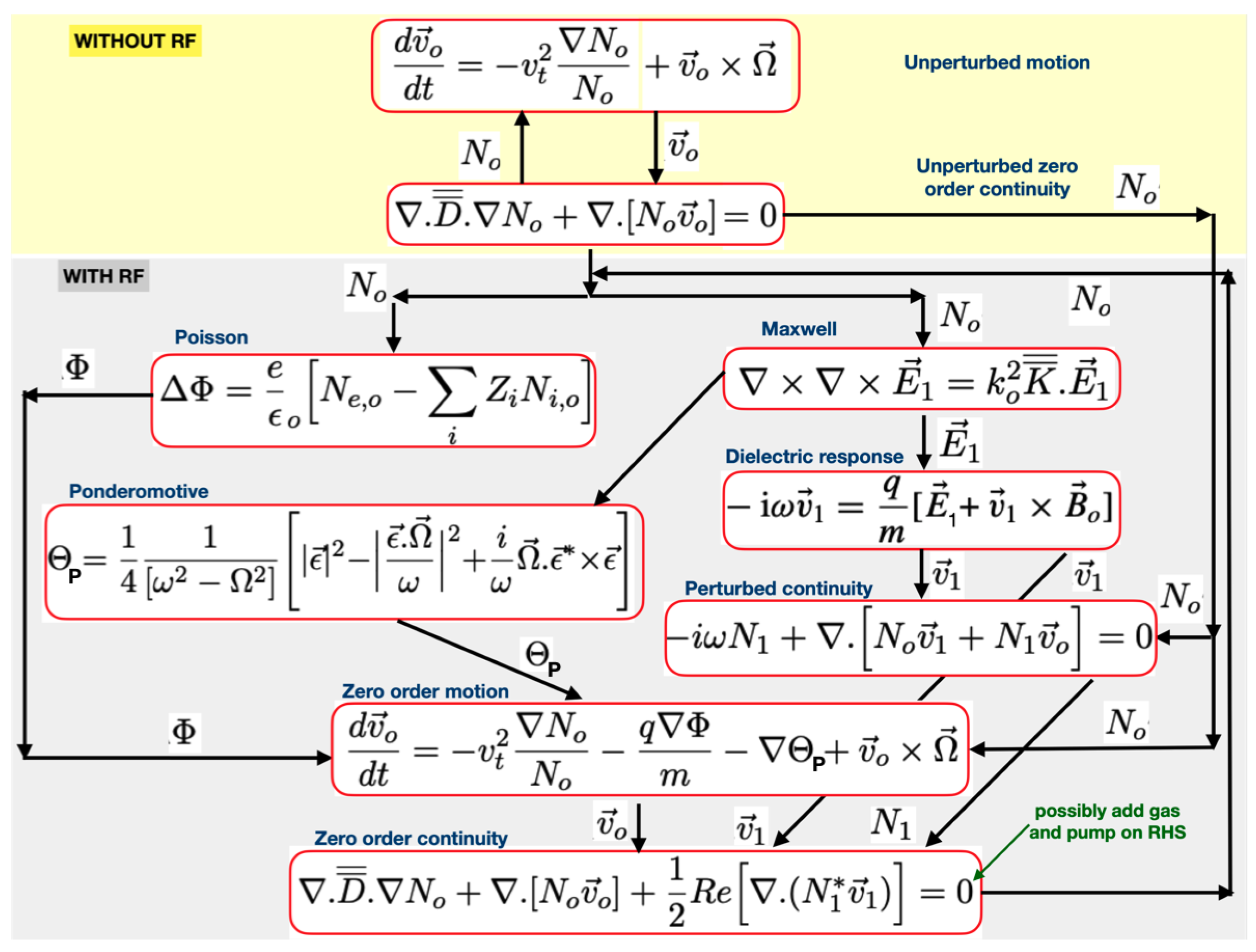
2. Adopted Set of Equations
3. Boundary Conditions
- For the rapidly varying electric field (Maxwell’s equations for waves in cold plasma):
- –
- 4th-order equation, so four boundary conditions in each direction,
- –
- imposed and at antenna side,
- –
- purely outgoing wave or metallic boundary conditions at the plasma edge (but—if desired—artificial damping imposed to ensure waves are damped before actually reaching the edge),
- –
- and and their poloidal derivatives identical at top and bottom.
- For the electrostatic potential (Poisson’s equation modelling the effect of charge neutrality breaking):
- –
- 2nd-order equation, so one boundary condition at each edge,
- –
- at the plasma side, force the potential to be zero: no RF perturbations far away from the antenna,
- –
- at the antenna side and since the antenna is a metallic object, either impose a zero normal derivative (electric field perpendicular to metallic object) or impose a potential (imposed by the loading of the metallic wall when field lines not fully parallel to it),
- –
- on the poloidal side impose the potential and its normal derivative to be identical on top and bottom.
- For the slowly varying density ( continuity equation):
- –
- 2nd-order equation, so one boundary condition at each side,
- –
- impose to be identical to the imposed one at the plasma side: no perturbation far away from the wave launcher,
- –
- impose negligible density at the antenna side (except for small corrections, exponential decay beyond the last closed flux surface),
- –
- impose same and normal derivative at top and bottom (poloidal) side.
- For the fast-varying density ( continuity equation):
- –
- 1st-order equation, so one boundary condition only on one side in each direction,
- –
- no perturbation at plasma side well away from antenna,
- –
- same density top/bottom.
- For the slowly varying velocity for each of the species (equation of motion):
- –
- check if the non-linear term is significant; if not, simply omit it and solve this equation analytically,
- –
- if the term is required: transform the non-linear equation into a series of linear “adiabatic switch-on” artificial time steps with the non-linear solution as the asymptotic solution of the linearized problem,
- –
- 1st-order vector equation, so one boundary for each unknown only on one side,
- –
- at plasma side: no RF-induced perturbation far away from the RF launcher,
- –
- same velocity top and bottom.
4. General Purpose Solver
Equation and Boundary Conditions
5. Examples
5.1. Solution of the Wave Equation
5.2. Poisson’s Equation
5.3. Perturbed Density
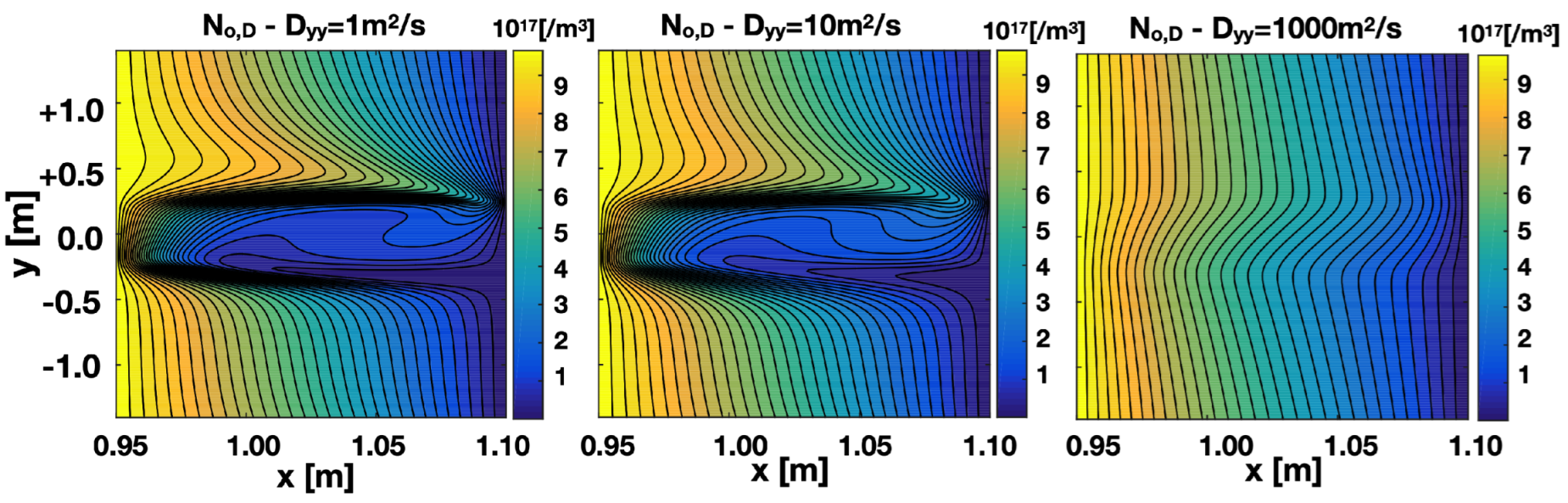
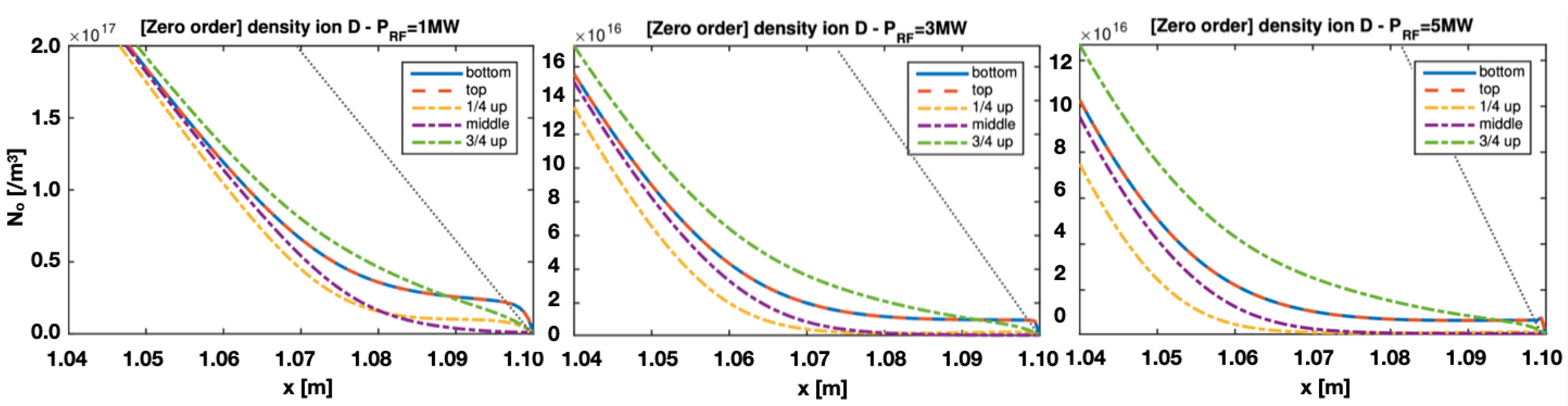
5.4. Zero-Order Density Correction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DTE2 | Second Deuterium–Tritium Experimental campaign |
| ICRH | ion cyclotron resonance heating |
| JET | Joint European Torus |
| MUMPS | MUltifrontal Massively Parallel Solver |
| RF | radio frequency |
| 1D | one-dimensional |
References
- Mailloux, J.; Abid, N.; Abraham, K.; Abreu, P.; Adabonyan, O.; Adrich, P.; Afanasev, V.; Afzal, M.; Ahlgren, T.; Aho-Mantila, L.; et al. Overview of JET results for optimising ITER operation. Nucl. Fusion 2022, 62, 042026. [Google Scholar] [CrossRef]
- Garzotti, L. Overview of results of scenario development for high fusion performance from DTE2 campaign at JET. In Proceedings of the 48th Annual Plasma Physics Conference, Liverpool, UK, 11–14 April 2022. [Google Scholar]
- Maggi, C.; JET contributors. Tritium experiments in JET-ILW in support of JET and ITER D-T plasmas. In Proceedings of the 48th EPS Conference on Plasma Physics, online, 27 June–1 July 2022; Available online (abstract): https://indico.fusenet.eu/event/28/contributions/216/ (accessed on 17 December 2022).
- Challis, C.; Hobirk, J.; Kappatou, A.; Lerche1, E.; Auriemma, F.; Belonohy, E.; Casson, F.J.; Coffey, I.; Eriksson, J.; Field, A.R.; et al. JET contributors. Development of hybrid (high beta) plasmas for deuterium-tritium operation in JET. In Proceedings of the 48th EPS Conference on Plasma Physics, online, 27 June–1 July 2022; Available online: https://indico.fusenet.eu/event/28/contributions/219/ (accessed on 17 December 2022).
- Maslov, M.; Lerche, E.; Challis, C.D.; Hobirk, J.; Kappatou, A.; King, D.B.; Keeling, D.; Rimini, F.; De La Luna, E.; Monakhov, I.; et al. T-rich scenario for the record fusion energy plasma in JET DT. In Proceedings of the 64th] Annual Meeting of the APS Division of Plasma Physics (APS), Spokane, WA, USA, 17–21 October 2022; Available online (abstract): https://meetings.aps.org/Meeting/DPP22/Session/BI01.3 (accessed on 17 December 2022).
- Noterdaeme, J.M.; Eriksson, L.-G.; Mantsinen, M.; Mayoral, M.-L.; Eester, D.V.; Mailloux, J.; Gormezano, C.; Jones, T.T.C. Physics studies with the additional heating systems in JET. Fusion Sci. Technol. 2008, 53, 1103–1151. [Google Scholar] [CrossRef]
- Koch, R. Plasma Heating by neutral beam injection. Fusion Sci. Technol. 2004, 45, 183–192. [Google Scholar] [CrossRef]
- Messiaen, A.; Maquet, V. Coaxial and surface mode excitation by an ICRF antenna in large machines like DEMO and ITER. Nucl. Fusion 2020, 60, 076014. [Google Scholar] [CrossRef]
- Maquet, V.; Druart, A.; Messiaen, A. Analytical edge power loss at the lower hybrid resonance: ANTITER IV validation and application to ion cyclotron resonance heating systems. J. Plasma Phys. 2021, 87, 905870617. [Google Scholar] [CrossRef]
- Giroud, C.; Pitts, R.A.; Kaveeva, E.; Rozhansky, V.; Brezinsek, S.; Huber, A.; Mailloux, J.; Marin, M.; Tomes, M.; Veselova, I.; et al. JET contributors. High performance Ne-seeded baseline scenario in JET-ILW in support of ITER. In Proceedings of the 48th EPS Conference on Plasma Physics, Maastricht, The Netherlands, 27 June–1 July 2022; Available online (abstract): https://indico.fusenet.eu/event/28/contributions/500/ (accessed on 17 December 2022).
- Colas, L.; Urbanczyk, G.; Goniche, M.; Hillairet, J.; Bernard, J.M.; Bourdelle, C.; Fedorczak, N.; Guillemaut, C.; Helou, W.; Bobkov, V.V.; et al. The geometry of the ICRF-induced wave-SOL interaction. A multi-machine experimental review in view of the ITER operation. Nucl. Fusion 2022, 62, 016014. [Google Scholar] [CrossRef]
- Colas, L.; Lu, L.; Jacquot, J.; Tierens, W.; Křivská, A.; Heuraux, S.; Faudot, E.; Tamain, P.; Després, B.; Van Eester, D.; et al. SOL RF physics modelling in Europe, in support of ICRF experiments. EPJ Web Conf. 2017, 157, 01001. [Google Scholar] [CrossRef] [Green Version]
- Colas, L.; Gunn, J.P.; Nanobashvili, I.; Petržílka, V.; Goniche, M.; Ekedahl, A.; Heuraux, S.; Joffrin, E.; Saint-Laurent, F.; Balorin, C.; et al. 2-D mapping of ICRF-induced SOL perturbations in Tore Supra tokamak. J. Nucl. Mater. 2007, 363–365, 555–559. [Google Scholar] [CrossRef]
- Bobkov, V.; Balden, M.; Bilato, R.; Braun, F.; Dux, R.; Herrmann, A.; Faugel, H.; Fünfgelder, H.; Giannone, L.; Kallenbach, A.; et al. ICRF operation with improved antennas in ASDEX Upgrade with W wall. Nucl. Fusion 2013, 53, 093018. [Google Scholar] [CrossRef] [Green Version]
- Bobkov, V.; Aguiam, D.; Bilato, R.; Brezinsek, S.; Colas, L.; Faugel, H.; Fünfgelder, H.; Herrmann, A.; Jacquot, J.; Kallenbach, A.; et al. Making ICRF power compatible with a high-Z wall in ASDEX Upgrade. Plasma Phys. Control. Fusion 2016, 59, 014022. [Google Scholar] [CrossRef]
- Bobkov, V.; Bilato, R.; Colas, L.; Dux, R.; Faudot, E.; Faugel, H.; Fünfgelder, H.; Herrmann, A.; Jacquot, J.; Kallenbach, A.; et al. Characterization of 3-strap antennas in ASDEX Upgrade. EPJ Web Conf. 2017, 157, 03005. [Google Scholar] [CrossRef]
- Tournay, N. Modelling Near-Antenna Plasma-Wave Interaction. Master’s Thesis, Université Libre de Bruxelles, Brussels, Belgium, 2022. [Google Scholar]
- Lancellotti, V.; Milanesio, D.; Maggiora, R.; Vecchi, G.; Kyrytsya, V. TOPICA: An accurate and efficient numerical tool for analysis and design of ICRF antennas. Nucl. Fusion 2006, 46, S476–S499. [Google Scholar] [CrossRef]
- Louche, F.; Lamalle, P.U.; Dumortier, P.; Messiaen, A.M. Three-dimensional electromagnetic modeling of the ITER ICRF antenna (external matching design). AIP Conf. Proc. 2005, 787, 190–193. [Google Scholar] [CrossRef]
- Usoltceva, M.; Tierens, W.; Kostic, A.; Noterdaeme, J.-M.; Ochoukov, R.; Zhang, W. 3D RAPLICASOL model of simultaneous ICRF FW and SW propagation in ASDEX upgrade conditions. AIP Conf. Proc. 2020, 2254, 050003. [Google Scholar] [CrossRef]
- Klima, R. The drifts and hydrodynamics of particles in a field with a high-frequency component. Czech. J. Phys. B 1968, 18, 1280–1291. [Google Scholar] [CrossRef]
- Stix, T.H. Waves in Plasmas; AIP: Melville, NY, USA, 1992. [Google Scholar]
- Swanson, D.G. Plasma Waves; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- MUMPS: MUltifrontal Massively Parallel Sparse Direct Solver. Available online: https://graal.ens-lyon.fr/MUMPS/index.php (accessed on 17 December 2017).
- Van Eester, D.; Crombé, K.; Kyrytsya, V. Ion cyclotron resonance heating-induced density modification near antennas. Plasma Phys. Control. Fusion 2013, 55, 025002. [Google Scholar] [CrossRef]
- Bora, D.; Ivanov, R.S.; Van Oost, G.; Samm, U. Effects of ICRH on electrostatic fluctuations and particle transport in the boundary plasma of TEXTOR. Nucl. Fusion 1991, 31, 2383–2391. [Google Scholar] [CrossRef]
- Lee, N.C.; Parks, G.K. Ponderomotive force in a warm two-fluid plasma. Phys. Fluids 1983, 26, 724–729. [Google Scholar] [CrossRef]
- Stratham, G.; Ter Haar, D. Strong turbulence of a magnetized plasma. II. The ponderomotive force. Plasma Phys. 1983, 25, 681–698. [Google Scholar] [CrossRef]
- Sawley, M.L. Self-consistent calculation of the ponderomotive force in a magnetized plasma column. Plasma Phys. Control. Fusion 1985, 27, 957–968. [Google Scholar] [CrossRef] [Green Version]
- Smithe, D.N.; Jenkins, T.G.; King, J.R. Improvements to the ICRH antenna time-domain 3D plasma simulation model. AIP Conf. Proc. 2015, 1689, 050004. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Bilato, R.; Bobkov, V.; Cathey, A.; Di Siena, A.; Hoelzl, M.; Messiaen, A.; Myra, J.R.; Suárez López, G.; Tierens, W.; et al. Recent progress in modeling ICRF-edge plasma interactions with application to ASDEX Upgrade. Nucl. Fusion 2022, 62, 075001. [Google Scholar] [CrossRef]
- Barnett, R.L.; Green, D.L.; Waters, C.L.; Lore, J.D.; Smithe, D.N.; Myra, J.R. RF-transpond: A 1D coupled cold plasma wave and plasma transport model for ponderomotive force driven density modification parallel to B0. Comp. Phys. Comm. 2022, 274, 108286. [Google Scholar] [CrossRef]
- Barnett, R.L.; Green, D.L.; Waters, C.L.; Lore, J.D.; Smithe, D.N.; Myra, J.R.; Lau, C.; Van Compernolle, B.; Vincena, S. Ponderomotive force driven density modifications parallel to B0 on the LAPD. Phys. Plasmas 2022, 29, 042508. [Google Scholar] [CrossRef]
- Jenkins, T.G.; Smithe, D.N.; Umansky, M.V.; Dimits, A.M.; Rognlien, T.D. Modeling RF-induced ponderomotive effects on edge/SOL transport: NSTX and beyond. In Proceedings of the 24th Topical Conference on Radio-Frequency Power in Plasmas, Annapolis, MD, USA, 26–28 September 2022; Available online (Book of Abstracts): https://web.cvent.com/event/4a35efca-19ed-47cc-9ba9-388d856ade7d/websitePage:eddac876-adfd-40bb-99cd-66eaa4414435 (accessed on 17 December 2022).






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Eester, D.; Tournay, N. The Impact of Radio Frequency Waves on the Plasma Density in the Tokamak Edge. Physics 2023, 5, 116-130. https://doi.org/10.3390/physics5010009
Van Eester D, Tournay N. The Impact of Radio Frequency Waves on the Plasma Density in the Tokamak Edge. Physics. 2023; 5(1):116-130. https://doi.org/10.3390/physics5010009
Chicago/Turabian StyleVan Eester, Dirk, and Nil Tournay. 2023. "The Impact of Radio Frequency Waves on the Plasma Density in the Tokamak Edge" Physics 5, no. 1: 116-130. https://doi.org/10.3390/physics5010009
APA StyleVan Eester, D., & Tournay, N. (2023). The Impact of Radio Frequency Waves on the Plasma Density in the Tokamak Edge. Physics, 5(1), 116-130. https://doi.org/10.3390/physics5010009




