Abstract
The photon production by conversion of gluons via quark loop in the framework of the mean-field approach to the QCD (quantunm chromodynamics) vacuum is studied here. According to the domain model of QCD vacuum, the confinement phase is dominated by Abelian (anti-)self-dual gluon fields, while the deconfinement phase is characterized by a strong chromomagnetic field. In the confinement phase, photon production is impossible due to the random spacial orientation of the statistical ensemble of vacuum fields. However, the conditions of Furry theorem are not satisfied in the deconfinement phase, the conversion of gluons is nonzero and, in addition, photon distribution has a strong angular anisotropy. Thus, the photon production in the discussed process acts as one of the important features of transition in quark-gluon plasma to the deconfinement phase.
1. Introduction
An extremely high photon signal was detected for the first time in CERN (the European Organization for Nuclear Research, Geneva, Switzerland) experiment during heavy ion collisions [1]. The photon excess became one of the first experimental indication of quark–gluon plasma (QGP) in hadronic matter under extreme conditions. The experimental data were confirmed and refined later by PHENIX [2] and ALICE [3] experiments. In addition, photons had strong angular anisotropy which had not been predicted. This effect is called direct photon flow puzzle. In Refs. [4,5], it was shown that the strong short-living magnetic field with a singled direction is generated in collision processes of relativistic heavy ions which can lead to various observed effects. Among these effects, there are additional photonic sources which have been discussed in [6,7,8,9,10].
Here, we calculate the photon production in the conversion process of gluons, , via quark loop (see Figure 1) in the presence of a homogeneous Abelian gauge field. Our calculation is based on the mean-field approach within the domain model of QCD (quantum chromodynamics) vacuum and hadronization [11,12,13]. According to this approach, in the confinement phase, the entire space is filled by the domain-structured Abelian that is almost entirely made up of homogeneous (anti-)self-dual gluon fields, whereas the chromomagnetic field dominates in the walls that separate (anti-)self–dual space areas. The quasiparticles with a color charge exist in the chromomagnetic field, and these quasiparticles are interpreted as quarks and gluons that correspond to the deconfinement phase. The described interpretation seems to be consistent with studies of lattice QCD [14]. Importantly, the short-living strong magnetic field with a singled space direction generated in heavy ion collisions is a catalyst for deconfinement [11]; that is, the magnetic field induces the long-living chromomagnetic field with the same space direction. This paper is mainly based on our earlier study [15], for which the results are outlined below.
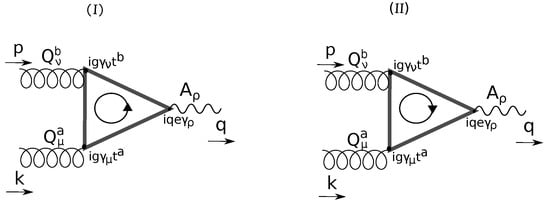
Figure 1.
The diagrams of process via quark loop in the presence of homogeneous Abelian gauge field. p and k are momenta of gluons and respectively, q is the photon () momentum. The closed arrows inside the triangle diagrams (I,II) indicate the direction of quark loop momentum. See text for more details.
2. Gluon Conversion in the Confinement Phase
Let us discuss the photon production in the confinement phase. According the domain model of a QCD vacuum and hadronization, this phase is dominated by a random ensemble of the Abelian (anti-)self-dual gluon field:
where is the Gell-Mann matrix and field strength B sets the scale related to the value of the scalar gluon condensate. The Greek letters denote the temporal (0) and spacial (1, 2, and 3) components. is the Levi-Civita symbol and is the Kronecker delta. The quark propagator with mass in the presence of the field (1) has the form [12]
where the anti-Hermitean representation of Dirac matrices () in Euclidean space-time is used. x, y, and z are the space coordinates, and , where . Sign “±” corresponds to (anti-)self-duality of the background field (1). The invariant part of the propagator is an entire analytical function in the complex momentum plane; thus, the propagator demonstrates confinement. The amplitudes for diagrams (I,II) in Figure 1 are given by
Here, g is the strong coupling constant, p and k are momenta of gluons, q is the photon momentum, e is the electron charge, Q is diagonal matrix of quark charges in units of e, vectors define the polarization of the gluons and photon (not to be confused with the Levi-Civita tensor .). “Tr” denotes trace with respect to color, Dirac and flavor indices, and denotes averaging of the amplitude over different random configurations of the background vacuum field, (anti-)self-duality and spacial orientation.
The expressions for amplitudes and differ in the sign of the phase factor: for diagram (I) and for diagram (II), where is an arbitrary antisymmetric tensor. Integration over spacial direction of the background field is achieved by using the master formula [12]:
where and the results of averaging over the spacial direction of the vacuum field are related to the phase sign as follows:
where n denotes the quantity of tensor in terms of amplitudes and .
As a consequence, the terms in the amplitude with an odd number of the field tensors cancel each other out because of averaging over the background vacuum field direction, while the terms with an even number of cancel each other out according to the Furry theorem (or charge parity). Therefore, in the confinement phase the gluon conversion does not lead to photon production.
3. Gluon Conversion and Photon Production in the Deconfinement Phase
The strong short-living magnetic field generated in relativistic heavy ion collisions is a trigger for the deconfinement phase transition, which is characterized by the long-living chromomagnetic field [11,12]. The lifetime and strength of the chromomagnetic field are related to the scalar gluon condensate, . A relevance of nonzero absolute value of topological charge density (or, equivalently, the condensate ) to confinement has been discussed in recent lattice QCD studies [16,17]. Let us estimate the photon production due to the gluon conversion in the constant background chromomagnetic field. The long-living chromomagnetic field and initially generated magnetic field are co-directed [11]. For clarity, we select the third spacial axis, , along the direction of the background (chromo)magnetic field:
all other components of are equal to zero. Respectively, we denote spacial transverse ⊥ and longitudinal ‖ coordinates and momenta (in Euclidean space-time):
respectively.
The quark propagator with mass including the contribution of all Landau levels in the presence of an external chromomagnetic field has the form,
After the evaluation of trace and integration over spacial variables, one obtains the expression for the amplitude :
where denotes the tensor structure, denotes the form factor (some of are shown in Figure 2). The full expression for each of the tensors and form factors can be found in our recent study [15].
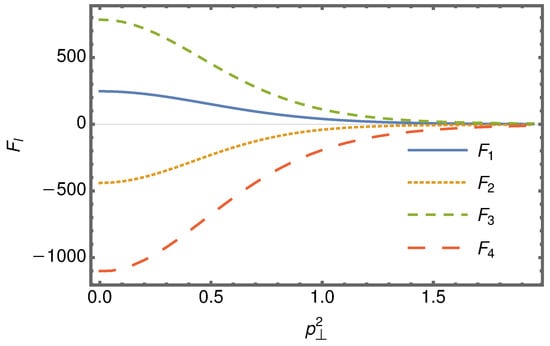
Figure 2.
Some form factors, such as the function of transverse gluon momenta, , for longitudinal momenta, . Dimensionless notations and are used, form factors are dimensionless. See [15] for the detailed form of and .
The details of the calculation of the on-shell amplitude squared (analytical continuation to Minkowsky space, integration of quark proper time s) are given in Ref. [15]. Let us now turn attention to a brief description of the results. The squared amplitude for photon production by gluon conversion in the limit of a strong field, alongside massless quarks with the lowest (LLL) and first Landau levels (1LL) as the propagators [8] take the form
where is the strength of the magnetic field, B is the strength of the chromomagnetic field, and are the electromagnetic and strong coupling constants, respectively, is the colors quantity, denotes the color trace, and is the quark charge in units of electron charge. As one can see from the dependence of the squared amplitude, , in Figure 3, the chromomagnetic field (dotted line) enhances the conversion at small transverse momenta, , in comparison with the pure magnetic field (dashed line). As mentioned above, the strength of the chromomagnetic field is much greater than the magnetic one [11] since the lifetime and strength of chromofield are related to the scalar gluon condensate, . Therefore, we also expect an increase in the photon production probability for a wide range of momenta (solid line).
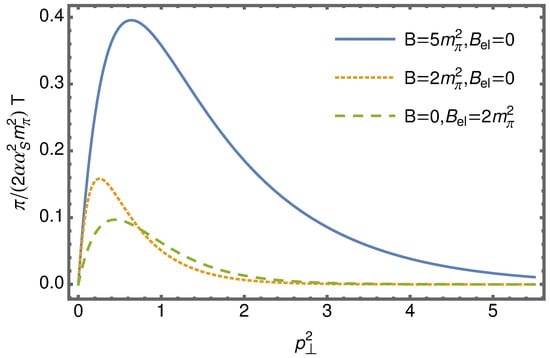
Figure 3.
The squared amplitude, (6), as a function of gluon momenta for . The dashed line corresponds to the pure magnetic field, [8], dotted and solid lines represent the case of a pure chromomagnetic field B with different strengths. The mass of the pion, , is chosen as the scale. Dimensionless notation is used. The quarks are considered massless.
One can check the dependence of the squared amplitude for massive and massless quarks in the specific range of gluon momenta . The full expression for in the case of massive quarks and the details related to the limit of gluon momenta can be found in Ref. [15]. From Figure 4, One can see that an increase in the quark mass leads to a result that differs from the massless case. Additionally, the expansion of the propagator in Landau levels is not correct for the strange quark.
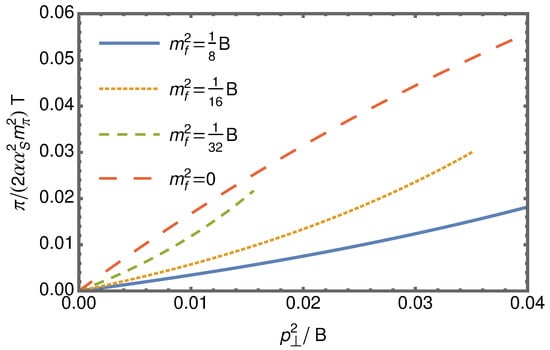
Figure 4.
The squared amplitude (6) taking into account all Landau levels for different quark masses [15] at gluon momenta and the case of massless quarks. The chromomagnetic field strength and magnetic field . Dimensionless notation is used.
The invariant photon energy distribution in the presence of chromomagnetic and magnetic fields takes the form [8]:
where
and and are the modified Bessel functions of the first kind. represents the high gluon occupation factor and is the . The factor is obtained by squaring the delta function for energy-momentum conservation in the amplitude. Some arguments and comments about the numerical values of the parameters can be found in Ref. [10]. The comparison of the differential energy distribution (7) for generated photons in the background magnetic, , and chromomagnetic, B, fields is shown in Figure 5. One can see that the chromomagnetic field (dotted line) enhances the effect in comparison with the pure magnetic field (dashed line) with the same strength. We also expect a significant increase in the photon signal due to the high strength of the chromomagnetic field, which is determined by gluon condensate (solid line).
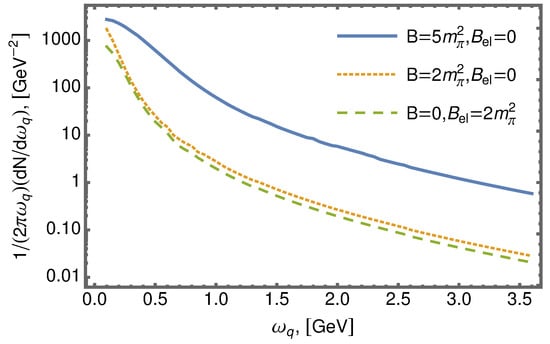
Figure 5.
Differential energy distribution of the generated photons for a pure magnetic field (dashed line) and pure chromomagnetic field B (the dotted and solid lines).
4. Conclusions
In conclusion, we notice that the gluon conversion process via quark loop is a feature of the confinement–deconfinement transition in hadronic matter under extreme conditions, QGP. In the confinement phase, the production of photons is impossible due to the random spacial orientation of the statistical ensemble of (anti-)self-vacuum gluon fields. However, the conditions of the Furry theorem are not satisfied in the deconfinement phase and the gluon conversion is nonzero. In addition, photon distribution has a strong angular anisotropy since the production amplitude retains the singled direction of the external magnetic and chromomagnetic fields. This anisotropy may be related to the direct photon flow puzzle.
As shown in Figure 3 and Figure 5, the chromomagnetic field enhances photon production in comparison with the pure magnetic field with the same strength. We also expect a significant increase in the photon signal due to the high strength and longer lifetime of the chromomagnetic field in comparison with the magnetic one. It is clearly seen from Figure 4 that an increase in the quark mass leads to a result which is very different from the case of massless quarks, and the expansion of the propagator in Landau levels is not correct for the strange quark.
Author Contributions
Conceptualization, S.N. and A.N.; methodology, S.N.; software, A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This paper is theoretical. The data used can be obtained in the references cited and on request from the corresponding author.
Acknowledgments
The discussions and recommendations from Vladimir Voronin are gratefully acknowledged. We would like to thank the organizers of the 6th International Conference on Particle Physics and Astrophysics (ICPPA-2022) where the results of this paper were partially presented.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agakichiev, G. et al. [CERES Collaboration] Low mass e+e− pair production in 158 A GeV Pb-Au collisions at the CERN SPS, its dependence on multiplicity and transverse momentum. Phys. Lett. B 1998, 422, 405–412. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration] Observation of direct-photon collective flow in = 200 GeV Au+Au collisions. Phys. Rev. Lett. 2012, 109, 122302. [Google Scholar] [CrossRef] [PubMed]
- Adam, J. et al. [ALICE Collaboration] Direct photon production in Pb-Pb collisions at = 2.76 TeV. Phys. Lett. B 2016, 754, 235–248. [Google Scholar] [CrossRef]
- Skokov, V.; Illarionov, A.Y.; Toneev, V. Estimate of the magnetic field strength in heavy-ion collisions. Int. J. Mod. Phys. A 2009, 24, 5925–5932. [Google Scholar] [CrossRef]
- Voronyuk, V.; Toneev, V.D.; Cassing, W.; Bratkovskaya, E.L.; Konchakovski, V.P.; Voloshin, S.A. Electromagnetic field evolution in relativistic heavy-ion collisions. Phys. Rev. C 2011, 83, 054911. [Google Scholar] [CrossRef]
- Bzdak, A.; Skokov, V. Anisotropy of photon production: Initial eccentricity or magnetic field. Phys. Rev. Lett. 2013, 110, 192301. [Google Scholar] [CrossRef] [PubMed]
- Tuchin, K. Particle production in strong electromagnetic fields in relativistic heavy-ion collisions. Adv. High Energy Phys. 2013, 2013, 490495. [Google Scholar] [CrossRef]
- Ayala, A.; Castaño-Yepes, J.D.; Dominguez, C.A.; Hernández, L.A.; Hernández-Ortiz, S.; Tejeda-Yeomans, M.E. Prompt photon yield and elliptic flow from gluon fusion induced by magnetic fields in relativistic heavy-ion collisions. Phys. Rev. D 2017, 96, 014023, Erratum in Phys. Rev. D 2017, 96, 119901. [Google Scholar] [CrossRef]
- Goloviznin, V.V.; Nikolskii, A.V.; Snigirev, A.M.; Zinovjev, G.M. Probing confinement by direct photons and dileptons. Eur. Phys. J. A 2019, 55, 142. [Google Scholar] [CrossRef]
- Ayala, A.; Castaño Yepes, J.D.; Dominguez Jimenez, I.; Salinas San Martín, J.; Tejeda-Yeomans, M.E. Centrality dependence of photon yield and elliptic flow from gluon fusion and splitting induced by magnetic fields in relativistic heavy-ion collisions. Eur. Phys. J. A 2020, 56, 53. [Google Scholar] [CrossRef]
- Galilo, B.V.; Nedelko, S.N. Impact of the strong electromagnetic field on the QCD effective potential for homogeneous Abelian gluon field configurations. Phys. Rev. D 2011, 84, 094017. [Google Scholar] [CrossRef]
- Nedelko, S.N.; Voronin, V.E. Domain wall network as QCD vacuum and the chromomagnetic trap formation under extreme conditions. Eur. Phys. J. A 2015, 51, 45. [Google Scholar] [CrossRef][Green Version]
- Nedelko, S.N.; Voronin, V.E. Energy-driven disorder in mean field QCD. Phys. Rev. D 2021, 103, 114021. [Google Scholar] [CrossRef]
- Bonati, C.; Calì, S.; D’Elia, M.; Mesiti, M.; Negro, F.; Rucci, A.; Sanfilippo, F. Effects of a strong magnetic field on the QCD flux tube. Phys. Rev. D 2018, 98, 054501. [Google Scholar] [CrossRef]
- Nedelko, S.; Nikolskii, A. Photons production in heavy-ion collisions as a signal of deconfinement phase. Eur. Phys. J. A 2023, 59, 70. [Google Scholar] [CrossRef]
- Astrakhantsev, N.Y.; Braguta, V.V.; Kotov, A.Y.; Kuznedelev, D.D.; Nikolaev, A.A. Lattice study of QCD at finite chiral density: Topology and confinement. Eur. Phys. J. A 2021, 57, 15. [Google Scholar] [CrossRef]
- Lombardo, M.P.; Trunin, A. Topology and axions in QCD. Int. J. Mod. Phys. A 2020, 35, 2030010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).