Abstract
In this study, we develop the colour string model of particle production, based on the multi-pomeron exchange scenario, to address the controversial origin of the flow signal measured in proton–proton inelastic interactions. Our approach takes into account the string–string interactions but does not include a hydrodynamic phase. We consider a comprehensive three-dimensional dynamics of strings that leads to the formation of strongly heterogeneous string density in an event. The latter serves as a source of particle creation. The string fusion mechanism, which is a major feature of the model, modifies the particle production and creates azimuthal anisotropy. Model parameters are fixed by comparing the model distributions with the ATLAS experiment proton–proton data at the centre-of-mass energy TeV. The results obtained for the two-particle angular correlation function, , with and differences in, respectively, pseudorapidities and azimuthal angles between two particles, reveal the resonance contributions and the near-side ridge. Model calculations of the two-particle cumulants, , and second order flow harmonic, , also performed using the two-subevent method, are in qualitative agreement with the data. The observed absence of the away-side ridge in the model results is interpreted as an imperfection in the definition of the time for the transverse evolution of the string system.
1. Introduction
In recent decades, a significant effort has been made in the study of a unique state of matter called [1] quark–gluon plasma (QGP). The first experimental evidence of QGP formation was claimed by CERN in 2000 [2]. In 2005, this statement was quantitatively confirmed by RHIC experiments [3,4,5,6], whose studies raised questions about the properties of QGP.
Among numerous illuminating hints of a QGP signal, there was evidence [4,5] of the azimuthal anisotropy of particles produced in semi-peripheral heavy ion collisions. The measurements were done in a model-independent way [7] using transverse flow harmonics, , of different orders, n: directed flow (), elliptic flow (), triangular flow () etc. A considerable magnitude of was observed [4], whose contribution is assumed to be a dominant one following the almond shape of the intersection region of two nuclei. The values of were comparable to the calculations [8] obtained when relativistic hydrodynamical fluid was considered in the early times of the collision. Therefore, it is the collective motion of thermally equilibrated partonic degrees of freedom that is believed to convert spatial anisotropies into momentum space under pressure gradients of the compressed medium. This rejected the view that QGP is a gas, but nevertheless, left still to establish whether this represents a perfect or viscous fluid.
Since then, plenty of flow measures have been proposed that vary in sensitivity to non-flow effects. Those are pair correlations [9], multi-particle correlations [10] measured with cumulants [11] or with subevent cumulant method [12], symmetric [13] and asymmetric [12] cumulants considered in subevent method and a peculiar combination of flow-mean particle transverse momentum correlations [14].
The surprising evidence that connects these studies and the present paper is the experimental observation of collective behaviour in small systems. Namely, the unexpected ridge signal [15,16] and associated flow harmonics [17] seen in high-multiplicity proton–proton (pp) interactions at the LHC. These observations should not be explained by the fluid nature of the medium produced in such a small droplet of matter as it should not be able to reach thermal equilibrium prior to hadronization [18]. Nevertheless, there are successful attempts [19] to apply hydro description even in this case, which raises questions about the use of the same approach in all colliding systems [20].
On the one hand, from the first principles of the theory of strong interaction, the description of multi-particle production is complicated by the feature that the majority of the particles are produced in soft processes. It means that their transverse momenta, , do not exceed about 1 GeV, therefore, the perturbative calculations in quantum chromodynamics (QCD) are inapplicable in this regime. This forces us to work in phenomenological approaches that can effectively describe the transition from, for instance, a few colliding hadrons to hundreds and thousands of particles produced.
One of the successful techniques is based on the concept of formation of colour strings between colliding partons which then fragment into observable hadrons [21]. This method appeared to be effective both in phenomenological calculations (see e.g., dual parton model [22], string percolation model [23], colour-glass condensate and glasma model [24]) and as the basis of many Monte-Carlo event generators, such as, e.g., EPOS [25], PYTHIA [26], HIJING [27], AMPT [28] models. In this paper, we consider the colour string picture of multi-particle production to model the transverse flow effect measured in pp collisions. It is the strings’ interaction in the form of fusion [23] that plays a primary role in the model.
Our interest in this topic is inspired by the approach developed in the series of papers [29,30,31] in which the flow signal appears due to the quenching of particle transverse momentum in a string medium [30]. Namely, it is assumed that particles emit gluons while passing through the strings, which is similar to the energy losses of charged particles moving in the electromagnetic field in quantum electrodynamics (QED). Hence, the appearance of forbidden azimuthal angles changes the distribution of particles in the transverse plane. Here, the fusion of strings creates a heterogeneous medium density along the path of a particle.
In addition, we consider that the fusion accelerates the overlapped strings, resulting in a boost of the produced particles. It creates distinct directions of motion in the transverse plane for particles originating from the rearranged colour field. This approach originates from the pioneering paper [32] and has already been tested in more recent models [33,34]. The interplay of these two mechanisms, driven by string fusion, allows one to obtain specific joint correlations in pseudorapidity and azimuthal angle, and , respectively, of the same origin in collision systems of different types.
In this paper, we extend our model [35,36] that provided a thorough description of particle correlations and fluctuations in , for inelastic pp interactions at top RHIC and LHC energies. In this paper, we follow up [37] and test the model application to the problem of describing flow in pp interactions, aiming to obtain characteristic – correlations at the pp system centre-of-mass energy TeV.
In Ref. [36], we emphasized that the previous model implementation lacks the short-range correlations introduced. It did not allow us to fully describe the ALICE experiment data, but we were able to catch the trend. In the present investigation, on the contrary, we aim to take advantage of this drawback of the model since getting rid of non-flow effects is the main challenge in flow studies. However, there is still a need to partially modify the model.
In the present study, the basic model features, as in Ref. [36], are the 3D (three-dimensional) dynamics of strings and string fusion. The strings consideration is slightly modified, but the main point stays intact: longitudinal contraction and shift of strings in the rapidity space, inspired by [38], and their transverse motion governed by an attractive Yukawa potential via the -meson exchange, following [39].
The main set of changes introduced in this study concerns the string fusion mechanism [40,41]. Namely, we abandon the consideration of the simplified cellular approach [42] to find the overlapped strings by looking after their centres. Instead, we divide the transverse plane into pixels that are much smaller than the string’s size. The contribution of a pixel to particle production is determined by the degree of strings fusion that occurs inside it. We apply these changes with an eye toward future studies of nucleus-nucleus (AA) collisions.
It is worth noting separately that the mechanisms of momentum loss and string boosts applied to AA collisions provide a good description of the observed flow signal [43,44]. However, the additional introduction of the transverse motion of strings would naively result in the formation of a single colour flux tube after string fusion is taken into account. Therefore, the problem with the previous implementation of the model [36] is that a modified but uniform colour field could not serve as a source of azimuthal anisotropy.
The approach with the fine granularity of the configuration–momentum space that we propose in the present paper solves this issue, but we first test it in the description of pp collision results. Although the interpretation of pp results on azimuthal anisotropy provokes some tension in the flow community, it is technically more convenient for us to start the model development with the small colliding system, since keeping the fine cellular structure is much more challenging in AA, CPU-time wise. Furthermore, there are other improvements of the model mostly at the stage of proton assembly and event simulation implemented in this work.
To summarize, we develop the Monte-Carlo model based on the colour strings approach that addresses the problem of azimuthal particle correlations via the string–string interactions and particles’ momentum loss. Thus, we anticipate that our preliminary estimates will demonstrate whether the nature of collective effects observed in pp collisions can be revealed using such a simplified but authentic model.
The paper is organized as follows. Section 2 presents the model framework, with special attention given to improvements introduced to the model compared to its previous version [36]. The description of the flow mechanism implemented in the model is included in a separate Section 3. In Section 4, we demonstrate the inference of free model parameters based on comparison with ATLAS experiment pp collision data at TeV [45]. Section 5 introduces the flow measures that we calculate in the model. Results obtained are presented in Section 6 and discussed in Section 7.
2. Colour String Model
The colour string model [21] is a phenomenological approach that is used to describe the soft particle production regime where the perturbative QCD calculations are not applicable. Strings that are extended colour field objects (also called tubes of gluon field) are stretched between partons participating in the collision. We consider them all to be parallel with neither kinks nor twists. It is believed that strings have a finite size in the transverse dimension, which enables them to overlap and interact. String longitudinal dynamics is described by a yo-yo solution, which means that a string periodically stretches and contracts with time. The energy of the colour field inside the tube grows as the string extends, while its massive endpoints slow down. It causes a probabilistic break-up of the colour field via the creation of quark–antiquark, q–, pairs and the breaking of strings into observed particles.
2.1. Multi-Pomeron Exchange in pp Collisions
In this paper, we consider inelastic pp interactions at TeV in the context of multi-pomeron exchange, with each pomeron represented by a cylindrical diagram. The uncut diagrams contribute to the elastic cross-section, while their unitarity cut creates two colour strings [22] that fragment into observed particles. Therefore, in this approach, the number of strings, , in an event is determined by the number of exchanged pomerons, , as .
With the natural assumption of the Gaussian distribution of the transverse positions of partons inside the proton, one can calculate a probability of parton-parton interaction that can be interpreted as the probability of string formation [46]. The resulting distribution of the number of pomeron exchanges coincides with the Regge-theory parametrization [47] that neglects the three-pomeron vertices:
where is a normalising coefficient, , is the quasi-eikonal parameter related to the small-mass diffraction dissociation of incoming hadrons, is the residue of the pomeron trajectory, is the intercept of the pomeron trajectory, and characterise the coupling of the pomeron trajectory with the initial hadrons, is the slope of the pomeron trajectory.
Figure 1 presents the event distribution in the number of strings, , obtained with these parameters and used in our simulation.
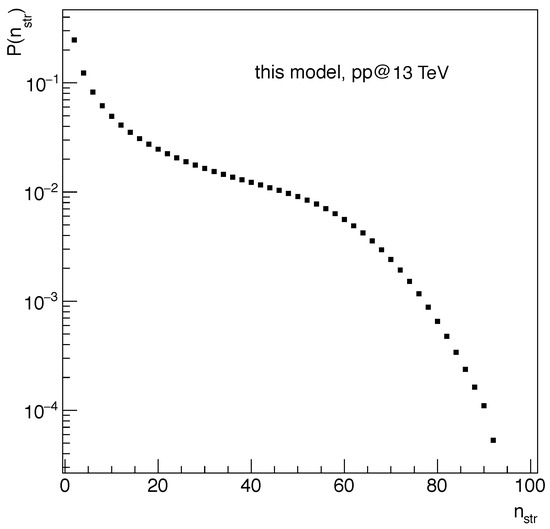
Figure 1.
Model event distribution, , of the number of strings for inelastic pp interactions at the centre-of mass energy TeV.
To determine the values of parameters in Equation (1), the data on multiplicity distributions and cross sections were used. We substitute into Equation (1) the parameters from Ref. [48], where it is assumed that strings that were initially formed in an event can overlap to various degrees and fuse, forming the string clusters with the modified fragmentation characteristics, which changes the obtained multiplicity. This is in contrast to another approach used in Ref. [49], where string fusion is effectively implemented already at the moment of string formation. Therefore, there are a number of free strings in Ref. [48] and a number of string clusters in Ref. [49]. The values of parameters in Equation (1) for these two methods will differ, but both the models should lead to the same charged particle multiplicity distribution, (see Equation (2) below), corresponding to the data. We follow the first approach that allows us to track the 3D evolution of string density.
Thus, the proton no longer consists of a single quark and a diquark and forms not only two strings in pp interaction, as we move away from the conventional picture. Instead, we take into account the multi-parton configurations of sea quarks whose independent and simultaneous interactions result in the formation of the number of pomerons in an event.
In this approach, is determined as a convolution of (1) and the multiplicity distribution at fixed number of pomerons, ,
Due to the complexity of the analytical formulation of , we treat it using a Monte-Carlo simulation. In Ref. [35], we demonstrated that for quite a simple case of non-interacting strings, the correlation observables calculated numerically and analytically are in good agreement.
2.2. Proton Assembly
Our current study is based on the assumption that all partons of a proton form strings with all partons of another proton. Therefore, we call an event the creation of between two protons, each with the number of partons, , which is equal to the number of strings in an event, .
To fulfil this requirement, we prepare an extensive set of protons with all the possible even numbers of partons, , k = 1, …, 50. In this study, we consider the parton composition of a proton as one valence quark, one valence diquark, and sea quarks. The algorithm provided in Appendix A is more time- and CPU-efficient than the permutations of partons between two selected protons that were implemented in Ref. [36].
2.3. Event Simulation
The first step of a simulation of an event is to sample the number of exchanged pomerons, , from Equation (1). Thus, we know the number of strings that should be created in an event, . By creating the event, we mean searching for two protons, with the same number of partons, , so that all their partons can form strings under certain conditions (see Section 2.3.1 and Section 2.3.2).
First, we select two random protons from the prepared set (Section 2.2) with the certain . Second, we permute partons in one of the two protons by performing replacements and checking whether this leads to the formation of good pairs (see the requirements in the next two subsections). If not, we select another pair of protons.
2.3.1. String Formation: Electric Charge
In this study, we ensure the conservation of electric charge. Thus, we accept a string candidate if the electric charge of the string, , defined as the sum of the partons’ charges that form a string, equals one of the possible integer numbers: , 0, , .
2.3.2. String Formation: Energy and Mass of Decay Products
We calculate the string energy, , by summing the energies of partons at the ends of the string, and , as
where is the initial momentum of a parton and is a dynamically defined parton mass (for details of their definitions, see Appendix A.3).
We accept the string candidate if is sufficient to decay at least in two hadrons at rest, with masses and , i.e., .
In order to test this condition, it is necessary to identify the species of the pair of daughter particles based on the flavours of the string ends, e.g., the quark–diquark string should decay at least to a baryon and a meson. For completeness, we provide the list of minimum permitted combinations of daughter products, based on the flavours of quarks that we consider in the model: , , , , , , , and . We use GeV, GeV, GeV, GeV for nucleons, pions, kaons, and D-mesons, respectively.
2.4. String Transverse Dynamics
In general, the colour confinement in QCD, a non-abelian gauge theory, is viewed as the gathering of the colour field between two colour charges in the flux tube of finite transverse size [50]. However, lattice QCD demonstrates that the presence of a colour string modifies the QCD vacuum. For example, the correlator between the quark–antiquark chiral condensate, , and the Wilson loop, W, is appeared to be not a constant as a function of the transverse distance from a string [51]. Indeed, at large distances it reaches the value of unity, meaning that there is no string influence. In the meantime, its values decrease in the vicinity of the string, which indicates a partial restoration of chiral symmetry in this region of the space.
We follow the approach of Refs. [39,52], where the authors interpret these lattice calculations (left-hand side of Equation (4)), as a field created by a cloud of -mesons (right-hand side of Equation (4)):
where is the regularized distance in the transverse plane, is a 2D distance between strings in a pair of strings, fm [39] is a genuine string width, unlike the effective string width, which is a result of quantum fluctuations, is zero-th modified second-kind Bessel function corresponding to a massive scalar propagator in two dimensions and GeV [39] is the mass of the -meson that is proposed to be a mediator of the force between strings.
In this paradigm, one can consider string–string interactions in the created Yukawa potential, which results in the non-relativistic attraction between them similar to nuclear forces. Thus, the equations of motion of the string system in an event are defined by the 2D Yukawa interaction [39],
where and correspond to and , respectively, from Equation (4). The i and j subscripts indicate that the quantities are constructed for the i-th and j-th strings. Here, is the QCD string self-interaction coupling and is the string tension, whose dimensionless product is selected as [52], and is the first modified second-kind Bessel function. Strings are considered to be moving as a whole according to Equations (5), without whatever kinks.
To solve this system of differential equations, the set of initial conditions is required. The Gaussian distribution of width (model parameter) is used to sample the initial 2D transverse coordinates of string centres in an event. This simplification is to decrease the program’s running time: instead of applying the Glauber approach at the partonic level and finding which partons are to form strings, we assume that some configuration of strings has already been created in an event.
Transverse strings’ evolution, governed by Equation (5), can be terminated at some proper time, , which affects the final string density. In Ref. [36], we showed that the largest number of overlaps between strings occurs after the time that we called . The latter is the time it takes for a string transverse configuration to attain the global minimum of the potential energy, evolving according to Equation (5). Ref. [36] considers other cases, including no transverse evolution and transverse evolution until the conventional time fm [52] that is unsuccessful in describing the data, especially the –N correlation, where is the event-averaged transverse momentum of a particle and N denotes the particle multiplicity. Thus, in the present study, we consider . It varies event-by-event and depends not only on the initial transverse positions of the strings, but also on the number of strings, and thus on the collision energy. It is worth noting that cannot be found for any event. This means that for some configurations of strings, the minimum of the potential energy of the system can only be reached at fm. In this case, we set fm as the typical time for string hadronization and restrict system evolution to it.
Figure 2 shows how a few events (one event a row) with different numbers of strings look before and after the transverse evolution of string density. Figure 2 (left half, left to right) demonstrates the event projections to the transverse plane, X–Y, before and after the transverse dynamics of strings. Figure 2 (right half, left to right) present the projections to the X–rapidity plane before and after the transverse evolution. The corresponding time of the transverse motion, , is indicated as relevant. One can see that the string system is highly compressed and the 2D distribution (Figure 2, second left) approaches a more spherical shape in comparison to the initial positions of the strings (Figure 2, most left). In the rapidity dimension, one obtains quite uniform distribution up to large rapidities (Figure 2, most right).

Figure 2.
The simulated events (one event a row) with 2, 16, 38, and 74 strings (top to bottom) for an event projection to the transverse plane, X–Y, before and after the transverse evolution and to the X–rapidity plane before and after the transverse evolution (left to right) for the time of the transverse evolution, , as indicated. The evolution runs till (second left and most right). Z axis is not to scale. See text for more details.
2.5. String Longitudinal Dynamics
In the model considered here, special attention is given to the simulation of partonic degrees of freedom for colliding protons (see Appendix A). It is because the initial rapidities of the string’s ends, , are determined by using the momenta of partons that form it as
However, the string tension, , slows down the massive partons flying outwards with momentum according to , where t denotes the time. As a result, the rapidity of the string end decreases [38] by value
where is the proper time of the string longitudinal evolution.
The aim is to relate the from Equation (7) with the time for the transverse evolution, , to synchronise the dynamics of the string system in rapidity and X–Y dimensions. However, one has to take into account that the compressions and stretchings of a string are periodic (yo-yo solution [21]) and are followed one by another. Moreover, the movement of massive endpoints of different masses, and , in the case here is not symmetrical (we denote by 1 or 2 one of the string ends). Therefore, we define the maximum proper time for each string end, , after which the string’s endpoint fully stops the deceleration (acceleration) after acceleration (deceleration) as
where are the initial rapidities of the string ends converted to the string rest frame.
To convert the rapidity of a string end from the laboratory frame, , to the string rest frame, , one has to know the rapidity of the string in the laboratory frame, . It is calculated as follows. First, let us define strings’ momentum, , and strings’ energy, (3). Thus, the rapidity of a string, , is
As soon as is known, one can recalculate the rapidities of the string ends in the string’s rest frame:
and substitute Equation (10) into Equation (8).
It is necessary to account for the periodicity of string motion. Namely, after the time (8), the sign of flips. Therefore, it is crucial to correctly connect the , which is found from the transverse dynamics for the whole event, with , which varies for two ends of the string and for each individual string in the event.
To summarize, the time of the movement of a string end only during the last period should be used in Equation (7). The rapidities of the string ends after such loss, , are found by subtraction of from with the correct signs.
It is worth remarking that the longitudinal evolution changes not only the length of the strings but also their positions with respect to midrapidity. Figure 3 demonstrates how the string density of the model events from Figure 2 (already after the transverse evolution) changes after the longitudinal losses are taken into account. For clarity, we repeat Figure 2 (most right) in Figure 3 (most left). In Figure 3 (left half, left to right), one can see the event projections on the X–rapidity plane before and after the longitudinal dynamics. Figure 3 (right half, left to right) shows the Y–rapidity plane projections also before and after the longitudinal dynamics.

Figure 3.
The simulated events (one event a row) with 2, 16, 38, and 74 strings (top to bottom) for an event projection to the X–rapidity plane before and after the longitudinal evolution and to the Y–rapidity plane before and after the longitudinal evolution (left to right) for the time of the longitudinal evolution, , as indicated. The evolution runs till (second left and most right). Z axis is not to scale.
It can be seen that the string system in the final state (Figure 3, second left and most right) has a significant compression in the longitudinal direction. The cloud of a high density of strings is no longer infinitely extended as it is often assumed in the string models [53]; thus, our model loses the translational invariance in rapidity. The transverse evolution of the strings, as described in Section 2.2, also leads to varying string density, which makes an event strongly heterogeneous.
2.6. String Fusion
As a result of the reductions and shifts of strings in the rapidity dimension (Section 2.5), the system of strings is a spaghetti-like structure [39], although the lengths and positions of strings vary with respect to mid-rapidity. Furthermore, due to the attractive motion of strings in the transverse plane (Section 2.4), the clusters of fully or partially overlapped strings are formed (taking into account that they have a finite transverse size). Since this overlap changes with rapidity, one obtains a non-trivial string density 3D distribution.
In this study, we follow the consideration from Ref. [23], where the colour field of fused gluonic tubes changes, which impacts particle production. This can also be interpreted as the appearance of string clusters with higher effective tension.
Apparently, there are several options for addressing the overlap and fusion of strings [42]. In our previous study [36], we employed a cellular approach that involves the fusion of strings that have the centres in the same cell in the transverse plane. In this case, the cell size is equivalent to the diameter of a string. Thus, a cluster of k overlapped strings in Ref. [36] was replaced by one string with a decreased mean multiplicity per rapidity unit, an increased mean transverse momentum of produced particles and an increased probability of producing heavier particles. The transverse position of the cluster of k fused strings can be assumed to be the mean value of their k transverse positions.
Therefore, if one considers AA collision in the approach [36] discussed just above, one can expect that after the transverse dynamics (Section 2.4) the centres of all strings appear in the same cell. This leads to the replacement of all the variety of the degrees of strings’ overlaps by a single string with enhanced tension. In this scenario, it is impossible to create the anisotropy of produced particles since the information about matter density fluctuations is lost. Let us note that in the models without attractive string dynamics in the transverse plane, this is not an issue since an event picture is less dense. Thus, in the current study, we do not consider simplifying string fusion on a coarse lattice but work using fine division of the transverse plane into small enough pixels.
In the approach considered here, the transverse plane is tessellated into square bins (pixels), each of which counts the occupation numbers of strings (number of strings that cover this pixel). In order to have a fine grid, one has to select the area of the bin, , so that the latter is much smaller than the string transverse area, . In the current implementation, we use a string diameter, , of fm and a pixel width, , of fm.
The resembling procedure is done for the rapidity space with a slice size of . In the previous study [36], we applied a longitudinal grid separately to each string. In this paper, we use a uniform splitting for the entire longitudinal dimension.
Finally, one can calculate the number of strings that occupy each 3D bin in the mixed configuration–momentum space. Thus, in a sense, we move away from the concept of particle-producing strings towards the concept of particle-producing pixels.
Note that the program’s running time is significantly impacted by the number of 3D bins, as it must iterate over all 3D cells. Hence, it is necessary to restrict the volume permitted for simulations. Actually, the collision energy determines the longitudinal (in rapidity) size of the defined space, as the beam rapidity rises with . In turn, the required transverse area depends on the initial distribution of strings and their final positions after the transverse dynamics. Since, in this investigation, we focus on the evolution of the system until the global minimum of its potential energy, after the motion according to Equation (5), the system becomes even more compact.
2.7. Fusion and the Kinetic Energy of Strings
Since the total energy of the system of strings in an event to be conserved, we assume that when strings overlap, a redistribution of their potential, U, and kinetic, T, energies occur. It is because the overlap of colour strings modifies the strength of the colour field inside the strings, which affects the string tension. Therefore, the partial overlap of a few strings leads to a decrease in the potential energy of each of them in this region. This modification causes an opposite change in the kinetic energy of strings, pulling them towards each other similar to that considered in Ref. [32]. The formation of a string cluster, as a consequence of the strings attraction increases the string tension in comparison to a free string. Interestingly enough, the alternative option, also mentioned in Ref. [32], includes the decrease in the effective string tension and, therefore, should lead to the string repulsion (see also Ref. [33]).
As a result, one needs to parameterize the gain of kinetic energy, , that the i-th string in an event obtains from the overlap with the j-th string. The functional form of should reflect the feature that the full overlap of two strings means that their fusion is completed and those strings stop. On the other hand, should decrease with the distance between the strings’ centres. Thus, the following dependence on —the 2D distance between the i-th and j-th strings—is proposed:
Here, , where fm is the string radius, while is a dimensional constant measured in GeV/fm that is a free model parameter. Hence, to get a new value of the kinetic energy of a string we iterate over its neighbouring overlapping strings in every rapidity slice.
We assume that the string motion according to Equation (5) is non-relativistic; therefore, in the following, we neglect the initial momentum of a string. As a result, the i-th string gains the extra transverse momentum from the j-th string:
where is the sum of the dynamically obtained masses of partons forming the i-th string (see Appendix A.3).
The azimuthal direction of the vector from the centre of the i-th string to the centre of the j-th string, , is determined by the distances on X and Y axes between the centres of the strings, and . The projections and of the total momentum that the i-th string gains from all its overlapping neighbours, , are found by summing the projections of as
Thus, the 2D vector of the string’s transverse momentum, , is determined by its overlap with other strings in each rapidity slice. It is this extra momentum that is transmitted to particles produced by the string (see Section 3.1).
2.8. Particle Production
In this study, we define string hadronisation in each 3D bin. The strength of the colour field inside it determines the average number of charged particles produced and their average transverse momentum. Particles’ rapidities are found from the uniform distribution in each rapidity slice.
2.8.1. Mean Multiplicity with String Fusion
Let us consider a rapidity slice of a free single string. The colour field, , inside it can be represented as a sum of colour fields inside all transverse (2D) bins that tessellate the area of this string,
Thus, the field inside a 2D bin, , is proportional to the ratio of its area, , to the area of a string, .
Let us now consider a random 3D bin in the space that is populated with k strings. The resulting colour field, , inside the string, is
where is the field of a string in the bin.
For simplicity, the present study considers all strings to have the same transverse area, , which does not vary along the rapidity direction, albeit the study can be more complex [54]. The colour field of a free string, , is assumed to be constant and is defined by the confinement properties [55]. Therefore, in the case considered here, Equation (15) can be simplified to
The average multiplicity from a free string, , is proportional to the field of a string, . Thus, by transitivity, for the k strings that overlap in a 3D bin, one obtains .
One can define the average multiplicity from a 3D bin with the length and transverse area as
with a free parameter defining the average multiplicity of a unit of rapidity of a free string and . For comparison, in our previous study [36], we calculated the mean multiplicity from the cluster of k strings (without division in the transverse plane), , as , following Ref. [40].
The actual multiplicity per 3D bin, , is sampled from the Poisson distribution with a given mean, (17). Then, is a sum of the multiplicities of from all the 3D bins.
2.8.2. Mean Transverse Momentum with String Fusion
The mean transverse momentum of the particles produced by a free string, , does not depend on the string’s length in rapidity or its transverse area. Thus, remains unchanged despite the division of a strings into pixels. Therefore, we keep the modification of for the cluster of k fused strings, , from Ref. [36]. Namely,
where is found in Refs. [49,56] from the fits to data and is a free model parameter.
Particles’ transverse momentum is sampled from distribution
corresponding to Schwinger mechanism of quark–antiquark pair creation in the colour field of a string that leads to its break-up and the formation of final hadrons [57,58,59], with the mean transverse momentum, (18), from the cluster.
2.8.3. Probabilities of Producing Different Particle Species
The particle species with masses are determined by Schwinger-like probabilities with the modified effective string tension, , according to ∝, which is consistent with Equation (19). Typically, in the models that rely on the Schwinger mechanism of particle production [60], slightly differs from (see Equation (7)) to effectively take into account the mechanism of particles re-scatterings.
Pions, kaons, protons and -resonances are included in the model, with the -resonance decaying into two charged pions. With particle masses, the longitudinal component of the particle momentum, , is calculated and, thus, the pseudorapidity is
where is an absolute value of the particle momentum.
3. The Origin of Particle Flow in the Model
A purpose of introducing the fine grid in the transverse plane as described in Section 2.6 above is to account for particle azimuthal flow in our model. We follow the consideration in Refs. [29,32] on the way of introducing collective behaviour in the colour string model without a hydro phase. There are three main ingredients.
First, in this type of models, the strings in an event form some clusters [23] distributed anisotropically. Alone, these fluctuations in string density do not produce whatever flow. However, this initial state anisotropy is crucial for the two mechanisms described below as controlling the strength of the effect of those mechanisms.
Second, we consider the change in the strings’ kinetic energy that occurs when the strings overlap in 3D space. As a result, the boost from a string is transferred to the particles that it is fragmented to [32]. The boost creates correlations in and between particles produced from strings that interact with each other. What is essential is that string hadronisation is considered at the moment of the minimum of the potential energy of the system of strings (at ). This results in the high similarity of the geometry of events with the close number of strings, which leads to the same picture of particle boosts. For instance, Figure 2 (second top, second left) shows a typical event with 16 strings. We argue that all events with this resemble each other up to the event rotation and some statistical fluctuations. It means that the events have a non-zero flow of comparable value; therefore, the signal survives after averaging over such group of events.
Third, the particles passing through single strings or string clusters lose some part of the energy due to gluon radiation in the medium [29]. When a particle loses its entire momentum, it means that this particle failed to escape. Thus, the azimuthal directions that are forbidden appear in the event. Consequently, the particles can no longer move in a whatever direction and s of those particles become narrowed and correlated. Moreover, the complicated geometry of the string medium leads to different path lengths in different azimuthal directions and to different losses.
The first mechanism of those listed just above is naturally introduced into our model: transverse dynamics of strings result in the formation of string clusters of different degrees of overlap. Longitudinal dynamics make the fluctuations of string density dependent on the rapidity coordinate.
The other two mechanisms are the new features implemented in the model and are described in Section 3.1 and Section 3.2 just below. Let us note that different degrees of string overlaps cause variations in the magnitude of energy loss and particle boosts bin-by-bin in the transverse plane–rapidity space. As a result, the particle production in a given event becomes highly asymmetric in azimuthal angle and pseudorapidity.
3.1. Transverse Momentum Boost
Particle’s transverse momentum sampled from Equation (19) receives a Lorenz boost if the particle originates from the string piece that was accelerated due to string fusion [32].
The procedure iterates over all 3D bins and finds the strings that cover each bin. A bin is assigned the momentum projections, and , that are found as fractions of the momentum projections of the i-th string, and , defined in Equation (13) as
where fm is the bin size in X and Y in the transverse plane, is the length of i-th string in rapidity which is calculated as the difference between the rapidities of the ends of the string, and , and highly fluctuates.
Second, we find the part of the mass of the i-th string, , which belongs to this bin in a similar way
If this 3D bin is covered by k strings in an event, their from Equation (21) and from Equation (23) should be included in its total momentum, , and the total energy inside it, , as
We perform particle production from each 3D bin in the bin rest frame as described in Section 2.8. In this frame, the particle’s azimuthal angle, , is sampled from the uniform distribution from to . To obtain the laboratory reference frame, one boosts the four-momenta of the produced particles using the boost vector with , and .
Thus, we obtain the correlated transverse motion of particles produced by a 3D bin.
3.2. Transverse Momentum Loss
When a particle traverses a 2D bin with a certain density of strings (occupation number), it loses part of its initial momentum, , due to gluon radiation, reaching the value, . In an analogy with the QED process of photon radiation by charged particles moving in the external electromagnetic field, it can be expressed in the following way [29]
where is a quenching coefficient that is a free model parameter. It is necessary to apply the Equation (26) iteratively since varies bin-by-bin based on the number of overlapped strings, k. That is why l, a 2D path that a particle accomplishes, can be approximated by (the length of the 2D bin’s diagonal) for each step. Since the density of strings fluctuates with rapidity (see Section 2.4 and Section 2.5), l differs not only at different azimuthal angles, , but also within different rapidity slices, .
Let us remark that, in general, the value of can become negative after a number of iterations of Equation (26). We interpret this as the impossibility of the particle to escape in a given azimuthal direction; thus, it is absorbed by the string environment. In this case, the energy of the particle is spent on producing another particle to replace the former one. For a new particle, the model regenerates the transverse momentum and azimuthal angle of this particle; thus, the particle gets a chance to escape in a new direction. As soon as the required number of particles to be produced from this 3D bin (from Poisson distribution with the mean from Equation (17)) is known, new particles are to be regenerated until the particle leaves the string medium.
To find the trajectory of a particle in the transverse plane, the Bresenham’s line algorithm [61] is applied for each rapidity slice.
4. Inference of the Model Parameters
We determine the model parameters by comparing the model distributions with the ATLAS experiment data on inelastic proton–proton interactions at TeV [45] (Figure 4). We describe not only the global observables such as -distribution, and spectra, but also the – correlation function.
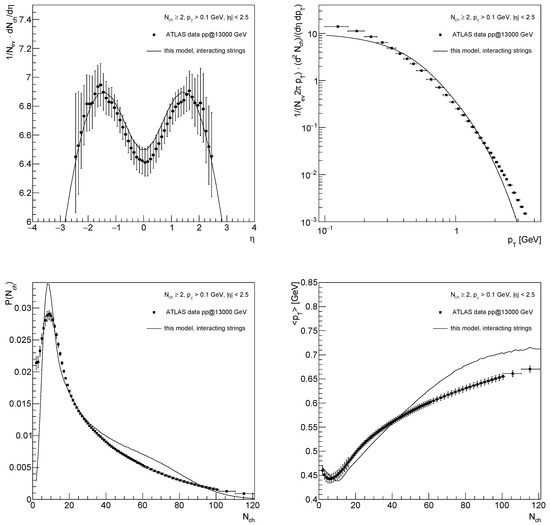
Figure 4.
Model results (lines) compared to the ATLAS experiment data [45] (solid squares) for inelastic pp interactions at TeV: charged-particle pseudorapidity, , distribution (upper left), transverse momentum, , spectrum (upper right), multiplicity distribution, , (lower left), and – correlation function (lower right) within the experimental GeV, , and limits.
The region (Figure 4, upper left) is adjusted by finding the appropriate value of the mean particle multiplicity (see Equation (17)) from a 3D bin of a free string. In turn, the width of the distribution is controlled by the value of the string tension, (see Equation (7)).
By tuning (see Equation (18)), we settle the at low (Figure 4, lower right). With the proper selection of (see Equation (26)), we are able to modify the slope of the – correlation function at moderate and high . The is influenced by the value of (see Equation (11)) at high , when string fusion is most significant.
In the charged particle multiplicity distribution (Figure 4, lower left) the events with are removed as in the data; thus, we plot . Here, denotes the charged particle multiplicity distribution that includes events without registered particles (). These events are highly influenced by diffractive processes that are not considered in the model. Moreover, even with the selection the experimental results at low and low are affected. Therefore, our predictions could not be directly compared in this region, but we are mostly interested in the high events as those events are more relevant in the studies of collective behaviour. The resulting -spectrum is presented in Figure 4 (upper right).
The following values of the free model parameters were simultaneously selected to fit the ATLAS experiment data: , GeV/fm, GeV, , and GeV/fm.
5. Flow Measurements and the Quantities of Interest
One can estimate the flow signal by performing the Fourier expansion of the single-particle distribution in the azimuthal angle, , [7]. It is necessary to take into account the intrinsic symmetry of particle production in every event, the latter being determined by its reaction plane, . The plane is formed by the direction of the beam and the impact parameter and creates a preferred azimuthal orientation in an event. Thus, the relative particle azimuthal angles, –, should be used in the calculations instead of the measured . Therefore, in a given part of phase-space, one can expand the distribution into a Fourier series as
where n is the Fourier harmonic number and is the corresponding Fourier coefficient. The full set of s describes the amplitudes of particle distribution asymmetry in the transverse plane averaged over particles in one event. Let us note that both and fluctuate event-by-event and, typically, only the moments of the corresponding distributions are measured experimentally.
The validity of the Fourier expansion in the real case of finite event multiplicity (especially in pp collisions) is questionable. Moreover, the reaction plane, , cannot be directly measured, so one may substitute it by proxy [62] called the event plane, . However, there is no unique event plane in an event; instead, one determines a set of event planes, , depending on n as
where the numerator and denominator are calculated from the distributions of the particles in per event.
More recent studies have shown [63] that imprecise estimation of the event plane significantly spoils the flow signal in this approach. Therefore, more sophisticated measures to be used such as two-particle correlations that, under certain assumptions, naturally exclude the dependence on in .
For example, the two-particle angular correlation function, , is defined by the differences in pseudorapidities, , and azimuthal angles, , for particle pairs such as
where S and B represent the –-distributions calculated for particle pairs from the same and mixed events, respectively. The S and B distributions are scaled by the numbers of pairs, and , respectively. The experimental analysis of this observable revealed the impressive ridge structure in both AA collisions [64,65] and inelastic pp interactions [15,16].
Another method to quantify the strength of azimuthal correlations is to compute the two-particle cumulant [9], ,
where the number in denotes the number of particles that were correlated, and represents the average over all particle pairs an event after been averaged over all events. Moreover, the estimate, , of the elliptic flow harmonic, , can be found [11] as
under the assumption of independent particle production (flow is the only source of correlations, providing that all non-flow effects are suppressed), which implies that should be positive.
The observed change in sign from positive to negative for in Ref. [66] demonstrated that contributions from non-flow correlations remain in . To exclude these non-flow contributions, it was proposed [12] to study cumulants in subevents separated in rapidity. Thus, by introducing a pseudorapidity gap, , between particles with and , one can eliminate the short-range correlations (coming from resonance decays, jets, and momentum conservation laws) and measure and the corresponding .
The study [11] of multi-particle cumulants, , that measure the correlation between particles in an event [10], is a natural extension of this method. Another generalisation is to consider higher, , orders of flow harmonics. However, the measurement of cumulants requires larger statistics. We have not tried to go beyond , as the simulation procedure is too CPU-demanding at the moment.
6. Model Results for Inelastic pp Interactions at TeV
Here, we repeat the procedure for event classification as in Ref. [66] based on charged-particle multiplicity in a certain acceptance. Then, the selected charged particle multiplicity, , distributions were obtained for particles with acceptance and for one of the following intervals: GeV, GeV, GeV or GeV. The distributions were split up into percentiles, which allows one to find to which event class based on a given event belongs.
In Figure 5, the model result for the two-particle angular correlation function, , calculated for particles with and GeV, is presented for the event class based on the multiplicity of particles with and GeV.

Figure 5.
Model result for the two-particle correlation function, (29), calculated for particles with and GeV and presented for event class 0–10% based on charged particles multiplicity, , under particle selection criteria and GeV for inelastic pp interactions at TeV.
Remarkably, the shape of (Figure 5) contains a near-side ridge at extended over the entire presented range. The ridge indicates the emission of particles in narrowly collimated azimuthal directions that is roughly boost-invariant at the given range. In the model framework, this structure is created by particles produced from the boosted string cluster that is of elongated shape in rapidity.
The prominent peak at , and the extended structure along come from the decays of the -resonances [67]. However, the developed model does not reproduce the away-side ridge seen in the data [15,16,68].
To plot the results on cumulants (Figure 6 and Figure 7) in a unified way for different event classifications, we correlate with the charged-particle multiplicity calculated on particles with and GeV. We find the event-mean for every event class based on and plot it along the X-axis.

Figure 6.
Model results for two-particle cumulant, (30), (upper) and the corresponding second flow harmonic, (see Equation (27)), (lower) calculated for charged particles with GeV and as a function of estimated for different event selections of width of distribution of particles with different (as indicated) and in inelastic pp interactions at TeV.

Figure 7.
Model results for two-particle cumulant, , (upper) and the corresponding second flow harmonic, , (lower) calculated by two-subevent method for particles with GeV and or as a function of estimated for different event selections of width of distribution calculated for particles with different (as indicated) and in inelastic pp interactions at TeV. See text for details.
Figure 6 shows the model results for (Figure 6, upper) and (Figure 6, lower) calculated for particles with and GeV, as a function of . Results are presented for event classes with a width of the distribution calculated for different event classifications based on , as indicated.
The values of are positive and show an increasing trend towards high-multiplicity collisions. The associated second flow harmonic, , repeats this behaviour. We interpret it as follows. The string fusion plays a more significant role with the increased string density, therefore, both quenching and boosting of particles become stronger, leading to a greater flow signal.
Figure 7 presents (Figure 7, upper) and (Figure 7, lower) calculated in the two-subevent method for particles with GeV and or . This selection is used to suppress the non-flow correlations that may remain in the calculation of (). One can see in Figure 7 that and repeat the trend of and from Figure 6 with the values being slightly higher. Thus, we assume that the two-subevent method indeed eliminated some of the remaining impacts of the -resonance decays, even though its usage requires larger statistics of simulated events.
A similar dependence was presented by ALICE experiment (see [69]) for the two-particle correlation, , integrated over rapidity, that grows with the event multiplicity. The results were also presented for the near-side ridge, but those differ in particle selection and acceptance.
For large in Figure 6 and Figure 7, one can see a slight splitting of the results with different definitions. The primary goal of the analysis with the different selections is to test the sensitivity of the flow to particles’ transverse momenta.
To make it more visible, we show in Figure 8 the dependence of two-particle cumulants, and , for 0–5% event class of distribution for particles with GeV and . To achieve a similar number of particles for all model points, we perform the calculation of cumulants in the -intervals of a varying size.
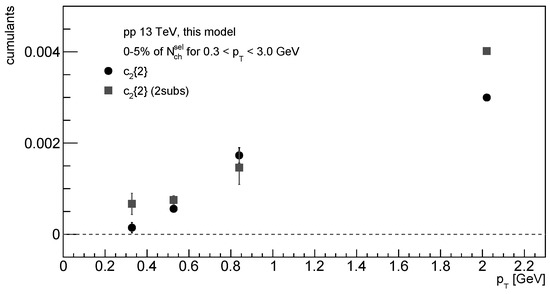
Figure 8.
Model results for two-particle cumulants, and , as a function of of charged particles for 0– event class based on calculated for GeV, in inelastic pp interactions at TeV. See text for details.
Figure 8 shows that and values gradually increase as the functions of the momentum of particles that are used in their calculations. This is in qualitative agreement with the ATLAS results [66] showing a similar trend.
In the model workflow, the behaviour of and can be explained as follows. First of all, the quenching mechanism that was introduced produces larger anisotropy for particles with higher . It is because it becomes increasingly more difficult for particles to escape the string matter while saving sufficiently large transverse momentum. In turn, string–string interactions and their acceleration in the transverse plane increase the of correlated particles, leading to larger anisotropy from these boosts.
7. Discussion
In this study, we developed the workflow of the colour string model to address the challenging question of the origin of the collective flow observed in inelastic proton–proton interactions. It is interesting to draw parallels between our simplified model and the cognate event generators also based on colour string fragmentation such as in the EPOS [25] and PYTHIA [26] models.
The core concept of our model is the description of pp inelastic interaction via the multi-pomeron exchange, Equation (1), find which resembles the parallel scatterings of partons that occur in the EPOS4 event generator. The way to find momenta of string endpoints combines methods of energy-momentum sharing and saturation implemented in the EPOS4 model. All this is strikingly different from the consideration of hard scattering a starting point of multi-parton interactions in the PYTHIA model. The concept that was not implemented in any existing event generator is attractive string dynamics [39] introduced to the workflow of our model. It modifies the shape of the string density in an event resulting in the collapse of particle-producing sources. This leads to the fusion of overlapped strings into an event hot spot, which is analogues to the formation of core in the EPOS4 model. On the other hand, the concept of the formation of the fused particle source with higher tension is realised in the PYTHIA generator by using the rope mechanism. Finally, in the EPOS4 generator, evolution of the core is considered in hydro-regime, which results in a transverse flow signal. In the presented model, particle boosts (similar to the effect of string shoving mechanism in PYTHIA) and their momentum losses in string medium are the sources of azimuthal anisotropy of produced particles.
Moving on to discussing the obtained results, let us note that an event picture prior to hadronisation looks like a highly inhomogeneous string medium. Originating from the multi-pomeron exchange, the system of particle-producing strings is disordered by the longitudinal and transverse dynamics of the system. One observes the peculiar grouping of strings in the mixed configuration–momentum space. Some of them are isolated forming the debris of pp interaction. Other strings participate in the event hot spot, partially overlapping, while the most lucky ones form a dense cluster of strings, overlapping to the highest degree. It is the presence of such a core that determines the crucial collective features of the soft particle production in pp collisions. In particular, in the model, the particle anisotropy appears due to this complex structure of event shape and the effect of particle momentum quenching.
Thus, a recognisable core-corona picture of the string system [70] is observed. This picture represents the interplay of these two characteristic event regions that governs the transverse flow in the model. Namely, in the corona region, it is only the loss of the particle’s momentum that plays a role. On the other hand, the impact of the complex core structure is quite complicated to deduce. The relatively low occupancy regions of the core create correlated multi-directional particle boosts, while the hottest region determines a single dominant direction and, therefore, strongly boosts particles with .
For example, the model result for the angular correlation function, ), reveals the familiar near-side ridge that is formed by the collimated emission of particles, boosted by the clusters of strings.
On the other hand, the away-side ridge is missing from the model results. We interpret that as due to an excessive approach of strings at the moment, which results in the formation of the over-condensed string region.
In this case, the production of particles with separation in the model framework with boost should come from the peripheral, low-occupancy parts of the core. It seems that, in the current implementation, this area is too scarce to create the away-side ridge. A similar observation was made in Ref. [71], where the absence of the away-side ridge is caused by complications in defining the cutoff between the core and corona.
The model results obtained for the second-order two-particle cumulants are in qualitative agreement with the data by the ALICE and ATLAS experiments on inelastic pp interactions at TeV. In our future studies, higher statistics would be needed to calculate multi-particle cumulants and to access high-multiplicity events.
The flow signal obtained in the model grows with the transverse momentum of charged particles in high-multiplicity events. This reflects the flow origin from the particles formed by interacting strings.
In conclusion, let us note that in this study, it was expected that the time—the time of the string system evolution in the transverse plane—that results in the highest density of strings would provide the best description of the collective behaviour of particles in pp interactions. However, it appeared that, in terms of this model, controls a degree of core-corona separation. The obtained – correlation result indicates that one would have to tune more precisely, which is a subject for further studies.
Author Contributions
Conceptualization, D.P. and E.A.; methodology, D.P. and E.A.; software, D.P. and E.A.; validation, D.P. and E.A.; formal analysis, D.P.; writing—original draft preparation, D.P.; writing—review and editing, E.A.; visualization, D.P. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge Saint-Petersburg State University for a research project 95413904.
Data Availability Statement
The data presented in this study are available on request from the authors.
Acknowledgments
The authors are grateful to Grigory Feofilov, Vladimir Vechernin and Vladimir Kovalenko for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AA | nucleus-nucleus |
| AMPT | A Multi-Phase Transport |
| ATLAS | A Toroidal LHC ApparatuS |
| CERN | Conseil Européen pour la Recherche Nucléaire (the European Organization for Nuclear Research) |
| CPU | central processing unit |
| CTEQ | Coordinate Theoretical-Experimental Project on QCD |
| CT10nnlo | CTEQ version 10 next-to-next-to-leading order |
| EPOS | Energy conserving quantum mechanical multiple scattering approach, based on Partons (parton ladders), Off-shell remnants, and Saturation of parton ladders |
| HIJING | Heavy Ion Jet INteraction Generator |
| LHA | Les Houches Accord |
| LHC | Large Hadron Collider |
| parton density function | |
| pp | proton–proton |
| QCD | quantum chromodynamics |
| QED | quantum electrodynamics |
| QGP | quark-gluon plasma |
| RHIC | Relativistic Heavy Ion Collider |
| 2D, 3D | 2-, 3-dimensional |
Appendix A
Here, we describe the procedure for creating a proton with .
Appendix A.1. Valence Quarks and Diquark
We start with the creation of valence u and d quarks by sampling their proton momentum fractions, and , from their valence parton distribution functions (PDFs), and . We find as the difference between PDFs for u (d) quark and () antiquark taken from CT10nnlo approximation [72] based on CT10 PDFs [73], set 1 by LHAPDF [74] at the momentum transferred, GeV2.
We consider three possible combinations of selecting 2 out of 3 valence quarks in order to create a diquark (either or ). We define diquark momentum, , as the sum of the proton momentum fractions of the two selected valence quarks, . The three combinations are ordered by the largest of the valence quark that is not included in the diquark.
We set the diquark mass, , equal to GeV. For quarks, both valence and sea, we start with the current (not constituent) masses: GeV, GeV, GeV, and GeV that are dynamically changed later, see Appendix A.3.
For each parton representing a quark or a diquark and enumerated by , we calculate its energy, , and its fraction of proton energy, , as
where , GeV, .
Appendix A.2. Sea Quarks
In case of a number of pomeron exchanges greater than 1, we take into account the presence of sea quarks that participate in the interaction. We sample the proton momentum fraction for each sea quark, , where i runs over values from 1 to , using the sum of PDFs for all flavours, . For a given sea quark (sampled ), we define its flavour from the relative probability that is known at any given x (i.e., from the ratio between PDFs for different flavours, , at x). Gluons are not considered at this stage because they are accounted for differently (see Appendix A.3). For each sea quark, we also calculate according to Equation (A1).
Appendix A.3. Energy-Momentum Conservation for a Proton
At this point, we take a step back and verify that the sums of partons’ and are less than 1. Otherwise, a proton is to be regenerated.
As soon as the goal is achieved, the energy-momentum conservation is to be taken into account within a proton. Namely, the sums of the and for all should be equal to 1 each. However, at this step, there is no guarantee these conditions are fulfilled. Therefore, we find the deficiencies, and , as
In this study, we distribute and between all the created partons (both valence and sea), which may be interpreted as a gluon contribution. For example, in the event with we split and in half between valence quark and diquark. Thus, for the bare valence quark and diquark one gets the modified fractions of proton momentum, , and proton energy, , from
As soon as the gluon contribution is taken into account, one can define the initial parton momentum as
and the initial parton energy as
The modifications of partons’ momenta (A3) and energies (A4) change the partons’ masses from “bare” (current) values, or , to the “dressed” ones, , according to
This approach can be naturally extrapolated to any arbitrary number of sea quarks. Namely, we assign and to each of the valence quark and the diquark and split the remaining between all the sea quarks in a proton. This procedure increases the masses of quarks and diquark (for valence ones to a greater extent), which makes the distributions of the string ends’ rapidities more realistic.
However, it is also possible that after the procedure described, parton’s energy decreases compared to parton’s momentum. Therefore, one cannot calculate parton’s dressed mass, . In this case, the remaining two different groupings of valence quarks into diquark should be considered (see Appendix A.1). If none of the combinations allows finding , the proton is to be regenerated.
References
- Shuryak, E.V. Theory of hadron plasma. Sov. Phys. JETP 1978, 47, 212–219. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/47/2/p212?a=list (accessed on 30 January 2024).
- Heinz, U.W.; Jacob, M. Evidence for a new state of matter: An Assessment of the results from the CERN lead beam program. arXiv 2000, arXiv:nucl-th/0002042. [Google Scholar] [CrossRef]
- Arsene, I. et al. [BRAHMS Collaboration] Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Back, B.B. et al. [PHOBOS Collaboration] The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28–101. [Google Scholar] [CrossRef]
- Adams, J. et al. [STAR Collaboration] Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Adcox, K. et al. [PHENIX Collaboration] Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX Collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef]
- Voloshin, S.; Zhang, Y. Flow study in relativistic nuclear collisions by Fourier expansion of Azimuthal particle distributions. Z. Phys. C 1996, 70, 665–672. [Google Scholar] [CrossRef]
- Kolb, P.F.; Huovinen, P.; Heinz, U.W.; Heiselberg, H. Elliptic flow at SPS and RHIC: From kinetic transport to hydrodynamics. Phys. Lett. B 2001, 500, 232–240. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, Y.Z.; Liu, Y.M.; Keane, D.; Beavis, D.; Chu, S.Y.; Fung, S.Y.; Vient, M.; Hartnack, C.; Stoecker, H. Measurement of collective flow in heavy ion collisions using particle pair correlations. Phys. Rev. C 1991, 44, 1091–1095. [Google Scholar] [CrossRef]
- Adler, C. et al. [STAR Collaboration] Elliptic flow from two and four particle correlations in Au+Au collisions at = 130 GeV. Phys. Rev. C 2002, 66, 034904. [Google Scholar] [CrossRef]
- Borghini, N.; Dinh, P.M.; Ollitrault, J.Y. Flow analysis from multiparticle azimuthal correlations. Phys. Rev. C 2001, 64, 054901. [Google Scholar] [CrossRef]
- Jia, J.; Zhou, M.; Trzupek, A. Revealing long-range multiparticle collectivity in small collision systems via subevent cumulants. Phys. Rev. C 2017, 96, 034906. [Google Scholar] [CrossRef]
- Bilandzic, A.; Christensen, C.H.; Gulbrandsen, K.; Hansen, A.; Zhou, Y. Generic framework for anisotropic flow analyses with multiparticle azimuthal correlations. Phys. Rev. C 2014, 89, 064904. [Google Scholar] [CrossRef]
- Bożek, P. Transverse-momentum–flow correlations in relativistic heavy-ion collisions. Phys. Rev. C 2016, 93, 044908. [Google Scholar] [CrossRef]
- Khachatryan, V. et al. [CMS Collaboration] Observation of long-range near-side angular correlations in proton-proton collisions at the LHC. J. High Energy Phys. 2010, 09, 091. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Observation of long-range elliptic azimuthal anisotropies in = 13 and 2.76 TeV pp collisions with the ATLAS detector. Phys. Rev. Lett. 2016, 116, 172301. [Google Scholar] [CrossRef] [PubMed]
- Aaboud, M. et al. [ATLAS Collaboration] Measurements of long-range azimuthal anisotropies and associated Fourier coefficients for pp collisions at = 5.02 and 13 TeV and p+Pb collisions at = 5.02 TeV with the ATLAS detector. Phys. Rev. C 2017, 96, 024908. [Google Scholar] [CrossRef]
- Ambrus, V.E.; Schlichting, S.; Werthmann, C. Establishing the range of applicability of hydrodynamics in high-energy collisions. Phys. Rev. Lett. 2023, 130, 152301. [Google Scholar] [CrossRef]
- Weller, R.D.; Romatschke, P. One fluid to rule them all: Viscous hydrodynamic description of event-by-event central p+p, p+Pb and Pb+Pb collisions at = 5.02 TeV. Phys. Lett. B 2017, 774, 351–356. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, W.; Murase, K.; Song, H. One fluid might not rule them all. Nucl. Phys. A 2021, 1005, 121908. [Google Scholar] [CrossRef]
- Artru, X. Classical string phenomenology. How strings work. Phys. Rep. 1983, 97, 147–171. [Google Scholar] [CrossRef]
- Capella, A.; Sukhatme, U.; Tan, C.-I.; Tran Thanh Van, J. Dual parton model. Phys. Rep. 1994, 236, 225–329. [Google Scholar] [CrossRef]
- Braun, M.; Pajares, C. A Probabilistic model of interacting strings. Nucl. Phys. B 1993, 390, 542–558. [Google Scholar] [CrossRef]
- Gelis, F. Color glass gondensate and glasma. Int. J. Mod. Phys. A 2013, 28, 1330001. [Google Scholar] [CrossRef]
- Werner, K. Revealing a deep connection between factorization and saturation: New insight into modeling high-energy proton–proton and nucleus-nucleus scattering in the EPOS4 framework. Phys. Rev. C 2023, 108, 064903. [Google Scholar] [CrossRef]
- Sjöstrand, T. The PYTHIA event generator: Past, resent and future. Comput. Phys. Commun. 2020, 246, 106910. [Google Scholar] [CrossRef]
- Wang, X.N.; Gyulassy, M. HIJING: A Monte Carlo model for multiple jet production in pp, pA and AA collisions. Phys. Rev. D 1991, 44, 3501–3516. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Ko, C.M.; Li, B.A.; Lin, Z.w. A multiphase transport model for nuclear collisions at RHIC. Phys. Rev. C 2000, 61, 067901. [Google Scholar] [CrossRef]
- Braun, M.A.; Pajares, C. Elliptic flow from color strings. Eur. Phys. J. C 2011, 71, 1558. [Google Scholar] [CrossRef]
- Braun, M.A.; Pajares, C.; Vechernin, V.V. Anisotropic flows from colour strings: Monte-Carlo simulations. Nucl. Phys. A 2013, 906, 14–27. [Google Scholar] [CrossRef]
- Braun, M.A.; Pajares, C.; Vechernin, V.V. Ridge from strings. Eur. Phys. J. A 2015, 51, 44. [Google Scholar] [CrossRef]
- Abramovsky, V.A.; Gedalin, E.V.; Gurvich, E.G.; Kancheli, O.V. Long range azimuthal correlations in multiple production processes at high energies. JETP Lett. 1988, 47, 337–339. Available online: http://jetpletters.ru/ps/1093/article_16503.shtml (accessed on 30 January 2024).
- Altsybeev, I. Mean transverse momenta correlations in hadron-hadron collisions in MC toy model with repulsing strings. AIP Conf. Proc. 2016, 1701, 100002. [Google Scholar] [CrossRef]
- Bierlich, C.; Gustafson, G.; Lönnblad, L. Collectivity without plasma in hadronic collisions. Phys. Lett. B 2018, 779, 58–63. [Google Scholar] [CrossRef]
- Andronov, E.V.; Prokhorova, D.S.; Belousov, A.A. Influence of quark–gluon string interactions on particle correlations in p+p collisions. Theor. Math. Phys. 2023, 216, 1265–1277. [Google Scholar] [CrossRef]
- Prokhorova, D.; Andronov, E.; Feofilov, G. Interacting colour strings approach in modelling of rapidity correlations. Physics 2023, 5, 636–654. [Google Scholar] [CrossRef]
- Braun, M.A.; Pajares, C. pt dependence of the flow coefficients for pp collisions in the color string scenario: Monte Carlo simulations. Eur. Phys. J. A 2018, 54, 185. [Google Scholar] [CrossRef]
- Shen, C.; Schenke, B. Dynamical initial state model for relativistic heavy-ion collisions. Phys. Rev. C 2018, 97, 024907. [Google Scholar] [CrossRef]
- Kalaydzhyan, T.; Shuryak, E. Collective interaction of QCD strings and early stages of high-multiplicity pA collisions. Phys. Rev. C 2014, 90, 014901. [Google Scholar] [CrossRef]
- Braun, M.A.; Pajares, C.; Ranft, J. Fusion of strings versus percolation and the transition to the quark gluon plasma. Int. J. Mod. Phys. A 1999, 14, 2689–2704. [Google Scholar] [CrossRef]
- Braun, M.A.; Del Moral, F.; Pajares, C. Percolation of strings and the first RHIC data on multiplicity and tranverse momentum distributions. Phys. Rev. C 2002, 65, 024907. [Google Scholar] [CrossRef]
- Braun, M.A.; Kolevatov, R.S.; Pajares, C.; Vechernin, V.V. Correlations between multiplicities and average transverse momentum in the percolating color strings approach. Eur. Phys. J. C 2004, 32, 535–546. [Google Scholar] [CrossRef]
- Braun, M.A.; Dias de Deus, J.; Hirsch, A.S.; Pajares, C.; Scharenberg, R.P.; Srivastava, B.K. De-Confinement and Clustering of Color Sources in Nuclear Collisions. Phys. Rep. 2015, 599, 1–50. [Google Scholar] [CrossRef]
- Altsybeev, I.; Feofilov, G. Azimuthal flow in hadron collisions from quark-gluon string repulsion. EPJ Web Conf. 2016, 125, 04011. [Google Scholar] [CrossRef]
- Aaboud, M. et al. [ATLAS Collaboration] Charged-particle distributions at low transverse momentum in = 13 TeV pp interactions measured with the ATLAS detector at the LHC. Eur. Phys. J. C 2016, 76, 502. [Google Scholar] [CrossRef] [PubMed]
- Vechernin, V.; Lakomov, I. The dependence of the number of pomerons on the impact parameter and the long-range rapidity correlations in pp collisions. PoS 2012, Baldin ISHEPP XXI, 072. [Google Scholar] [CrossRef][Green Version]
- Kaidalov, A.B.; Ter-Martirosyan, K.A. Pomeron as quark-gluon strings and multiple hadron production at SPS collider energies. Phys. Lett. B 1982, 117, 247–251. [Google Scholar] [CrossRef]
- Vechernin, V.V.; Belokurova, S.N. The strongly intensive observable in pp collisions at LHC energies in the string fusion model. J. Phys. Conf. Ser. 2020, 1690, 012088. [Google Scholar] [CrossRef]
- Armesto, N.; Derkach, D.A.; Feofilov, G.A. pt–multiplicity correlations in a multi-pomeron-exchange model with string collective effects. Phys. Atom. Nucl. 2008, 71, 2087–2095. [Google Scholar] [CrossRef]
- Wilson, K.G. Confinement of quarks. Phys. Rev. D 1974, 10, 2445–2459. [Google Scholar] [CrossRef]
- Iritani, T.; Cossu, G.; Hashimoto, S. Analysis of topological structure of the QCD vacuum with overlap-Dirac operator eigenmode. PoS 2014, LATTICE 2013, 376. [Google Scholar] [CrossRef][Green Version]
- Kalaydzhyan, T.; Shuryak, E. Self-interacting QCD strings and string balls. Phys. Rev. D 2014, 90, 025031. [Google Scholar] [CrossRef]
- Belokurova, S.; Vechernin, V. Long-range correlations between observables in a model with translational invariance in rapidity. Symmetry 2020, 12, 1107. [Google Scholar] [CrossRef]
- Lüscher, M.; Münster, G.; Weisz, P. How thick are chromo-electric flux tubes? Nucl. Phys. B 1981, 180, 1–12. [Google Scholar] [CrossRef]
- Baker, M.; Cea, P.; Chelnokov, V.; Cosmai, L.; Cuteri, F.; Papa, A. The confining color field in SU(3) gauge theory. Eur. Phys. J. C 2020, 80, 514. [Google Scholar] [CrossRef]
- Kovalenko, V.; Feofilov, G.; Puchkov, A.; Valiev, F. Multipomeron model with collective effects for high-energy hadron collisions. Universe 2022, 8, 246. [Google Scholar] [CrossRef]
- Schwinger, J. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Gurvich, E.G. The quark anti-quark pair production mechanism in a quark jet. Phys. Lett. B 1979, 87, 386–388. [Google Scholar] [CrossRef]
- Casher, A.; Neuberger, H.; Nussinov, S. Chromoelectric flux tube model of particle production. Phys. Rev. D 1979, 20, 179–188. [Google Scholar] [CrossRef]
- Bodnia, E.; Derkach, D.; Feofilov, G.; Kovalenko, V.; Puchkov, A. Multi-pomeron exchange model for pp and collisions at ultra-high energy. PoS 2014, QFTEP 2013, 060. [Google Scholar] [CrossRef]
- Bresenham, J.E. Algorithm for computer control of a digital plotter. IBM Syst. J. 1965, 4, 25–30. [Google Scholar] [CrossRef]
- Poskanzer, A.M.; Voloshin, S.A. Methods for analyzing anisotropic flow in relativistic nuclear collisions. Phys. Rev. C 1998, 58, 1671–1678. [Google Scholar] [CrossRef]
- Luzum, M.; Ollitrault, J.Y. Eliminating experimental bias in anisotropic-flow measurements of high-energy nuclear collisions. Phys. Rev. C 2013, 87, 044907. [Google Scholar] [CrossRef]
- Adams, J. et al. [STAR Collaboration] Minijet deformation and charge-independent angular correlations on momentum subspace (η, ϕ) in Au-Au collisions at = 130 GeV. Phys. Rev. C 2006, 73, 064907. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration] Centrality dependence of dihadron correlations and azimuthal anisotropy harmonics in PbPb collisions at = 2.76 TeV. Eur. Phys. J. C 2012, 72, 2012. [Google Scholar] [CrossRef]
- Aaboud, M. et al. [ATLAS Collaboration] Measurement of multi-particle azimuthal correlations in pp, p+Pb and low-multiplicity Pb+Pb collisions with the ATLAS detector. Eur. Phys. J. C 2017, 77, 428. [Google Scholar] [CrossRef] [PubMed]
- Graczykowski, L.K.; Janik, M.A. Unfolding the effects of final-state interactions and quantum statistics in two-particle angular correlations. Phys. Rev. C 2021, 104, 054909. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Long- and short-range correlations and their event-scale dependence in high-multiplicity pp collisions at = 13 TeV. JHEP 2021, 05, 290. [Google Scholar] [CrossRef]
- Parkkila, J.E. Long-range correlations in low-multiplicity pp collisions at = 13 TeV. In Proceedings of the 57th Rencontres de Moriond. 2023 QCD and High Energy Interactions, La Thuile, Italy, 25 March–1 April 2023; Augé, E., Dumarchez, J., Trân Thanh Vân, J., Eds.; ARISF: Lausanne, Switzerland, 2023; pp. 247–250. [Google Scholar]
- Kanakubo, Y.; Tachibana, Y.; Hirano, T. Interplay between core and corona from small to large systems. EPJ Web Conf. 2023, 276, 01017. [Google Scholar] [CrossRef]
- Werner, K.; Karpenko, I.; Pierog, T. The ’ridge’ in proton-proton scattering at 7 TeV. Phys. Rev. Lett. 2011, 106, 122004. [Google Scholar] [CrossRef]
- Gao, J.; Guzzi, M.; Huston, J.; Lai, H.L.; Li, Z.; Nadolsky, P.; Pumplin, J.; Stump, D.; Yuan, C.P. CT10 next-to-next-to-leading order global analysis of QCD. Phys. Rev. D 2014, 89, 033009. [Google Scholar] [CrossRef]
- Lai, H.L.; Guzzi, M.; Huston, J.; Li, Z.; Nadolsky, P.M.; Pumplin, J.; Yuan, C.P. New parton distributions for collider physics. Phys. Rev. D 2010, 82, 074024. [Google Scholar] [CrossRef]
- Buckley, A.; Ferrando, J.; Lloyd, S.; Nordström, K.; Page, B.; Rüfenacht, M.; Schönherr, M.; Watt, G. LHAPDF6: Parton density access in the LHC precision era. Eur. Phys. J. C 2015, 75, 132. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).