Atoms Dressed by Virtual and Real Photons
Abstract
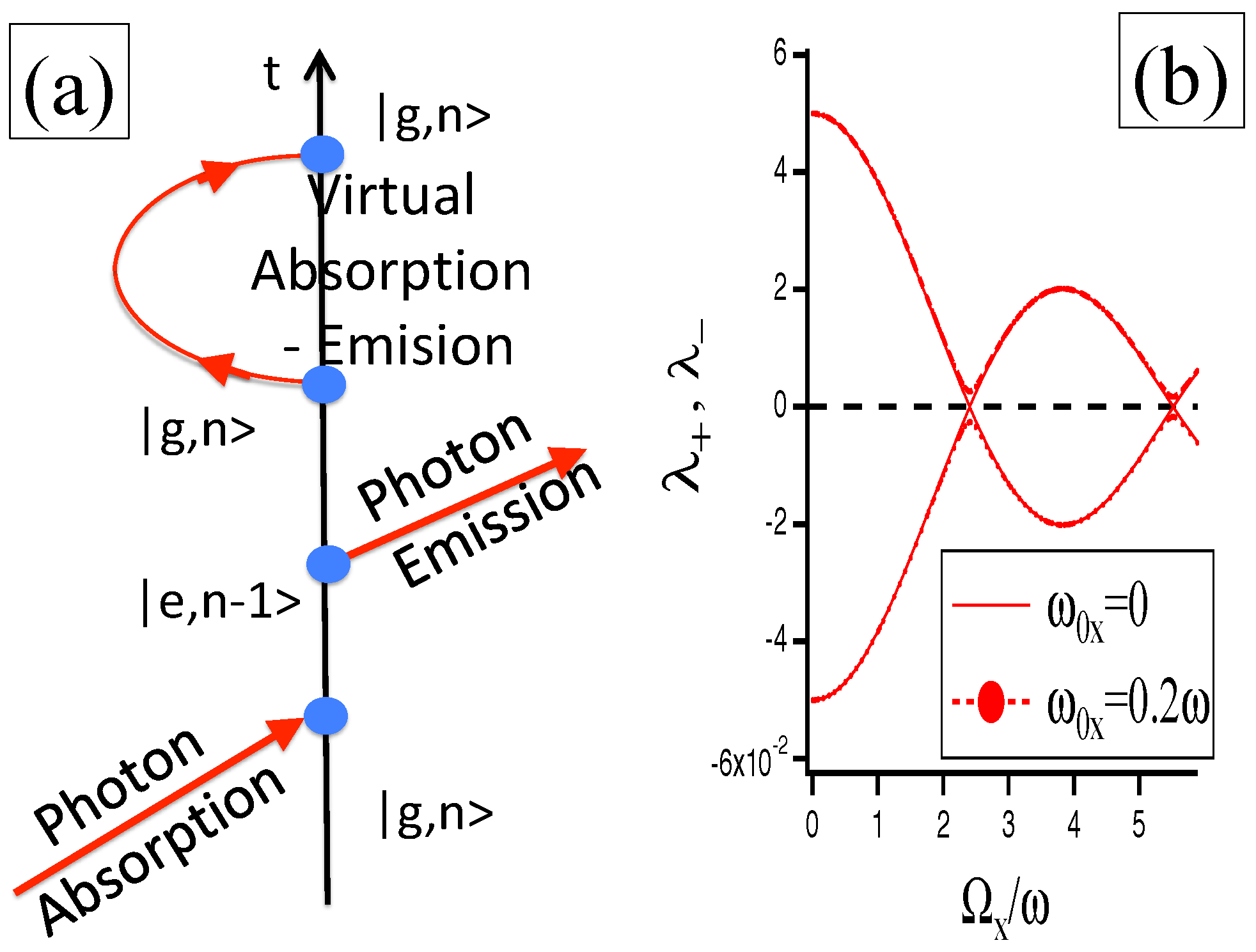
:1. Introduction
2. Dressed States
3. Results
3.1. Dressed Hamiltonian and Spin Detection
3.2. Single x Strong Dressing
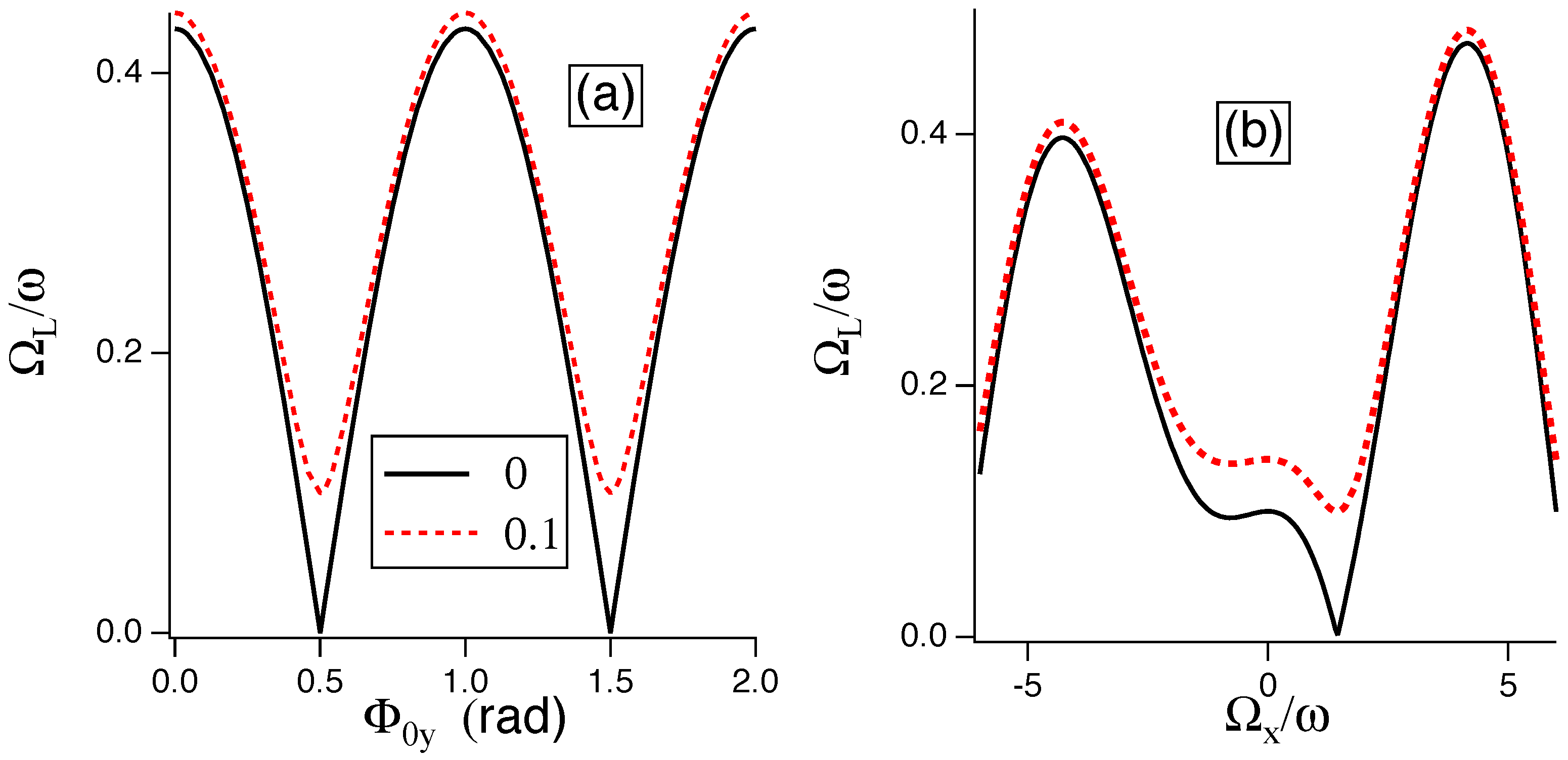
3.3. Dual (x,y) Dressing
3.4. Rotating Dressing
3.5. Dual (x,z) Dressing
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Compagno, G.; Passante, R.; Persico, F. Atom-Field Interactions and Dressed Atoms; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Goldman, N.; Dalibard, J. Periodically driven quantum systems: Effective Hamiltonians and engineered gauge fields. Phys. Rev. X 2014, 4, 031027. [Google Scholar] [CrossRef]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal high-frequency behavior of periodically driven systems: From dynamical stabilization to Floquet engineering. Adv. Phys. 2015, 64, 139–226. [Google Scholar] [CrossRef]
- Eckardt, A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004. [Google Scholar] [CrossRef]
- Compagno, G.; Passante, R.; Persico, F. Edwin Power and the birth of dressed atoms. Contemp. Phys. 2006, 47, 269–278. [Google Scholar] [CrossRef]
- Van Hove, L. The approach to equilibrium in quantum statistics: A perturbation treatment to general order. Physica 1957, 23, 441–480. [Google Scholar] [CrossRef]
- Feynman, R.P. QED: The Strange Theory of Light and Matter; Princeton University Press: Princeton, NJ, USA, 1985; Available online: https://archive.org/details/qedstrangetheory00feyn (accessed on 5 December 2023).
- Pekar, S.I.; Deigen, M.F. Quantum states and optical transitions of electron in a polaron and at a color center of a crystal. Zh. Eksp. Teor. Fiz. 1948, 18, 481–486. (In Russian). English translation: Ukr. J. Phys. 2008, 53, 78–82. Available online: http://archive.ujp.bitp.kiev.ua/files/journals/53/si/53SI17p.pdf (accessed on 5 December 2023).
- Landau, L.D.; Pekar, S.I. Effective mass of a polaron. Zh. Eksp. Teor. Fiz. 1948, 18, 419–423. (In Russian). English translation: Ukr. J. Phys. 2008, 53, 71–74. Available online: http://archive.ujp.bitp.kiev.ua/files/journals/53/si/53SI15p.pdf (accessed on 5 December 2023).
- Devreese, J.T.; Alexandrov, A.S. Fröhlich polaron and bipolaron: Recent developments. Rep. Progr. Phys. 2009, 72, 066501. [Google Scholar] [CrossRef]
- Massignan, P.; Zaccanti, M.; Bruun, G.M. Polarons, dressed molecules and itinerant ferromagnetism in ultracold Fermi gases. Rep. Progr. Phys. 2014, 77, 034401. [Google Scholar] [CrossRef]
- Compagno, G.; Passante, R.; Persico, F.; Salamone, G. Cloud of virtual photons surrounding a nonrelativistic electron. Acta Phys. Pol. A 1994, 85, 676–677. [Google Scholar] [CrossRef]
- Compagno, G.; Passante, R.; Persico, F. The role of the cloud of virtual photons in the shift of the ground state energy of a hydrogen atom. Phys. Lett. A 1983, 98, 253–255. [Google Scholar] [CrossRef]
- Passante, R.; Compagno, G.; Persico, F. Cloud of virtual photons in the ground state of the hydrogen atom. Phys. Rev. A 1985, 31, 2827–2841. [Google Scholar] [CrossRef] [PubMed]
- Passante, R.; Power, E.A. Electromagnetic-energy-density distribution around a ground-state hydrogen atom and connection with van der Waals forces. Phys. Rev. A 1987, 35, 188–197. [Google Scholar] [CrossRef] [PubMed]
- Passante, R. Dispersion interactions between neutral atoms and the quantum electrodynamical vacuum. Symmetry 2018, 10, 735. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Guéry-Odelin, D. Advances in Atomic Physics: An Overview; World Scientific: Singapore, 1994. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Haroche, S. Modification et annulation de facteur de Landé d’un atome couplage avec un champ de radiofréquence. Comp. Rend. Acad. Sci. Paris B 1966, 262, 268–271. Available online: https://gallica.bnf.fr/ark:/12148/bpt6k64298075/f288.item (accessed on 5 December 2023).
- Cohen-Tannoudji, C.; Haroche, S. Absorption et diffusion de photons optiques par un atome en interaction avec des photons de radiofréquence. J. Phys. France 1969, 30, 153–168. [Google Scholar] [CrossRef]
- Landré, C.; Cohen-Tannoudji, C.; Dupont-Roc, J.; Haroche, S. Anisotropie des propriétés magnétiques d’un atome “habillé” par des photons de RF. J. Phys. France 1970, 31, 971–983. [Google Scholar] [CrossRef]
- Ashhab, S.; Johansson, J.R.; Zagoskin, A.M.; Nori, F. Two-level systems driven by large-amplitude fields. Phys. Rev. A 2007, 75, 063414. [Google Scholar] [CrossRef]
- Hausinger, J.; Grifoni, M. Dissipative two-level system under strong ac driving: A combination of Floquet and Van Vleck perturbation theory. Phys. Rev. A 2010, 81, 022117. [Google Scholar] [CrossRef]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Holthaus, M. Towards coherent control of a Bose-Einstein condensate in a double well. Phys. Rev. A 2001, 64, 011601. [Google Scholar] [CrossRef]
- Bevilacqua, G.; Biancalana, V.; Dancheva, Y.; Moi, L. Larmor frequency dressing by a nonharmonic transverse magnetic field. Phys. Rev. A 2012, 85, 042510. [Google Scholar] [CrossRef]
- Happer, W., Jr. Observations of transitions between stationary states in a rotating magnetic field. Phys. Rev. 1964, 136, A35–A42. [Google Scholar] [CrossRef]
- Hofferberth, S.; Fischer, B.; Schumm, T.; Schmiedmayer, J.; Lesanovsky, I. Ultracold atoms in radio-frequency dressed potentials beyond the rotating-wave approximation. Phys. Rev. A 2007, 76, 013401. [Google Scholar] [CrossRef]
- Allegrini, M.; Arimondo, E. Radiofrequency transitions in a dressed atom. J. Phys. B At. Mol. Phys. 1971, 4, 1008–1012. [Google Scholar] [CrossRef]
- Harper, P.G.; Allegrini Arimondo, M. Resonant polaron damping of de Haas-Van Alphen oscillations in polar semiconductors. J. Phys. C Solid State Phys. 1971, 4, 181–186. [Google Scholar] [CrossRef]
- Shirley, J.H. Solution of the Schrödinger equation with a hamiltonian periodic in time. Phys. Rev. 1965, 138, B979–B987. [Google Scholar] [CrossRef]
- Sambe, H. Steady states and quasienergies of a quantum-mechanical system in an oscillating field. Phys. Rev. A 1973, 7, 2203–2213. [Google Scholar] [CrossRef]
- Guccione-Gush, R.; Gush, H.P. Two-level system in a bichromatic field. Phys. Rev. A 1974, 10, 1474–1487. [Google Scholar] [CrossRef]
- Chu, S.I.; Telnov, D.A. Beyond the Floquet theorem: Generalized Floquet formalisms and quasienergy methods for atomic and molecular multiphoton processes in intense laser fields. Phys. Rep. 2004, 390, 1–131. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F.; Oteo, J.A.; Ros, J. The Magnus expansion and some of its applications. Phys. Rep. 2009, 470, 151–238. [Google Scholar] [CrossRef]
- Leskes, M.; Madhu, P.K.; Vega, S. Floquet theory in solid-state nuclear magnetic resonance. Prog. Nucl. Magn. Reson. Spectrosc. 2010, 57, 345–380. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, K.L.; Mote, K.R.; Ernst, M.; Equbal, A.; Madhu, P.M. Floquet theory in magnetic resonance: Formalism and applications. Prog. Nucl. Magn. Reson. Spectrosc. 2021, 126–127, 17–58. [Google Scholar] [CrossRef] [PubMed]
- Arnal, M.; Chatelain, G.; Cabrera-Gutiérrez, C.; Fortun, A.; Michon, E.; Billy, J.; Schlagheck, P.; Guéry-Odelin, D. Beyond effective Hamiltonians: Micromotion of Bose-Einstein condensates in periodically driven optical lattices. Phys. Rev. A 2020, 101, 013619. [Google Scholar] [CrossRef]
- Desbuquois, R.; Messer, M.; Görg, F.; Sandholzer, K.; Jotzu, G.; Esslinger, T. Controlling the Floquet state population and observing micromotion in a periodically driven two-body quantum system. Phys. Rev. A 2017, 96, 053602. [Google Scholar] [CrossRef]
- Martin, I.; Refael, G.; Halperin, B. Topological frequency conversion in strongly driven quantum systems. Phys. Rev. X 2017, 7, 041008. [Google Scholar] [CrossRef]
- Fregosi, A.; Marinelli, C.; Gabbanini, C.; Bevilacqua, G.; Biancalana, V.; Arimondo, E.; Fioretti, A. Floquet space exploration for the dual-dressing of a qubit. Sci. Rep. 2023, 13, 15304. [Google Scholar] [CrossRef]
- Pegg, D.T. Semi-classical model of magnetic resonance in intense RF fields. J. Phys. B At. Mol. Phys. 1973, 6, 246–253. [Google Scholar] [CrossRef]
- Ruyten, W.M. Magnetic and optical resonance of two-level quantum systems in modulated fields. II. Floquet Hamiltonian approach. Phys. Rev. A 1990, 42, 4246–4254. [Google Scholar] [CrossRef]
- Buckley, B.B.; Fuchs, G.D.; Bassett, L.C.; Awschalom, D.D. Spin-light coherence for single-spin measurement and control in diamond. Science 2010, 330, 1212–1215. [Google Scholar] [CrossRef]
- Budker, D.; Kimball, D.F.; Rochester, S.M.; Yashchuk, V.V.; Zolotorev, M. Sensitive magnetometry based on nonlinear magneto-optical rotation. Phys. Rev. A 2000, 62, 043403. [Google Scholar] [CrossRef]
- Fregosi, A.; Gabbanini, C.; Gozzini, S.; Lenci, L.; Marinelli, C.; Fioretti, A. Magnetic induction imaging with a cold-atom radio frequency magnetometer. Appl. Phys. Lett. 2020, 117, 144102. [Google Scholar] [CrossRef]
- Bevilacqua, G.; Biancalana, V.; Vigilante, A.; Zanon-Willette, T.; Arimondo, E. Harmonic fine tuning and triaxial spatial anisotropy of dressed atomic spins. Phys. Rev. Lett. 2020, 125, 093203. [Google Scholar] [CrossRef]
- Yabuzaki, T.; Tsukada, N.; Ogawa, T. Modification of atomic g-factor by the oscillating rf field. J. Phys. Soc. Jpn. 1972, 32, 1069–1077. [Google Scholar] [CrossRef]
- Kunitomo, M.; Hashi, T. Modification of Zeeman energy by non-resonant oscillating field in the rotating frame. Phys. Lett. A 1972, 40, 75–76. [Google Scholar] [CrossRef]
- Muskat, E.; Dubbers, D.; Schärpf, O. Dressed Neutrons. Phys. Rev. Lett. 1987, 58, 2047–2050. [Google Scholar] [CrossRef] [PubMed]
- Gerbier, F.; Widera, A.; Fölling, S.; Mandel, O.; Bloch, I. Resonant control of spin dynamics in ultracold quantum gases by microwave dressing. Phys. Rev. A 2006, 73, 041602. [Google Scholar] [CrossRef]
- Esler, A.; Peng, J.C.; Chandler, D.; Howell, D.; Lamoreaux, S.K.; Liu, C.Y.; Torgerson, J.R. Dressed spin of 3He. Phys. Rev. C 2007, 76, 051302. [Google Scholar] [CrossRef]
- Chu, P.H.; Esler, A.M.; Peng, J.C.; Beck, D.H.; Chandler, D.E.; Clayton, S.; Hu, B.Z.; Ngan, S.Y.; Sham, C.H.; So, L.H.; et al. Dressed spin of polarized 3He in a cell. Phys. Rev. C 2011, 84, 022501. [Google Scholar] [CrossRef]
- Beaufils, Q.; Zanon, T.; Chicireanu, R.; Laburthe-Tolra, B.; Maréchal, E.; Vernac, L.; Keller, J.C.; Gorceix, O. Radio-frequency-induced ground-state degeneracy in a Bose-Einstein condensate of chromium atoms. Phys. Rev. A 2008, 78, 051603(R). [Google Scholar] [CrossRef]
- Pervishko, A.A.; Kibis, O.V.; Morina, S.; Shelykh, I.A. Control of spin dynamics in a two-dimensional electron gas by electromagnetic dressing. Phys. Rev. B 2015, 92, 205403. [Google Scholar] [CrossRef]
- Hao, C.P.; Qiu, Z.R.; Sun, Q.; Zhu, Y.; Sheng, D. Interactions between nonresonant rf fields and atoms with strong spin-exchange collisions. Phys. Rev. A 2019, 99, 053417. [Google Scholar] [CrossRef]
- Haroche, S. L’atome habillé: Une étude théorique et expérirmentale des propriétés physiques d’atomes en interaction avec des photons de radiofréquence. Première partie. Ann. Phys. Paris 1971, 14, 189–326. [Google Scholar] [CrossRef]
- Haroche, S. L’atome habillé: Une étude théorique et expérirmentale des propriétés physiques d’atomes en interaction avec des photons de radiofréquence. Deuxième partie. Ann. Phys. Paris 1971, 14, 327–387. [Google Scholar] [CrossRef]
- Bevilacqua, G.; Biancalana, V.; Dancheva, Y.; Vigilante, A. Sub-millimetric ultra-low-field MRI detected in situ by a dressed atomic magnetometer. Appl. Phys. Lett. 2019, 115, 174102. [Google Scholar] [CrossRef]
- Haroche, S.; Cohen-Tannoudji, C. Resonant transfer of coherence in nonzero magnetic field between atomic levels of different g factors. Phys. Rev. Lett. 1970, 24, 974–978. [Google Scholar] [CrossRef]
- Ito, H.; Ito, T.; Yabuzaki, T. Accumulative Transfer of transverse magnetic moment between spin-locked Rb and Cs atoms. J. Phys. Soc. Jpn. 1994, 63, 1337–1344. [Google Scholar] [CrossRef]
- Golub, R.; Lamoreaux, S.K. Neutron electric-dipole moment, ultracold neutrons and polarized 3He. Phys. Rep. 1994, 237, 1–62. [Google Scholar] [CrossRef]
- Swank, C.M.; Webb, E.K.; Liu, X.; Filippone, B.W. Spin-dressed relaxation and frequency shifts from field imperfections. Phys. Rev. A 2018, 98, 053414. [Google Scholar] [CrossRef]
- Pegg, D.T.; Series, G.W. Semi-classical theory of the Hanle effect with transverse static and oscillating magnetic fields. J. Phys. B At. Mol. Phys. 1970, 3, L33–L35. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Fabre, C. An experimental check of higher order terms in the radiative shift of a coherence resonance. J. Phys. B At. Mol. Phys. 1973, 6, L218–L221. [Google Scholar] [CrossRef]
- Hannaford, P.; Pegg, D.T.; Series, G.W. Analytical expressions for the Bloch-Siegert shift. J. Phys. B At. Mol. Phys. 1973, 6, L222–L225. [Google Scholar] [CrossRef]
- Ahmad, F.; Bullough, R.K. Theory of the Bloch-Siegert shift. J. Phys. B At. Mol. Phys. 1974, 7, L275. [Google Scholar] [CrossRef]
- Series, G.W. A semi-classical approach to radiation problems. Phys. Rep. 1978, 43, 1–41. [Google Scholar] [CrossRef]
- Stoneman, R.C.; Thomson, D.S.; Gallagher, T.F. Microwave multiphoton transitions between Rydberg states of potassium. Phys. Rev. A 1988, 37, 1527–1540. [Google Scholar] [CrossRef] [PubMed]
- Zanon-Willette, T.; de Clercq, E.; Arimondo, E. Magic radio-frequency dressing of nuclear spins in high-accuracy optical clocks. Phys. Rev. Lett. 2012, 109, 223003. [Google Scholar] [CrossRef]
- Bevilacqua, G.; Biancalana, V.; Zanon-Willette, T.; Arimondo, E. Harmonic dual dressing of spin-1/2 systems. Phys. Rev. A 2022, 105, 022619. [Google Scholar] [CrossRef]
- Lo Cascio, L.; Persico, F. Strong-field theory of dressed atoms and dressed photons. J. Mod. Optics 1992, 39, 87–101. [Google Scholar] [CrossRef]
- Pegg, D.T. Misalignment effects in magnetic resonance. J. Phys. B At. Mol. Phys. 1973, 6, 241–245. [Google Scholar] [CrossRef]
- Yabuzaki, T.; Nakayama, S.; Murakami, Y.; Ogawa, T. Interaction between a spin-1/2 atom and a strong rf field. Phys. Rev. A 1974, 10, 1955–1963. [Google Scholar] [CrossRef]
- Yabuzaki, T.; Murakami, Y.; Ogawa, T. Power shifts of multiphoton transitions in a spin 1/2 system. J. Phys. B At. Mol. Phys. 1976, 9, 9–19. [Google Scholar] [CrossRef]
- Ni, Y.; Xu, P.; Martin, J.D.D. Reduction of the dc-electric-field sensitivity of circular Rydberg states using nonresonant dressing fields. Phys. Rev. A 2015, 92, 063418. [Google Scholar] [CrossRef]
- Booth, D.W.; Isaacs, J.; Saffman, M. Reducing the sensitivity of Rydberg atoms to dc electric fields using two-frequency ac field dressing. Phys. Rev. A 2018, 97, 012515. [Google Scholar] [CrossRef]
- Tommey, J.D.R.; Hogan, S.D. Resonant Rydberg-atom–microwave-field interactions in the ultrastrong-driving regime: Beyond the rotating-wave approximation. Phys. Rev. A 2019, 100, 053417. [Google Scholar] [CrossRef]
- Kumar, A.; Suleymanzade, A.; Stone, M.; Taneja, L.; Anferov, A.; Schuster, D.; Simon, J. Quantum-enabled millimetre wave to optical transduction using neutral atoms. Nature 2023, 615, 614–619. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allegrini, M.; Arimondo, E. Atoms Dressed by Virtual and Real Photons. Physics 2024, 6, 60-74. https://doi.org/10.3390/physics6010005
Allegrini M, Arimondo E. Atoms Dressed by Virtual and Real Photons. Physics. 2024; 6(1):60-74. https://doi.org/10.3390/physics6010005
Chicago/Turabian StyleAllegrini, Maria, and Ennio Arimondo. 2024. "Atoms Dressed by Virtual and Real Photons" Physics 6, no. 1: 60-74. https://doi.org/10.3390/physics6010005
APA StyleAllegrini, M., & Arimondo, E. (2024). Atoms Dressed by Virtual and Real Photons. Physics, 6(1), 60-74. https://doi.org/10.3390/physics6010005




