Relations between Shot Noise, Gain Bandwidth, and Saturation of Instabilities
Abstract
:1. Introduction
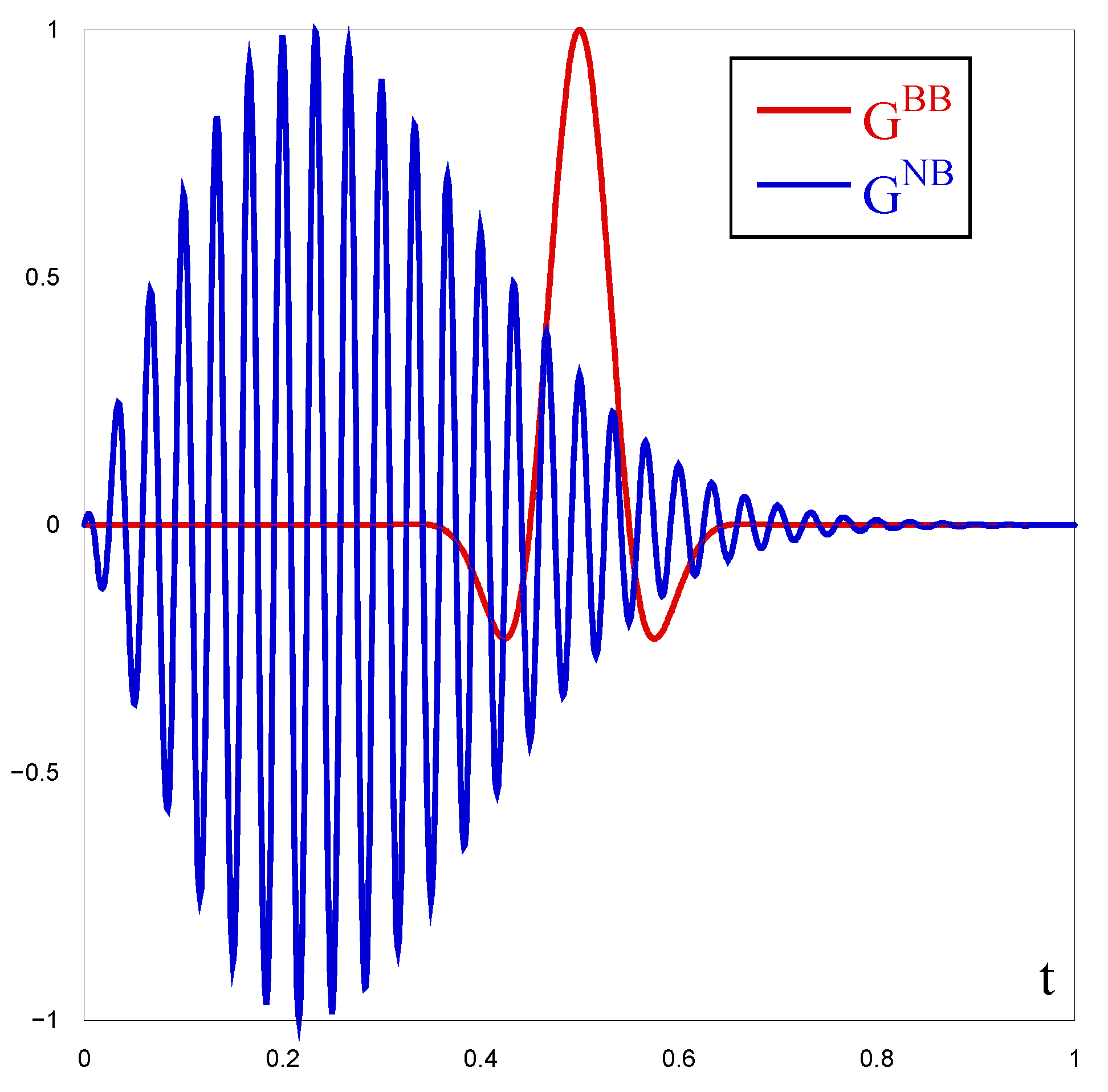
2. Limitation for the Green Function
3. Numerical Tests
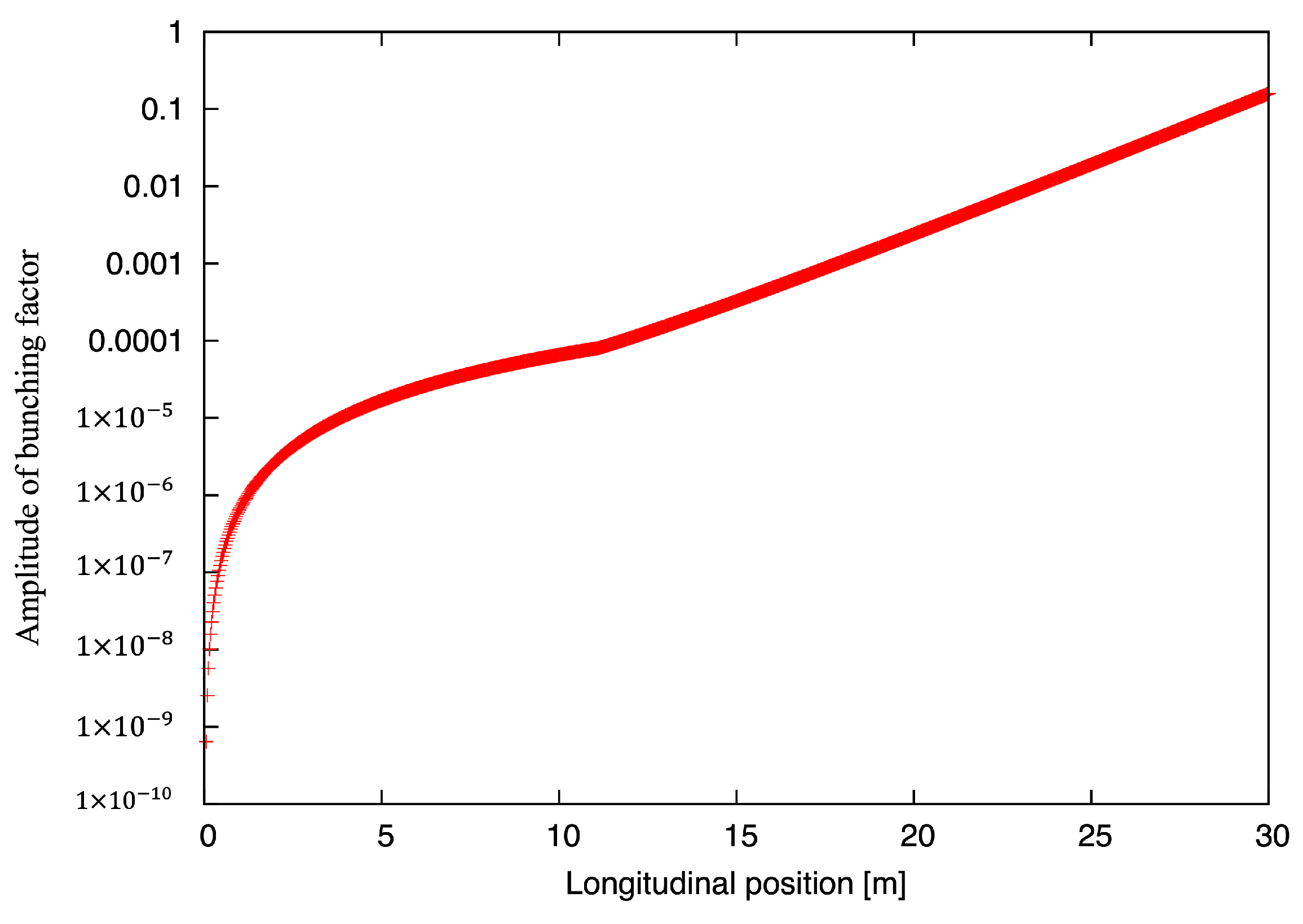
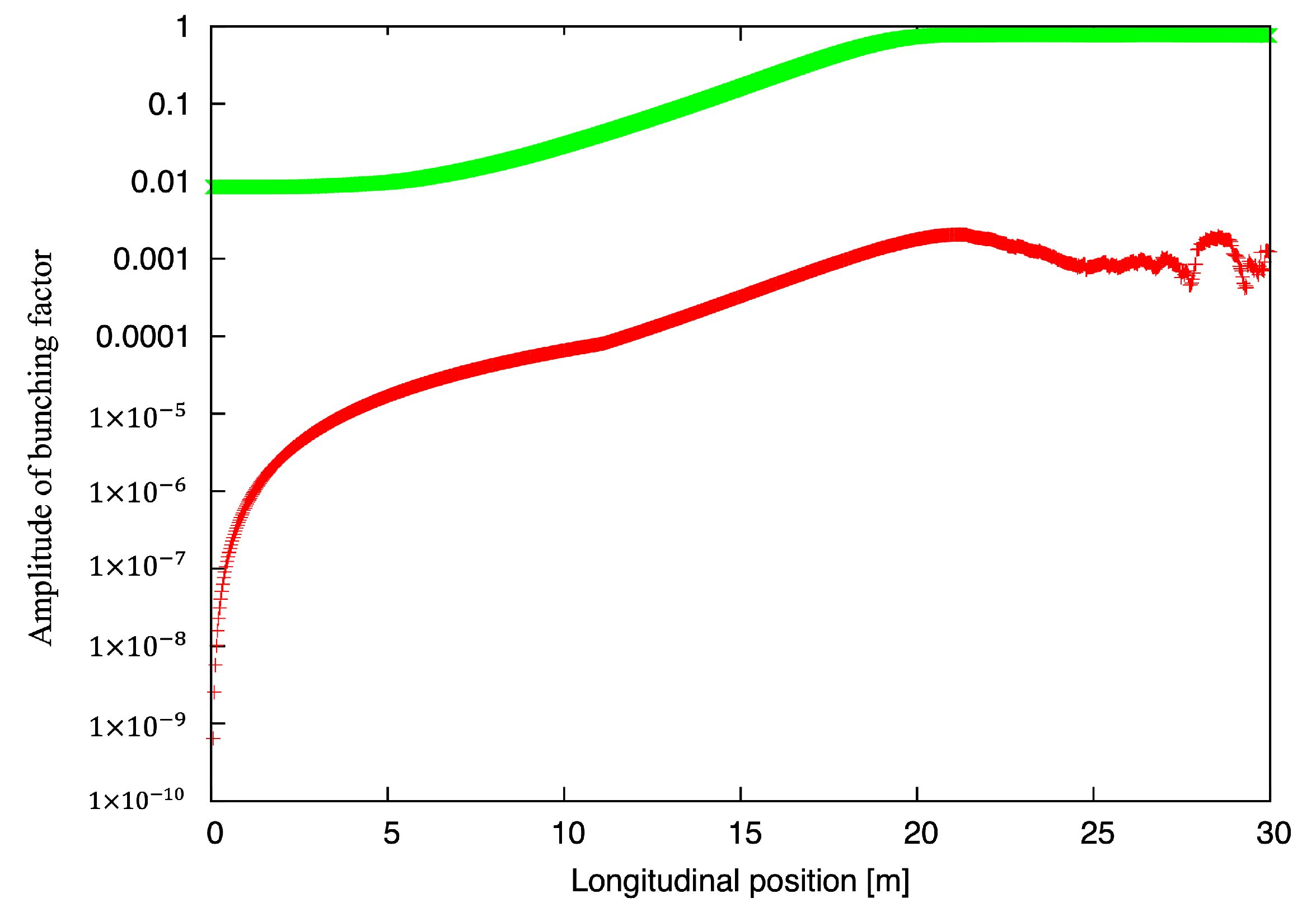
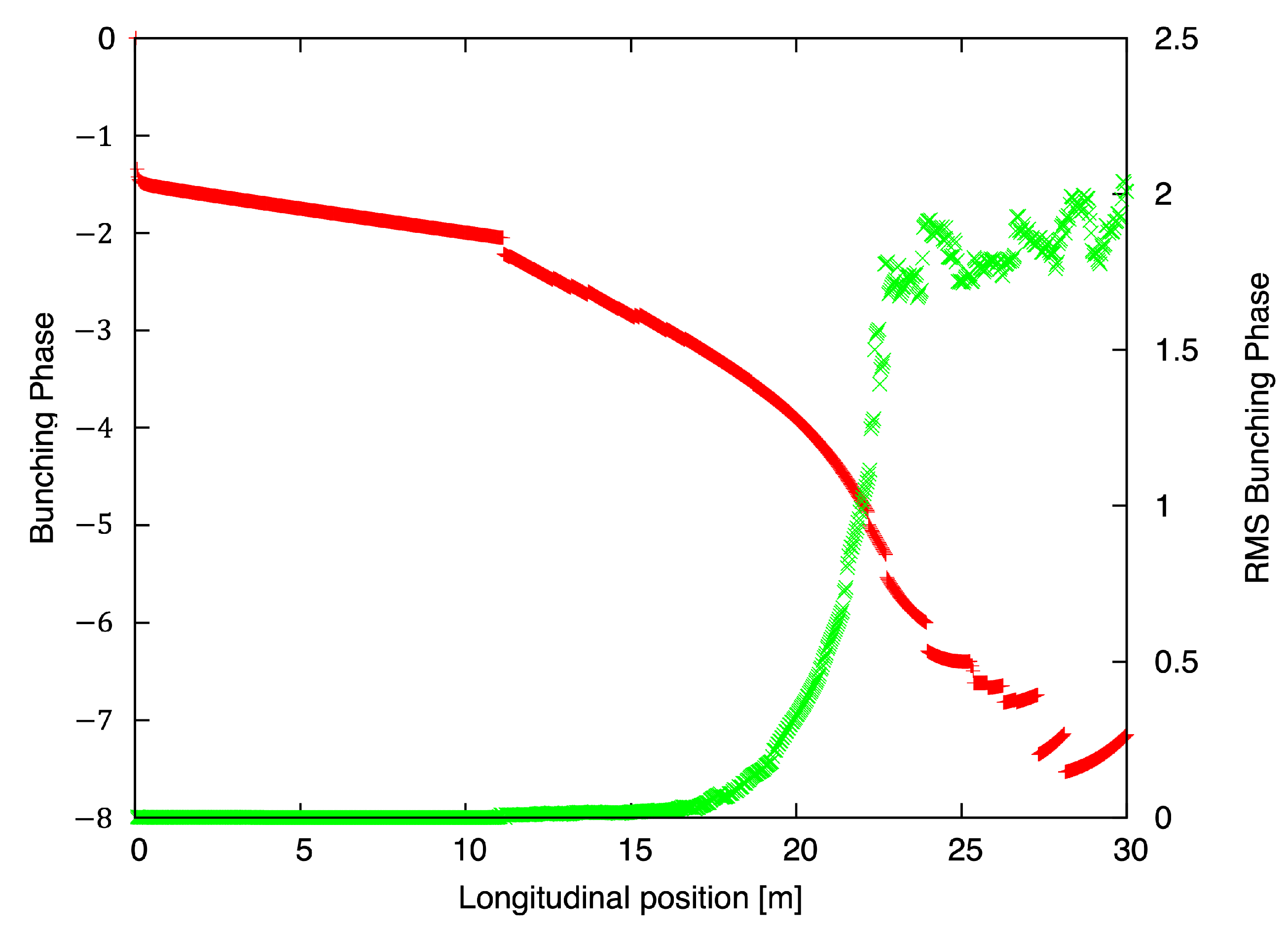
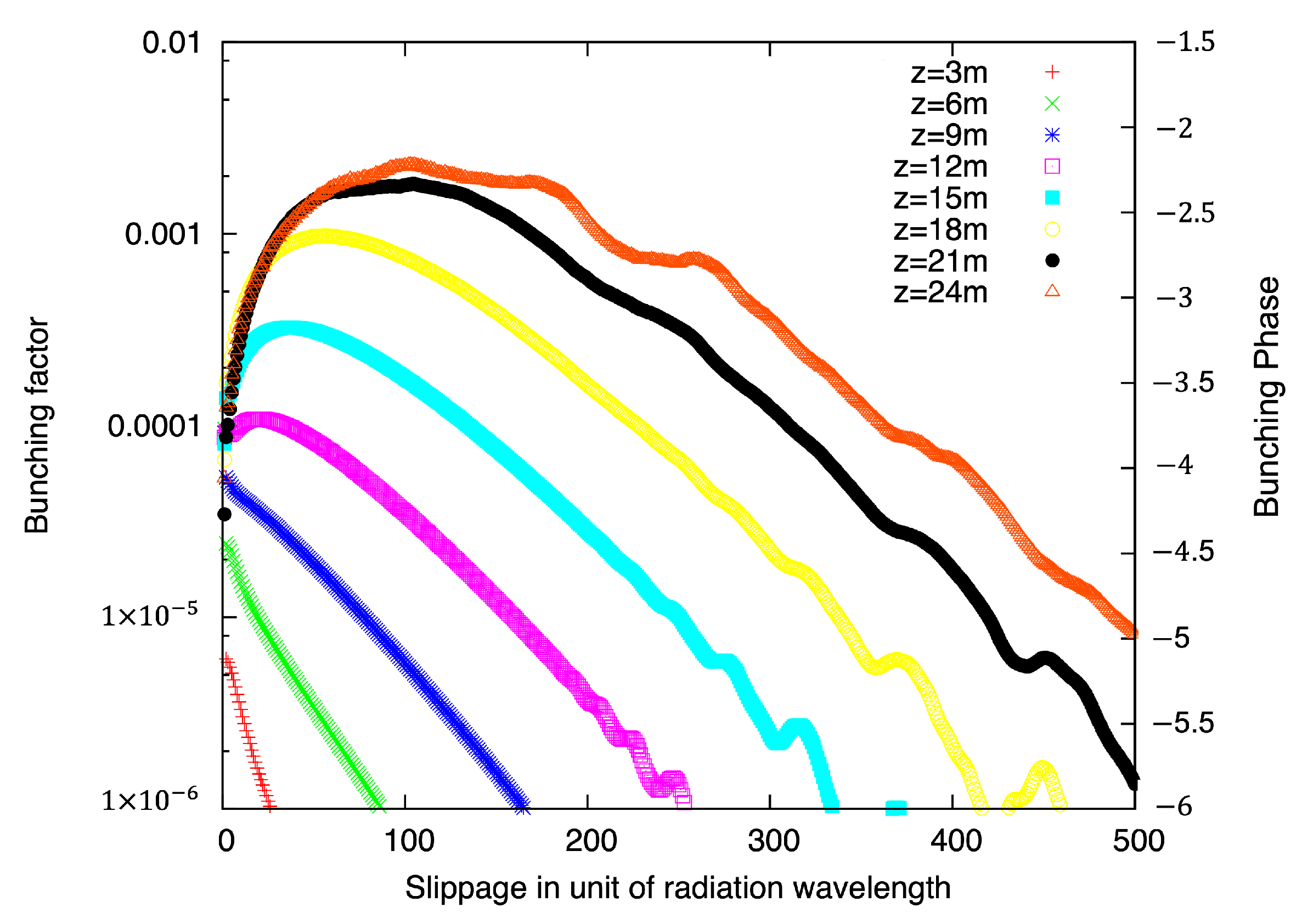
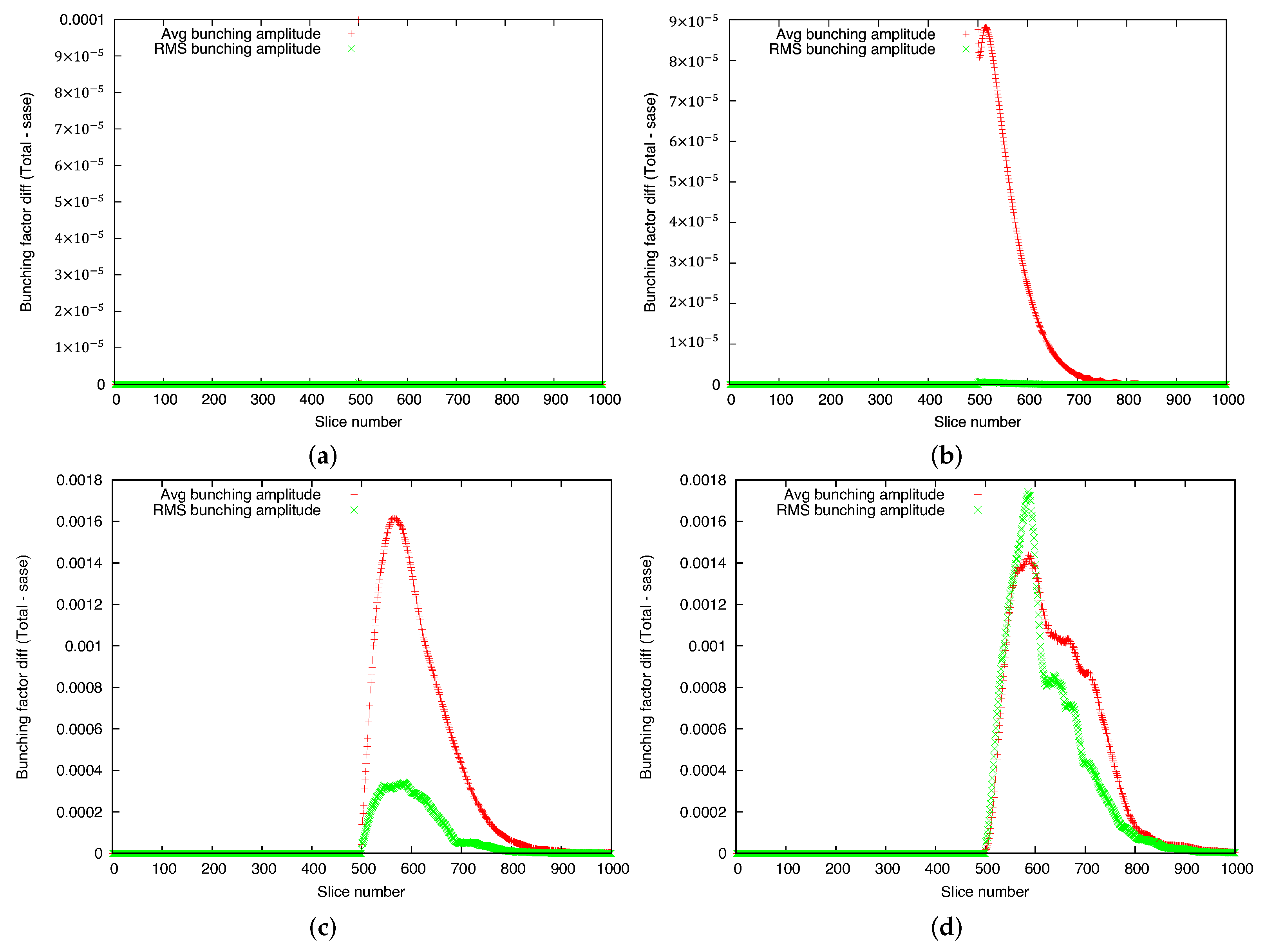
3.1. FEL Simulations
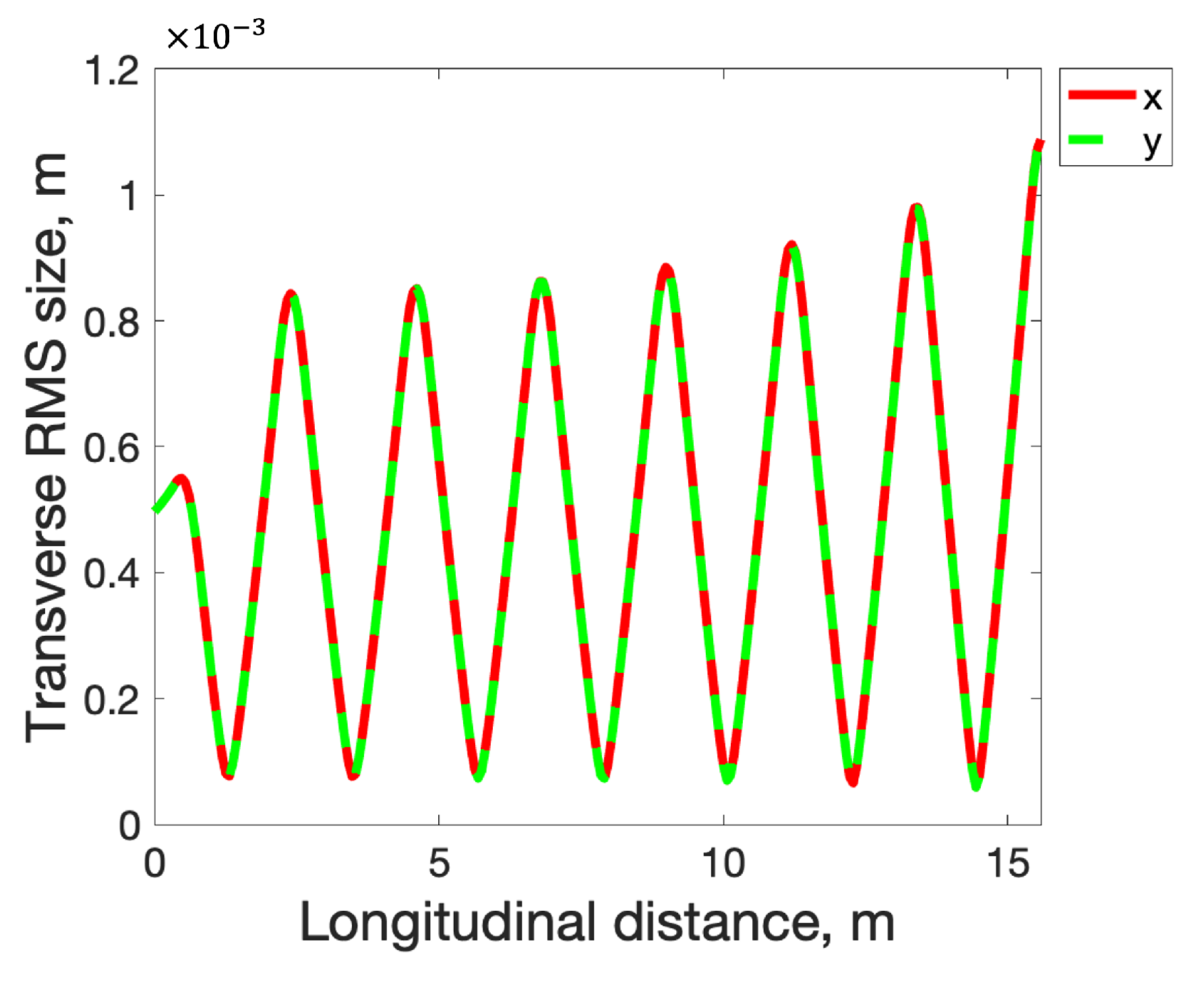
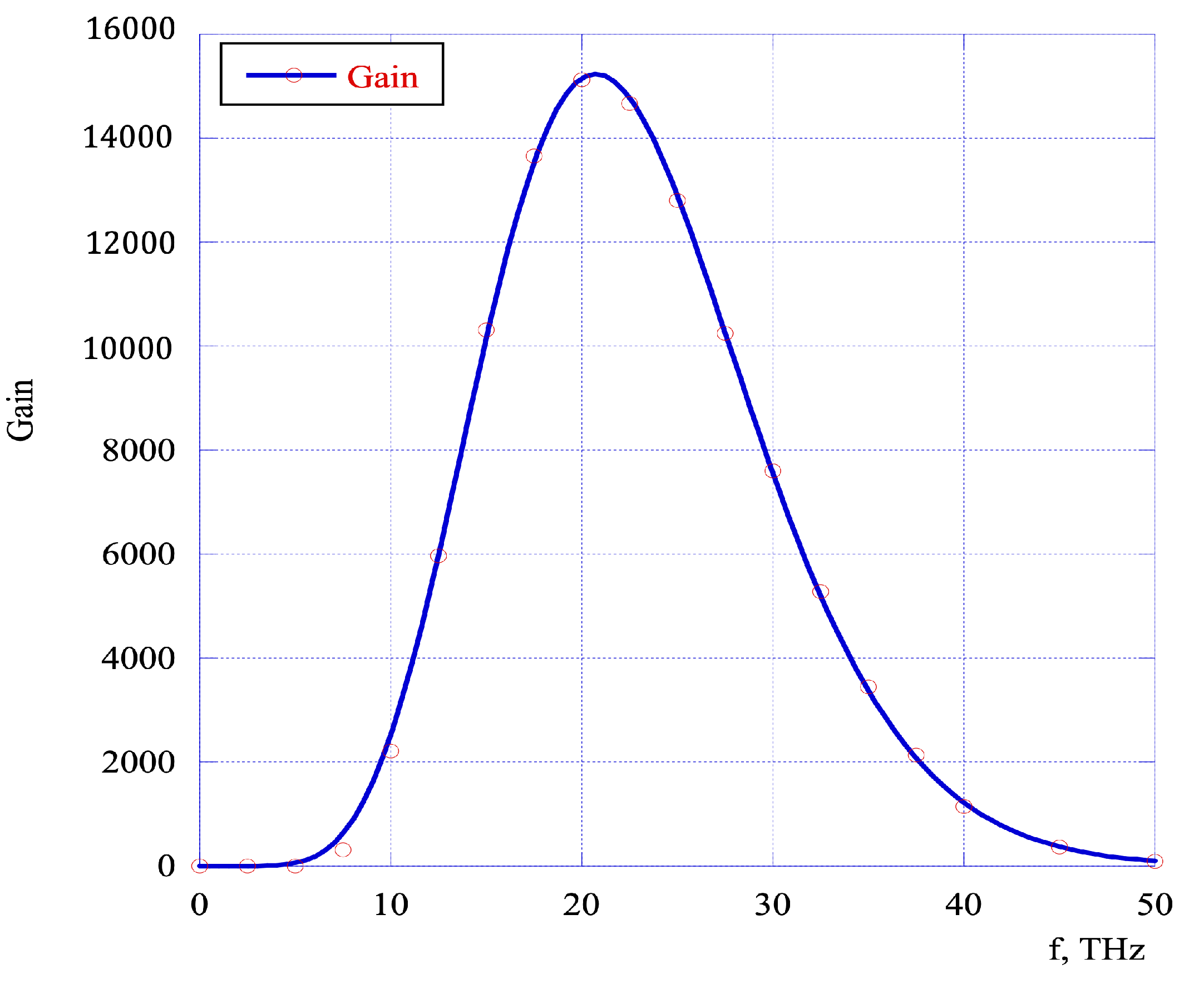
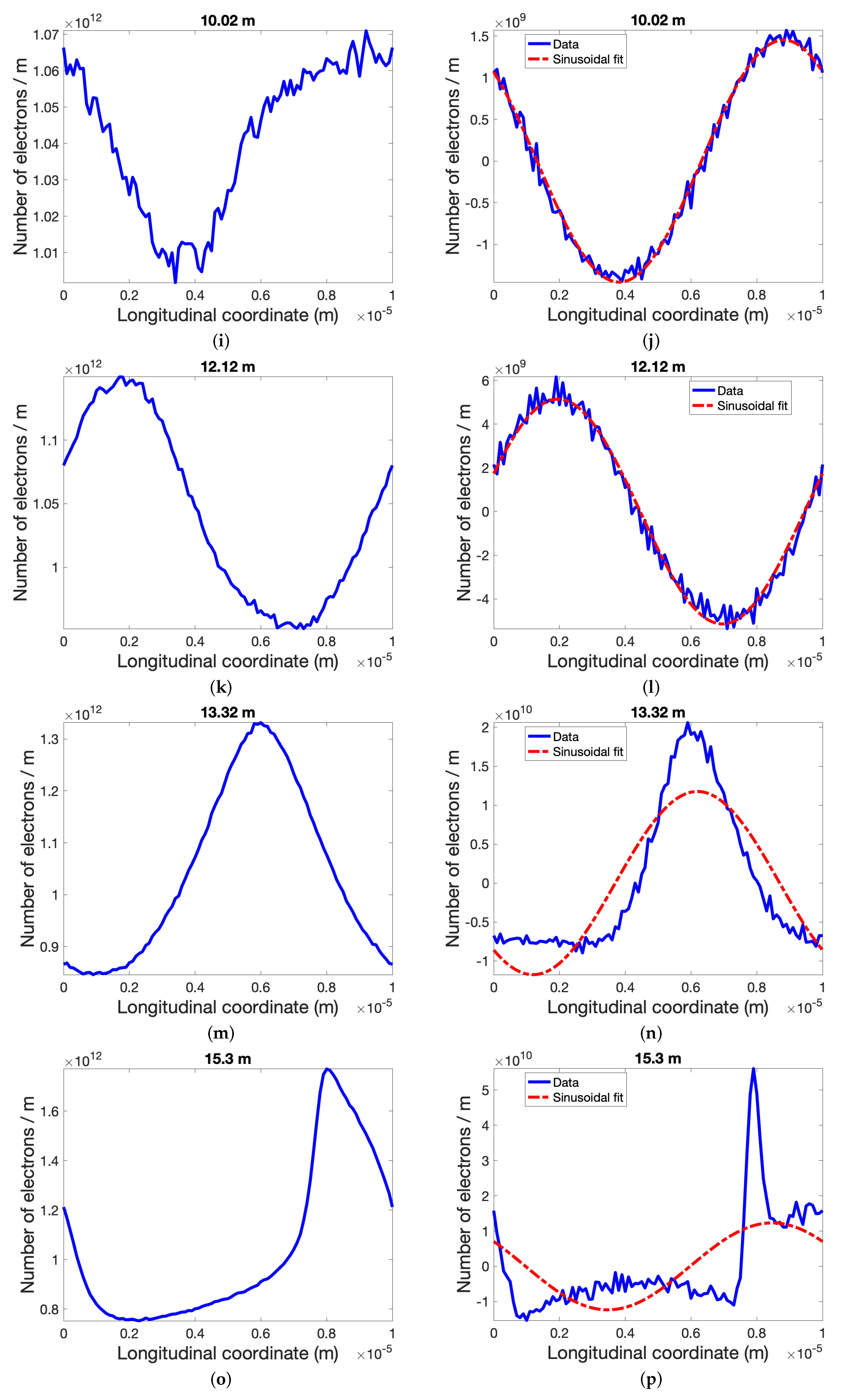
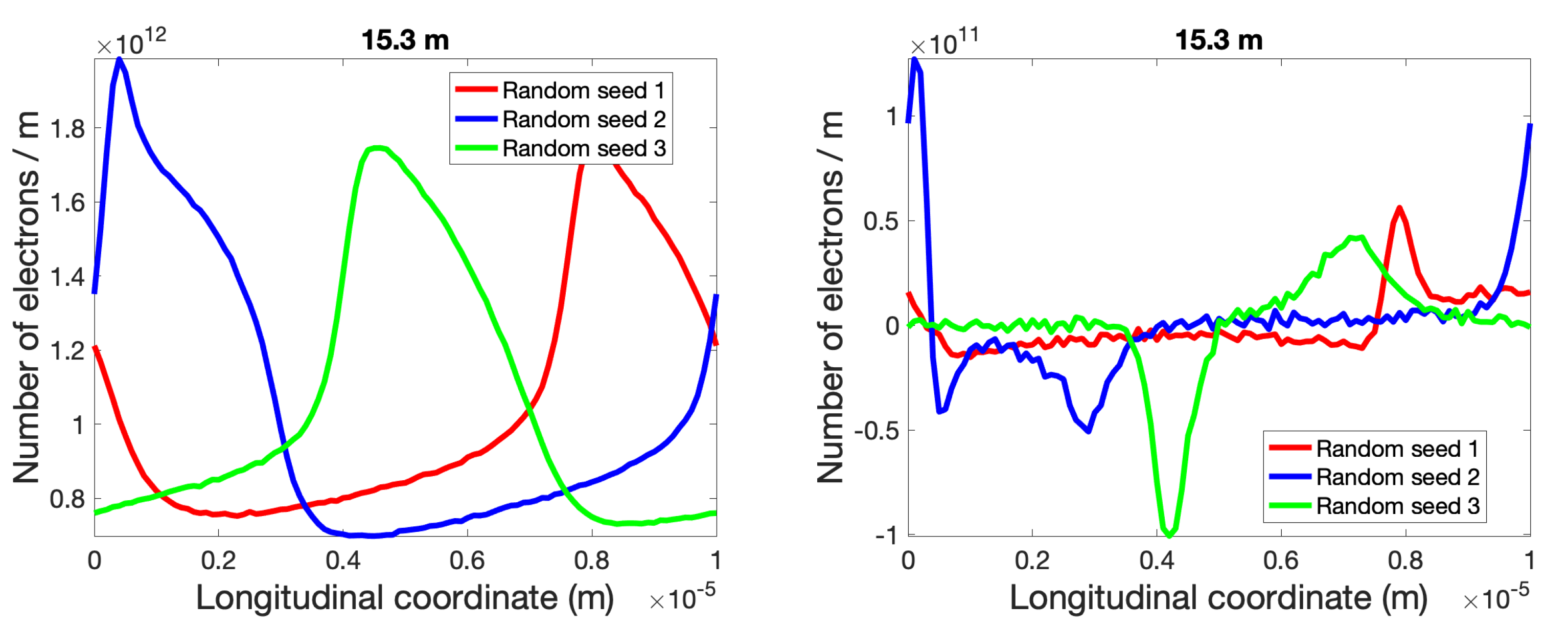
3.2. Simulations of Plasma-Cascade Instability (PCI)
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Extension for the 6D Phase Space
References
- Dattoli, G.; Renieri, A.; Voykov, G. Storage-ring free-electron-laser amplifiers and the microwave instability. Phys. Rev. E 1997, 55, 2056–2058. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. An analytical description of longitudinal phase space distortions in magnetic bunch compressors. Nucl. Istrum. Meth. Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2002, 483, 516–520. [Google Scholar] [CrossRef]
- Huang, Z.; Borland, M.; Emma, P.; Wu, J.; Limborg, C.; Stupakov, G.; Welch, J. Suppression of microbunching instability in the linac coherent light source. Phys. Rev. Spec. Top. Accel. Beams 2004, 7, 074401. [Google Scholar] [CrossRef]
- Madey, J.M.J. Stimulated emission of bremsstrahlung in a periodic magnetic field. J. Appl. Phys. 1971, 42, 1906–1913. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. The physics of free electron lasers. An introduction. Phys. Rep. 1995, 260, 187–327. [Google Scholar] [CrossRef]
- Yu, L.-H.; Babzien, M.; Ben-Zvi, I.; Dimauro, L.F.; Doyuran, A.; Graves, W.; Johnson, E.; Krinsky, S.; Malone, R.; Pogorelsky, I.; et al. High-gain harmonic-generation free-electron laser. Science 2000, 289, 932–934. [Google Scholar] [CrossRef] [PubMed]
- Krinsky, S. The physics and properties of free-electron lasers. AIP Conf. Proc. 2002, 648, 23–43. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Review of x-ray free-electron laser theory. Phys. Rev. Spec. Top. Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Amann, J.; Berg, W.; Blank, V.; Decker, F.-J.; Ding, Y.; Emma, P.; Feng, Y.; Frisch, J.; Fritz, D.; Hastings, J.; et al. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nat. Photon. 2012, 6, 693–698. [Google Scholar] [CrossRef]
- Derbenev, Y.S.; Rossbach, J.; Saldin, E.L.; Shiltsev, V.D. Microbunch Radiative Tail-Head Interaction; Report TESLA-FEL-95-05; DESY: Hamburg, Germany, 1995; Available online: http://cds.cern.ch/record/291102 (accessed on 2 March 2024).
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. On the coherent radiation of an electron bunch moving in an arc of a circle. Nucl. Istrum. Meth. Phys. Res. A Accel. Spectrom. Detect. Assoc. 1997, 398, 373–394. [Google Scholar] [CrossRef]
- Heifets, S.; Stupakov, G.V.; Krinsky, S. Coherent synchrotron radiation instability in a bunch compressor. Phys. Rev. Spec. Top. Accel. Beams 2002, 5, 064401. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Klystron instability of a relativistic electron beam in a bunch compressor. Nucl. Istrum. Meth. Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2002, 490, 1–8. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Formulas for coherent synchrotron radiation microbunching in a bunch compressor chicane. Phys. Rev. Spec. Top. Accel. Beams 2002, 5, 074401. [Google Scholar] [CrossRef]
- Litvinenko, V.N.; Derbenev, Y.S. Coherent electron cooling. Phys. Rev. Lett. 2009, 102, 114801. [Google Scholar] [CrossRef] [PubMed]
- Ratner, D. Microbunched electron cooling for high-energy hadron beams. Phys. Rev. Lett. 2013, 111, 084802. [Google Scholar] [CrossRef] [PubMed]
- Litvinenko, V.N.; Wang, G.; Kayran, D.; Jing, Y.; Ma, J.; Pinayev, I. Plasma-cascade micro-bunching amplifier and coherent electron cooling of a hadron beams. arXiv 2018, arXiv:1802.08677. [Google Scholar] [CrossRef]
- Stupakov, G. Cooling rate for microbunched electron cooling without amplification. Phys. Rev. Accel. Beams 2018, 21, 114402. [Google Scholar] [CrossRef]
- Stupakov, G.; Baxevanis, P. Microbunched electron cooling with amplification cascades. Phys. Rev. Accel. Beams 2019, 22, 034401. [Google Scholar] [CrossRef]
- Litvinenko, V.N.; Jing, Y.; Kayran, D.; Inacker, P.; Ma, J.; Miller, T.; Petrushina, I.; Pinayev, I.; Shih, K.; Wang, G.; et al. Plasma-cascade instability. Phys. Rev. Accel. Beams 2021, 24, 014402. [Google Scholar] [CrossRef]
- Litvinenko, V.N.; Jing, Y.; Ma, J.; Petrushina, I.; Shih, K.; Wang, G. 3D theory of microscopic instabilities driven by space-charge forces. Phys. Rev. Accel. Beams 2023, 26, 054402. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidermiller, E.A.; Yurkov, M.V. The Physics of FELs; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Vlasov, A.A. On vibration properties of electron gas. Zh. Experim. Teor. Fiz. [J. Exp. Theor. Phys.] 1938, 8, 291–318. (In Russian) [Google Scholar]
- Vlasov, A.A. The vibrational properties of an electron gas. Sov. Phys. Usp. 1968, 10, 721–733. [Google Scholar] [CrossRef]
- Lee, H.J. Fundamentals of Theoretical Plasma Physics. Mathematical Description of Plasma Waves; World Scientific: Singapore, 2019. [Google Scholar] [CrossRef]
- Landau, L. On the vibrations of the electronic plasma. J. Phys. (USSR) 1946, 10, 25–34, Reprinted in Collected Papers of L.D. Landau; Ter Haar, D., Ed.; Pergamon Press Ltd.: London, UK and Gordon and Breach, Science Publishers, Inc.: New York, NY, USA; pp. 445–460. [Google Scholar] [CrossRef]
- Van Kampen, N.G. On the theory of stationary waves in plasma. Physica 1955, 21, 949–963. [Google Scholar] [CrossRef]
- Larsson, J. Hermitian structure for the linearized Vlasov–Poisson and Vlasov–Maxwell equations. Phys. Rev. Lett. 1991, 66, 1466–1468. [Google Scholar] [CrossRef] [PubMed]
- Van Kampen, N.G.; Felderhof, B.U. Theoretical Methods in Plasma Physics; North-Holland Publishing, Co.: Amsterdam, The Netherlands; John Wiley & Sons, Inc.: New York, NY, USA, 1967; Available online: https://archive.org/details/theoreticalmetho0000kamp/ (accessed on 2 March 2024).
- Abraham-Shrauner, B. Lie transformation group solutions nonlinear one-dimensional Vlasov equation. J. Math. Phys. 1985, 26, 1428–1435. [Google Scholar] [CrossRef]
- Kheifets, S. Application of the Green’s function method to some nonlinear problems of an electron storage ring. Part IV. Study of a weak beam interaction with a flat strong beam. Part. Accel. 1984, 15, 153–175. Available online: https://inspirehep.net/literature/191782 (accessed on 2 March 2024).
- Duffy, D.G. Green’s Functions with Applications; Chapman & Hall/CRC//Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Kac, M. Statistical Independence on Probability, Number Theory and Analysis; The Mathematical Association of America: Washington, DC, USA, 1959; Available online: https://www.jstor.org/stable/10.4169/j.ctt5hh8tq (accessed on 2 March 2024).
- Klimontovich, Y.L. Kinetic Theory of Nonideal Gases and Nonideal Plasmas; Pergamon Press Ltd.: Oxford, UK, 1982. [Google Scholar] [CrossRef]
- Klimontovich, Y.L. The Kinetic Theory of Electromagnetic Processes; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Reiche, S. Genesis 1.3. Available online: http://genesis.web.psi.ch/ (accessed on 2 March 2024).
- Milton, S.V.; Gluskin, E.; Arnold, N.D.; Benson, C.; Berg, W.; Biedron, S.G.; Borland, M.; Chae, Y.-C.; Dejus, R.J.; Den Hartog, P.K.; et al. Exponential gain and saturation of a self-amplified spontaneous emission free-electron laser. Science 2001, 292, 2037–2041. [Google Scholar] [CrossRef]
- Yu, K.; Kumar, P.; Yuan, S.; Cheng, A.; Samulyak, R. SPACE: 3D parallel solvers for Vlasov–Maxwell and Vlasov–Poisson equations for relativistic plasmas with atomic transformations. Comput. Phys. Commun. 2022, 277, 108396. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Wang, G.; Yu, K.; Samulyak, R.; Litvinenko, V. Simulation studies of modulator for coherent electron cooling. Phys. Rev. Accel. Beams 2018, 21, 111001. [Google Scholar] [CrossRef]
- Ma, J.; Wang, G.; Litvinenko, V. Simulations of coherent electron cooling with two types of amplifiers. Int. J. Mod. Phys. A 2019, 34, 1942029. [Google Scholar] [CrossRef]




| Parameters | FEL Type | |||
|---|---|---|---|---|
| Infrared | Visible | VUV | Hard X-rays | |
| Beam energy (MeV) | 21.8 | 136 | 3812.3 | 13,643.7 |
| Beam current (peak, A) | 100 | 10 | 30 | 3400 |
| Normalized emittance (μm rad) | 5 | 1 | 1 | 1.2 |
| Momentum spread (σp/p) | 1 × 10−3 | 1.5 × 10−5 | 2.5 × 10−5 | 1.05 × 10−4 |
| Undulator period (cm) | 4 | 3 | 10 | 3 |
| Undulator strength, aw | 0.4 | 1 | 10 | 2.4756 |
| Radiation wavelength | 12.7 μm | 423.5 nm | 90.7 nm | 0.15 nm |
| Nc = | 35.8 | 102 | 70.6 | 14.5 |
| Parameter | Value |
|---|---|
| Beam energy | 14.56 MeV |
| Beam current (peak) | 50 A |
| Normalized emittance (RMS) | 1.5 μm rad |
| Momentum spread (RMS, σp/p) | 2 × 10−4 |
| Peak solenoid field | 0.2503 T |
| Solenoid length | 0.42672 m |
| Focal length of solenoids | 0.49 m |
| Distance between solenoids | 2.2 m |
| FEL Type | gmax, Equation (21) | gmax, Genesis Simulations |
|---|---|---|
| Infrared FEL | 858 | 777 |
| Visible FEL | 29 | 27 |
| VUV FEL | 28 | 18.7 |
| Hard X-ray FEL | 27 | 21.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, Y.; Litvinenko, V.N.; Ma, J.; Wang, G. Relations between Shot Noise, Gain Bandwidth, and Saturation of Instabilities. Physics 2024, 6, 921-944. https://doi.org/10.3390/physics6030057
Jing Y, Litvinenko VN, Ma J, Wang G. Relations between Shot Noise, Gain Bandwidth, and Saturation of Instabilities. Physics. 2024; 6(3):921-944. https://doi.org/10.3390/physics6030057
Chicago/Turabian StyleJing, Yichao, Vladimir N. Litvinenko, Jun Ma, and Gang Wang. 2024. "Relations between Shot Noise, Gain Bandwidth, and Saturation of Instabilities" Physics 6, no. 3: 921-944. https://doi.org/10.3390/physics6030057
APA StyleJing, Y., Litvinenko, V. N., Ma, J., & Wang, G. (2024). Relations between Shot Noise, Gain Bandwidth, and Saturation of Instabilities. Physics, 6(3), 921-944. https://doi.org/10.3390/physics6030057





