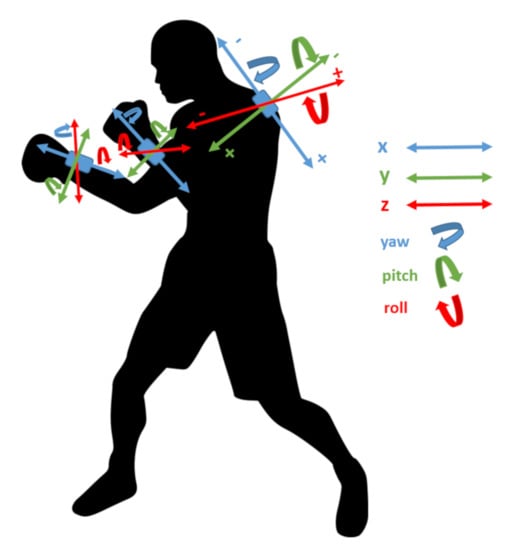
An Evaluation of Wearable Inertial Sensor Configuration and Supervised Machine Learning Models for Automatic Punch Classification in Boxing
Abstract
:1. Introduction
- (i)
- There is no consensus among the scientific literature for measurement protocol (i.e., number of sensors used, sensor placement, properties of sensor used);
- (ii)
- There is no consensus among the scientific literature for the signal processing of the data extracted from the sensors. The algorithms may not be shared amongst the wider scientific community;
- (iii)
- Many of the inertial sensor classification algorithms rely on inertial sensor suits or external technologies such as optical motion capture to be available.
- -
- Inertial sensors positioned near the glove are likely to over-range if the sensor properties are not suitable for high impact events such as punching. However due to the vast array of sensor channels available in a 9DOF sensor, this may not have a drastic effect on classification. However, high-range sensors are required for accurate measurements of punch impact acceleration, velocity and angular velocity etc.
- -
- One less sensor is needed for a complete configuration.
- -
- The complete algorithm can be implemented by embedding sensors into boxing gloves to produce smart boxing gloves, like those developed by Move it Swift™ [36].
- -
- In this configuration, the glove positioned sensors are being used purely for punch detection (high impact event) and thus over-range on these sensors is not a concern for classification model training. The supervised machine learning models are trained using features obtained from the T3 positioned sensor. As the T3 is positioned nearer the user’s centre of mass (CoM) and the punch impact acceleration is attenuated by the musculoskeletal structure, the sensor is not likely to over range.
- -
- Boxing punch form is highly dependent on the movement of the kinetic chain which starts at the torso (requires high rotation for power and stability). Using only boxing glove sensors for classification means that the torso movement must be inferred. Valuable performance metrics regarding more of the kinetic chain can be obtained by using glove sensors in combination with a T3 positioned sensor.
- -
- Many sporting organisations already use Catapult sensors in their training and competitive games. Thus, athletes are used to wearing a sensor in the T3 region. It is advantageous to deliver more metrics from this location.
2. Experimental Section
2.1. Participants
2.2. Materials
2.3. Methods
2.4. Data Pre-Processing and Feature Engineering
2.5. Supervised Machine Learning Model Training and Evaluation
- -
- LR: Inverse of regularization strength (C) = 100, solver = newton-cg, penalty = l2.
- -
- SVM: Regularization parameter (C) = 1, kernel = Radial basis function, Kernel coefficient (gamma) = 0.001.
- -
- MLP-NN: Activation = tanh, alpha = 0.0001, hidden layer sizes = 8, 8, 8 (3 hidden layers with 8 nodes each), learning rate = constant, solver = lbfgs.
- -
- RF: criterion = gini, maximum features =, number of estimators = 70.
- -
- XGB: criterion = mae, loss = deviance, max depth = 6, maximum features = log2 (number of features), number of estimators = 150.
- -
- LR: Inverse of regularization strength (C) = 100, solver = newton-cg, penalty = l2.
- -
- SVM: Regularization parameter (C) = 1, kernel = Radial basis function, Kernel coefficient (gamma) = 0.001.
- -
- MLP-NN: Activation = tanh, alpha = 0.0001, hidden layer sizes = 10 (1 hidden layer with 10 nodes), learning rate = constant, solver = lbfgs.
- -
- RF: criterion = gini, maximum features =, number of estimators = 60.
- -
- XGB: criterion = friedman_mse, loss = deviance, max depth = 1, maximum features = log2 (number of features), number of estimators = 150.
2.6. Statistical Analysis
- -
- Prediction accuracy of sensor configuration 1 and 2;
- -
- Prediction accuracy of tuned and untuned supervised machine learning models;
- -
- Computational training time of tuned and untuned supervised machine learning models.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Feature | Accelerometer | Gyroscope | Sensor Orientation |
|---|---|---|---|
| Mean | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Standard deviation | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Maximum | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Sample number of maximum | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Minimum | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Sample number of minimum | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Skewness | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Kurtosis | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Frequency amplitude | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Frequency | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Energy | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Absolute difference | x,y,z, mag | x,y,z, mag | Roll,pitch,yaw |
| Model | Hyper-Parameters |
|---|---|
| LR | C = 1.0, solver = lbfgs, penalty =l2 |
| LSVM | C = 1.0. kernel = linear, gamma =scale |
| GSVM | C = 1.0, kernel = rbf, gamma = scale |
| MLP-NN | Activation = relu, alpha = 0.0001, hidden layer sizes = 8,8,8, (3 hidden layers with 8 nodes each) learning rate = constant, solver = adam |
| RF | , number of estimators = 20 |
| XGB | Criterion = friedman_mse, loss = deviance, max depth = 3, maximum features = None, number of estimators = 100 |
References
- Espinosa, H.G.; Shepherd, J.B.; Thiel, D.V.; Worsey, M.T.O. Anytime, anywhere! Inertial sensors monitor sports performance. IEEE Potentials 2019, 38, 11–16. [Google Scholar] [CrossRef]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends supporting the in-field use of wearable inertial sensors for sport performance evaluation: A systematic review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef] [Green Version]
- Bai, L.; Efstratiou, C.; Ang, C.S. weSport: Utilising wrist-band sensing to detect player activities in basketball games. In Proceedings of the 2016 IEEE International Conference on Pervasive Computing and Communication Workshops (PerCom Workshops), Sydney, Australia, 14–18 March 2016; pp. 1–6. [Google Scholar]
- Buckley, C.; O’Reilly, M.A.; Whelan, D.; Farrell, A.V.; Clark, L.; Longo, V.; Gilchrist, M.D.; Caulfield, B. Binary classification of running fatigue using a single inertial measurement unit. In Proceedings of the 2017 IEEE 14th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Eindhoven, The Netherlands, 9–12 May 2017; pp. 197–201. [Google Scholar]
- Crema, C.; Depari, A.; Flammini, A.; Sisinni, E.; Haslwanter, T.; Salzmann, S. IMU-based solution for automatic detection and classification of exercises in the fitness scenario. In Proceedings of the 2017 IEEE Sensors Applications Symposium (SAS), Glassboro, NJ, USA, 13–15 March 2017; pp. 1–6. [Google Scholar]
- Cust, E.E.; Sweeting, A.J.; Ball, K.; Robertson, S. Machine and deep learning for sport-specific movement recognition: A systematic review of model development and performance. J. Sports Sci. 2019, 37, 568–600. [Google Scholar] [CrossRef]
- Davey, N.; Anderson, M.; James, D.A. Validation trial of an accelerometer-based sensor platform for swimming. Sports Technol. 2008, 1, 202–207. [Google Scholar] [CrossRef]
- Groh, B.H.; Reinfelder, S.J.; Streicher, M.N.; Taraben, A.; Eskofier, B.M. Movement prediction in rowing using a Dynamic Time Warping based stroke detection. In Proceedings of the 2014 IEEE Ninth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 21–24 April 2014; pp. 1–6. [Google Scholar]
- Hachaj, T.; Piekarczyk, M.; Ogiela, M. Human actions analysis: Templates generation, matching and visualization Applied to motion capture of highly-skilled karate athletes. Sensors 2017, 17, 2590. [Google Scholar] [CrossRef] [Green Version]
- Jensen, U.; Prade, F.; Eskofier, B.M. Classification of kinematic swimming data with emphasis on resource consumption. In Proceedings of the 2013 IEEE International Conference on Body Sensor Networks, Cambridge, MA, USA, 6–9 May 2013; pp. 1–5. [Google Scholar]
- Karmaker, D.; Chowdhury, A.Z.M.E.; Miah, M.S.U.; Imran, M.A.; Rahman, M.H. Cricket shot classification using motion vector. In Proceedings of the 2015 Second International Conference on Computing Technology and Information Management (ICCTIM), Johor, Malaysia, 21–23 April 2015; pp. 125–129. [Google Scholar]
- Khan, A.; Nicholson, J.; Plötz, T. Activity recognition for quality assessment of batting shots in cricket using a hierarchical representation. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2017, 1, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Kos, M.; Zenko, J.; Vlaj, D.; Kramberger, I. Tennis stroke detection and classification using miniature wearable IMU device. In Proceedings of the 2016 International Conference on Systems, Signals and Image Processing (IWSSIP), Bratislava, Slovakia, 23–25 May 2016; pp. 1–4. [Google Scholar]
- McGrath, J.W.; Neville, J.; Stewart, T.; Cronin, J. Cricket fast bowling detection in a training setting using an inertial measurement unit and machine learning. J. Sports Sci. 2019, 37, 1220–1226. [Google Scholar] [CrossRef]
- Mooney, R.; Corley, G.; Godfrey, A.; Quinlan, L.; ÓLaighin, G. Inertial sensor technology for elite swimming performance analysis: A systematic review. Sensors 2016, 16, 18. [Google Scholar] [CrossRef] [Green Version]
- Ohgi, Y.; Kaneda, K.; Takakura, A. Sensor data mining on the cinematical characteristics of the competitive swimming. Procedia Eng. 2014, 72, 829–834. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, M.A.; Whelan, D.F.; Ward, T.E.; Delahunt, E.; Caulfield, B.M. Classification of deadlift biomechanics with wearable inertial measurement units. J. Biomech. 2017, 58, 155–161. [Google Scholar] [CrossRef]
- O’Reilly, M.; Whelan, D.; Chanialidis, C.; Friel, N.; Delahunt, E.; Ward, T.; Caulfield, B. Evaluating squat performance with a single inertial measurement unit. In Proceedings of the 2015 IEEE 12th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Cambridge, MA, USA, 9–12 June 2015; pp. 1–6. [Google Scholar]
- Rawashdeh, S.; Rafeldt, D.; Uhl, T. Wearable IMU for shoulder injury prevention in overhead sports. Sensors 2016, 16, 1847. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Arora, J.; Khan, P.; Satapathy, S.; Agarwal, S.; Sengupta, S.; Mridha, S.; Ganguly, N. CommBox: Utilizing sensors for real-time cricket shot identification and commentary generation. In Proceedings of the 2017 9th International Conference on Communication Systems and Networks (COMSNETS), Bengaluru, India, 4–8 January 2017; pp. 427–428. [Google Scholar]
- Siirtola, P.; Laurinen, P.; Roning, J.; Kinnunen, H. Efficient accelerometer-based swimming exercise tracking. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence and Data Mining (CIDM), Paris, France, 11–15 April 2011; pp. 156–161. [Google Scholar]
- Soekarjo, K.M.W.; Orth, D.; Warmerdam, E. Automatic classification of strike techniques using limb trajectory data. In Proceedings of the 2018 Workshop on Machine Learning and Data Mining for Sports Analytics, Dublin, Ireland, 10 September 2018. [Google Scholar]
- Steven Eyobu, O.; Han, D. Feature representation and data augmentation for human activity classification based on wearable IMU sensor data using a deep LSTM neural network. Sensors 2018, 18, 2892. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Li, W.; Li, C.; Hou, Y. Action recognition based on joint trajectory maps with convolutional neural networks. Knowl. Based Syst. 2018, 158, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Whelan, D.; O’Reilly, M.; Huang, B.; Giggins, O.; Kechadi, T.; Caulfield, B. Leveraging IMU data for accurate exercise performance classification and musculoskeletal injury risk screening. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 659–662. [Google Scholar]
- Whiteside, D.; Cant, O.; Connolly, M.; Reid, M. Monitoring hitting load in tennis using inertial sensors and machine learning. Int. J. Sports Physiol. Perform. 2017, 12, 1212–1217. [Google Scholar] [CrossRef]
- Worsey, M.T.O.; Espinosa, H.G.; Shepherd, J.B.; Thiel, D.V. A systematic review of performance analysis in rowing using inertial sensors. Electronics 2019, 8, 1304. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Xu, D.; Zhou, Z.; Mai, J.; He, Z.; Wang, Q. IMU-based underwater sensing system for swimming stroke classification and motion analysis. In Proceedings of the 2017 IEEE International Conference on Cyborg and Bionic Systems (CBS), Beijing, China, 17–19 October 2017; pp. 268–272. [Google Scholar]
- Ashker, S.E. Technical and tactical aspects that differentiate winning and losing performances in boxing. Int. J. Perform. Anal. Sport 2011, 11, 356–364. [Google Scholar] [CrossRef]
- Kraemer, W.J.; Fleck, S.J. Optimizing Strength Training: Designing Nonlinear Periodization Workouts; Human Kinetics: Champaign, IL, USA, 2007; ISBN 10-0-7360-6068-5. [Google Scholar]
- Farrow, D.; Robertson, S. Development of a skill acquisition periodisation framework for high-performance Sport. Sports Med. 2017, 47, 1043–1054. [Google Scholar] [CrossRef]
- Catapult Sports. Available online: https://www.catapultsports.com/ (accessed on 14 November 2018).
- Catapult Fundamentals: What Can PlayerLoad Tell Me about Athlete Work? Available online: https://www.catapultsports.com/blog/fundamentals-playerload-athlete-work (accessed on 3 October 2019).
- Marshall, B.; Elliott, B.C. Long-axis rotation: The missing link in proximal-to-distal segmental sequencing. J. Sports Sci. 2000, 18, 247–254. [Google Scholar] [CrossRef]
- Worsey, M.T.O.; Espinosa, H.G.; Shepherd, J.B.; Thiel, D.V. Inertial sensors for performance analysis in combat sports: A systematic review. Sports 2019, 7, 28. [Google Scholar] [CrossRef] [Green Version]
- Move It Swift: Smart Boxing Gloves. Available online: https://www.indiegogo.com/projects/move-it-swift-smart-boxing-gloves?utm_source=KOL&utm_medium=Reedy%20Kewlus&utm_campaign=MoveItSwift#/ (accessed on 6 October 2020).
- Shepherd, J.B.; Thiel, D.V.; Espinosa, H.G. Evaluating the use of inertial-magnetic sensors to assess fatigue in boxing during intensive training. IEEE Sens. Lett. 2017, 1, 1–4. [Google Scholar] [CrossRef]
- Attal, F.; Mohammed, S.; Dedabrishvili, M.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. Physical human activity recognition using wearable sensors. Sensors 2015, 15, 31314–31338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGrath, J.; Neville, J.; Stewart, T.; Cronin, J. Upper body activity classification using an inertial measurement unit in court and field-based sports: A systematic review. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2020. [Google Scholar] [CrossRef]
- Shepherd, J.; James, D.; Espinosa, H.G.; Thiel, D.V.; Rowlands, D. A literature review informing an operational guideline for inertial sensor propulsion measurement in wheelchair court sports. Sports 2018, 9, 55. [Google Scholar] [CrossRef] [PubMed]
- Thiel, D.V.; Shepherd, J.; Espinosa, H.G.; Kenny, M.; Fischer, K.; Worsey, M.; Matsuo, A.; Wada, T. Predicting Ground Reaction Forces in Sprint Running Using a Shank Mounted Inertial Measurement Unit. Proceedings 2018, 6, 34. [Google Scholar] [CrossRef] [Green Version]
- Worsey, M.T.O.; Espinosa, H.G.; Shepherd, J.; Lewerenz, J.; Klodzinski, F.; Thiel, D.V. Features observed using multiple inertial sensors for running track and hard-soft sand running: A comparison study. Proceedings 2020, 49, 12. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Wada, T.; Nagahara, R.; Gleadhill, S.; Ishizuka, T.; Ohnuma, H.; Ohgi, Y. Measurement of pelvic orientation angles during sprinting using a single inertial sensor. Proceedings 2020, 49, 10. [Google Scholar] [CrossRef]
- Shepherd, J.B.; Giblin, G.; Pepping, G.-J.; Thiel, D.; Rowlands, D. Development and validation of a single wrist mounted inertial sensor for biomechanical performance analysis of an elite netball shot. IEEE Sens. Lett. 2017, 1, 1–4. [Google Scholar] [CrossRef]
- Schuldhaus, D.; Zwick, C.; Körger, H.; Dorschky, E.; Kirk, R.; Eskofier, B.M. Inertial sensor-based approach for shot/pass classification during a soccer match. In Proceedings of the 21st ACM KDD Workshop on Large-Scale Sports Analytics, Sydney, Australia, 10–13 August 2015; pp. 1–4. [Google Scholar]
- Anand, A.; Sharma, M.; Srivastava, R.; Kaligounder, L.; Prakash, D. Wearable motion sensor based analysis of swing sports. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 261–267. [Google Scholar]
- Ó Conaire, C.; Connaghan, D.; Kelly, P.; O’Connor, N.E.; Gaffney, M.; Buckley, J. Combining inertial and visual sensing for human action recognition in tennis. In Proceedings of the First ACM International Workshop on Analysis and Retrieval of Tracked Events and Motion in Imagery Streams—ARTEMIS ’10, Firenze, Italy, 25–29 October 2010; p. 51. [Google Scholar]
- Kautz, T.; Groh, B.H.; Hannink, J.; Jensen, U.; Strubberg, H.; Eskofier, B.M. Activity recognition in beach volleyball using a Deep Convolutional Neural Network: Leveraging the potential of Deep Learning in sports. Data Min. Knowl. Discov. 2017, 31, 1678–1705. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference (SciPy 2010), Austin, TX, USA, June 28–July 3 2010; pp. 56–61. [Google Scholar]
- Scikit-Learn: Machine Learning in Python. Available online: https://scikit-learn.org/stable/index.html (accessed on 6 October 2020).
- Hahn, A.G.; Helmer, R.J.N.; Kelly, T.; Partridge, K.; Krajewski, A.; Blanchonette, I.; Barker, J.; Bruch, H.; Brydon, M.; Hooke, N.; et al. Development of an automated scoring system for amateur boxing. Procedia Eng. 2010, 2, 3095–3101. [Google Scholar] [CrossRef] [Green Version]
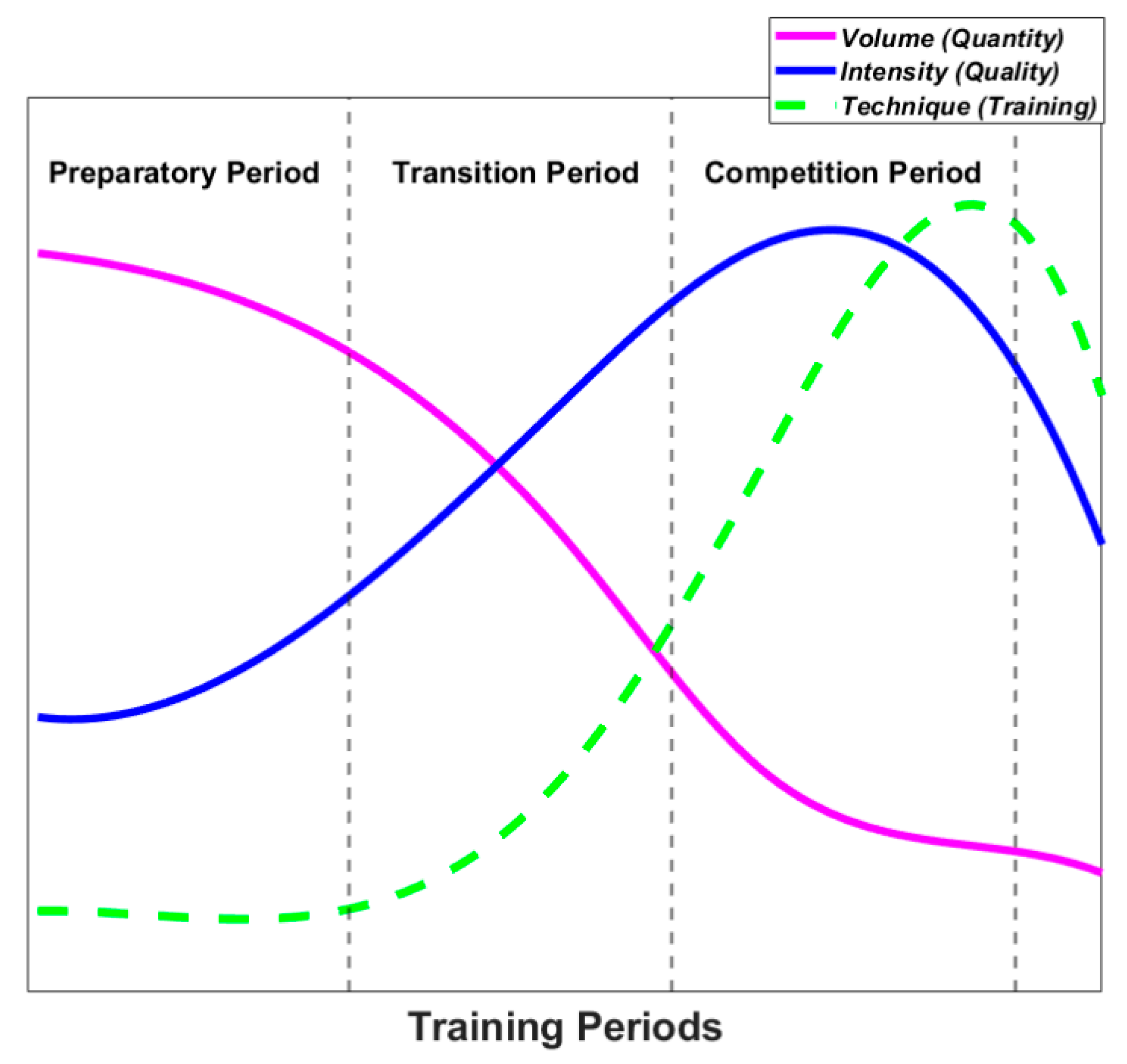

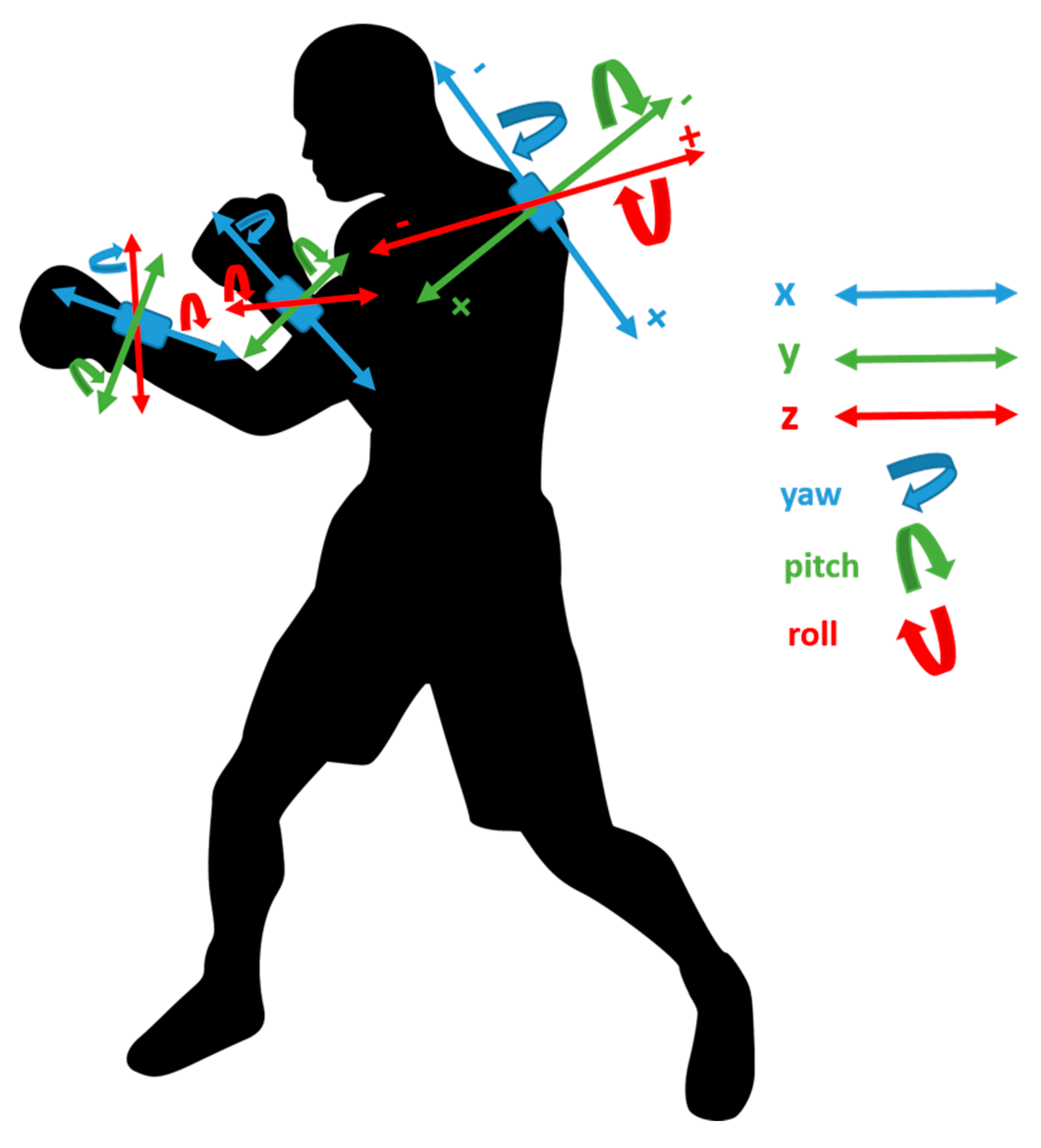



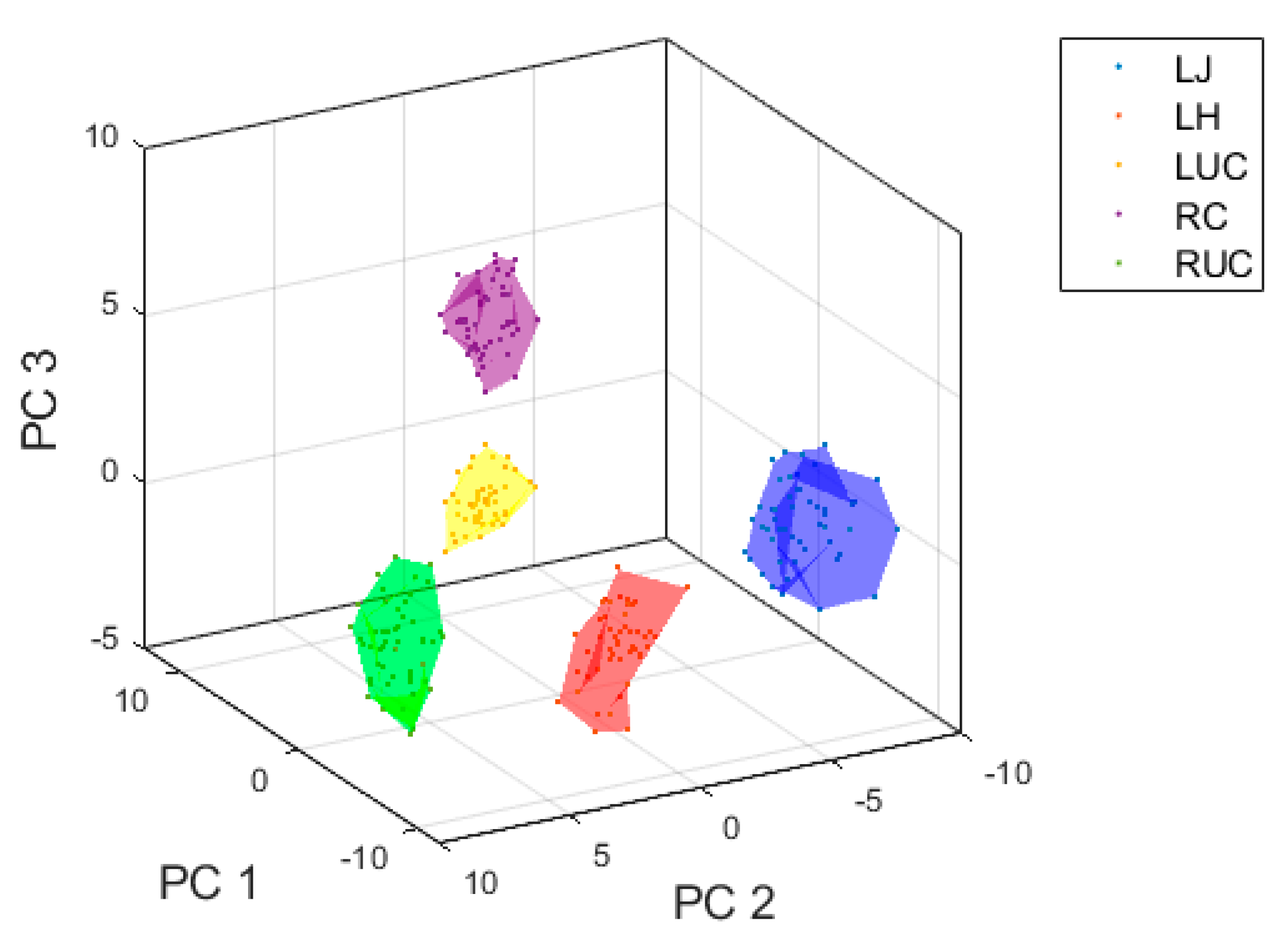
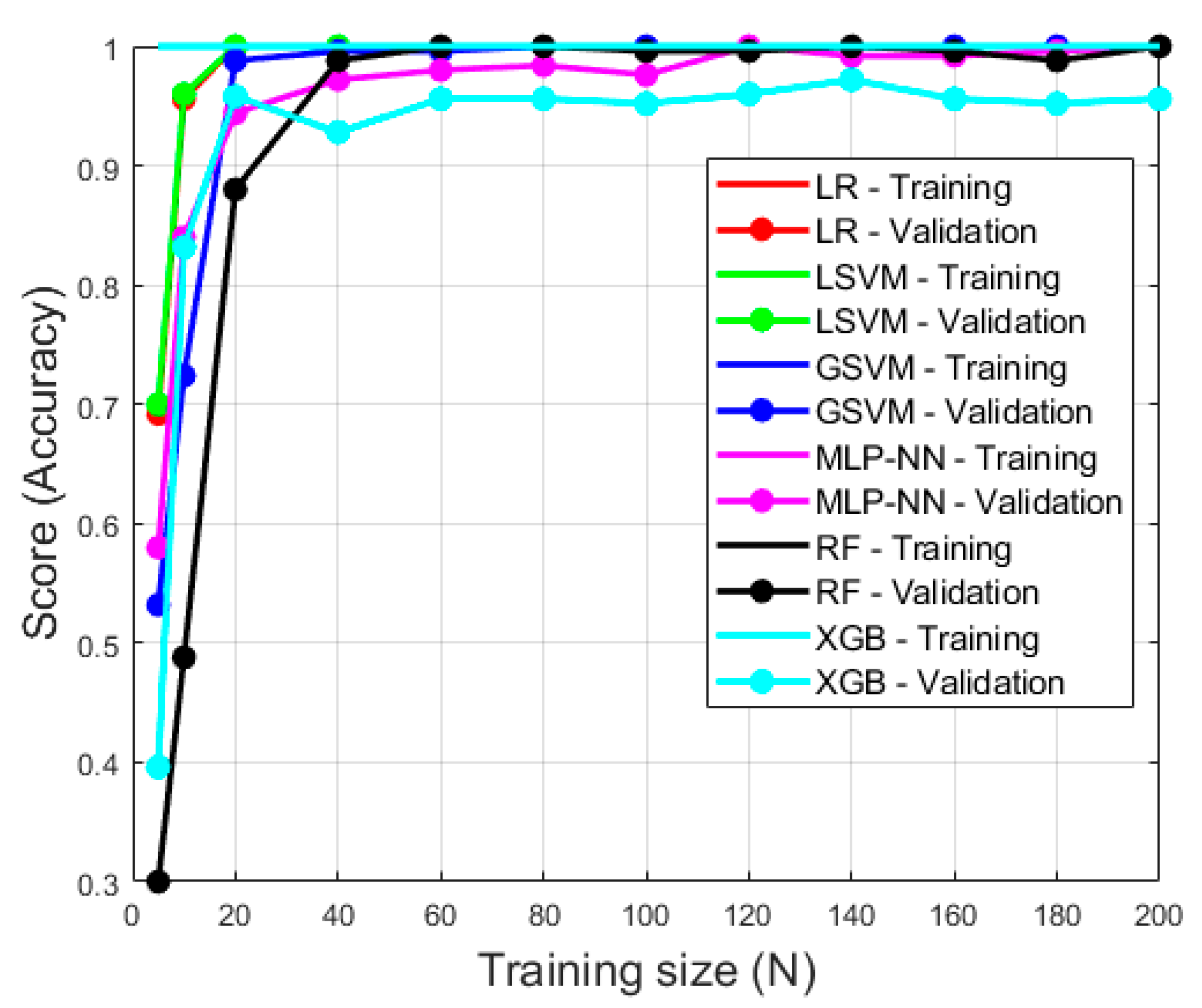
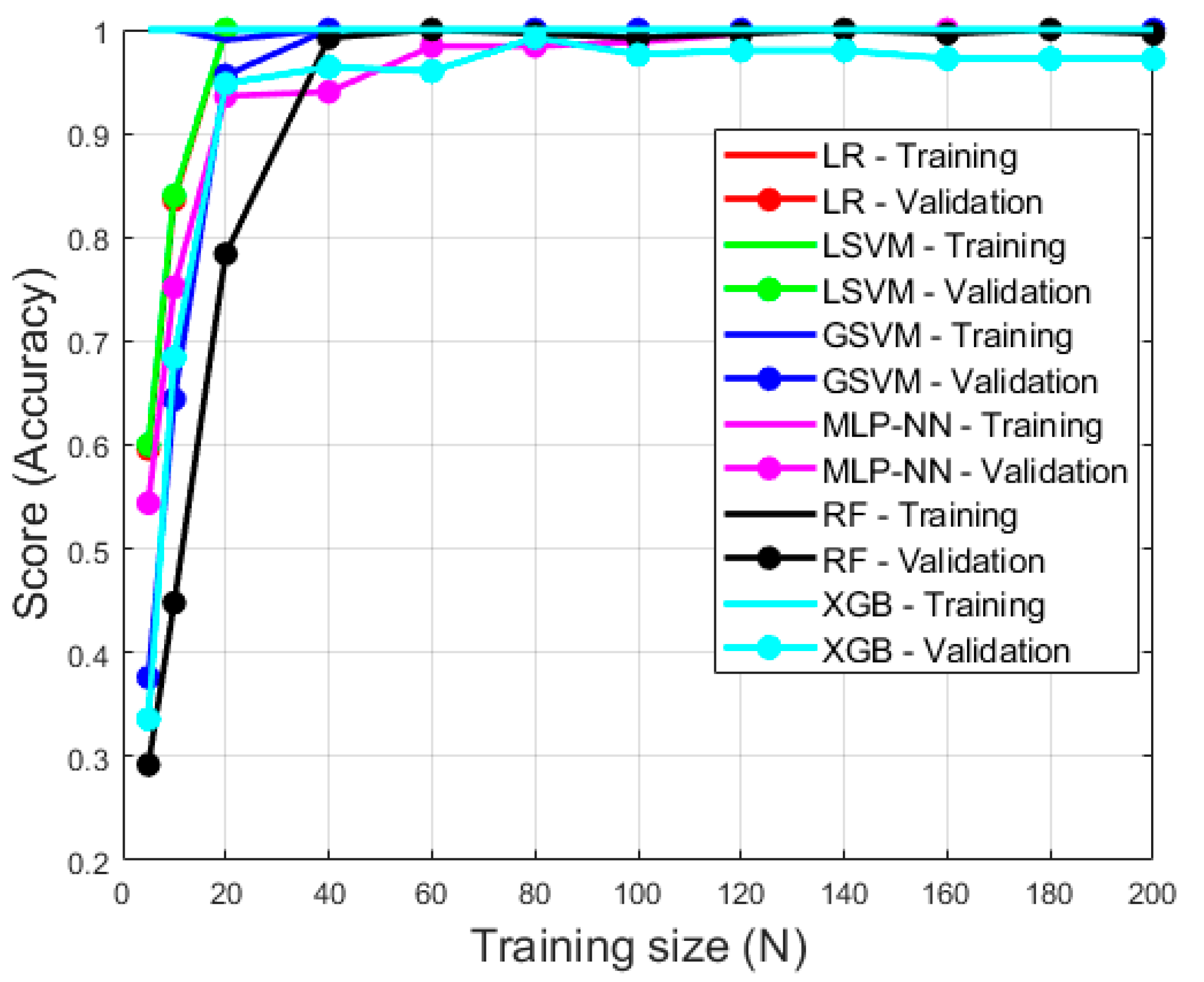
| Model Type | Punch Type | Precision | Recall | F1-Score | Overall Accuracy | Training Time (s) | Prediction Time (s) |
|---|---|---|---|---|---|---|---|
| LR | LH | 0.88 | 0.93 | 0.90 | 0.96 | 0.02 | <1 × 10−4 |
| LJ | 0.94 | 0.89 | 0.91 | ||||
| LUC | 1.00 | 1.00 | 1.00 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| LR’ | LH | 0.88 | 0.93 | 0.90 | 0.96 | 0.82 | 5 × 10−4 |
| LJ | 0.94 | 0.89 | 0.91 | ||||
| LUC | 1.00 | 1.00 | 1.00 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| LSVM | LH | 0.82 | 0.93 | 0.87 | 0.95 | 0.002 | <1 × 10−4 |
| LJ | 0.94 | 0.83 | 0.88 | ||||
| LUC | 1.00 | 1.00 | 1.00 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| GSVM | LH | 0.93 | 0.93 | 0.93 | 0.96 | 0.004 | <1 × 10−4 |
| LJ | 1.00 | 0.94 | 0.97 | ||||
| LUC | 0.95 | 0.95 | 0.95 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 0.93 | 1.00 | 0.96 | ||||
| SVM’ | LH | 0.88 | 0.93 | 0.90 | 0.94 | 0.24 | 5 × 10−4 |
| LJ | 0.94 | 0.89 | 0.91 | ||||
| LUC | 1.00 | 0.90 | 0.95 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 0.87 | 1.00 | 0.93 | ||||
| MLP-NN | LH | 0.88 | 0.93 | 0.90 | 0.90 | 0.41 | 5 × 10−4 |
| LJ | 0.82 | 0.78 | 0.80 | ||||
| LUC | 0.95 | 1.00 | 0.98 | ||||
| RC | 0.93 | 0.88 | 0.90 | ||||
| RUC | 0.92 | 0.92 | 0.92 | ||||
| MLP-NN’ | LH | 0.67 | 0.93 | 0.78 | 0.84 | 40.7 | 5 × 10−4 |
| LJ | 0.88 | 0.83 | 0.86 | ||||
| LUC | 1.00 | 0.80 | 0.89 | ||||
| RC | 0.92 | 0.69 | 0.79 | ||||
| RUC | 0.81 | 1.00 | 0.90 | ||||
| RF | LH | 0.83 | 1.00 | 0.91 | 0.87 | 0.03 | 0.016 |
| LJ | 0.92 | 0.67 | 0.77 | ||||
| LUC | 0.78 | 0.90 | 0.84 | ||||
| RC | 1.00 | 0.88 | 0.93 | ||||
| RUC | 0.86 | 0.92 | 0.89 | ||||
| RF’ | LH | 0.79 | 1.00 | 0.88 | 0.90 | 7.53 | <1 × 10−4 |
| LJ | 0.93 | 0.78 | 0.85 | ||||
| LUC | 0.90 | 0.95 | 0.93 | ||||
| RC | 1.00 | 0.88 | 0.93 | ||||
| RUC | 0.92 | 0.92 | 0.92 | ||||
| XGB | LH | 0.79 | 1.00 | 0.88 | 0.79 | 0.61 | <1 × 10−4 |
| LJ | 0.91 | 0.56 | 0.69 | ||||
| LUC | 0.85 | 0.85 | 0.85 | ||||
| RC | 0.59 | 0.81 | 0.68 | ||||
| RUC | 1.00 | 0.77 | 0.87 | ||||
| XGB’ | LH | 0.60 | 1.00 | 0.75 | 0.83 | 103.02 | <1 × 10−4 |
| LJ | 0.86 | 0.67 | 0.75 | ||||
| LUC | 0.95 | 0.95 | 0.95 | ||||
| RC | 1.00 | 0.62 | 0.77 | ||||
| RUC | 0.92 | 0.92 | 0.92 |
| Predicted | |||||||
|---|---|---|---|---|---|---|---|
| Model | LH | LJ | LUC | RC | RUC | ||
| Observed | LH | LR | 14 | 1 | 0 | 0 | 0 |
| (n = 15) | LR’ | 14 | 1 | 0 | 0 | 0 | |
| LSVM | 14 | 1 | 0 | 0 | 0 | ||
| GSVM | 14 | 0 | 1 | 0 | 0 | ||
| SVM’ | 14 | 1 | 0 | 0 | 0 | ||
| MLP-NN | 14 | 1 | 0 | 0 | 0 | ||
| MLP-NN’ | 14 | 1 | 0 | 0 | 0 | ||
| RF | 15 | 0 | 0 | 0 | 0 | ||
| RF’ | 15 | 0 | 0 | 0 | 0 | ||
| XB | 15 | 0 | 0 | 0 | 0 | ||
| XB’ | 15 | 0 | 0 | 0 | 0 | ||
| LJ | LR | 2 | 16 | 0 | 0 | 0 | |
| (n = 18) | LR’ | 2 | 16 | 0 | 0 | 0 | |
| LSVM | 3 | 15 | 0 | 0 | 0 | ||
| GSVM | 1 | 17 | 0 | 0 | 0 | ||
| SVM’ | 2 | 16 | 0 | 0 | 0 | ||
| MLP-NN | 2 | 14 | 0 | 1 | 0 | ||
| MLP-NN’ | 3 | 15 | 0 | 0 | 1 | ||
| RF | 2 | 12 | 4 | 0 | 0 | ||
| RF’ | 3 | 14 | 1 | 0 | 0 | ||
| XB | 1 | 10 | 2 | 5 | 0 | ||
| XB’ | 5 | 12 | 1 | 0 | 0 | ||
| LUC | LR | 0 | 0 | 20 | 0 | 0 | |
| (n = 20) | LR’ | 0 | 0 | 20 | 0 | 0 | |
| LSVM | 0 | 0 | 20 | 0 | 0 | ||
| GSVM | 0 | 0 | 19 | 0 | 1 | ||
| SVM’ | 0 | 0 | 18 | 0 | 0 | ||
| MLP-NN | 0 | 0 | 20 | 0 | 0 | ||
| MLP-NN’ | 0 | 0 | 16 | 0 | 3 | ||
| RF | 0 | 0 | 18 | 1 | 2 | ||
| RF’ | 0 | 0 | 19 | 0 | 1 | ||
| XB | 0 | 0 | 17 | 3 | 0 | ||
| XB’ | 0 | 0 | 19 | 0 | 1 | ||
| RC | LR | 0 | 0 | 0 | 16 | 0 | |
| (n = 16) | LR’ | 0 | 0 | 0 | 16 | 0 | |
| LSVM | 0 | 0 | 0 | 16 | 0 | ||
| GSVM | 0 | 0 | 0 | 16 | 0 | ||
| SVM’ | 0 | 0 | 0 | 16 | 0 | ||
| MLP-NN | 0 | 2 | 0 | 14 | 0 | ||
| MLP-NN’ | 4 | 1 | 0 | 11 | 0 | ||
| RF | 1 | 1 | 0 | 14 | 0 | ||
| RF’ | 1 | 1 | 0 | 14 | 0 | ||
| XB | 3 | 0 | 0 | 13 | 0 | ||
| XB’ | 4 | 2 | 0 | 10 | 0 | ||
| RUC | LR | 0 | 0 | 0 | 0 | 13 | |
| (n = 13) | LR’ | 0 | 0 | 0 | 0 | 13 | |
| LSVM | 0 | 0 | 0 | 0 | 13 | ||
| GSVM | 0 | 0 | 0 | 0 | 13 | ||
| SVM’ | 0 | 0 | 0 | 0 | 13 | ||
| MLP-NN | 0 | 0 | 1 | 0 | 12 | ||
| MLP-NN’ | 0 | 0 | 0 | 0 | 13 | ||
| RF | 0 | 0 | 1 | 0 | 12 | ||
| RF’ | 0 | 0 | 1 | 0 | 12 | ||
| XB | 0 | 1 | 1 | 1 | 10 | ||
| XB’ | 1 | 0 | 0 | 0 | 12 |
| Model Type | Punch Type | Precision | Recall | F1-Score | Overall Accuracy | Training Time (s) | Prediction Time (s) |
|---|---|---|---|---|---|---|---|
| LR | LH | 0.62 | 1.00 | 0.77 | 0.89 | 0.02 | <1 × 10−4 |
| LJ | 1.00 | 0.50 | 0.67 | ||||
| LUC | 1.00 | 1.00 | 1.00 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| LR’ | LH | 0.60 | 1.00 | 0.75 | 0.88 | 0.87 | <1 × 10−4 |
| LJ | 1.00 | 0.44 | 0.62 | ||||
| LUC | 1.00 | 1.00 | 1.00 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| LSVM | LH | 0.60 | 1.00 | 0.75 | 0.88 | 0.002 | <1 × 10−4 |
| LJ | 1.00 | 0.44 | 0.62 | ||||
| LUC | 1.00 | 1.00 | 1.00 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| GSVM | LH | 0.68 | 1.00 | 0.81 | 0.89 | 0.004 | <1 × 10−4 |
| LJ | 1.00 | 0.50 | 0.67 | ||||
| LUC | 0.91 | 1.00 | 0.95 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| SVM’ | LH | 0.62 | 1.00 | 0.77 | 0.89 | 0.19 | <1 × 10−4 |
| LJ | 1.00 | 0.50 | 0.67 | ||||
| LUC | 1.00 | 1.00 | 1.00 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| MLP-NN | LH | 0.88 | 1.00 | 0.94 | 0.98 | 0.46 | 5 × 10−4 |
| LJ | 1.00 | 0.94 | 0.97 | ||||
| LUC | 1.00 | 0.95 | 0.97 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| MLP-NN’ | LH | 0.60 | 1.00 | 0.75 | 0.88 | 42.54 | <1 × 10−4 |
| LJ | 1.00 | 0.50 | 0.67 | ||||
| LUC | 1.00 | 0.95 | 0.97 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| RF | LH | 0.54 | 0.93 | 0.68 | 0.83 | 0.038 | 0.002 |
| LJ | 1.00 | 0.28 | 0.43 | ||||
| LUC | 0.95 | 1.00 | 0.98 | ||||
| RC | 0.94 | 1.00 | 0.97 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| RF’ | LH | 0.54 | 0.93 | 0.68 | 0.84 | 5.24 | 0.016 |
| LJ | 1.00 | 0.33 | 0.50 | ||||
| LUC | 0.95 | 1.00 | 0.98 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 | ||||
| XGB | LH | 0.79 | 1.00 | 0.88 | 0.79 | 0.61 | <1 × 10−4 |
| LJ | 0.91 | 0.56 | 0.69 | ||||
| LUC | 0.85 | 0.85 | 0.85 | ||||
| RC | 0.59 | 0.81 | 0.68 | ||||
| RUC | 1.00 | 0.77 | 0.87 | ||||
| XGB’ | LH | 0.54 | 0.93 | 0.68 | 0.85 | 73.46 | 0.001 |
| LJ | 1.00 | 0.33 | 0.60 | ||||
| LUC | 0.95 | 1.00 | 0.98 | ||||
| RC | 1.00 | 1.00 | 1.00 | ||||
| RUC | 1.00 | 1.00 | 1.00 |
| Predicted | |||||||
|---|---|---|---|---|---|---|---|
| Model | LH | LJ | LUC | RC | RUC | ||
| Observed | LH | LR | 15 | 0 | 0 | 0 | 0 |
| (n = 15) | LR’ | 15 | 0 | 0 | 0 | 0 | |
| LSVM | 15 | 0 | 0 | 0 | 0 | ||
| GSVM | 15 | 0 | 0 | 0 | 0 | ||
| SVM’ | 15 | 0 | 0 | 0 | 0 | ||
| MLP-NN | 15 | 0 | 0 | 0 | 0 | ||
| MLP-NN’ | 15 | 0 | 0 | 0 | 0 | ||
| RF | 14 | 0 | 1 | 0 | 0 | ||
| RF’ | 14 | 0 | 1 | 0 | 0 | ||
| XGB | 14 | 0 | 1 | 0 | 0 | ||
| XGB’ | 14 | 0 | 1 | 0 | 0 | ||
| LJ | LR | 9 | 9 | 0 | 0 | 0 | |
| (n = 18) | LR’ | 10 | 8 | 0 | 0 | 0 | |
| LSVM | 10 | 8 | 0 | 0 | 0 | ||
| GSVM | 7 | 9 | 2 | 0 | 0 | ||
| SVM’ | 9 | 9 | 0 | 0 | 0 | ||
| MLP-NN | 1 | 17 | 0 | 0 | 0 | ||
| MLP-NN’ | 9 | 9 | 0 | 0 | 0 | ||
| RF | 12 | 5 | 0 | 1 | 0 | ||
| RF’ | 12 | 6 | 0 | 0 | 0 | ||
| XGB | 12 | 4 | 2 | 0 | 0 | ||
| XGB’ | 12 | 6 | 0 | 0 | 0 | ||
| LUC | LR | 0 | 0 | 20 | 0 | 0 | |
| (n = 20) | LR’ | 0 | 0 | 20 | 0 | 0 | |
| LSVM | 0 | 0 | 20 | 0 | 0 | ||
| GSVM | 0 | 0 | 20 | 0 | 0 | ||
| SVM’ | 0 | 0 | 20 | 0 | 0 | ||
| MLP-NN | 1 | 0 | 19 | 0 | 0 | ||
| MLP-NN’ | 1 | 0 | 19 | 0 | 0 | ||
| RF | 0 | 0 | 20 | 0 | 0 | ||
| RF’ | 0 | 0 | 20 | 0 | 0 | ||
| XGB | 0 | 0 | 20 | 0 | 0 | ||
| XGB’ | 0 | 0 | 20 | 0 | 0 | ||
| RC | LR | 0 | 0 | 0 | 16 | 0 | |
| (n = 16) | LR’ | 0 | 0 | 0 | 16 | 0 | |
| LSVM | 0 | 0 | 0 | 16 | 0 | ||
| GSVM | 0 | 0 | 0 | 16 | 0 | ||
| SVM’ | 0 | 0 | 0 | 16 | 0 | ||
| MLP-NN | 0 | 2 | 0 | 14 | 0 | ||
| MLP-NN’ | 0 | 0 | 0 | 16 | 0 | ||
| RF | 0 | 0 | 0 | 16 | 0 | ||
| RF’ | 0 | 0 | 0 | 16 | 0 | ||
| XGB | 0 | 0 | 1 | 15 | 0 | ||
| XGB’ | 0 | 0 | 0 | 16 | 0 | ||
| RUC | LR | 0 | 0 | 0 | 0 | 13 | |
| (n = 13) | LR’ | 0 | 0 | 0 | 0 | 13 | |
| LSVM | 0 | 0 | 0 | 0 | 13 | ||
| GSVM | 0 | 0 | 0 | 0 | 13 | ||
| SVM’ | 0 | 0 | 0 | 0 | 13 | ||
| MLP-NN | 0 | 0 | 0 | 0 | 13 | ||
| MLP-NN’ | 0 | 0 | 0 | 0 | 13 | ||
| RF | 0 | 0 | 0 | 0 | 13 | ||
| RF’ | 0 | 0 | 0 | 0 | 13 | ||
| XGB | 0 | 0 | 0 | 0 | 13 | ||
| XGB’ | 0 | 0 | 0 | 0 | 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Worsey, M.T.O.; Espinosa, H.G.; Shepherd, J.B.; Thiel, D.V. An Evaluation of Wearable Inertial Sensor Configuration and Supervised Machine Learning Models for Automatic Punch Classification in Boxing. IoT 2020, 1, 360-381. https://doi.org/10.3390/iot1020021
Worsey MTO, Espinosa HG, Shepherd JB, Thiel DV. An Evaluation of Wearable Inertial Sensor Configuration and Supervised Machine Learning Models for Automatic Punch Classification in Boxing. IoT. 2020; 1(2):360-381. https://doi.org/10.3390/iot1020021
Chicago/Turabian StyleWorsey, Matthew T. O., Hugo G. Espinosa, Jonathan B. Shepherd, and David V. Thiel. 2020. "An Evaluation of Wearable Inertial Sensor Configuration and Supervised Machine Learning Models for Automatic Punch Classification in Boxing" IoT 1, no. 2: 360-381. https://doi.org/10.3390/iot1020021
APA StyleWorsey, M. T. O., Espinosa, H. G., Shepherd, J. B., & Thiel, D. V. (2020). An Evaluation of Wearable Inertial Sensor Configuration and Supervised Machine Learning Models for Automatic Punch Classification in Boxing. IoT, 1(2), 360-381. https://doi.org/10.3390/iot1020021