A Model Study on the Dynamics of the Amino Acid Content in Micrometeoroids during Atmospheric Entry

Abstract

A model for the survival of the amino acid content in micrometeorites and its possible transformations upon atmospheric entry is described. Since any organic species released in the atmosphere at high altitudes would exhibit a limited lifetime with respect to the typical timescale for atmospheric mixing (due to the substantial radiation field of the early Sun), only the organic content inside the meteorites could have contributed to prebiotic chemistry. It is thus important to determine both the amino acid loss from meteorites, due to both degassing and chemical degradation, and the extent of the chemical transformation of amino acids subjected to the increased temperature due to friction with the atmosphere. According to the interplay between the potential energy barrier and the pre-exponential factor in rate coefficients, either diffusion or chemical processing might be the dominant process following the rising temperature upon atmospheric entry. The possibility of the elimination of water from glycine to form aminoketene, or ${\mathrm{CO}}_2$ to form methylamine, ultimately driven by gravitational energy, was examined along with the more conventional formation of a peptide bond between two glycine units to afford Gly–Gly. While retention, degassing, and decarboxylation are the fastest processes, each dominating in different ranges of the initial velocity and radius, the formation of either Gly–Gly from bimolecular water elimination or aminoketene from unimolecular water elimination appears to be negligible.

1. Introduction

One of the hypotheses concerning the origin of complex organic chemistry on the early Earth entails the continuous supply of small organic molecules in the flux of micrometeorites and interplanetary dust particles. Inside dust particles, organic molecules are thought to have found their way from the envelopes of AGB stars, to molecular clouds, and, finally, to Earth and nearby planets in the solar system [1,2,3]. Although the driving force for the polymerization of relatively simple organic compounds to form large molecular species with significant catalytic activity has been shown to be a demanding requirement [4], necessary conditions for aqueous polymerization are a steady influx of monomers and substantial environmental catalysis. In the case of polypeptides, the infalling flux of amino acids from interplanetary dust particles was found to be one of the key parameters regulating the maximum length of polypeptide chains that could spontaneously form in the primordial ocean [5]. If micrometeorites were the carriers of this source, it is crucial that the load of organic species would survive the atmospheric heating and reach the Earth surface [6]. Although leucine was shown to withstand solar radiation for three months when embedded in a $5\mathsf{\mu }\mathrm{m}$ layer of montmorillonite clay [7], the delivery of the organic species directly to the atmosphere at high altitudes would subject the organics to the substantial UV radiation field of the early Sun, limiting the lifetime of the organic species to less than the typical timescale for atmospheric mixing [8]. Both the nature of the content of a meteoroid and its survival are thus crucial to the possibility of considering the extraterrestrial source of amino acids as viable for the appearance of functional biomolecules on the early Earth.

Moreover, the possibility that the raised temperature in micrometeoroids in the atmospheric entry phase could promote chemical processes conducting to an increase of complexity has been put forward [9]. This work also explores this possibility by investigating both the unimolecular elimination of water from glycine to afford aminoketene and the direct bimolecular formation of a peptide bond between two glycine units. In fact, aminoketene has the ability to add to itself or to a glycine molecule to form either the dehydrated form of the glycine dimer or the glycine dimer itself. Along with the above processes, the possibility of degassing and decarboxylation has been taken into account, leading to the destruction of the original amino acid content of the micrometeoroid.

The non-protein amino acid $\alpha$-amino isobutyric acid was found in ≈ 14% of micrometeorites collected at the South Pole [10], and $\alpha$-amino isobutyric acid along with other amino acids were found in Antarctic micrometeorites [11]. Glycine was found to sublimate out of the CM-type carbonaceous chondrite Murchison at ≈423 K while being heated to 823 K [12]. After the release, the fate of an organic molecule at high altitude in the primordial atmosphere would be affected by the strong UV solar radiation.

To the author’s knowledge, the modeling of micrometeoroids entry in the atmosphere has been so far limited to the equations of motion, the evaluation of temperature along the trajectory [13,14], and ablation of inorganic material [15,16]. This study aims to determine if a significant fraction of the amino acid content of micrometeoroids was able to reach the Earth surface as such or as useful intermediates or products. To this effect, the complex dynamics of an infalling micrometeorite was studied by coupling the kinetics equations for amino acid degassing and chemical reactivity to the time-dependent temperature of the micrometeorite, which is in turn coupled to its equations of motion along the trajectory in the primordial atmosphere.

2. Model

The heating of micrometeoroids entering the Earth’s atmosphere was studied by Love and Brownlee [14]. Since, according to their study, particles with initial radius above ≈300 $\mathsf{\mu }$m rarely survive atmospheric entry, we limit our study to micrometeoroid below that size. Furthermore, micrometeoroids in this range of initial radius exhibit homogeneous temperature.

The events associated with the chemical evolution from relatively simple organic compounds to the highly organized network of processes taking place in a living cell are constrained between the cooling of the Earth’s crust with the formation of the hydrosphere $3.9\mathrm{Gyr}$ ago and the first fossilized unicellular organisms $3.5\mathrm{Gyr}$ ago [17]. The initial 40 bar ${\mathrm{CO}}_2$ atmosphere was replaced by a mixture of ${\mathrm{N}}_2$, ${\mathrm{CO}}_2$, and ${\mathrm{H}}_2\mathrm{O}$ at the beginning of the Archean [18]. The exact partial pressures of ${\mathrm{N}}_2$ and ${\mathrm{CO}}_2$ in that era are unknown, but are estimated to be around ≈0.5–1 bar. For the purpose of the simulation, the density ${\rho }_a$ of the primordial atmosphere was calculated at $1\mathrm{bar}$ of ${\mathrm{CO}}_2$ pressure by the ideal gas equation of state, with the empirical dependence of temperature (in Celsius) on elevation h (in meters) of the standard atmosphere: $T_C=15.04-0.00649h$ for $0\le h\le 11.0\mathrm{km}$, $T_C=-56.46$ for $11.0<h\le 25.0\mathrm{km}$, $T_C=-131.21+0.00299h$ for $h>25.0\mathrm{km}$[19]. We derive the atmospheric pressure P from the condition for its hydrostatic equilibrium

$$\frac{P}{P_0}=e^{-x},\mathrm{with}x=\frac{GM{\mu }_a}{N_{A}k}{\int }_R^r\frac{\mathrm{d}s}{T{s}^2},$$

(1)

where G is the gravitational constant, M the mass of the Earth, $N_A$ Avogadro’s number, k the Boltzmann’s constant, and ${\mu }_a$ the molecular mass of ${\mathrm{CO}}_2$. The change in momentum per unit time of an infalling spherical meteoroid of radius R and velocity v caused by friction with the atmosphere of density ${\rho }_a$ is ${\rho }_a\pi R^2{v}^2$. It is convenient to define the friction coefficient per unit mass of a meteoroid of density ${\rho }_m\approx 3\times {10}^3\mathrm{kg}{\mathrm{m}}^{-3}$ as

$$k_f=\frac{3}{4R}\frac{{\rho }_a}{{\rho }_m}$$

(2)

with dimensions $L^{-1}$. With this definition, we write the equations of motion for the infalling meteoroid as

$$\begin{array}{ccc}\hfill \ddot{r}& =& r{\dot{\phi }}^2-\frac{GM}{r^2}-k_{f}v\dot{r}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \ddot{\phi }& =& -\dot{\phi }\left(k_{f}v+2\frac{\dot{r}}{r}\right)\hfill \end{array}$$

(4)

where r is the distance from the Earth, $\phi$ the orbital angle, and $v^2={\dot{r}}^2+r^2{\dot{\phi }}^2$. If the average atomic mass of the meteoroid is ${\mu }_m$ and its specific heat of sublimation $\gamma$, the reduced energy of sublimation is ${\zeta }_s=\gamma {\mu }_m/kT$. Integrating the time derivative of the specific energy of a micrometeoroid of specific heat $C_p$

$$C_p\dot{T}=k_{f}v\left(\frac{v^2}{2}-\frac{4\epsilon \sigma T^4}{{\rho }_{a}v}-\gamma e^{-{\zeta }_s}\right)$$

(5)

we obtain the time-dependent temperature T of the meteoroid. Along with sublimation, the emission of radiation is a factor that cools off the meteoroid ($\epsilon$ is the emissivity and $\sigma$ the Stefan–Boltzmann constant), and is given by the black body expression

$$\epsilon =\frac{{\int }_{x_l}^{\infty }\frac{x^3}{e^x-1}\mathrm{d}x}{{\int }_0^{\infty }\frac{x^3}{e^x-1}\mathrm{d}x}$$

(6)

in terms of the variable $x=h\nu /kT$, where the limit of integration

$$\begin{array}{ccc}\hfill x_l& =& \frac{h{\nu }_l}{kT}\hfill \\ & =& \frac{hc}{2RkT}\hfill \end{array}$$

(7)

is the lowest reduced frequency of the radiation emitted by a particle of radius R. Finally, the relative rate of change of the radius of the meteoroid due to ablation is given by

$$\frac{\dot{R}}{R}=-\frac{1}{3}{k}_{f}v{e}^{-{\zeta }_s}$$

(8)

One of the chemical processes taken into consideration in this study is the formation from glycine (1, concentration y) of the dipeptide Gly–Gly (2, concentration d) and water (concentration w) with a rate represented as a second-order process with rate coefficients $k_1$ for the forward reaction and $k_{-1}$ for the backward reaction, each of the form

$$k_r=\frac{kT}{h}\frac{q_{TS}}{q_A{q}_B}{e}^{-{\zeta }_r}\mathrm{with}{\zeta }_r=u_{TS}/kT,$$

(10)

h being the Planck constant, and q the partition functions per unit volume of the species involved. The rate of the unimolecular elimination of water from glycine with the formation of aminoketene (3, concentration z) is represented by a rate coefficient of the form

$$k_{{\mathrm{H}}_2\mathrm{O}}=\frac{kT}{h}\frac{q_{TS}}{q_A}{e}^{-{\zeta }_r}$$

(12)

Since a proper transition structure for the decarboxylation of glycine could not be located on its potential energy surface, pyrolysis will be represented as the dissociation of ${\mathrm{CO}}_2$ with formation of the intermediate tautomer of methylamine ${}^{-}{\mathrm{CH}}_2{\mathrm{NH}}_3^{+}$. Fragmenting an amino acid molecule of mass $M_a$ in two parts of mass m (${\mathrm{CO}}_2$) and $M_a-m$ entails the loss of one vibrational degrees of freedom from reactants to transition structure. If we replace the vibrational partition function of the transition structure with the product of the vibrational partition functions of the two fragments, we have five missing degrees of freedom, which are being replaced by three translational plus two rotational degrees of freedom of ${\mathrm{CO}}_2$, obtaining

$$k_{{\mathrm{CO}}_2}=\frac{kT}{h}{\left(\frac{2\pi mkT}{h^2}\right)}^{3/2}{L}^3\frac{z_r\left({\mathrm{CO}}_2\right)z_v\left({\mathrm{CO}}_2\right)z_r\left({}_{TS}\right)z_v\left({}^{-}{\mathrm{CH}}_2{\mathrm{NH}}_3^{+}\right)}{z_r\left(\mathrm{gly}\right)z_v\left(\mathrm{gly}\right)}{e}^{-{\zeta }_r}$$

(13)

with

$$z_r=\frac{{\pi }^{1/2}}{\sigma }\prod _{i=1}^3{\left(\frac{\pi kT}{h{B}_i}\right)}^{1/2}{z}_v=\prod _{i=1}^n{\left[2sinh\left(\frac{\hslash {\omega }_i}{2kT}\right)\right]}^{-1}$$

(14)

L being the typical length of free translation as defined by the Lennard–Jones Devonshire theory [20], $B_i$ the rotational constants, ${\omega }_i$ the angular vibrational frequencies, and z the partition functions. We observe that for temperatures that allow chemical reactions to take place, when both ${\left(k_1{y}_0\right)}^{-1}$ and $k_{{\mathrm{H}}_2\mathrm{O}}^{-1}$ are lower than the typical time of atmospheric entry $\left(\approx {10}^2\mathrm{s}\right)$, we have $k_{{\mathrm{CO}}_2}>k_{{\mathrm{H}}_2\mathrm{O}}>k_1{y}_0$.

The rates of decarboxylation, dimerization, formation of the aminoketene from glycine, and the corresponding degassing process will be represented by the equations

$$\begin{array}{ccc}\hfill \dot{y}& =& -\left(k_{{\mathrm{H}}_2\mathrm{O}}+k_{{\mathrm{CO}}_2}+k_{dg}\right)y-k_1{y}^2+k_{-1}dw\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill \dot{z}& =& k_{{\mathrm{H}}_2\mathrm{O}}y-k_{dg}z\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \dot{w}& =& k_{{\mathrm{H}}_2\mathrm{O}}y-k_{dg}w+k_1{y}^2-k_{-1}dw\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill \dot{d}& =& k_1{y}^2-k_{-1}dw\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(18)

The mass-transfer coefficient for degassing $k_{dg}$ depends on the the heat of sublimation $u_{dg}$ ($32.60\mathrm{kcal}{\mathrm{mol}}^{-1}$ for glycine) [21] and the heat of vaporization for water ($9.72\mathrm{kcal}{\mathrm{mol}}^{-1}$) through the relation

$$k_{dg}=\frac{3D_0}{R^2}{e}^{{\zeta }_{dg}\Delta T/T}{\zeta }_{dg}=u_{dg}/k{T}_0,$$

(19)

with $D_0$ the diffusion coefficient and $T_0=298\mathrm{K}$.

Although the barrier for the formation of the peptide bond through reaction (9) ($45.95\mathrm{kcal}{\mathrm{mol}}^{-1}$) is considerably lower than the corresponding barrier for the formation of aminoketene ($78.10\mathrm{kcal}{\mathrm{mol}}^{-1}$), the pre-exponential factor favors the latter process. Consequently, the loss of water becomes faster than the formation of the peptide bond above a threshold temperature. Taking into consideration also the degassing process, the value of the parameter $D_0$ turns out to be crucial in determining which process is the fastest at high temperatures. Once more, the pre-exponential factor determines which process is favored in the limit of high temperature.

Equations (3)–(5), (8), and (15)–(18) were numerically integrated with the program Scilab [22] starting with a 21.7 ppm initial concentration of glycine and initial temperature 10 K. The potential energy and thermochemistry of all species were computed with the suite of programs Gaussian [23] and all the molecular graphics were obtained with the program Moldraw [24].

3. Results

The mass and velocity distribution for the micrometeoroids under investigation was taken from the zodiacal dust cloud model [25] ($0.5\le v_0\le 10\mathrm{km}{\mathrm{s}}^{-1}$ and $7\le R_0\le 70\mathsf{\mu }\mathrm{m}$), including 50–70% of the incoming flux. The temperature profiles versus altitude for three micrometeoroids with trajectories starting at 200 km elevation and ending after 200 s are plotted in Figure 1. The curves represent different values of the initial radius of the micrometeoroids, all with initial velocity $3.7\mathrm{km}{\mathrm{s}}^{-1}$. At this value of the initial velocity, the actual chemical processing of glycine begins, while at lower values retention and degassing are the only outcomes. For the values of the initial radius of micrometeoroids examined in this work, the maximum temperature along the trajectory is never below ≈500 K. The maximum temperature along the atmospheric entry trajectory of a micrometeoroid of radius $70\mathsf{\mu }\mathrm{m}$ and initial velocity $0.5\mathrm{km}{\mathrm{s}}^{-1}$ would be 482.2 K, allowing the survival of 78.5% of the original glycine content. At the commonly observed higher temperatures, the amino acid fate depends on the values of the initial velocity, the mass, and the diffusivity.

In Figure 2 we explore the effect of the initial velocity $v_0$ on temperature. As it happened with the initial radius, the system is very sensitive to $v_0$, always exhibiting maximum temperatures above ≈500 K.

The maximum temperature along the trajectory versus $v_0$ and $R_0$ is reported in Figure 3. In the range of initial mass and velocity under investigation, the amount of ablation is negligible and virtually the whole mass of the micrometeoroid is retained during the atmospheric entry trajectory.

The value of the effective diffusivity depends on the porosity of the meteoroid, a quantity that can vary widely and is difficult to estimate. To have an idea of what the limiting cases could be, we first select upper and lower bounds for the diffusivity, and lastly we discuss the case of intermediate values. If we set the value $D_0=9.57\times {10}^{-10}{\mathrm{m}}^2{\mathrm{s}}^{-1}$, the value for the diffusivity of glycine in water [26], and $D_0=2.30\times {10}^{-9}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ for water itself [27], there would be no residual amino acid or aminoketene in the micrometeorite at the end of its trajectory. The degassing process in Equations (15)–(17) takes place first. In fact, glycine exhibits a heat of vaporization of $31.64\mathrm{kcal}{\mathrm{mol}}^{-1}$, and the elimination of water (reaction (11)) has a potential energy barrier of $78.10\mathrm{kcal}{\mathrm{mol}}^{-1}$. The pre-exponential factor for degassing would however be reduced at lower values of $D_0$, and possibly be smaller than the corresponding pre-exponential factor for reaction, an indication that the reaction process would be dominant above a threshold temperature that depends on the value of $D_0$. The loss of ${\mathrm{CO}}_2$, with a potential energy barrier of $66.94\mathrm{kcal}{\mathrm{mol}}^{-1}$, at sufficiently high temperatures exhibits a larger pre-exponential factor than the corresponding elimination of water and the highest reaction rate.

The value of L in Equation (13) was calculated according to the procedure described in [20] using a Lennard–Jones type potential $u\left(r\right)=u_{LJ}\left[{\left(r_{LJ}/r\right)}^{10}-2{\left(r_{LJ}/r\right)}^4\right]$ of the cluster ${}^{-}{\mathrm{CH}}_2{\mathrm{NH}}_3^{+}\cdots {\mathrm{CO}}_2$ between the tautomer of methylamine and carbon dioxide, obtaining $u_{LJ}=2.43\mathrm{kcal}{\mathrm{mol}}^{-1}$ and $L=3.574\times {10}^{-11}\mathrm{m}$.

In meteorites exhibiting the above value of $D_0$, and within the range of radius and initial velocity considered in this study, the initial content of glycine mostly evolves into retained, degassed, or decarboxylated glycine. It would be natural to infer that, once in the atmosphere, the degassed glycine would be subjected to degradation by the UV radiation of the early Earth before any further chemical transformation could take place.

Since micrometeoroids exhibit a wide range of variation in porosity, and diffusivity in turn depends strongly on pore diameter [28], we report the results obtained making use of an intermediate value of the effective diffusion coefficient, that is $D_0=1.0\times {10}^{-12}{\mathrm{m}}^2{\mathrm{s}}^{-1}$.

While the initial velocity and radius of the micrometeoroid are varied, the ratios $y/y_0$, $z/y_0$, $w/y_0$, and $d/y_0$ are computed for each 200 s trajectory. There is a threshold value around $3.3\mathrm{km}{\mathrm{s}}^{-1}$ on the initial velocity that allows for the survival of at least a fraction of amino acid within meteorites (Figure 4).

The initial velocity which is compatible with a significant retention of the original amino acid content depends rather weakly on the initial radius. The highest content (in the order of hundreds of ppm) of glycine, alanine, and $\alpha$-amino isobutyric acid was found in a set of Antarctic micrometeorites with radius ≈100 $\mathsf{\mu }\mathrm{m}$ [11]. A simulation of the trajectory of a micrometeorite with radius $100\mathsf{\mu }\mathrm{m}$ and initial velocity $1.5\mathrm{km}{\mathrm{s}}^{-1}$ gives a final fraction of retained glycine of 0.60, and 0.40 for degassed glycine. The fraction of retained glycine falls dramatically for higher values of the initial velocity.

The fraction of degassed glycine ($0.19\le y_{dg}/y_0\le 0.92$) is reported in Figure 5; it reaches a maximum at the lowest range of initial radius and approaches zero for $R_0>70\mathsf{\mu }\mathrm{m}$. Limited degassing allows both retention of the meteorite’s content of amino acids and some chemical processing, as discussed below. We observe that slow meteorites retain their amino acid content and fast micrometeorites lose most of their amino acids by both degassing and chemical processing. As pointed out earlier, we may not consider the degassed species as contributors to prebiotic chemistry on the Earth’s surface since they would have been destroyed in the atmosphere by the intense radiation flux of the early Sun [29,30]. This fact limits the carriers of organic species to the Earth’s surface to micrometeorites of size in excess of ≈20 $\mathsf{\mu }\mathrm{m}$.

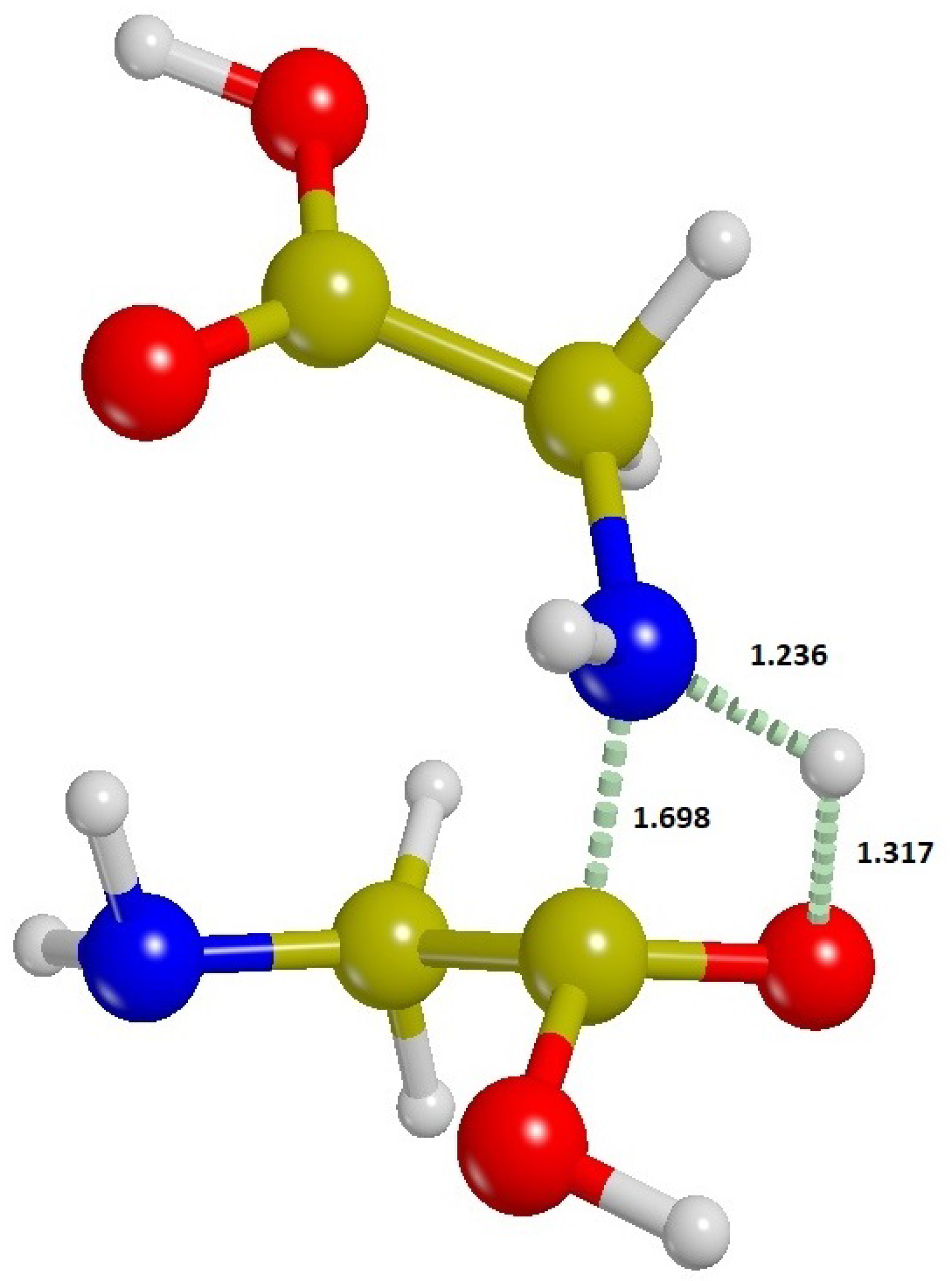
The observed high mobility of organic species at higher temperatures also allows the occurrence in principle of bimolecular chemical processes. Since reaction (9) is bimolecular and nearly thermoneutral ($\mathsf{\Delta }u=-0.41\mathrm{kcal}{\mathrm{mol}}^{-1}$), the spontaneous formation of polypeptides is not a favored process in equilibrium conditions. However, the rapid degassing of water compared to the backward rate of hydrolysis of the glycine dimer, could in principle drive the whole process in favor of the formation of the dimer. The transition structure for the formation of a peptide bond between two molecules of glycine (reaction barrier $45.95\mathrm{kcal}{\mathrm{mol}}^{-1}$) is shown in Figure 6, and the fraction of the amino acid dimer in Figure 7.

Although the formation of glycine dimer catalyzed by water has a low potential energy barrier ($13.89\mathrm{kcal}{\mathrm{mol}}^{-1}$), the fast degassing of any water content precludes this process. The formation of the peptide bond between two anhydrous glycine molecules exhibits the much higher barrier of $45.95\mathrm{kcal}{\mathrm{mol}}^{-1}$, and, moreover, the pre-exponential factor in the expression for the rate coefficient is the lowest, being this process bimolecular. These effects make the rate of dimerization lower with respect to decarboxylation at high temperatures.

In fact, for all values of $v_0$ and $R_0$, decarboxylation is the most relevant process determining the destruction of the amino acid content of micrometeoroids. In a pyrolysis experiment where a palagonite sample inoculated with Escherichia coli was heated to 500 ${}^{°}$C [12], only very limited amounts of methylamine and ethylamine were found. Since most of the initial content of glycine and alanine decomposed, amines are probably not the end products of decarboxylation. Experimental results on the pyrolysis of solid amino acids in bulk (5–6 mg) [31] show that glycine decomposes in the temperature range 499–846 K. A simulation of a micrometeoroid trajectory at the upper limit of validity of this model for the value of the radius ($300\mathsf{\mu }\mathrm{m}$) indicates that the fraction of decarboxylated glycine is negligible at 499 K, 0.52 at 845.2 K, and 0.996 (the maximum value, since a small fraction of $4.5\times {10}^{-3}$ degassed before 906.9 K) at 932.3 K. However, in the range of values for the radius of the micrometeoroids under investigation, the small size of the micrometeoroids makes degassing the dominant process in the lower region of the size range (see Figure 5). At higher values of the radius, decarboxylation becomes the exclusive process for the amino acid decomposition (Figure 8). A lower value of the diffusion coefficient, such as the one measured for bromide in basalt, $D_0=1.75\times {10}^{-14}{\mathrm{m}}^2{\mathrm{s}}^{-1}$[32], allows the loss of ${\mathrm{CO}}_2$ from glycine to become the dominant reaction above $v_0\approx 3.0\mathrm{km}{\mathrm{s}}^{-1}$ for micrometeoroids of any size. As we have seen, below $v_0\approx 2.0\mathrm{km}{\mathrm{s}}^{-1}$, most of the glycine content is retained inside the micrometeoroid.

Besides the loss of ${\mathrm{CO}}_2$, other interesting possibilities are open for reactions taking place upon heating. Among them the unimolecular loss of water with formation of aminoketene, exhibiting a potential energy barrier of $78.10\mathrm{kcal}{\mathrm{mol}}^{-1}$ (Figure 9).

As we have already discussed, the loss of ${\mathrm{CO}}_2$ dominates at sufficiently high temperature, but the high rate of the addition of glycine to aminoketene (Figure 10). proceeds with a barrier of only $17.14\mathrm{kcal}{\mathrm{mol}}^{-1}$, is exothermic by $12.00\mathrm{kcal}{\mathrm{mol}}^{-1}$, and consequently is much faster than the competitive addition of water that would transform the aminoketene back into glycine ($29.42\mathrm{kcal}{\mathrm{mol}}^{-1}$). This could lead to the formation of amino acid oligomers, otherwise very difficult to form in water solution [4]. Furthermore, the addition of aminoketene to itself takes place with a small barrier ($16.77\mathrm{kcal}{\mathrm{mol}}^{-1}$, Figure 11) and forms intermediate (4) that can easily add a water molecule to form Gly–Gly. The addition of aminoketene to Gly–Gly would be just as easy, with formation of oligomers of higher molecular weight, an overall process ultimately driven by gravitational energy. However, the average lifetime of a primordial polypeptide formed in this way inside the micrometeorites, once leaked into oceanic water, would be limited to $\approx 500\mathrm{yr}$ [33].

The formation and retention of aminoketene inside the meteorite occurs for initial velocities above $\approx 2\mathrm{km}{\mathrm{s}}^{-1}$ and peaks at $v_0\approx 3.7\mathrm{km}{\mathrm{s}}^{-1}$, growing monotonically with the value of the initial radius and approaching the maximum ($z/y_0\approx 3\times {10}^{-9}$) for values $R_0=70\mathsf{\mu }\mathrm{m}$ (Figure 12). Thus, the aminoketene formed in this range of the initial values of the radius and velocity is limited to a negligible fraction of the initial amino acid content of the micrometeoroid. As discussed above, the formed aminoketene could in turn add to glycine or to itself with formation of Gly–Gly and higher oligomers, but the minimal extent of this process does not make it a viable route to the formation of polypeptides inside micrometeorites.

Besides the very small extent of formation of aminoketene depicted in Figure 12, for initial velocities above $\approx 2\mathrm{km}{\mathrm{s}}^{-1}$, the aminoketene forms and quickly escapes micrometeorites with initial radius $R_0$ around $25\mathsf{\mu }\mathrm{m}$ (Figure 13).

4. Discussion

Previous research has investigated the evolution of amino acids on the surface of the Earth, with a focus on the possibility of oligomerization in aqueous solution. The formation of $\approx 1\mathrm{mM}$ diglycine and triglycine was experimentally observed from a 0.1 M glycine water solution cycled between a high temperature and pressure chamber and one at lower temperature simulating the environment of hydrothermal vents [34]. However, the possibility of the oligomerization of glycine in water at a prebiotic oceanic concentration (estimated at $2.4\times {10}^{-9}\mathrm{M}$ [35]) can be ruled out unless a hitherto unknown and very efficient mechanism for catalysis is uncovered [4,5]. This manuscript aims at determining if the oligomerization of amino acids could have been promoted in the absence of water by the heating of micrometeoroids during atmospheric entry.

We summarize the results detailed above with a plot of the rates of the four main processes among those taken into consideration, namely the decarboxylation, dimerization, dehydration, and degassing of glycine (Figure 14), along with the corresponding relative densities at the end of the trajectory (Figure 15). The curves in Figure 14 show that both dimerization and dehydration represent secondary processes along the trajectory. When the temperature equals $744.4\mathrm{K}$ (at $t=48.7\mathrm{s}$) decarboxylation attains the same rate as degassing, and after that time, it dominates all rates. This result is in agreement with the findings of [12] that found no evidence for the formation of dipeptides or diketopiperazines during the sublimation of amino acids from the Murchison meteorite. On the other hand, $11\mathrm{pmol}{\mathrm{g}}^{-1}$ of glycylglycine and $18\mathrm{pmol}{\mathrm{g}}^{-1}$ of cyclo(glycylglycine) were found in the Yamato–791198 and Murchinson meteorites, respectively [36]. These results indicate that, while the oligomerization of amino acids is a very unlikely process in micrometeorites, it may occur in a limited extent in larger meteorites. Besides retention of the unaltered amino acid, degassing dominates the initial part of the trajectory. In a pulse-heating series of experiments simulating the loss of organic material from model micrometeoroids, the survival of l-lysine was measured to be 10% upon heating at 623 K for 5 s [37]. The heated substrate was a layer of aluminum oxide of thickness $25\mathsf{\mu }\mathrm{m}$, corresponding to a surface to volume ratio of $0.1\mathsf{\mu }{\mathrm{m}}^{-1}$. The entry trajectory of a spherical micrometeoroid with the same surface to volume ratio (corresponding to a radius $R_0=30\mathsf{\mu }\mathrm{m}$) and initial velocity $v_0=3.0\mathrm{km}{\mathrm{s}}^{-1}$ was simulated, and the maximum temperature of 626.8 K was attained at 59.7 s along the trajectory. In a 5 s interval centered on $t=59.7\mathrm{s}$, the fraction of glycine changed from 0.52 to 0.043, corresponding to a survival of 8.4%, in good agreement with the experimental result. The overall survival fraction of glycine along the entire trajectory is 0.013, and the degassing of the amino acid takes place in an interval of 20.4 s, during which the temperature changes from 152.2 K to the maximum temperature of 626.8, and to 350.2 K.

The relative densities in Figure 15 show that the decarboxylated glycine is the most likely outcome of the heating of a micrometeorite with size $70\mathsf{\mu }\mathrm{m}$ and initial velocity $3.7\mathrm{km}{\mathrm{s}}^{-1}$. Along with the main decarboxylation product (69%), about 31% of the original amino acid content is being degassed into the atmosphere, and a fraction $2\times {10}^{-9}$ survives as aminoketene. Despite the high rate of addition of aminoketene to itself, we may not consider the formation of glycine dimer once the product of addition makes contact with water. Figure 16 reports the prevailing product at the end of a trajectory of a micrometeorite. While the amount of retained glycine is significant, the corresponding yield of aminoketene and diglycine in the region of higher initial velocity is negligible.

The focus of this manuscript has been primarily on the possibility of oligomerization of the amino acids content of micrometeoroids falling on the prebiotic Earth. However, the set of Equations (1)–(8) and (15)–(18) can be extended to investigate the conditions on exoplanets of different mass and atmospheric composition with respect to the early Earth that could be more conductive towards the formation of amino acid oligomers.

5. Conclusions

The temperature of micrometeorites upon atmospheric entry is computed for different values of the initial velocity and radius at the edge of the atmosphere. Various evolutionary paths for the amino acid content of the micrometeorites are taken into consideration: degassing through heating and diffusion, elimination of ${\mathrm{CO}}_2$, elimination of water, formation of Gly–Gly through dimerization, addition of glycine to aminoketene or of aminoketene to itself. The dominant process depends on the maximum temperature along the trajectory and the value of diffusivity (porosity). The most common outcome of the atmospheric entry trajectory is a mixture of amino acid decarboxylation with small amounts of degassing and dehydration. Retention is significant only for very small values of the initial velocity ($v_0\le 2.8\mathrm{km}{\mathrm{s}}^{-1}$). The glycine dimer and aminoketene are formed only in negligible amounts.