Next Article in Journal / Special Issue
On the 3D → 2D Isomerization of Hexaborane(12)
Previous Article in Journal
Coordination Polymers Constructed from Semi-Rigid N,N′-Bis(3-pyridyl)terephthalamide and Dicarboxylic Acids: Effect of Ligand Isomerism, Flexibility, and Identity
Previous Article in Special Issue
The Photophysical Properties of Triisopropylsilyl-ethynylpentacene—A Molecule with an Unusually Large Singlet-Triplet Energy Gap—In Solution and Solid Phases
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemistry
Volume 3
Issue 1
10.3390/chemistry3010002
chemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom

by
Krishnan Thirumoorthy
1,
Vijayanand Chandrasekaran
1,
Andrew L. Cooksy
2 and
Venkatesan S. Thimmakondu
2,*
1
School of Advanced Sciences, Vellore Institute of Technology, Vellore 632 014, Tamil Nadu, India
2
Department of Chemistry and Biochemistry, San Diego State University, San Diego, CA 92182-1030, USA
*
Author to whom correspondence should be addressed.
Chemistry 2021, 3(1), 13-27; https://doi.org/10.3390/chemistry3010002
Submission received: 16 December 2020 / Revised: 25 December 2020 / Accepted: 28 December 2020 / Published: 31 December 2020
(This article belongs to the Special Issue A Special Issue in Honor of Professor Josef Michl)
Browse Figures
Versions Notes

Abstract

:
Dissociation pathways of the global minimum geometry of Si 2 C 5 H 2 with a planar tetracoordinate carbon (ptC) atom, 2,7-disilatricyclo[4.1.0.0 1 , 3 ]hept-2,4,6-trien-2,7-diyl (1), have been theoretically investigated using density functional theory and coupled-cluster (CC) methods. Dissociation of Si-C bond connected to the ptC atom leads to the formation of 4,7-disilabicyclo[4.1.0]hept-1(6),4(5)-dien-2-yn-7-ylidene (4) through a single transition state. Dissociation of C-C bond connected to the ptC atom leads to an intermediate with two identical transition states and leads back to 1 itself. Simultaneous breaking of both Si-C and C-C bonds leads to an acyclic transition state, which forms an acyclic product, cis-1,7-disilahept-1,2,3,5,6-pentaen-1,7-diylidene (19). Overall, two different products, four transition states, and an intermediate have been identified at the B3LYP/6-311++G(2d,2p) level of theory. Intrinsic reaction coordinate calculations have also been done at the latter level to confirm the isomerization pathways. CC calculations have been done at the CCSD(T)/cc-pVTZ level of theory for all minima. Importantly, all reaction profiles for 1 are found be endothermic in Si 2 C 5 H 2 . These results are in stark contrast compared to the structurally similar and isovalent lowest-energy isomer of C 7 H 2 with a ptC atom as the overall reaction profiles there have been found to be exothermic. The activation energies for Si-C, C-C, and Si-C/C-C breaking are found to be 30.51, 64.05, and 61.85 kcal mol − 1 , respectively. Thus, it is emphasized here that 1 is a kinetically stable molecule. However, it remains elusive in the laboratory to date. Therefore, energetic and spectroscopic parameters have been documented here, which may be of relevance to molecular spectroscopists in identifying this key anti-van’t-Hoff-Le Bel molecule.

Graphical Abstract

1. Introduction

Apart from chemical curiosity, interest in molecules with a planar tetracoordinate [1,2,3,4,5,6,7,8] or hypercoordinate carbon [9,10,11,12,13,14,15,16] atom (ptC or phC) stems from the fact that they could be used as potential new materials [17,18,19,20,21]. Though the experimental evidence on molecules with a ptC atom is limited as of today [22,23,24,25,26], more molecules have been continuously proposed from quantum chemical studies [27,28,29,30,31,32,33,34,35,36,37,38,39]. Importantly, two key questions are repeatedly being asked in the synthetic viability of these “anti-van’t Hoff-Le Bel molecules”: [40,41] (i) what is the energetic (thermodynamic) stability of the proposed molecule from a given elemental composition on the molecular potential energy surface (PES)? and (ii) what is its kinetic stability? A firm answer obtained from these two questions either directly or indirectly informs the experimentalists whether the theoretically proposed molecule could possibly be identified in the laboratory or not.
Experimentally, it was outlined in the past that molecules with a ptC atom can be enormously stabilized by the cooperative influence of metal pairs (Zr/Al or Zr/Zr + ) of atoms [22]. Experimental confirmation of pentaatomic ptC species (CAl 4 − , CAl 3 Si − / 0 , CAl 3 Ge − / 0 , CAl 4 2 − , etc.) [23,24,25] in the gas phase has given the much-needed momentum in the further search of these molecules. Stabilization of ptC by hydrogenation in the case of CAl 4 H − / 0 has been observed recently by Bowen and co-workers [26]. The effect of planar tetracoordinate silicon (ptSi) atom [18,33,42,43,44,45,46,47,48] in the stability of calix[4]pyrrole hydridosilicate [49] serves as the first experimental proof for ptSi, which motivated further study of these molecules. Very recently, room-temperature stable molecules containing a ptSi atom have been experimentally characterized including single-crystal x-ray diffraction measurements by Filippou and co-workers [50]. In 2017, isomers of X 2 C 5 H 2 (X = Si, Ge, Sn, and Pb) with a ptC atom have been theoretically proposed as global minimum geometries but to date they are yet to be identified in the laboratory [51]. This indirectly indicates that mere thermodynamic stability is not the only governing factor in the successful identification of molecules in the laboratory [52,53,54,55,56,57]. Thus, the objective here is to examine the kinetic stability of the global minimum geometry of Si 2 C 5 H 2 through dissociation studies. The knowledge of activation energies, reaction energies, and the reactive intermediates involved could give sufficient insights to experimentalists in devising successful synthetic routes–including what precursor molecules to choose.
Here, the kinetic stability of 2,7-disilatricyclo[4.1.0.0 1 , 3 ]hept-2,4,6-trien-2,7-diyl (1)—which is the global minimum geometry of Si 2 C 5 H 2 [51,58]—has been investigated in detail using density functional theory (DFT) and high-level coupled-cluster (CC) methods. Four low-lying isomers of Si 2 C 5 H 2 including 1 lying within 30 kcal mol − 1 have been reported at the CCSD(T)/def2-TZVP//PBE0/def2-TZVP level of theory elsewhere [51]. These results were obtained using search algorithms [59,60,61,62,63]. We recently explored the Si 2 C 5 H 2 PES in an exhaustive manner through a chemical intuition approach [58] instead of using search algorithms. Our study predicted more possible isomers in the low-lying region (see Figure 1). Upon further search, the AUTOMATON program [64], which is based on a genetic algorithm, had also suggested new isomers for Si 2 C 5 H 2 [58] in the low-lying region. Although the thermodynamic stabilities of various isomers have been examined at length, to the best of our knowledge, the kinetic stability of 1, which contains a ptC atom, is yet to be studied. Moreover, though it was reported as a global minimum nearly three years ago, the experimental evidence is completely absent not only on 1 but also on all other low-lying Si 2 C 5 H 2 isomers. Therefore, the kinetic stability of 1 has been examined here, which may possibly aid the detection of this peculiar molecule using infrared or rotational spectroscopy in the laboratory.

2. Computational Details

The geometries of all Si 2 C 5 H 2 isomers reported here have been optimized using DFT with the B3LYP hybrid-functional [65,66,67,68] and the 6-311++G(2d,2p) basis set [69,70]. All the transition states corresponding to the dissociation of C-C/Si-C bonds connected to the ptC atom, the intrinsic reaction coordinate (IRC) calculations [71,72], and the nucleus independent chemical shift (NICS) values [73,74,75] have been calculated at the latter level. It is also noted here that wavefunction stability analysis has been done for all minima (1–22) obtained at the B3LYP/6-311++G(2d,2p) level and no instabilities have been found [76]. All these DFT calculations have been carried out with the Gaussian suite of programs [77]. All the low-lying isomers (minima) obtained from the DFT calculations, which lie within 40 kcal mol − 1 , have been reoptimized with CC methods. All these CC calculations with single and double excitations (CCSD) [78] including a quasiperturbative triple excitations (CCSD(T)) [79,80] have been done with correlation-consistent polarized valence triple zeta (cc-pVTZ) basis set of Dunning’s [81]. The latter basis set consists of 246 basis functions for Si 2 C 5 H 2 . The frozen-core (fc) approximation is used for isomers 1–18 initially in the fc-CCSD(T)/cc-pVTZ calculations. For the global minimum geometry alone (1), all-electron (ae) calculations at the ae-CCSD(T)/cc-pwCVTZ [82] level of theory have also been done. This basis set consists of 361 basis functions for Si 2 C 5 H 2 and therefore these calculations have not been done for other isomers considering their expensive nature. All these calculations have been done with the CFOUR (2.00 beta version) program package [83]. We note that for all the stationary points obtained, harmonic vibrational frequencies have been calculated by analytic calculation of second derivatives [84].

3. Results and Discussion

Eighteen low-lying isomers of Si 2 C 5 H 2 obtained at the fc-CCSD(T)/cc-pVTZ level of theory are shown in Figure 1. Zero-point vibrational energy (ZPVE) corrected relative energies calculated with respect to 1, point group symmetry, and the absolute dipole moment value calculated for the corresponding geometry are given underneath each isomer. Optimal geometry parameters obtained at five different levels for isomer 1 are given in Table 1. Harmonic vibrational frequencies, infrared (IR) intensities, and various isotopic shifts ( 28 Si– 29 Si, 12 C–mono-substituted- 13 C, Si 2 13 C 5 H 2 , 1 H–mono-substituted- 2 D, and Si 2 C 5 D 2 ) in harmonic vibrational frequencies for isomer 1 are collected in Table 2. The activation energies ( Δ E ‡ ), reaction energies ( Δ E r ), and relative energies ( Δ E 0 ) calculated at different levels for the various dissociation pathways of 1 are given in Table 3. The atom numbering scheme, natural atomic charges, possible valence structures, and relevant occupied molecular orbitals contributing to the bonding of the ptC atom of isomer 1 are shown in Figure 2. Schematic reaction profile diagram connecting the reactant 1 and their dissociative products through appropriate transition states calculated at the B3LYP/6-311++G(2d,2p) level of theory is shown in Figure 3. Likewise, reaction profile diagram involving the isomerization of 1 to 2 is shown in Figure 4. For brevity, total electronic energies, ZPVEs, and final Cartesian coordinates of the optimized geometries of all isomers are given in the supporting information.

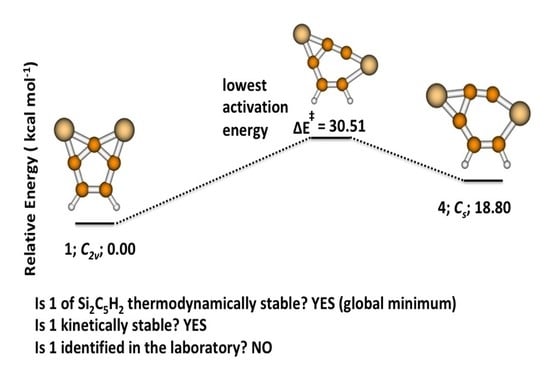
3.1. 2,7-Disilatricyclo[4.1.0.0 1 , 3 ]hept-2,4,6-trien-2,7-diyl (1)

All bond lengths of isomer 1 are systematically overestimated at the CCSD/cc-pVDZ and CCSD(T)/cc-pVDZ levels (see Table 1). One could notice a contraction in bond lengths with respect to the same methods using the cc-pVTZ basis set. They are slightly contracted further if we observe the change in bond lengths from CCSD(T)/cc-pVTZ to CCSD(T)/cc-pwCVTZ levels. These results (longer bond lengths with respect to cc-pVDZ basis set) are largely due to the lack of higher angular momentum polarization functions [85,86,87,88,89,90] and consistent with our earlier observations [91,92,93,94,95,96]. Considering the double bond characteristics of C 6 C 7 , C 2 Si 4 (C 3 Si 5 ; equal due to C 2 v symmetry) and single bond characteristics of C 1 C 2 (C 1 C 3 ) and C 2 C 6 (C 3 C 7 ), we have come to the conclusion that valence structure 1a shown in Figure 2 is dominant. However, based on the natural atomic charges, one could also assume an equally dominant resonance contributor where the molecule behaves like a zwitterion (Si and H atoms having a partial positive charge whereas all carbon atoms having a partial negative charge). The second most stable isomer, 2-ethynylmethylene-1,4-disilabicyclo[1.1.0]but-1(3)-en-4-ylidene (2), is 21.39 kcal mol − 1 above 1 at the fc-CCSD(T)/cc-pVTZ level of theory (see Figure 1). Therefore, isomer 1 is thermodynamically well-separated from others. It is worth noting here that the singlet-triplet energy gap ( Δ E S T ) calculated for isomer 1 is 72.26 kcal mol − 1 (positive value indicates singlet being more stable) at the (U)B3LYP/6-311++G(2d,2p) level of theory [58].
Harmonic vibrational frequencies calculated for 1 reveal that three vibrational modes (modes 4, 8, and 17) are dominant (see Table 2). One is the Si-C-Si rocking ( b 2 ) calculated at 427.7 cm − 1 , another is the Si-C-Si breathing motion ( a 1 ) calculated at 616.0 cm − 1 , and yet another is the C-C stretching motion ( a 1 ) calculated at 1340.0 cm − 1 at the ae-CCSD(T)/cc-pwCVTZ level of theory. Various isotopic shift values calculated by us can help in resolving potential ambiguities in assigning vibrational modes. It is also possible to identify isomer 1 and all other low-lying isomers (2–18) using Fourier transform microwave spectroscopy as the net dipole moment is non-zero ( μ ≠ 0 ) in all cases. The net dipole moment value calculated for isomer 1 is 0.39 Debye at the fc-CCSD(T)/cc-pVTZ level of theory. Rotational and centrifugal distortion constants of all 18 isomers are given in our previous article [58] and detailed discussion related to rotational constants are not repeated here for brevity. It is also noted here that for the low-lying C 7 H 2 isomer with a ptC atom, tricyclo[4.1.0.0 1 , 3 ]hept-2,4,6-trien-2,7-diyl [92], the net dipole moment value calculated at the same level of theory is 5.84 Debye. Such a large deviation is not surprising considering the fact that silicon is more electropositive than carbon and the overall charge (see Figure 2) is more balanced and thus the net dipole moment has a smaller value for isomer 1. Also, compared with the iso-valent C 7 H 2 isomer with a ptC atom, isomer 1 exhibits higher aromatic characteristic. The NICS (1 Å) value obtained for 1 is −20.28 ppm at the B3LYP/6-311++G(2d,2p) level. At the latter level, the NICS (1 Å) value obtained for C 7 H 2 isomer with a ptC atom is −12.21 ppm. Nevertheless, both the molecules remain elusive to date. To analyze the aromatic characteristics further, we have carried out NICS calculations in 3D grid points (see supporting information). The out-of-plane NICS values are negative for all the three rings. On the other hand, the in-plane NICS value (NICS (0 Å)) is positive for the C 5 ring and negative for the SiC 2 rings. Thus, the entire molecule is π -aromatic (see the MOs in Figure 2; HOMO, HOMO-2, HOMO-6) but σ -aromaticity is not completely there in the C 5 ring (HOMO-1, HOMO-3, HOMO-4, HOMO-5). Therefore, isomer 1 of Si 2 C 5 H 2 can be characterized as a molecule, which exhibits pseudo-double aromaticity [97,98,99]. To assess the multi-reference characteristic of isomer 1, we have calculated the T 1 diagnostic value suggested elsewhere [100] and found that it is below 0.02. The value obtained for isomer 1 at the fc-CCSD/cc-pVTZ level of theory is 0.015. Thus, we have not carried out multi-reference CC calculations for this molecule.

3.2. Activation and Reaction Energies

To calculate the activation and reaction energies, different bonds connected to the ptC atom of 1 were broken. Four different transition states (TS-1 to TS-4), one intermediate (20), and three different products, 1, 4,7-disilabicyclo[4.1.0]hept-1(6),4(5)-dien-2-yn-7-ylidene (4), and cis-1,7-disilahept-1,2,3,5,6-pentaen-1,7-diylidene (19), respectively, have been identified (see Figure 3) along three different dissociation pathways A, B, and C connected to the ptC atom of isomer 1. It is noted here that for pathway A, both the reactant and the product are one and the same. Breaking of C-ptC bond requires an Δ E ‡ of 64.05 kcal mol − 1 at the B3LYP/6-311++G(2d,2p) level. IRC calculations through this transition state (TS-1) leads to an intermediate (20), which lies at 54.64 kcal mol − 1 above 1. Another identical transition state, TS-2, which is a half-chair equivalent conformer of TS-1, has been identified along pathway A. IRC calculations along these two transition states (TS-1 and TS-2) either leads to the same non-planar intermediate (20—in one direction) or to the global minimum isomer itself (1—in the other direction). The lowest activation energy required was estimated to be 30.51 kcal mol − 1 at the same level of theory, which occurs through Si-ptC bond breaking (pathway B). Along pathway C, where simultaneous breaking of both C-ptC and Si-ptC bonds has been taken into consideration, an acyclic transition state has been identified (TS-4), which requires an activation energy of 61.85 kcal mol − 1 and leads to an acyclic product, 19. Overall, the reaction profiles along these three different dissociation pathways are found to be endothermic with a reaction energy of 54.64, 18.80, and 43.03 kcal mol − 1 , respectively, for dissociation pathways A, B, and C. For the lowest activation energy path (B), we have also estimated rate constant values using Rice–Ramsperger–Kassel–Marcus (RRKM) theory [101]. It was estimated that the rate of the reverse reaction (4 to 1) is three orders of magnitude faster than the forward reaction. This clearly implies that 1 is kinetically stable.

3.3. Isomerization of 1 to 2

Isomerization of 1 to 2 has also been considered though 2 lies 21.39 kcal mol − 1 above 1 (see Figure 4). Considering the structural similarity between 1 and 2, the Si-C double bond and the ptC-C bonds on one side are initially broken. This requires an activation energy of 71.45 kcal mol − 1 at the B3LYP/6-311++G(2d,2p) level. IRC calculations from this transition state (TS-5) lead us to a new intermediate (22). Upon rotating the C-C bond, we found a new transition state (TS-6). IRC calculations from TS-6 lead to new intermediate (21), where the hydrogen atoms are in the trans position. A 1,2-H shift must happen to reach the geometry of 2. Therefore, using this new intermediate 22 and slightly elongating the C-C-C angle, we found a new transition state geometry TS-7, which requires an activation energy of 62.71 kcal mol − 1 . It is noted here that the energy barrier between 21 and TS-7 is negative after ZPVE-correction at the B3LYP/6-311++G(2d,2p) level. Without ZPVE-corrections, the activation energy ( Δ E * ; see Figure 4) is 66.96 kcal mol − 1 . It is well-known in the literature that various DFT functionals including the popular B3LYP underestimate the barrier-heights [102,103]. Doubly hybrid density functionals such as B2PLYP [104,105] and XYG3 [102] offer promising alternatives for accurate description of barrier-heights. We leave this discussion with a caveat that currently we have not tried these alternatives and in a future work we would be exploring these avenues. IRC calculations in one direction from TS-7 lead us to isomer 2, whose reaction energy is 17.53 kcal mol − 1 . It is also noted here that the Gibbs free energy change is minimal for almost all stationary points.

3.4. Rate Co-Efficient for the Isomerization Reaction

The activation energies and reaction energies estimated among the low-lying isomers of Si 2 C 5 H 2 reveal that pathway B is the most feasible based on energetics. Therefore, for this isomerization process alone, we have calculated the rate coefficients for the forward ( k 1 ) and reverse ( k − 1 ) reactions using RRKM theory [101] given by the expression
k = N ( E − E T S ) c / ρ
where E T S is the energy of the transition state from the ground state of the isomers under consideration, E is the total energy of the isomer, N(E- E T S ) is the sum of states of the transition state that would be available for the given energy E of the isomer, c is the velocity of light, and ρ is the density of the vibrational states. The densities of the vibrational states are calculated by Beyer and Swinehart direct count algorithm [106].
The rate of forward and reverse reactions are given in Figure 5 as a function of energy. The reverse reaction is found to be around three orders of magnitude faster than the forward reaction. The equilibrium constant for the isomerization reaction is calculated using the expression K = k 1 / k − 1 and it is given in Figure 6. The equilibrium constant is much below 1. This is due to the high density of vibrational states for isomer 1 (global minimum structure) compared to isomer 4 at energies above the isomerization barrier. This favors the reverse reaction than the forward reaction. Figure 6 clearly indicates that over a wide range of energies, isomer 1 is kinetically as well as energetically more stable.

4. Conclusions

The most stable isomer (global minimum) of Si 2 C 5 H 2 containing a ptC atom and its dissociation pathways have been theoretically characterized using DFT and CC methods. The lowest activation energy barrier for 1 has been calculated as 30.51 kcal mol − 1 at the B3LYP/6-311++G(2d,2p) level of theory. Possible interconversion of 1 to 2 is highly unlikely as the initial activation energy required for this process is 71.45 kcal mol − 1 at the same level. Hence, it is concluded that 1 is a kinetically stable molecule. Also, the rate co-efficient for the reverse reaction (4 to 1; exothermic) is ∼3 orders of magnitude faster than the forward reaction (1 to 4; endothermic). This clearly indicates further that isomer 1 is kinetically stable. In fact, our extensive search for various structural isomers of Si 2 C 5 H 2 indicates that there are no other isomers lying close to 1 within 20 kcal mol − 1 [58] at the fc-CCSD(T)/cc-pVTZ level of theory (see Figure 1). Thus, 1 is not only the energetically most stable molecule but also thermodynamically well-separated from other isomers. Perhaps, synthetic challenges may remain as one of the potential issues in the laboratory identification of this molecule considering the pyrophoric nature of some of the precursor molecules such as SiH 4 in the preparation of this isomer or silicon-doped hydrocarbons, in general. Nevertheless, it is believed that the current theoretical efforts may motivate and assist the experimentalists in devising successful synthetic strategies and in characterizing this potential “anti-van’t Hoff-Le Bel” molecule in the laboratory. The kinetic stability of 1,7-disilatricyclo[4.1.0.0 1 , 3 ]hept-2,4,6-trien-2,7-diyl (6), which contains a ptSi atom will be examined in a future work.

Supplementary Materials

The following are available online at https://www.mdpi.com/2624-8549/3/1/2/s1.

Author Contributions

Conceptualization, V.S.T. and K.T.; methodology, K.T., V.S.T. and V.C.; software, K.T., V.C. and V.S.T.; validation, V.S.T. and K.T.; formal analysis, V.S.T., K.T. and V.C.; investigation, V.S.T., K.T. and V.C.; resources, K.T., V.C., A.L.C. and V.S.T.; data curation, K.T., V.C. and V.S.T.; writing—original draft preparation, V.S.T.; writing—review and editing, V.S.T. and A.L.C.; visualization, K.T. and V.S.T.; supervision, V.S.T.; project administration, V.S.T. All authors have read and agreed to the published version of the manuscript.

Funding

Computational support provided at the SDSU by DURIP Grant W911NF-10-1-0157 from the U.S. Department of Defense and by NSF CRIF Grant CHE-0947087 is gratefully acknowledged. Additional computational support provided at the VIT, Vellore, India, through a research grant (Project. No. YSS/2014/001019) from the Science and Engineering Research Board, Department of Science and Technology, New Delhi, Government of India, is gratefully acknowledged. Computing time provided (to VST) at the National Computational Infrastructure (NCI), which is supported by the Australian Government, is also gratefully acknowledged.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in inside the article or the supplementary material.

Acknowledgments

This publication is dedicated to Josef Michl on the occasion of his 80th birthday. VST thanks Amir Karton (UWA, Perth) for helpful discussions during the initial stages of this work and providing access to the computational resources. VST also thanks Anoop Ayyappan (Indian Institute of Technology, Kharagpur) for helpful discussions related to search algorithms.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
aeall-electron
fcfrozen-core
DFTDensity functional theory
CCSDCoupled-cluster singles, doubles
CCSD(T)Coupled-cluster singles, doubles including perturbative triples
ptCplanar tetracoordinate carbon
ptSiplanar tetracoordinate silicon

References

  1. Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
  2. Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.V.R.; Seeger, R.; Pople, J.A. Stabilization of Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
  3. Keese, R. Carbon Flatland: Planar Tetracoordinate Carbon and Fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef] [PubMed]
  4. Radom, L.; Rasmussen, D.R. The Planar Carbon Story. Pure Appl. Chem. 1998, 70, 1977. [Google Scholar] [CrossRef]
  5. Merino, G.; Méndez-Rojas, M.A.; Beltrán, H.I.; Corminboeuf, C.; Heine, T.; Vela, A. Theoretical Analysis of the Smallest Carbon Cluster Containing a Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 2004, 126, 16160–16169. [Google Scholar] [CrossRef]
  6. Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar Tetracoordinate Carbon in Extended Systems. J. Am. Chem. Soc. 2004, 126, 15309–15315. [Google Scholar] [CrossRef]
  7. Roy, D.; Corminboeuf, C.; Wannere, C.S.; King, R.B.; Schleyer, P.V.R. Planar Tetracoordinate Carbon Atoms Centered in Bare Four-membered Rings of Late Transition Metals. Inorg. Chem. 2006, 45, 8902–8906. [Google Scholar] [CrossRef]
  8. Nandula, A.; Trinh, Q.T.; Saeys, M.; Alexandrova, A.N. Origin of Extraordinary Stability of Square-Planar Carbon Atoms in Surface Carbides of Cobalt and Nickel. Angew. Chem. Int. Ed. 2015, 54, 5312–5316. [Google Scholar] [CrossRef] [Green Version]
  9. Yang, L.M.; Ganz, E.; Chen, Z.; Wang, Z.X.; Schleyer, P.v.R. Four Decades of the Chemistry of Planar Hypercoordinate Compounds. Angew. Chem. Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef]
  10. Yañez, O.; Báez-Grez, R.; Garza, J.; Pan, S.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Embedding a Planar Hypercoordinate Carbon Atom into a [4n+2] π-System. ChemPhysChem 2020, 21, 145–148. [Google Scholar] [CrossRef]
  11. Guo, J.C.; Feng, L.Y.; Dong, C.; Zhai, H.J. Planar Pentacoordinate versus Tetracoordinate Carbons in Ternary CBe4Li4 and CBe4 Li 4 2 − Clusters. J. Phys. Chem. A 2018, 122, 8370–8376. [Google Scholar] [CrossRef] [PubMed]
  12. Zhang, C.F.; Han, S.J.; Wu, Y.B.; Lu, H.G.; Lu, G. Thermodynamic Stability versus Kinetic Stability: Is the Planar Hexacoordinate Carbon Species D3h CN3 Mg 3 + Viable? J. Phys. Chem. A 2014, 118, 3319–3325. [Google Scholar] [CrossRef] [PubMed]
  13. Wu, Y.B.; Duan, Y.; Lu, H.G.; Li, S.D. CAl2 Be 3 2 − and Its Salt Complex LiCAl2 Be 3 − : Anionic Global Minima with Planar Pentacoordinate Carbon. J. Phys. Chem. A 2012, 116, 3290–3294. [Google Scholar] [CrossRef] [PubMed]
  14. Guo, J.C.; Feng, L.Y.; Zhang, X.Y.; Zhai, H.J. Star-Like CBe5 Au 5 + Cluster: Planar Pentacoordinate Carbon, Superalkali Cation, and Multifold (π and σ) Aromaticity. J. Phys. Chem. A 2018, 122, 1138–1145. [Google Scholar] [CrossRef]
  15. Wang, M.H.; Dong, X.; Ding, Y.H.; Cui, Z.H. Avoided Spin Coupling: An Unexpected σ-σ Diradical in Global Planar Pentacoordinate Carbon. Chem. Commun. 2020, 56, 7285–7288. [Google Scholar] [CrossRef]
  16. Guo, J.C.; Feng, L.Y.; Barroso, J.; Merino, G.; Zhai, H.J. Planar or Tetrahedral? A Ternary 17-Electron CBe5 H 4 + Cluster with Planar Pentacoordinate Carbon. Chem. Commun. 2020, 56, 8305–8308. [Google Scholar] [CrossRef]
  17. Wang, Y.; Li, F.; Li, Y.; Chen, Z. Semi-Metallic Be5C2 Monolayer Global Minimum with Quasi-Planar Pentacoordinate Carbons and Negative Poisson’s Ratio. Nat. Commun. 2016, 7, 11488. [Google Scholar] [CrossRef] [Green Version]
  18. Li, Y.; Li, F.; Zhou, Z.; Chen, Z. SiC2 Silagraphene and Its One-Dimensional Derivatives: Where Planar Tetracoordinate Silicon Happens. J. Am. Chem. Soc. 2011, 133, 900–908. [Google Scholar] [CrossRef]
  19. Wang, M.H.; Dong, X.; Cui, Z.H.; Orozco-Ic, M.; Ding, Y.H.; Barroso, J.; Merino, G. Planar Pentacoordinate Silicon and Germanium Atoms. Chem. Commun. 2020, 56, 13772–13775. [Google Scholar] [CrossRef]
  20. Jimenez-Izal, E.; Saeys, M.; Alexandrova, A.N. Metallic and Magnetic 2D Materials Containing Planar Tetracoordinated C and N. J. Phys. Chem. C 2016, 120, 21685–21690. [Google Scholar] [CrossRef] [Green Version]
  21. Zhang, C.; Tian, Z.; Jia, W.; Mo, Y. Rational Design of Porous Organic Molecules (POMs) Based on B-Heterocyclic Carbenes. Mol. Syst. Des. Eng. 2021. [Google Scholar] [CrossRef]
  22. Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chem. Int. Ed. Engl. 1997, 36, 812–827. [Google Scholar] [CrossRef]
  23. Li, X.; Wang, L.S.; Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in the Al4C− Anion. A Combined Photoelectron Spectroscopy and ab Initio Study. J. Am. Chem. Soc. 1999, 121, 6033–6038. [Google Scholar] [CrossRef]
  24. Wang, L.S.; Boldyrev, A.I.; Li, X.; Simons, J. Experimental Observation of Pentaatomic Tetracoordinate Planar Carbon-Containing Molecules. J. Am. Chem. Soc. 2000, 122, 7681–7687. [Google Scholar] [CrossRef]
  25. Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.; Boldyrev, A. Pentaatomic Tetracoordinate Planar Carbon, [CAl4]2−: A New Structural Unit and Its Salt Complexes. Angew. Chem. Int. Ed. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
  26. Xu, J.; Zhang, X.; Yu, S.; Ding, Y.H.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef] [Green Version]
  27. Priyakumar, U.D.; Reddy, A.S.; Sastry, G.N. The Design of Molecules Containing Planar Tetracoordinate Carbon. Tetrahedron Lett. 2004, 45, 2495–2498. [Google Scholar] [CrossRef]
  28. Perez, N.; Heine, T.; Barthel, R.; Seifert, G.; Vela, A.; Mendez-Rojas, M.A.; Merino, G. Planar Tetracoordinate Carbons in Cyclic Hydrocarbons. Org. Lett. 2005, 7, 1509–1512. [Google Scholar] [CrossRef]
  29. Sateesh, B.; Srinivas Reddy, A.; Narahari Sastry, G. Towards Design of the Smallest Planar Tetracoordinate Carbon and Boron Systems. J. Comput. Chem. 2007, 28, 335–343. [Google Scholar] [CrossRef]
  30. Cui, Z.H.; Ding, Y.H.; Cabellos, J.L.; Osorio, E.; Islas, R.; Restrepo, A.; Merino, G. Planar Tetracoordinate Carbons with A Double Bond in CAl3E Clusters. Phys. Chem. Chem. Phys. 2015, 17, 8769–8775. [Google Scholar] [CrossRef]
  31. Suresh, C.H.; Frenking, G. Direct 1-3 Metal-Carbon Bonding and Planar Tetracoordinated Carbon in Group 6 Metallacyclobutadienes. Organometallics 2010, 29, 4766–4769. [Google Scholar] [CrossRef]
  32. Cui, Z.H.; Contreras, M.; Ding, Y.H.; Merino, G. Planar Tetracoordinate Carbon versus Planar Tetracoordinate Boron: The Case of CB4 and Its Cation. J. Am. Chem. Soc. 2011, 133, 13228–13231. [Google Scholar] [CrossRef] [PubMed]
  33. Thimmakondu, V.S.; Thirumoorthy, K. Si3C2H2 Isomers with A Planar Tetracoordinate Carbon or Silicon atom(s). Comput. Theor. Chem. 2019, 1157, 40–46. [Google Scholar] [CrossRef] [Green Version]
  34. Thirumoorthy, K.; Karton, A.; Thimmakondu, V.S. From High-Energy C7H2 Isomers with A Planar Tetracoordinate Carbon Atom to An Experimentally Known Carbene. J. Phys. Chem. A 2018, 122, 9054–9064. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Thirumoorthy, K.; Thimmakondu, V.S. Flat Crown Ethers with Planar Tetracoordinate Carbon Atoms. Int. J. Quantum Chem. 2020, e26479. [Google Scholar] [CrossRef]
  36. Raghunathan, S.; Yadav, K.; Rojisha, V.C.; Jaganade, T.; Prathyusha, V.; Bikkina, S.; Lourderaj, U.; Priyakumar, U.D. Transition Between [R]- and [S]-Stereoisomers without Bond Breaking. Phys. Chem. Chem. Phys. 2020, 22, 14983–14991. [Google Scholar] [CrossRef]
  37. Job, N.; Karton, A.; Thirumoorthy, K.; Cooksy, A.L.; Thimmakondu, V.S. Theoretical Studies of SiC4H2 Isomers Delineate Three Low-Lying Silylidenes Are Missing in the Laboratory. J. Phys. Chem. A 2020, 124, 987–1002. [Google Scholar] [CrossRef]
  38. Zhang, C.; Wang, P.; Liang, J.; Jia, W.; Cao, Z. Theoretical Study on a Family of Organic Molecules with Planar Tetracoordinate Carbon. J. Mol. Struct. THEOCHEM 2010, 941, 41–46. [Google Scholar] [CrossRef]
  39. Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon Rings Decorated with Group 14 Elements: New Aromatic Clusters Containing Planar Tetracoordinate Carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar]
  40. Van’t Hoff, J.H. A Suggestion Looking to the Extension Into Space of the Structural Formulas at Present Used in Chemistry. And A Note Upon the Relation Between the Optical Activity and the Chemical Constitution of Organic Compounds. Arch. Neerl. Sci. Exactes Nat. 1874, 9, 445–454. [Google Scholar]
  41. Le-Bel, J.A. On the Relations Which Exist Between the Atomic Formulas of Organic Compounds and the Rotatory Power of Their Solutions. Bull. Soc. Chim. Fr. 1874, 22, 337–347. [Google Scholar]
  42. Würthwein, E.U.; von Ragué Schleyer, P. Planar Tetracoordinate Silicon. Angew. Chem. Int. Ed. Engl. 1979, 18, 553–554. [Google Scholar] [CrossRef]
  43. Guo, J.C.; Miao, C.Q.; Ren, G.M. Planar Tetracoordinate Si and Ge in π-Aromatic X3 Cu 3 + (X=Si, Ge) Cations. Comput. Theor. Chem. 2014, 1032, 7–11. [Google Scholar] [CrossRef]
  44. Guo, J.C.; Wu, H.X.; Ren, G.M.; Miao, C.Q.; Li, Y.X. D3h X3 Li 3 + (X=C, Si and Ge): Superalkali Cations Containing Three Planar Tetracoordinate X Atoms. Comput. Theor. Chem. 2016, 1083, 1–6. [Google Scholar] [CrossRef] [Green Version]
  45. Li, S.D.; Miao, C.Q.; Guo, J.C.; Ren, G.M. Planar Tetra-, Penta-, Hexa-, Hepta-, and Octacoordinate Silicons: A Universal Structural Pattern. J. Am. Chem. Soc. 2004, 126, 16227–16231. [Google Scholar] [CrossRef]
  46. Sui, J.J.; Xu, J.; Ding, Y.H. A Template for A Planar Tetracoordinate Heavier Group 14 Atom: A Global Study of C2Si2Xq (X = C, Si, Ge, Sn, Pb; q = +1, 0, −1). Dalton Trans. 2016, 45, 56–60. [Google Scholar] [CrossRef]
  47. Xu, J.; Ding, Y.H. Pentaatomic Planar Tetracoordinate Silicon with 14 Valence Electrons: A Large-Scale Global Search of SiXn Y q m (n + m = 4; q = 0, ±1, −2; X, Y = Main Group Elements From H to Br). J. Comput. Chem. 2015, 36, 355–360. [Google Scholar] [CrossRef]
  48. Zhang, Y.; Zhang, C.; Mo, Y.; Cao, Z. Planar Tetracoordinate Silicon in Organic Molecules As Carbenoid-Type Amphoteric Centers: A Computational Study. Chem. Eur. J. 2020, 26, 1–9. [Google Scholar] [CrossRef]
  49. Ebner, F.; Greb, L. Calix[4]pyrrole Hydridosilicate: The Elusive Planar Tetracoordinate Silicon Imparts Striking Stability to Its Anionic Silicon Hydride. J. Am. Chem. Soc. 2018, 140, 17409–17412. [Google Scholar] [CrossRef]
  50. Ghana, P.; Rump, J.; Schnakenburg, G.; Arz, M.I.; Filippou, A.C. Planar Tetracoordinated Silicon (ptSi): Room-Temperature Stable Compounds Containing Anti-van’t Hoff/Le Bel Silicon. J. Am. Chem. Soc. 2020. [Google Scholar] [CrossRef]
  51. Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting Electronic Strategies to Stabilize A Planar Tetracoordinate Carbon in Cyclic Aromatic Hydrocarbons. Chem. Commun. 2017, 53, 12112–12115. [Google Scholar] [CrossRef] [PubMed]
  52. Reusch, E.; Kaiser, D.; Schleier, D.; Buschmann, R.; Krueger, A.; Hermann, T.; Engels, B.; Fischer, I.; Hemberger, P. Pentadiynylidene and Its Methyl-Substituted Derivates: Threshold Photoelectron Spectroscopy of R1-C5-R2 Triplet Carbon Chains. J. Phys. Chem. A 2019, 123, 2008–2017. [Google Scholar] [CrossRef] [PubMed]
  53. Bouwman, J.; Bodi, A.; Hemberger, P. Nitrogen Matters: The Difference Between PANH and PAH Formation. Phys. Chem. Chem. Phys. 2018, 20, 29910–29917. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  54. Henkel, S.; Huynh, Y.A.; Neuhaus, P.; Winkler, M.; Sander, W. Tunneling Rearrangement of 1-Azulenylcarbene. J. Am. Chem. Soc. 2012, 134, 13204–13207. [Google Scholar] [CrossRef]
  55. Fulara, J.; Nagy, A.; Filipkowski, K.; Thimmakondu, V.S.; Stanton, J.F.; Maier, J.P. Electronic Transitions of C6 H 4 + Isomers: Neon Matrix and Theoretical Studies. J. Phys. Chem. A 2013, 117, 13605–13615. [Google Scholar] [CrossRef]
  56. Thimmakondu, V.S. MgC2H2 isomers—Simple Penta-Atomic Molecules Missing in the Laboratory. Chem. Phys. 2020, 538, 110899. [Google Scholar] [CrossRef]
  57. Pandey, A.P.; Padidela, U.K.; Thulasiraman, L.K.; Sethu, R.; Vairaprakash, P.; Thimmakondu, V.S. MgC6H2 Isomers: Potential Candidates for Laboratory and Radioastronomical Studies. J. Phys. Chem. A 2020, 124, 7518–7525. [Google Scholar] [CrossRef]
  58. Thirumoorthy, K.; Cooksy, A.; Thimmakondu, V.S. Si2C5H2 Isomers—Search Algorithms Versus Chemical Intuition. Phys. Chem. Chem. Phys. 2020, 22, 5865–5872. [Google Scholar] [CrossRef]
  59. Saunders, M. Stochastic Search for Isomers on a Quantum Mechanical Surface. J. Comput. Chem. 2004, 25, 621–626. [Google Scholar] [CrossRef]
  60. Bera, P.P.; Sattelmeyer, K.W.; Saunders, M.; Schaefer, H.F.; Schleyer, P.V.R. Mindless Chemistry. J. Phys. Chem. A 2006, 110, 4287–4290. [Google Scholar] [CrossRef]
  61. Zhao, J.; Xie, R.H. Genetic Algorithms for the Geometry Optimization of Atomic and Molecular Clusters. J. Comput. Theor. Nanosci. 2004, 1, 117–131. [Google Scholar] [CrossRef]
  62. Grande-Aztatzi, R.; Martínez-Alanis, P.R.; Cabellos, J.L.; Osorio, E.; Martínez, A.; Merino, G. Structural Evolution of Small Gold Clusters Doped by One and Two Boron Atoms. J. Comput. Chem. 2014, 35, 2288–2296. [Google Scholar] [CrossRef] [PubMed]
  63. Ramirez-Manzanares, A.; Peña, J.; Azpiroz, J.M.; Merino, G. A Hierarchical Algorithm for Molecular Similarity (H-FORMS). J. Comput. Chem. 2015, 36, 1456–1466. [Google Scholar] [CrossRef] [PubMed]
  64. Yañez, O.; Báez-Grez, R.; Inostroza, D.; Rabanal-León, W.A.; Pino-Rios, R.; Garza, J.; Tiznado, W. AUTOMATON: A Program That Combines a Probabilistic Cellular Automata and a Genetic Algorithm for Global Minimum Search of Clusters and Molecules. J. Chem. Theory Comput. 2019, 15, 1463–1475. [Google Scholar]
  65. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
  66. Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
  67. Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  68. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  69. Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
  70. Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
  71. Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
  72. Hratchian, H.P.; Schlegel, H.B. Chapter 10—Finding Minima, Transition States, and Following Reaction Pathways On Ab Initio Potential Energy Surfaces. In Theory and Applications of Computational Chemistry; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 195–249. [Google Scholar]
  73. Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
  74. Fallah-Bagher-Shaidaei, H.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.V.R. Which NICS Aromaticity Index for Planar π Rings Is Best? Org. Lett. 2006, 8, 863–866. [Google Scholar] [CrossRef] [PubMed]
  75. Seal, P.; Chakrabarti, S. Is Nucleus-Independent Chemical Shift Scan a Reliable Aromaticity Index for Planar Heteroatomic Ring Systems? J. Phys. Chem. A 2007, 111, 9988–9994. [Google Scholar] [CrossRef]
  76. Bauernschmitt, R.; Ahlrichs, R. Stability Analysis for Solutions of the Closed Shell Kohn–Sham Equation. J. Chem. Phys. 1996, 104, 9047–9052. [Google Scholar] [CrossRef]
  77. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  78. Purvis, G.D.; Bartlett, R.J. A Full Coupled-Cluster Singles and Doubles Model: The Inclusion of Disconnected Triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
  79. Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A Fifth-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
  80. Bartlett, R.J.; Watts, J.; Kucharski, S.; Noga, J. Non-Iterative Fifth-Order Triple and Quadruple Excitation Energy Corrections in Correlated Methods. Chem. Phys. Lett. 1990, 165, 513–522. [Google Scholar] [CrossRef]
  81. Dunning, T.H. Gaussian Basis Sets for Use In Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  82. Peterson, K.A.; Dunning, T.H. Accurate Correlation Consistent Basis Sets for Molecular Core–Valence Correlation Effects: The Second Row Atoms Al-Ar, and the First Row Atoms B-Ne Revisited. J. Chem. Phys. 2002, 117, 10548–10560. [Google Scholar] [CrossRef] [Green Version]
  83. Stanton, J.F.; Gauss, J.; Cheng, L.; Harding, M.E.; Matthews, D.A.; Szalay, P.G. CFOUR, Coupled-Cluster Techniques for Computational Chemistry, a Quantum-Chemical Program Package. With Contributions from A.A. Auer, R.J. Bartlett, U. Benedikt, C. Berger, D.E. Bernholdt, Y.J. Bomble, O. Christiansen, F. Engel, R. Faber, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, W.J. Lauderdale, F. Lipparini, T. Metzroth, L.A. Mück, D.P. O’Neill, D.R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J.D. Watts and the integral packages MOLECULE (J. Almlöf and P.R. Taylor), PROPS (P.R. Taylor), ABACUS (T. Helgaker, H.J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the Current Version. Available online: http://www.cfour.de (accessed on 11 December 2020).
  84. Gauss, J.; Stanton, J.F. Analytic CCSD(T) Second Derivatives. Chem. Phys. Lett. 1997, 276, 70–77. [Google Scholar] [CrossRef]
  85. Spackman, P.R.; Jayatilaka, D.; Karton, A. Basis Set Convergence of CCSD(T) Equilibrium Geometries Using a Large and Diverse Set of Molecular Structures. J. Chem. Phys. 2016, 145, 104101. [Google Scholar] [CrossRef] [Green Version]
  86. Feller, D.; Peterson, K.A. Probing the Limits of Accuracy in Electronic Structure Calculations: Is Theory Capable of Results Uniformly Better Than “Chemical Accuracy”? J. Chem. Phys. 2007, 126, 114105. [Google Scholar] [CrossRef]
  87. Wang, S.; Schaefer, H.F. The Small Planarization Barriers for the Amino Group in the Nucleic Acid Bases. J. Chem. Phys. 2006, 124, 044303. [Google Scholar] [CrossRef] [PubMed]
  88. Bak, K.L.; Gauss, J.; Jørgensen, P.; Olsen, J.; Helgaker, T.; Stanton, J.F. The Accurate Determination of Molecular Equilibrium Structures. J. Chem. Phys. 2001, 114, 6548. [Google Scholar] [CrossRef]
  89. Martin, J.M.L.; Taylor, P.R. Structure and Vibrations of Small Carbon Clusters from Coupled-Cluster Calculations. J. Phys. Chem. 1996, 100, 6047. [Google Scholar] [CrossRef]
  90. Xie, Y.; Scuseria, G.E.; Yates, B.F.; Yamaguchi, Y.; Schaefer, H.F. Methylnitrene: Theoretical Predictions of its Molecular Structure and Comparison with the Conventional C-N Single Bond in Methylamine. J. Am. Chem. Soc. 1989, 111, 5181. [Google Scholar] [CrossRef]
  91. Thimmakondu, V.S. The Equilibrium Geometries of Heptatriynylidene, Cyclohepta-1,2,3,4-tetraen-6-yne, and Heptahexaenylidene. Comput. Theor. Chem. 2016, 1079, 1–10. [Google Scholar] [CrossRef]
  92. Thimmakondu, V.S.; Karton, A. Energetic and Spectroscopic Properties of the Low-Lying C7H2 Isomers: A High-Level Ab Initio Perspective. Phys. Chem. Chem. Phys. 2017, 19, 17685–17697. [Google Scholar] [CrossRef] [Green Version]
  93. Thimmakondu, V.S.; Karton, A. The Quest for the Carbene Bent-Pentadiynylidene Isomer of C5H2. Chem. Phys. 2018, 515, 411–417. [Google Scholar] [CrossRef]
  94. Thirumoorthy, K.; Viji, M.; Pandey, A.P.; Netke, T.G.; Sekar, B.; Yadav, G.; Deshpande, S.; Thimmakondu, V.S. Many Unknowns Below or Close to the Experimentally Known Cumulene Carbene—A Case Study of C9H2 Isomers. Chem. Phys. 2019, 527, 110496. [Google Scholar] [CrossRef]
  95. Thimmakondu, V.S.; Ulusoy, I.; Wilson, A.K.; Karton, A. Theoretical Studies of Two Key Low-Lying Carbenes of C5H2 Missing in the Laboratory. J. Phys. Chem. A 2019, 123, 6618–6627. [Google Scholar] [CrossRef] [PubMed]
  96. Thimmakondu, V.S. Molecules in Laboratory and in Interstellar Space? In Proceedings of the 71st International Symposium on Molecular Spectroscopy, Urbana, IL, USA, 20–24 June 2016; p. RH05. [Google Scholar]
  97. Tsipis, A.C.; Depastas, I.G.; Tsipis, C.A. Diagnosis of the σ-, π-and (σ+ π)-Aromaticity by the Shape of the NICSzz-Scan Curves and Symmetry-Based Selection Rules. Symmetry 2010, 2, 284–319. [Google Scholar] [CrossRef]
  98. Furukawa, S.; Fujita, M.; Kanatomi, Y.; Minoura, M.; Hatanaka, M.; Morokuma, K.; Ishimura, K.; Saito, M. Double Aromaticity Arising From σ- and π-Rings. Commun. Chem. 2018, 1, 60. [Google Scholar] [CrossRef] [Green Version]
  99. Kalita, A.J.; Rohman, S.S.; Kashyap, C.; Ullah, S.S.; Guha, A.K. Double Aromaticity in a BBe6 H 6 + Cluster with A Planar Hexacoordinate Boron Structure. Chem. Commun. 2020, 56, 12597–12599. [Google Scholar] [CrossRef] [PubMed]
  100. Lee, T.J.; Taylor, P.R. A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods. Int. J. Quantum Chem. 1989, 36, 199–207. [Google Scholar] [CrossRef] [Green Version]
  101. Petrie, S.; Herbst, E. Some Interstellar Reactions Involving Electrons and Neutral Species: Attachment and Isomerization. Astrophys. J. 1997, 491, 210–215. [Google Scholar] [CrossRef]
  102. Zhang, Y.; Xu, X.; Goddard, W.A. Doubly Hybrid Density Functional for Accurate Descriptions of Nonbond Interactions, Thermochemistry, and Thermochemical Kinetics. Proc. Natl. Acad. Sci. USA 2009, 106, 4963–4968. [Google Scholar] [CrossRef] [Green Version]
  103. Zhang, I.Y.; Wu, J.; Xu, X. Extending the Reliability and Applicability of B3LYP. Chem. Commun. 2010, 46, 3057–3070. [Google Scholar] [CrossRef] [Green Version]
  104. Grimme, S. Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [Green Version]
  105. Grimme, S.; Neese, F. Double-Hybrid Density Functional Theory for Excited Electronic States of Molecules. J. Chem. Phys. 2007, 127, 154116. [Google Scholar] [CrossRef] [PubMed]
  106. Beyer, T.; Swinehart, D.F. Algorithm 448: Number of Multiply-Restricted Partitions. Commun. ACM 1973, 16, 379. [Google Scholar] [CrossRef]
Chemistry 03 00002 g001 550
Figure 1. Eighteen low-lying isomers of Si 2 C 5 H 2 currently considered on the singlet PES. Relative energies including ZPVE correction (in kcal mol − 1 ) and dipole moments (in Debye) are calculated at the fc-CCSD(T)/cc-pVTZ level of theory. Isomers identified by search algorithms are marked with an asterisk symbol. All the isomers depicted here are minima and all of them remain elusive in the laboratory to date.
Figure 1. Eighteen low-lying isomers of Si 2 C 5 H 2 currently considered on the singlet PES. Relative energies including ZPVE correction (in kcal mol − 1 ) and dipole moments (in Debye) are calculated at the fc-CCSD(T)/cc-pVTZ level of theory. Isomers identified by search algorithms are marked with an asterisk symbol. All the isomers depicted here are minima and all of them remain elusive in the laboratory to date.
Chemistry 03 00002 g001
Chemistry 03 00002 g002 550
Figure 2. Atom numbering scheme, valence structures, and key occupied molecular orbitals of isomer 1. Natural atomic charges (in a.u) calculated at the B3LYP/6-311++G(2d,2p) level of theory are also shown.
Figure 2. Atom numbering scheme, valence structures, and key occupied molecular orbitals of isomer 1. Natural atomic charges (in a.u) calculated at the B3LYP/6-311++G(2d,2p) level of theory are also shown.
Chemistry 03 00002 g002
Chemistry 03 00002 g003 550
Figure 3. Schematic outline of the dissociation pathways of Si 2 C 5 H 2 global minimum isomer (1) with a ptC atom. ZPVE-corrected relative energies are calculated at the B3LYP/6-311++G(2d,2p) level of theory. Gibbs free energy corrected values (at 298.15 K) are given in red color.
Figure 3. Schematic outline of the dissociation pathways of Si 2 C 5 H 2 global minimum isomer (1) with a ptC atom. ZPVE-corrected relative energies are calculated at the B3LYP/6-311++G(2d,2p) level of theory. Gibbs free energy corrected values (at 298.15 K) are given in red color.
Chemistry 03 00002 g003
Chemistry 03 00002 g004 550
Figure 4. Schematic outline of the isomerization pathway of isomer 1 to 2 of Si 2 C 5 H 2 . ZPVE-corrected relative energies are calculated at the B3LYP/6-311++G(2d,2p) level of theory. Gibbs free energy corrected values (at 298.15 K) are given in red color. Negative barrier between 21 and TS-7 is due to ZPVE-corrections. Activation energy ( Δ E * ) for the latter route without ZPVE-corrections is 66.96 kcal mol − 1 (see Section 3.3 for further discussion).
Figure 4. Schematic outline of the isomerization pathway of isomer 1 to 2 of Si 2 C 5 H 2 . ZPVE-corrected relative energies are calculated at the B3LYP/6-311++G(2d,2p) level of theory. Gibbs free energy corrected values (at 298.15 K) are given in red color. Negative barrier between 21 and TS-7 is due to ZPVE-corrections. Activation energy ( Δ E * ) for the latter route without ZPVE-corrections is 66.96 kcal mol − 1 (see Section 3.3 for further discussion).
Chemistry 03 00002 g004
Chemistry 03 00002 g005 550
Figure 5. Rate co-efficient for the forward ( k 1 ; 1 to 4) and reverse ( k − 1 ; 4 to 1) isomerization reaction.
Figure 5. Rate co-efficient for the forward ( k 1 ; 1 to 4) and reverse ( k − 1 ; 4 to 1) isomerization reaction.
Chemistry 03 00002 g005
Chemistry 03 00002 g006 550
Figure 6. Calculated equilibrium constant for the isomerization reaction of isomers 1 and 4.
Figure 6. Calculated equilibrium constant for the isomerization reaction of isomers 1 and 4.
Chemistry 03 00002 g006
Table
Table 1. Optimal geometry parameters (Å and degrees) of isomer 1 of Si 2 C 5 H 2 calculated at different levels.
Table 1. Optimal geometry parameters (Å and degrees) of isomer 1 of Si 2 C 5 H 2 calculated at different levels.
ParameterB3LYPCCSDCCSD(T)CCSDCCSD(T)CCSD(T)
6-311++G(2d,2p)cc-pVDZcc-pVTZcc-pwCVTZ
R(C 1 Si 4 ;C 1 Si 5 )1.92901.95491.96121.91771.92381.9081
R(C 1 C 2 ;C 1 C 3 )1.46791.47771.48751.46771.47811.4727
R(C 2 Si 4 ;C 3 Si 5 )1.75061.76791.78031.74881.76121.7475
R(C 2 C 6 ;C 3 C 7 )1.41791.43791.43931.42281.42441.4197
R(C 6 C 7 )1.38131.39141.39931.37921.38761.3832
R(C 6 H 8 ;C 7 H 9 )1.08001.09461.09681.07961.08201.0806
θ (C 2 C 1 C 3 )104.00104.49104.21104.44104.11104.10
θ (C 2 C 1 Si 4 ;C 3 C 1 Si 5 )60.2460.1060.3260.4960.6960.64
θ (C 1 C 2 C 6 ;C 1 C 3 C 7 )108.81108.57108.66108.48108.60108.63
θ (C 2 C 6 H 8 ;C 3 C 7 H 9 )124.87124.82124.78124.71124.67124.69
Table
Table 2. Harmonic vibrational frequencies, IR Intensities, and isotopic shifts of isomer 1 calculated at the ae-CCSD(T)/cc-pwCVTZ level of theory.
Table 2. Harmonic vibrational frequencies, IR Intensities, and isotopic shifts of isomer 1 calculated at the ae-CCSD(T)/cc-pwCVTZ level of theory.
ModeIsomer 1Isotopic Shifts (cm − 1 )
SymmetryFrequencyIntensity 28 Si– 29 Si 12 C– 13 C 1 H– 2 D
cm − 1 km mol − 1 Si(4)  a 29 Si 2 C 5 H 2 C(1)C(2)C(6)Si 2 13 C 5 H 2 H(8)Si 2 C 5 D 2
1 a 2 195.20.00.40.70.01.91.05.44.37.7
2 b 1 219.414.70.30.63.91.00.36.63.58.0
3 a 1 232.82.01.83.60.60.10.11.10.10.3
4 b 2 427.7106.70.71.43.34.01.012.77.914.9
5 b 2 513.217.82.95.70.60.32.76.65.89.8
6 a 2 576.70.00.00.00.05.35.019.037.656.1
7 b 1 606.80.00.00.010.64.70.322.94.426.7
8 a 1 616.043.62.65.45.32.01.411.54.811.0
9 a 1 787.90.90.61.15.95.26.927.485.0118.1
10 b 1 829.820.60.00.00.00.53.27.350.676.7
11 b 2 887.00.10.10.12.97.18.433.043.5125.1
12 a 2 915.70.00.00.00.00.04.69.433.796.6
13 a 1 991.330.40.00.116.59.20.136.6104.1142.1
14 b 2 1004.517.30.30.721.10.83.532.49.490.5
15 a 1 1103.82.30.00.00.11.73.811.280.299.1
16 b 2 1272.813.30.40.72.29.31.619.354.5171.6
17 a 1 1340.048.50.61.20.017.95.648.69.924.1
18 a 1 1461.54.20.00.00.01.624.547.223.245.3
19 b 2 1484.78.60.30.60.811.18.149.113.528.7
20 b 2 3208.92.00.00.00.00.06.49.9825.3841.2
21 a 1 3227.921.10.00.00.00.04.311.49.4828.5
a TDue to symmetry, Si(4) and Si(5); C(2) and C(3); C(6) and C(7); H(8) and H(9) are equivalent.
Table
Table 3. Dissociation pathways of Si 2 C 5 H 2 isomers (1 and 2) and their corresponding activation energies ( Δ E ‡ ) and reaction energies ( Δ E r ) computed at the B3LYP/6-311++G(2d,2p) level of theory.
Table 3. Dissociation pathways of Si 2 C 5 H 2 isomers (1 and 2) and their corresponding activation energies ( Δ E ‡ ) and reaction energies ( Δ E r ) computed at the B3LYP/6-311++G(2d,2p) level of theory.
IsomerDissociation Δ E ‡ , a Δ E r b Δ E 0 c
Pathwaykcal mol − 1 kcal mol − 1 kcal mol − 1
1A64.05 (TS-1;TS-2)54.64 (20)0.00
B30.51 (TS-3)18.80 (4)22.76
C61.85 (TS-4)43.03 (19)– d
D71.45 (TS-5)64.36 (22)– d
68.94 (TS-6)63.35 (21)– d
62.71 (TS-7)17.53 (2)21.39
a The dissociation pathway leading to the corresponding transition state(s) is (are) given in parenthesis. b The dissociation pathway leading to the corresponding product is given in parenthesis. The reaction path is confirmed by IRC calculations. c ZPVE-corrected relative energies of the final product calculated at the fc-CCSD(T)/cc-pVTZ level of theory. In pathway A, the final product is 1 and not isomer 20. d Not calculated at this level of theory.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Thirumoorthy, K.; Chandrasekaran, V.; Cooksy, A.L.; Thimmakondu, V.S. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry 2021, 3, 13-27. https://doi.org/10.3390/chemistry3010002

AMA Style

Thirumoorthy K, Chandrasekaran V, Cooksy AL, Thimmakondu VS. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry. 2021; 3(1):13-27. https://doi.org/10.3390/chemistry3010002

Chicago/Turabian Style

Thirumoorthy, Krishnan, Vijayanand Chandrasekaran, Andrew L. Cooksy, and Venkatesan S. Thimmakondu. 2021. "Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom" Chemistry 3, no. 1: 13-27. https://doi.org/10.3390/chemistry3010002

APA Style

Thirumoorthy, K., Chandrasekaran, V., Cooksy, A. L., & Thimmakondu, V. S. (2021). Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry, 3(1), 13-27. https://doi.org/10.3390/chemistry3010002

Article Metrics

Back to TopTop