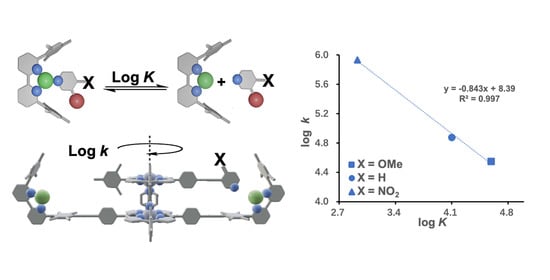
Exchange Speed of Four-Component Nanorotors Correlates with Hammett Substituent Constants †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. Determination of Binding Constants
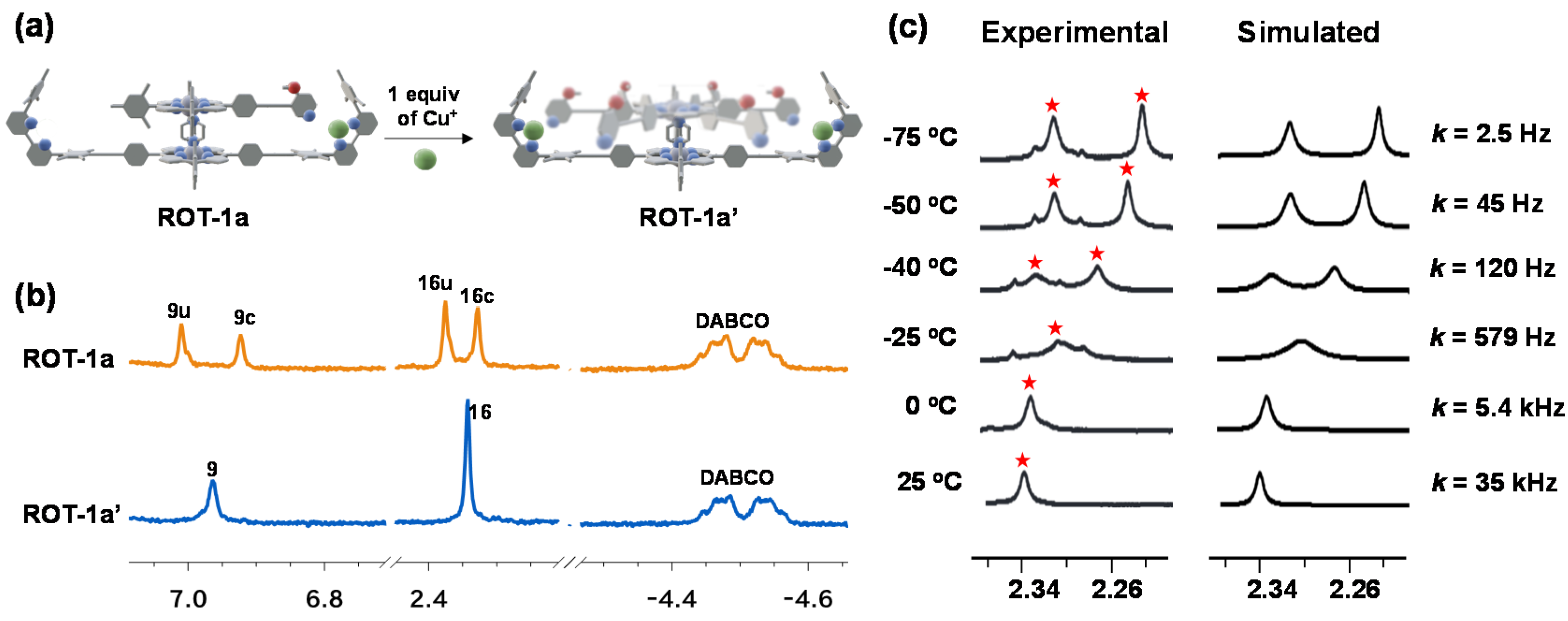
2.3. NMR Simulation
3. Results
3.1. Design
3.2. Synthesis and Characterization of Four-Component Nanorotors
4. Discussion
4.1. Bipyridine vs. Phenanthroline Stator in Nanorotors
4.2. Hammett Equation Applies to Rotational Exchange in Nanorotors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yoshida, M.; Muneyuki, E.; Hisabori, T. ATP synthase-a marvelous rotary engine of the cell. Nat. Rev. Mol. Cell Biol. 2001, 3, 669–677. [Google Scholar] [CrossRef]
- Schliwa, M.; Woehlke, G. Molecular motors. Nature 2003, 422, 759–765. [Google Scholar] [CrossRef]
- Sowa, Y.; Berry, R.M. Bacterial Flagellar Motor. Q. Rev. Biophys. 2008, 41, 103–132. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Nasr, M.; Kim, Y.; Matthews, H.R. Genistein Inhibits Protein Histidine Kinase. J. Biol. Chem. 1992, 267, 15511–15515. [Google Scholar]
- Kassem, S.; van Leeuwen, T.; Lubbe, A.S.; Wilson, M.R.; Feringa, B.L.; Leigh, D.A. Artificial molecular motors. Chem. Soc. Rev. 2017, 46, 2592–2621. [Google Scholar] [CrossRef] [Green Version]
- Lubbe, A.S.; van Leeuwen, T.; Wezenberg, S.J.; Feringa, B.L. Designing dynamic functional molecular systems. Tetrahedron 2017, 73, 4837–4848. [Google Scholar] [CrossRef]
- Dattler, D.; Fuks, G.; Heiser, J.; Moulin, E.; Perrot, A.; Yao, X.; Giuseppone, N. Design of Collective Motions from Synthetic Molecular Switches, Rotors, and Motors. Chem. Rev. 2020, 120, 310–433. [Google Scholar] [CrossRef] [Green Version]
- Erbas-Cakmak, S.; Fielden, S.D.P.; Karaca, U.; Leigh, D.A.; McTernan, C.T.; Tetlow, D.J.; Wilson, M.R. Rotary and linear molecular motors driven by pulses of a chemical fuel. Science 2017, 358, 340–343. [Google Scholar] [CrossRef] [Green Version]
- Uhl, E.; Thumser, S.; Mayer, P.; Dube, H. Transmission of Unidirectional Molecular Motor Rotation to a Remote Biaryl Axis. Angew. Chem. Int. Ed. 2018, 57, 11064–11068. [Google Scholar] [CrossRef]
- Pezzato, C.; Nguyen, M.T.; Kim, D.J.; Anamimoghadam, O.; Mosca, L.; Stoddart, J.F. Controlling dual molecular pumps electrochemically. Angew. Chem. Int. Ed. 2018, 57, 9325–9329. [Google Scholar] [CrossRef]
- Pfeifer, L.; Scherübl, M.; Fellert, M.; Danowski, W.; Cheng, J.; Pol, J.; Feringa, B.L. Photoefficient 2nd generation molecular motors responsive to visible light. Chem. Sci. 2019, 10, 8768–8773. [Google Scholar] [CrossRef] [Green Version]
- Rapenne, G. Synthesis of technomimetic molecules: Towards rotation control in single-molecular machines and motors. Org. Biomol. Chem. 2005, 3, 1165–1169. [Google Scholar] [CrossRef]
- Michl, J.; Sykes, E.C.H. Molecular rotors and motors: Recent advances and future challenges. ACS Nano 2009, 3, 1042–1048. [Google Scholar] [CrossRef]
- Zhao, K.; Dron, P.I.; Kaleta, J.; Rogers, C.T.; Michl, J. Arrays of dipolar molecular rotors in Tris(o-phenylenedioxy) cyclotriphosphazene. Top. Curr. Chem. 2014, 354, 163–211. [Google Scholar] [CrossRef]
- Takara, Y.; Kusamoto, T.; Masui, T.; Nishikawa, M.; Kume, S.; Nishihara, H. A single-molecular twin rotor: Correlated motion of two pyrimidine rings coordinated to copper. Chem. Commun. 2015, 51, 2896–2898. [Google Scholar] [CrossRef]
- Godde, B.; Jouaiti, A.; Fluck, A.; Kyritsakas, N.; Mauro, M.; Hosseini, M.W. Symmetrical or non-symmetrical luminescent turnstiles based on hydroquinone stators and rotors bearing pyridyl or p-dimethylaminopyridyl coordinating units. Dalton Trans. 2017, 46, 14897–14906. [Google Scholar] [CrossRef]
- Lee, S.-C.; Heo, J.; Woo, H.C.; Lee, J.-A.; Seo, Y.H.; Lee, C.-L.; Kim, S.; Kwon, O.-P. Fluorescent Molecular Rotors for Viscosity Sensors. Chem. Eur. J. 2018, 24, 13706–13718. [Google Scholar] [CrossRef]
- Ogi, S.; Ikeda, T.; Wakabayashi, R.; Shinkai, S.; Takeuchi, M. A bevel-gear-shaped rotor bearing a double-decker porphyrin complex. Chem. Eur. J. 2010, 16, 8285–8290. [Google Scholar] [CrossRef]
- Frantz, D.K.; Linden, A.; Baldridge, K.K.; Siegel, J.S. Molecular spur gears comprising triptycene rotators and bibenzimidazole-based stators. J. Am. Chem. Soc. 2012, 134, 1528–1535. [Google Scholar] [CrossRef]
- Sanada, K.; Ube, H.; Shionoya, M. Rotational control of a dirhodium-centered supramolecular four-gear system by ligand exchange. J. Am. Chem. Soc. 2016, 138, 2945–2948. [Google Scholar] [CrossRef]
- Nakamura, M.; Kishimoto, K.; Kobori, Y.; Abe, T.; Yoza, K.; Kobayashi, K. Self-Assembled Molecular Gear: A 4:1 Complex of Rh(III)Cl Tetraarylporphyrin and Tetra(p-pyridyl)cavitand. J. Am. Chem. Soc. 2016, 138, 12564–12577. [Google Scholar] [CrossRef]
- Cheng, C.; McGonigal, P.R.; Schneebeli, S.T.; Li, H.; Vermeulen, N.A.; Ke, C.; Stoddart, J.F. An artificial molecular pump. Nat. Nanotechnol. 2015, 10, 547–553. [Google Scholar] [CrossRef]
- Ragazzon, G.; Baroncini, M.; Silvi, S.; Venturi, M.; Credi, A. Light-powered autonomous and directional molecular motion of a dissipative self-assembling system. Nat. Nanotechnol. 2015, 10, 70–75. [Google Scholar] [CrossRef]
- Cai, K.; Shi, Y.; Zhuang, G.; Qiu, Y.; Shen, D.; Stoddart, J.F. Molecular-Pump-Enabled Synthesis of a Daisy Chain Polymer. J. Am. Chem. Soc. 2020, 142, 10308–10313. [Google Scholar] [CrossRef]
- von Delius, M.; Geertsema, E.M.; Leigh, D.A. A synthetic small molecule that can walk down a track. Nat. Chem. 2010, 2, 96–101. [Google Scholar] [CrossRef]
- Qu, D.-H.; Tian, H. Synthetic small-molecule walkers at work. Chem. Sci. 2013, 4, 3031–3035. [Google Scholar] [CrossRef]
- Liu, M.; Cheng, J.; Tee, S.R.; Sreelatha, S.; Loh, I.Y.; Wang, Z. Biomimetic Autonomous Enzymatic Nanowalker of High Fuel Efficiency. ACS Nano 2016, 10, 5882–5890. [Google Scholar] [CrossRef]
- Liu, S.; Kondratuk, D.V.; Rousseaux, S.A.L.; Gil-Ramírez, G.; O’Sullivan, M.C.; Cremers, J.; Claridge, T.D.W.; Anderson, H.L. Caterpillar track complexes in template-directed synthesis and correlated molecular motion. Angew. Chem. Int. Ed. 2015, 54, 5355–5359. [Google Scholar] [CrossRef] [Green Version]
- Hiraoka, S.; Hisanaga, Y.; Shiro, M.; Shionoya, M. A molecular double ball bearing: An Ag(I)-Pt(II) dodecanuclear quadruple-decker complex with three rotors. Angew. Chem. Int. Ed. 2010, 49, 1669–1673. [Google Scholar] [CrossRef]
- Kai, H.; Nara, S.; Kinbara, K.; Aida, T. Toward long-distance mechanical communication: Studies on a ternary complex interconnected by a bridging rotary module. J. Am. Chem. Soc. 2008, 130, 6725–6727. [Google Scholar] [CrossRef]
- Ferris, D.P.; Zhao, Y.L.; Khashab, N.M.; Khatib, H.A.; Stoddart, J.F.; Zink, J.I. Light-operated mechanized nanoparticles. J. Am. Chem. Soc. 2009, 131, 1686–1688. [Google Scholar] [CrossRef]
- Goswami, A.; Saha, S.; Biswas, P.K.; Schmittel, M. (Nano)mechanical Motion Triggered by Metal Coordination. Chem. Rev. 2020, 120, 125–199. [Google Scholar] [CrossRef]
- Isaac, N.S. Physical Organic Chemistry, 2nd ed.; Pearson: Essex, UK, 1995. [Google Scholar]
- Ashton, P.R.; Fyfe, M.C.T.; Hickingbottom, S.K.; Fraser Stoddart, J.; White, A.J.P.; Williams, D.J. Hammett correlations ‘beyond the molecule’. J. Chem. Soc. Perkin Trans. 1998, 2, 2117–2128. [Google Scholar] [CrossRef]
- Schultz, D.; Nitschke, J.R. Designing multistep transformations using the Hammett equation: Imine exchange on a copper(I) template. J. Am. Chem. Soc. 2006, 128, 9887–9892. [Google Scholar] [CrossRef]
- Schmidt, J.; Schmidt, R.; Würthner, F. Synthesis, optical properties, and LFER analysis of solvent-dependent binding constants of Hamilton-receptor-connected merocyanine chromophores. J. Org. Chem. 2008, 73, 6355–6362. [Google Scholar] [CrossRef]
- Biswas, P.K.; Saha, S.; Paululat, T.; Schmittel, M. Rotating Catalysts Are Superior: Suppressing Product Inhibition by Anchimeric Assistance in Four-Component Catalytic Machinery. J. Am. Chem. Soc. 2018, 140, 9038–9041. [Google Scholar] [CrossRef]
- Samanta, S.K.; Schmittel, M. Four-component supramolecular nanorotors. J. Am. Chem. Soc. 2013, 135, 18794–18797. [Google Scholar] [CrossRef]
- Biswas, P.K.; Saha, A.; Gaikwad, S.; Schmittel, M. Reversible Multicomponent AND Gate Triggered by Stoichiometric Chemical Pulses Commands the Self-Assembly and Actuation of Catalytic Machinery. J. Am. Chem. Soc. 2020, 142, 7889–7897. [Google Scholar] [CrossRef]
- Samanta, S.K.; Bats, J.W.; Schmittel, M. A five-component nanorotor with speed regulation. Chem. Commun. 2014, 50, 2364–2366. [Google Scholar] [CrossRef]
- Samanta, S.K.; Rana, A.; Schmittel, M. Conformational Slippage Determines Rotational Frequency in Five-Component Nanorotors. Angew. Chem. Int. Ed. 2016, 55, 2267–2272. [Google Scholar] [CrossRef]
- Biswas, P.K.; Saha, S.; Nanaji, Y.; Rana, A.; Schmittel, M. Influence of Rotator Design on the Speed of Self-Assembled Four-Component Nanorotors: Coordinative Versus Dispersive Interactions. Inorg. Chem. 2017, 56, 6662–6670. [Google Scholar] [CrossRef]
- Saha, S.; Biswas, P.K.; Schmittel, M. Reversible Interconversion of a Static Metallosupramolecular Cage Assembly into a High-Speed Rotor: Stepless Adjustment of Rotational Exchange by Nucleophile Addition. Inorg. Chem. 2019, 58, 3466–3472. [Google Scholar] [CrossRef]
- Hammett, L.P. Some Relations Between Reaction Rates and Equilibrium Constants. Chem. Rev. 1935, 17, 125–136. [Google Scholar] [CrossRef]
- Wells, P.R. Linear Free Energy Relationships. Chem. Rev. 1963, 63, 171–219. [Google Scholar] [CrossRef]
- Schmittel, M.; Ganz, A.; Schenk, W.A.; Hagel, M. Synthesis and Coordination Properties of 6,6’-Dimesityl-2,2’-bipyridine. Z. Naturforsch. B 1999, 54b, 559–563. [Google Scholar] [CrossRef]
- Gampp, H.; Maeder, M.; Meyer, C.J.; Zuberbühler, A.D. Calculation of Equilibrium Constants From Multiwavelength Spectroscopic data-IV Model-free Least-Squares Refinement by Use of Evolving Factor Analysis. Talanta 1986, 33, 943. [Google Scholar] [CrossRef]
- Reich, H.J. WinDNMR: Dynamic NMR Spectra for Windows. J. Chem. Educ. 1995, 72, 1086. [Google Scholar] [CrossRef] [Green Version]
- Eyring, H.L. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107. [Google Scholar] [CrossRef]
- Neogi, S.; Schnakenburg, G.; Lorenz, Y.; Engeser, M.; Schmittel, M. Implications of Stoichio metry-Controlled Structural Changeover between Heteroleptic Trigonal [Cu(phenAr2)(py)2]+ Motifs for Solution and Solid-State Supramolecular Self-Assembly. Inorg. Chem. 2012, 51, 10832–10841. [Google Scholar] [CrossRef]
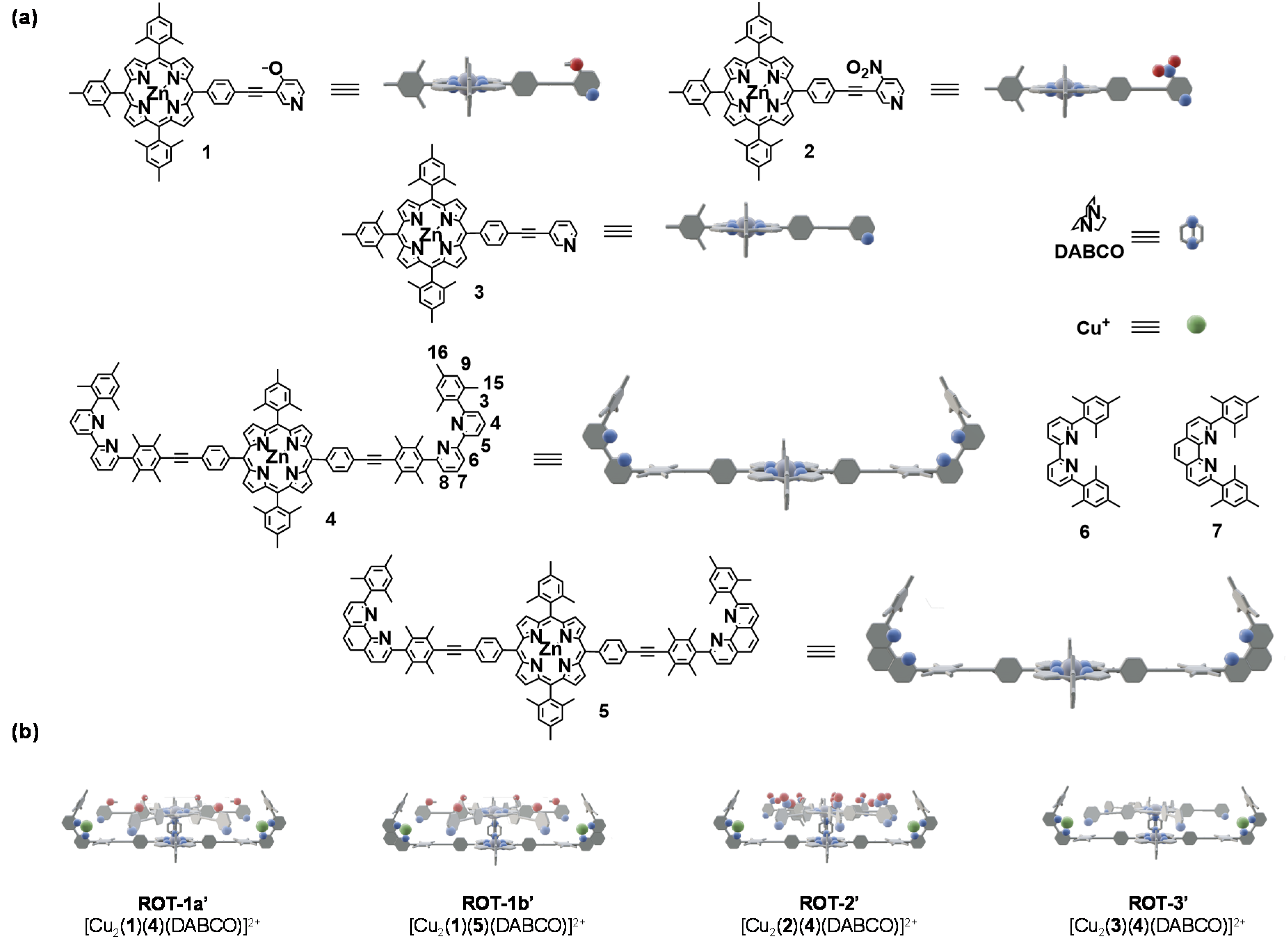
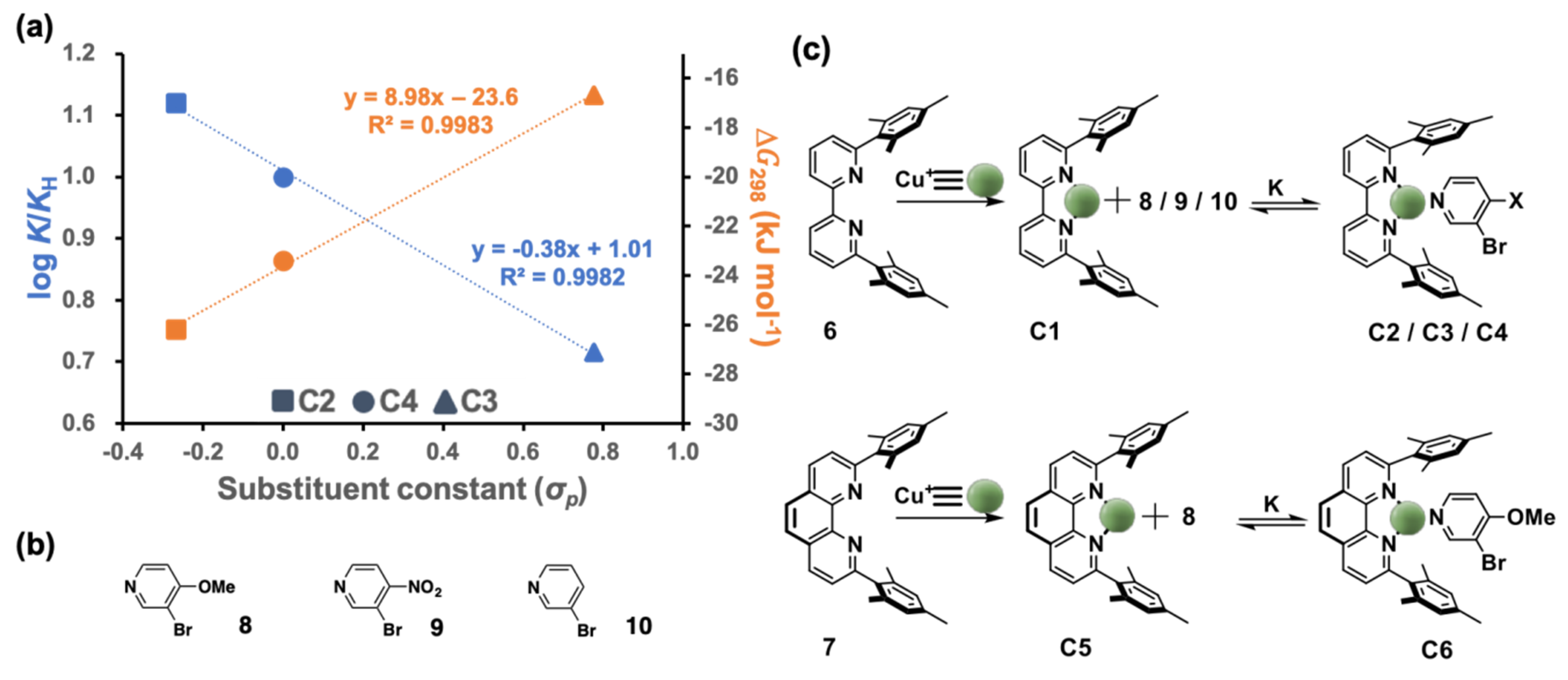



| Motifs | 4-X a | σp | log K | ΔG298 (kJ mol−1) |
|---|---|---|---|---|
| C2 = [Cu(6)(8)]+ | OMe | −0.268 | 4.59 | −26.2 |
| C3 = [Cu(6)(9)]+ | NO2 | 0.778 | 2.93 | −16.7 |
| C4 = [Cu(6)(10)]+ | H | 0.000 | 4.10 | −23.4 |
| C6 = [Cu(7)(8)]+ | OMe | −0.268 | 4.63 | −26.4 |
| Nanorotor | 4-X | ΔG‡298 (kJ mol−1) | k298 (Hz) | log k |
|---|---|---|---|---|
| ROT-1a’ | 4-OMe | 47.1 | 3.5 × 104 | 4.55 |
| ROT-1b’ | 4-OMe | 48.6 | 2.0 × 104 | 4.30 |
| ROT-2′ | 4-NO2 | 39.2 | 8.4 × 105 | 5.93 |
| ROT-3′ | 4-H | 45.2 | 7.7 × 104 | 4.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-F.; Ghosh, A.; Biswas, P.K.; Saha, S.; Schmittel, M. Exchange Speed of Four-Component Nanorotors Correlates with Hammett Substituent Constants. Chemistry 2021, 3, 116-125. https://doi.org/10.3390/chemistry3010009
Li Y-F, Ghosh A, Biswas PK, Saha S, Schmittel M. Exchange Speed of Four-Component Nanorotors Correlates with Hammett Substituent Constants. Chemistry. 2021; 3(1):116-125. https://doi.org/10.3390/chemistry3010009
Chicago/Turabian StyleLi, Yi-Fan, Amit Ghosh, Pronay Kumar Biswas, Suchismita Saha, and Michael Schmittel. 2021. "Exchange Speed of Four-Component Nanorotors Correlates with Hammett Substituent Constants" Chemistry 3, no. 1: 116-125. https://doi.org/10.3390/chemistry3010009
APA StyleLi, Y.-F., Ghosh, A., Biswas, P. K., Saha, S., & Schmittel, M. (2021). Exchange Speed of Four-Component Nanorotors Correlates with Hammett Substituent Constants. Chemistry, 3(1), 116-125. https://doi.org/10.3390/chemistry3010009