Spatial Contributions to 1H NMR Chemical Shifts of Free-Base Porphyrinoids
Abstract
:1. Introduction
2. Theory
3. Computational Methods
3.1. Electronic and Molecular Structure Calculations
3.2. Magnetic Shielding-Density Calculations
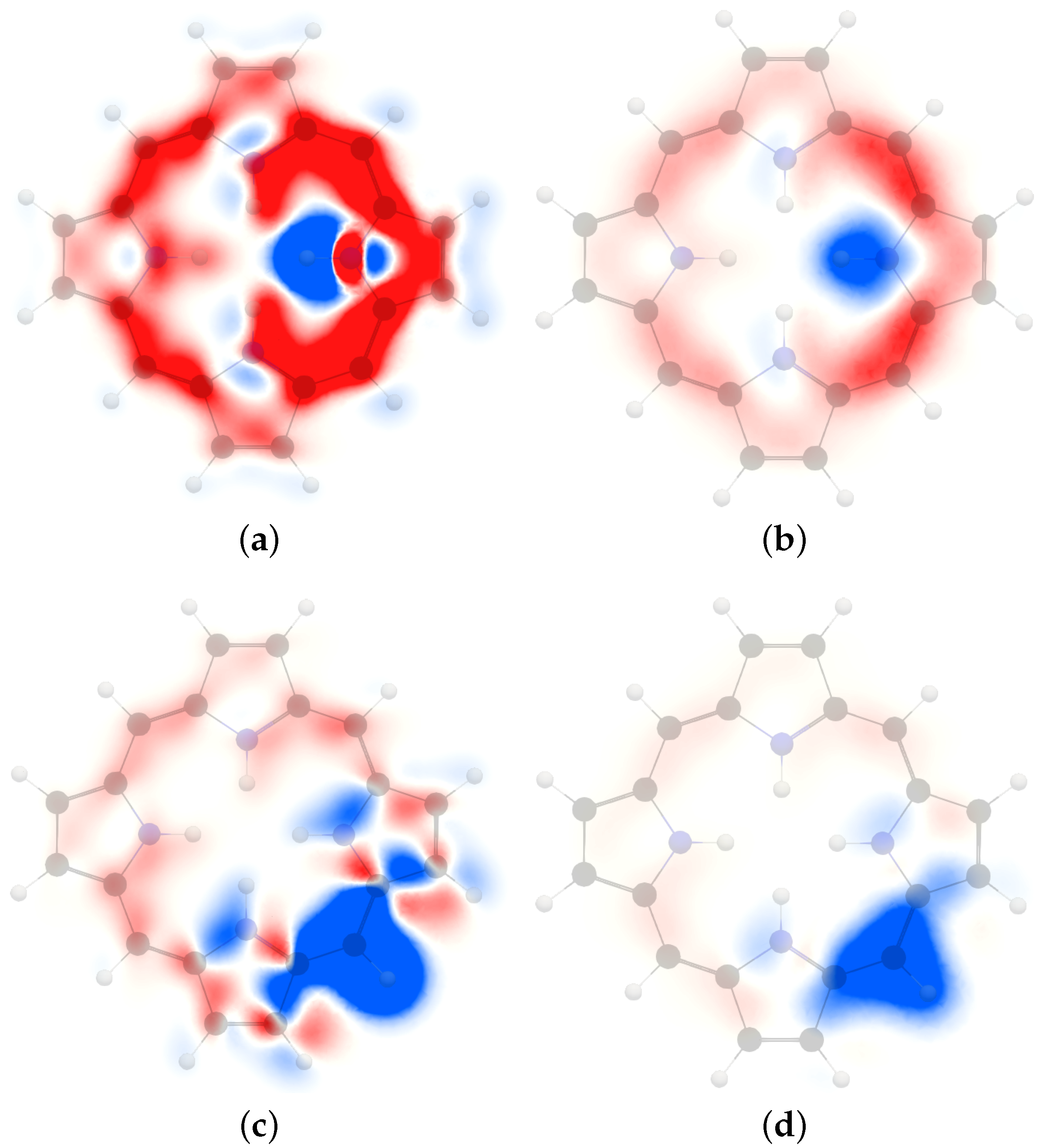
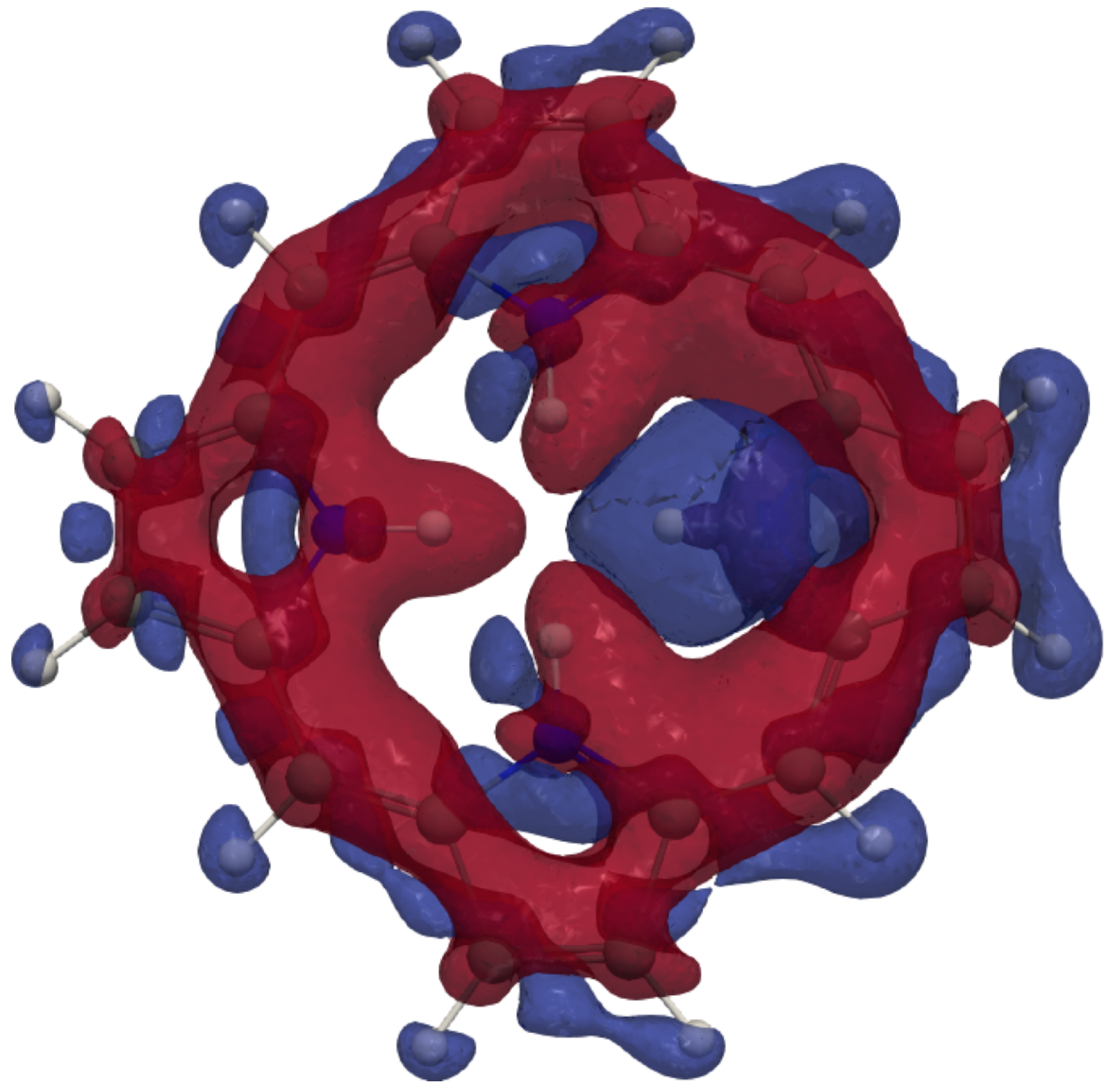
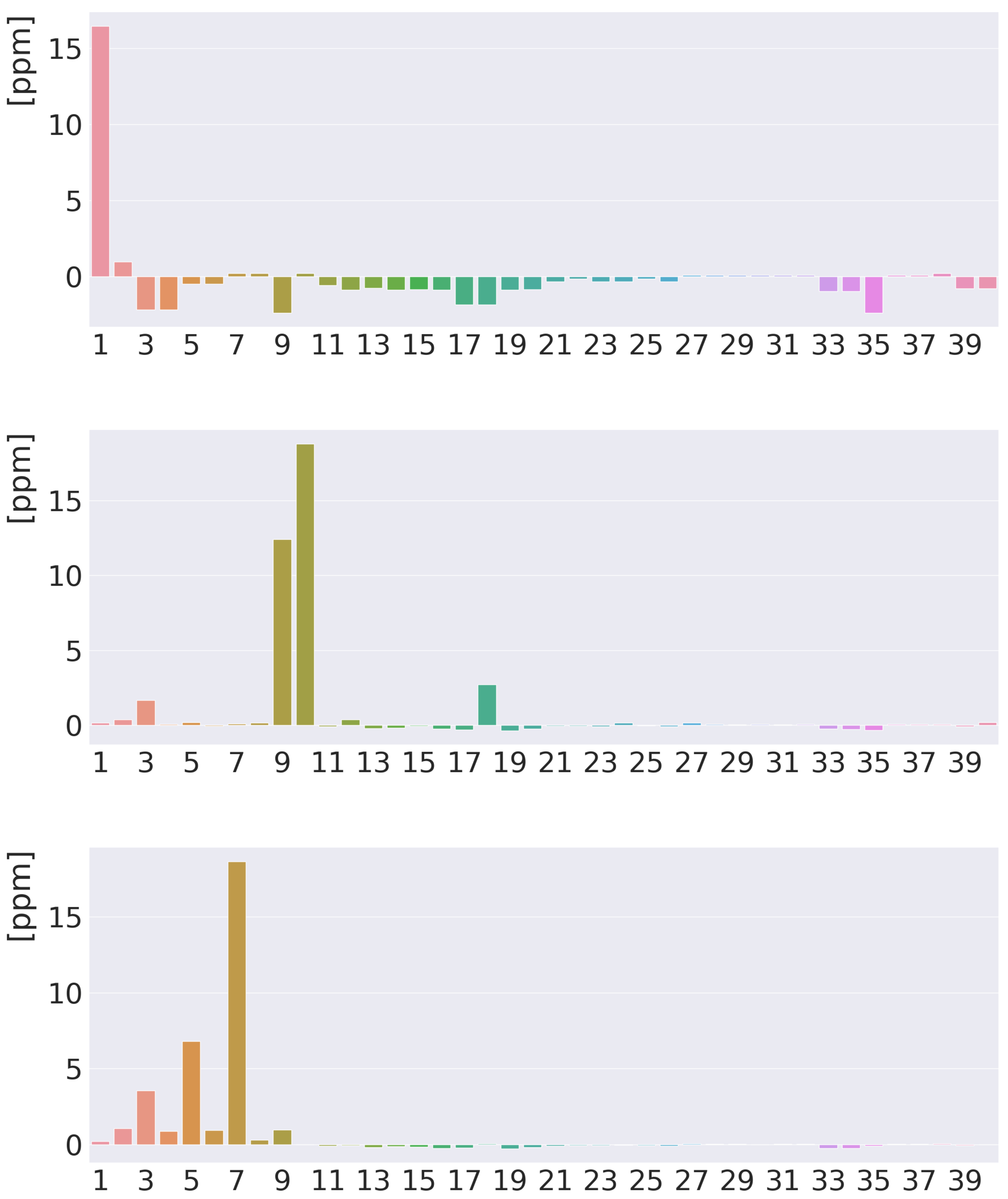
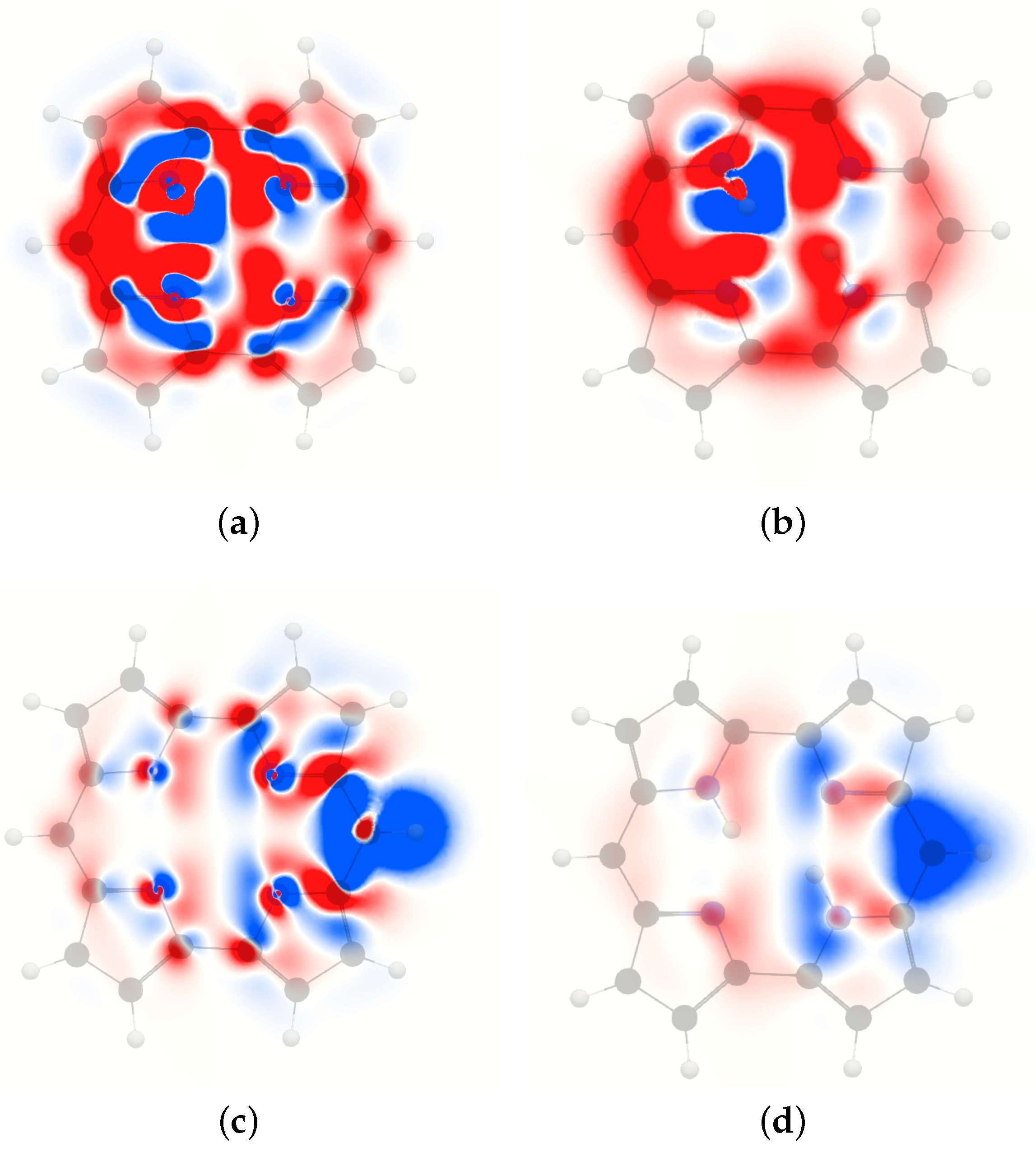
4. Results and Discussion
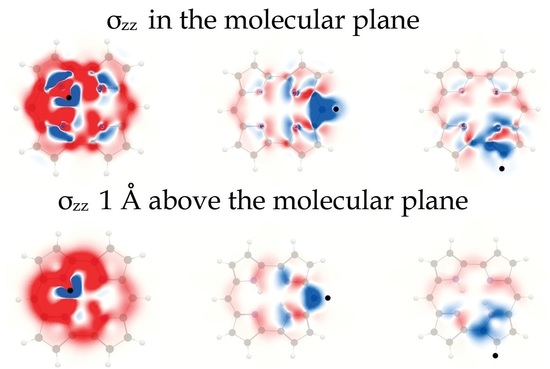
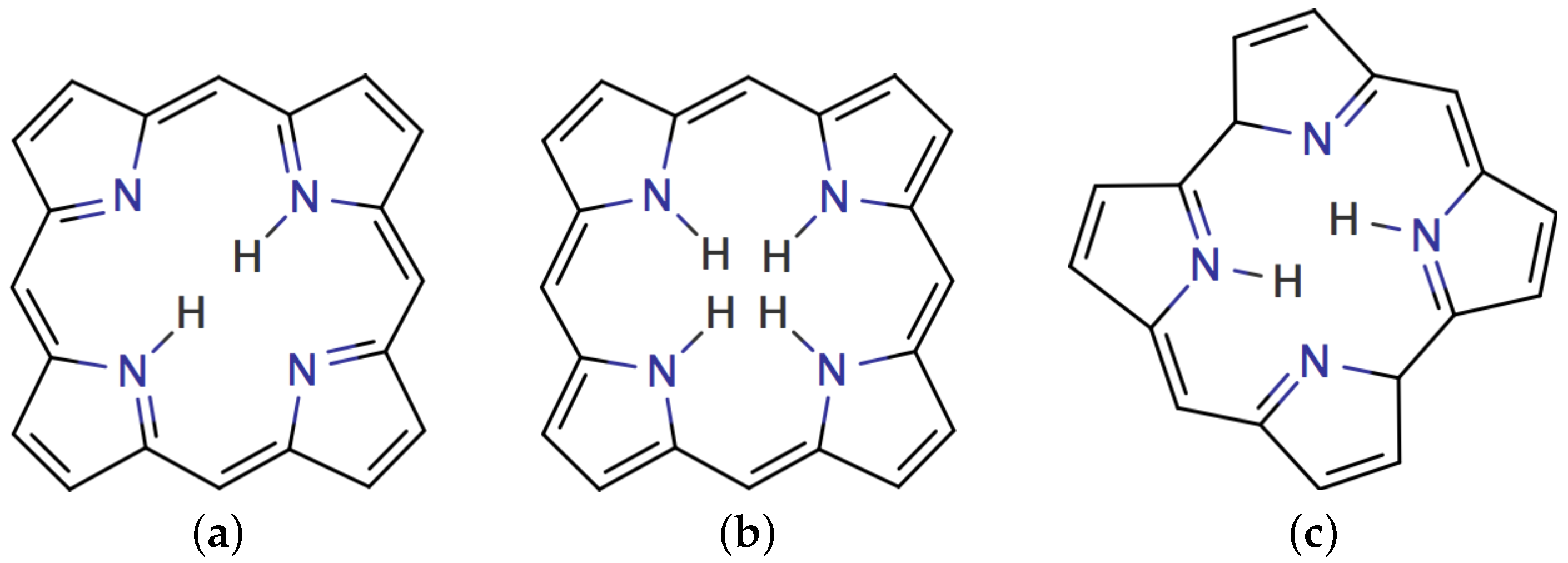
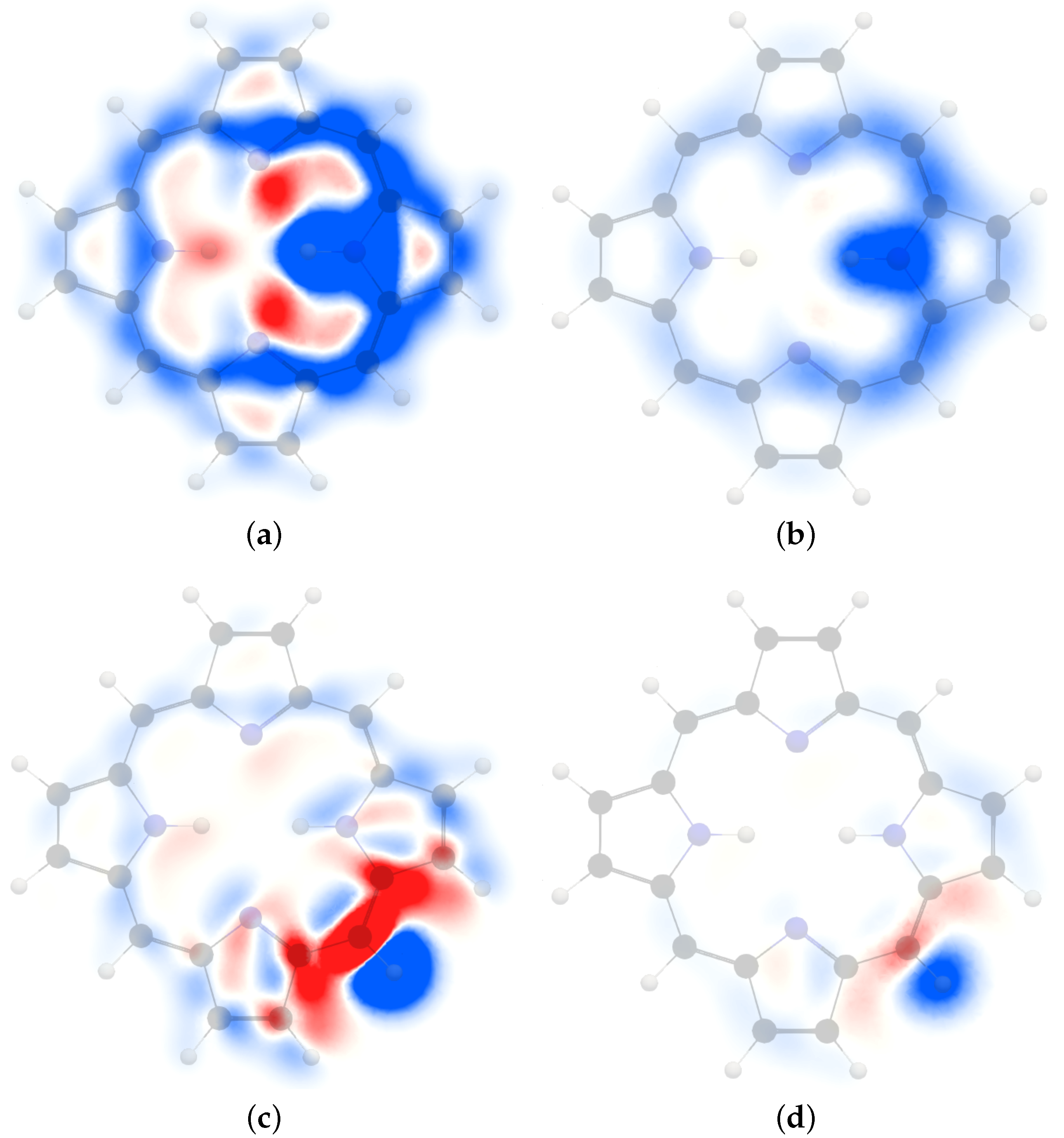
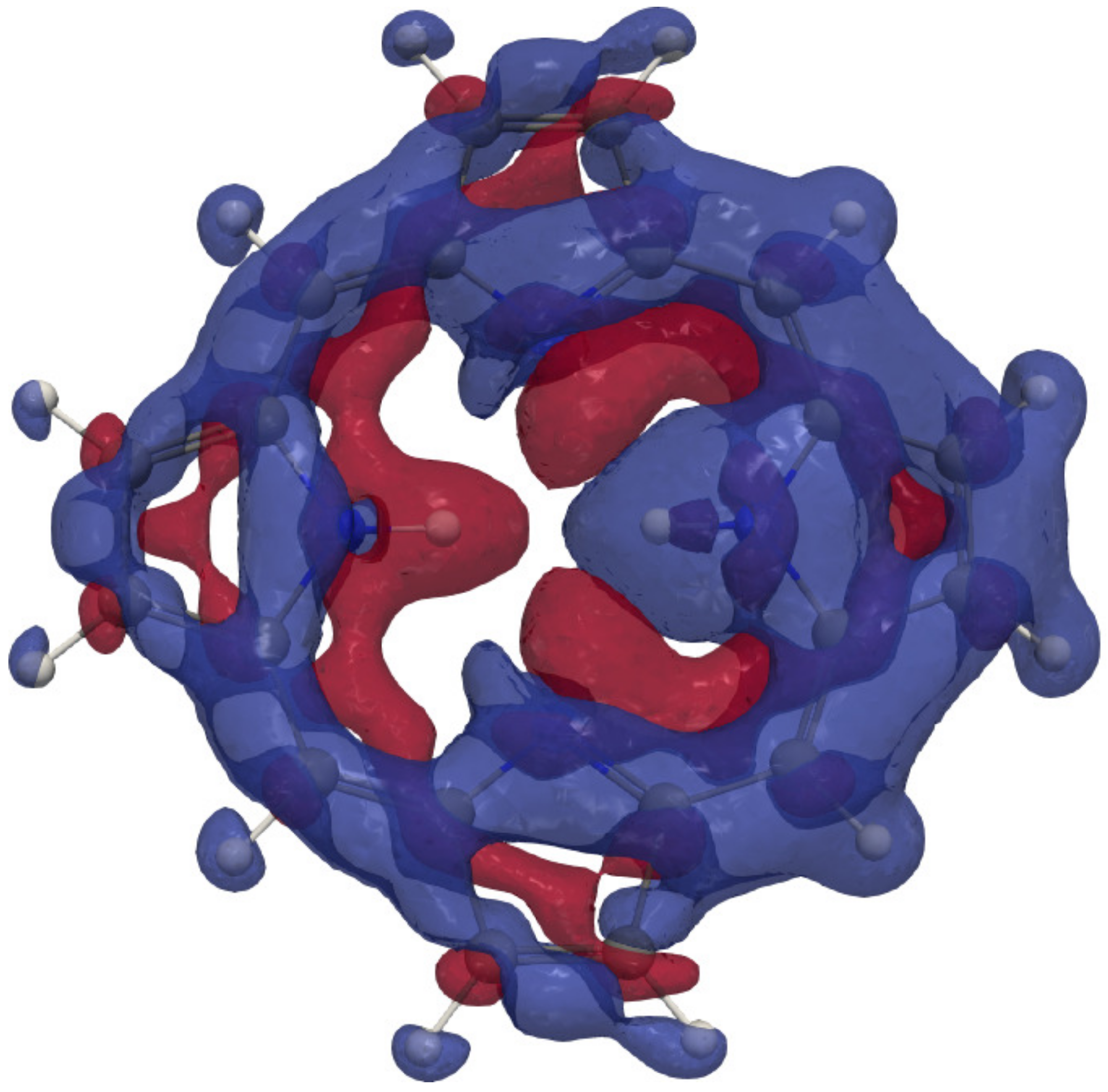
4.1. Free-Base trans-Porphyrin
4.2. Free-Base Isophlorin
4.3. Free-Base trans-Norcorrole
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lazzeretti, P.; Zanasi, R. Inconsistency of the ring-current model for the cyclopropenyl cation. Chem. Phys. Lett. 1981, 80, 533–536. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Malagoli, M.; Zanasi, R. Computational Approach to Molecular Magnetic Properties by Continuous Transformation of the Origin of the Current Density. Chem. Phys. Lett. 1994, 220, 299–304. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Malagoli, M.; Zanasi, R. SYSMO Package; Technical Report on Project ”Sistemi Informatici e Calcolo, Parallelo”; Research Report, 1/67; Additional routines for the evaluation and plotting of current densities by E. Steiner, P.W. Fowler, R.W.A. Havenith, A. Soncini; University of Exeter: Exeter, UK; University of Modena: Modena, Italy; University of Salerno: Rome, Italy, 1991. [Google Scholar]
- Monaco, G.; Summa, F.F.; Zanasi, R. Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems. J. Chem. Inf. Model. 2021, 61, 270–283. [Google Scholar] [CrossRef]
- Jinger, R.K.; Fliegl, H.; Bast, R.; Dimitrova, M.; Lehtola, S.; Sundholm, D. Spatial Contributions to Nuclear Magnetic Shieldings. J. Phys. Chem. A 2021, 125, 1778–1786. [Google Scholar] [CrossRef]
- Jusélius, J.; Sundholm, D. The aromatic pathways of porphins, chlorins and bacteriochlorins. Phys. Chem. Chem. Phys. 2000, 2, 2145–2151. [Google Scholar] [CrossRef] [Green Version]
- Fliegl, H.; Pichierri, F.; Sundholm, D. Antiaromatic Character of 16 π Electron Octaethylporphyrins: Magnetically Induced Ring Currents from DFT-GIMIC Calculations. J. Phys. Chem. A 2015, 119, 2344–2350. [Google Scholar] [CrossRef]
- Valiev, R.R.; Fliegl, H.; Sundholm, D. The aromatic character of thienopyrrole-modified 20π-electronporphyrinoids. Phys. Chem. Chem. Phys. 2014, 16, 11010–11016. [Google Scholar] [CrossRef]
- Pople, J.A. Molecular orbital theory of aromatic ring currents. Mol. Phys. 1958, 1, 175–180. [Google Scholar] [CrossRef]
- McWeeny, R. Ring currents and proton magnetic resonance in aromatic molecules. Mol. Phys. 1958, 1, 311–321. [Google Scholar] [CrossRef]
- von Ragué Schleyer, P.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Klod, S.; Kleinpeter, E. Ab initio calculation of the anisotropy effect of multiple bonds and the ring current effect of arenes-application in conformational and configurational analysis. J. Chem. Soc. Perkin Trans. 2001, 2, 1893–1898. [Google Scholar]
- Merino, G.; Heine, T.; Seifert, G. The Induced Magnetic Field in Cyclic Molecules. Chem. Eur. J. 2004, 10, 4367–4371. [Google Scholar] [CrossRef] [PubMed]
- Stevens, R.M.; Pitzer, R.M.; Lipscomb, W.N. Perturbed Hartree-Fock Calculations. I. Magnetic Susceptibility and Shielding in the LiH Molecule. J. Chem. Phys. 1963, 38, 550–560. [Google Scholar] [CrossRef]
- Woodward, R.B. Totalsynthese des chlorophylls. Angew. Chem. Int. Ed. 1960, 72, 651–662. [Google Scholar] [CrossRef]
- Reddy, B.K.; Basavarajappa, A.; Ambhore, M.D.; Anand, V.G. Isophlorinoids: The Antiaromatic Congeners of Porphyrinoids. Chem. Rev. 2017, 117, 3420–3443. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Wasbotten, I.H.; Davis, W.; Swarts, J.C. Norcorrole and Dihydronorcorrole: A Predictive Quantum Chemical Study. Eur. J. Inorg. Chem. 2005, 2005, 4479–4485. [Google Scholar] [CrossRef]
- Bröring, M.; Köhler, S.; Kleeberg, C. Norcorrole: Observation of the Smallest Porphyrin Variant with a N4 Core. Angew. Chem. Int. Ed. 2008, 47, 5658–5660. [Google Scholar] [CrossRef]
- Ito, T.; Hayashi, Y.; Shimizu, S.; Shin, J.Y.; Kobayashi, N.; Shinokubo, H. Gram-Scale Synthesis of Nickel(II) Norcorrole: The Smallest Antiaromatic Porphyrinoid. Angew. Chem. Int. Ed. 2012, 51, 8542–8545. [Google Scholar] [CrossRef] [PubMed]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Ruud, K. Ab initio Methods for the Calculation of NMR Shielding and Indirect Spin-Spin Coupling Constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef]
- Gauss, J.; Stanton, J.F. Electron-correlated approaches for the calculation of NMR chemical shifts. Adv. Chem. Phys. 2002, 123, 355–422. [Google Scholar]
- Facelli, J.C. Calculations of chemical shieldings: Theory and applications. Concepts Magn. Reson. Part A 2004, 20A, 42–69. [Google Scholar] [CrossRef]
- Helgaker, T.; Coriani, S.; Jørgensen, P.; Kristensen, K.; Olsen, J.; Ruud, K. Recent Advances in Wave Function-Based Methods of Molecular-Property Calculations. Chem. Rev. 2012, 112, 543–631. [Google Scholar] [CrossRef] [PubMed]
- Jameson, C.J.; Buckingham, A.D. Nuclear magnetic shielding density. J. Phys. Chem. 1979, 83, 3366–3371. [Google Scholar] [CrossRef]
- Jameson, C.J.; Buckingham, A.D. Molecular electronic property density functions: The nuclear magnetic shielding density. J. Chem. Phys. 1980, 73, 5684–5692. [Google Scholar] [CrossRef]
- Bieger, W.; Seifert, G.; Eschrig, H.; Grossmann, G. LCAO Xα calculations of nuclear magnetic shielding in molecules. Chem. Phys. Lett. 1985, 115, 275–280. [Google Scholar] [CrossRef]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2014. J. Phys. Chem. Ref. Data 2016, 45, 043102. [Google Scholar] [CrossRef] [Green Version]
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of Current Densities using Gauge-Including Atomic Orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef] [PubMed]
- Taubert, S.; Sundholm, D.; Jusélius, J. Calculation of spin-current densities using gauge-including atomic orbitals. J. Chem. Phys. 2011, 134, 054123. [Google Scholar] [CrossRef]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The gauge including magnetically induced current method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef]
- Sundholm, D.; Fliegl, H.; Berger, R.J.F. Calculations of magnetically induced current densities: Theory and applications. WIREs Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
- Dimitrova, M.; Sundholm, D. Current density, current-density pathways and molecular aromaticity. In Aromaticity: Modern Computational Methods and Applications; Fernández López, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 5; pp. 155–194. [Google Scholar]
- GIMIC, Version 2.0, a Current Density Program. December 2020. Available online: https://github.com/qmcurrents/gimic (accessed on 3 September 2021).
- Sambe, H. Properties of induced electron current density of a molecule under a static uniform magnetic field. J. Chem. Phys. 1973, 59, 555. [Google Scholar] [CrossRef]
- Lazzeretti, P. Current density tensors. J. Chem. Phys. 2018, 148, 134109. [Google Scholar] [CrossRef] [PubMed]
- Lazzeretti, P. Ring currents. Prog. Nucl. Magn. Reson. Spectrosc. 2000, 36, 1–88. [Google Scholar] [CrossRef]
- Pelloni, S.; Lazzeretti, P. On the existence of a natural common gauge-origin for the calculation of magnetic properties of atoms and molecules via gaugeless basis sets. J. Chem. Phys. 2012, 136, 164110. [Google Scholar] [CrossRef] [PubMed]
- Lazzeretti, P.; Malagoli, M.; Zanasi, R. Electronic Current-Density Induced by Nuclear Magnetic Dipoles. J. Mol. Struct. THEOCHEM 1994, 119, 299–304. [Google Scholar] [CrossRef]
- Komorovsky, S.; Jakubowska, K.; Świder, P.; Repisky, M.; Jaszuński, M. NMR Spin-Spin Coupling Constants Derived from Relativistic Four-Component DFT Theory-Analysis and Visualization. J. Phys. Chem. A 2020, 124, 5157–5169. [Google Scholar] [CrossRef]
- Lehtola, S.; Dimitrova, M.; Fliegl, H.; Sundholm, D. Benchmarking Magnetizabilities with Recent Density Functionals. J. Chem. Theory Comput. 2021, 17, 1457–1468. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Calculation of Magnetic Response Properties Using a Continuous Set of Gauge Transformations. Chem. Phys. Lett. 1993, 210, 223–231. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W. Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions. J. Phys. Chem. A 2001, 105, 9553–9562. [Google Scholar] [CrossRef]
- Soncini, A.; Fowler, P.; Lazzeretti, P.; Zanasi, R. Ring-current signatures in shielding-density maps. Chem. Phys. Lett. 2005, 401, 164–169. [Google Scholar] [CrossRef]
- Pelloni, S.; Ligabue, A.; Lazzeretti, P. Ring-Current Models from the Differential Biot-Savart Law. Org. Lett. 2004, 6, 4451–4454. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, M.; Lazzeretti, P.; Viglione, R.; Zanasi, R. Understanding proton magnetic shielding in the benzene molecule. Chem. Phys. Lett. 2004, 390, 268–271. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W. On the orbital analysis of magnetic properties. Phys. Chem. Chem. Phys. 2004, 6, 261–272. [Google Scholar] [CrossRef]
- Ferraro, M.B.; Faglioni, F.; Ligabue, A.; Pelloni, S.; Lazzeretti, P. Ring current effects on nuclear magnetic shielding of carbon in the benzene molecule. Magn. Res. Chem. 2005, 43, 316–320. [Google Scholar] [CrossRef]
- Acke, G.; Van Damme, S.; Havenith, R.W.A.; Bultinck, P. Interpreting the behavior of the NICSzz by resolving in orbitals, sign, and positions. J. Comp. Chem. 2018, 39, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Acke, G.; Van Damme, S.; Havenith, R.W.A.; Bultinck, P. Quantifying the conceptual problems associated with the isotropic NICS through analyses of its underlying density. Phys. Chem. Chem. Phys. 2019, 21, 3145–3153. [Google Scholar] [CrossRef]
- Balasubramani, S.G.; Chen, G.P.; Coriani, S.; Diedenhofen, M.; Frank, M.S.; Franzke, Y.J.; Furche, F.; Grotjahn, R.; Harding, M.E.; Hättig, C.; et al. TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations. J. Chem. Phys. 2020, 152, 184107. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chim. Acta 1997, 97, 119–124. [Google Scholar] [CrossRef]
- Treutler, O.; Ahlrichs, R. Efficient molecular numerical integration schemes. J. Chem. Phys. 1995, 102, 346–354. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-Consistent Perturbation-Theory Of Diamagnetism 1. Gauge-Invariant LCAO Method For NMR Chemical-Shifts. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Kollwitz, M.; Häser, M.; Gauss, J. Non-Abelian point group symmetry in direct second-order many-body perturbation theory calculations of NMR chemical shifts. J. Chem. Phys. 1998, 108, 8295–8301. [Google Scholar] [CrossRef] [Green Version]
- Reiter, K.; Mack, F.; Weigend, F. Calculation of Magnetic Shielding Constants with meta-GGA Functionals Employing the Multipole-Accelerated Resolution of the Identity: Implementation and Assessment of Accuracy and Efficiency. J. Chem. Theory Comput. 2018, 14, 191–197. [Google Scholar] [CrossRef]
- Jensen, F. Unifying General and Segmented Contracted Basis Sets. Segmented Polarization Consistent Basis Sets. J. Chem. Theory Comput. 2014, 10, 1074–1085. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibsom, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef] [PubMed]
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef] [Green Version]
- Pecul, M.; Ruud, K. The ab initio calculation of optical rotation and electronic circular dichroism. Adv. Quantum Chem. 2005, 50, 185–212. [Google Scholar]
- Fliegl, H.; Sundholm, D.; Taubert, S.; Jusélius, J.; Klopper, W. Magnetically Induced Current Densities in Aromatic, Antiaromatic, Homoaromatic, and Nonaromatic Hydrocarbons. J. Phys. Chem. A 2009, 113, 8668–8676. [Google Scholar] [CrossRef] [PubMed]
- Bast, R. April 2020. Numgrid v1.1.2: Numerical Integration Grid for Molecules. Available online: https://zenodo.org/record/4815722#.YThHNty-s2w (accessed on 3 September 2021).
- Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Lebedev, V.I. A quadrature formula for the sphere of 59th algebraic order of accuracy. Russ. Acad. Sci. Dokl. Math. 1995, 50, 283–286. [Google Scholar]
- Lindh, R.; Malmqvist, P.Å.; Gagliardi, L. Molecular integrals by numerical quadrature. I. Radial integration. Theor. Chem. Acc. 2001, 106, 178–187. [Google Scholar] [CrossRef] [Green Version]
- Fliegl, H.; Sundholm, D. Aromatic Pathways of Porphins, Chlorins and Bacteriochlorins. J. Org. Chem. 2012, 77, 3408–3414. [Google Scholar] [CrossRef] [Green Version]
- Nozawa, R.; Kim, J.; Oh, J.; Lamping, A.; Wang, Y.; Shimizu, S.; Hisaki, I.; Kowalczyk, T.; Fliegl, H.; Kim, D.; et al. Three-dimensional aromaticity in an antiaromatic cyclophane. Nat. Commun. 2019, 10, 3576. [Google Scholar] [CrossRef]
- Sundholm, D.; Fliegl, H. Aromatic Pathways in Porphyrinoids by Magnetically Induced Ring Currents. In Handbook of Porphyrin Science; Kadish, K.M., Smith, K.M., Guilard, R., Eds.; World Scientific: Singapore, 2021; Volume 46, in press. [Google Scholar]
- Kawashima, H.; Ukai, S.; Nozawa, R.; Fukui, N.; Fitzsimmons, G.; Kowalczyk, T.; Fliegl, H.; Shinokubo, H. Determinant Factors of Three-Dimensional Aromaticity in Antiaromatic Cyclophanes. J. Am. Chem. Soc. 2021, 143, 10676–10685. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fliegl, H.; Dimitrova, M.; Berger, R.J.F.; Sundholm, D. Spatial Contributions to 1H NMR Chemical Shifts of Free-Base Porphyrinoids. Chemistry 2021, 3, 1005-1021. https://doi.org/10.3390/chemistry3030072
Fliegl H, Dimitrova M, Berger RJF, Sundholm D. Spatial Contributions to 1H NMR Chemical Shifts of Free-Base Porphyrinoids. Chemistry. 2021; 3(3):1005-1021. https://doi.org/10.3390/chemistry3030072
Chicago/Turabian StyleFliegl, Heike, Maria Dimitrova, Raphael J. F. Berger, and Dage Sundholm. 2021. "Spatial Contributions to 1H NMR Chemical Shifts of Free-Base Porphyrinoids" Chemistry 3, no. 3: 1005-1021. https://doi.org/10.3390/chemistry3030072
APA StyleFliegl, H., Dimitrova, M., Berger, R. J. F., & Sundholm, D. (2021). Spatial Contributions to 1H NMR Chemical Shifts of Free-Base Porphyrinoids. Chemistry, 3(3), 1005-1021. https://doi.org/10.3390/chemistry3030072