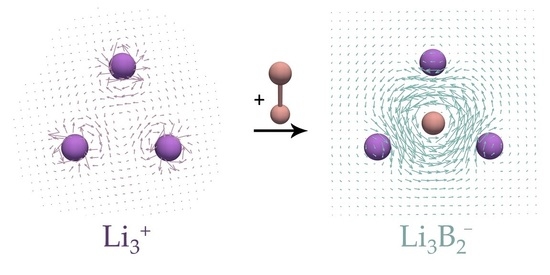
The B2 Structural Motif as a Tool for Modulating Ring Currents in Monocyclic Li Clusters
Abstract
:1. Introduction
2. Computational Methods
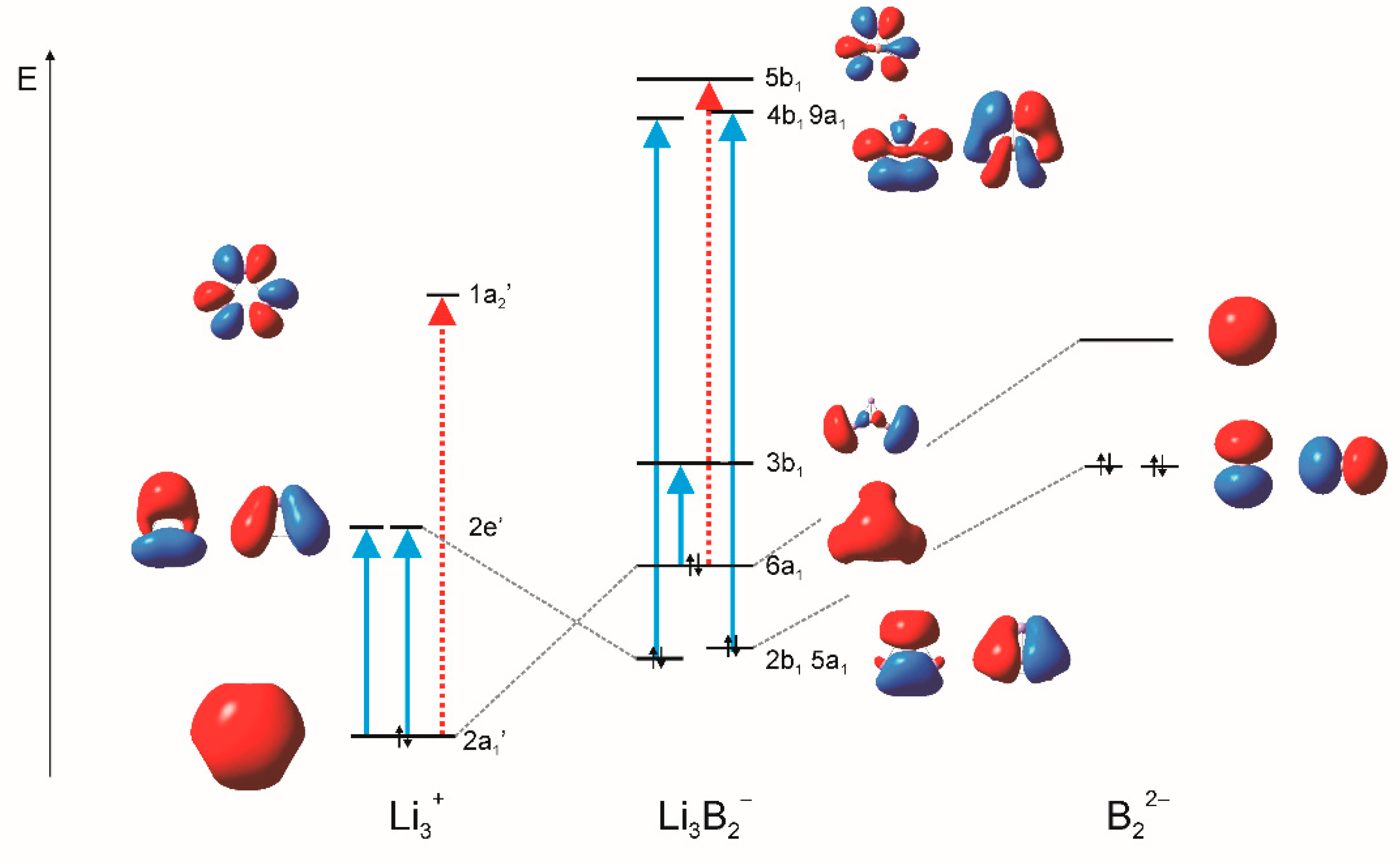
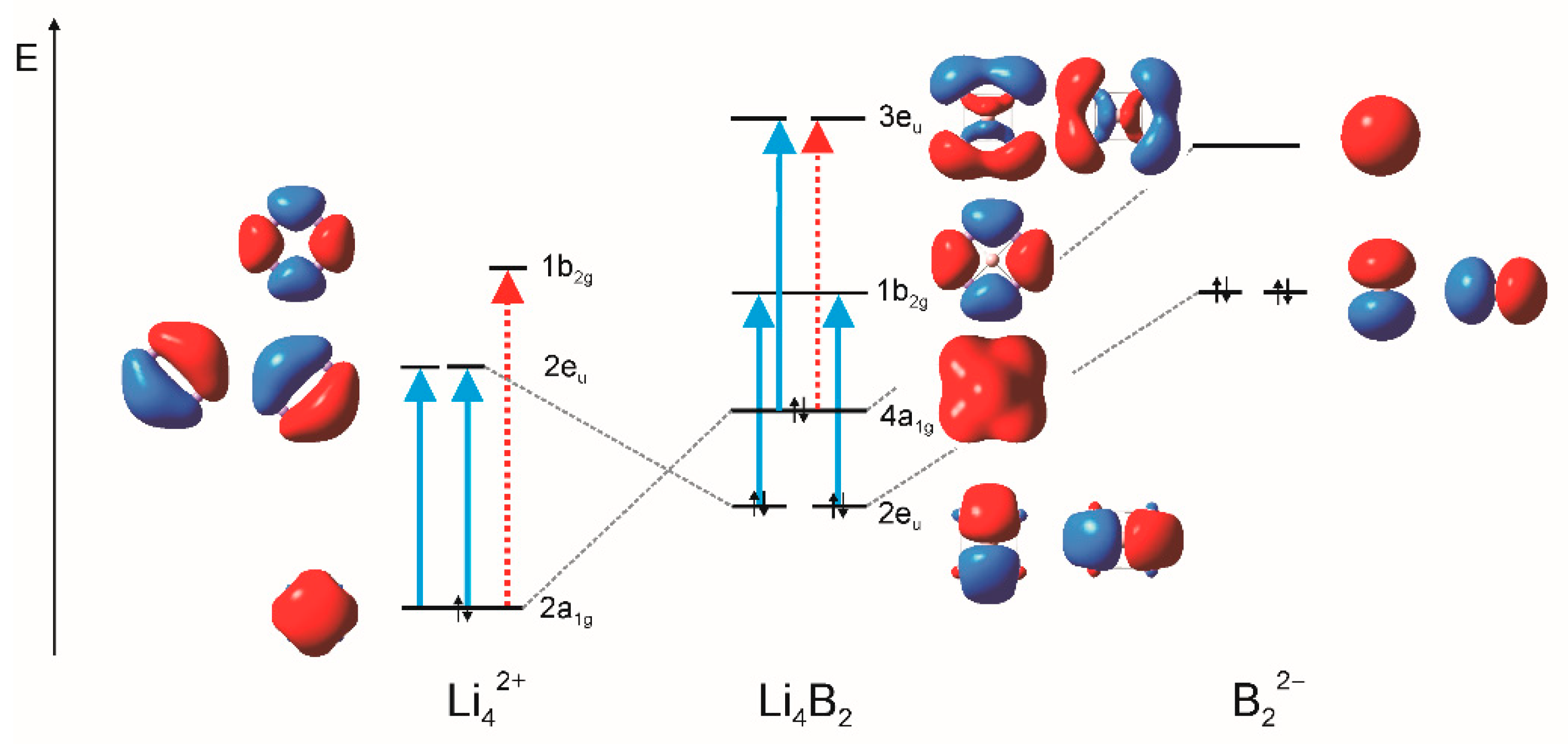
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cyrański, M.K. Energetic Aspects of Cyclic π-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R.; Stanger, A. Magnetic Criteria of Aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef] [PubMed]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying Aromaticity with Electron Delocalisation Measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lazzeretti, P. Ring Currents. Prog. Nucl. Magn. Reson. Spectrosc. 2000, 36, 1–88. [Google Scholar] [CrossRef]
- Gomes, J.A.N.F.; Mallion, R.B. Aromaticity and Ring Currents. Chem. Rev. 2001, 101, 1349–1384. [Google Scholar] [CrossRef] [PubMed]
- London, F. Théorie Quantique des Courants Interatomiques dans les Combinaisons Aromatiques. J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef] [Green Version]
- Geuenich, D.; Hess, K.; Köhler, F.; Herges, R. Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef]
- Sundholm, D.; Fliegl, H.; Berger, R.J.F. Calculations of Magnetically Induced Current Densities: Theory and Applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; Hommes, N.J.v.R.E. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Lazzeretti, P. Assessment of Aromaticity via Molecular Response Properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. [Google Scholar] [CrossRef]
- Van Damme, S.; Acke, G.; Havenith, R.W.A.; Bultinck, P. Can the Current Density Map Topology Be Extracted from the Nucleus Independent Chemical Shifts? Phys. Chem. Chem. Phys. 2016, 18, 11746–11755. [Google Scholar] [CrossRef]
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of Current Densities Using Gauge-Including Atomic Orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Calculation of Magnetic Response Properties Using a Continuous Set of Gauge Transformations. Chem. Phys. Lett. 1993, 210, 223–231. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Topological Analysis of Magnetically Induced Molecular Current Distributions. J. Chem. Phys. 1993, 99, 3669–3682. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Malagoli, M.; Zanasi, R. Computational Approach to Molecular Magnetic Properties by Continuous Transformation of the Origin of the Current Density. Chem. Phys. Lett. 1994, 220, 299–304. [Google Scholar] [CrossRef]
- Lazzeretti, P. Methods of Continuous Translation of the Origin of the Current Density Revisited. Theor. Chem. Acc. 2012, 131, 1222. [Google Scholar] [CrossRef]
- Zanasi, R. Coupled Hartree-Fock Calculations of Molecular Magnetic Properties Annihilating the Transverse Paramagnetic Current Density. J. Chem. Phys. 1996, 105, 1460–1469. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Zanasi, R. SYSMO Package; University of Modena: Modena, Italy, 1980. [Google Scholar]
- Monaco, G.; Summa, F.F.; Zanasi, R. Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems. J. Chem. Inf. Model. 2021, 61, 270–283. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W. Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions. J. Phys. Chem. A 2001, 105, 9553–9562. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W. Four- and Two-Electron Rules for Diatropic and Paratropic Ring Currents in Monocyclic π Systems. Chem. Commun. 2001, 2220–2221. [Google Scholar] [CrossRef]
- Soncini, A.; Teale, A.M.; Helgaker, T.; De Proft, F.; Tozer, D.J. Maps of Current Density Using Density-Functional Methods. J. Chem. Phys. 2008, 129, 74101. [Google Scholar] [CrossRef] [PubMed]
- Havenith, R.W.A.; De Proft, F.; Fowler, P.W.; Geerlings, P. σ-Aromaticity in H3+ and Li3+: Insights from Ring-Current Maps. Chem. Phys. Lett. 2005, 407, 391–396. [Google Scholar] [CrossRef]
- Badri, Z.; Pathak, S.; Fliegl, H.; Rashidi-Ranjbar, P.; Bast, R.; Marek, R.; Foroutan-Nejad, C.; Ruud, K. All-Metal Aromaticity: Revisiting the Ring Current Model among Transition Metal Clusters. J. Chem. Theory Comput. 2013, 9, 4789–4796. [Google Scholar] [CrossRef] [PubMed]
- Foroutan-Nejad, C. Is NICS a Reliable Aromaticity Index for Transition Metal Clusters? Theor. Chem. Acc. 2015, 134, 1–9. [Google Scholar] [CrossRef]
- Foroutan-Nejad, C.; Vícha, J.; Ghosh, A. Relativity or Aromaticity? A First-Principles Perspective of Chemical Shifts in Osmabenzene and Osmapentalene Derivatives. Phys. Chem. Chem. Phys. 2020, 22, 10863–10869. [Google Scholar] [CrossRef] [PubMed]
- Radenković, S.; Bultinck, P. Ring Currents in Polycyclic Sodium Clusters. J. Phys. Chem. A 2011, 115, 12493–12502. [Google Scholar] [CrossRef] [Green Version]
- Kalita, A.; Rohman, S.; Kashyap, C.; Ullah, S.; Baruah, I.; Marumder, L.; Das, K.; Guha, A. Boron-Boron Quadruple Bond in Li3B2− and Li4B2 Clusters. Phys. Chem. Chem. Phys. 2021. [Google Scholar] [CrossRef]
- Zhang, X.; Popov, I.A.; Lundell, K.A.; Wang, H.; Mu, C.; Wang, W.; Schnöckel, H.; Boldyrev, A.I.; Bowen, K.H. Realization of an Al≡Al Triple Bond in the Gas-Phase Na3Al2− Cluster via Double Electronic Transmutation. Angew. Chem. Int. Ed. 2018, 57, 14060–14064. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Foster, J.P.; Weinhold, F. Natural Hybrid Orbitals. J. Am. Chem. Soc. 1980, 102, 7211–7218. [Google Scholar] [CrossRef]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware: New York, NY, USA, 2015; ISBN 978-1930934306. [Google Scholar]
- Irons, T.J.P.; Spence, L.; David, G.; Speake, B.T.; Helgaker, T.; Teale, A.M. Analyzing Magnetically Induced Currents in Molecular Systems Using Current-Density-Functional Theory. J. Phys. Chem. A 2020, 124, 1321–1333. [Google Scholar] [CrossRef]
- Elhay, S.; Kautsky, J. Algorithm 655: IQPACK: FORTRAN Subroutines for the Weights of Interpolatory Quadratures. ACM Trans. Math. Softw. 1987, 13, 399–415. [Google Scholar] [CrossRef]
- Bochicchio, R.; Ponec, R.; Torre, A.; Lain, L. Multicenter Bonding Within the AIM Theory. Theor. Chem. Acc. 2001, 105, 292–298. [Google Scholar] [CrossRef]
- Heyndrickx, W.; Salvador, P.; Bultinck, P.; Solà, M.; Matito, E. Performance of 3D-Space-Based Atoms-in-Molecules Methods for Electronic Delocalization Aromaticity Indices. J. Comput. Chem. 2011, 32, 386–395. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bultinck, P.; Rafat, M.; Ponec, R.; Van Gheluwe, B.; Carbó-Dorca, R.; Popelier, P. Electron Delocalization and Aromaticity in Linear Polyacenes: Atoms in Molecules Multicenter Delocalization Index. J. Phys. Chem. A 2006, 110, 7642–7648. [Google Scholar] [CrossRef] [PubMed]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A Comparison of Models for Calculating Nuclear Magnetic Resonance Shielding Tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0: New Vistas in Localized and Delocalized Cbonding Theory. J. Comput. Chem. 2019, 40, 2234–2241. [Google Scholar] [CrossRef]
- Ghorai, S.; Jemmis, E.D. A DFT Study on the Stabilization of the B≡B Triple Bond in a Metallaborocycle: Contrasting Electronic Structures of Boron and Carbon Analogues. Chem.–A Eur. J. 2017, 23, 9746–9751. [Google Scholar] [CrossRef]
- Alexandrova, A.; Boldyrev, A. σ-Aromaticity and σ-Antiaromaticity in Alkali Metal and Alkaline Earth Metal Small Clusters. J. Phys. Chem. A 2003, 107, 554–560. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]








| Dissociation Path | DE |
|---|---|
| 343.24 | |
| 569.61 | |
| 233.26 | |
| 358.96 | |
| −18.92 |
| Molecule | ||||
|---|---|---|---|---|
| 0.4214 (0.4012) | −54.62 (−53.58) | −45.48 | −6.2 | |
| 0.3176 (0.3081) | −46.21 (−46.50) | −36.17 | −6.64 | |
| 0.7631 (0.7631) | −9.00 (−9.06) | −11.47 | - | |
| 0.6575 (0.6575) | −9.59 (−9.73) | −11.08 | - |
| Δd | Charge of B | |||||
|---|---|---|---|---|---|---|
| 0.0 | −1.175 | −1.265 | −54.62 | −46.21 | 0.4213 | 0.3178 |
| 0.3 | −1.179 | −1.265 | −49.89 | −46.03 | 0.2581 | 0.3146 |
| 0.6 | −1.161 | −1.148 | −40.86 | −36.03 | 0.1613 | 0.1495 |
| 0.9 | −1.089 | −0.947 | −31.87 | −28.46 | 0.2728 | 0.2141 |
| 1.2 | −0.886 | −0.717 | −25.67 | −24.02 | 0.2571 | 0.1968 |
| 1.5 | −0.740 | −0.551 | −22.21 | −22.17 | 0.2444 | 0.1821 |
| 1.8 | −0.621 | −0.414 | −20.16 | −21.45 | 0.2315 | 0.1899 |
| 2.1 | −0.513 | −0.293 | −19.01 | −21.55 | 0.2237 | 0.2258 |
| Bond | ||||
|---|---|---|---|---|
| Li1–Li2 | 2.28 | 1.59 | 8.81 | 8.11 |
| Li2–Li3 | 8.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Đorđević, S.; Radenković, S. The B2 Structural Motif as a Tool for Modulating Ring Currents in Monocyclic Li Clusters. Chemistry 2021, 3, 1063-1073. https://doi.org/10.3390/chemistry3030077
Đorđević S, Radenković S. The B2 Structural Motif as a Tool for Modulating Ring Currents in Monocyclic Li Clusters. Chemistry. 2021; 3(3):1063-1073. https://doi.org/10.3390/chemistry3030077
Chicago/Turabian StyleĐorđević, Slađana, and Slavko Radenković. 2021. "The B2 Structural Motif as a Tool for Modulating Ring Currents in Monocyclic Li Clusters" Chemistry 3, no. 3: 1063-1073. https://doi.org/10.3390/chemistry3030077
APA StyleĐorđević, S., & Radenković, S. (2021). The B2 Structural Motif as a Tool for Modulating Ring Currents in Monocyclic Li Clusters. Chemistry, 3(3), 1063-1073. https://doi.org/10.3390/chemistry3030077