Photoelectron Circular Dichroism as a Probe of Chiral Hydrocarbons

Abstract

The sensitivity of Photoelectron Circular Dichroism (PECD) in the angular distribution of photoelectrons, a recent chiral technique, to detect chirality in pure hydrocarbons is investigated in a number of benchmark molecules. It is found that a very large chiral signal is expected, surpassing most current examples, giving a sure fingerprint of absolute configuration. On the other hand, the sensitivity to specific isomers or closely related molecules is relatively modest.

1. Introduction

Molecular chirality is an important topic in chemistry and is also fundamental for applications in the life sciences and the pharmaceutical industry. However, not very many physical techniques are available for the detection and characterization of molecular chirality, the oldest and most consolidated are circular dichroism (CD) in absorption, both electronic and more recently vibrational, and optical rotation (ORD) [1,2]. Clearly the former requires the presence of an absorption band and the availability of a suitable circularly polarized light source, while ORD, showing a dispersive signal, dies off very slowly from absorption bands, and may give a detectable signal far from those [1,2]. In fact, it was recently pointed out that while optical CD may often be unusable in the case of absorption bands in the VUV, e.g., in saturated hydrocarbon molecules, ORD is still usable [3,4].

An important point is that optical techniques require the chirality of the light, which translates into necessitating both the electric and magnetic vectors of the field. The optical signal depends on the magnitude of a mixed electric dipole-magnetic dipole transition matrix element between the states involved in the excitation [1,2]. This makes the signal very weak in comparison to pure electric dipole transitions, and makes experimental detection very difficult for diluted samples, as in the gas phase, requiring very specialized instruments available in few laboratories [5]. This limitation is obviated in solution because of the much larger concentration of the sample. Still, solution experiments, although the most common practice, may have some drawbacks. The solvent itself may have a limited wavelength window of transparency. Furthermore, from a fundamental point of view, it may significantly alter the chiral response of the isolated sample, both changing the electronic and vibrational properties, and the molecular conformation.

A last important remark is the role of the theory and the availability of accurate models for the simulation of the experimental results. It is fair to say that up to the development of dependable Quantum Chemistry approaches to the calculation of optical chirality the crucial assignment of the absolute configuration was very difficult, as few empirical rules, as well as the chemical similarity of two related molecules, had very limited predictive power, and led to wrong assignments in the past [3,4].

A relatively recent technique, that works very well in the gas phase, is the detection of circular dichroism in the emission of electrons from molecules ionized by high energy radiation, called PECD (PhotoElectron Circular Dichroism) [6,7,8]. The basic experiment measures the angular distribution of photoelectrons. VUV radiation ionizes a molecule, and the detector reveals photoelectron at an angle θ with respect to the light propagation vector The intensity of emission (cross-section) for left circularly polarized light is given by the simple formula:

$$\mathrm{I}=\mathrm{const}[1+{\mathsf{\beta }}_1\cos \mathsf{\theta }-\frac{1}{2}{\mathsf{\beta }}_2{\mathrm{P}}_2(\cos \mathsf{\theta })]$$

(1)

which defines the two parameters β₁ and β₂. (P₂ is the second-order Legendre polynomial). β₁ reverses with reversing light polarization from left (+1) to right (−1) as well as interchanging the enantiomers. For non-chiral molecules β₁ = 0 and emission at θ (forward) and (π − θ) (backward) have equal intensities, but for chiral molecules, this is not true, and the normalized difference in the intensity

$$\left(\mathsf{\theta }\right)=\frac{\mathrm{I}\left(\mathsf{\theta }\right)-\mathrm{I}\left(\mathsf{\pi }-\mathsf{\theta }\right)}{\mathrm{I}\left(\mathsf{\theta }\right)+\mathrm{I}\left(\mathsf{\pi }-\mathsf{\theta }\right)}=\frac{{\mathrm{I}}_{\mathrm{L}}\left(\mathsf{\theta }\right)-{\mathrm{I}}_{\mathrm{R}}\left(\mathsf{\theta }\right)}{{\mathrm{I}}_{\mathrm{L}}\left(\mathsf{\theta }\right)+{\mathrm{I}}_{\mathrm{R}}\left(\mathsf{\theta }\right)}$$

(2)

allows the retrieval of the dichroic parameter β₁ (actually β₁ = Δ(θ_M), θ_M = 54.4° is the so-called magic angle, such that P₂(cos θ_M) = 0).

The information content of β₁ is rich, as it depends on the specific final ionic state I probed, that is on its ionization potential (IP), and also on the photon energy ℏω of the ionizing radiation, a typical profile for methyloxirane being shown in Figure 1. The effect is large at low kinetic energies (KE), close to the threshold, and then fades away after a few tens of electronvolts (eV), but is orders of magnitude larger than in optical absorption, as it is due to a pure electric dipole matrix element between initial and final states. Here chirality of the probe is provided by the additional vector given by the electron momentum. The value of β₁ is typically in the range of a few percent, occasionally surpassing 0.1 units, and can be rather easily measured with current facilities [8]. Like for optical absorption also for PECD simulations are very useful to extract the most information from the spectra, and unavoidable for the absolute configuration assignment. Actually, this requires a rather accurate description of the electronic continuum wavefunction which describes the photoelectron. This is a more difficult problem than the calculation of bound states and requires special computational techniques [9,10,11]. Given the complexity of chiral systems, it is difficult to go beyond an effective single-particle description of the continuum electron, employing either a density functional (DFT) potential or a static Hartree-Fock one [12,13,14]. Generally, the results are more erratic very close to the threshold, at low electron kinetic energies, but are sufficiently accurate to be predictive from about 5 eV KE, which is amply sufficient to obtain a sure fingerprint.

Speaking of saturated hydrocarbons, there is no reason why these systems would be dark for PECD, as photoionization is always an open channel for photon energies above the IP. On the other hand, it might be feared that the signal would be very small, given the very simple electronic structure, comprising only C–C and C–H single bonds. Moreover, the capability of distinguishing isomers, or in any case molecules closely similar is a further important point. Prompted by the recent investigation underlying the limitations of CD for saturated hydrocarbons and the need for different techniques, we have considered it interesting to test a number of benchmark cases from a previous publication [3] to assess the capability of PECD in this class of compounds. Given the current level of accuracy in theoretical simulations, we are pretty confident that the qualitative features and the level of the expected signal are correctly predicted.

2. The Theoretical Approach

The cross-section in the molecular frame (a molecule fixed in space) is given (in atomic units (au)) by [15]:

$$\frac{{\mathrm{d}\mathsf{\sigma }}_{\mathrm{I}}}{\mathrm{dk}}=4{\mathsf{\pi }}^2\mathsf{\alpha }\mathsf{\omega }>|<{\mathsf{\Psi }}_{\mathrm{Ik}}^{(-)}\left|\mathrm{E}·\mathrm{D}\right|{\mathsf{\Psi }}_0>{|}^2$$

(3)

where α is the fine structure constant, ω the photon energy, Ψ⁽⁻⁾_Ik represents asymptotically an ion with wavefunction Ψ_I and an electron with momentum k, and appropriate boundary conditions. E is the electric field vector and D the dipole operator. If both initial and final states are represented as single Slater determinants with a common set of orbitals, the dipole matrix element reduces to a single particle one:

E <φ⁽⁻⁾_k | r | φ_i>

(4)

where φ_i is the initial orbital ionized. It is convenient to employ for the continuum a basis of angular momentum states, which leads to matrix elements of the form:

E <φ_εlm | rY_1m | φ_i>

(5)

which are those effectively computed. For a sample of randomly oriented molecules, an average of the cross-section over all molecular orientations leads to the expression (1) for the angular distribution in the laboratory frame, with explicit expressions for β₁ which are involved but easily calculated [15].

In the present work, we employ orbitals, both bound and continuum, that are eigenvectors of a fixed DFT (or Kohn-Sham) Hamiltonian (static-DFT approach) [16]:

h_KS = −½ Δ + V_N + V_C + V_XC

(6)

where V_N, V_C, V_XC are the nuclear attraction, the classical coulomb and the DFT exchange-correlation potentials, the latter being defined by the molecular ground state density ρ(r).

Then we compute

h_KS φ_i = ε_i φ_i and h_KS φ_εlm = ε φ_εlm

(7)

both for the bound and continuum eigenvectors. To this end, a special basis is employed, made of products of B-spline radial functions and real spherical harmonics.

χ_nlm = B_n (r) Y_lm(θ,φ)

(8)

B-splines [17] are piecewise polynomial functions defined over a grid of points that span a fixed interval, [0, Rmax] in the present case. The full basis comprises a large one-center expansion (OCE) about a common origin plus short expansions around all nuclei, in the spirit of the LCAO approach [16]. In the present calculation, the OCE expansion employed Rmax = 25 au (30 for chiralane) with a linear grid with stepsize = 0.50 au, and angular expansion up to Lmax = 15 (13 for dimethylcyclopropane, 19 for chiralane). Expansions around the nuclei used Rmax = 1.0 au with step size 0.2 au for all atoms, and Lmax = 2 for carbon, Lmax = 1 for hydrogen. The initial density was obtained from a preliminary SCF calculation with the ADF program [18,19], and the DZP basis from the ADF library. The LB94 exchange-correlation potential [20] was employed. All geometries were taken from [3] except for chiralane from [21].

3. Results and Discussion

The molecules that have been considered are dimethylcyclopropane, brexane, twistane, twistbrendane, ditwistbrendane, trishomocubane, taken from ref [3].

In addition, we chose to study chiralane, a hydrocarbon with the rare T symmetry, purely rotational and so chiral, which is deemed to represent maximal chirality [21]. Their carbon skeleton is depicted in Figure 2. Only the outermost ionizations, which will give well-resolved photoelectron peaks, are reported. They are listed, together with the IP estimates from LB94 eigenvalues, in

Table 1. Orbital ionizations and ionization energies from LB94 DFT eigenvalues.

Dimethylcyclopropane
8B	13.34
10A	13.22
9B	11.64
11A	11.41
Brexane
18A	11.74
16B	11.63
Twistane
19A	11.45
20A	11.42
18B	11.31
Twistbrendane
17A	11.85
16B	11.67
18A	11.65
Ditwistbrendane
18B	11.94
18A	11.84
19A	11.74
Trishomocubane
11E1	12.31
12E1	12.04
9A1	11.76
Chiralane
22T	11.46
23T	10.18

. When more than one ionization lie very close, an average value of β₁ weighted by the corresponding cross-section, is also reported.

We shall briefly point out salient features of the β₁ profile for each molecule and then summarize the important general points.

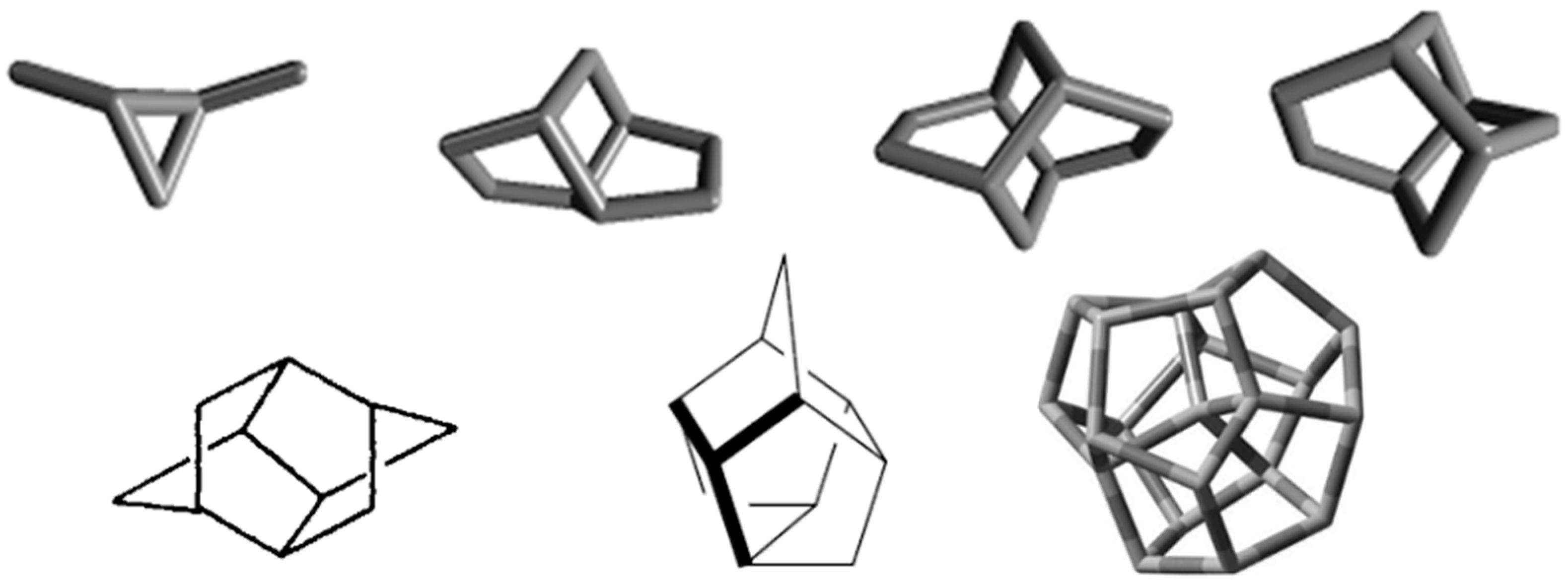
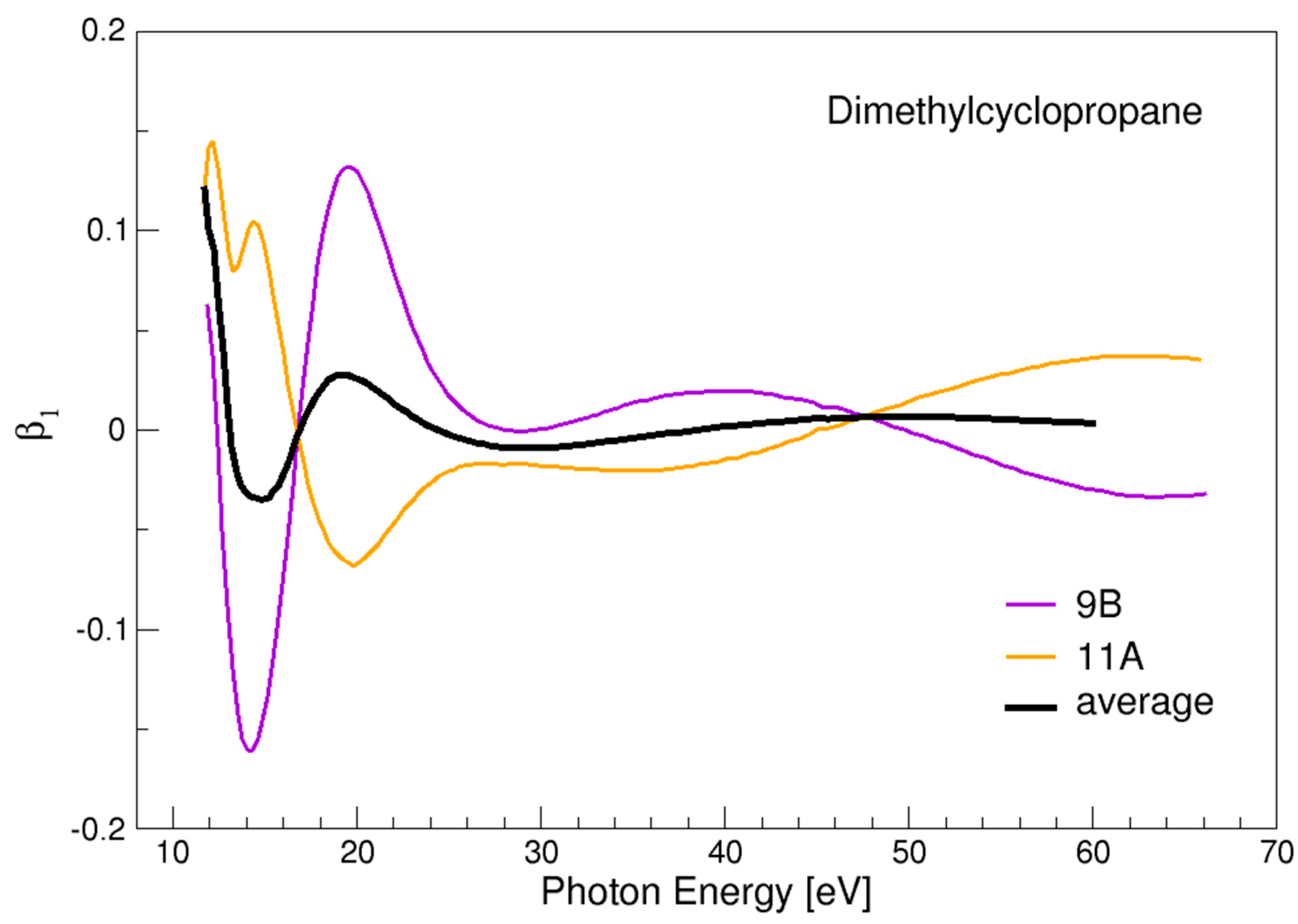
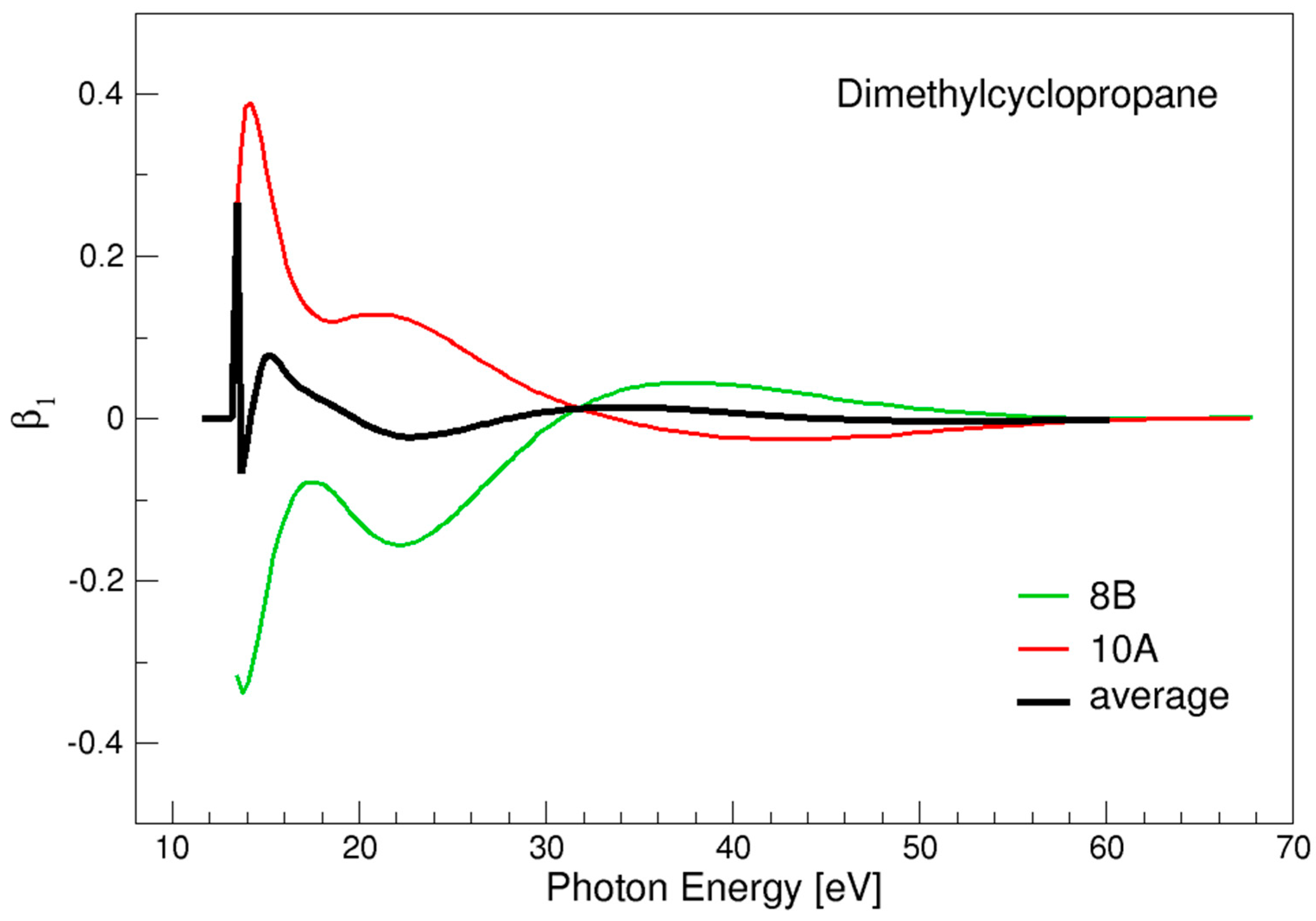
3.1. Dimethylcyclopropane

In this case (Table 1) there are two well-separated couples of close outermost ionizations so that two well-resolved bands will show in the photoelectron spectrum, and the average β₁ is reported, together with the separate components, in Figure 3 and Figure 4. In both cases, it can be seen that the separate components mostly show opposite β₁ behavior, so that the average is much less intense and structured and dies relatively fast. This is probably due to the fact that each couple of orbitals amount to a symmetric or antisymmetric combination of faraway methyl orbitals so that the energy splitting is very small. Nonetheless, both average profiles show a distinct smooth β₁ oscillation, sharper in the higher energy 10A, 8B couple, in the typical range of a few percent, which will give a characteristic well-identified signal.

3.2. Brexane

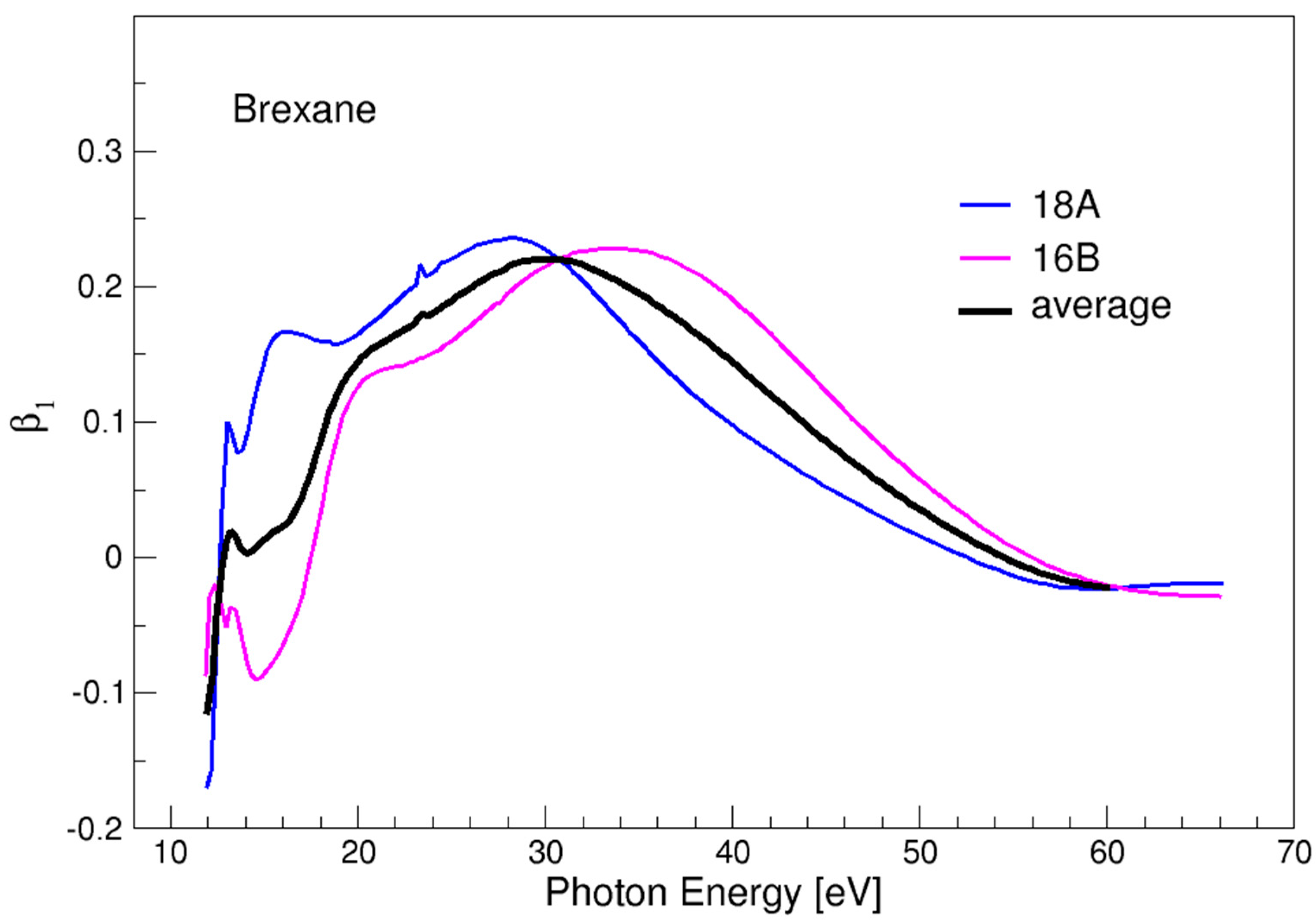
A very different pattern is displayed by brexane. Here again, two close-lying ionizations give rise to an average β₁ profile (Figure 5). In this case, however, except at the lowest energies, the individual profiles are very close and give rise to a very wide almost unstructured profile, that will produce a strong signal, up to 20 percent, spanning almost 30 eV, an unmistakable signature of the molecule.

3.3. Twistane

The situation is similar in twistane. Here three almost degenerate ionizations are present, all with rather close profiles past 20 eV photon energy (Figure 6). The result is again a very wide, rather flat β₁ profile, reaching up to 30 percent before declining smoothly after 40 eV, and reaching important negative values, up to 10 percent above 50 eV, where generally the β₁ signals become very weak.

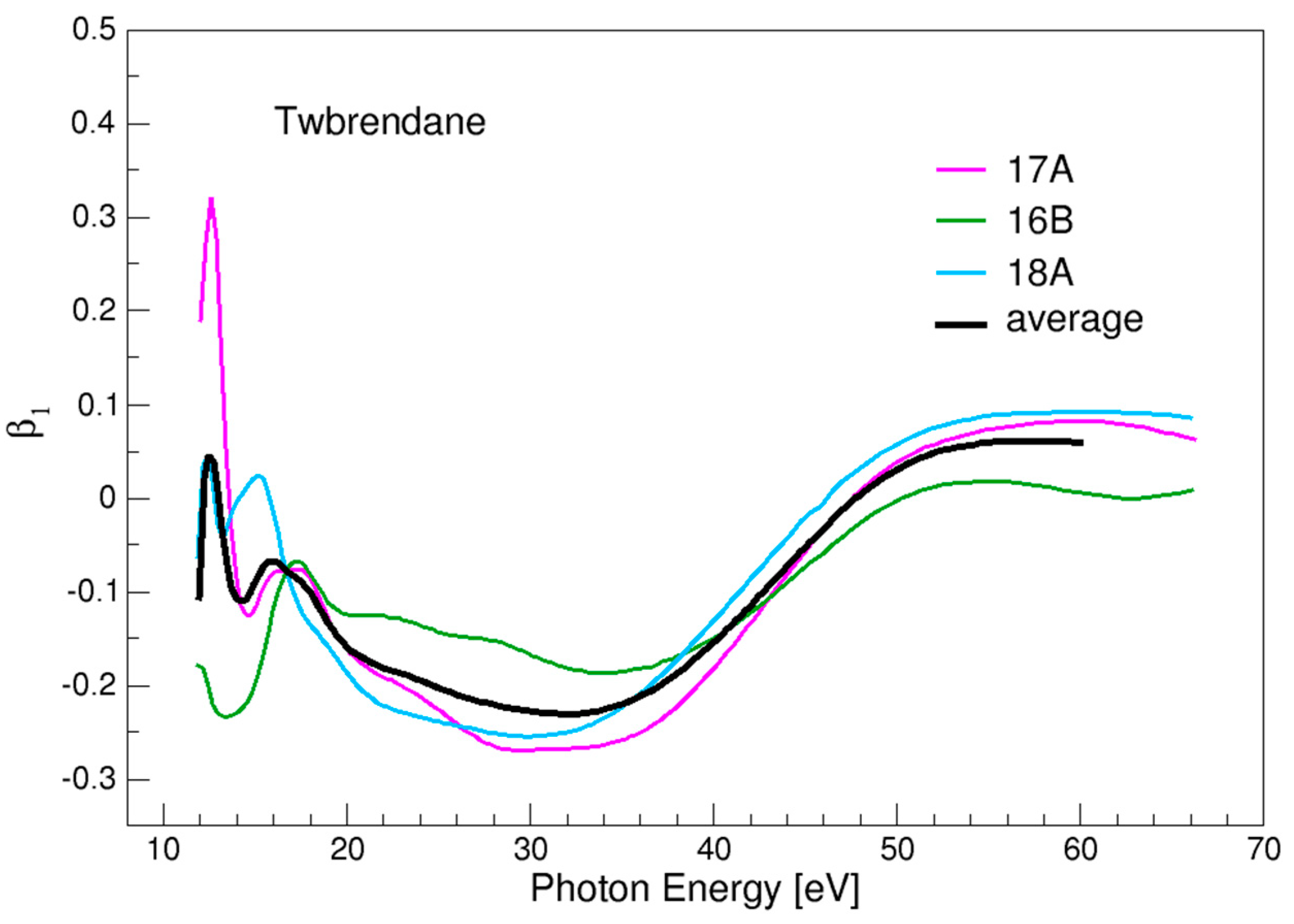
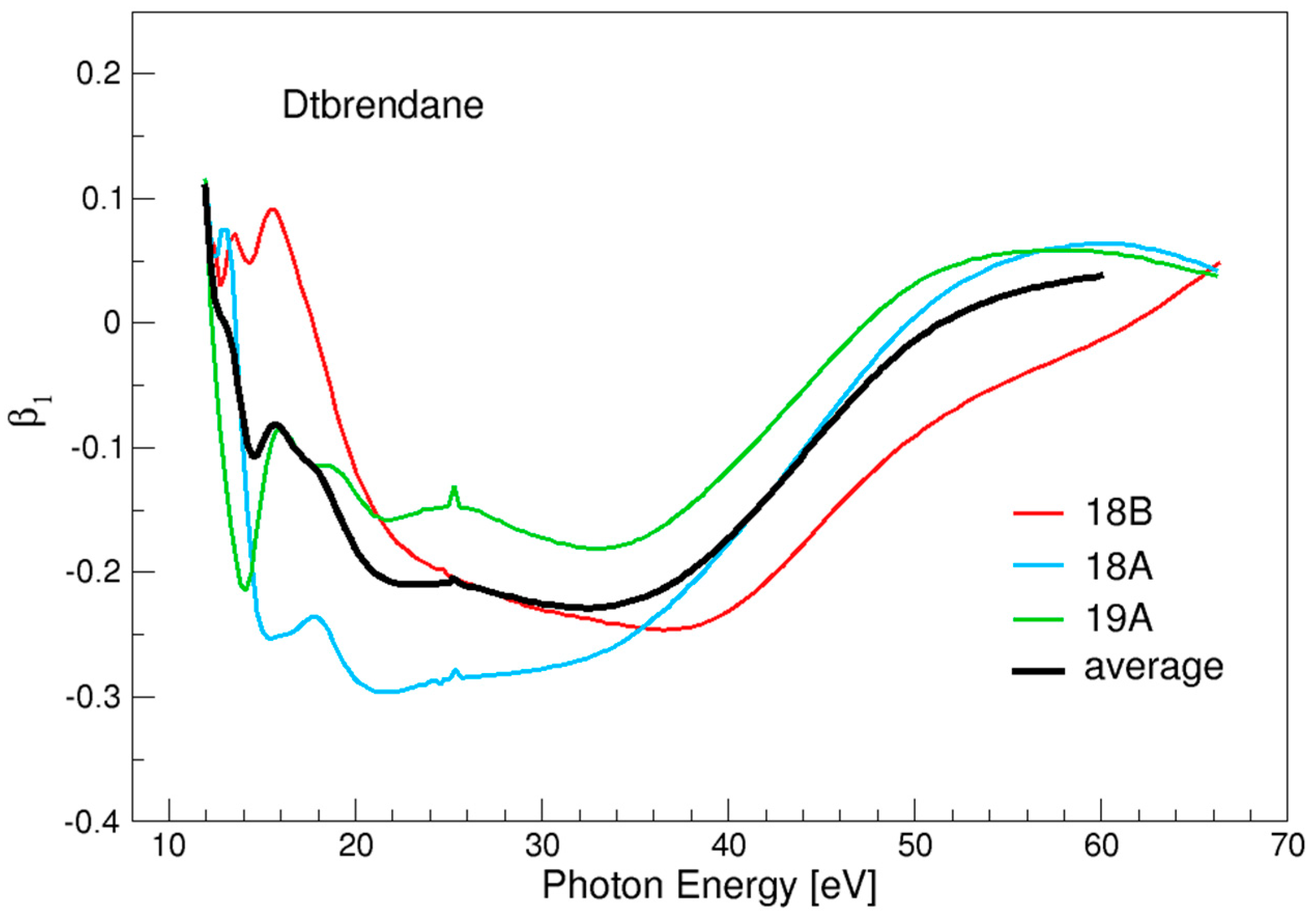
3.4. Twistbrendane and Ditwistbrendane

The average profiles for both molecules, shown in Figure 7 and Figure 8, are quite similar, although the individual components show significant differences in the latter. Apart from the opposite sign, which amounts to reverse the enantiomer, the average profile also bears some similarity to that of twistane, which has a significantly different shape. So, in this case, the outermost β₁ profile is probably not sufficient to differentiate between the two molecules. The signal is however quite strong over a large energy interval and gives a solid characterization of the absolute configuration.

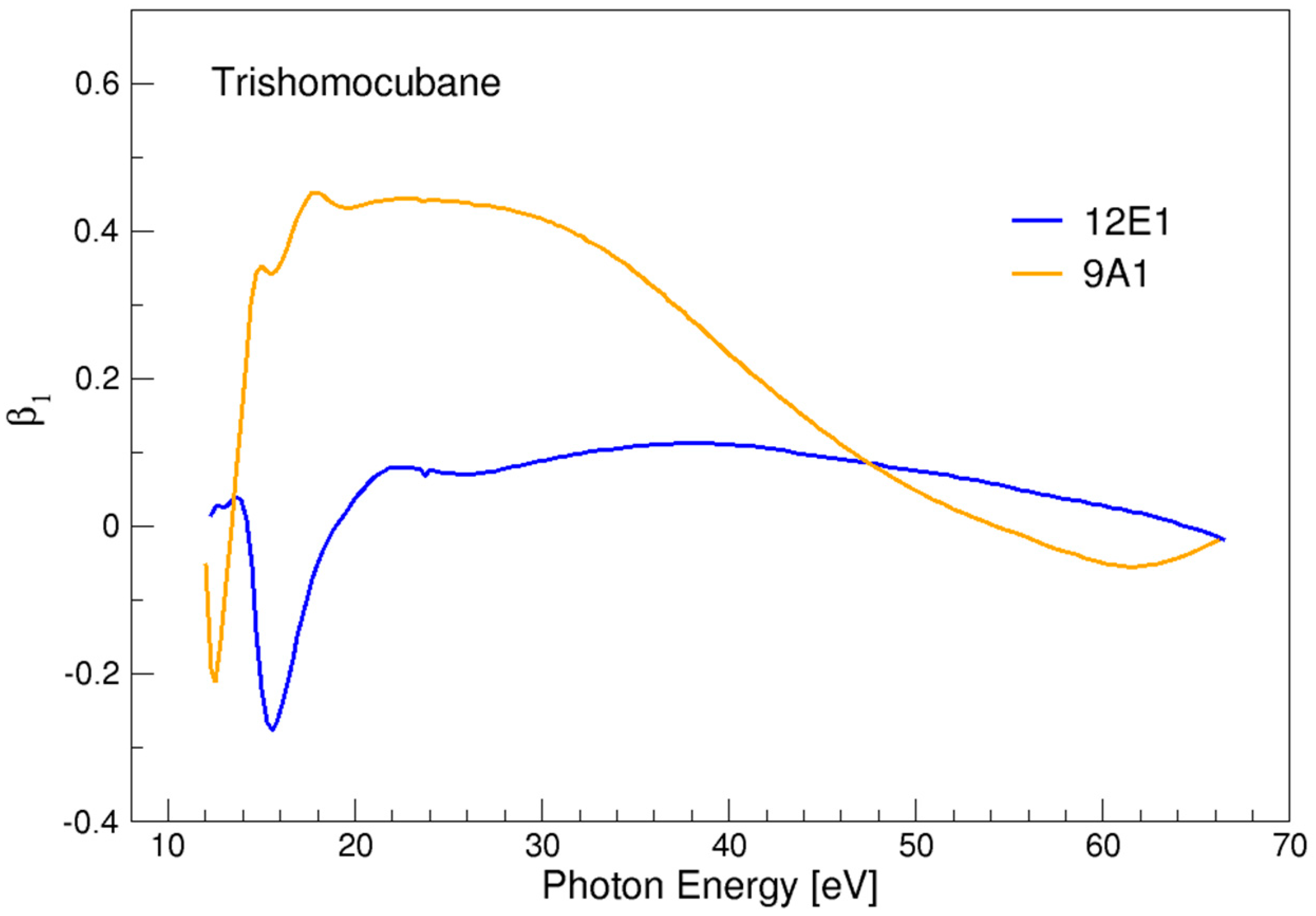
3.5. Trishomocubane

In this case, the separation between consecutive ionizations is estimated to be only 0.3 eV (Table 1) and some band overlap may be expected. We have considered the two ionizations as isolated. The difference in the profiles (Figure 9), as well as the maximum rise of β₁, almost −0.3 for the HOMO 9A₁, and over 0.4 for the next 12E₁, is remarkable. HOMO shows a narrow negative peak, confined in a few eV, and then becomes positive and quite flat. 12E₁, apart from a narrower negative minimum, close to the threshold, presents a wide energy region of very positive values, before declining slowly towards zero.

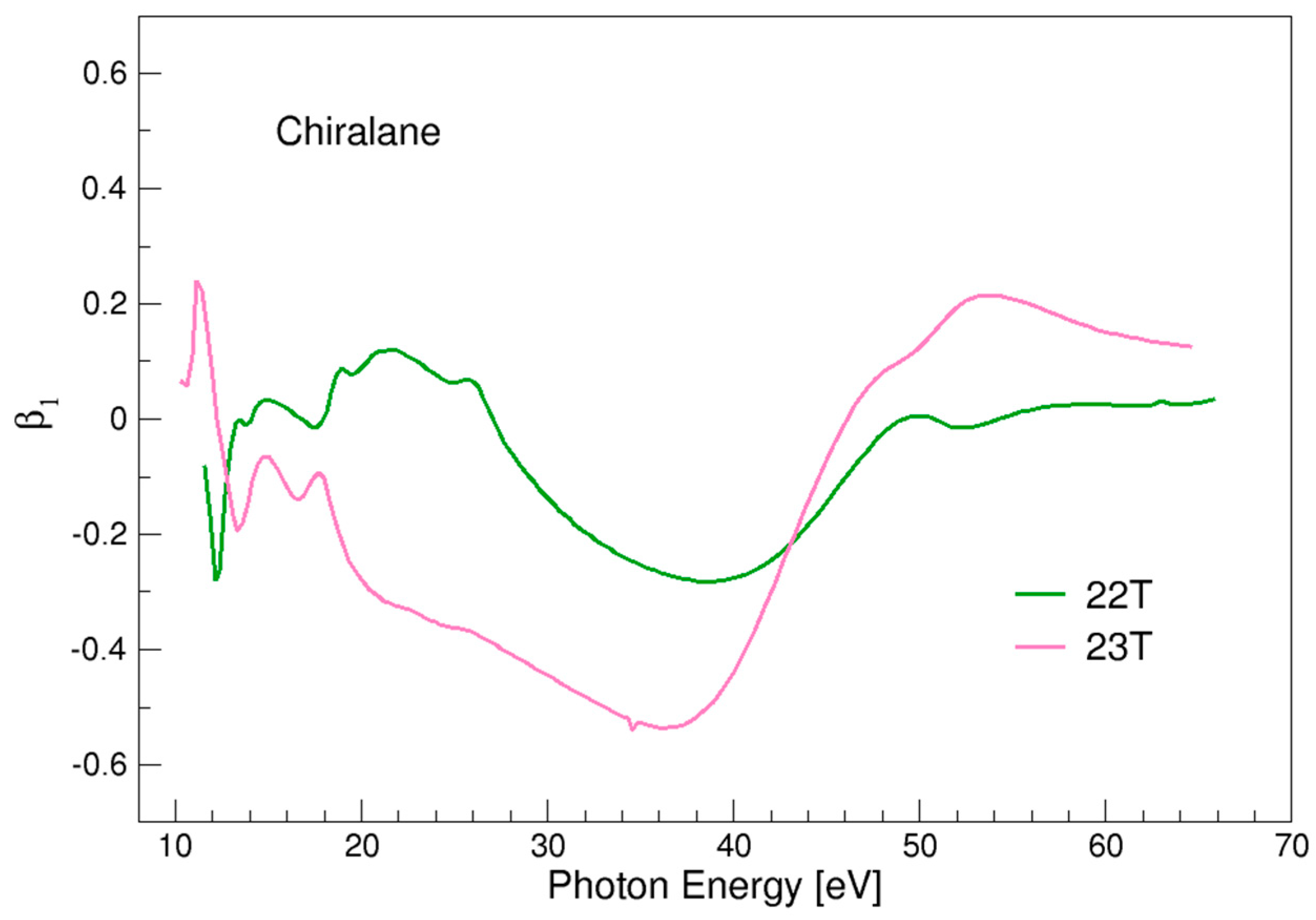
3.6. Chiralane

This hypothetical molecule is significantly larger, and due to the high T symmetry is expected to have well separated outer ionizations. We have considered HOMO 23T and HOMO-1 22T. The β₁ profiles are presented in Figure 10. Apart from the low energy region, the two profiles show some similarity, with a wide negative region, followed by a decline. However, the amplitude covered by HOMO is significantly larger, so the two curves cross and while HOMO-1 goes close to zero at high energy, HOMO after a negative peak of more than −0.5 β₁ units, reaches a positive value of 0.2 at high energy, above 50 eV, a truly remarkable excursion, confirming the “maximum chirality” claim.

We may summarize the important points in this study:

-

PECD is sensitive to chirality in saturated hydrocarbons, and gives generally a rather large signal, apart from the special case of dimethylcyclopropane, probably associated with a peculiar interference-effect.

-

The signature of absolute configuration is therefore very strong and unmistakable in the cases considered.

-

For most of the systems considered the magnitude of β₁ values is among the strongest recorded, and in trishomocubane and chiralane vastly exceeds the values previously known. For comparison, a record value of β₁~0.18 was reported for α-pinene [22] (note that in the literature often chiral asymmetry is reported as 2 β₁). The results seem to suggest that the chiral response increases with molecular size in this class of compounds.

-

Furthermore, the energy range covered by β₁ profiles is remarkably large, extending from threshold to several tens of eV, again significantly exceeding current known cases.

-

In the case of relatively similar molecules, with the same type of atoms and bonds, the β₁ profiles are not very specific. This similarity has been appreciated only recently [23], also because of the limited number, and quite different nature, of the systems hitherto analyzed, often by the trivial requirement of being readily available.

4. Conclusions

PECD is found to be a very sensitive probe of molecular chirality, also in the nondescriptive class of pure saturated hydrocarbons. The predicted signal is generally very strong and the imprint of absolute configuration unmistakable. Because of this, the current level of theoretical simulations is amply sufficient to give an unequivocal assignment of the absolute configuration in the compounds studied. The discrimination of different structures among similar molecules is instead not very strong. In this respect, it is probably the very low kinetic energy region, close to the threshold, that can prove most sensitive, a region however more difficult to simulate accurately. One may add however that only the outermost ionizations have been considered here, and most systems will still present some additional well-defined bands that could provide further discrimination.

It must be reminded that several refinements are already possible with respect to the pure DFT approach presented in this exploratory study [24,25,26], although the features examined are so clear and strong that we believe are realistically described. More work in the development of theoretical approaches is needed, as already mentioned, to capture finer details, and especially to describe the first few eV after threshold. Due to the complexity of chiral molecules, it will be difficult to employ approaches beyond a single channel description. However, improvements of the single-particle effective potential used, and inclusion of polarization effects by inclusion of a limited set of virtual excited states may significantly improve the near-threshold accuracy.

Finally, the technique is presently applied to gas-phase systems, which may be an advantage and is anyway not a significant limitation for most samples. Recent advancements in liquid jet photoelectron spectroscopy may further lift this limitation. A second limitation is the availability of suitable laboratory sources, as most experiments have been performed at synchrotrons. However, the fast developments in laser sources will again remove this limitation, and in fact, a first study employing high harmonic generation sources has been already performed [27]. Furthermore, the possibility of multiphoton PECD with a laboratory setting has been demonstrated, with good performance [28,29]. This still requires the development of predictive theoretical tools.