Theoretical Study on the Structures, Electronic Properties, and Aromaticity of Thiophene Analogues of Anti-Kekulene
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
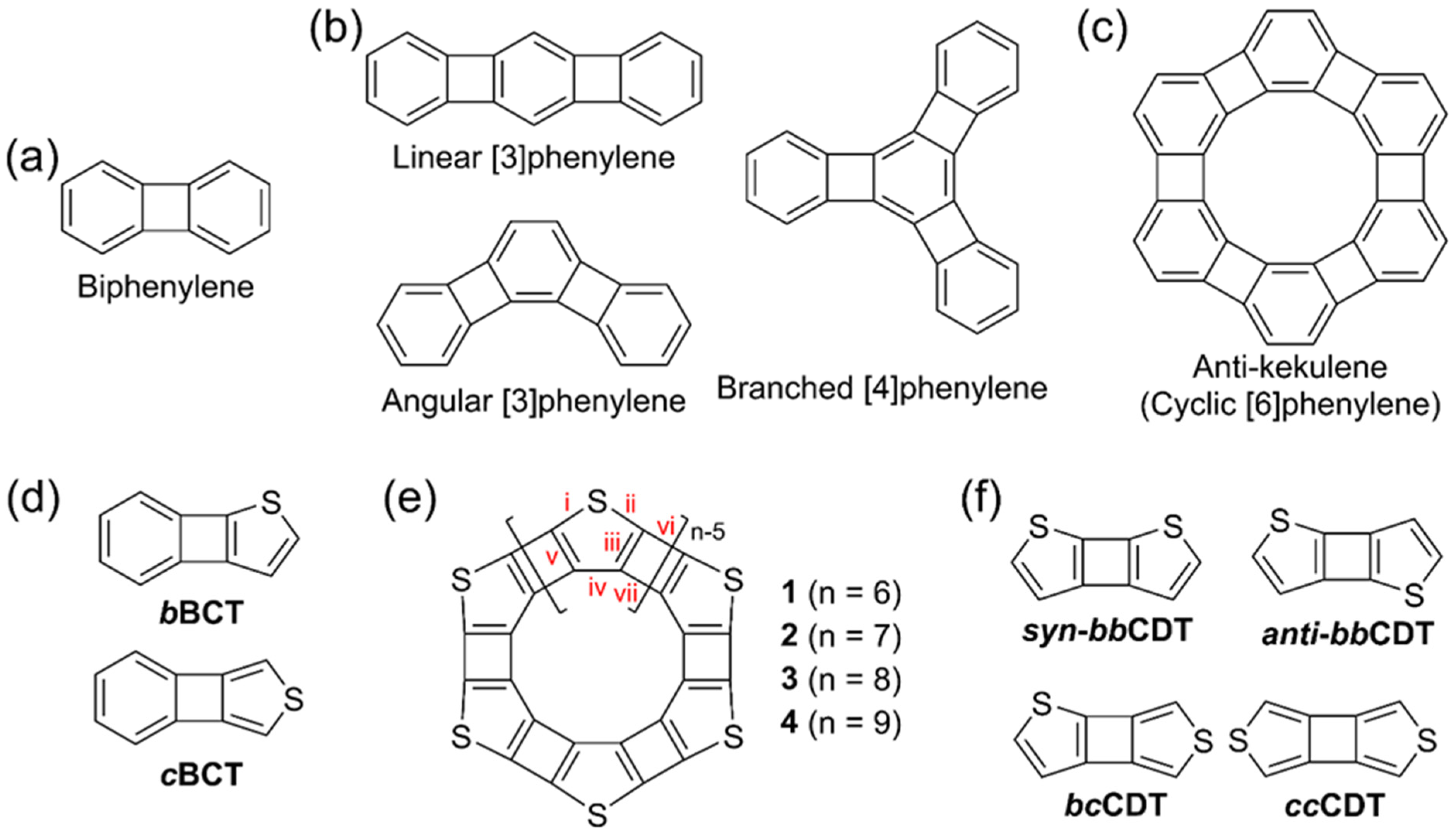
3.1. Structures, Electronic Properties, and Aromaticity of Cyclobutadithiophenes
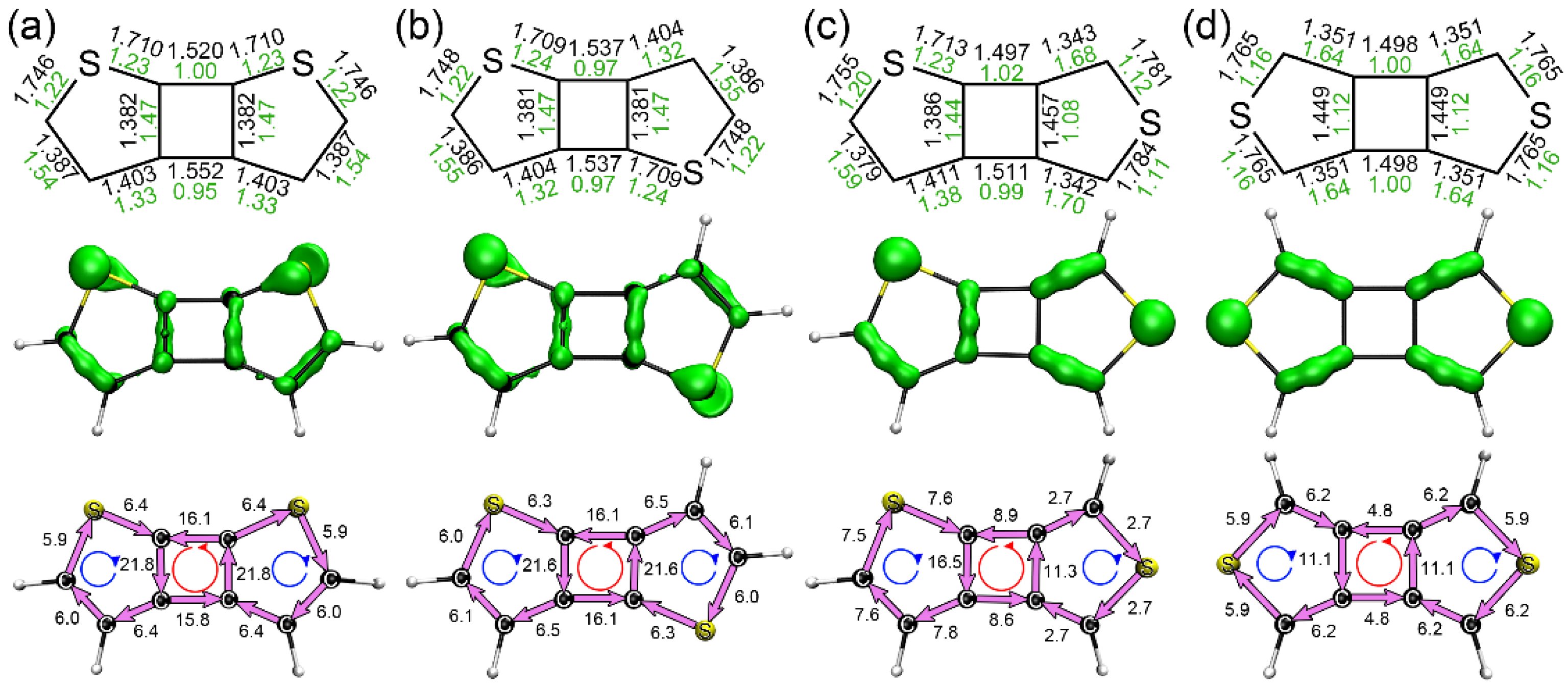
3.2. Structure and Aromaticity of Anti-Kekulene
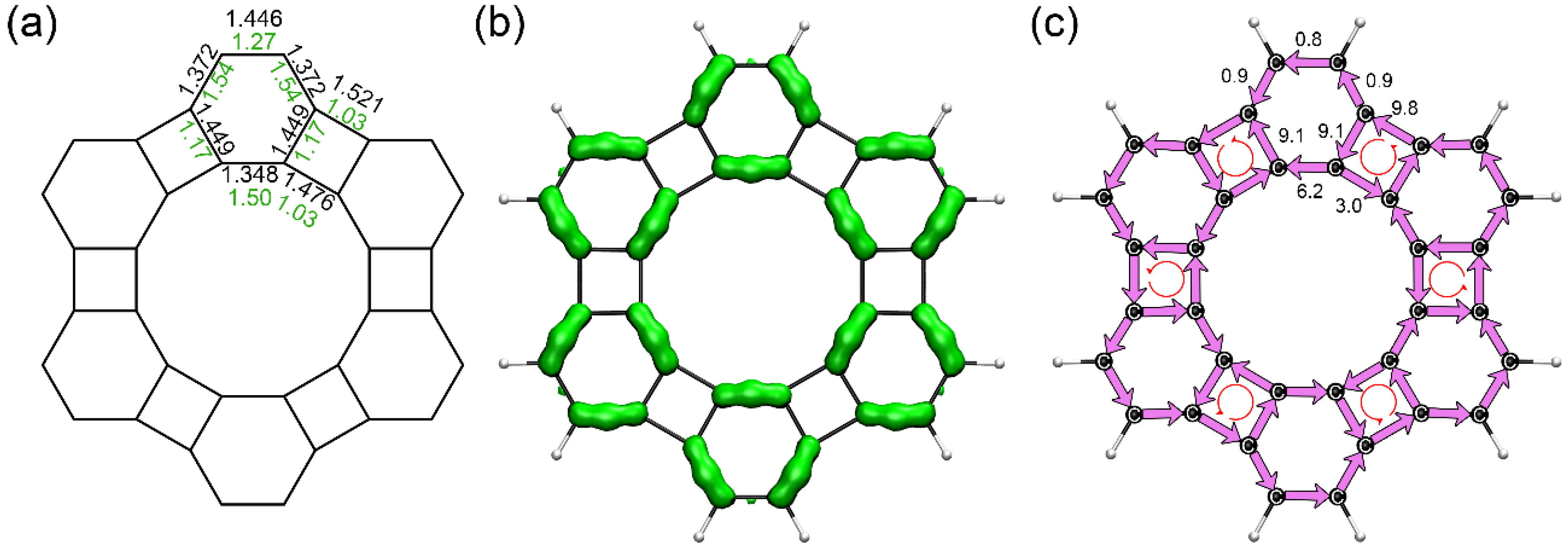
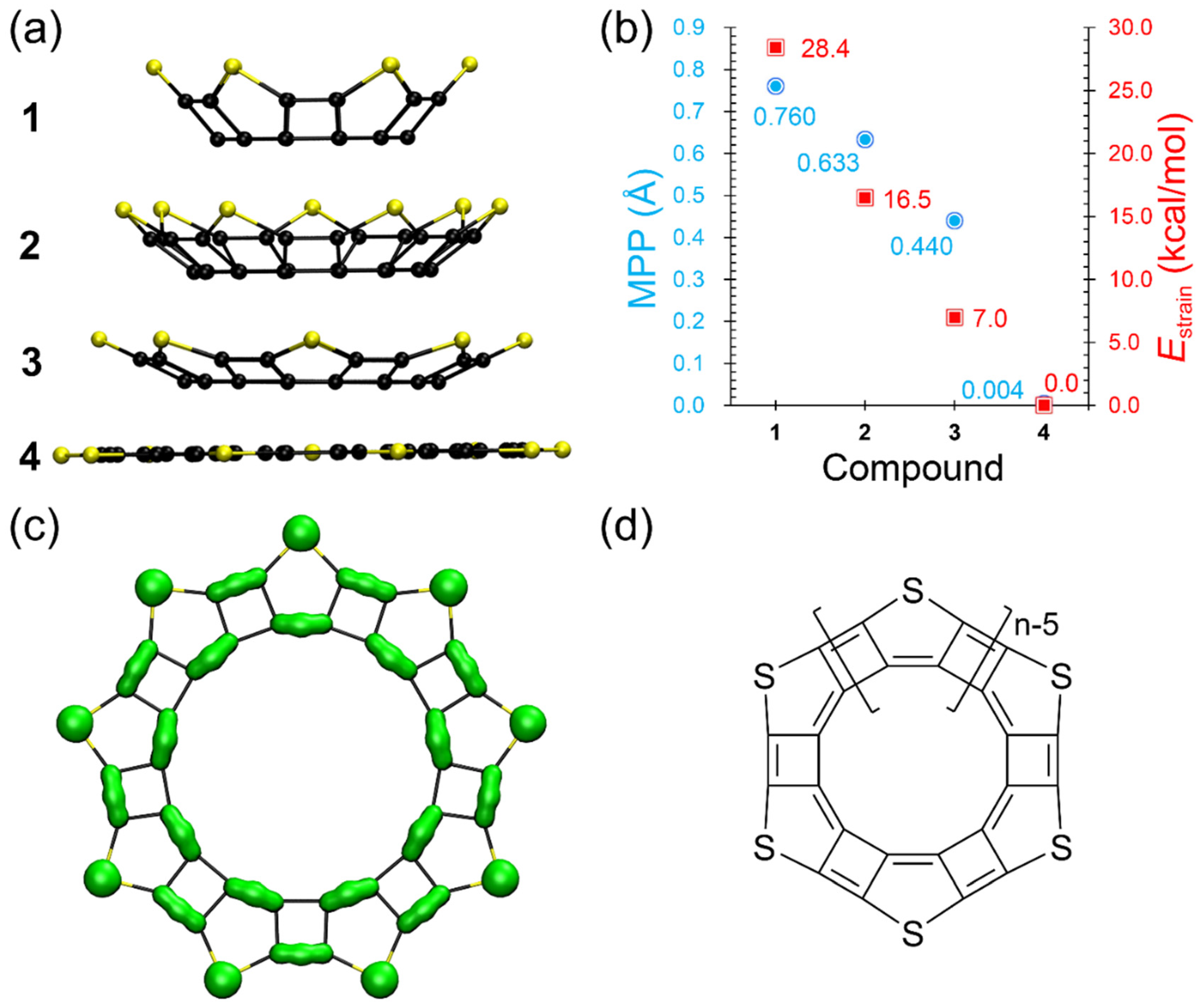
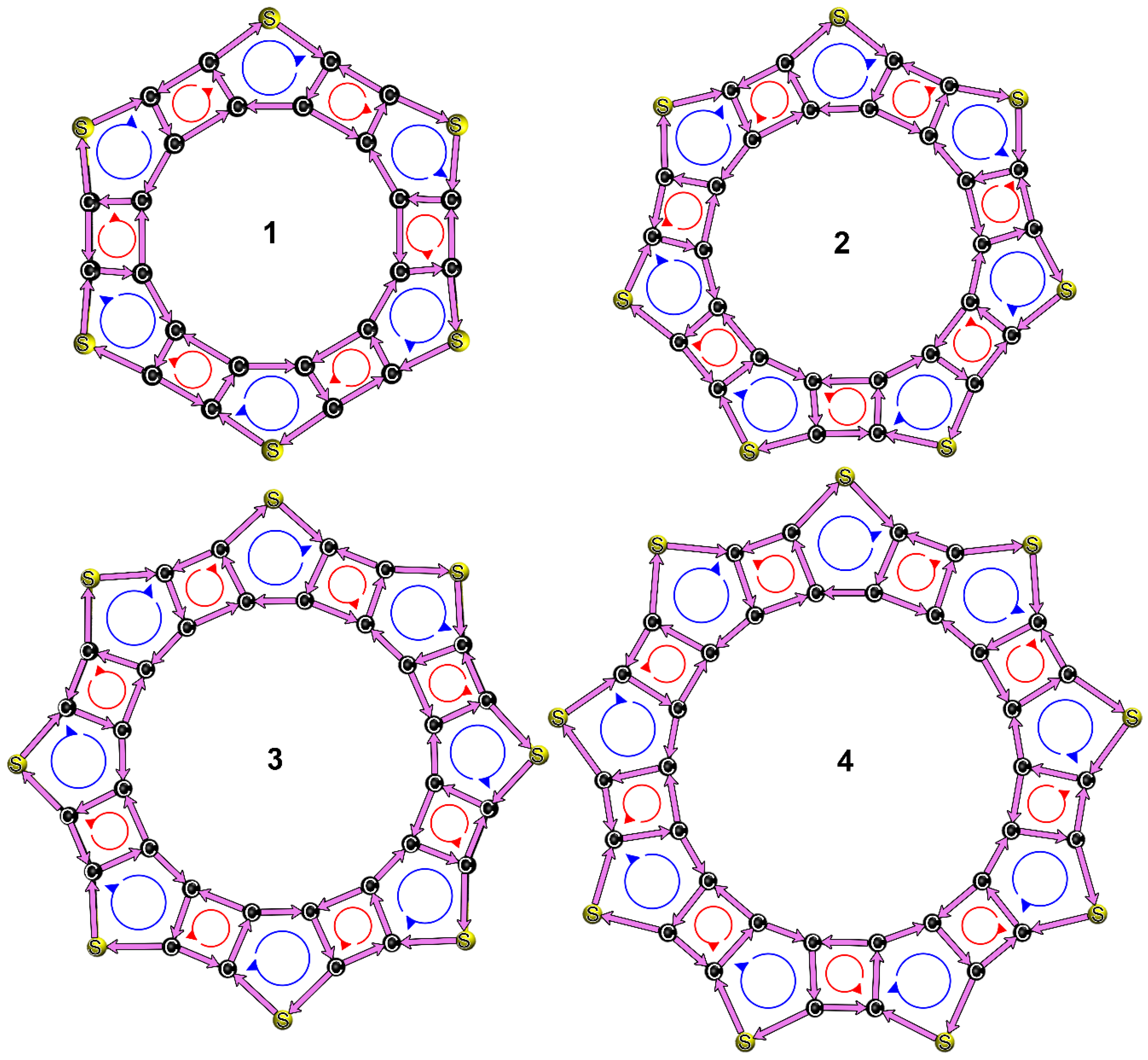
3.3. Structures, Electronic Properties, and Aromaticity of Thiophene Analogues of Anti-Kekulene
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, C.; Baltazar, J.; Tovar, J.D. Manifestations of Antiaromaticity in Organic Materials: Case Studies of Cyclobutadiene, Borole, and Pentalene. Eur. J. Org. Chem. 2022, 2022, e202101343. [Google Scholar] [CrossRef]
- Miyoshi, H.; Sugiura, R.; Kishi, R.; Spisak, S.N.; Wei, Z.; Muranaka, A.; Uchiyama, M.; Kobayashi, N.; Chatterjee, S.; Ie, Y.; et al. Dianion and Dication of Tetracyclopentatetraphenylene as Decoupled Annulene-within-an-Annulene Models. Angew. Chem. Int. Ed. 2022, 61, e202115316. [Google Scholar] [CrossRef]
- Konishi, A.; Okada, Y.; Kishi, R.; Nakano, M.; Yasuda, M. Enhancement of Antiaromatic Character via Additional Benzoannulation into Dibenzo[a,f]Pentalene: Syntheses and Properties of Benzo[a]Naphtho[2,1-f]Pentalene and Dinaphtho[2,1-a,f]Pentalene. J. Am. Chem. Soc. 2019, 141, 560–571. [Google Scholar] [CrossRef]
- Esser, B.; Wössner, J.S.; Hermann, M. Conjugated Nanohoops with Dibenzo[a,e]Pentalenes as Nonalternant and Antiaromatic π-Systems. Synlett 2022, 33, 737–753. [Google Scholar] [CrossRef]
- Kalapos, P.P.; Mayer, P.J.; Gazdag, T.; Demeter, A.; Oruganti, B.; Durbeej, B.; London, G. Photoswitching of Local (Anti)Aromaticity in Biphenylene-Based Diarylethene Molecular Switches. J. Org. Chem. 2022, 87, 9532–9542. [Google Scholar] [CrossRef]
- Liu, J.; Ma, J.; Zhang, K.; Ravat, P.; Machata, P.; Avdoshenko, S.; Hennersdorf, F.; Komber, H.; Pisula, W.; Weigand, J.J.; et al. π-Extended and Curved Antiaromatic Polycyclic Hydrocarbons. J. Am. Chem. Soc. 2017, 139, 7513–7521. [Google Scholar] [CrossRef]
- Akahori, S.; Kaga, A.; Kim, J.; Yorimitsu, H.; Kim, D.; Shinokubo, H.; Miyake, Y. Protonation-Induced Antiaromaticity in Octaaza[8]Circulenes: Cyclooctatetraene Scaffolds Constrained with Four Amidine Moieties. Chem. Asian J. 2022, 17, e202200244. [Google Scholar] [CrossRef]
- Tahara, K.; Kozuma, H.; Venkatesh, V.; Ryomura, E.; Miyoshi, H.; Nakamachi, K.; Kishi, R.; Takahashi, H.; Nakano, M.; Tobe, Y. Generation of Aromatic (Dehydro)Benzoannulene Dications Stabilized by Platinum Catecholate Complexes. ChemPlusChem 2017, 82, 1052–1056. [Google Scholar] [CrossRef]
- Takano, H.; Ito, T.; Kanyiva, K.S.; Shibata, T. Recent Advances of Biphenylene: Synthesis, Reactions and Uses. Eur. J. Org. Chem. 2019, 2019, 2871–2883. [Google Scholar] [CrossRef]
- Lothrop, W.C. Biphenylene. J. Am. Chem. Soc. 1941, 63, 1187–1191. [Google Scholar] [CrossRef]
- Miljanić, O.Š.; Vollhardt, K.P.C. [N]Phenylenes: A Novel Class of Cyclohexatrienoid Hydrocarbon. In Carbon-Rich Compounds: From Molecules to Materials; Haley, M.M., Tykwinski, R.R., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2006; pp. 140–197. [Google Scholar] [CrossRef]
- Berris, B.C.; Hovakeemian, G.H.; Lai, Y.H.; Mestdagh, H.; Vollhardt, K.P.C. A New Approach to the Construction of Biphenylenes by the Cobalt-Catalyzed Cocyclization of o-Diethynylbenzenes with Alkynes. Application to an Iterative Approach to [3]Phenylene, the First Member of a Novel Class of Benzocyclobutadienoid Hydrocarbons. J. Am. Chem. Soc. 1985, 107, 5670–5687. [Google Scholar] [CrossRef]
- Diercks, R.; Vollhardt, K.P.C. Novel Synthesis of the Angular [3]Phenylene (Terphenylene) by Cobalt-Catalyzed Cyclization of Bis(2-Ethynylphenyl)Ethyne: A Molecule with an Internal Cyclohexatriene Ring. Angew. Chem. Int. Ed. Engl. 1986, 25, 266–268. [Google Scholar] [CrossRef]
- Diercks, R.; Vollhardt, K.P.C. Tris(Benzocyclobutadieno)Benzene, the Triangular [4]Phenylene with a Completely Bond-Fixed Cyclohexatriene Ring: Cobalt-Catalyzed Synthesis from Hexaethynylbenzene and Thermal Ring Opening to 1,2:5,6:9,10-Tribenzo-3,4,7,8,11,12-Hexadehydro[12]Annulene. J. Am. Chem. Soc. 1986, 108, 3150–3152. [Google Scholar] [CrossRef]
- Gershoni-Poranne, R.; Gibson, C.M.; Fowler, P.W.; Stanger, A. Concurrence between Current Density, Nucleus-Independent Chemical Shifts, and Aromatic Stabilization Energy: The Case of Isomeric [4]- and [5]Phenylenes. J. Org. Chem. 2013, 78, 7544–7553. [Google Scholar] [CrossRef]
- Radenković, S.; Tošović, J.; Havenith, R.W.A.; Bultinck, P. Ring Currents in Benzo- and Benzocyclobutadieno-Annelated Biphenylene Derivatives. ChemPhysChem 2015, 16, 216–222. [Google Scholar] [CrossRef] [PubMed]
- Holmes, D.; Kumaraswamy, S.; Matzger, A.J.; Vollhardt, K.P.C. On the Nature of Nonplanarity in the [N]Phenylenes. Chem. Eur. J. 1999, 5, 3399–3412. [Google Scholar] [CrossRef]
- Dosche, C.; Mickler, W.; Löhmannsröben, H.-G.; Agenet, N.; Vollhardt, K.P.C. Photoinduced Electron Transfer in [N]Phenylenes. J. Photochem. Photobiol. A 2007, 188, 371–377. [Google Scholar] [CrossRef][Green Version]
- Schulman, J.M.; Disch, R.L. Theoretical Studies of the [N]Phenylenes. J. Am. Chem. Soc. 1996, 118, 8470–8474. [Google Scholar] [CrossRef]
- Schulman, J.M.; Disch, R.L.; Jiao, H.; Schleyer, P.v.R. Chemical Shifts of the [N]Phenylenes and Related Compounds. J. Phys. Chem. A 1998, 102, 8051–8055. [Google Scholar] [CrossRef]
- Anjalikrishna, P.K.; Gadre, S.R.; Suresh, C.H. Antiaromaticity–Aromaticity Interplay in Fused Benzenoid Systems Using Molecular Electrostatic Potential Topology. J. Phys. Chem. A 2021, 125, 5999–6012. [Google Scholar] [CrossRef]
- Babić, D.; Trinajstić, N. Kekulene and Antikekulene. J. Mol. Struct. THEOCHEM 1994, 314, 321–327. [Google Scholar] [CrossRef]
- Aihara, J. A Simple Method for Estimating the Superaromatic Stabilization Energy of a Super-Ring Molecule. J. Phys. Chem. A 2008, 112, 4382–4385. [Google Scholar] [CrossRef] [PubMed]
- Dickens, T.K.; Mallion, R.B. Topological Ring-Current Assessment of the ‘Annulene-within-an-Annulene’ Model in [N]-Circulenes and Some Structures Related to Kekulene. Chem. Phys. Lett. 2011, 517, 98–102. [Google Scholar] [CrossRef]
- Gribanova, T.N.; Minyaev, R.M.; Minkin, V.I. Parquet Compounds on the Basis of Eight- and Twelve-Membered Structure Blocks: Quantum-Chemical Study. Russ. J. Org. Chem. 2016, 52, 268–282. [Google Scholar] [CrossRef]
- Randić, M.; Balaban, A.T.; Plavšić, D. Applying the Conjugated Circuits Method to Clar Structures of [n]Phenylenes for Determining Resonance Energies. Phys. Chem. Chem. Phys. 2011, 13, 20644–20648. [Google Scholar] [CrossRef]
- Miyoshi, H.; Nobusue, S.; Shimizu, A.; Tobe, Y. Non-Alternant Non-Benzenoid Kekulenes: The Birth of a New Kekulene Family. Chem. Soc. Rev. 2015, 44, 6560–6577. [Google Scholar] [CrossRef]
- Dickens, T.K.; Mallion, R.B. An Analysis of Topological Ring-Currents and Their Use in Assessing the Annulene-within-an-Annulene Model for Super-Ring Conjugated Systems. Croat. Chem. Acta 2013, 86, 387–406. [Google Scholar] [CrossRef]
- Dickens, T.K.; Mallion, R.B. Topological Ring-Currents in Conjugated Systems. MATCH Commun. Math. Comput. Chem. 2016, 76, 297–356. [Google Scholar]
- Yates, K. Hückel Molecular Orbital Theory. In Hückel Molecular Orbital Theory; Academic Press Inc.: New York, NY, USA, 1978; pp. 27–87. [Google Scholar] [CrossRef]
- London, F. Théorie Quantique Des Courants Interatomiques Dans Les Combinaisons Aromatiques. J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- Eickmeier, C.; Junga, H.; Matzger, A.J.; Scherhag, F.; Shim, M.; Vollhardt, K.P.C. 5,6,11,12,17,18-Hexadehydro-1,4,7,10,13,16-Hexaethynyltribenzo[a,e,i,]Cyclododecene: Synthesis and CpCo-Catalyzed Cycloisomerization to the First Superdelocalized Oligophenylenes. Angew. Chem. Int. Ed. Engl. 1997, 36, 2103–2108. [Google Scholar] [CrossRef]
- Fonari, A.; Röder, J.C.; Shen, H.; Timofeeva, T.V.; Vollhardt, K.P.C. Toward Antikekulene: Angular 1,2-Di-, 2,3-Di-, and 1,2,15,16-Tetrachloro[6]Phenylene. Synlett 2014, 25, 2429–2433. [Google Scholar] [CrossRef]
- Dahlmann, U.; Vollhardt, K.P.C. Oligoether-Substituted Derivatives of Carbon-Rich 1,4,7,10,13,16-Hexaethynyltribenzo[a,e,i]Cyclododeca-5,11,17-Triyne (C36H12) and 1,4,9,12-Tetrakis(Ethynyl)Dibenzo[a,g]Cyclododeca-5,7,13,15-Tetrayne (C28H8): Potential Precursors to the Circular [6]Phenylene (‘Antikekulene’) Frame. Synthesis 2020, 52, 1287–1300. [Google Scholar] [CrossRef]
- Mamada, M.; Yamashita, Y. S-Containing Polycyclic Heteroarenes: Thiophene-Fused and Thiadiazole-Fused Arenes as Organic Semiconductors. In Polycyclic Arenes and Heteroarenes: Synthesis, Properties, and Applications; Miao, Q., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 277–308. [Google Scholar] [CrossRef]
- Okamoto, T.; Mitsui, C.; Yamagishi, M.; Nakahara, K.; Soeda, J.; Hirose, Y.; Miwa, K.; Sato, H.; Yamano, A.; Matsushita, T.; et al. V-Shaped Organic Semiconductors with Solution Processability, High Mobility, and High Thermal Durability. Adv. Mater. 2013, 25, 6392–6397. [Google Scholar] [CrossRef]
- Irie, M.; Fukaminato, T.; Matsuda, K.; Kobatake, S. Photochromism of Diarylethene Molecules and Crystals: Memories, Switches, and Actuators. Chem. Rev. 2014, 114, 12174–12277. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, K.; Sannohe, Y.; Kaieda, S.; Tanaka, K.; Osuga, H.; Tahara, H.; Xu, Y.; Kawase, T.; Bando, T.; Sugiyama, H. A Chiral Wedge Molecule Inhibits Telomerase Activity. J. Am. Chem. Soc. 2010, 132, 3778–3782. [Google Scholar] [CrossRef] [PubMed]
- di Maria, F.; Zangoli, M.; Barbarella, G. Supramolecular Thiophene-Based Materials: A Few Examples of the Interplay between Synthesis, Optoelectronic Properties and Applications. Org. Mater. 2021, 3, 321–336. [Google Scholar] [CrossRef]
- Ueda, M.; Aoki, T.; Akiyama, T.; Nakamuro, T.; Yamashita, K.; Yanagisawa, H.; Nureki, O.; Kikkawa, M.; Nakamura, E.; Aida, T.; et al. Alternating Heterochiral Supramolecular Copolymerization. J. Am. Chem. Soc. 2021, 143, 5121–5126. [Google Scholar] [CrossRef]
- Li, G.; Gopalakrishna, T.Y.; Phan, H.; Herng, T.S.; Ding, J.; Wu, J. From Open-Shell Singlet Diradicaloid to Closed-Shell Global Antiaromatic Macrocycles. Angew. Chem. Int. Ed. 2018, 57, 7166–7170. [Google Scholar] [CrossRef]
- Chernichenko, K.Y.; Sumerin, V.V.; Shpanchenko, R.V.; Balenkova, E.S.; Nenajdenko, V.G. “Sulflower”: A New Form of Carbon Sulfide. Angew. Chem. Int. Ed. 2006, 45, 7367–7370. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Suzuki, T. Tetrabenzo[8]Circulene: Aromatic Saddles from Negatively Curved Graphene. J. Am. Chem. Soc. 2013, 135, 14074–14077. [Google Scholar] [CrossRef]
- Feng, C.-N.; Kuo, M.-Y.; Wu, Y.-T. Synthesis, Structural Analysis, and Properties of [8]Circulenes. Angew. Chem. Int. Ed. 2013, 52, 7791–7794. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, T.; Suizu, R.; Yoshikawa, H.; Awaga, K. Molecular, Crystal, and Thin-Film Structures of Octathio[8]Circulene: Release of Antiaromatic Molecular Distortion and Lamellar Structure of Self-Assembling Thin Films. Chem. Eur. J. 2008, 14, 6053–6056. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, T.; Matsushita, M.M.; Awaga, K. Ionic-Liquid Component Dependence of Carrier Injection and Mobility for Electric-Double-Layer Organic Thin-Film Transistors. J. Phys. Chem. C 2012, 116, 5240–5245. [Google Scholar] [CrossRef]
- Fujimoto, T.; Matsushita, M.M.; Awaga, K. Dual-Gate Field-Effect Transistors of Octathio[8]Circulene Thin-Films with Ionic Liquid and SiO2 Gate Dielectrics. Appl. Phys. Lett. 2010, 97, 123303. [Google Scholar] [CrossRef]
- Takimiya, K.; Shinamura, S.; Osaka, I.; Miyazaki, E. Thienoacene-Based Organic Semiconductors. Adv. Mater. 2011, 23, 4347–4370. [Google Scholar] [CrossRef]
- Dressler, J.J.; Teraoka, M.; Espejo, G.L.; Kishi, R.; Takamuku, S.; Gómez-García, C.J.; Zakharov, L.N.; Nakano, M.; Casado, J.; Haley, M.M. Thiophene and Its Sulfur Inhibit Indenoindenodibenzothiophene Diradicals from Low-Energy Lying Thermal Triplets. Nat. Chem. 2018, 10, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Usuba, J.; Fukazawa, A. Thiophene-Fused 1,4-Diazapentalene: A Stable C=N-Containing Π-Conjugated System with Restored Antiaromaticity. Chem. Eur. J. 2021, 27, 16127–16134. [Google Scholar] [CrossRef]
- Aita, K.; Ohmae, T.; Takase, M.; Nomura, K.; Kimura, H.; Nishinaga, T. Dithieno[3,4-b:3′,4′-d]Thiophene-Annelated Antiaromatic Planar Cyclooctatetraene with Olefinic Protons. Org. Lett. 2013, 15, 3522–3525. [Google Scholar] [CrossRef]
- Ohmae, T.; Nishinaga, T.; Wu, M.; Iyoda, M. Cyclic Tetrathiophenes Planarized by Silicon and Sulfur Bridges Bearing Antiaromatic Cyclooctatetraene Core: Syntheses, Structures, and Properties. J. Am. Chem. Soc. 2010, 132, 1066–1074. [Google Scholar] [CrossRef]
- Fringuelli, F.; Marino, G.; Taticchi, A.; Grandolini, G. A Comparative Study of the Aromatic Character of Furan, Thiophen, Selenophen, and Tellurophen. J. Chem. Soc. Perkin Trans. 1974, 2, 332–337. [Google Scholar] [CrossRef]
- Frederickson, C.K.; Zakharov, L.N.; Haley, M.M. Modulating Paratropicity Strength in Diareno-Fused Antiaromatics. J. Am. Chem. Soc. 2016, 138, 16827–16838. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.R.; Brown, J.M.; Sondheimer, F. Annelated 14π-Electron Systems. The Synthesis of a Dimethylbisdehydro[14]Annuleno[c]Thiophene, -[b]Thiophene and -[b]Furan. Tetrahedron Lett. 1975, 16, 4183–4186. [Google Scholar] [CrossRef]
- Boydston, A.J.; Haley, M.M.; Williams, R.V.; Armantrout, J.R. Diatropicity of 3,4,7,8,9,10,13,14-Octadehydro[14]Annulenes: A Combined Experimental and Theoretical Investigation. J. Org. Chem. 2002, 67, 8812–8819. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, M.J.; Yelle, R.B.; Zakharov, L.N.; Haley, M.M. Structure−Property Investigations of Conjugated Thiophenes Fused onto a Dehydro[14]Annulene Scaffold. J. Org. Chem. 2008, 73, 4424–4432. [Google Scholar] [CrossRef]
- Sarkar, A.; Haley, M.M. Synthesis and Characterization of Dehydrothieno[18]Annulenes. Chem. Commun. 2000, 1733–1734. [Google Scholar] [CrossRef]
- Ohtomo, Y.; Ishiwata, K.; Hashimoto, S.; Kuroiwa, T.; Tahara, K. Revisiting Dehydrothiopheno[12]Annulenes: Synthesis, Electronic Properties, and Aromaticity. J. Org. Chem. 2021, 86, 13198–13211. [Google Scholar] [CrossRef]
- Usuba, J.; Hayakawa, M.; Yamaguchi, S.; Fukazawa, A. Dithieno[a,e]Pentalenes: Highly Antiaromatic Yet Stable π-Electron Systems without Bulky Substituents. Chem. Eur. J. 2021, 27, 1638–1647. [Google Scholar] [CrossRef]
- Gazdag, T.; Mayer, P.J.; Kalapos, P.P.; Holczbauer, T.; El Bakouri, O.; London, G. Unsymmetrical Thienopentalenes: Synthesis, Optoelectronic Properties, and (Anti)Aromaticity Analysis. ACS Omega 2022, 7, 8336–8349. [Google Scholar] [CrossRef]
- Engelhardt, V.; Gabriel Garcia, J.; Hubaud, A.A.; Lyssenko, K.A.; Spyroudis, S.; Timofeeva, T.V.; Tongwa, P.; Vollhardt, K.P.C. The Cobalt-Way to Heterophenylenes: Syntheses of 2-Thianorbiphenylenes, Monoazabiphenylenes, and Linear 1-Aza[3]Phenylene {biphenyleno[2,3-a] Cyclobuta[1,2- b ]Pyridine}. Synlett 2011, 2011, 280–284. [Google Scholar] [CrossRef][Green Version]
- Garratt, P.J.; Vollhardt, K.P.C. Benzo[3,4]Cyclobuta[1,2-c]Thiophen (2-Thianorbiphenylene). J. Chem. Soc. D 1970, 109. [Google Scholar] [CrossRef]
- Barton, J.W.; Lapham, D.J. Benzo[3,4]Cyclobuta[1,2-b]Thiophene. Tetrahedron Lett. 1979, 20, 3571–3572. [Google Scholar] [CrossRef]
- Hashimoto, S.; Tahara, K. Theoretical Study on the Geometry, Aromaticity, and Electronic Properties of Benzo[3,4]Cyclobutathiophenes and Their Homologues. J. Org. Chem. 2019, 84, 9850–9858. [Google Scholar] [CrossRef] [PubMed]
- Párkányl, C.; Huang, D.-L.; Kalsotra, B.L.; Jeffries, A.T.I.; Lloyd, W.D. Attempted Synthesis of the Dithiophene Analogs of Biphenylene. Bull. Soc. Chim. Belg. 1987, 96, 237–244. [Google Scholar] [CrossRef]
- Shepherd, M.K. Cyclobuta[1,2-c:3,4-c’]Dithiophene. J. Chem. Soc. Chem. Commun. 1985, 880–881. [Google Scholar] [CrossRef]
- Ponce Ortiz, R.; Casado, J.; Rodríguez González, S.; Hernández, V.; López Navarrete , J.T.; Viruela, P.M.; Ortí, E.; Takimiya, K.; Otsubo, T. Quinoidal Oligothiophenes: Towards Biradical Ground-State Species. Chem. Eur. J. 2010, 16, 470–484. [Google Scholar] [CrossRef]
- Takahashi, T.; Matsuoka, K.; Takimiya, K.; Otsubo, T.; Aso, Y. Extensive Quinoidal Oligothiophenes with Dicyanomethylene Groups at Terminal Positions as Highly Amphoteric Redox Molecules. J. Am. Chem. Soc. 2005, 127, 8928–8929. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16; Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Boese, R.; Bläser, D.; Latz, R. Redetermination of Biphenylene at 130K. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1999, 55, IUC9900067. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Stability Analysis for Solutions of the Closed Shell Kohn–Sham Equation. J. Chem. Phys. 1996, 104, 9047–9052. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView (Ver. 6. 0. 16); Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lu, T. Simple, Reliable, and Universal Metrics of Molecular Planarity. J. Mol. Model. 2021, 27, 263. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Kruszewski, J.; Krygowski, T.M. Definition of Aromaticity Basing on the Harmonic Oscillator Model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic Studies of Inter- and Intramolecular Interactions Reflected in Aromatic Character of π-Electron Systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; Van Damme, S. Multicenter Bond Indices as a New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Casademont-Reig, I.; Ramos-Cordoba, E.; Torrent-Sucarrat, M.; Matito, E. Aromaticity Descriptors Based on Electron Delocalization. In Aromaticity: Modern Computational Methods and Applications; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 235–259. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO Version 3.1; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 1998. [Google Scholar]
- Wiberg, K.B. Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Schmider, H.L.; Becke, A.D. Chemical Content of the Kinetic Energy Density. J. Mol. Struct. THEOCHEM 2000, 527, 51–61. [Google Scholar] [CrossRef]
- Steinmann, S.N.; Mo, Y.; Corminboeuf, C. How Do Electron Localization Functions Describe π-Electron Delocalization? Phys. Chem. Chem. Phys. 2011, 13, 20584–20592. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Fallah-Bagher-Shaidaei, H.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Which NICS Aromaticity Index for Planar π Rings Is Best? Org. Lett. 2006, 8, 863–866. [Google Scholar] [CrossRef] [PubMed]
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of Current Densities Using Gauge-Including Atomic Orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The Gauge Including Magnetically Induced Current Method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef]
- Myrvold, W.; Fowler, P.W.; Clarke, J. Partitioning Hückel–London Currents into Cycle Contributions. Chemistry 2021, 3, 1138–1156. [Google Scholar] [CrossRef]
- Aihara, J. Graph Theory of Ring-Current Diamagnetism. Bull. Chem. Soc. Jpn. 2018, 91, 274–303. [Google Scholar] [CrossRef]
- Pasquarello, A.; Schlüter, M.; Haddon, R.C. Ring Currents in Topologically Complex Molecules: Application to C60, C70, and Their Hexa-Anions. Phys. Rev. A 1993, 47, 1783–1789. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Malagoli, M.; Zanasi, R. Computational Approach to Molecular Magnetic Properties by Continuous Transformation of the Origin of the Current Density. Chem. Phys. Lett. 1994, 220, 299–304. [Google Scholar] [CrossRef]
- Monaco, G.; Summa, F.F.; Zanasi, R. Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems. J. Chem. Inf. Model. 2021, 61, 270–283. [Google Scholar] [CrossRef]
- Rauhalahti, M.; Taubert, S.; Sundholm, D.; Liégeois, V. Calculations of Current Densities for Neutral and Doubly Charged Persubstituted Benzenes Using Effective Core Potentials. Phys. Chem. Chem. Phys. 2017, 19, 7124–7131. [Google Scholar] [CrossRef]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware, Inc.: New York, NY, USA, 2015; ISBN 978-1-930934-30-6. [Google Scholar]
- Christoph, H.; Grunenberg, J.; Hopf, H.; Dix, I.; Jones, P.G.; Scholtissek, M.; Maier, G. MP2 and DFT Calculations on Circulenes and an Attempt to Prepare the Second Lowest Benzolog, [4]Circulene. Chem. Eur. J. 2008, 14, 5604–5616. [Google Scholar] [CrossRef] [PubMed]
- Fabian, J.; Hartmann, H. Structure and Properties of α-Cyclo[N]Thiophenes as Potential Electronic Materials—A Theoretical Study. J. Phys. Org. Chem. 2007, 20, 554–567. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Handgraaf, J.-W.; Baerends, E.J.; Bickelhaupt, F.M. Voronoi Deformation Density (VDD) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD Methods for Charge Analysis. J. Comput. Chem. 2004, 25, 189–210. [Google Scholar] [CrossRef] [PubMed]
- Davidson, E.R.; Chakravorty, S. A Test of the Hirshfeld Definition of Atomic Charges and Moments. Theor. Chim. Acta 1992, 83, 319–330. [Google Scholar] [CrossRef]
- Saha, S.; Roy, R.K.; Ayers, P.W. Are the Hirshfeld and Mulliken Population Analysis Schemes Consistent with Chemical Intuition? Int. J. Quantum Chem. 2009, 109, 1790–1806. [Google Scholar] [CrossRef]
| Compound | HOMA Value | MCI Value | NICS(1)zz Value (ppm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Thiophene Ring | Benzene Ring | Thiophene Ring | Benzene Ring | 4MR | Thiophene Ring | Benzene Ring | Macrocylic Center | ||||
| b-TR | c-TR | b-TR | c-TR | b-TR | c-TR | ||||||
| syn-bbCDT (C2) a | 0.875 | --- | --- | 0.0758 | --- | --- | 52.5 | −16.3 | --- | --- | |
| anti-bbCDT (Ci) a | 0.870 | --- | --- | 0.0766 | --- | --- | 53.0 | −16.4 | --- | --- | |
| bcCDT (Cs) a | 0.831 | 0.126 | --- | 0.0685 | 0.0401 | --- | 29.2 | −19.1 | −5.2 | --- | |
| ccCDT (D2h) a | --- | 0.373 | --- | --- | 0.0514 | --- | 17.8 | --- | −14.3 | --- | |
| anti-kekulene (D6) a | --- | --- | 0.448 | --- | --- | 0.0484 | 24.3 | --- | --- | 1.9 | 16.6 |
| 1 (C6v) a | −0.707 | --- | --- | 0.0121 | --- | --- | 8.9 | −0.9 | --- | --- | 5.7 |
| 2 (C7v) a | −0.683 | --- | --- | 0.0121 | --- | --- | 10.7 | −0.9 | --- | --- | 4.7 |
| 3 (C8) a | −0.661 | --- | --- | 0.0128 | --- | --- | 10.9 | −0.8 | --- | --- | 4.9 |
| 4 (D9) a | −0.643 | --- | --- | 0.0129 | --- | --- | 11.6 | −0.5 | --- | --- | 4.3 |
| Compound | EGap Value (eV) | Erela Value (kcal/mol) |
|---|---|---|
| syn-bbCDT | 3.13 | 22.7 |
| anti-bbCDT | 3.23 | 22.4 |
| bcCDT | 3.94 | 7.0 |
| ccCDT | 4.35 | 0.0 |
| anti-kekulene | 2.77 | --- |
| 1 | 2.74 | --- |
| 2 | 2.85 | --- |
| 3 | 2.67 | --- |
| 4 | 2.78 | --- |
| Compound | Bond Position a | |||||||
|---|---|---|---|---|---|---|---|---|
| i | ii | iii | iv | v | vi | vii | ||
| 1 | bond length (Å) | 1.781 | 1.781 | 1.494 | 1.334 | 1.494 | 1.379 | 1.481 |
| WBI value | 1.08 | 1.08 | 1.02 | 1.64 | 1.02 | 1.53 | 1.02 | |
| current strength (nA/T) | 0.91 | 0.91 | 2.89 | 0.96 | 2.89 | 1.68 | 1.29 | |
| 2 | bond length (Å) | 1.778 | 1.778 | 1.493 | 1.333 | 1.493 | 1.378 | 1.479 |
| WBI value | 1.09 | 1.09 | 1.02 | 1.64 | 1.02 | 1.53 | 1.02 | |
| current strength (nA/T) | 1.40 | 1.40 | 3.44 | 0.99 | 3.44 | 2.46 | 2.47 | |
| 3 | bond length (Å) | 1.777 | 1.777 | 1.492 | 1.332 | 1.493 | 1.378 | 1.479 |
| WBI value | 1.09 | 1.09 | 1.02 | 1.64 | 1.02 | 1.52 | 1.02 | |
| current strength (nA/T) | 1.72 | 1.72 | 4.32 | 1.52 | 4.32 | 3.01 | 2.61 | |
| 4 | bond length (Å) | 1.773 | 1.773 | 1.493 | 1.334 | 1.493 | 1.375 | 1.483 |
| WBI value | 1.09 | 1.09 | 1.02 | 1.65 | 1.02 | 1.52 | 1.01 | |
| current strength (nA/T) | 2.13 | 2.13 | 5.10 | 1.56 | 5.10 | 3.43 | 3.29 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashimoto, S.; Tahara, K. Theoretical Study on the Structures, Electronic Properties, and Aromaticity of Thiophene Analogues of Anti-Kekulene. Chemistry 2022, 4, 1546-1560. https://doi.org/10.3390/chemistry4040102
Hashimoto S, Tahara K. Theoretical Study on the Structures, Electronic Properties, and Aromaticity of Thiophene Analogues of Anti-Kekulene. Chemistry. 2022; 4(4):1546-1560. https://doi.org/10.3390/chemistry4040102
Chicago/Turabian StyleHashimoto, Shingo, and Kazukuni Tahara. 2022. "Theoretical Study on the Structures, Electronic Properties, and Aromaticity of Thiophene Analogues of Anti-Kekulene" Chemistry 4, no. 4: 1546-1560. https://doi.org/10.3390/chemistry4040102
APA StyleHashimoto, S., & Tahara, K. (2022). Theoretical Study on the Structures, Electronic Properties, and Aromaticity of Thiophene Analogues of Anti-Kekulene. Chemistry, 4(4), 1546-1560. https://doi.org/10.3390/chemistry4040102




