Five Bonds to Carbon through Tri-Coordination in
Abstract
1. Introduction
2. Computational Methodology
3. Results and Discussion
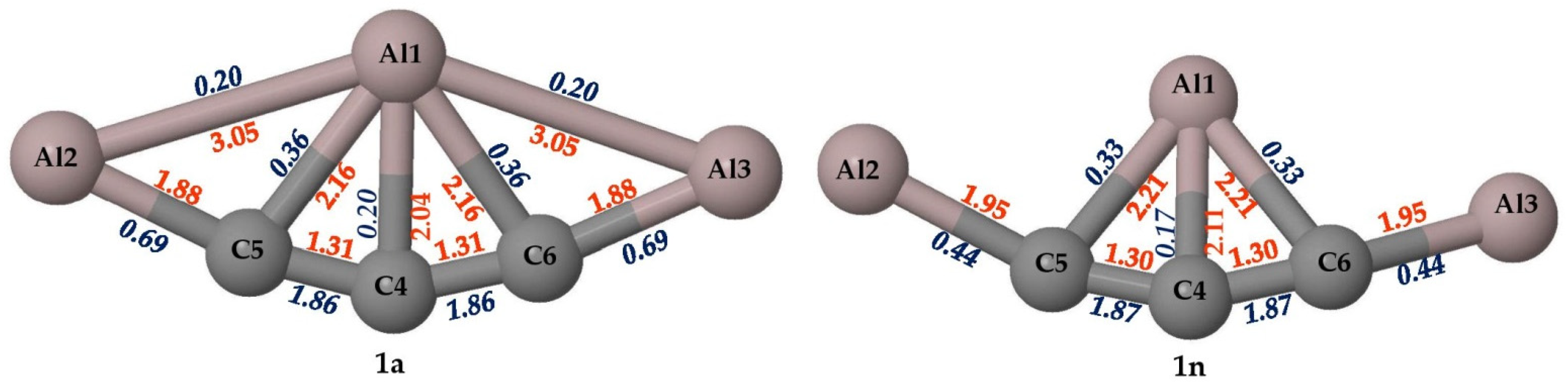
3.1. Wiberg Bond Indices
3.2. Adaptive Natural Density Partitioning (AdNDP) Analysis
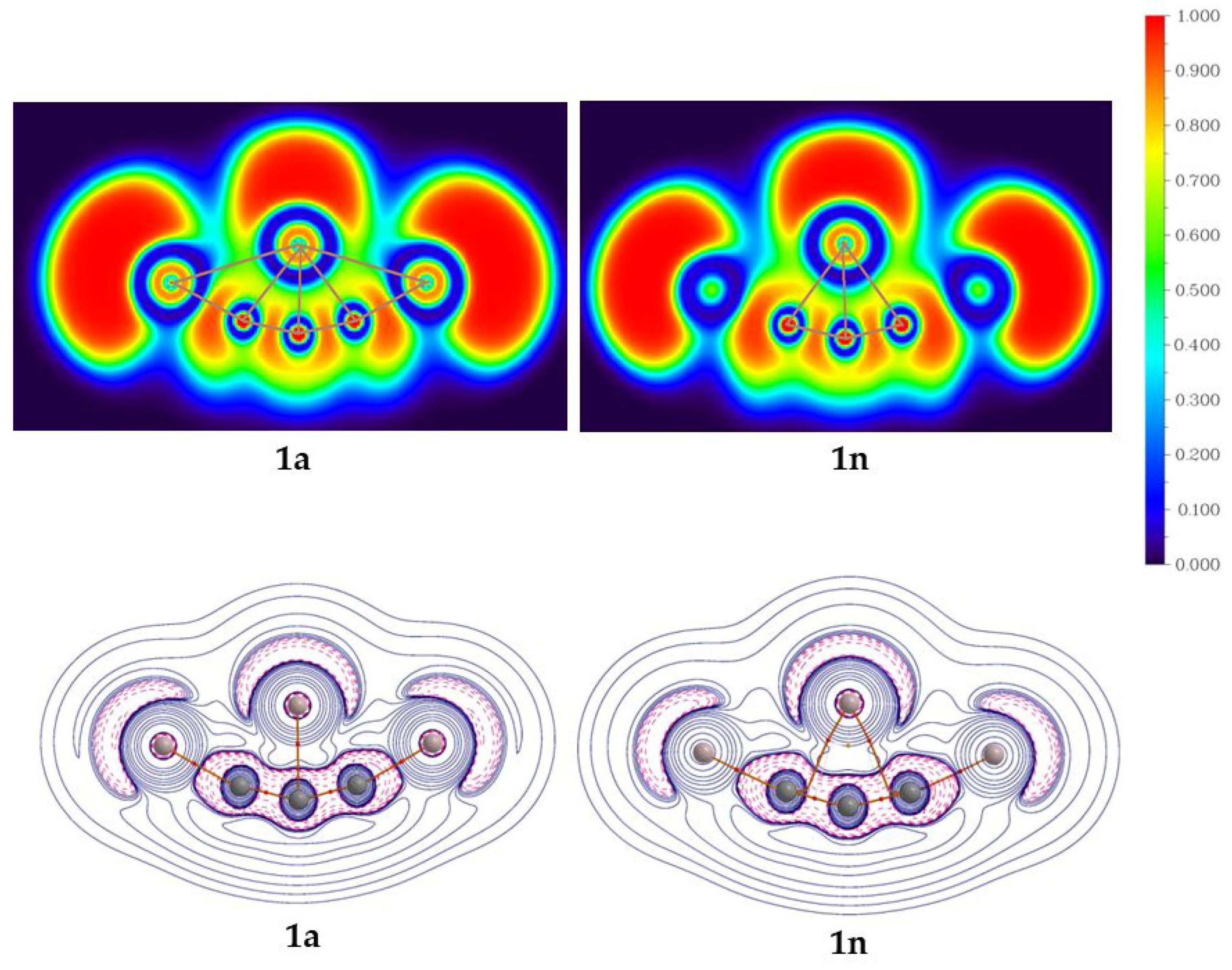
3.3. Atoms in Molecule (AIM) Analysis
3.4. Kinetic Stability
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tal’rose, V.L.; Lyubimova, A.K. Secondary Processes in the Ion Source of the Mass Spectrometer. Dokl. Akad. Nauk SSSR 1952, 86, 909–912. [Google Scholar]
- White, E.T.; Tang, J.; Oka, T. CH5+: The Infrared Spectrum Observed. Science 1999, 284, 135–137. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Wuerthwein, E.U.; Kaufmann, E.; Clark, T.; Pople, J.A. Effectively Hypervalent Molecules. 2. Lithium Carbide (CLi5), Lithium Carbide (CLi6), and the Related Effectively Hypervalent First Row Molecules, CLi5-NHn and CLi6-NHn. J. Am. Chem. Soc. 1983, 105, 5930–5932. [Google Scholar] [CrossRef]
- Kudo, H. Observation of Hypervalent CLi6 by Knudsen-Effusion Mass Spectrometry. Nature 1992, 355, 432–434. [Google Scholar] [CrossRef]
- Dávalos, J.Z.; Herrero, R.; Abboud, J.-L.M.; Mó, O.; Yáñez, M. How can a Carbon Atom Be Covalently Bound to Five Ligands? The Case of Si2(CH3)7+. Angew. Chem. Int. Ed. 2006, 46, 381–385. [Google Scholar] [CrossRef]
- McKee, W.C.; Agarwal, J.; Schaefer, H.F.; Schleyer, P.V.R. Covalent Hypercoordination: Can Carbon Bind Five Methyl Ligands? Angew. Chem. Int. Ed. 2014, 53, 7875–7878. [Google Scholar] [CrossRef]
- Hogeveen, H.; Kwant, P.W. Direct observation of a remarkably stable dication of unusual structure: (CCH3)62+. Tetrahedron Lett. 1973, 14, 1665–1670. [Google Scholar] [CrossRef]
- Schmidbaur, H.; Gabbaie, F.; Schier, A.; Riede, J. Hypercoordinate Carbon in Protonated Tetraauriomethane Molecules. Organometallics 1995, 14, 4969–4971. [Google Scholar] [CrossRef]
- Scherbaum, F.; Grohmann, A.; Müller, G.; Schmidbaur, H. Synthesis, Structure, and Bonding of the Cation [(C6H5)3PAu5C]+. Angew. Chem. Int. Ed. 1989, 28, 463–465. [Google Scholar] [CrossRef]
- Scherbaum, F.; Grohmann, A.; Huber, B.; Krüger, C.; Schmidbaur, H. “Aurophilicity” as a Consequence of Relativistic Effects: The Hexakis (Triphenylphosphaneaurio) Methane Dication [(Ph3PAu)6C]2+. Angew. Chem. Int. Ed. 1988, 27, 1544–1546. [Google Scholar] [CrossRef]
- Malischewski, M.; Seppelt, K. Crystal Structure Determination of the Pentagonal-Pyramidal Hexamethylbenzene Dication C6 (CH3)62+. Angew. Chem. Int. Ed. 2017, 56, 368–370. [Google Scholar] [CrossRef]
- Akiba, K.; Yamashita, M.; Yamamoto, Y.; Nagase, S. Synthesis and Isolation of Stable Hypervalent Carbon Compound (10-C-5) Bearing a 1,8-Dimethoxyanthracene Ligand. J. Am. Chem. Soc. 1999, 121, 10644–10645. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Yamamoto, Y.; Kinoshita, D.; Akiba, K.; Zhang, Y.; Reed, C.A.; Hashizume, D.; Iwasaki, F. Synthesis and Structure of a Hexacoordinate Carbon Compound. J. Am. Chem. Soc. 2008, 130, 6894–6895. [Google Scholar] [CrossRef]
- Lancaster, K.M.; Roemelt, M.; Ettenhuber, P.; Hu, Y.; Ribbe, M.W.; Neese, F.; Bergmann, U.; DeBeer, S. X-Ray Emission Spectroscopy Evidences a Central Carbon in the Nitrogenase Iron-Molybdenum Cofactor. Science 2011, 334, 974–977. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.-S.; Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in the Al4C− Anion. A Combined Photoelectron Spectroscopy and Ab Initio Study. J. Am. Chem. Soc. 1999, 121, 6033–6038. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.-F.; Wang, L.-S.; Geske, G.D.; Boldyrev, A.I. Pentaatomic Tetracoordinate Planar Carbon, [CAl4]2−: A New Structural Unit and Its Salt Complexes. Angew. Chem. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
- Keese, R. Carbon Flatland: Planar Tetracoordinate Carbon and Fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Yu, S.; Ding, Y.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H–. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Du, Z. 18-Valence-Electron Rule Lighted Planar Tetracoordinate Carbon and Nitrogen: The Global Energy Minima of CAl4Zn and NAl4Zn+. Phys. Chem. Chem. Phys. 2023, 25, 4211–4215. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Khatun, M.; Anoop, A.; Chattaraj, P.K. CSinGe4−n2+ (n = 1–3): Prospective Systems Containing Planar Tetracoordinate Carbon (PtC). Phys. Chem. Chem. Phys. 2022, 24, 16701–16711. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Chattaraj, P.K. CSiGaAl2−/0 and CGeGaAl2−/0 Having Planar Tetracoordinate Carbon Atoms in Their Global Minimum Energy Structures. J. Comput. Chem. 2022, 43, 894–905. [Google Scholar] [CrossRef] [PubMed]
- Leyva-Parra, L.; Inostroza, D.; Yañez, O.; Cruz, J.C.; Garza, J.; García, V.; Tiznado, W. Persistent Planar Tetracoordinate Carbon in Global Minima Structures of Silicon-Carbon Clusters. Atoms 2022, 10, 27. [Google Scholar] [CrossRef]
- Liu, F.-L.; Guo, J.-C. Ternary CE2Ba2 (E = As, Sb) Clusters: New Pentaatomic Planar Tetracoordinate Carbon Species with 18 Valence Electrons. J. Mol. Model. 2022, 28, 230. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Chandrasekaran, V.; Cooksy, A.L.; Thimmakondu, V.S. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry 2020, 3, 13–27. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Karton, A.; Thimmakondu, V.S. From High-Energy C7H2 Isomers with a Planar Tetracoordinate Carbon Atom to an Experimentally Known Carbene. J. Phys. Chem. A 2018, 122, 9054–9064. [Google Scholar] [CrossRef] [PubMed]
- Thimmakondu, V.S.; Thirumoorthy, K. Si3C2H2 Isomers with a Planar Tetracoordinate Carbon or Silicon Atom(s). Comput. Theor. Chem. 2019, 1157, 40–46. [Google Scholar] [CrossRef]
- Jayakumari, C.; Nag, P.; Isukapalli, S.; Vennapusa, S. Exploring the Excited-State Nonadiabatic Effects in the Semisaturated Planar Tetracoordinated Carbon Molecule C7H4. Atoms 2022, 10, 10. [Google Scholar] [CrossRef]
- Job, N.; Khatun, M.; Thirumoorthy, K.; CH, S.S.R.; Chandrasekaran, V.; Anoop, A.; Thimmakondu, V.S. CAl4Mg0/−: Global Minima with a Planar Tetracoordinate Carbon Atom. Atoms 2021, 9, 24. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Thimmakondu, V.S. Flat Crown Ethers with Planar Tetracoordinate Carbon Atoms. Int. J. Quantum Chem. 2021, 121, e26479. [Google Scholar] [CrossRef]
- Pei, Y.; An, W.; Ito, K.; Schleyer, P.V.R.; Xiao, C.Z. Planar Pentacoordinate Carbon in CAI5+: A Global Minimum. J. Am. Chem. Soc. 2008, 130, 10394–10400. [Google Scholar] [CrossRef] [PubMed]
- Jimenez-Halla, J.O.C.; Wu, Y.-B.; Wang, Z.-X.; Islas, R.; Heine, T.; Merino, G. CAl4Be and CAl3Be2−: Global Minima with a Planar Pentacoordinate Carbon Atom. Chem. Commun. 2010, 46, 8776. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Cabellos, J.L.; Orozco-Ic, M.; Chattaraj, P.K.; Zhao, L.; Merino, G. Planar Pentacoordinate Carbon in CGa5+ Derivatives. Phys. Chem. Chem. Phys. 2018, 20, 12350–12355. [Google Scholar] [CrossRef]
- Das, P.; Chattaraj, P.K. Structure and Bonding in Planar Hypercoordinate Carbon Compounds. Chemistry 2022, 4, 1723–1756. [Google Scholar] [CrossRef]
- Sarkar, P.; Thirumoorthy, K.; Anoop, A.; Thimmakondu, V.S. Planar Pentacoordinate Carbon in [XC7H2]2+ (X = Be and Mg) and Its Derivatives. Phys. Chem. Chem. Phys. 2022, 24, 27606–27611. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Jin, B.; Huo, B.; Yuan, C.; Zhai, H.-J.; Wu, Y.-B. Planar Pentacoordinate Carbon in a Sulphur-Surrounded Boron Wheel: The Global Minimum of CB5S5+. Chem. Commun. 2022, 58, 2552–2555. [Google Scholar] [CrossRef]
- Sun, R.; Zhao, X.-F.; Jin, B.; Huo, B.; Bian, J.-H.; Guan, X.-L.; Yuan, C.; Wu, Y.-B. Influence of Stepwise Oxidation on the Structure, Stability, and Properties of Planar Pentacoordinate Carbon Species CAl5+. Phys. Chem. Chem. Phys. 2020, 22, 17062–17067. [Google Scholar] [CrossRef]
- Das, P.; Pan, S.; Chattaraj, P.K. Planar Hypercoordinate Carbon. In Atomic Clusters with Unusual Structure, Bonding and Reactivity; Elsevier: Amsterdam, The Netherlands, 2023; pp. 357–372. [Google Scholar]
- Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar Pentacoordinate Carbons. Nat. Rev. Chem. 2018, 2, 0114. [Google Scholar] [CrossRef]
- Yang, L.-M.; Ganz, E.; Chen, Z.; Wang, Z.-X.; Schleyer, P.V.R. Four Decades of the Chemistry of Planar Hypercoordinate Compounds. Angew. Chem. Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef]
- Exner, K.; Schleyer, P.V.R. Planar Hexacoordinate Carbon: A Viable Possibility. Science 2000, 290, 1937–1940. [Google Scholar] [CrossRef]
- Ito, K.; Chen, Z.F.; Corminboeuf, C.; Wannere, C.S.; Zhang, X.H.; Li, Q.S.; Schleyer, P.v.R. Myriad Planar Hexacoordinate Carbon Molecules Inviting Synthesis. J. Am. Chem. Soc. 2007, 129, 1510–1511. [Google Scholar] [CrossRef]
- Inostroza, D.; Leyva-Parra, L.; Yañez, O.; Solar-Encinas, J.; Vásquez-Espinal, A.; Valenzuela, M.L.; Tiznado, W. Searching for Systems with Planar Hexacoordinate Carbons. Atoms 2023, 11, 56. [Google Scholar] [CrossRef]
- Leyva-Parra, L.; Diego, L.; Yañez, O.; Inostroza, D.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Planar Hexacoordinate Carbons: Half Covalent, Half Ionic. Angew. Chem. Int. Ed. 2021, 60, 8700–8704. [Google Scholar] [CrossRef] [PubMed]
- Bradley, J.S.; Ansell, G.B.; Leonowicz, M.E.; Hill, E.W. Synthesis and Molecular Structure of. Mu.4-Carbido-.Mu.2-Carbonyl-Dodecacarbonyltetrairon, a Neutral Iron Butterfly Cluster Bearing an Exposed Carbon Atom. J. Am. Chem. Soc. 1981, 103, 4968–4970. [Google Scholar] [CrossRef]
- Radius, U.; Silverio, S.J.; Hoffmann, R.; Gleiter, R. A Five-Coordinate Carbon Center and Zr to H, B, and C Bonding in Cp2Zr[CH2(BH{C6F5}2)2]. Organometallics 1996, 15, 3737–3745. [Google Scholar] [CrossRef]
- Vicente, J.; Chicote, M.T.; Guerrero, R.; Jones, P.G. Synthesis of the First Complex with a Hypercoordinate Ylidic Carbon Atom. Crystal and Molecular Structure of [{Au(PPh3)}4CS(=O)Me2](ClO4)2. J. Am. Chem. Soc. 1996, 118, 699–700. [Google Scholar] [CrossRef]
- Shajan, S.; Guo, J.-C.; Sinjari, A.; Thirumoorthy, K.; Thimmakondu, V.S. Pentacoordinate Carbon Atoms in a Ferrocene Dication Derivative—[Fe(Si2-H5-C5H2)2]2+. Chemistry 2022, 4, 1092–1100. [Google Scholar] [CrossRef]
- Zhang, C.-J.; Wang, P.; Xu, X.-L.; Xu, H.-G.; Zheng, W.-J. Photoelectron Spectroscopy and Theoretical Study of AlnC5 −/0 (n = 1–5) Clusters: Structural Evolution, Relative Stability of Star-like Clusters, and Planar Tetracoordinate Carbon Structures. Phys. Chem. Chem. Phys. 2021, 23, 1967–1975. [Google Scholar] [CrossRef] [PubMed]
- Ravell, E.; Jalife, S.; Barroso, J.; Orozco-Ic, M.; Hernández-Juárez, G.; Ortiz-Chi, F.; Pan, S.; Cabellos, J.L.; Merino, G. Structure and Bonding in CE5− (E=Al-Tl) Clusters: Planar Tetracoordinate Carbon versus Pentacoordinate Carbon. Chem. Asian J. 2018, 13, 1467–1473. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, J.; Lu, H.; Wang, Z.; Perez-Peralta, N.; Islas, R.; Contreras, M.; Merino, G.; Wu, J.I.; von Ragué Schleyer, P. Starlike Aluminum–Carbon Aromatic Species. Chem. A Eur. J. 2011, 17, 714–719. [Google Scholar] [CrossRef]
- Bai, L.-X.; Guo, J.-C. CAl4X4 (X = Te, Po): Double Aromatic Molecular Stars Containing Planar Tetracoordinate Carbon Atoms. Molecules 2023, 28, 3280. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Zhang, Y.; Chen, H. Dissociation of H2 on Carbon Doped Aluminum Cluster Al6C. J. Chem. Phys. 2014, 141, 064302. [Google Scholar] [CrossRef] [PubMed]
- Ermoline, A.; Schoenitz, M.; Dreizin, E.; Yao, N. Production of Carbon-Coated Aluminium Nanopowders in Pulsed Microarc Discharge. Nanotechnology 2002, 13, 638–643. [Google Scholar] [CrossRef]
- Kotov, Y.A.; Beketov, I.V.; Medvedev, A.I.; Murzakaev, A.M.; Timoshenkova, O.P.; Demina, T.M. Forming a Carbide Coating on the Surface of Aluminum Nanoparticles and Producing Nanopowders from Al-Al4C3 Using the Method of Electric Explosion of Wire. Nanotechnol. Russ. 2010, 5, 831–836. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Schleyer, P.v.R.; Chen, Z. Al2C Monolayer: The Planar Tetracoordinate Carbon Global Minimum. Nanoscale 2014, 6, 10784. [Google Scholar] [CrossRef]
- Zhang, C.-J.; Xu, H.-G.; Xu, X.-L.; Zheng, W.-J. Anion Photoelectron Spectroscopy and Theoretical Studies of Al4C6–/0: Global Minimum Triangle-Shaped Structures and Hexacoordinated Aluminum. J. Phys. Chem. A 2021, 125, 302–307. [Google Scholar] [CrossRef]
- Kalita, A.J.; Sarmah, K.; Yashmin, F.; Borah, R.R.; Baruah, I.; Deka, R.P.; Guha, A.K. σ-Aromaticity in Planar Pentacoordinate Aluminium and Gallium Clusters. Sci. Rep. 2022, 12, 10041. [Google Scholar] [CrossRef]
- Malhan, A.H.; Sobinson, S.; Job, N.; Shajan, S.; Mohanty, S.P.; Thimmakondu, V.S.; Thirumoorthy, K. Al2C4H2 Isomers with the Planar Tetracoordinate Carbon (PtC)/Aluminum (PtAl). Atoms 2022, 10, 112. [Google Scholar] [CrossRef]
- Zhai, H.-J.; Alexandrova, A.N.; Birch, K.A.; Boldyrev, A.I.; Wang, L.-S. Hepta- and Octacoordinate Boron in Molecular Wheels of Eight- and Nine-Atom Boron Clusters: Observation and Confirmation. Angew. Chem. 2003, 115, 6186–6190. [Google Scholar] [CrossRef]
- Li, S.D.; Miao, C.Q.; Ren, G.M. D5h Cu5H5X: Pentagonal Hydrocopper Cu5H5 Containing Pentacoordinate Planar Nonmetal Centers (X = B, C, N, O). Eur. J. Inorg. Chem. 2004, 2232–2234. [Google Scholar] [CrossRef]
- Khatun, M.; Roy, S.; Giri, S.; CH, S.S.R.; Anoop, A.; Thimmakondu, V.S. BAl4Mg−/0/+: Global Minima with a Planar Tetracoordinate or Hypercoordinate Boron Atom. Atoms 2021, 9, 89. [Google Scholar] [CrossRef]
- Das, P.; Patra, S.G.; Chattaraj, P.K. CB6Al0/+: Planar Hexacoordinate Boron (PhB) in the Global Minimum Structure. Phys. Chem. Chem. Phys. 2022, 24, 22634–22644. [Google Scholar] [CrossRef]
- Thompson, E.J.; Myers, T.W.; Berben, L.A. Synthesis of Square-Planar Aluminum(III) Complexes. Angew. Chem. Int. Ed. 2014, 53, 14132–14134. [Google Scholar] [CrossRef]
- Ebner, F.; Wadepohl, H.; Greb, L. Calix [4]Pyrrole Aluminate: A Planar Tetracoordinate Aluminum(III) Anion and Its Unusual Lewis Acidity. J. Am. Chem. Soc. 2019, 141, 18009–18012. [Google Scholar] [CrossRef]
- Bai, L.-X.; Barroso, J.; Orozco-Ic, M.; Ortiz-Chi, F.; Guo, J.-C.; Merino, G. : A Molecular Rotor with a Quasi-Planar Tetracoordinate Carbon. Chem. Commun. 2023, 59, 4966–4969. [Google Scholar] [CrossRef] [PubMed]
- Leskiw, B.D.; Castleman, A.W. The Interplay between the Electronic Structure and Reactivity of Aluminum Clusters: Model Systems as Building Blocks for Cluster Assembled Materials. Chem. Phys. Lett. 2000, 316, 31–36. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, B.; Zhai, H.; Zhou, R.; Ni, G.; Xu, Z. Mass Spectrometric and First Principles Study of AlnC− Clusters. Solid State Commun. 2002, 122, 543–547. [Google Scholar] [CrossRef]
- Maatallah, M.; Guo, M.; Cherqaoui, D.; Jarid, A.; Liebman, J.F. Aluminium Clusters for Molecular Hydrogen Storage and the Corresponding Alanes as Fuel Alternatives: A Structural and Energetic Analysis. Int. J. Hydrogen Energy 2013, 38, 5758–5767. [Google Scholar] [CrossRef]
- Dai, J.; Wu, X.; Yang, J.; Zeng, X.C. AlxC Monolayer Sheets: Two-Dimensional Networks with Planar Tetracoordinate Carbon and Potential Applications as Donor Materials in Solar Cell. J. Phys. Chem. Lett. 2014, 5, 2058–2065. [Google Scholar] [CrossRef]
- Dong, F.; Heinbuch, S.; Xie, Y.; Rocca, J.J.; Bernstein, E.R. Experimental and Theoretical Study of Neutral AlmCn and AlmCnHx Clusters. Phys. Chem. Chem. Phys. 2010, 12, 2569. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Perdew, J.P. Generalized Gradient Approximation to the Angle- and System-Averaged Exchange Hole. J. Chem. Phys. 1998, 109, 3313–3320. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Revealing Intuitively Assessable Chemical Bonding Patterns in Organic Aromatic Molecules via Adaptive Natural Density Partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Richard, F.W. Bader Atoms in Molecules. A Quantum Theory; Oxford University Press: Oxford, UK, 1990; ISBN 9780198558651. [Google Scholar]
- Becke, A.D.; Edgecombe, K.E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Schlegel, H.B.; Millam, J.M.; Iyengar, S.S.; Voth, G.A.; Daniels, A.D.; Scuseria, G.E.; Frisch, M.J. Ab Initio Molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. J. Chem. Phys. 2001, 114, 9758–9763. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malhan, A.H.; Thimmakondu, V.S.; Thirumoorthy, K.
Five Bonds to Carbon through Tri-Coordination in
Malhan AH, Thimmakondu VS, Thirumoorthy K.
Five Bonds to Carbon through Tri-Coordination in
Malhan, Abdul Hamid, Venkatesan S. Thimmakondu, and Krishnan Thirumoorthy.
2023. "Five Bonds to Carbon through Tri-Coordination in
Malhan, A. H., Thimmakondu, V. S., & Thirumoorthy, K.
(2023). Five Bonds to Carbon through Tri-Coordination in






