Computational Models for Analyzing the Thermodynamic Properties of Linear Triatomic Molecules

Abstract

This study presents analytical models for simulating the thermal properties of linear triatomic systems, using the modified Rosen–Morse oscillator and harmonic oscillator potential to represent vibrational modes. The models employ existing partition functions to derive the thermodynamic functions for the symmetric, asymmetric, and 2-fold degenerate bending modes. These thermodynamic functions are applied to gaseous triatomic molecules such as BO₂, HCN, N₃, and Si₂N. The results demonstrate high accuracy, with mean percentage absolute deviations (MPAD) of less than 0.17% for molar entropy and Gibbs free energy. For enthalpy and heat capacity, MPAD values are below 2% compared to National Institute of Standards and Technology (NIST) data. The findings are in strong agreement with the existing literature on gaseous triatomic molecules, confirming the reliability of the proposed models.

1. Introduction

Thermodynamics is a branch of physical science focused on the study of heat, work, energy, and how these quantities interact with matter. It provides insights into energy conversion processes and the transformation of energy between systems. Thermodynamic processes are governed by key state variables, such as temperature, pressure, volume, and energy, and are described by the following four fundamental laws: the Zeroth, First (energy conservation), Second (entropy), and Third (Nernst heat theorem) laws [1].

A deep understanding of thermodynamics is essential for advancing technologies such as fuel cells, enhanced oil recovery techniques, carbon capture and storage systems, and battery management systems. It also plays a critical role in manufacturing heat exchangers, which are widely used in industries like nuclear power, dyeing and printing, and steel production [2,3,4,5]. Furthermore, thermodynamics aids in determining equilibrium constants in chemical reactions [6,7,8], with applications in hydrogen production, carbon emission control, water treatment, material selection, and corrosion prevention [9].

Quantum mechanical methods, particularly non-fitting models, are increasingly embraced for analyzing the thermodynamic properties of molecular systems. These models offer a computationally efficient alternative for studying diatomic and polyatomic molecules. Fitted models, while supported by experimental data to improve accuracy, rely on data availability and are system-specific. They also require new data for different systems or conditions and are sensitive to temperature and pressure, limiting their broader use. In contrast, non-fitting models, based on fundamental physical principles, do not rely on experimental data and are valuable when such data are unavailable, offering a simplified approach to predicting thermal properties.

In polyatomic molecule analysis, both the number of atoms (atomicity) and the molecular shape are fundamental to identifying the vibrational modes. Each of these modes is associated with an oscillator similar to that of a diatomic molecule. The energy levels and partition function can then be calculated to explore different thermodynamic models. For a linear polyatomic molecule with N atoms, the number of vibrational modes is determined by the formula 3N–5.

A diatomic molecule (N = 2) has only one vibrational mode—the symmetric stretching mode. Different oscillator models, such as exponential-type and hyperbolic-type models, have been used to represent these vibrational modes [10,11,12,13,14,15]. Thermodynamic models derived from these oscillators, such as Helmholtz free energy, Gibbs free energy, mean thermal energy, heat capacities, enthalpy, and entropy, have been applied to various diatomic molecules [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

Despite these successes, the thermodynamic properties of triatomic molecules remain underexplored, particularly when analyzed using non-fitting computational models. Analytical expressions for Gibbs free energy, entropy, heat capacity, and enthalpy have been derived by using appropriate representations of the vibrational, rotational, and translational partition functions, and by being applied to molecules such as MgCl₂, Si₂N, BeF₂, CNC, BO₂, and N₃ [32]. Non-fitting models have also been employed to study the thermodynamic properties of nonlinear triatomic molecules, such as NO₂, BF₂, and AlCl₂ [33]. However, the exploration of thermodynamic properties using these non-fitting models remains limited. Further studies on polyatomic molecules using non-fitting models are listed in [34,35,36,37,38,39,40].

Unlike diatomic molecules, which have a single vibrational mode, triatomic molecules are more complex. A linear triatomic molecule has the following four vibrational modes: symmetric, asymmetric, and two bending modes (degenerate). Thus, accurately formulating the thermodynamic functions for these molecules requires incorporating all four vibrational modes. Previous models for both linear and nonlinear polyatomic systems have used the improved Tietz (IMTZ) oscillator [10] to approximate the internal stretching vibrations. These models are based on three molecular constants (equilibrium dissociation energy, chemical bond length, and harmonic frequency of vibration) and two oscillator parameters (screening parameter α and dimensionless parameter q). A key limitation of the IMTZ model is the need to adjust the dimensionless parameter for each molecular system.

To address this issue, this study employs the modified Rosen–Morse (MRM) oscillator [11], which has proven effective in modeling the internuclear potential energy curve of diatomic molecules and handling anharmonicity in molecular systems. The MRM oscillator is widely used in fields such as solid-state physics, chemical physics, computational chemistry, and material science. Despite its versatility, the MRM oscillator has yet to be applied to study the thermodynamic properties of linear triatomic molecules. This study is the first to employ the MRM oscillator to derive computational models for the thermodynamic properties of these molecules, providing novel insights into the thermodynamics of triatomic systems.

The paper is organized as follows: Section 2 derives the thermodynamic functions; Section 3 uses these functions to generate numerical data for linear triatomic molecules such as BO₂ (boron oxide), HCN (hydrogen cyanide), N₃ (azide), and Si₂N (silicon nitride); and Section 4 provides a brief conclusion.

2. Computational Method

This section outlines the computational models that do not rely on fitting parameters for determining the thermodynamic properties of linear triatomic molecules. The non-fitting computational method uses quantum mechanics to develop model equations that analyze the physical properties of substances. Unlike the fitting functional approach, which is restricted to systems or conditions similar to those used for parameter calibration, the non-fitting method is more adaptable and can be applied to a variety of chemical and physical systems. In this approach, the thermal properties of a linear triatomic molecule are predicted through analytical formulations that start with the canonical partition function, given by $\mathrm{Q}={\mathrm{Q}}_{\mathrm{vib}}{\mathrm{Q}}_{\mathrm{rot}}{\mathrm{Q}}_{\mathrm{tra}}$, where ${\mathrm{Q}}_{\mathrm{vib}}$, ${\mathrm{Q}}_{\mathrm{rot}}$, and ${\mathrm{Q}}_{\mathrm{tra}}$ correspond to the vibrational, rotational, and translational partition functions, respectively [30].

2.1. Formulating the Vibrational Partition Function

In a linear triatomic molecule of the form XZY, where X, Y, and Z represent atoms, the system exhibits the following three distinct vibrational modes: symmetric stretching, asymmetric stretching, and two degenerate bending modes. The vibrational partition function ${\mathrm{Q}}_{\mathrm{vib}}$ is expressed as ${\mathrm{Q}}_{\mathrm{vib}}={\mathrm{Q}}_{\mathrm{s}}{\mathrm{Q}}_{\mathrm{a}}{\mathrm{Q}}_{\mathrm{b}}^2$, where ${\mathrm{Q}}_{\mathrm{s}}$, ${\mathrm{Q}}_{\mathrm{a}}$, and ${\mathrm{Q}}_{\mathrm{b}}$ represent the partition functions for the symmetric, asymmetric, and bending vibrations, respectively. The square in ${\mathrm{Q}}_{\mathrm{b}}^2$ accounts for the two-fold degeneracy of the bending modes. If the molecule consists of more than three atoms while remaining linear, additional vibrational modes emerge, requiring an adjustment to the vibrational partition function to include these modes.

In a linear triatomic molecule XZY, where atoms X, Y, and Z are bonded in a straight line, symmetric stretching occurs when both the X-Z and Z-Y bonds stretch and compress in unison. If atoms X and Y are identical, the central atom Z shifts along the molecular axis, and both X and Y move symmetrically toward or away from Z. Since X and Y are the same, their movements are identical, resulting in equal changes in bond lengths and preserving the molecule’s symmetry.

In an asymmetric linear triatomic molecule, where X, Y, and Z are all different, the central atom Z moves along the molecular axis, and atoms X and Y move in phase. However, due to differences in atomic size, mass, and electronegativity, the displacements of X and Y are unequal. This leads to one bond (X-Z or Z-Y) stretching more than the other, causing an asymmetric vibration despite the motion occurring in phase.

However, anharmonicity causes deviations from perfect harmonic motion, particularly at higher energy levels, leading to the uneven spacing of vibrational energy levels. While previous studies modeled anharmonicity using the IMTZ potential, the present work employs the simpler MRM oscillator, which avoids the need for an adjustable dimensionless parameter that varies across molecules. The energy–distance relationship for a system modeled by the MRM oscillator is given by [11]

$$\mathrm{U}\left(r\right)=D_{\mathrm{e}}{\left\{1-{\displaystyle \frac{\exp \alpha \left(r_{\mathrm{e}}-r_{\mathrm{ij}}\right)+1}{\exp \alpha \left(r-r_{\mathrm{ij}}\right)+1}}\right\}}^2$$

(1)

where

$$\alpha =\sqrt{{\displaystyle \frac{{\mathrm{k}}_{\mathrm{es}}}{2D_{\mathrm{e}}}}}+{\displaystyle \frac{1}{r_{\mathrm{e}}-r_{\mathrm{ij}}}}\mathrm{W}\left\{\left(r_{\mathrm{e}}-r_{\mathrm{ij}}\right)\sqrt{{\displaystyle \frac{{\mathrm{k}}_{\mathrm{es}}}{2D_{\mathrm{e}}}}}\exp \left[-\left(r_{\mathrm{e}}-r_{\mathrm{ij}}\right)\sqrt{{\displaystyle \frac{{\mathrm{k}}_{\mathrm{es}}}{2D_{\mathrm{e}}}}}\right]\right\}$$

(2)

is the potential screening parameter; $D_{\mathrm{e}}$ is the equilibrium dissociation energy; ${\mathrm{k}}_{\mathrm{es}}={\mu }_{\mathrm{XY}}(2\mathsf{\pi }c{\omega }_{\mathrm{es}}{)}^2$ is the equilibrium force constant for symmetric vibrations; ${\mu }_{\mathrm{XY}}$ is the reduced mass of atoms X and Y; c is the speed of light; ${\omega }_{\mathrm{es}}$ is the symmetric harmonic vibrational frequency; and the parameters $r_{\mathrm{ij}}$ and $r_{\mathrm{e}}$ are defined as $r_{\mathrm{ij}}=r_{\mathrm{e}}-2\sqrt{{\mathrm{k}}_{\mathrm{es}}^{-1}{D}_{\mathrm{e}}}$ and $r_{\mathrm{e}}=r_{\mathrm{eZX}}+r_{\mathrm{eZY}}$, where $r_{\mathrm{eZX}}$ is the equilibrium bond length between atoms Z and X, $r_{\mathrm{eZY}}$ is the equilibrium bond length between atoms Z and Y, W is the Lambert W function, and r is the internuclear separation between atoms X and Y.

Deng and Jia previously derived the vibrational partition function for a diatomic molecule using the MRM oscillator. Their expression for the symmetric stretching vibrations is adopted here, given by [41]

$${\mathrm{Q}}_{\mathrm{s}}={\displaystyle \frac{1}{2}}\exp \left({\omega }_1^2-{\omega }^2-\lambda \right)-{\displaystyle \frac{1}{2}}\exp \left({\omega }_2^2-{\omega }^2-\lambda \right)+{\displaystyle \frac{\sqrt{\mathsf{\pi }}}{4{\omega }_3}}\left[{\displaystyle \frac{\mathrm{Erfi}{\omega }_1+\mathrm{Erfi}{\omega }_2}{\exp \left({\omega }^2+\lambda \right)}}-{\displaystyle \frac{\mathrm{Erfi}{\overline{\omega }}_1+\mathrm{Erfi}{\overline{\omega }}_2}{\exp \left({\omega }^2+\lambda +4{\omega }_3^2{\omega }_4\right)}}\right],$$

(3a)

$${\omega }_1={\omega }_3\left({\omega }_5-{\omega }_4{\omega }_5^{-1}\right),$$

(3b)

$${\omega }_2={\omega }_3\left[{\nu }_{\max }+1-{\omega }_5-{\omega }_4{\left({\nu }_{\max }+1-{\omega }_5\right)}^{-1}\right],$$

(3c)

$${\overline{\omega }}_1={\omega }_3\left({\omega }_5+{\omega }_4{\omega }_5^{-1}\right),$$

(3d)

$${\overline{\omega }}_2={\omega }_3\left[{\nu }_{\max }+1-{\omega }_5+{\omega }_4{\left({\nu }_{\max }+1-{\omega }_5\right)}^{-1}\right],$$

(3e)

$${\omega }_3=\alpha \hslash \left(\frac{1}{8}\beta {\mu }_{\mathrm{XY}}^{-1}\right)$$

(3f)

$${\omega }_4={\displaystyle \frac{2{\mu }_{\mathrm{XY}}{D}_{\mathrm{e}}}{{\alpha }^2{\hslash }^2}}\left[\exp 2\alpha \left(r_{\mathrm{e}}-r_{\mathrm{ij}}\right)-1\right],$$

(3g)

$${\omega }_5=-{\displaystyle \frac{1}{2}}+\sqrt{{\displaystyle \frac{1}{2}}+{\displaystyle \frac{2{\mu }_{\mathrm{XY}}{D}_{\mathrm{e}}}{{\alpha }^2{\hslash }^2}}{\left[\exp \alpha \left(r_{\mathrm{e}}-r_{\mathrm{ij}}\right)+1\right]}^2},$$

(3h)

In Equation (3), $\omega ={\left(\beta D_{\mathrm{e}}\right)}^{\frac{1}{2}}$, where β⁻¹ = k_BT (with T representing the temperature and k_B the Boltzmann constant); Erfi(z) denotes the imaginary error function evaluated at z. ${\nu }_{\max }=-{\omega }_5+{\omega }_4^{\frac{1}{2}}$ refers to the number of excited bonded molecular states, which can be deduced by applying ${\left.\frac{\partial E_{\nu }}{\partial \nu }\right|}_{{\nu }_{\max }}=0$, where ν = 0, 1, 2, … is the vibrational quantum number, E_ν represents the vibrational energy eigenvalues, ℏ is the reduced Planck constant, and λ is an optimization parameter. As noted in Ref. [42], $\exp \left(-4{\omega }_3^2{\omega }_4\right)$ is negligibly small for the molecular system. By neglecting the terms involving this factor, the partition function simplifies to

$${\mathrm{Q}}_{\mathrm{s}}={\displaystyle \frac{1}{2}}\exp \left({\omega }_1^2-{\omega }^2-\lambda \right)-{\displaystyle \frac{1}{2}}\exp \left({\omega }_2^2-{\omega }^2-\lambda \right)+{\displaystyle \frac{\sqrt{\mathsf{\pi }}}{4{\omega }_3}}{\displaystyle \frac{\mathrm{Erfi}{\omega }_1+\mathrm{Erfi}{\omega }_2}{\exp \left({\omega }^2+\lambda \right)}}.$$

(4)

In the asymmetric stretching vibration, the bonds (X-Z and Z-Y) stretch and compress in opposite directions, causing unequal changes in bond lengths. During this vibration, atom Z moves along the molecular axis, while atoms X and Y move in opposite directions. This mode is termed “asymmetric” because the two sides of Z behave differently. The bending vibration, on the other hand, changes the angle between the bonds (X-Z and Z-Y), rather than the bond lengths. In this mode, atoms X and Y move perpendicular to the molecular axis, causing the bond angle to increase or decrease. There are two degenerate bending modes with the same frequency but different atomic motion directions, typically referred to as in-plane and out-of-plane bending. These bending vibrations occur at lower frequencies than the stretching modes.

Anharmonicity plays an important role in selecting oscillator models to represent the internal motion of molecular systems. It refers to how molecular vibrations deviate from the idealized harmonic oscillator behavior. In simpler systems, deviations are typically less pronounced in asymmetric and bending modes than in symmetric stretching modes. At typical temperatures, these deviations are smaller in asymmetric and bending vibrations compared to symmetric stretching vibrations, likely due to the lower vibrational frequencies of the atoms involved. Therefore, at standard temperatures, these vibrations can often be accurately modeled using harmonic oscillator potentials. As a result, the partition functions for the asymmetric and bending modes are given in compact form as [43]

$${\mathrm{Q}}_{\mathrm{A}}={\displaystyle \frac{1}{2}}\mathrm{csch}\left(2\mathsf{\pi }\hslash c{\omega }_{\mathrm{e}\mathrm{A}}\beta \right),\hspace{1em}\mathrm{A}\equiv \left(\mathrm{a},\mathrm{b}\right),$$

(5)

where ${\omega }_{\mathrm{e}\mathrm{a}}$ and ${\omega }_{\mathrm{e}\mathrm{b}}$ are the equilibrium frequencies for the asymmetric and bending vibrations, respectively.

2.2. Formulating the Rotational and Translational Partition Functions

Using the rigid rotor approximation for molecular systems and neglecting molecular interactions, the rotational and translational partition functions can be expressed as [43]

$${\mathrm{Q}}_{\mathrm{rot}}= \frac{1}{3}+{\Omega }^{-1}{\beta }^{-1}+\frac{1}{15}\Omega \beta +\frac{4}{315}{\Omega }^2{\beta }^2,$$

(6)

$${\mathrm{Q}}_{\mathrm{tra}}={\displaystyle \frac{1}{p}}{\left({\displaystyle \frac{m}{2\mathsf{\pi }{\hslash }^2}}\right)}^{\frac{3}{2}}{\beta }^{-\frac{5}{2}}.$$

(7)

In these expressions, $\Omega = \frac{1}{2}{\left(\mu r_{\mathrm{e}}^2\right)}^{-1}{\hslash }^2$, m denotes the molar mass, and p represents the pressure exerted by the system in a container of volume V.

2.3. Formulating the Thermodynamic Functions

In this work, analytical equations for assessing the thermal properties of a linear triatomic molecule are derived from the following expressions [43]

$$\mathrm{S}=\mathrm{R}\left(\ln \mathrm{Q}-{\gamma }_1\right),$$

(8)

$$\mathrm{H}=-{\mathrm{N}}_{\mathrm{A}}{\gamma }_1,$$

(9)

$$\mathrm{G}=-\mathrm{R}T\ln \mathrm{Q},$$

(10)

$${\mathrm{C}}_p=\mathrm{R}\left(-{\gamma }_1^2+{\gamma }_2\right).$$

(11)

In these equations, ${\gamma }_1={\displaystyle \frac{\beta }{\mathrm{Q}}}{\displaystyle \frac{\partial \mathrm{Q}}{\partial \beta }}$, ${\gamma }_2={\displaystyle \frac{{\beta }^2}{\mathrm{Q}}}{\displaystyle \frac{{\partial }^2\mathrm{Q}}{\partial {\beta }^2}}$, and the Avogadro number, ${\mathrm{N}}_{\mathrm{A}}$, with R denotes the universal gas constant. Additionally, S represents the molar entropy, H the molar enthalpy, G the molar Gibbs free energy, and ${\mathrm{C}}_p$ is the constant-pressure (or isobaric) molar heat capacity. The thermodynamic functions are computed by substituting $\mathrm{Q}={\mathrm{Q}}_{\mathrm{vib}}{\mathrm{Q}}_{\mathrm{rot}}{\mathrm{Q}}_{\mathrm{tra}}$ and ${\mathrm{Q}}_{\mathrm{vib}}={\mathrm{Q}}_{\mathrm{s}}{\mathrm{Q}}_{\mathrm{a}}{\mathrm{Q}}_{\mathrm{b}}^2$ into Equations (8)–(11). The first- and second-order derivatives required for these evaluations are derived from Equations (4)–(7), with the corresponding expressions for the first and second derivatives provided in (12) and (13), respectively.

$${\displaystyle \frac{\beta }{{\mathrm{Q}}_{\mathrm{s}}}}{\displaystyle \frac{\partial {\mathrm{Q}}_{\mathrm{s}}}{\partial \beta }}=-{\omega }^2-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{2{\omega }_1^2+{\omega }_1{\omega }_3^{-1}+1}{{4\mathrm{Q}}_{\mathrm{s}}\exp \left({\omega }^2-{\omega }_1^2+\lambda \right)}}-{\displaystyle \frac{2{\omega }_2^2-{\omega }_2{\omega }_3^{-1}+1}{{4\mathrm{Q}}_{\mathrm{s}}\exp \left({\omega }^2-{\omega }_2^2+\lambda \right)}},$$

(12a)

$${\displaystyle \frac{\beta }{{\mathrm{Q}}_{\mathrm{A}}}}{\displaystyle \frac{\partial {\mathrm{Q}}_{\mathrm{A}}}{\partial \beta }}=-2\mathsf{\pi }\hslash c{\omega }_{\mathrm{e}\mathrm{A}}\beta \sqrt{1+4{\mathrm{Q}}_{\mathrm{A}}^2},\hspace{1em}\mathrm{A}\equiv \left(\mathrm{a},\mathrm{b}\right),$$

(12b)

$${\displaystyle \frac{\beta }{{\mathrm{Q}}_{\mathrm{rot}}}}{\displaystyle \frac{\partial {\mathrm{Q}}_{\mathrm{rot}}}{\partial \beta }}=-{\displaystyle \frac{\beta }{{\mathrm{Q}}_{\mathrm{rot}}}}\left({\Omega }^{-1}{\beta }^{-2}-\frac{1}{15}\Omega -\frac{8}{315}{\Omega }^2\beta \right),$$

(12c)

$${\displaystyle \frac{\beta }{{\mathrm{Q}}_{\mathrm{tra}}}}{\displaystyle \frac{\partial {\mathrm{Q}}_{\mathrm{tra}}}{\partial \beta }}=-{\displaystyle \frac{5}{2}},$$

(12d)

$${\displaystyle \frac{{\beta }^2}{{\mathrm{Q}}_{\mathrm{s}}}}{\displaystyle \frac{{\partial }^2{\mathrm{Q}}_{\mathrm{s}}}{\partial {\beta }^2}}={\omega }^4+{\omega }^2+{\displaystyle \frac{3}{4}}+{\displaystyle \frac{4{\left({\omega }_1^2-{\omega }^2\right)}^2-{\left(2{\omega }^2+1\right)}^2+{\omega }_1{\omega }_3^{-1}\left(2{\omega }_1^2-4{\omega }^2-3\right)-2}{{8\mathrm{Q}}_{\mathrm{s}}\exp \left({\omega }^2-{\omega }_1^2+\lambda \right)}},$$

(13a)

$${\displaystyle \frac{{\beta }^2}{{\mathrm{Q}}_{\mathrm{A}}}}{\displaystyle \frac{{\partial }^2{\mathrm{Q}}_{\mathrm{A}}}{\partial {\beta }^2}}=4{\mathsf{\pi }}^2{\hslash }^2{c}^2{\omega }_{\mathrm{eA}}^2\beta \left(1+8{\mathrm{Q}}_{\mathrm{A}}^2\right),\hspace{1em}\mathrm{A}\equiv \left(\mathrm{a},\mathrm{b}\right),$$

(13b)

$${\displaystyle \frac{{\beta }^2}{{\mathrm{Q}}_{\mathrm{rot}}}}{\displaystyle \frac{{\partial }^2{\mathrm{Q}}_{\mathrm{rot}}}{\partial {\beta }^2}}={\displaystyle \frac{{\beta }^2}{{\mathrm{Q}}_{\mathrm{rot}}}}\left(2{\Omega }^{-1}{\beta }^{-3}+\frac{8}{315}{\Omega }^2\right),$$

(13c)

$${\displaystyle \frac{{\beta }^2}{{\mathrm{Q}}_{\mathrm{tra}}}}{\displaystyle \frac{{\partial }^2{\mathrm{Q}}_{\mathrm{tra}}}{\partial {\beta }^2}}={\displaystyle \frac{35}{4}}.$$

(13d)

This work introduces the application of these equations specifically to the thermal properties of linear triatomic molecules, providing new insights into the calculation of thermodynamic properties. The use of the MRM oscillator, a tool previously underexplored in this context, represents a significant advancement in computational thermodynamics.

3. Results and Discussion

The accuracy of the new model equations for analyzing the thermal properties of linear triatomic molecules is assessed using data on equilibrium dissociation energy ($D_{\mathrm{e}}$), harmonic vibrational frequencies (${\omega }_{\mathrm{e}\mathrm{s}}$, ${\omega }_{\mathrm{e}\mathrm{a}}$, ${\omega }_{\mathrm{e}\mathrm{b}}$), and bond lengths ($r_{\mathrm{e}\mathrm{ZX}}$, $r_{\mathrm{e}\mathrm{ZY}}$). The molecules considered, including boron oxide (BO₂), hydrogen cyanide (HCN), azide (N₃), and silicon nitride (Si₂N), are selected for their relevance to computational and theoretical chemistry, atomic and molecular physics, materials science, and chemical physics. The equilibrium dissociation energy represents the energy required to break a molecule XZY into X and ZY. For these molecules, the dissociation reactions are as follows: BO₂ dissociates into O and BO [44], HCN dissociates into H and CN [45], N₃ dissociates into N and N₂ [46], and Si₂N dissociates into Si and NSi [47]. Model parameters, along with experimental values for $D_{\mathrm{e}}$, $r_{\mathrm{e}\mathrm{ZX}}$, $r_{\mathrm{e}\mathrm{ZY}}$, ${\omega }_{\mathrm{e}\mathrm{s}}$, ${\omega }_{\mathrm{e}\mathrm{a}}$, and ${\omega }_{\mathrm{e}\mathrm{b}}$, are provided in

Table 1. Equilibrium dissociation energy, bond lengths, vibrational frequencies, and screening and optimization parameters for linear triatomic molecules in this study.

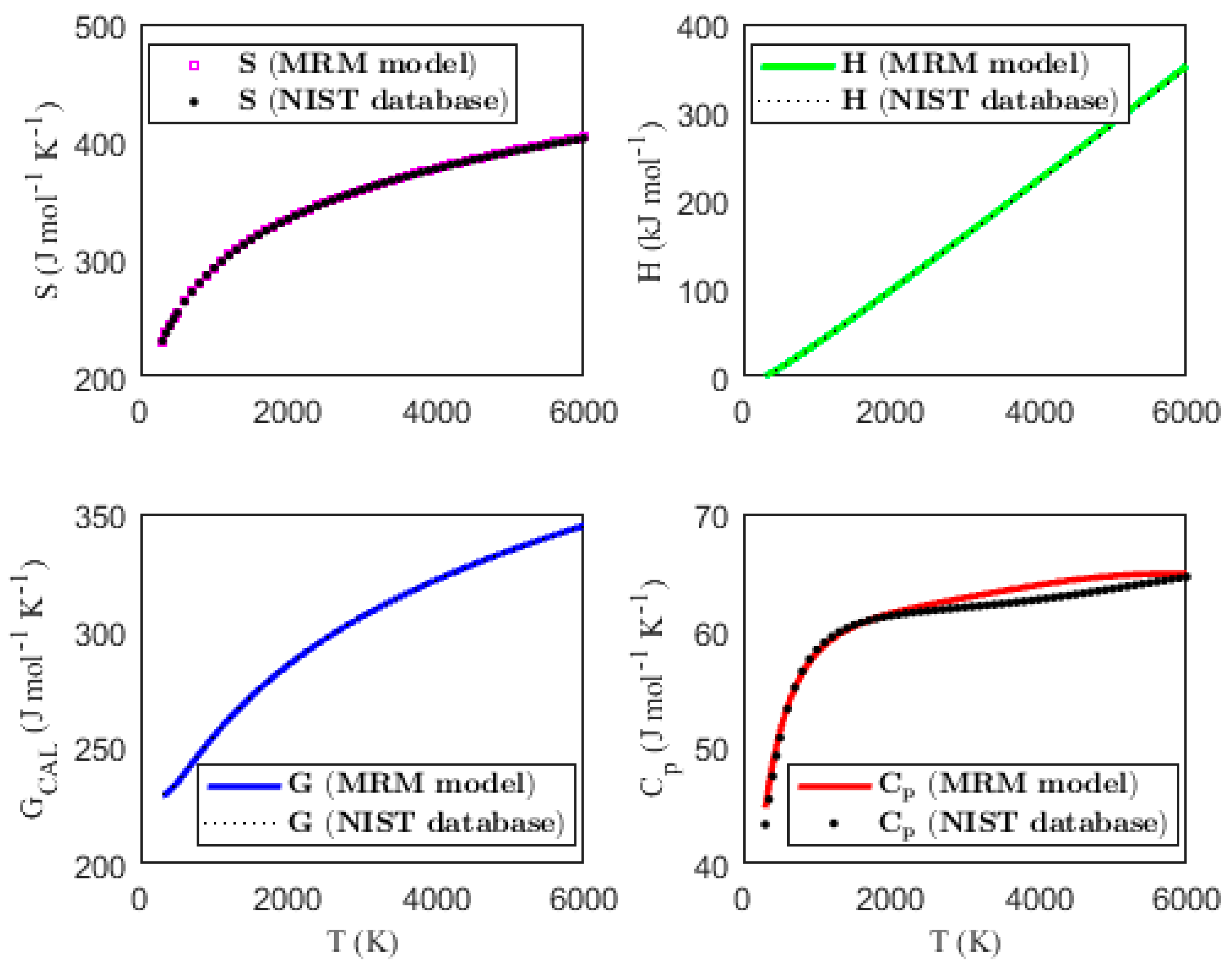
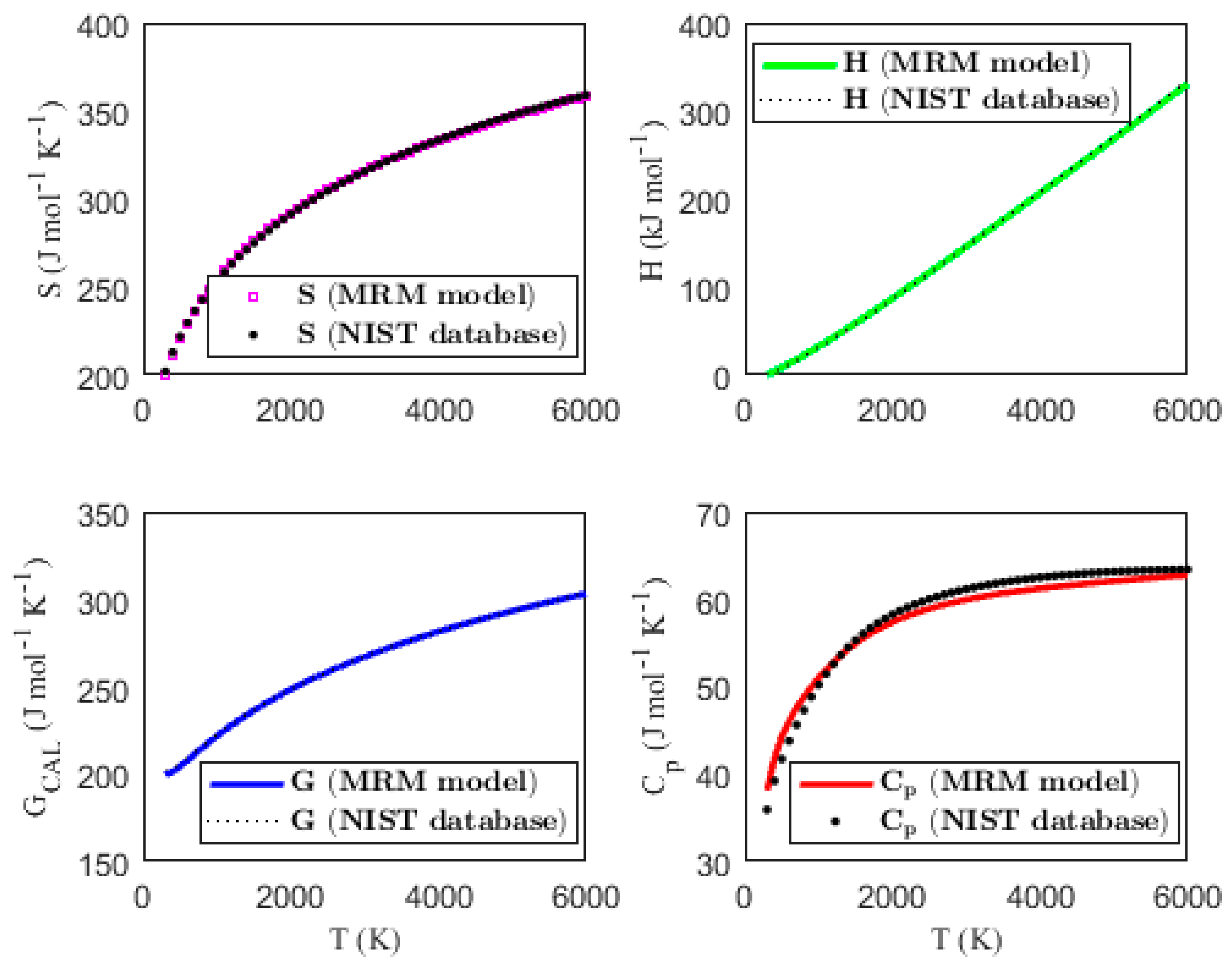
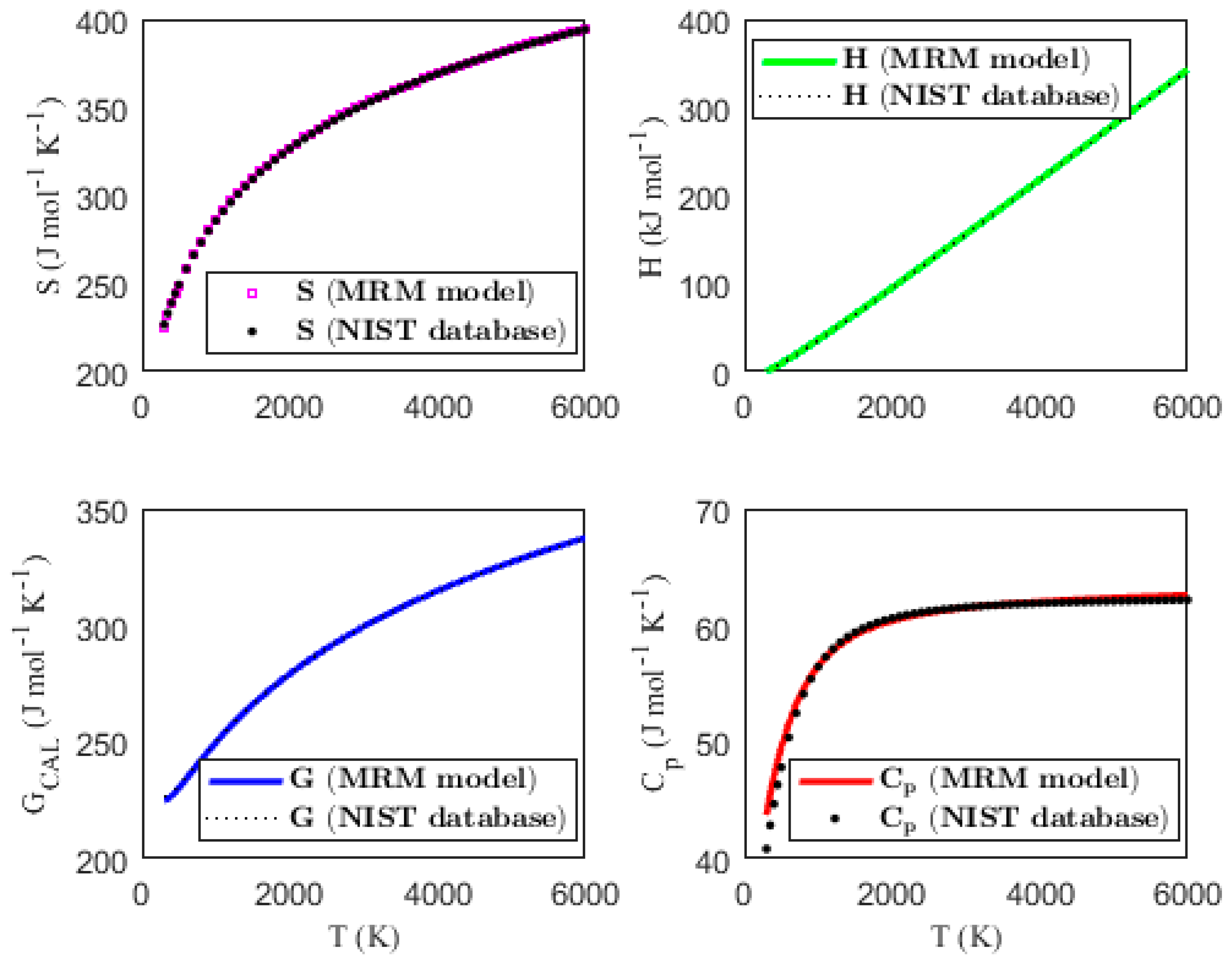
Molecule	Atoms in Molecule			Molecular Parameter [32,34,44,45,46,47]						α (Å−1)	λ
	X	Z	Y	De (kcalmol−1)	reZX (Å)	reZY (Å)	ωes (cm−1)	ωea (cm−1)	ωeb (cm−1)
BO2	O	B	O	68.33	1.263	1.263	1056	1321.7	454	2.7917	0.913
HCN	H	C	N	130.0184 #	1.066	1.153	2096.3	3311.5	713.5	1.3775	2.300
N3	N	N	N	219.6	1.18115	1.18115	1320	1645	457	1.8216	1.130
Si2N	Si	N	Si	123	1.70	1.70	600	1000	240	1.5666	0.812

130.0184 ^# kcalmol⁻¹ = 544 kJmol⁻¹.

, with data drawn from Refs. [32,34,44,45,46,47].

3.1. Significance of the Optimization Parameter

Before exploring the applicability of the model equations, it is important to consider the role of the optimization parameter, λ, introduced into the partition function. By expressing the symmetric partition function as ${\mathrm{Q}}_{\mathrm{s}}=\mathrm{F}\left(\beta \right){\mathrm{e}}^{-\lambda }$, where F(β) is solely a function of temperature, the combined partition function $\mathrm{Q}={\mathrm{Q}}_{\mathrm{vib}}{\mathrm{Q}}_{\mathrm{rot}}{\mathrm{Q}}_{\mathrm{tra}}$, where ${\mathrm{Q}}_{\mathrm{vib}}={\mathrm{Q}}_{\mathrm{s}}{\mathrm{Q}}_{\mathrm{a}}{\mathrm{Q}}_{\mathrm{b}}^2$, can also be expressed as

$$\mathrm{lnQ}=\ln \mathrm{F}\left(\beta \right){+\mathrm{lnQ}}_{\mathrm{a}}{+2\mathrm{lnQ}}_{\mathrm{b}}{+\mathrm{lnQ}}_{\mathrm{rot}}{+\mathrm{lnQ}}_{\mathrm{tra}}-\lambda .$$

(14)

The first derivative of this equation is given by

$${\displaystyle \frac{\partial }{\partial \beta }}\mathrm{lnQ}={\displaystyle \frac{\partial }{\partial \beta }}\ln \mathrm{F}\left(\beta \right)+{\displaystyle \frac{\partial }{\partial \beta }}{\mathrm{lnQ}}_{\mathrm{a}}+2{\displaystyle \frac{\partial }{\partial \beta }}{\mathrm{lnQ}}_{\mathrm{b}}+{\displaystyle \frac{\partial }{\partial \beta }}{\mathrm{lnQ}}_{\mathrm{rot}}+{\displaystyle \frac{\partial }{\partial \beta }}{\mathrm{lnQ}}_{\mathrm{tra}}.$$

(15)

Equation (14) clearly depends on λ, which in turn affects the molar entropy and Gibbs free energy (Equations (8) and (10)). However, Equation (15) is independent of λ, meaning the molar enthalpy (Equation (9)) and heat capacity (Equation (11)) are unaffected by changes in the optimization parameter. Setting λ = 0 effectively disables the optimization parameter, which, in turn, recovers the original model equations. This recovery ensures that the system returns to the unoptimized form, where the entropy and Gibbs free energy models are no longer adjusted by λ, but the enthalpy and heat capacity remain unchanged. The optimization parameter, λ, is varied manually until optimized data for molar entropy and reduced Gibbs free energy are achieved.

3.2. Validating the Thermodynamic Models

This section explores the use of model equations to evaluate the thermodynamic properties of linear triatomic molecules, as listed in Table 1. The model equations generate numerical data, which are then compared to available experimental data. The accuracy of the model is assessed based on Lippincott’s specifications, which dictate that the mean percentage absolute deviation (MPAD) between observed and experimental values should not exceed 1%.

To calculate the MPAD, the following equation is applied: $\mathrm{MPAD}=N_{\mathrm{p}}^{-1}{\displaystyle \sum _j{\left(\mathrm{PAD}\right)}_j}$, where N_p denotes the total number of experimental data points and ${\mathrm{PAD}}_j=100\left(1-{\mathrm{A}}_j{\mathrm{B}}_j^{-1}\right)$ represents the percentage absolute deviation [25]. The terms A_j and B_j refer to the predicted and experimental values at data point j, respectively. One source of experimental data for comparison is the NIST database [48]. NIST employs a fitting functional approach, using various fitting parameters to model the thermal properties of a substance, though its applicability is limited to certain temperature and pressure ranges.

The approach presented here offers a more efficient alternative by reducing the need for extensive experimental setups and the large number of fitting parameters used in the NIST method. Instead, only a few key molecular constants—such as equilibrium dissociation energy, vibrational frequencies, and bond lengths—are required to predict the thermal properties of linear triatomic systems. Since NIST results for molar enthalpy and Gibbs free energy are standardized to molar enthalpy at T = 298.15 K and p = 0.1 MPa, this study introduces theoretical adjustments to calibrate enthalpy and Gibbs free energy using the following equations

$${\mathrm{H}}_{\mathrm{STA}}=\mathrm{H}-{\mathrm{H}}_0,$$

(16)

$${\mathrm{G}}_{\mathrm{STA}}=T^{-1}\left({\mathrm{H}}_0-\mathrm{G}\right),$$

(17)

Here, H₀ represents the enthalpy calculated from Equation (9) at T = 298.15 K and p = 0.1 MPa. The thermodynamic functions from Equations (8), (11), (16) and (17) are applied to the data in Table 1, where pressure is held constant at 0.1 MPa and temperature varies from 300 to 6000 K. MATLAB (version 2016a) is utilized for numerical computations and to generate graphical plots. The program includes molecular constants and other necessary parameters, such as those defining the canonical partition function.

The computational procedure is illustrated using data for the HCN molecule. When T = 298.15 K, p = 0.1 MPa, and λ is set to zero, the dimensionless parameters γ₁ and γ₂ are calculated as −20.3332 and 10.2903, respectively. These values are substituted into Equation (9), yielding H₀ = 51.48 kJmol⁻¹. This value of H₀ is required for the calculation of H_STA and G_STA at other temperatures.

When T = 300 K, p = 0.1 MPa, and λ set to 2.3, the dimensionless parameters are γ₁ = −20.2361 and γ₂ = 8.9915. These values are inserted into Equations (8), (11), (16) and (17), resulting in S = 200.095 Jmol⁻¹K⁻¹, C_p = 38.146 Jmol⁻¹K⁻¹, H_STA = 0.070 kJmol⁻¹, and G_STA = 199.860 Jmol⁻¹K⁻¹. The same procedure is repeated for the other temperature values.

The program algorithm also calculates the MPAD values, enabling λ to be adjusted gradually to optimize S and G_STA. The numerical results for BO₂, HCN, N₃, and Si₂N, along with the NIST data and MPAD values, are summarized in

Table 2. Comparison of thermodynamic properties of the BO₂ molecule at 0.1 MPa: NIST data vs. MRM model predictions.

T [48]	S (J mol−1K−1)		H (kJ mol−1)		G (J mol−1K−1)		Cp (J mol−1K−1)
	Equation (8)	NIST [48]	Equation (16)	NIST [48]	Equation (17)	NIST [48]	Equation (11)	NIST [48]
300	229.618	230.082	0.083	0.080	229.342	229.815	44.763	43.359
350	236.676	236.931	2.373	2.303	229.895	230.351	46.805	45.527
400	243.042	243.141	4.758	4.630	231.147	231.567	48.548	47.495
450	248.849	248.838	7.224	7.049	232.796	233.174	50.052	49.246
500	254.192	254.108	9.760	9.550	234.672	235.007	51.356	50.780
…	…	…	…	…	…	…	…	…
2900	356.949	356.752	153.495	152.949	304.020	304.011	62.664	61.904
3000	359.076	358.852	159.768	159.142	305.820	305.804	62.781	61.961
3100	361.136	360.884	166.052	165.341	307.571	307.548	62.897	62.019
3200	363.135	362.854	172.347	171.546	309.276	309.246	63.012	62.078
3300	365.076	364.765	178.654	177.757	310.938	310.900	63.126	62.138
…	…	…	…	…	…	…	…	…
5600	398.976	398.069	326.275	322.804	340.713	340.425	64.836	64.169
5700	400.124	399.206	332.759	329.226	341.745	341.447	64.845	64.273
5800	401.252	400.324	339.244	335.658	342.762	342.452	64.848	64.377
5900	402.360	401.426	345.729	342.101	343.762	343.443	64.845	64.480
6000	403.450	402.510	352.213	348.554	344.748	344.418	64.836	64.582
MPAD (%)	0.103		0.822		0.050		1.190

,

Table 3. Comparison of thermodynamic properties of the HCN molecule at 0.1 MPa: NIST data vs. MRM model predictions.

T [48]	S (J mol−1K−1)		H (kJ mol−1)		G (J mol−1K−1)		Cp (J mol−1K−1)
	Equation (8)	NIST [48]	Equation (16)	NIST [48]	Equation (17)	NIST [48]	Equation (11)	NIST [48]
300	200.095	202.050	0.070	0.066	199.860	201.829	38.146	35.928
400	211.600	212.863	4.079	3.833	201.403	203.281	41.788	39.229
500	221.210	221.894	8.390	7.885	204.430	206.125	44.291	41.731
600	229.454	229.690	12.914	12.164	207.930	209.417	46.116	43.806
700	236.676	236.583	17.601	16.638	211.531	212.815	47.577	45.643
…	…	…	…	…	…	…	…	…
3100	317.712	317.718	151.976	152.072	268.687	268.663	60.116	61.347
3200	319.623	319.669	157.995	158.215	270.249	270.226	60.270	61.513
3300	321.479	321.564	164.030	164.374	271.774	271.754	60.415	61.669
3400	323.285	323.407	170.078	170.548	273.262	273.246	60.551	61.814
3500	325.042	325.201	176.140	176.736	274.717	274.705	60.680	61.948
…	…	…	…	…	…	…	…	…
5600	354.002	354.707	305.679	308.689	299.416	299.584	62.505	63.358
5700	355.108	355.829	311.933	315.026	300.383	300.561	62.573	63.378
5800	356.197	356.931	318.194	321.364	301.336	301.524	62.640	63.395
5900	357.269	358.015	324.461	327.705	302.275	302.472	62.707	63.407
6000	358.323	359.081	330.735	334.046	303.201	303.407	62.773	63.417
MPAD (%)	0.162		1.666		0.131		1.980

,

Table 4. Comparison of thermodynamic properties of the N₃ molecule at 0.1 MPa: NIST data vs. MRM model predictions.

T [48]	S (J mol−1K−1)		H (kJ mol−1)		G (J mol−1K−1)		Cp (J mol−1K−1)
	Equation (8)	NIST [48]	Equation (16)	NIST [48]	Equation (17)	NIST [48]	Equation (11)	NIST [48]
300	225.361	226.721	0.081	0.075	225.092	226.470	43.755	40.842
350	232.244	233.172	2.314	2.169	225.631	226.974	45.534	42.864
400	238.425	239.016	4.630	4.359	226.851	228.120	47.044	44.686
450	244.044	244.377	7.016	6.635	228.454	229.633	48.371	46.339
500	249.203	249.338	9.465	8.990	230.274	231.358	49.556	47.838
…	…	…	…	…	…	…	…	…
2900	349.441	349.221	150.092	149.614	297.686	297.630	61.432	61.503
3000	351.525	351.307	156.239	155.767	299.446	299.385	61.505	61.558
3100	353.543	353.327	162.393	161.926	301.159	301.093	61.574	61.607
3200	355.499	355.283	168.553	168.089	302.826	302.756	61.638	61.652
3300	357.397	357.181	174.720	174.256	304.451	304.376	61.697	61.693
…	…	…	…	…	…	…	…	…
5600	390.254	389.944	317.700	316.788	333.522	333.374	62.513	62.153
5700	391.360	391.044	323.952	323.004	334.527	334.377	62.537	62.165
5800	392.448	392.125	330.207	329.222	335.516	335.363	62.561	62.177
5900	393.518	393.188	336.464	335.440	336.490	336.334	62.584	62.189
6000	394.570	394.234	342.724	341.659	337.449	337.290	62.607	62.202
MPAD (%)	0.098		1.199		0.097		0.793

and

Table 5. Comparison of thermodynamic properties of the Si2N molecule at 0.1 MPa: NIST data vs. MRM model predictions.

T [48]	S (J mol−1K−1)		H (kJ mol−1)		G (J mol−1K−1)		Cp (J mol−1K−1)
	Equation (8)	NIST [48]	Equation (16)	NIST [48]	Equation (17)	NIST [48]	Equation (11)	NIST [48]
300	256.930	256.795	0.094	0.092	256.618	256.488	50.663	49.965
350	264.863	264.652	2.668	2.642	257.241	257.104	52.251	51.951
400	271.930	271.699	5.315	5.281	258.643	258.495	53.598	53.570
450	278.311	278.087	8.024	7.994	260.480	260.323	54.732	54.886
500	284.128	283.927	10.785	10.766	262.558	262.395	55.687	55.958
…	…	…	…	…	…	…	…	…
2800	387.749	387.821	150.997	151.094	333.822	333.859	62.417	62.097
2900	389.940	390.000	157.241	157.305	335.719	335.757	62.463	62.118
3000	392.058	392.106	163.489	163.517	337.562	337.601	62.507	62.137
3100	394.109	394.144	169.742	169.732	339.353	339.392	62.549	62.156
3200	396.095	396.118	175.999	175.949	341.096	341.134	62.590	62.175
…	…	…	…	…	…	…	…	…
5600	431.355	431.093	327.320	326.046	372.905	372.871	63.538	63.112
5700	432.480	432.211	333.676	332.361	373.940	373.902	63.583	63.179
5800	433.586	433.310	340.037	338.682	374.959	374.917	63.629	63.248
5900	434.674	434.392	346.402	345.010	375.962	375.916	63.675	63.318
6000	435.745	435.457	352.771	351.346	376.950	376.899	63.721	63.391
MPAD (%)	0.036		0.299		0.016		0.583

. A MATLAB script for computing the thermodynamic properties of nonlinear triatomic molecules is available upon request.

The results show that the MPAD values for all molecules fall within the acceptable range. However, the models for enthalpy and heat capacity slightly deviate from the NIST data for the HCN molecule, with the MPAD exceeding the Lippincott error threshold. These discrepancies may result from the exclusion of quantum correction terms in the partition function for the MRM oscillator [41]. Nevertheless, the models for molar enthalpy and heat capacity provide accurate predictions for most molecules.

Figure 1, Figure 2, Figure 3 and Figure 4 present the temperature dependence of the thermal functions, with the corresponding NIST data shown for comparison. The alignment of the predicted thermal functions with the NIST data further supports the validity of the proposed thermodynamic models in predicting the thermal properties of the selected triatomic molecules.

Finally,

Table 6. Benchmarking APAD (%) data for MRM thermodynamic models against the literature-based IMTZ models.

Model	BO2		HCN		N3		Si2N
	MRM	IMTZ [32]	MRM	IMTZ [34]	MRM	IMTZ [32]	MRM	IMTZ [32]
Entropy	0.103	0.132	0.162	0.176	0.098	0.106	0.036	0.044
Enthalpy	0.822	1.118	1.666	1.705	1.199	1.378	0.299	0.323
Gibbs free energy	0.050	0.053	0.131	0.098	0.097	0.047	0.016	0.014
Heat capacity	1.190	1.334	1.980	1.899	0.793	0.881	0.583	0.640

compares the performance of the MRM models (developed in the present work) with the existing IMTZ models from the literature. The MPAD values for the MRM models are smaller than those for the IMTZ models, indicating that the MRM models offer improved accuracy in predicting the thermal properties of BO₂, HCN, N₃, and Si₂N. Both the MRM and IMTZ models incorporate optimization parameters for efficiency and rely on the same input data. However, the simplicity of the MRM models lies in their ability to predict thermal properties without requiring a dimensionless parameter.

4. Conclusions

In this study, computational models are developed to estimate the thermodynamic properties of linear triatomic molecules, including molar enthalpy, molar Gibbs free energy, constant pressure molar heat capacity, and molar entropy. These models are derived from the partition functions of the modified Rosen–Morse (MRM) potential, which simulates symmetric vibrational modes, and the harmonic oscillator, which represents asymmetric and 2-fold degenerate bending vibrational modes. The models incorporate key parameters such as equilibrium dissociation energy (D_e), vibrational frequencies (ω_es, ω_ea, ω_eb), and bond lengths (r_eZX, r_eZY). Additionally, an optimization parameter (λ) is introduced to refine the expressions for molar entropy and Gibbs free energy. The models are then applied to determine the thermodynamic properties of linear triatomic molecules, including BO₂, HCN, N₃, and Si₂N. The determined values are compared to experimental data from the National Institute of Standards and Technology (NIST) database. When assessed using the mean percentage absolute deviation (MPAD), the models show strong accuracy, as follows: the MPAD for molar entropy and Gibbs free energy is no greater than 0.17%, while the MPAD for molar enthalpy and isobaric heat capacity does not exceed 2%. The determined thermodynamic properties agree with values found in the literature for triatomic molecules. These computational models provide an efficient and straightforward approach for estimating thermodynamic properties, making them highly relevant for applications in the chemical industry, environmental chemistry, materials science, and chemical engineering.